Introduction

Metal Halide perovskite (MHP) materials with chemical formula ABX3 have demonstrated astonishing features that make them to be compatible in optoelectronic applications including, perovskite-based light emitting diodes (PeLEDs)1,2,3,4,5,6,7,8,9,10, perovskite solar cells (PSCs)11,12,13,14,15,16,17,18,19,20, photodetectors21,22,23,24, lasers25,26,27,28, sensing elements29,30,31, and other solid-state technologies. These semiconductors possess long carrier diffusion lengths, allowing excitons to go further without significant lost or recombination. Moreover, MHPs can be fabricated at room temperature, without requiring high-temperature or vacuum conditions, making them favorable for research in the mentioned technologies.

Their narrow emission bandwidths due to their full width at half-maximum (FWHM) value lower than 20 nm, low exciton binding energy, low turn-on voltage, color tunability by changing their halides, high quantum yield, and low power consumption in comparison with organic semiconductors make them highly attractive for next-generation optoelectronics.1,2,3,4,5,6,7,8,9,10.

However, perovskite semiconductors have some weaknesses unlike their advantageous. Due to their ionic bond in their crystalline structures, they are highly sensitive when exposed to humidity, oxygen, heat, or UV radiation. Additionally, when electric field applied to these structures, their ionic migration can occur, increasing trap density in their structures that could hinder the carrier transport, even non-radiative recombination, which reduces device stability and operational lifetime resulted in less commercialization opportunities32,33,34,35,36,37,38.

To overcome these limitations, several tactics have been explored for enhancing performance of PeLEDs from visible to near-infrared (NIR) ranges. Device engineering, perovskite solution preparation, advanced encapsulation and optical manipulation have been investigated to minimize trap densities and enhance radiative recombination39,40. For instance, by using lower bandgap MHPs, the density of trap energy levels inside the bandgap will be lowered and it can extend the emission wavelength toward the NIR region. So, leakage current and non-radiative recombination will suppress and this will help gain higher lifetime of thin film perovskite material41.

Beneficially, the applications of NIR-emitting PeLEDs (700–900 nm) have found in night vision, biosensing, and optical communications42,43. In this aspect, considering perovskite materials that are made of formamidinium (FA) cations instead of methylammonium (MA)12,13,14,15,16,17,18, would be beneficial for some reasons like, smaller bandgap of FAPbI3 (1.4–1.55 eV) compared with MAPbI3 (~ 1.57 eV), longer carrier diffusion length in FAPbI3 and higher quality of thin films that were made up with FAPbI3 material.43,44,45,46,47,48 Other tactics to get the desired potential from MHPs can be achieved through precise control of crystal growth, using ligand inside the pre-solution of perovskite material and passivation strategies in parallel with considering the relationship between structural dimension, and careful energy-level alignment across layers16,17,18.

In the aspect of dimensional engineering, the 1D and quasi-1D perovskite nanowires or nanorods are adaptable to flexible devices and they indicated desired features in carrier transport and emission characteristics49,50. As an example, in 2019, by applying MAPbI3 nanowires in PeLED the photoluminescence quantum yield (PLQY) of device reached to 42.6%, due to enhanced radiative recombination rate under low-injection region that carrier density is highly bigger than the photogenerated carrier density51. In 2020, by growing the perovskite nanowires (PNW) inside porous alumina membrane (PAM) the stability and external quantum efficiency (EQE) increased from 11% to 16%, because of the protection that PAM provides by avoiding oxygen and humidity penetration to the perovskite52. As a result by considering mentioned tactics the higher values of PLQY have obtained even near unit1,2,53. However, due to the high refractive index of perovskites (~ 2.5)1,2,54,55 in comparison with organic (< 2) and other materials in PeLED, total internal reflection (TIR) causes substantial optical losses through waveguiding and absorption modes.

In this case considering thin perovskite layers, especially between 20 and 40 nm can enhance light outcoupling efficiency (LEE) while decreasing the speed of degradation in the following of lower joule heating and temperature rise inside the layer56,57. In 2024, the effect of photon recycling on electroluminescence quantum efficiency of NIR PeELD were indicated that thinner ITO electrode (15 nm) in parallel with thinner perovskite material layer (≤ 40 nm) could enhance the LEE of PeLED to the range of 20–30%57. In general, the whole efficiency of PeLEDs, EQE, is a combination of optoelectrical efficiency and optical efficiency (LEE) of the device. Thus, addressing the optical loss mechanisms and enhancing light extraction remain key steps toward realizing efficient and stable PeLED devices.

In the following of our previous paper, the number of photons that were lost inside AL by propagating horizontally confined in a bounded area to conduct them to go straight perpendicular to x_y plane, and then reach to air. For this purpose, AL designed by FAPbI3 nanorods inside two different specially chosen membranes consist of Fluoride based materials, Magnesium Fluoride (MgF2) and Lithium Fluoride (LiF) with 2 different arrangements of square and hexagonal. These 4 new nanostructured based NIR PeLEDs simulated optically to obtain optical modes with and accurate computational electromagnetics method named by Finite-difference time-domain (FDTD) which is based in Maxwell’s equations to calculate in every mesh inside the structure. By considering these new designs the LEE of PeLEDs 3 to 4 times enhanced in comparison with same volume of perovskite in planar structure and reached to about 45%.

Optical efficiency of PeLED

The EQE that indicates the ratio of number of extracted photons from the device to number of injected electron-hole pair from the electrical field through electrodes to the device. This efficiency divided into two parts consist of internal quantum efficiency (IQE) and light extraction efficiency (LEE) or outcoupling, in general. According to Eq. (1), IQE is the ratio of number of photons that produced inside the emissive material to number of carriers that injected through electric field. When electric field applied the electrons from cathode and holes from anode separated and through the force of field collected inside the active layer (AL). These carrier pairs by columbic force combine and create excitons. Then these excitons through radiative recombination will produce photons that this whole process is called as electroluminescence phenomena. As a result, collecting balanced carriers and feasible transmission of carriers form the electrodes to the other layers inside the structure named as carrier transporting layers (CTLs) will be used. The electron transporting layer (ETL) and hole transporting layer (HTL) will be placed beside cathode and anode around AL, respectively. These ETL and HTL not only transport easily carriers to AL by lowering the difference of energy levels between electrodes and AL, but also, they block diffusion of corresponding carriers to the AL to make balanced number of carriers. By placing these CTLs the probability of higher number of excitons will increase which results in higher possibility of photon production. In the following, these generated photons inside AL will interact with the structure to get out of the device through glass substrate. This part of efficiency that is dedicating to completely optical efficiency of the PeLED is LEE that shows the ratio of number of photons that generated inside AL to number of photons that were able to escape from the device and is given in Eq. (2)1,2,58,59. To conclude, in Eq. (3), the EQE value obtains by the product of IQE and LEE to each other that can be used to as a significant parameter to compare PeLEDs.

$$\:IQE=\:\frac{\#\:\text{G}\text{e}\text{n}\text{e}\text{r}\text{t}\text{e}\text{d}\:\text{p}\text{h}\text{o}\text{t}\text{o}\text{n}\text{s}\:\text{i}\text{n}\text{s}\text{i}\text{d}\text{e}\:\text{e}\text{m}\text{i}\text{s}\text{s}\text{i}\text{v}\text{e}\:\text{l}\text{a}\text{y}\text{e}\text{r}}{\#\:\text{I}\text{n}\text{j}\text{e}\text{c}\text{t}\text{e}\text{d}\:\text{c}\text{a}\text{r}\text{r}\text{i}\text{e}\text{r}\text{s}\:\text{i}\text{n}\:\text{t}\text{o}\:\text{t}\text{h}\text{e}\:\text{d}\text{e}\text{v}\text{i}\text{c}\text{e}}$$
(1)
$$\:LEE=\:\frac{\#\:\text{E}\text{x}\text{t}\text{r}\text{a}\text{c}\text{t}\text{e}\text{d}\:\text{p}\text{h}\text{o}\text{t}\text{o}\text{n}\text{s}\:\text{f}\text{r}\text{o}\text{m}\:\text{t}\text{h}\text{e}\:\text{d}\text{e}\text{v}\text{i}\text{c}\text{e}}{\#\:\text{G}\text{e}\text{n}\text{e}\text{r}\text{a}\text{t}\text{e}\text{d}\:\text{p}\text{h}\text{o}\text{t}\text{o}\text{n}\text{s}\:\text{i}\text{n}\text{s}\text{i}\text{d}\text{e}\:\text{e}\text{m}\text{i}\text{s}\text{s}\text{i}\text{v}\text{e}\:\text{l}\text{a}\text{y}\text{e}\text{r}}$$
(2)

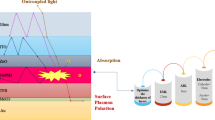
During electroluminescnce phenomena, if the excitons were singlet (with opposite spins) during recombination their energy will appear as optical photons that if they do not waste inside the structure, and their lifetime passed they will reach out to the air from substrate. In PeLEDs, the optical losses are in a group contains of waveguide mode, substrate mode, surface plasmon polariton (SPP), absorption of each material inside which are affecting the air mode or LEE as desired mode of PeLED. These optical modes happen in different parts of the PeLED structure. For example, from the bottom of the structure, if the photons go in opposite direction, at the interface of metallic electrode and upper semiconductor layer, the photons would be waste and resonance at the boundary and this is surface plasmon mode. Waveguiding mode, is also related to TIR mode that due to refractive index (RI) difference between perovskite and other layers around it will happen. And when the photons could pass these layers, at the substrate and due to the difference of RI between substrate and air, the photons will stock inside the substrate mode. Finally, the desired mode that shows the photons which were extracted from the device will be go in the group of air mode or LEE of the optical modes.

$$\:EQE=IQE\:\times\:LEE=\:{\upgamma\:}.{\text{r}}_{\text{s}\text{t}}.\:\frac{\stackrel{-}{{\text{h}}_{\text{v}}\:}\:}{\text{q}{\text{V}}_{\text{i}\text{n}}}.\:\left(\frac{{\text{K}}_{\text{r}}}{{\text{K}}_{\text{r}}+{\text{K}}_{\text{n}\text{r}}}\right).{{\upphi\:}\:}_{\text{o}\text{u}\text{t}}$$
(3)

In Eq. (3), the relation between each part of EQE is explained. In this equation, IQE as optoelectrical efficiency of PeLED is related to different parameters like \(\:{\text{r}}_{\text{s}\text{t}}\) that is a fraction of excitons which can be converted to photons, and \(\:\:{\upgamma\:}\) as charge balance factor that refers to ratio of created excitons to the number of carriers that injected by the external electric circuit, and there is \(\:\text{q}\) as symbol of charge, \(\:{\text{V}}_{\text{i}\text{n}}\) which is dedicated to applied voltage and \(\:{h_{\text{v}}}\) is the average energy of the emitted photons. The optical part \(\:{{\upphi\:}}_{\text{o}\text{u}\text{t}}\) which is referred to as the light outcoupling efficiency or LEE part of efficiency. Also, there is the efficiency of the radiative recombination which are related to \(\:{\text{K}}_{\text{r}}\:\)and \(\:{\text{K}}_{\text{n}\text{r}}\) and representing the rate constants for radiative and non-radiative decay of an exciton1,2.

Simulation method

Among simulation methods for LEDs, there are several computational electromagnetic methods (CEM) that are implemented by Maxwell’s equation like finite element method (FEM), fine difference time domain (FDTD), beam propagation method (BPM) and so on. FEM and FDTD are based on iterative process of solving equations in each defined mesh inside the structure. Their computational expense depends on the number of grid divisions1,2,60. The mechanism of FDTD is highly versatile and simple to implement on volumetrically complex structures to incorporate dispersion61.

In this paper like the previous one, by using this accurate and robust FDTD method which is also excellent for field visualization, the NIR nanostructured AL PeLEDs will be designed and simulated.

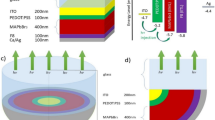
To begin with, the selected PeLED has 6 different layers that produces light in NIR region of electromagnetic spectrum that 803 nm of wavelength is the peak of emission of FAPbI3 as active material in the structure. According to Figure (1a), each layer from electrodes to carrier transport layers and emissive one are consist of Gold (Au) as anode with a thin layer of Molybdenum trioxide (MoO3) as anode buffer layer (ABL) on top of the anode, Poly (9,9-dioctylfluorene-alt-N-(4-sec-butyl phenyl)-diphenylamine) (TFB) as hole transporting layer (HTL), Formamidinium lead iodide (FAPbI3) as active layer (AL), Zinc oxide (ZnO) as electron transporting layer (ETL) and Indium thin oxide (ITO) as cathode. Au was selected as the anode due to its high work function (~ 5.1 eV) which is stable due to its chemical properties, that prevents it from oxidation and degradation. MoO₃ and TFB act as efficient hole-injection and transport layers; MoO₃ provides favorable energy alignment with Au, while TFB enhances hole mobility and blocks electrons, improving carrier balance. ZnO, with its wide bandgap (~ 3.6 eV) and suitable conduction‐band level, serves as a transparent electron‐transport layer ensuring selective electron extraction. ITO is used as the transparent cathode because of its high transmittance (~ 85–90%) and compatible work function (~ 4.8 eV), enabling light emission through the top electrode. This combination provides stable interfaces, efficient charge injection/extraction, and high optical performance, consistent with prior experimental PeLED architectures1,62,63,64.

In the Figure (1b), the band diagram of each layer is given that illustrates that according to the energy levels that the electrons from LUMO (Least Unoccupied Molecular Orbital) of ITO go through the ZnO and then step by step reach the LUMO of AL (perovskite layer). On the other side, hole injection will occur from the HOMO (Highest Occupied Molecular Orbital) of the anode and ABL to the HOMO of TFB. Then the carriers will be collected in an emissive layer to create excitons and after the recombination process the energy will convert to photons. To be precise, HTL and ETL will confine the electron and hole respectively in the EML, in parallel with facilitating the injection of hole and electron to the EML and balancing the number of carrier pairs to enhance the possibility of exciton formation in the AL. According to Figure (1c), the refractive index of each layer with its material were collected65,66,67 at 803 nm of wavelength is given that the highest value of RI is for perovskite material which is about 2.2.

Fig. 1
figure 1

(a) Structure of PeLED with its different layers and their thicknesses, (b) the band diagram energy of each material inside the structure and their energy levels (c) the RI of different materials in the PeLED structure1,65,66,67.

Full size image

The CEM method that used to investigate the optical efficiency of the structure is Finite-Difference Time-Domain (FDTD) that by this method, electromagnetic fields solve by iterating Maxwell’s equations in the time domain1,2,61,68.

In the Finite-Difference method, the whole region of simulation will be divided into square single meshes. In each single mesh the Maxwell’s equation of electric field will solved differentially and then by solving these equations (Eqs. (4), (5), (6)) in each frequency of defined span of wavelength, the transient response of the numerical equations will obtain.

$$\:\nabla\:\times\:\:\overrightarrow{\text{E}}\left(\text{t}\right)=\:-{\upmu\:}\:\partial\:\:\overrightarrow{\text{H}\left(\text{t}\right)}/\partial\:\text{t}$$
(4)
$$\:\nabla\:\times\:\:\overrightarrow{\text{H}}\left(\text{t}\right)=\:-{\upepsilon\:}\:\:\partial\:\:\overrightarrow{\text{E}\left(\text{t}\right)}/\partial\:\text{t}$$
(5)
$$\:\overrightarrow{\text{E}}{|}_{\text{t}+\varDelta\:\text{t}}=\:\overrightarrow{\text{E}}{|}_{\text{t}}+\:\varDelta\:t/\epsilon\:\left(\nabla\:\:\times\:\:\overrightarrow{\text{H}}{|}_{\text{t}+\varDelta\:t/2}\right)$$
(6)

Where the \(\:\overrightarrow{\text{E}}\left(\text{t}\right)\) and \(\:\overrightarrow{\text{H}}\left(\text{t}\right)\:\)are dedicated to electric and magnetic field intensity in time domain, respectively. The \(\:{\upmu\:}\) and \(\:{\upepsilon\:}\) parameters are indicating the ability of media to store magnetic and electric energy which are named by permeability and permittivity. In Eq. (6), time steps in calculations will be applied by \(\:\varDelta\:\text{t}\) that the best stable method of computation is related to half-time steps for magnetic fields and unit-time steps for electric fields1,2,61,68.

In the simulation, in the x and y directions, periodic boundary conditions (BCs) applied to consider repetitive arrays of a unit cell of the nanostructures. Considering periodic BC not only will decrease the simulation time, but also it will allow to define more meshes in the repetitive cell to gain more accurate results. In z direction, each layer defined with their specific thickness that the light will extract in this direction from the structure from the ITO and substrate of the structure. In this direction, with a space region equal to wavelength of interest, the perfect matched layer (PML) BC applied in top of the simulation region to prevent from any additional and undesired backward optical waves into the simulation region and the structure. Generally, in this simulation method, we suppose that the electric field were applied through the electrodes to the device and the process of radiative recombination of excitons were done that we have photons that will help us to investigate the interaction between photons and the structure. So, to model photons as dipole oscillations in the center of the active material, dipole source with electric field placed. This dipole source will oscillate in 3 different directions which is exact model of photon production in a PeLED that photons in 3 cartesian direction will spread. To calculate the pure emission power of the source a power box around it considered. Due to the multilayer structure of the PeLED and different RI of each layer the possibility of reflections and resonances inside the layers increase that will create cavities within the structure that could affect any wavelength in defined bandwidth, constructively or destructively, known as Purcell effect in PeLED. So, the power box in each direction around the source (for 3D simulation) placed. As a result, this transmission box will neutralize the amplification and attenuation of the optical power emitted inside the cavities that could occur. Finally, the LEE and other optical modes will be calculated by using far_field monitor in specific region of the structure inside the simulation region. The information about the simulation software, parameters, and scripts that used in this research is provided in the Supplementary Information section.

Selecting membrane materials

According to the previous research1, when the dipole source starts to oscillate inside the active material, not only photons pass the layers and reach out to the air, but also, they spread along x_y plane inside the AL which is impact the optical losses. In this case, to suppress the horizontally light spread, we designed 4 different nanostructured AL with same material and same thickness of CTLs and electrodes in the PeLED. To obtain this purpose and limit optical loss of photons in x_y plane along the surface of the AL in parallel with increasing the vertically production of light we selected 2 different Fluoride based membranes to set them around the perovskite nanorods. There are 3 reasons for choosing these membrane materials that they have to have some specific features included in:

  1. 1.

    Less value of the refractive index in comparison with the perovskite material.

  2. 2.

    Minimal extinction coefficient to lower the absorption.

  3. 3.

    Wide bandgap to be electrically insulator.

Based on Snell’s law, when an optical wave come across to the interface of two media, if the second material have lower RI compared with first material that wave was produced in, the wave will go back ward to the first material, which is also called as TIR in the first region. In Eq. (7), the Snell’s law explained that the \(\:{\text{n}}_{1\:}\)is referred to as the RI of material that light generated in it, and here is dedicated to the RI of perovskite material. The \(\:{\text{n}}_{2\:}\)is referred to as the RI of material that light will go into, and may collide and at the interface of these two materials, and then reflects into the first material that in this structure is dedicated to the RI of the membrane around FAPbI3 nanorods. In addition, the angle of light at the interface between two media, in the first material and the second one is shown by\(\:\:{{\uptheta\:}}_{1}\) and \(\:{{\uptheta\:}}_{2}\), respectively.

$$\:{\text{n}}_{1\:}\text{sin}{{\uptheta\:}}_{1}=\:\:\:{\text{n}}_{2\:}\text{sin}{{\uptheta\:}}_{2\:}$$
(7)

In Eq. (8), and (9), more specified version of Snell’s law is given that are Fresnel’s equations with the same parameters of Eq. (7). The Fresnel equations describe the reflection of light when it encounters an interface between two different materials for both s and p polarizations of light that are written below:

For s-polarized light (electric field perpendicular to the plane of incidence):

$$\:\:{\text{r}}_{\text{s}}\:=\:\frac{{\text{n}}_{1}\:\text{cos}\left({{\uptheta\:}}_{1}\right)\:-\:{\text{n}}_{2}\:\text{cos}\left({{\uptheta\:}}_{2}\right)}{{\text{n}}_{1}\:\text{cos}\left({{\uptheta\:}}_{1}\right)\:+\:{\text{n}}_{2}\:\text{cos}\left({{\uptheta\:}}_{2}\right)}$$
(8)

For p-polarized light (electric field parallel to the plane of incidence):

$$\:\:{\text{r}}_{\text{p}}\:=\:\frac{{\text{n}}_{1}\:\text{cos}\left({{\uptheta\:}}_{2}\right)\:-\:{\text{n}}_{2}\:\text{cos}\left({{\uptheta\:}}_{1}\right)}{{\text{n}}_{1}\:\text{cos}\left({{\uptheta\:}}_{2}\right)\:+\:{\text{n}}_{2}\:\text{cos}\left({{\uptheta\:}}_{1}\right)}$$
(9)

According to Eqs. (8) and (9), if the RI of membrane would be lower than the RI of perovskite material, the probability to increase the TIR will increase. Due to this we selected materials that have lower RI in comparison with FAPbI3 material at 803 nm of wavelength. Moreover, the extinction coefficient of these membranes should be minimum (near zero) in a case that if light could be able to go inside of them because of the transparency of those membranes, the light would be able to escape from the membrane to reach out to the substrate without being absorbed by membrane material. Based on these two discussed factors, metallic membrane would be the best choice because of its lower RI between materials and highest reflection that they have in parallel with their lowest possibility to absorb light. However, there is a third factor that is essential to choose these membrane materials and it is related to the electrical features of the membrane. These new materials should be electrically insulator to prevent short circuit happening. In other words, the bandgap of membrane materials should be more than 5 eV to avoid any carrier to get trapped inside them and prevent electrically function of the PeLED.

To wrap things up, Fluoride-based materials such as Lithium Fluoride (LiF) and Magnesium Fluoride (MgF2), are one of the best choices to design a new nanostructured emissive layer inside the PeLED. In several types of research, an ultrathin layer of LiF has been deposited on top of the cathode electrode in PeLEDs to improve the electron injection due to its wide optical applications69,70,71,72. For instance, LiF has been used in perovskite-based solar cells as a buffer layer to suppress the degradation of the perovskite layer and increase stability by preventing ions and moisture diffusion from metallic electrodes73,74,75. Also, LiF has strong covalent bonding within its ionic structure, which increases its chemical and structural stability, exhibiting a direct bandgap of 14.0 eV76,77,78. Furthermore, MgF2 like LiF, is a wide bandgap insulator with a value of approximately 10.8 eV, which may vary depending on its structural shapes79,80,81. Both, LiF and MgF2 have lower RI than FAPbI3 equal to 1.389, and 1.375 at 803 nm of wavelength with zero extinction coefficients, making them highly suitable for confining light within perovskite nanorods. Due to the transparency of these materials, even if part of the light propagates into these membranes, the minimal imaginary component of their refractive indices prevents significant absorption losses, thereby facilitating efficient light conduction toward the upper layers for extraction. In addition to their optical advantages, the thermal properties of these fluoride materials play a key role in improving the overall stability of the nanostructure. The thermal conductivity of LiF and MgF2 are 13.89 W/m·K and about 21–33.6 W/m·K, respectively, at room temperature82,83, whereas FAPbI3 exhibits a much lower value of approximately 0.63 W/m·K45. This significant difference indicates that FAPbI3 cannot efficiently dissipate heat, potentially leading to localized heating and thermal degradation. Therefore, incorporating LiF and MgF2 in the nanostructured design not only enhances optical confinement and outcoupling efficiency but also substantially improves heat management and long-term device stability.

Designing nanostructured AL

For designing the perovskite nanorods, 2 different arrangements within each Fluoride-based material were considered, Square and Hexagonal. Figures (2a) is dedicated to square arrangements of nanorods, and Figure (2b) is for hexagonal arrangement that in structure, red cylinders are dedicated to FAPbI3, and the pink area is MgF2 or LiF. These new designs swept in 2 general steps to be optimized dimensionally in 3D simulation and investigated the LEE of them.

Fig. 2
figure 2

The nanostructures inside EML of PeLED with (a) Square and (b) Hexagonal arrangement of FAPbI3 nanorods inside LiF or MgF2 in with x_y plane and the middle and the right one is in 3D view. (The pink area is for LiF or MgF2 and the red cylinders are dedicated to FAPbI3).

Full size image

To begin optimization process, the primary value for the dimensions for each arrangement extracted by considering same volume of perovskite with previous paper results for planar PeLED. The whole volume of perovskite in the planar PeLED were obtained as 0.025\(\:{\mu\:m}^{3}\) with 25 nm of thickness. To maintain the dimension values for each arrangements’ unit cell, the radius set by R parameter and the unit cell’s horizontal dimensions set to D. So, in square arrangement of nanorods, the x and y dimensions of each unit cell are equal to D and in hexagonal arrangement in x direction the dimension of unit cell is equal to D and in y direction it will be D\(\:\sqrt{3}\). In addition, the height of these nanostructures will be same as thickness of perovskite nanorods and their membranes which is defined by H parameter. As a result, to obtain 0.025\(\:{\mu\:m}^{3}\) of perovskite in square and hexagonal arrangement of nanorods, the R and D parameter of each arrangement could be 200 nm and 1000 nm, with the H parameter of nanorods equal to 200 nm and 100 nm for each arrangement, respectively. So, we have same fixed R and D parameter value equal to 200 nm and 1000 nm, respectively with height that could be swept from 100 to 1000 nm with 50 nm of steps. Then by setting the optimized height that is related to the maximum value of LEE in each nanostructure, the D and R parameters simultaneously will be optimized.

In the simulation, same as planar PeLED, the BCs in the x_y plane, set to the periodic FDTD region of simulation contain one sample of a periodic arrangement of nanorods like the sample illustrated in Figure (2a) and Figure (2b), with purple dashed lines. The dimensions of the FDTD region for each arrangement are controlled by 2 factors named D and Fill Factor (FF) in Eq. (10).

$$\:\text{R}=\text{F}\text{F}\:\times\:\:\text{D}$$
(10)

In Eq. (10) the FF is a parameter without a unit, and D is the dimension of the simulation area in the scale of a nanometer, accordingly, R which is the radius of nanowires will be obtained in the nanometer scale. So, to sweep the structure, the D swept between 0.1 μm and 1 μm and FF swept for each of those D dimensions between 0.1 and 0.5, in 5 steps. In Figure (3) and Figure (4), the illustration of the way that FF affects the area of nanorods when the D parameter is constant (1000 nm) is given for square and hexagonal arrangements of nanostructures, respectively.

Fig. 3
figure 3

Different dimensions of FDTD region of a single sample of square arrangement of perovskite nanorods when D is equal to 1 μm and FF parameter is equal to: (a) 0.1, (b) 0.2, (C) 0.3, (d) 0.4, (e) 0.5, (f) 0.6.

Full size image
Fig. 4
figure 4

Different dimensions of FDTD region of a single sample of a hexagonal arrangement of perovskite nanorods when D is equal to 1 μm and FF parameter is equal to: (a) 0.1, (b) 0.2, (C) 0.3, (d) 0.4, (e) 0.5, (f) 0.6.

Full size image

As it can be observed, in both arrangements in Figure (3) and (4), by considering the value of FF more than 0.5, structures will convert to planar structures, especially in a hexagonal arrangement that all the area of the FDTD region will be same as a planar film of perovskite material. As a result, the suitable span of the FF parameter is from 0.1 to 0.5.

Optimization of nanostructured EML

To optimize the nanostructured EML, we swept the horizontal and vertical dimensions of unit cell of each nanostructure to get the optimized dimensions of EML on order to maintain maximum possible LEE in order to decrease optical losses.

Optimizing vertical dimension of nanostructures

To get the best dimensions of perovskite nanorods, we start with optimizing the vertical dimension of the EML. Firstly, by considering the same volume of perovskite with previous paper results, we set the D parameter of unit cell of each arrangement of nanorods to 1000 nm and the radius of nanorods to 200 nm, then we swept the height of nanorods from 100 to 1000 nm with 50 nm steps. The results of the simulation, collected in Figure (5), according to the volume of perovskite which is related to the photon generation rate, the appropriate height of nanorods in a square arrangement is about double of a hexagonal one.

Fig. 5
figure 5

LEE results for each nanostructured AL by sweeping the height of FAPbI3 nanorods in Fluoride-based materials from 100 to 1000 nm and fixed D = 1000 nm and R = 200 nm.

Full size image

According to Figure (5), the maximum value for LEE in square arrangement of nanorods occurs when the height will be equal to 800 nm and 850 nm for LiF and MgF2 membranes, respectively. In the hexagonal arrangement we expect to get maximum LEE values at half value of nanorods thickness in comparison with square arrangement, in case of getting same volume of perovskite, that it is also happened at 400 nm of height. To be precise, some minimum and maximum peaks occurred which are happened due to the destructive and constructive interactions. For picking the suitable radius of nanorods to continue calculations, we should obtain the best match between the results from Eqs. (11) and (12) and the results of simulations.

$$\:\text{L}=\left(2\text{n}-1\right)\frac{{\uplambda\:}}{4}\:;\:\text{n}=\text{1,2},3,...\:$$
(11)
$$\:\text{L}=\text{n}\frac{{\uplambda\:}}{2}\:;\:\text{n}=\text{1,2},3,...\:$$
(12)

According to the wavelength of interest for FAPbI3, 803 nm, due to resonance phenomena, the destructive and constructive interferences would be happened at 200.75 nm, 602.25 nm, and 401.5 nm, 803 nm in the span of 100 to 1000 nm of height, respectively. These values according to the accuracy of the simulation that we had, are nearly happened at 200 nm, 600 nm for minimum peaks and 400 nm and 800 nm (or 850 nm) for maximum peaks in the Figure (5). As a result, by considering the optimized height of nanorods, the horizontal dimensions of nanorods in the following will be optimized.

Optimizing horizontal dimensions of nanostructures

In the following, we changed the horizontal dimensions of unit cell of the nanostructure arrays. By considering the described range of FF in Figs. 3 and 4, and the D parameter from 0.1 to 1 μm with 100 nm steps, the sweep range set. The results of this simulation are collected in Figure (6) that the light outcoupling occurred almost at the same dimensions due to the highly close values of RI values for both Fluoride-based materials.

Fig. 6
figure 6

LEE results for optimization of horizontal dimensions of FAPbI3 nanorods with different membranes and arrangement at 803 nm of wavelength.

Full size image

The contrast between RI values of LiF and MgF2 with FAPbI3 is equal to 0.9 and 0.91 at 803 nm of wavelength, respectively. This difference between RI values is not that much different and has nearly the same results in the light outcoupling from the AL. Although the difference even about 0.01, made the photons to be more bounded, then more TIR happens which causes growth in LEE value about 1%. In other words, the optical efficiency for both arrangements of FAPbI3 nanorods, with MgF2 obtained at about 45% which are nearly 1% more than the structures that are surrounded by LiF membrane. The exact results of LEE and optimized dimensions of nanostructured EML are given in Table 1.

Table 1 The optimized dimensions of FAPbI3 nanorods in NIR PeLED and LEE results at 803 nm of wavelength.
Full size table

To conclude, by setting an optical barrier around emissive material, we reached about 45% optical efficiency for the NIR PeLED. During the optimization process, the volume of perovskite has been changed that in Fig. 7, the LEE values for each structure with their perovskite volume are shown. To make a general comparison, the same volume of perovskite material of the nanostructures was set to the planar structure and the LEE was extracted. For 0.1 \(\:{\upmu\:}{\text{m}}^{3}\)of FAPbI3, the LEE achieved 11.19% that in a new design by using perovskite nanorods, the LEE value is bigger about 4 times. Moreover, for the 0.064 \(\:{\upmu\:}{\text{m}}^{3}\)of FAPbI3, the LEE achieved 16.18% in planar structure, that indicates by using a hexagonal arrangement of nanorods in the MgF2 membrane the LEE value will be tripled.

Fig. 7
figure 7

Comparison between nanostructured and planar EML in NIR PeLED at 803 nm of wavelength base on perovskite volume.

Full size image

To consider the optical modes, in Fig. 8, the waveguide mode and other modes like Surface Plasmon Polariton (SPP) and absorption, substrate mode are collected that in comparison with nanostructured patterned EML (Fig. 9), the waveguide value lowered.

Fig. 8
figure 8

The optical modes at 803 nm of wavelength for planar NIR PeLED when the periodic area is equal to 1\(\:{\:\mu\:m}^{2}\) and the volume of FAPbI3 perovskite is equal to (a) 0.064\(\:\:\mu\:{m}^{3}\) and (b) 0.1 \(\:\mu\:{m}^{3}\).

Full size image
Fig. 9
figure 9

Optical modes for each optimized nanostructured NIR PeLED at 803 nm of wavelength.

Full size image

According to Fig. 10, and Fig. 11, the electric field profile also shows how the light is bounded in the perovskite region, that when photons try to escape horizontally, the highest percentage of light reflected from the interface of perovskite and Fluoride-based membranes to inside the nanorod. Furthermore, due to the transparency of Fluoride-based materials, when the light diffuses inside the optical barriers, due to zero absorption of theses membranes, it can escape from them and go to the upside and reach the substrate, which is decrease the light trapping.

Fig. 10
figure 10

Electric field profile for the hexagonal arrangement of FAPbI3 nanorods in (a) LiF and (b) MgF2 membrane.

Full size image
Fig. 11
figure 11

Electric field profile for square arrangement of FAPbI3 nanorods in (a) LiF and (b) MgF2 membrane.

Full size image

Finally, the whole nanostructured EML NIR PeLED with two arrangements is given in Figure (12) that they are containing planar CTLs and electrodes with nanorods of FAPbI3 inside Fluoride_based membranes.

Fig. 12
figure 12

The new nanostructure NIR PeLED structures with (a) square and (b) hexagonal arrangements.

Full size image

Perovskite volume per surface area

Generally, to compare the planar PeLED of last paper and the new designed nanostructures, total volume of perovskite which is directly related to the photon production volume is crucial. In this case, a diagram of data for each structure collected that illustrates the volume of perovskite per surface area in Fig. 13. In the nanostructured design, not only the volume of perovskite is closely near to the area of it, but also the ratio of them is higher than that of planar one. In 1 \(\:\mu\:{m}^{2}\) area for the planar PeLED, the area of the optimized nanorod contained designs, have 0.125 \(\:\mu\:{m}^{2}\) for both LiF and MgF2 membranes in square arrangement, and 0.25 \(\:\mu\:{m}^{2}\), and 0.16 \(\:\mu\:{m}^{2}\) for hexagonal arrangement of nanorods with LiF and MgF2 membranes, respectively to outcouple light from the PeLED. This means that more perovskite is actively contributing in light emission in lower area which leads to more light emission. To conclude, these nanostructures, has increases the LEE near 2 to 3 percentages in comparison with planar PeLED, in parallel with creating the situation that we can get high brightness in lower area from each part of array.

Fig. 13
figure 13

The volume of photon production per area for each structure of NIR PeLED.

Full size image

Conclusion

By considering TIR phenomena, the available area to produce photons from dipole sources inside emissive material is limited, by designing nanostructured AL. In the new designs, FAPbI3 nanorods are surrounded by Fluoride-based materials (LiF and MgF2) which bound light in the nanorods and conduct it out of the substrate of the device. By considering the same volume of perovskite in comparison with planar EML, the light outcoupling efficiency of the nanostructured-based designs gained 3 to 4 times better optical efficiency, in parallel with a higher light production per surface area.

Due to the chemically stable ionic crystal with a strong, rigid lattice structure, the thermochemical properties of LiF and MgF2 are higher than those of FAPbI3 which has an ionic lattice structure and the presence of organic components, which scatter phonons (heat carriers) effectively. These properties included thermal conductivity, heat capacity, and melting point of LiF and MgF2 are significantly higher than that of FAPbI3 which could be beneficial for heat dissipation by achieving more uniform temperature across the structure, preventing localized hotspots that could cause the perovskite to decompose or degrade prematurely. As a result, by fabricating the new nanostructured designs, these materials not only manage heat effectively but also protect the perovskite from environmental degradation. The chemically stable feature of MgF₂ or LiF acts as coating around perovskite nanorods that protect them from humidity and oxygen and other environmental factors that are destructive for perovskite. As a result, these new designs can increase the device lifetime.