Introduction

The Qinghai-Xizang Plateau, known as the “Roof of the World,” plays an important role in global climate and environmental systems due to its unique geographic position and dramatic topographic variations1,2. Its eastern edge serves as a key transition zone between the Qinghai-Xizang Plateau and the Sichuan Basin3. This region is characterized by rugged terrain, steep elevation gradients, and diverse landforms, which exerts substantial influence on local climate patterns and hydrological processes4,5. Regional geographic segmentation is vital for comprehensively understanding climatic and geographic characteristics of this area, facilitating the identification of key drivers influencing soil, vegetation, and other environmental elements6,7. However, this process remains challenging due to the region’s complex topography and climate variability.

Spatial clustering is a fundamental geographic technique that partitions areas based on both attribute similarity and spatial continuity8,9. Traditional clustering methods such as K-means and hierarchical clustering primarily focus on attribute-based similarity10,11,12. While spatial clustering integrates geographic relationships to ensure that regions are not only internally homogeneous but also spatially contiguous13,14,15. Traditional clustering methods often overlook spatial dependencies8, leading to fragmented clusters, particularly in complex terrains or climate zones. By integrating spatial constraints, spatial clustering produces more geographically coherent results, making it an essential tool in modern geographical analysis16. This approach has been widely applied across various disciplines, including epidemiology17,18, ecological zoning19,20, geomorphology21,22, and environmental management23.

Spatial clustering incorporates spatial constraints into traditional clustering methods to maintain spatial connectivity, often represented by geographic adjacency24. A straightforward approach extends the traditional K-means algorithm by treating spatial coordinates as attributes and assigning appropriate weights to reflect spatial constraints8. Recent studies have applied spatial distances24 or spatial adjacency relationships16 to construct spatial weight matrices, enabling more precise spatial continuity constraints. However, achieving an optimal balance between spatial continuity and attribute similarity remains a major challenge. Several studies have demonstrated that enforcing spatial continuity often leads to the low attribute similarity within regions8,9, and this trade-off is determined subjectively in most cases. Wolf (2021) have proposed a method that applied multiplicative kernel combinations to adjust the bandwidths of geographic and feature kernels. Nevertheless, these bandwidths are usually determined subjectivity based on prior experience or specific clustering objectives. Therefore, the development of automated and data-driven methods for objectively determining the balance between spatial continuity and attribute similarity remains a crucial challenge in spatial clustering research25.

Distance-based methods are common in spatial clustering26,27,28. The main distance metrics include Euclidean distance, Manhattan distance, and Minkowski distance29,30. Euclidean distance is simple to compute and works well in most31. Manhattan distance is better for cities because movement follows straight paths along a grid32. Minkowski distance is more flexible through parameter adjustments, allowing a smooth transition between Euclidean and Manhattan distances33. However, using these distance metrics alone does not work well in mountainous environments, where critical terrain factors such as slope and elevation are often overlooked despite their importance in spatial partitioning. Recent studies have changed distance measures to include terrain and climate variables34,35. For example, Dehghan et al. (2018) used a weighted Euclidean distance framework that considering climate and geographic attribute35. This method worked better than regular distance measures for spatial clustering. Therefore, developing better distance metrics that effectively capture terrain characteristics is still an important research topic in mountainous regions.

To address these limitations and develop a more reliable method for boundary delineation in small-scale mountainous environments, we propose a spatial clustering framework designed for county-level regions. We selected six key indicators that represent terrain and climate features to calculate attribute distance. Principal Component Analysis (PCA) was applied to simplify the environmental data and determine attribute distance weights based on the variance contribution of each principal component. To capture spatial non-stationarity in complex terrain, attribute distances were further adjusted with Gaussian weighted functions. Furthermore, the optimal weighting combination was systematically examined by fixing attribute distance weights and varying geographic distance weights. The clustering performance was assessed using three clustering metrics (Davies-Bouldin, Silhouette, and Calinski-Harabasz indices) and two spatial autocorrelation metrics (Moran’s I and Moran’s Z score). The most effective geographically weighted distance was then applied to delineate spatial partitions in Kangding county, revealing spatial patterns and providing insights for targeted environmental management and regional analysis at a small spatial scale.

Materials and methods

Study area and datasets

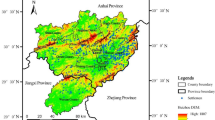
Kangding county lies in the transition zone between the eastern edge of the Qinghai-Xizang Plateau and the Sichuan Basin, encompassing an area of approximately 11,595 km2 (Fig. 1). The region exhibits diverse landforms, including plateau gorges, hilly plateaus, and alpine valleys. The terrain gradually decreases from west to east, averaging 4,002 m. Kangding experiences a monsoon-influenced climate, characterized by an annual average temperature of approximately 7.1 ℃ and an annual precipitation of around 800 mm.Vegetation and soil distributions demonstrate distinct vertical zonation patterns. Vegetation transitions from forests at lower altitudes to shrubs and meadows at higher elevations. Similarly, soil types follow an elevational gradient, ranging from cinnamon soil and brown soil at lower altitudes to alpine meadow soil and frigid frozen soil at higher elevations. The vertical differentiation of the natural environment, driven by topography and climate, serves as a fundamental basis for boundary delineation and spatial partitioning at Kangding county.

Fig. 1
figure 1

Location of the study area in the Qinghai-Xizang Plateau, China. Base map provided by Esri. Administrative boundaries from the Geographic Information Public Service Platform (https://www.tianditu.gov.cn/). Tibetan Plateau boundary from the National Tibetan Plateau Data Center (https://data.tpdc.ac.cn).

Full size image

The environmental data for this study including 6 variables related to climate and terrain (Fig. 2). Climate data, specifically annual precipitation and temperature, were obtained from the National Tibetan Plateau Data Center (https://data.tpdc.ac.cn) at a spatial resolution of 1 km36,37. The mean annual precipitation and temperature from 2018 to 2022 were computed and incorporated as environmental variables. The Digital Elevation Model (DEM) was acquired from the Shuttle Radar Topography Mission (SRTM) at a resolution of 30 m. Slope, plan curvature, and profile curvature were derived from the DEM using the System for Automated Geoscientific Analyses (SAGA GIS), version 9.10.1, developed by the Department of Physical Geography, University of Hamburg, Hamburg, Germany (https://saga-gis.sourceforge.io/).

To enhance computational efficiency and maintain a consistent spatial resolution, all datasets were resampled. The final dataset comprised 45,647 raster pixels at a spatial resolution of 500 m × 500 m, with all data projected to the CGCS2000 3 Degree GK Zone 34 coordinate system. All data pre-processing was conducted in ArcGIS Pro (Esri, Redlands, USA).

Fig. 2
figure 2

Spatial variability of topographic and climatic variables for principal component analysis (PCA)-driven spatial clustering: (a) Annual precipitation (mm), ​(b) Mean annual temperature (°C), ​(c) Elevation (m), ​(d) Slope gradient (°), ​(e) Plan curvature, ​(f) Profile curvature. Maps were generated using ArcGIS Pro.

Full size image

Clustering methodology

The PCA method

In this study, we used PCA to simplify environmental variables and assign weights to attribute distances. PCA is a common statistical method that converts original variables into fewer principal components while keeping most of the data’s variance35. Before applying PCA, we standardized all environmental variables using Z-score normalization to reduce the effect of different units on the results6,38. In this study, we kept principal components that explained more than 80% of the total variance for clustering analysis. The standardization process and PCA computations were performed in ArcGIS Pro.

Spatial cluster

This study uses the Aggregate coordinate and attributes for spatial cluster (ACA-Cluster) method developed by Dong et al. (2022)39. This method applies the K-means algorithm to combine spatial continuity and attribute similarity in clustering. ACA-Cluster integrates spatial and attribute distances, allowing effective grouping of spatially continuous data. The clustering process uses Euclidean distance to maintain spatial continuity while incorporating attribute distance into the distance matrix. The conceptual framework is shown in Fig. 3. The total spatial distance (D) is calculated as:

$$\:D={d}_{p}+{d}_{a}$$
(1)

Where\(\:{d}_{p}\) is the spatial distance, indicating how close the pixels are; and \(\:{d}_{a}\) denotes the attribute distance, measuring the similarity of attribute between pixels. The spatial distance \(\:{d}_{p}\) is computed as Euclidean distance between pixel i and j:

$$\:{d}_{p}={d}_{ij}=\sqrt{{({x}_{i}-{x}_{j})}^{2}+{({y}_{i}-{y}_{j})}^{2}}$$
(2)

Where (xi, yi) and (xj, yj) are the coordinates of pixels i and j, respectively. \(\:{d}_{a}\) is formulated as follows:

$$\:{d}_{a}=\frac{1}{m}\sum\:_{k=1}^{m}\left|{a}_{ik}-{a}_{jk}\right|$$
(3)

Where, m represents the number of attribute variables, while aik and ajk denote the attribute values of pixel i and j at the k-th attribute variable. Given the complex mountainous terrain of Kangding County, conventional distance measures often struggle to adequately capture the influence of topography on spatial continuity. To overcome this limitation, we incorporate Gaussian weighting functions into attribute distance computation. This is formulated as follows:

$$\:{d}_{a}=\frac{1}{m}\sum\:_{k=1}^{m}exp(-\beta\:\cdot\:{{d}_{ij}}^{2})\left|{a}_{ik}-{a}_{jk}\right|$$
(4)

where \(\:{d}_{ij}\) denotes the Euclidean geographical distance, and is the bandwidth parameter that regulates the spread of the Gaussian function. To mitigate the influence of the Gaussian function’s bandwidth on the results, we set β to 0.1. The final spatial distance combines the weighted geographical and attribute distance, computed as follows:

$$\:D=\:{w}_{p}\cdot\:{d}_{p}+\sum\:_{k=1}^{m}{w}_{ak}\cdot\:{d}_{ak}$$
(5)

where and ak represent the weights of geographic distance and attribute distances of different principal components, respectively. The term m indicates the number of principal components, while represents the attribute distance of the k-th principal component. In this study, the weights of principal component attribute distances were assigned according to the proportion of eigenvalues, ensuring that their sum equals 1. The geographic distance weights were specified as 0.15, 0.25, 0.50, 0.75, and 1.00 respectively. For each weight combination, clustering analyses were performed with three cluster numbers (k = 3, 5, 8) to evaluate clustering performance and spatial dependency under different configurations.

Fig. 3
figure 3

Technical workflow of the spatial clustering framework integrating PCA and spatial constraints.

Full size image

Evaluation

Evaluating unsupervised clustering methods is challenging because there is no definitive standard for result assessment10. To address this issue, this study applied two types of metrics to evaluate clustering performance.

The first type measures how well clusters are separated and how compact they are. These metrics help determine the best clustering algorithm and the optimal number of clusters for a dataset40. The selected metrics include the Davies-Bouldin (DB) index, Silhouette score, and Calinski-Harabasz (CH) index. The DB index assesses clustering compactness by comparing intra-cluster and inter-cluster distances across all cluster pairs. A lower DB index indicates better clustering quality34. The Silhouette score evaluates clustering effectiveness by comparing how similar each sample is to its assigned cluster versus other clusters. It ranges from − 1 to 1, with higher values indicating well-separated clusters10. The CH index measures clustering performance by comparing inter-cluster variance to intra-cluster variance, where higher values suggest better clustering quality10.

The second type of metric examines the spatial distribution of clusters. According to Ohana-Levi et al. (2019), well-formed spatial clusters should show strong similarity among nearby points34. Moran’s I index and Moran’s Z-score were used to measure spatial segregation and global spatial autocorrelation in the clustering results. Moran’s I index quantifies global spatial autocorrelation, while Moran’s Z-score evaluates whether the observed clustering pattern differs from a random distribution. Higher values of both metrics indicate stronger spatial autocorrelation and better clustering performance.

Results

Weighting attribute distances using PCA

PCA was used to reduce the dimensionality of variables in the clustering analysis, helping to lower computational complexity41. Table 1 shows the eigenvalues and variance contributions of each principal component. The first four principal components (PC1–PC4) were selected for spatial clustering, as they accounted for over 85% of the total variance. PC1 accounted for 34.07% of the total variance, while PC2, PC3, and PC4 accounted for 20.18%, 19.74%, and 13.31%, respectively (Table 1). To determine the weights of the attribute distances, the variance contributions of these four principal components were normalized, yielding weights of 0.39 (PC1), 0.23 (PC2), 0.22 (PC3), and 0.15 (PC4). In the clustering analysis, the total weight of the four principal component attributes was fixed at 1, while the optimal weight combination was determined by adjusting the weight of geographic distance. Furthermore, Table 2 presents the loadings of different variables in the first four principal components. The results indicate that PC1 is primarily associated with elevation and temperature, PC2 and PC4 are dominated by plan curvature and profile curvature, whereas PC3 is primarily related to rainfall and slope. PC2 and PC4 exhibit a high degree of similarity, both being predominantly influenced by terrain curvature indicators.

Table 1 PCA results of topographic and Climatic variables: Eigenvalues, explained variance, and cumulative variance for six principal components (PCs).
Full size table
Table 2 PCA loadings of topographic and Climatic variables for the first four principal components (PC1–PC4).
Full size table

Regionalization results of different k and

Figure 3 illustrate the clustering results under different geographic distance weights () when k equals 3, 5, and 8, respectively. The results indicate that clustering based solely on attribute distances tends to result in complex spatial boundaries and fragmented spatial distributions. As increases, the spatial continuity of the clusters gradually improves, and the clustering boundaries become more simplified. However, the influence of on spatial continuity differs with the number of clusters. When k = 3, distinct clustering patterns emerge at = 0.25. In contrast, when k = 5 or 8, clear spatial continuity is observed only when reaches 0.5 or 0.75. Furthermore, as increases, the clustering boundaries progressively simplify, and small fragmented clusters near the boundaries gradually decrease.

Visualizing clustering maps with different k values and selecting an appropriate k based on subjective judgment provides a more intuitive approach42. When k = 3, Kangding county is divided into three spatial clusters: the northeast, central, and southern areas (Fig. 3a). However, this division may result in grouping areas with distinct geographic features into the same cluster. For instance, the central-western region is relatively flat, while the eastern region is characterized by steep terrain, with the two regions also experiencing different climatic conditions. When k = 5, the clustering results reveal more detailed spatial differentiation (Fig. 3b). The central area is divided into eastern and western subregions, whereas the southern area is further split into southeastern and southwestern parts. The southeastern area corresponds to the Gongga Mountain region, which is characterized by high elevation, steep terrain, and increased rainfall. In contrast, the southwestern area lies within the Yalong River Valley, characterized by similarly steep terrain but lower elevation and reduced rainfall. When k = 8, the spatial segmentation becomes even more detailed (Fig. 3c). The Dadu River Valley in the northeastern region, which was previously classified as a single cluster when k = 3 or k = 5, is further subdivided into two distinct clusters: one for the river valley itself and another for the more distant northeastern area.

Fig. 4
figure 4

Spatial clustering partitions under varying cluster numbers (k) and geographic distance weight (): (a) k = 3 with weight configurations: (a-1) only attribute, (a-2) =0.15, (a-3) =0.25, (a-4) =0.50, (a-5) =0.75, (a-6) =1.00; (b) k = 5 with weights analogously assigned (b-1 to b-6); (c) k = 8 configurations (c-1 to c-6).

Full size image

Clustering performance comparison and analysis

Figure 4 presents the clustering performance and spatial dependence of the model under varying cluster numbers and weight combinations. The results indicate that the DB index, Silhouette score, and CH index reach their optimal values when the geographic distance weight () is set to 0.25. As exceeds 0.25, the clustering performance gradually deteriorates. Among different k values, the clustering performance is optimal when k = 5, yielding a DB index of 1.02, a Silhouette score of 0.33, and a CH index of 29932.99. Moran’s I index and Moran’s Z-score results indicate that the spatial dependence of the clustering results peaks when reaches 0.5. When exceeds 0.5, both Moran’s I index and Moran’s Z-score stabilize. Moreover, a comparison of different cluster numbers reveals that a smaller number of clusters corresponds to higher spatial dependence. Once the spatial structure stabilizes, the performance of k = 3 and k = 5 becomes comparable, whereas that of k = 8 is less effective.

Fig. 5
figure 5

Sensitivity of clustering performance and spatial autocorrelation metrics to geographical distance weights (Wp) across cluster numbers (k = 3, 5, 8): (a) Davies-Bouldin (DB) index, ​(b) Silhouette score, ​(c) Calinski-Harabasz (CH) index, ​ (d) Moran’s I index, ​(e) Moran’s Z-score.

Full size image

Figure 5 compares the inter-cluster distributions of key attribute (e.g., elevation) under different spatial weights and cluster numbers (k = 3, 5, 8). The results indicate that the variation patterns of attributes among clusters remain generally consistent across different cluster numbers. When clustering relies solely on attribute distances, the differences in attributes among clusters are most pronounced. As the geographic distance weight increases, the differences in attributes among clusters gradually decrease. However, when the geographic distance weight reaches 0.5, the differences in attributes among clusters tend to stabilize. Furthermore, the results indicate that elevation and temperature exhibit the most pronounced differences among clusters, which is consistent with the PCA results showing that PC1 is primarily driven by elevation and temperature (Fig. S2).

Fig. 6
figure 6

Elevation heterogeneity across spatially clustering partitions: Effects of geographic distance weights () and cluster numbers (k). (a) k = 3: (a-1) only attribute, (a-2) =0.15, (a-3) =0.25, (a-4) =0.50, (a-5) =0.75, (a-6) =1.00; (b) k = 5 with analogous configurations (b-1–b-6); (c) k = 8 partitions (c-1–c-6).

Full size image

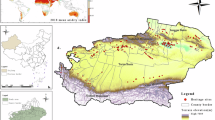
Regionalization results

After evaluating clustering performance, spatial continuity, and attribute similarity, we determined that k = 5 and = 0.5 were the optimal parameters for boundary delineation in Kangding county. The corresponding spatial clustering map is presented in Fig. 6. The consistency between cluster boundaries and attribute patterns further reinforces the reliability of the partitioning results. As indicated in Table 3, the environmental characteristics of the five spatial clusters display distinct patterns. Specifically, Cluster 1 represents the Dadu River Valley, which has the lowest average elevation but exhibits the greatest elevation variation, steep slopes, and the highest temperatures in Kangding county. In contrast, Cluster 2 features higher elevations, lower temperatures, and less topographic variation. Cluster 3 represents the Tagong Grassland-Xinduqiao region, characterized by relatively flat terrain and the lowest precipitation. Cluster 4 represents the Gongga Mountain region, which has the highest elevations and considerable elevation variation; it experiences persistent snow cover, leading to the lowest temperatures and the highest precipitation. Cluster 5 represents the Yalong River Valley, characterized by pronounced elevation variation and steep slopes, similar to Cluster 1 (Dadu River Valley).

Fig. 7
figure 7

Optimal spatial partitioning of Kangding county based on spatial clustering (k = 5, =0.50).

Full size image
Table 3 Statistical characteristics (mean and std) of topographic and Climatic variables in optimal Spatial clusters of Kangding County (k = 5, =0.50).
Full size table

Discussion

This study shows that combining Gaussian-weighted attribute distance with geographic distance in spatial clustering performs better than traditional methods that use only attribute distance. This approach is especially effective in maintaining spatial continuity. Traditional clustering methods may create clusters with lower attribute similarity but often result in fragmented spatial partitions, making interpretation difficult. This observation aligns with findings by Gao and Kupfer (2018)13. Additionally, our study finds that increasing the number of clusters worsens spatial fragmentation in traditional clustering results, supporting the conclusions of Rodrigues et al. (2015)43. Adding geographic distance as a constraint significantly improves spatial continuity, making clustering results more consistent with real geographic patterns24. For example, the REDCAP model proposed by Guo (2008) introduced spatial continuity constraints in clustering, improving the coherence of clustered regions14. Building on this, we integrated geographic distance constraints into raster data clustering, further demonstrating the advantage of spatial clustering in defining continuous geographic regions. Moreover, applying Gaussian weighting to attribute distances smooths variations between adjacent regions, reducing the impact of spatial non-stationarity in complex terrain44.

Balancing spatial continuity and attribute similarity is a key challenge in geographic spatial clustering. Spatial continuity keeps neighboring geographic units together, while attribute similarity focuses on clustering based on feature differences. Too much emphasis on spatial continuity can merge clusters with distinct characteristics45, while relying only on attribute similarity can break natural spatial relationships34. Kang et al. (2022) proposed a method that models attribute dependency within subregions using a Markov random field while maintaining cluster boundary continuity through a spatial consistency strategy46. This approach evaluates clustering performance using the Adjusted Rand Index and Macro-F1 score, while spatial continuity is measured using Join Count Statistics, achieving a balance between spatial structure and attribute similarity. In this study, we evaluated clustering performance and spatial autocorrelation under different geographic distance weighting schemes. We prioritized spatial continuity while maintaining attribute differentiation as much as possible. However, as Kupfer et al. (2012) pointed out, in some large-scale geographic classifications, internal homogeneity should be more important than spatial continuity47. Therefore, the role of spatial continuity constraints should be adjusted based on the goals of regionalization to ensure a proper balance between spatial structure and attribute characteristics.

PCA results indicate that elevation and temperature are the main factors driving spatial differences in Kangding County (Table 2). This is largely due to Kangding’s location at the transition between the Hengduan Mountains and the Qinghai-Xizang Plateau. The area’s varied terrain increases the influence of elevation on temperature, shaping natural regional differences. This aligns with previous studies, which have also identified elevation and temperature as key factors in environmental diversity48,49. For example, Wei et al. (2024) highlighted that elevation gradients are crucial in regulating terrestrial ecosystem net primary productivity50. In mountainous areas with significant elevation changes, variations in height affect solar radiation distribution, which in turn influences climate, soil, vegetation, and energy availability49. Our findings support this view. The strong match between clustering boundaries in Kangding and the DEM further confirms the role of elevation in spatial partitioning. Temperature is also a key ecological factor. It affects vegetation diversity, productivity, and soil nutrients, shaping ecosystem characteristics51. This explains the strong link between Kangding’s cluster patterns and its climate. Similarly, Hu et al. (2020) used topographic and temperature variables to study vegetation patterns, identifying the Qinling-Daba Mountain climate transition zone and reinforcing the importance of temperature in regional ecosystems3. In summary, our study confirms that elevation and temperature play a dominant role in spatial differentiation. In complex mountainous landscapes, geographic diversity is mainly shaped by the interaction between these two factors.

This study presents a spatial clustering method that combines geographic distance with Gaussian-weighted attribute distance. This method improves attribute similarity within clusters while maintaining spatial continuity. Applied in the Kangding region, it effectively identifies spatial clusters at a county-level spatial scale in areas with significant topographic variation. To regulate the influence of Gaussian-weighted attribute distance in clustering, the decay coefficient (β) was set at 0.01. While principal component analysis was used to determine attribute weights, the balance between geographical distance and attribute distance remains manually assigned. Future research should explore dynamic optimization of parameters such as β and weights using clustering objectives and advanced algorithms, including Bayesian optimization and adaptive methods. Additionally, this study employed an unsupervised classification method to segment Kangding’s natural geographic environment, considering topography and climate as primary driving factors. This approach could be extended to spatial partitioning in future studies to enhance predictive model performance.

Conclusion

This study introduces a geographically weighted clustering framework that integrates multiple topographic and climatic factors using PCA-based dimensionality reduction and Gaussian spatial weighting functions. Through a joint evaluation mechanism incorporating both clustering performance and spatial autocorrelation, this framework provides a novel, objective method that contributes to geographical regionalization research at a small spatial scale. Compared to traditional spatial clustering methods, the proposed framework enhances attribute similarity while preserving spatial continuity, thereby reducing the subjectivity in weight assignment. The resulting small-scale spatial partitioning in Kangding County distinctly delineates regional environmental characteristics, underscoring the dominant role of topographic gradients in shaping climatic, vegetation, and other natural geographic features. The derived boundary delineation results supports ecological environment management and provides a foundational framework for partition-based models used in prediction and classification tasks. Future research should refine this framework by automating the optimization of geographic and attribute distance weights, enabling adaptive trade-offs between spatial continuity and attribute similarity across diverse research scenarios.