Hybrid Fennec Fox–Sand Cat optimized cascaded ANFIS MPPT for enhanced control of DFIG-based WECS with grid support

Abstract

The Doubly Fed Induction Generator (DFIG)-based Wind Energy Conversion System (WECS) has gained significant attention due to its capability to operate efficiently over a wide range of wind speeds and in various modes. To enhance the performance and reliability of such systems, advanced control strategies are essential. This study introduces a Hybrid Fennec Fox–Sand Cat Optimization Algorithm (HFFSCOA) integrated with a Cascaded Adaptive Neuro-Fuzzy Inference System (ANFIS) for Maximum Power Point Tracking (MPPT) control of DFIG-based WECS. The proposed hybrid algorithm adaptively tunes ANFIS membership functions and parameters, improving its learning capability and ensuring accurate maximum power tracking with minimal oscillations. The coordinated control of the Rotor Side Converter (RSC) and Grid Side Converter (GSC) maintains a stable DC-link voltage and facilitates smooth power delivery to the grid. Moreover, d–q transformation is employed for harmonic suppression, enhancing overall power quality and ensuring compliance with grid standards. Simulation results in MATLAB/Simulink demonstrate the proposed controller’s effectiveness in minimizing active (Ps) and reactive (Qs) power fluctuations while achieving a remarkably low total harmonic distortion (THD) of 0.09%. Consequently, the proposed HFFSCOA-Cascaded ANFIS MPPT offers an intelligent, efficient, and scalable solution for sustainable wind energy systems seamlessly integrated into modern smart grids.

Introduction

The production of toxic gases like$\:{\:CO}_{2}$ and $\:CO\:$ from fossil fuels contributes to environmental contamination and global warming. However, there are plenty of renewable resources that are widely available everywhere in the world¹. Therefore, the best alternative to natural fossil fuels is renewable energy. The best approach to mitigate the issue of global warming and widely promote ecologically friendly energy is through renewable energy^2,3. This emphasis on wind power is in accordance with the widespread acknowledgement that wind energy is an essential renewable resource because of its affordability, sustainability, cleanliness and environmental friendliness^4,5. Vertical and horizontal axis wind turbines are the 2 categories of wind turbines^6,7. Because they only require small converters, double-fed induction generator (DFIG)-based units are popular among different wind turbine (WT) technologies. This lowers costs in comparison to other variable speed WTs while maintaining the capability to independently control reactive and active power^8,9.

Since a power electronic converter separates its rotating mass from the grid, DFIG is unable to use the kinetic energy that is naturally stored in its revolving masses to provide additional power¹⁰. The stator is attached to the grid, where the rotor winding is fed by a voltage source converter that utilizes pulse width modulation (PWM)¹¹. Among the DFIG and the grid, the RSC keeps the flow of active and reactive power¹². A faster response and lower steady-state error are demonstrated using an MPPT¹³ controller based on an Artificial Neural Network (ANN). In order to properly reflect wind speed variations, turbine features, and environmental factors, ANN models need large datasets¹⁴. Fuzzy logic¹⁵ monitors the system’s nonlinearity and produces the maximum output given the wind speed. The FLC approach enhances the fuzzy system’s membership parameters, enabling it to achieve the highest output power. Its intricate rule design necessitates precise tuning and in-depth domain knowledge to generate an efficient fuzzy rule base and membership functions, which take a lot of effort.

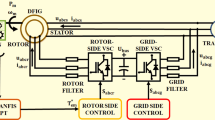
To raise the DFIG system’s performance, the MPPT is employed that has the ability to track the utmost power. An ANFIS¹⁶ that uses fuzzy logic in a sophisticated, networked ANN to make it easier to transform system inputs into desired outputs. Furthermore, the quality and diversity of training data have a significant impact on ANFIS performance; if the dataset is insufficient in capturing wind condition variability, the system is not be able to monitor the maximum power point, in rapid variations in wind speed. The metaheuristic algorithm is employed to increase the performance of MPPT approach. The robust global search ability of grey wolf optimization¹⁷ helps steer clear of local optima and guarantees highest power’s accurate tracking even in wind circumstances that change quickly. Minor power losses are result from oscillations near the ideal point. Fast convergence, fewer power fluctuations and improved energy capture efficiency are benefits of the crow search algorithm¹⁸. Particularly when used in real-time systems with constrained processing power, it is computationally demanding. Because of its well-balanced exploration and exploitation approach, the Equilibrium Optimizer Algorithm¹⁹ is effectively traverse intricate solution spaces without experiencing premature convergence. Real-time implementation in low-resource situations is hampered by its processing cost and the requirement for meticulous parameter tuning. The common block diagram of proposed DFIG system is depicted in Fig. 1.

Fig. 1

General block diagram of proposed DFIG system.

When wind conditions changed, the Modified Golden Section²⁰ has dynamic adaptation. Limited scalability in highly nonlinear or multi-variable systems is one of its disadvantages. High flexibility to nonlinear and changing wind circumstances, strong tracking capability and quick convergence speed are all features of the African Vulture Optimization²¹. Its performance is also susceptible to parameter adjustment, and instability or less-than-ideal tracking result from incorrect configuration. By reducing the searching space, the searching space minimization-PSO (SSM-PSO) scheme reduces the tracking time. Additionally, because of its straightforward searching mechanism, the SSM-PSO have reduced oscillation and is simple to implement. Under quickly shifting wind conditions, it is incapable to track the upmost power point due to premature convergence²². Significantly less oscillations, quicker transient response, more efficiency and enhanced speed tracking are the benefits of EVOA. Slow convergence is a problem for Energy Valley Optimization (EVO) in DFIG-based wind systems, especially when wind conditions change quickly²³. To reduce sub synchronous torsional oscillations in series-compensated induction generator-based wind turbines, STATCOM-based damping controllers optimised using the Bacterial Foraging Optimisation Algorithm (BFOA) is developed in²⁴. The Whale Optimisation Algorithm (WOA) have increased oscillation damping and system stability²⁵. In order to preserve overall stability and control in multimachine power systems, hybrid wind-photovoltaic farms employed as static compensators²⁶. Furthermore, sub-synchronous oscillations in DFIG-based wind farms have been effectively suppressed by damping controllers based on battery energy storage. Although these methods significantly improve certain aspects of wind power regulation, they frequently lack integrated solutions for real-time flexibility and optimal MPPT under quickly changing wind conditions²⁷.

Due to their early convergence, susceptibility to parameter adjustment, and inadequate balance between exploration and exploitation, earlier hybrid controllers resulted in local optima and unstable MPPT tracking under different wind conditions. These problems are addressed by the HFFSCOA, which combines the fine local exploitation of the Sand Cat optimizer with the robust global search capability of the Fennec Fox algorithm. Faster convergence, improved stability, and avoidance of local minima are all guaranteed by this approach. Thus, the Hybrid Fennec Fox-Sand Cat Optimized Cascaded ANFIS MPPT control method is exploited in this research. The key objectives are:

• The DFIG-based WECS is incorporated owing to its capability to function efficiently across an extensive range of wind speeds while ensuring grid compatibility.

• To improvise the performance of DFIG system, the Cascaded ANFIS MPPT control approach is exploited, and its parameters are tuned by Hybrid Fennec Fox-Sand Cat optimization algorithm.

Proposed methodology

The turbine blades absorb wind energy, which is then conveyed via the gearbox to power the DFIG. By joining the DFIG’s stator directly to the transformer and subsequently to the grid, partial direct power is transferred. An RSC converts the AC to DC power and controls rotor currents, guarantee torque control and support reactive power. The RSC is controlled by a cascaded ANFIS MPPT algorithm that is tuned for hybrid Fennec Fox–Sand Cat, ensuring optimal power extraction in fluctuating wind situations. The DFIG-WECS’s block diagram is presented in Fig. 2.

Fig. 2

Block diagram of DFIG-WECS.

Then, the GSC transforms this DC power back to a synchronized AC form to given into the grid. Between the GSC and the RSC, the DC-link capacitor keeps the steady voltage balance. Along with controlling the flow of reactive and active power, the GSC steadies the DC-link voltage. Harmonic distortions are reduced to electricity injection into the grid due to the addition of filters. The quality and stability of grid power are improved by GSC control. The transformer raises the voltage level for seamless grid integration and long-distance transmission. This hybrid control structure enhances the wind system’s efficiency, flexibility and dynamic performance.

DFIG based wind system

The DFIG is exploited to produce and deliver power in a constant frequency. Figure 3 displays the circuit for the DFIG in the $\:d-q$ frame.

$$\:{V}_{ds}={I}_{ds}{R}_{s}+\dot{{\phi\:}_{ds}}-{{\upphi\:}}_{qs}{\omega\:}_{s}$$

(1)

$$\:{V}_{qs}={I}_{qs}{R}_{s}+\dot{{\phi\:}_{qs}}-{{\upphi\:}}_{ds}{\omega\:}_{s}$$

(2)

$$\:{V}_{dr}={I}_{dr}{R}_{r}+\dot{{\phi\:}_{dr}}-{{\upphi\:}}_{qr}{\omega\:}_{r}$$

(3)

$$\:{V}_{qr}={I}_{qr}{R}_{r}+\dot{{\phi\:}_{qr}}-{{\upphi\:}}_{dr}{\omega\:}_{r}$$

(4)

$$\:{I}_{dr}{L}_{m}+{{I}_{ds}L}_{s}={{\upphi\:}}_{ds}$$

(5)

$$\:{I}_{qr}{L}_{m}+{{I}_{qs}L}_{s}={{\upphi\:}}_{qs}$$

(6)

$$\:{I}_{ds}{L}_{m}{{+I}_{dr}L}_{r}={{\upphi\:}}_{dr}$$

(7)

$$\:{{I}_{qs}L}_{m}+{I}_{qr}{L}_{r}={{\upphi\:}}_{qr}$$

(8)

The self-inductance coefficients of rotor and stator side windings are represented by$\:{L}_{r}$ and$\:{L}_{s}$, whereas the rotor and stator’s resistances are indicated by $\:{R}_{r}\:$and$\:\:{R}_{s}$. The mutual coupling coefficient among the rotor and stator sides is $\:{L}_{m}$.

Fig. 3

Circuit of DFIG.

Here, $\:{I}_{qs},{I}_{ds},{V}_{qs},{V}_{ds},{{I}_{qr},{I}_{dr},V}_{qr}$ and $\:{V}_{dr}$ represents the current and voltage components of stator and rotor. It is assumed that the EM torque expression in the d-q frame as,

$$\:{T}_{e}={{\upphi\:}}_{ds}{I}_{qs}-{{\upphi\:}}_{qs}{I}_{ds}={I}_{qr}{{\upphi\:}}_{qr}-{I}_{dr}{{\upphi\:}}_{dr}=\left({I}_{dr}{I}_{qs}-{I}_{ds}{I}_{qr}\right){L}_{m}$$

(9)

The reactive and active stator powers are,

$$\:\left({{I}_{ds}V}_{ds}+{I}_{qs}{V}_{qs}\right)\times\:1.5\:={P}_{s}$$

(10)

$$\:\left({{I}_{ds}V}_{qs}-{I}_{qs}{V}_{ds}\right)\times\:1.5={Q}_{s}$$

(11)

The active and reactive rotors’ power are,

$$\:\left({{I}_{dr}V}_{dr}+{{V}_{qr}I}_{qr}\right)\times\:1.5={P}_{r}$$

(12)

$$\left( {I_{{dr}} V_{{qr}} - I_{{qr}} V_{{dr}} } \right) \times 1.5 = Q_{r}$$

(13)

The number of pole sets is represented by p. The stator and rotor side current’s $\:q\:and\:d\:$components are $\:{I}_{qs}$ and $\:{I}_{qr}$ and stator voltage are $\:{V}_{qs}\:$and$\:{V}_{ds}$. The EM torque and the stator and rotor side’s flux linkages are,

$$\:{I}_{r}{L}_{m}+{I}_{s}{L}_{s}={{\Psi\:}}_{s}$$

(14)

$$\:{{I}_{r}L}_{r}+{I}_{s}{L}_{m}={{\Psi\:}}_{r}$$

(15)

These flux and torque correlations serve as state equations in the optimization framework that connect the electrical behavior of the DFIG to the MPPT controller’s decision.

$$\:{T}_{m}=\frac{3}{2}p\frac{{L}_{m}}{{L}_{s}}\left({{\Psi\:}}_{qs}{I}_{dr}-{{\Psi\:}}_{ds}{I}_{qr}\right)$$

(16)

The control strategy utilizes a combination of RSC and GSC techniques to manage power flow and assure smooth incorporation by the grid. Subsequently, the regulation of RSC and GSC in DFIG based WECS is discussed in the next section.

Control of RSC and GSC

The RSC sustains DC-link voltage stability, where the GSC facilitates power transmission to the grid and regulates voltage.

Control of GSC

Figure 4 illustrates the GSC’s control system. The grid-side PWM converter’s vector-control strategy aims to regulate the flow of reactive power into the grid though sustaining a steady DC link voltage. By aligning the reference frame with the grid voltage position, it is possible to decouple the regulation of the reactive power flow and DC-link voltage among the grid and the GSC. The voltage balance between the across the inductor is,

$$\:\left[\begin{array}{c}{v}_{a}\\\:{v}_{b}\\\:{v}_{c}\end{array}\right]=\left[\begin{array}{c}{i}_{a}\\\:{i}_{b}\\\:{i}_{c}\end{array}\right]R+\frac{d}{dt}\left[\begin{array}{c}{i}_{a}\\\:{i}_{b}\\\:{i}_{c}\end{array}\right]L+\left[\begin{array}{c}{v}_{al}\\\:{v}_{bl}\\\:{v}_{cl}\end{array}\right]$$

(17)

Where, $\:L\:and\:R$ denotes the inductance and resistance.

Fig. 4

Block diagram of the GSC control.

$$\:{Ri}_{d}+L\frac{{di}_{d}}{dt}-{Li}_{q}{\omega\:}_{e}+{v}_{dl}={v}_{d}$$

(18)

$$\:{i}_{q}R+\frac{{di}_{q}}{dt}L+{Li}_{d}{\omega\:}_{e}+{v}_{ql}={v}_{q}$$

(19)

The active power and reactive power are,

$$\:1.5\:\left({i}_{d}{v}_{d}+{{i}_{q}v}_{q}\right)={P}_{s}$$

(20)

$$\:1.5\:\left({i}_{q}{v}_{d}+{{i}_{d}v}_{q}\right)={Q}_{s}$$

(21)

The grid voltage’s angular position is,

$$\:{\theta\:}_{e}=\int\:{\omega\:}_{e}dt={tan}^{-1}\frac{{v}_{\beta\:}}{{v}_{\alpha\:}}$$

(22)

Ignoring the switching-related harmonics as well as losses in the converter and inductor resistance, the DC-link voltage and current expressions are,

$$\:{Ei}_{os}=3{v}_{d}{i}_{d}$$

(23)

$$\:{v}_{d}=\frac{{m}_{1}}{2\surd\:2}E$$

(24)

$$\:{i}_{os}=\frac{3}{2\surd\:2}{m}_{1}{i}_{d}$$

(25)

$$\:C\frac{dE}{dt}={i}_{os}-{i}_{or}$$

(26)

Reference values for the stator side converter is,

$$\:{v}_{dl}^{*}=-{v}_{d}^{,}+\left({\omega\:}_{e}{Li}_{q}+{v}_{d}\right)$$

(27)

$$\:{v}_{ql}^{*}=-{v}_{q}^{,}+\left({\omega\:}_{e}{Li}_{d}\right)$$

(28)

Where, the GSC’s reference values are denoted by $\:{v}_{dl}^{*}$ and $\:{v}_{ql}^{*}.$ The instantaneous power errors that are fed into the ANFIS-based MPPT controller are produced by these control loops.

Control of RSC

The structure of RSC control is displayed in Fig. 5. The actuation is provided by the rotor-side PWM converter. Since the stator is grid-connected and the stator resistance has no effect, the stator magnetizing current $\:{i}_{ms}$ is regarded as constant. The stator and rotor flux expressions under stator flux orientation are expressed as,

$$\:\left[\begin{array}{c}{\lambda\:}_{ds}\\\:{\lambda\:}_{dr}\end{array}\right]=\left[\begin{array}{cc}{L}_{s}&\:{L}_{o}\\\:{L}_{o}&\:{L}_{r}\end{array}\right]\left[\begin{array}{c}{i}_{ds}\\\:{i}_{dr}\end{array}\right]$$

(29)

$$\:{L}_{o}{i}_{ms}={\lambda\:}_{ds}$$

(30)

$$\:{{{i}_{dr}L}_{o}+{i}_{ds}L}_{s}={i}_{ms}{L}_{o}$$

(31)

$$\:{i}_{ds}=\frac{{L}_{o}{i}_{ms}-{L}_{o}{i}_{dr}}{{L}_{s}}$$

(32)

Fig. 5

Structure of the RSC control.

The rotor flux expression as,

$$\:{\lambda\:}_{dr}=\frac{{L}_{o}^{2}}{{L}_{s}}{i}_{ms}+\left(1-\frac{{L}_{o}^{2}}{{L}_{r}{L}_{s}}\right){i}_{dr}{L}_{r}$$

(33)

$$\:{{L}_{m}i}_{ms}+{L}_{r}{\sigma\:i}_{r}={\lambda\:}_{r}$$

(34)

$$\:\raisebox{1ex}{${L}_{o}^{2}$}\!\left/\:\!\raisebox{-1ex}{${L}_{s}$}\right.={L}_{m}$$

(35)

$$\:\sigma\:=\left(1-{L}_{o}^{2}\right)/{L}_{s}{L}_{r}$$

(36)

$$\:{v}_{dr}={R}_{r}{i}_{dr}+\sigma\:{L}_{r}\frac{{di}_{dr}}{dt}-{\omega\:}_{slip}\sigma\:{L}_{r}{i}_{qr}$$

(37)

$$\:{{i}_{qr}R}_{r}+\frac{{di}_{qr}}{dt}\sigma\:{L}_{r}-{\omega\:}_{slip}\left({L}_{m}{i}_{ms}+\sigma\:{L}_{r}{i}_{dr}\right)={v}_{qr}$$

(38)

The reference voltage comprises,

$$\:{v}_{dr}^{{\prime\:}}-{\omega\:}_{slip}\left(\sigma\:{L}_{r}{i}_{qr}\right)={v}_{dr}^{*}$$

(39)

$$\:{v}_{qr}^{{\prime\:}}+{\omega\:}_{slip}\left({L}_{m}{i}_{ms}+\sigma\:{L}_{r}{i}_{dr}\right)={v}_{qr}^{*}$$

(40)

The flux angle on stator is,

$$\:\int\:\left({v}_{\alpha\:s}-{{R}_{s}i}_{\alpha\:s}\right)dt={\lambda\:}_{\alpha\:s}$$

(41)

$$\:\int\:\left({v}_{\beta\:s}-{R}_{s}{i}_{\beta\:s}\right)dt={\lambda\:}_{\beta\:s}$$

(42)

$$\:{\theta\:}_{s}={tan}^{-1}\frac{{\lambda\:}_{\beta\:s}}{{\lambda\:}_{\alpha\:s}}$$

(43)

Where, the stator flux vector’s position is indicated by $\:{\theta\:}_{s}.$ To raise the DFIG system’s performance, the HFFSCOA based cascaded ANFIS MPPT controller is utilized.

HFFSCOA based cascaded ANFIS MPPT controller

The HFF-SCO algorithm is presented to tune the cascaded ANFIS parameters, such as duty cycle adjustment, widths, rule weights, membership function centers and scaling gains to enhance accuracy and convergence speed. The ability of each pair of input variables to lower the Root Mean Square Error (RMSE) among the estimated and actual outcomes is evaluated in a consecutive feature selection process. For each pair, an ANFIS model with 2 inputs is trained and assessed. By contrasting the expected and actual results, the RMSE for each data pair is calculated. The specified optimization problem is,

$$\:\left\{{Z}_{1},{Z}_{2},{Z}_{3},{Z}_{4}\right\}=Input$$

(44)

$$\:\left\{{Z}_{1},{Z}_{3}\right\},\left\{{Z}_{2},{Z}_{1}\right\},\left\{{Z}_{3},{Z}_{4}\right\},\left\{{Z}_{4},{Z}_{1}\right\}={Input\:}_{pairs}$$

(45)

$$\:RMSE=\sqrt{{\left(A-P\right)}^{2}}$$

(46)

$$\:{RMSE}_{A,P}={\left[\sum\:_{i=1}^{N}\frac{{\left({O}_{Ai}-{O}_{Pi}\right)}^{2}}{N}\right]}^{\frac{1}{2}}$$

(47)

$$\:f=\frac{{\omega\:}_{1}}{{\omega\:}_{1}+{\omega\:}_{2}}{.f}_{1}+\frac{{\omega\:}_{2}}{{\omega\:}_{1}+{\omega\:}_{2}}\:.{f}_{2}+\frac{{\omega\:}_{3}}{{\omega\:}_{2}+{\omega\:}_{3}}\:.{f}_{3}+\frac{{\omega\:}_{4}}{{\omega\:}_{3}+{\omega\:}_{4}}\:.{f}_{4}$$

(48)

Where, the input variables are indicted as$\:{Z}_{1},{Z}_{2},{Z}_{3}$ and $\:{Z}_{4}$, actual results is $\:A$, predicted outcomes is P and sample size is $\:N.$ Fuzzification, rule generation, normalization, defuzzification, and output are the five levels that make up each ANFIS in the two-stage hierarchical structure of the cascaded ANFIS MPPT controller. Gaussian membership functions with three MFs per input are used to process four important inputs rotor speed error, change in speed of rotor, DC-link voltage error, and change in active power. This results in 81 fuzzy rules. The final MPPT control signal is produced by refining the initial duty cycle produced by the first ANFIS. While the Sand Cat Optimization (SCO) offers global exploration capacity by imitating prey finding and attacking mechanisms utilizing adaptive auditory sensitivity, the Fennec Fox Optimization (FFO) guarantees powerful local exploitation by fine-tuning parameters through its digging and escape behaviours. By combining these two approaches, a balance between local and global searches is maintained, allowing the cascaded ANFIS MPPT controller to achieve strong tracking efficiency, minimal oscillations, and fast convergence. The FFO initializes all parameters of cascaded ANFIS-MPPT controller like as membership function centers, widths, rule weights, output scaling gains and the duty cycle factor by encoding them into candidate solutions. Each fox indicates a parameter set and is randomly located in the search space.

$$\:{x}_{i,j}={lb}_{j}+\left({ub}_{j}-{lb}_{j}\right)r,\:j=\text{1,2},\cdots\:,m,i=\text{1,2},\cdots\:N.$$

(49)

Here, the number of decision variables are denoted by $\:m,$ total population of foxes are $\:N$ and$\:\:{ub}_{j}$ and $\:{lb}_{j}$are upper and lower bounds. The population matrix is,

$$\:\left[ {\begin{array}{*{20}c} {x_{{{\text{1,1}}}} } & {\: \cdots \:} & {\:\begin{array}{*{20}c} {x_{{1,j}} } & {\: \cdots \:} & {\:x_{{1,m}} } \\ \end{array} } \\ {\: \vdots } & {\: \ddots \:} & {\:\begin{array}{*{20}c} \vdots & {\: {\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}} } & {\: \vdots } \\ \end{array} } \\ {\:\begin{array}{*{20}c} {x_{{i,1}} } \\ {\: \vdots } \\ {\:x_{{N,1}} } \\ \end{array} } & {\:\begin{array}{*{20}c} { \cdots \:} \\ {\: {\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}} } \\ {\: \cdots \:} \\ \end{array} } & {\:\begin{array}{*{20}c} {\begin{array}{*{20}c} {x_{{i,j}} } \\ {\: \vdots } \\ {\:x_{{N,j}} } \\ \end{array} } & {\:\begin{array}{*{20}c} { \cdots \:} \\ {\: \ddots \:} \\ {\: \cdots \:} \\ \end{array} } & {\:\begin{array}{*{20}c} {x_{{i,m}} } \\ {\: \vdots } \\ {\:x_{{N,m}} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]_{{N \times \:m}} = X = \left[ {\begin{array}{*{20}c} {X_{1} } \\ {\: \vdots } \\ {\:\begin{array}{*{20}c} {X_{i} } \\ {\: \vdots } \\ {\:X_{N} } \\ \end{array} } \\ \end{array} } \right]_{{N \times \:m}}$$

(50)

Each row indicates a single fennec fox with a ANFIS parameter set whereas the each column corresponds to a candidate value of a specific parameter. The objective function is evaluated as,

$$\:\left[ {\begin{array}{*{20}c} {F\left( {X_{1} } \right)} \\ {\: \vdots } \\ {\:\begin{array}{*{20}c} {F\left( {X_{i} } \right)} \\ {\: \vdots } \\ {\:F\left( {X_{N} } \right)} \\ \end{array} } \\ \end{array} } \right]_{{N \times \:1}} = F = \left[ {\begin{array}{*{20}c} {F_{1} } \\ {\: \vdots } \\ {\:\begin{array}{*{20}c} {F_{i} } \\ {\: \vdots } \\ {\:F_{N} } \\ \end{array} } \\ \end{array} } \right]_{{N \times \:1}}$$

(51)

In the exploitation phase of FFA, it refines the parameters by performing local search in the neighbourhood of each candidate solution. Every fennec fox indicates a membership function centers, widths, rule weights, output scaling gains and the duty cycle factor. The digging behavior fine tunes the parameters within a localized search radius assuring that the solution converges to the global optimum of MPPT. The local update of each parameter dimension is,

$$\:{x}_{i,j}^{P1}={x}_{i,j}+\left(2.r-1\right).{R}_{i,j}$$

(52)

Where, the updated value of $\:{j}^{th}$parameter is $\:{x}_{i,j}^{P1},$ adaptive search radius is $\:{R}_{i,j}$ and random number is $\:r$.

$$\:{R}_{i,j}=\alpha\:.\left(1-\frac{1}{T}\right){x}_{i,j}$$

(53)

The flowchart of HFFSCO based Cascaded ANFIS MPPT controller is revealed in Fig. 6. Where, the total number of iterations are $\:T.$ The update rule for new solution is,

$$\:{X}_{i}=\left\{\begin{array}{c}{x}_{i,j}^{P1},\:{F}_{i}^{P1}<{F}_{i}\\\:{X}_{i},\:\:else\:\end{array}\right.$$

(54)

Here, the new parameter set is $\:{X}_{i}^{P1}$and its fitness value is $\:{F}_{i}^{P1}.$ In this phase, membership functions are shifted and resized, rule weights are adjusted, output scaling gains are more precisely tuned and duty cycle control step is refined. It assures that the MPPT parameters converge toward an accurate MPP under dynamic operating conditions. In the exploration phase, it improves the global search ability to evade being trapped in local optima while tuning the cascaded ANFIS parameters. It simulates the fox’s sudden change of position when escaping predators that corresponds to moving ANFIS parameter sets toward diverse regions of search space. The target position is randomly selected from the population as,

$$\:{X}_{i}^{rand}:{x}_{i,j}^{rand}={x}_{k,j},k\in\:\left\{\text{1,2},\cdots\:,N\right\},=\text{1,2},\cdots\:N$$

(55)

Where, the escape target is denoted by $\:{X}_{i}^{rand}$ and selected parameter dimension is $\:{x}_{i,j}^{rand}.$ The actual update of each parameter is,

$$\:{x}_{i,j}^{P2}=\left\{\begin{array}{c}{x}_{i,j}+r.\left({x}_{i,j}^{rand}-I.{x}_{i,j}\right),{F}_{i}^{rand}<{F}_{i}\\\:{x}_{i,j}+r.\left({x}_{i,j}-{x}_{i,j}^{rand}\right),\:\:\:\:\:\:\:\:\:\:else\end{array}\right.$$

(56)

Where, the random integer is denoted by $\:I.$

$$\:{X}_{i}=\left\{\begin{array}{c}{X}_{i}^{P2},\:{F}_{i}^{P2}<{F}_{i}\\\:{X}_{i},\:\:else\:\end{array}\right.$$

(57)

Here, the new parameter set is denoted by $\:{X}_{i}^{P2}$ and its fitness function is $\:{F}_{i}^{P2}.$ The algorithm efficiently explores the unexplored region of parameter space assures that the MPPT converge toward the global MPP rather than stuck in local solution.

Fig. 6

Flowchart of HFFSCO based Cascaded ANFIS MPPT controller.

In the initialization phase of SCO, each sand cat denotes a parameter of cascaded ANFIS MPPT controller. In the beginning, the positions of sand cats are randomly generated within their allowable limit to assure diversity in the search population.

$$\:{d}_{i,j}={d}_{j}^{min}+rand.\left({d}_{j}^{max}-{d}_{j}^{min}\right)$$

(58)

Here, the lower and upper bounds are denoted by $\:{d}_{j}^{max}$ and $\:{d}_{j}^{min}$. This phase offers a diverse set of MPPT parameters where some sand cats indicate parameter sets with broader membership functions. In the exploration phase, the MPPT parameters are tuned by simulating the auditory based hunting ability of sand cats.

$$\:{r}_{G}={S}_{M}\left(1-\frac{n}{{nter}_{max}}\right)$$

(59)

Where, the maximum number of iterations are $\:{nter}_{max},$ maximum auditory sensitivity is $\:SM\:$and current iteration number is $\:n.\:$ The efficient auditory range of each sand cat is randomized to sustain diversity in search space as,

$$\:{r=r}_{G}\times\:rand$$

(60)

It assures that distinct sand cats explore and exploit distinct neighbours of the MPPT parameter space. The exploration phase enables the algorithm to search broadly for global optima of MPPT parameters while the exploitation phase assures fine-tuning around the best solution. In the searching and attacking prey phase, the MPPT parameters are tuned based on the balance among the global exploitation and exploration.

$$\:R=2*{r}_{G}*rand-{r}_{G}$$

(61)

Since R reduces with time, the algorithm transits from global searching to local attacking assuring a smooth convergence process. If $\:\left|R\right|>1,$ it explores new regions of parameter space to avoid local optima.

$$\:d\left(n+1\right)=r.\left({d}_{bc}\left(n\right)-rand.{d}_{c}\left(n\right)\right)$$

(62)

Here, the cat’s current position is $\:{d}_{c}\left(n\right)$ and new position is $\:d\left(n+1\right).\:$ If $\:\left|R\right|\le\:1,$ the cat switches to attack mode.

$$\:{d}_{rnd}=\left|rand.{d}_{b}\left(n\right)-{d}_{c}\left(n\right)\right|$$

(63)

Where, the global best parameter set is $\:{d}_{b}\left(n\right).$ The new position is updated as,

$$\:d\left(n+1\right)={d}_{b}\left(n\right)-r.{d}_{rnd}.cos\left(\theta\:\right)$$

(64)

Here, the randomly selected angle is $\:\theta\:$ permits the cat to approach the global best solution from multiple directions. In search mode, it diversifies candidate ANFIS MPPT parameters to prevent premature convergence while in attack mode, it exploits the neighbourhood of global best solution. It assures that the MPPT parameters quickly converge and yield high tracking accuracy in fluctuating environmental conditions. Combining these two approaches allows the algorithm to strike a compromise between local fine-tuning and global search, guaranteeing reliable ANFIS parameter optimization. By avoiding local optima and avoiding premature convergence, it iteratively converges toward the optimal parameter set with less computational cost. With fewer oscillations, this hybrid technique offers better steady-state accuracy, faster dynamic responsiveness and increased MPPT efficiency. In the end, robust grid integration, dependable maximum power extraction, and improved wind energy system performance are all guaranteed by the HFFSCO based cascaded ANFIS MPPT controller.

Result and discussions

The analysis of DFIG based WECS with HFFSCO algorithm based Cascaded ANFIS MPPT controller in in MATLAB/Simulink tool is added in this section. The parameters of specification are depicted in Table 1.

Table 1 Specification of parameters.

Fig. 7

Waveform of WECS.

The waveform of wind system is presented in Fig. 7. The wind’s speed is stabilized at $\:15\left({\text{m}/\text{s}}\right)$ while the rotor speed is maintained a steady value at$\:1.2\left({\text{m}/\text{s}}\right)$, assures the synchronized operation with minimal fluctuations. Then, the torque has sustained at a less value and the pitch angle is gradually raised and settled at 5 rad, representing the active pitch control mechanism that regulates blade orientation to control power capture and defend the turbine.

Fig. 8

Waveform of DFIG.

The waveform of DFIG is illustrated in Fig. 8. The output current is sustained at 0.8 A, replicating effective current regulation and reduced harmonic distortion. Subsequently, the output voltage is maintained at 1 V, indicating the proper synchronization with the grid. The output voltage of PWM rectifier is randomly increased and settled at 600 V, endorsing effective DC-link regulation for power conversion.

Fig. 9

Waveform of grid.

Figure 9 depicts the waveform of grid. The grid’s voltage is stabilized at 320 V, denoting the stable voltage delivery in the system while grid’s current is randomly fluctuated in the beginning and maintained at 20 A, ensuring reliable power injection under varying dynamics.

Fig. 10

Waveform of power.

The waveform of power is shown in Fig. 10. The real power is slowly increased and settled at 1000 W and reactive power is settled at a reduced value, indicating the reliable power transfer and strong grid compliance is attained.

Fig. 11

Waveform of axis current.

The waveform of direct and quadrature axis current is represented in Fig. 11. The current of direct axis is reduced and sustained at 20 A, ensuring effective regulation of the reactive power. Consequently, the current of quadrature axis is suddenly increased and settled at less value, managing the active power flow.

Fig. 12

Waveform of current.

Figure 12 reveals the waveform of reference and actual current. The reference current is gradually reduced and sustained at 20 V while the actual current has minimal deviation after the initial transient period and settled at 20 A, denotes the improved stability of DFIG system.

Fig. 13

Waveform of grid.

The waveform of grid under 7KW load condition is depicted in Fig. 13. The voltage of grid is maintained at 320 V and current of grid is settled at 10 A, representing the system maintains voltage stability at rated conditions and efficiently controls grid currents.

Fig. 14

Waveform of power.

Figure 14 illustrates the waveform of power, and the real power is gradually raised and sustained at 1000 W with no oscillations and reactive power is settled at a small value that improves the performance of system.

Fig. 15

Waveform of axis current.

Figure 15 reveals the waveform of direct and quadrature axis current, in which the current of direct axis is suddenly reduced and sustained at 10 A and current of quadrature axis is stabilized at a small value.

Fig. 16

Waveform of current.

The waveform of reference and actual current is represented in Fig. 16. The reference current is maintained at 20 A while the actual current is suddenly reduced and sustained at 10 A throughout the system.

Fig. 17

Waveform of grid.

Figure 17 presents the waveform of grid under 9KW load conditions. The voltage of grid is sustained at 320 V throughout the system and current of grid is settled at 10 A with no oscillation in the complete system.

Fig. 18

Waveform of power.

The waveform of real and reactive power is displayed in Fig. 18. The real power is slowly increased and stabilized at 1000 W, and reactive power is maintained at small value throughout the system.

Fig. 19

Waveform of axis current.

Figure 19 presents the waveform of direct and quadrature axis current, in which current of direct axis is stabilized at 20 A while the current of quadrature axis is sustained at small value in the entire system.

Fig. 20

Waveform of current.

The waveform of reference and actual current is displayed in Fig. 20. The reference current is stabilized at 10 A while actual current is sustained at 20 A throughout the system.

Fig. 21

Waveform of THD.

The waveform of THD is represented in Fig. 21. For the R, Y, and B phases, the suggested HFFSCOA–Cascaded ANFIS controller achieves THD values of 0.18%, 0.17% and 0.15%, well within IEEE and IEC limits. Therefore, the developed controller validates its efficacy and grid compliance by achieving a 94–98% reduction in harmonic distortion when compared to the IEEE 519 benchmark.

Table 2 Analysis of response time.

Higher oscillations and inadequate reactive power control are indicated by the ISMC approach with PS = 0.5 and QS = 0.71. With lower PS = 0.22 and QS = 0.26 values, the PPFC approach performs better, indicating improved dynamic response and partial stability, as seen in Table 2. But the best results are obtained by the proposed approach, which achieves PS = 0.07 and QS = 0.06, indicating fewer fluctuations and accurate power regulation, demonstrate that the developed controller maintains balanced power quality while improving the DFIG system’s stability and efficiency.

Fig. 22

Analysis of THD.

An analysis of Total Harmonic Distortion (THD) for several control strategies is depicted in Fig. 22. With a THD value of 3.26%, the DTC²⁸ method exhibits the highest harmonic content and low power quality. The highest THD is attained by the IVC-ANFIS²⁹ than others. The THD of 0.83% and 0.77% is attained by the Third Order Sliding Mode Control (TOSMC)³⁰ and PPFC³¹ approaches significantly improve waveform quality and performance. However, the developed method’s greater capacity to minimize harmonic distortions is demonstrated by its lowest THD of 0.15%.

Fig. 23

Analysis of tracking efficiency.

The analysis of tracking efficiency for methods used for MPPT in a DFIG system is shown in Fig. 23. With the lowest tracking efficiency of 89%, the AD-HCS³² approach and ADPO³³ has 91%, shows its limitations in terms of maximizing power extraction under dynamic wind conditions. With an efficiency of 98%, the Adaptive MPPT³⁴ approach outperforms the others, demonstrating better response while still need for improvement. With the highest tracking efficacy of 99.90%, the developed approach beats both and guarantees almost optimal power extraction from the wind system.

Fig. 24

Analysis of response time.

An analysis of response time for ISMC¹⁴, IVC –ANFIS²⁹ and proposed approach is shown in Fig. 24, which reveals the proposed approach has the lowest response time of 0.015s, offers reliable incorporation into the grid.

Fig. 25

Analysis of ITAE.

The proposed approach is compared with PSO³⁵ and BFO³⁶ in terms of ITAE is displayed in Fig. 25. The ITAE for PSO and BFO and proposed approach are 582.48, 1.63 and 0.05, assures the upmost power is extracted from WECS.

Table 3 Analysis of settling time in seconds.

The settling time analysis of two methods for managing the DFIG system is displayed in the Table 3. With id = 0.891 s and iq = 1.8 s, the settling times in the traditional MPPT approach³⁷ are high, denoting a slower dynamic response. The developed approach has a notable improvement, obtaining significantly shorter settling times of id = 0.05 s and iq = 0.06 s. This notable decrease demonstrates the controller’s capacity for quicker convergence. It guarantees increased adaptation in a range of wind situations and enhanced transient performance. During transient conditions, the controller maintained a steady DC-link voltage and accurate MPPT tracking, with an output power deviation of less than 2%. The THD showed good harmonic suppression, staying below 0.2% even during abrupt load fluctuations. These findings reveals that the ANFIS parameters to system nonlinearities, guaranteeing grid stability, high tracking efficiency and robustness in real-time DFIG–WECS operation.

Conclusion

By combining a cascaded ANFIS-based MPPT approach with a HFFSCO algorithm, this paper presents a control mechanism for DFIG-based WECS. By constantly adjusting ANFIS parameters, it efficiently optimizes wind power extraction, leading to precise tracking and quick response in a range of wind conditions. The system guarantees balanced power flow and reliable operation by combining the GSC for active power supply and grid support with the RSC for reactive power and DC-link voltage stability. Grid current quality is further enhanced by the use of d-q based harmonic mitigation, which guarantees adherence to IEEE standards. The proposed approach performs better than traditional control schemes in terms of power extraction efficiency, harmonic reduction and grid support capabilities, according to simulation data from MATLAB/Simulink tool with lowest THD of 0.15%. It reveals an improved dynamic stability during disturbances and high adaptability to wind changes. Because several parameters must be tuned simultaneously, the HFFSCOA- cascaded ANFIS controller has a high computational load, which could make real-time implementation difficult. ANFIS’s broad parameterization raises the possibility of over fitting, especially when training data is sparse or noisy, which could impede generalization under different wind and grid conditions. Although the optimization increases accuracy and convergence, it need a lot of iterations, which would increase runtime and energy usage.