Introduction

Artificial Ground Freezing method is widely used for the reinforcement of rich–water and soft soil layers, which has successfully assisted in the construction of multiple subway tunnels both domestically and internationally, such as Fürth subway in German, Naples subway in Italy1, Cross passage of Harbin Metro Line 3 in China2, Tianhe Station of Guangzhou Metro Line 3 in China3, and so on. However, in the design phase of freezing engineering, there are many fundamental tasks that engineers need to consider, including hydrogeological exploration, layout of frozen pipes, inversion of freezing effects, prediction of geological deformation, etc. and each task is full of randomness and uncontrollability4,5,6. At present, researchers reach a consensus that the artificial freezing process is a coupled process of multiple physical fields, involving temperature field evolution, freeze–thaw effects, water migration, and geological displacement response, etc7,8,9,10. Therefore, establishing a reliable numerical simulation method will contribute to the study of the aforementioned physical processes.

Currently, numerical simulations of freezing temperature fields are mostly based on simplified two–dimensional models, which cannot fully reflect the asymmetric temperature diffusion characteristics in three–dimensional space11. The monitoring data of a freezing project in a connecting channel of Xiamen Metro Line 3 shows that factors such as the layout of freezing pipes, geological heterogeneity, and groundwater seepage lead to significant asymmetry in temperature field distribution, and traditional symmetric models are difficult to accurately predict the actual freezing range. In addition, the calculation accuracy of latent heat of frozen soil phase change is insufficient, resulting in deviations in the prediction of the formation time and thickness of frozen walls12. The monitoring data of a freezing project in a certain section of the Beijing subway tunnel shows that in the silty clay layer, the development of frozen walls exhibits obvious anisotropic characteristics, namely, the freezing speed in the horizontal direction is about 20% faster than that in the vertical direction, and traditional isotropic models cannot accurately simulate this difference13. In view of this, developing finite element control equations for three–dimensional temperature fields under multi–scale factors are of great significance for improving accurate temperature prediction14.

Besides, the ground displacement caused by freezing construction includes two stages, that is frost heave and thaw settlement. Existing research mostly focuses on a single process and lacks systematic simulation of the evolution of displacement throughout the entire cycle15. The monitoring data of Gongbei Tunnel shows that frost heave mainly occurs during freezing from 18 days to 45 days, while thaw settlement is concentrated in the first two months after thawing. However, existing numerical models are difficult to accurately simulate this temporal dependence16. In addition, the spatial distribution of frost heave displacement follows a normal pattern, with the maximum displacement reaching 3–5 times the ground surface deformation. However, the current model still has significant errors in describing this nonlinear distribution17. In a freezing project of Wuhan Metro, due to inaccurate prediction of frost heave displacement, the ground surface uplift exceeded the warning value, and emergency measures had to be taken18. In view of this, developing finite element control equations for three–dimensional displacement fields under multi–scale factors are of great significance for improving accurate deformation prediction19.

Overall, the numerical simulation study of artificial ground freezing method still faces the following key challenges and opportunities in the coupling analysis of temperature field and displacement field. Firstly, the theoretical system of multi field coupling is not yet perfect, which is manifested in the fact that most models adopt sequential coupling methods20,21. Secondly, the adaptability of the constitutive model for freeze–thaw soil is insufficient, which is manifested in low simulation accuracy of the anisotropic characteristics of frost heave and thaw settlement deformation22,23. Thirdly, the convergence of three–dimensional large models is poor, which is manifested in the discontinuous calculation of the model when considering the construction of tunnel structures24. In this paper, some measures have been taken to address the above–mentioned issues, with the aim of establishing a practical three–dimensional thermodynamic coupling method.

Establishment of finite element calculation method

Control equation of freeze–thaw temperature field

There are three zones for freeze–thaw soil, namely unfrozen zone, phase transition zone, and frozen zone, and each zone has its own unique temperature partial differential equation. According to heat transfer theory25,26, these temperature partial differential equations27 can be written as follows.

In unfrozen zone

$${C_u}\frac{{\partial T}}{{\partial t}}=\frac{\partial }{{\partial x}}\left( {{k_u}\frac{{\partial T}}{{\partial x}}} \right)+\frac{\partial }{{\partial y}}\left( {{k_u}\frac{{\partial T}}{{\partial y}}} \right)+\frac{\partial }{{\partial z}}\left( {{k_u}\frac{{\partial T}}{{\partial z}}} \right)$$
(1)

In phase transition zone

$${C_L}\frac{{\partial T}}{{\partial t}} - {L_w}{\rho _i}\frac{{\partial {\theta _i}}}{{\partial t}}=\frac{\partial }{{\partial x}}\left( {{k_L}\frac{{\partial T}}{{\partial x}}} \right)+\frac{\partial }{{\partial y}}\left( {{k_L}\frac{{\partial T}}{{\partial y}}} \right)+\frac{\partial }{{\partial z}}\left( {{k_L}\frac{{\partial T}}{{\partial z}}} \right)$$
(2)

In frozen zone

$${C_f}\frac{{\partial T}}{{\partial t}}=\frac{\partial }{{\partial x}}\left( {{k_f}\frac{{\partial T}}{{\partial x}}} \right)+\frac{\partial }{{\partial y}}\left( {{k_f}\frac{{\partial T}}{{\partial y}}} \right)+\frac{\partial }{{\partial z}}\left( {{k_f}\frac{{\partial T}}{{\partial z}}} \right)$$
(3)

where \({C_u}\), \({C_L}\), \({C_f}\) is the volumetric heat capacity of unfrozen soil, undergoing phase transition soil and frozen soil, respectively, (kcal/(m3⋅°C)). \({k_u}\), \({k_L}\), \({k_f}\) is the thermal conductivity of unfrozen soil, undergoing phase transition soil and frozen soil, respectively, (kcal/(m⋅d⋅°C)). \({L_w}\) is the latent heat of phase change per unit mass of water, (79.6 kcal/kg). \({\theta _i}\) is the volumetric ice content of soil, (m3/m3). \({\rho _i}\) is the density of ice, (kg/m3). T is the soil temperature, (°C). t is time, (day).

In phase transition zone, the specific heat and thermal conductivity values of soil fluctuate violently within the temperature range, [\({T_d}\), \({T_r}\)]. \({T_d}\) is the critical freezing temperature of unfrozen soil, and \({T_r}\) is the critical thawing temperature of frozen soil28. Here, using the volumetric moisture content to replace the volumetric ice content, then:

$$- {L_w}{\rho _i}\frac{{\partial {\theta _i}}}{{\partial t}}={L_w}{\rho _w}\frac{{\partial {\theta _w}}}{{\partial t}}={L_w}{\rho _w}\frac{{\partial {\theta _w}}}{{\partial T}}\frac{{\partial T}}{{\partial t}}={L_w}{\rho _w}\frac{{{\rho _d}\left( {{w_0} - {w_u}} \right)}}{{{\rho _w}\left( {{T_r} - {T_d}} \right)}}\frac{{\partial T}}{{\partial t}}=\frac{{{L_w}{\rho _d}\left( {{w_0} - {w_u}} \right)}}{{\left( {{T_r} - {T_d}} \right)}}\frac{{\partial T}}{{\partial t}}=\frac{L}{{{T_r} - {T_d}}}\frac{{\partial T}}{{\partial t}}$$
(4)

where \({\rho _w}\) is the density of water, (kg/m3). \({\rho _d}\) is the dry density of soil, (kg/m3). \({w_0}\) is the initial water content of soil, (%). \({w_u}\) is the unfrozen water content, (%). L is the freezing latent heat of soil per unit volume, (kcal/m3).

Therefore, the temperature partial differential equation in phase transition zone can be rewritten as

$$\left( {{C_L}+\frac{L}{{{T_r} - {T_d}}}} \right)\frac{{\partial T}}{{\partial t}}=\frac{\partial }{{\partial x}}\left( {{k_L}\frac{{\partial T}}{{\partial x}}} \right)+\frac{\partial }{{\partial y}}\left( {{k_L}\frac{{\partial T}}{{\partial y}}} \right)+\frac{\partial }{{\partial z}}\left( {{k_L}\frac{{\partial T}}{{\partial z}}} \right)$$
(5)

Furthermore, the temperature partial differential equation of freeze–thaw soil can be summarized as

$${C^ * }\frac{{\partial T}}{{\partial t}}=\frac{\partial }{{\partial x}}\left( {{k^ * }\frac{{\partial T}}{{\partial x}}} \right)+\frac{\partial }{{\partial y}}\left( {{k^ * }\frac{{\partial T}}{{\partial y}}} \right)+\frac{\partial }{{\partial z}}\left( {{k^ * }\frac{{\partial T}}{{\partial z}}} \right)$$
(6)

\({C^ * }\) and \({k^ * }\) are also given by

$${C^ * }=\left\{ \begin{gathered} \quad \quad \,\;\;\;\;{C_f}\quad \quad \quad \quad \;\;\;\;\;T<{T_d} \hfill \\ \frac{{{C_f}+{C_u}}}{2}+\frac{L}{{{T_r} - {T_d}}}\quad \quad {T_d} \leqslant T \leqslant {T_r} \hfill \\ \quad \quad \,\;\;\;\;{C_u}\quad \quad \quad \quad \quad \;\;T>{T_r} \hfill \\ \end{gathered} \right.$$
(7)
$${k^ * }=\left\{ \begin{gathered} \quad \quad \,\;\;{k_f}\quad \quad \quad \quad \quad \quad \quad \;T<{T_d} \hfill \\ {k_f}+\frac{{{k_u} - {k_f}}}{{{T_r} - {T_d}}}\left( {T - {T_d}} \right)\quad \quad {T_d} \leqslant T \leqslant {T_r} \hfill \\ \quad \quad \,\;\;{k_u}\quad \quad \quad \quad \quad \quad \quad \;T>{T_r} \hfill \\ \end{gathered} \right.$$
(8)

where \({C^ * }\) is the equivalent volumetric heat capacity, (kcal/(m3⋅°C)), and \({k^ * }\) is the equivalent thermal conductivity, (kcal/(m⋅d⋅°C)).

In actual freezing engineering, the cold source is continuously transported to the excavation position of the tunnel that is different from the freeze–thaw cycle of strata under natural conditions. Thus, here, a cold source Q is introduced to amplify this temperature conversion effect29.

$$c\frac{{\partial T}}{{\partial t}}+\frac{L}{{{T_r} - {T_d}}}=k\left( {\frac{{{\partial ^2}T}}{{\partial {x^2}}}+\frac{{{\partial ^2}T}}{{\partial {y^2}}}+\frac{{{\partial ^2}T}}{{\partial {z^2}}}} \right)+Q$$
(9)

where c is the specific heat capacity, (J/kg⋅℃);k is the thermal conductivity (W/m⋅℃)༛T is the formation temperature (℃)༛Q is the cold source.

The initial condition for freezing temperature field is

$${\left. T \right|_{t=0}}={T_0}$$
(10)

The temperature continuity condition at the frozen front is

$${T_f}\left[ {R\left( t \right)\;,\;t} \right]={T_d}$$
(11)

The conservation of heat condition is

$${k_f}\frac{{\partial {T_f}}}{{\partial n}} - {k_u}\frac{{\partial {T_u}}}{{\partial n}}=L\frac{{dR\left( t \right)}}{{dt}}$$
(12)

where T0 is the initial temperature of soil, Tf is the temperature of frozen soil, Tu is the temperature of unfrozen soil, R(t) is the phase transition boundary, n is the normal direction vector of phase transition boundary.

The boundary condition at the freezing pipe is

$${k_f}{\left. {\frac{{\partial T}}{{\partial {n_p}}}} \right|_{r={R_p}}}=Q$$
(13)

where Rp is the outer radius of freezing pipe, np is the normal vector direction of the outer surface of freezing pipe.

Assuming the cross-section of the freezing pipe as a particle, then

$${\left. T \right|_{\left( {{x_p},{y_p}} \right)}}={T_c}\left( t \right)$$
(14)

where (xp, yp) is the centroid coordinate of freezing pipe, Tc(t) is the temperature of salt water.

The boundary condition at infinity in the frozen zone is

$${\left. T \right|_{\left( {x=\infty \,or\,y=\infty } \right)}}={T_0}$$
(15)

The boundary condition for convective heat transfer between the ground surface and air is

$${k^ * }\frac{{\partial T}}{{\partial {n_1}}}={\alpha _1}\left( {{T_a} - T} \right)$$
(16)

where \({\alpha _1}\) is the convective heat transfer coefficient between ground surface and air, Ta is the air temperature at the ground surface, n1 is the normal direction vector of the ground surface.

The initial condition for thawing temperature field is

$${\left. T \right|_{t=0}}=T\left( {x{\kern 1pt} \,,\,y} \right)$$
(17)

where T(x, y) is the final freezing temperature field during the freezing period.

The temperature continuity condition at the thawed front is

$${T_u}\left[ {R\left( t \right)\;,\;t} \right]={T_r}$$
(18)

The conservation of heat condition is the same as freezing temperature field.

During the thawing period, in addition to meeting the convective heat transfer boundary condition between the ground surface and air, it is also necessary to meet the convective heat transfer boundary condition between the inner surface of the tunnel lining and the air.

$${k^ * }\frac{{\partial T}}{{\partial {n_2}}}={\alpha _2}\left( {{T_b} - T} \right)$$
(19)

where \({\alpha _2}\) is the convective heat transfer coefficient between the inner surface of tunnel lining and air, Tb is the air temperature inside the tunnel clearance, n2 is the normal direction vector of inner surface of tunnel lining.

The finite element basic equation of the tunnel freeze–thaw temperature field can be derived using the Galerkin weighted residual method30, the equivalent functional of Eq. (9) is

$${J^e}=\int\limits_{{{v^e}}} {\left\{ {\frac{1}{2}\left[ {{k_x}{{\left( {\frac{{\partial t}}{{\partial x}}} \right)}^2}+{k_y}{{\left( {\frac{{\partial t}}{{\partial y}}} \right)}^2}+{k_z}{{\left( {\frac{{\partial t}}{{\partial z}}} \right)}^2}} \right] - \left( {{q_v} - \rho c\frac{{\partial t}}{{\partial \tau }}} \right)} \right\}dv} {\kern 1pt} +\int\limits_{{{s_2}}} {qd{s_2}} {\text{+}}\int\limits_{{{{\text{s}}_3}}} {\alpha \left( {\frac{1}{2}{t^2} - t \cdot {t_f}} \right)} d{s_3}$$
(20)

The temperature interpolation function is defined as

$$t=t(x,y,z,\tau )=\left[ N \right]{t^e}=\left[ {{N_1},{N_2}, \cdot \cdot \cdot ,{N_p}} \right]{\left\{ {{t_1},{t_2}, \cdot \cdot \cdot ,{t_p}} \right\}^T}={N_1}{t_1}+{N_2}{t_2}+ \cdot \cdot \cdot +{N_p}{t_p}$$
(21)

where P is the calculation number of node, determined by the unit type and the number of interpolation functions.

Find partial derivatives on both sides of Eq. (21) simultaneously.

$$\frac{{\partial t}}{{\partial \tau }}=\left[ N \right]{\left\{ {\frac{{\partial t}}{{\partial \tau }}} \right\}^e}$$
(22)

The first–order differential equations of temperature t in the (x, y, z, ti) direction can be written as

$$\left\{ {\begin{array}{*{20}{l}} {\frac{{\partial t}}{{\partial x}}=\frac{{\partial \left[ N \right]}}{{\partial x}}=\left[ {\frac{{\partial {N_1}}}{{\partial x}},\frac{{\partial {N_2}}}{{\partial x}}, \cdot \cdot \cdot ,\frac{{\partial {N_p}}}{{\partial x}}} \right]} \\ {\frac{{\partial t}}{{\partial y}}=\frac{{\partial \left[ N \right]}}{{\partial y}}=\left[ {\frac{{\partial {N_1}}}{{\partial y}},\frac{{\partial {N_2}}}{{\partial y}}, \cdot \cdot \cdot ,\frac{{\partial {N_p}}}{{\partial y}}} \right]} \\ {\frac{{\partial t}}{{\partial z}}=\frac{{\partial \left[ N \right]}}{{\partial z}}=\left[ {\frac{{\partial {N_1}}}{{\partial z}},\frac{{\partial {N_2}}}{{\partial z}}, \cdot \cdot \cdot ,\frac{{\partial {N_p}}}{{\partial z}}} \right]} \\ {\frac{{\partial t}}{{\partial {t_i}}}=\frac{\partial }{{\partial {t_i}}}\left[ {\left[ N \right]{t^e}} \right]=\left[ {{N_1},{N_2}, \cdot \cdot \cdot ,{N_i}} \right]={N_i}} \end{array}} \right.$$
(23)

Also,

$$\left\{ {\begin{array}{*{20}{c}} {\frac{\partial }{{\partial {t_i}}}\left( {\frac{{\partial t}}{{\partial x}}} \right)=\frac{\partial }{{\partial x}}\left( {\frac{{\partial t}}{{\partial {t_i}}}} \right)=\frac{{\partial {N_i}}}{{\partial x}}} \\ {\frac{\partial }{{\partial {t_i}}}\left( {\frac{{\partial t}}{{\partial y}}} \right)=\frac{\partial }{{\partial y}}\left( {\frac{{\partial t}}{{\partial {t_i}}}} \right)=\frac{{\partial {N_i}}}{{\partial y}}} \\ {\frac{\partial }{{\partial {t_i}}}\left( {\frac{{\partial t}}{{\partial z}}} \right)=\frac{\partial }{{\partial z}}\left( {\frac{{\partial t}}{{\partial {t_i}}}} \right)=\frac{{\partial {N_i}}}{{\partial z}}} \end{array}} \right.$$
(24)

Then,

$$\left\{ {\begin{array}{*{20}{c}} {\frac{\partial }{{\partial x}}\left[ {\frac{1}{2}{k_x}{{\left( {\frac{{\partial t}}{{\partial x}}} \right)}^2}} \right]={k_x}\frac{{\partial t}}{{\partial x}}\left( {\frac{\partial }{{\partial {t_i}}}\left( {\frac{{\partial t}}{{\partial x}}} \right)} \right)={k_x}\frac{{\partial t}}{{\partial x}}\frac{{\partial {N_i}}}{{\partial x}}={k_x}\frac{{\partial \left[ N \right]}}{{\partial x}}{{\left\{ t \right\}}^e}\frac{{\partial {N_i}}}{{\partial x}}} \\ {\frac{\partial }{{\partial y}}\left[ {\frac{1}{2}{k_y}{{\left( {\frac{{\partial t}}{{\partial y}}} \right)}^2}} \right]={k_y}\frac{{\partial t}}{{\partial y}}\left( {\frac{\partial }{{\partial {t_i}}}\left( {\frac{{\partial t}}{{\partial y}}} \right)} \right)={k_y}\frac{{\partial t}}{{\partial y}}\frac{{\partial {N_i}}}{{\partial y}}={k_y}\frac{{\partial \left[ N \right]}}{{\partial y}}{{\left\{ t \right\}}^e}\frac{{\partial {N_i}}}{{\partial y}}} \\ {\frac{\partial }{{\partial z}}\left[ {\frac{1}{2}{k_z}{{\left( {\frac{{\partial t}}{{\partial z}}} \right)}^2}} \right]={k_z}\frac{{\partial t}}{{\partial z}}\left( {\frac{\partial }{{\partial {t_i}}}\left( {\frac{{\partial t}}{{\partial z}}} \right)} \right)={k_z}\frac{{\partial t}}{{\partial z}}\frac{{\partial {N_i}}}{{\partial z}}={k_z}\frac{{\partial \left[ N \right]}}{{\partial z}}{{\left\{ t \right\}}^e}\frac{{\partial {N_i}}}{{\partial z}}} \end{array}} \right.$$
(25)

Furthermore, Eq. (20) can be rewritten as

$$\begin{gathered} \frac{{\partial {J^e}}}{{\partial {t_i}}}=\int\limits_{{{v^e}}} {\left[ {{k_x}\frac{{\partial t}}{{\partial x}}\left( {\frac{\partial }{{\partial {t_i}}}\left( {\frac{{\partial t}}{{\partial x}}} \right)} \right)+{k_y}\frac{{\partial t}}{{\partial y}}\left( {\frac{\partial }{{\partial {t_i}}}\left( {\frac{{\partial t}}{{\partial y}}} \right)} \right)+{k_z}\frac{{\partial t}}{{\partial z}}\left( {\frac{\partial }{{\partial {t_i}}}\left( {\frac{{\partial t}}{{\partial z}}} \right)} \right)} \right]} dv{\kern 1pt} - \int\limits_{{{v^e}}} {\left( {{q_v} - \rho c\frac{{\partial t}}{{\partial \tau }}} \right){N_i}} dv+\int\limits_{{{s_2}}} {q{N_i}} d{s_2}+\int\limits_{{{s_3}}} {\alpha (t - {t_f})} {N_i}d{s_3} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} =\int\limits_{{{v^e}}} {\left( {{k_x}\frac{{\partial \left[ N \right]}}{{\partial x}}\frac{{\partial {N_i}}}{{\partial x}}+{k_y}\frac{{\partial \left[ N \right]}}{{\partial y}}\frac{{\partial {N_i}}}{{\partial y}}+{k_z}\frac{{\partial \left[ N \right]}}{{\partial z}}\frac{{\partial {N_i}}}{{\partial z}}} \right){{\left\{ t \right\}}^e}} dv{\kern 1pt} - \int\limits_{{{v^e}}} {\left( {{q_v} - \rho c\frac{{\partial t}}{{\partial \tau }}} \right){N_i}} dv+\int\limits_{{{s_2}}} {q{N_i}} d{s_2}+\int\limits_{{{s_3}}} {\alpha (t - {t_f})} {N_i}d{s_3} \hfill \\ \end{gathered}$$
(26)

By taking partial differentiation of the temperature at each node, it can be obtained

$$\frac{{\partial {J^e}}}{{\partial {{\left\{ t \right\}}^e}}}=\iiint {_{{{v^e}}}}{\left[ B \right]^T}\left[ D \right]\left[ B \right]dv - \int {_{{{v^e}}}} {\left[ N \right]^T}\left( {{q_v} - \rho c\frac{{\partial t}}{{\partial \tau }}} \right){N_i}dv{\kern 1pt} +\int\limits_{{{s_2}}} {{{\left[ N \right]}^T}} qd{s_2}+\int\limits_{{{s_3}}} {\left[ N \right]{{\left[ N \right]}^T}} {\left\{ t \right\}^e}d{s_3} - \int\limits_{{{s_3}}} {\alpha {N^T}} {t_f}d{s_3}$$
(27)

where,

$$\left[ D \right]{\text{=}}\left[ {\begin{array}{*{20}{c}} {{\lambda _x}}&0&0 \\ 0&{{\lambda _y}}&0 \\ 0&0&{{\lambda _z}} \end{array}} \right]$$
(28)
$$\left[ B \right]=\left[ {\begin{array}{*{20}{c}} {\frac{{\partial N}}{{\partial x}}} \\ {\frac{{\partial N}}{{\partial y}}} \\ {\frac{{\partial N}}{{\partial z}}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {\frac{{\partial {N_1}}}{{\partial x}}}&{\frac{{\partial {N_2}}}{{\partial x}}}&{ \cdot \cdot \cdot }&{\frac{{\partial {N_p}}}{{\partial x}}} \\ {\frac{{\partial {N_1}}}{{\partial y}}}&{\frac{{\partial {N_2}}}{{\partial y}}}&{ \cdot \cdot \cdot }&{\frac{{\partial {N_p}}}{{\partial y}}} \\ {\frac{{\partial {N_1}}}{{\partial z}}}&{\frac{{\partial {N_2}}}{{\partial z}}}&{ \cdot \cdot \cdot }&{\frac{{\partial {N_p}}}{{\partial z}}} \end{array}} \right]$$
(29)

Made,

$$\left\{ \begin{gathered} {\left[ {{K_1}} \right]^e}=\iiint {_{{{v^e}}}}{\left[ B \right]^T}\left[ D \right]\left[ B \right]dv \\ {\left[ {{K_2}} \right]^e}=\iint {_{{{s_3}}}}\alpha \left[ N \right]{\left[ N \right]^T}d{s_3} \\ {\left[ {{K_3}} \right]^e}=\iint {_{{{v^e}}}}\rho c\left[ N \right]{\left[ N \right]^T}dv \\ \end{gathered} \right.$$
(30)
$$\left\{ \begin{gathered} {\left[ {{P_1}} \right]^e}=\iiint {_{{{v^e}}}}{q_v}{\left[ N \right]^T}dv \\ {\left[ {{P_2}} \right]^e}=\iint {_{{{s_2}}}}{\left[ N \right]^T}qd{s_2} \\ {\left[ {{P_3}} \right]^e}=\iint {_{{{s_3}}}}\alpha {t_f}{\left[ N \right]^T}d{s_3} \\ \end{gathered} \right.$$
(31)

where, \({\left[ P \right]^e}={\left[ {{P_1}} \right]^e} - {\left[ {{P_2}} \right]^e}+{\left[ {{P_3}} \right]^e}\), correspondingly, Eq. (17) can be written as

$$\frac{{\partial {J^e}}}{{\partial \left\{ t \right\}_{{i=1,2, \cdot \cdot \cdot ,p}}^{e}}}={\left[ {{K_1}} \right]^e}{\left\{ t \right\}^e}+{\left[ {{K_2}} \right]^e}{\left\{ t \right\}^e}+{\left[ {{K_3}} \right]^e}{\left\{ t \right\}^e} - {\left[ P \right]^e}$$
(32)

If all sets of units satisfy that \(\partial J{\text{=}}0\), then,

$$\frac{{\partial J}}{{\partial {{\left\{ t \right\}}^e}}}=\frac{{\partial \sum {{J^e}} }}{{\partial {{\left\{ t \right\}}^e}}}=\sum\limits_{1}^{n} {\frac{{\partial J}}{{\partial {{\left\{ t \right\}}^e}}}} =0$$
(33)

By substituting Eq. (32) into Eq. (33), the finite element calculation equation for the freeze–thaw temperature field can be obtained31.

$$\sum\limits_{1}^{n} {\left\{ {{{\left[ {{K_1}} \right]}^e}{{\left\{ t \right\}}^e}+{{\left[ {{K_2}} \right]}^e}{{\left\{ t \right\}}^e}+{{\left[ {{K_3}} \right]}^e}{{\left\{ t \right\}}^e} - \left[ P \right]} \right\}} =0$$
(34)

Control equation of freeze–thaw deformation field

In local coordinate system, the instantaneous thermal strain component of freeze–thaw soil caused by temperature32 is

$$\left\{ {\begin{array}{*{20}{c}} {\varepsilon _{{11}}^{T}}&{\varepsilon _{{12}}^{T}}&{\varepsilon _{{13}}^{T}} \\ {\varepsilon _{{21}}^{T}}&{\varepsilon _{{22}}^{T}}&{\varepsilon _{{23}}^{T}} \\ {\varepsilon _{{31}}^{T}}&{\varepsilon _{{32}}^{T}}&{\varepsilon _{{33}}^{T}} \end{array}} \right\}=\left[ {\begin{array}{*{20}{c}} \eta &0&0 \\ 0&{{{\left( {1 - \eta } \right)} \mathord{\left/ {\vphantom {{\left( {1 - \eta } \right)} 2}} \right. \kern-0pt} 2}}&0 \\ 0&0&{{{\left( {1 - \eta } \right)} \mathord{\left/ {\vphantom {{\left( {1 - \eta } \right)} 2}} \right. \kern-0pt} 2}} \end{array}} \right]\varepsilon _{{{f \mathord{\left/ {\vphantom {f {th}}} \right. \kern-0pt} {th}}}}^{T}$$
(35)

where η is the deformation characteristic coefficient, a dimensionless quantity. When η = 1/3, freeze–thaw soil exhibits isotropic deformation characteristics; When η = 1, the freeze–thaw soil exhibits unidirectional deformation characteristics, along the direction of temperature gradient. \(\varepsilon _{{{f \mathord{\left/ {\vphantom {f {th}}} \right. \kern-0pt} {th}}}}^{T}\) is the instantaneous volumetric strain caused by temperature. \(\varepsilon _{{ij}}^{T}\) is the instantaneous volumetric strain component caused by temperature, i = 1, 2, 3. j = 1, 2, 3.

Fig. 1
figure 1

Spatial heat flux component in the three–dimensional local coordinate system.

Full size image

In Figs. 1, 2 and 3 represent the three principal directions of the local coordinate system, x, y, and z represent the three principal directions of the global coordinate system, and axis 1’ is the projection of axis 1 on the xoy plane. The global coordinate system can be obtained by rotating the local coordinate system twice, where θ is the angle between axis x and axis 1’, and φ is the angle between axis 1 (heat flow direction) and axis z. The positive and negative relationship of the rotation angle satisfies the right–hand screw rule.

Fig. 2
figure 2

Projection diagram of heat flux after rotating around axis 2.

Full size image

In Fig. 2, the angle between axis 1 and axis 1’ is β, the angle between axis 1 and axis z is φ, and φ = π/2–β. Assuming the coordinates before rotation are denoted as (x, y, z), and the coordinates after rotation are denoted as (x’, y’, z’), these two coordinate values have this relationship.

$$\left\{ \begin{gathered} \text{x}=\text{x}^{\prime}{\text{sin}}\varphi - z^{\prime}\cos \varphi \hfill \\ {\text{z}}=\text{x}^{\prime}\cos \varphi +z^{\prime}\sin \varphi \hfill \\ \end{gathered} \right.$$
(36)

Converting to matrix expression as

$$\left[ \begin{gathered} x \hfill \\ y \hfill \\ z \hfill \\ \end{gathered} \right]=\left[ {\begin{array}{*{20}{c}} {{\text{sin}}\varphi }&0&{ - \cos \varphi } \\ 0&1&0 \\ {\cos \varphi }&0&{\sin \varphi } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\text{x}^{\prime}} \\ {\text{y}^{\prime}} \\ {\text{z}^{\prime}} \end{array}} \right]$$
(37)

Correspondingly, the rotation matrix around axis 2 is

$$R_{2} \left( \varphi \right) = \left[ {\begin{array}{*{20}c} {\sin \varphi } & 0 & { - \cos \varphi } \\ 0 & 1 & 0 \\ {\cos \varphi } & 0 & {\sin \varphi } \\ \end{array} } \right]$$
(38)

The rotation matrix around axis 3 is

$$R_{3} \left( \theta \right) = \left[ {\begin{array}{*{20}c} {\cos \theta } & { - \sin \theta } & 0 \\ {\sin \theta } & {\cos \theta } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]$$
(39)

In the three–dimensional global coordinate system, the instantaneous thermal strain component caused by temperature is

$$\left[ {\begin{array}{*{20}{c}} {\varepsilon _{{\text{x}\text{x}}}^{T}}&{\varepsilon _{{\text{x}\text{y}}}^{T}}&{\varepsilon _{{\text{x}\text{z}}}^{T}} \\ {\varepsilon _{{\text{y}\text{x}}}^{T}}&{\varepsilon _{{\text{y}\text{y}}}^{T}}&{\varepsilon _{{\text{y}\text{z}}}^{T}} \\ {\varepsilon _{{\text{z}\text{x}}}^{T}}&{\varepsilon _{{\text{z}\text{y}}}^{T}}&{\varepsilon _{{\text{z}\text{z}}}^{T}} \end{array}} \right]=\left[ R \right]\left[ {\begin{array}{*{20}{c}} {\varepsilon _{{11}}^{T}}&{\varepsilon _{{12}}^{T}}&{\varepsilon _{{13}}^{T}} \\ {\varepsilon _{{21}}^{T}}&{\varepsilon _{{22}}^{T}}&{\varepsilon _{{23}}^{T}} \\ {\varepsilon _{{31}}^{T}}&{\varepsilon _{{32}}^{T}}&{\varepsilon _{{33}}^{T}} \end{array}} \right]$$
(40)

where R is the rotation matrix,

$$\left[ R \right]={R_3}{R_2}=\left[ {\begin{array}{*{20}{c}} {\cos \theta \sin \varphi }&{ - \sin \theta }&{ - \cos \theta \cos \varphi } \\ {\sin \theta \sin \varphi }&{\cos \theta }&{ - \sin \theta \cos \varphi } \\ {\cos \varphi }&0&{\sin \varphi } \end{array}} \right]$$
(41)

Simplify as

$$\left\{ \begin{gathered} \varepsilon _{x}^{T} = \left[ {\eta \cos ^{2} \theta \sin ^{2} \varphi + \frac{1}{2}\left( {1 - \eta } \right)\sin ^{2} \theta + \frac{1}{2}(1 - \eta )\cos ^{2} \theta \cos ^{2} \varphi } \right]\varepsilon _{{{f \mathord{\left/ {\vphantom {f {th}}} \right. \kern-\nulldelimiterspace} {th}}}}^{T} \hfill \\ \varepsilon _{y}^{T} = \left[ {\eta \sin ^{2} \theta \sin ^{2} \varphi + \frac{1}{2}\left( {1 - \eta } \right)\cos ^{2} \theta + \frac{1}{2}(1 - \eta )\sin ^{2} \theta \cos ^{2} \varphi } \right]\varepsilon _{{{f \mathord{\left/ {\vphantom {f {th}}} \right. \kern-\nulldelimiterspace} {th}}}}^{T} \hfill \\ \varepsilon _{z}^{T} = \left[ {\eta \cos ^{2} \varphi + \frac{1}{2}\left( {1 - \eta } \right)\sin ^{2} \varphi } \right]\varepsilon _{{{f \mathord{\left/ {\vphantom {f {th}}} \right. \kern-\nulldelimiterspace} {th}}}}^{T} \hfill \\ \varepsilon _{{xy}}^{T} = \left[ {\eta \cos \theta \sin \theta \sin ^{2} \varphi - \frac{1}{2}\left( {1 - \eta } \right)\cos \theta \sin \theta + \frac{1}{2}(1 - \eta )\cos \theta \sin \theta \cos ^{2} \varphi } \right]\varepsilon _{{{f \mathord{\left/ {\vphantom {f {th}}} \right. \kern-\nulldelimiterspace} {th}}}}^{T} \hfill \\ \varepsilon _{{yz}}^{T} = \left[ {\eta \sin \theta \sin \varphi \cos \varphi - \frac{1}{2}\left( {1 - \eta } \right)\sin \theta \sin \varphi \cos \varphi } \right]\varepsilon _{{{f \mathord{\left/ {\vphantom {f {th}}} \right. \kern-\nulldelimiterspace} {th}}}}^{T} \hfill \\ \varepsilon _{{zx}}^{T} = \left[ {\eta \cos \theta \cos \varphi \sin \varphi - \frac{1}{2}(1 - \eta )\cos \theta \cos \varphi \sin \varphi } \right]\varepsilon _{{{f \mathord{\left/ {\vphantom {f {th}}} \right. \kern-\nulldelimiterspace} {th}}}}^{T} \hfill \\ \end{gathered} \right.$$
(42)

where E is the elastic modulus of freeze–thaw soil. µ is Poisson’s ratio of freeze–thaw soil.

Three–dimensional thermodynamic coupling equation

For the problem of spatial strain, the equilibrium equation of the stress field is

$$\left\{ \begin{gathered} \frac{{\partial {\sigma _x}}}{{\partial x}}+\frac{{\partial {\tau _{xy}}}}{{\partial y}}+\frac{{\partial {\tau _{xz}}}}{{\partial z}}=0 \hfill \\ \frac{{\partial {\tau _{yx}}}}{{\partial x}}+\frac{{\partial {\sigma _y}}}{{\partial y}}+\frac{{\partial {\tau _{yx}}}}{{\partial z}}=0 \hfill \\ \frac{{\partial {\tau _{xz}}}}{{\partial x}}+\frac{{\partial {\tau _{yz}}}}{{\partial y}}+\frac{{\partial {\sigma _z}}}{{\partial z}}= - \gamma \hfill \\ \end{gathered} \right.$$
(43)

where γ is the gravity of soil.

The geometric equation is

$$\left\{ {\begin{array}{*{20}{l}} {{\varepsilon _x}=\frac{{\partial u}}{{\partial x}}} \\ {{\varepsilon _y}=\frac{{\partial v}}{{\partial y}}} \\ {{\varepsilon _z}=\frac{{\partial w}}{{\partial z}}} \\ {{\varepsilon _{xy}}=\frac{{\partial v}}{{\partial x}}+\frac{{\partial u}}{{\partial y}}} \\ {{\varepsilon _{yz}}=\frac{{\partial w}}{{\partial y}}+\frac{{\partial v}}{{\partial z}}} \\ {{\varepsilon _{zx}}=\frac{{\partial w}}{{\partial x}}+\frac{{\partial u}}{{\partial z}}} \end{array}} \right.$$
(44)

For the assumed anisotropic elastic freeze–thaw soil, its mechanical parameter is the function of temperature, thus the thermodynamic coupling constitutive equation of freeze–thaw soil is

$$\left\{ {\begin{array}{*{20}{l}} {{\varepsilon _x}=\frac{1}{{E(T)}}\left( {{\sigma _x} - \mu (T)\left( {{\sigma _y}+{\sigma _z}} \right)} \right)+\varepsilon _{x}^{T}} \\ {{\varepsilon _y}=\frac{1}{{E(T)}}\left( {{\sigma _y} - \mu (T)\left( {{\sigma _x}+{\sigma _z}} \right)} \right)+\varepsilon _{y}^{T}} \\ {{\varepsilon _z}=\frac{1}{{E(T)}}\left( {{\sigma _z} - \mu (T)\left( {{\sigma _z}+{\sigma _y}} \right)} \right)+\varepsilon _{z}^{T}} \\ {{\varepsilon _{xy}}=\frac{{1+\mu (T)}}{{E(T)}}{\tau _{xy}}+\varepsilon _{{xy}}^{T}} \\ {{\varepsilon _{yz}}=\frac{{1+\mu (T)}}{{E(T)}}{\tau _{yz}}+\varepsilon _{{yz}}^{T}} \\ {{\varepsilon _{zx}}=\frac{{1+\mu (T)}}{{E(T)}}{\tau _{zx}}+\varepsilon _{{zx}}^{T}} \end{array}} \right.$$
(45)

where \(\varepsilon _{x}^{T}\), \(\varepsilon _{y}^{T}\), \(\varepsilon _{{xy}}^{T}\), \(\varepsilon _{{yz}}^{T}\), \(\varepsilon _{{zx}}^{T}\) is the instantaneous temperature strain component under the thermodynamic coupling.

For the assumed isotropic elastic–plastic unfrozen soil, its constitutive equation is expressed using incremental theory33 as

$$d\left\{ \sigma \right\}={\left[ D \right]_{ep}}d\left\{ \varepsilon \right\}=\left( {{{\left[ D \right]}_e} - {{\left[ D \right]}_p}} \right)d\left\{ \varepsilon \right\}$$
(46)

where \({\left[ D \right]_{ep}}\) is the elastic–plastic matrix, \({\left[ D \right]_e}\) is the elastic matrix, \({\left[ D \right]_p}\) is the plastic matrix.

$${\left[ D \right]_e}=\frac{{E\left( {1 - \mu } \right)}}{{\left( {1+\mu } \right)\left( {1 - 2\mu } \right)}}\left[ {\begin{array}{*{20}{c}} 1&{\mu /(1 - \mu )}&{\mu /(1 - \mu )}&0&0&0 \\ {\mu /(1 - \mu )}&1&{\mu /(1 - \mu )}&0&0&0 \\ {\mu /(1 - \mu )}&{\mu /(1 - \mu )}&1&0&0&0 \\ 0&0&0&{(1-2\mu )/\left[ {2(1 - \mu )} \right]}&0&0 \\ 0&0&0&0&{(1-2\mu )/\left[ {2(1 - \mu )} \right]}&0 \\ 0&0&0&0&0&{(1-2\mu )/\left[ {2(1 - \mu )} \right]} \end{array}} \right]$$
(47)
$${\left[ D \right]_p}=\frac{{{{\left[ D \right]}_e}\left\{ {\frac{{\partial P}}{{\partial \sigma }}} \right\}{{\left\{ {\frac{{\partial F}}{{\partial \sigma }}} \right\}}^T}{{\left[ D \right]}_e}}}{{{{\left\{ {\frac{{\partial F}}{{\partial \sigma }}} \right\}}^T}{{\left[ D \right]}_e}\left\{ {\frac{{\partial P}}{{\partial \sigma }}} \right\}+A}}$$
(48)

where F is the yield function, P is the plastic potential function, A is the hardening function.

Case analysis

Project overview

Fuzhou Metro Line 5 Phase I project has the starting station at Agriculture and Forestry University Station, and the ending station at Hongtang Road Station shown in Fig. 3. A double–line tunnel is built between the two stations, passing through Shangxiadian and Minjiang Avenue. This line consists of three sections of circular curves, with a horizontal spacing of 11.00 ~ 34.78 m between the two tunnels and a total length of 2391.413 m. A connecting channel is constructed using artificial ground freezing technology at the downstream “eight” shaped curve section of Shangxiadian, which also serves as a wastewater pump room. At the construction location of the connecting passage, the centerline of the left tunnel is only 18.6 m away from the bank of the Minjiang River, and the centerline of the right tunnel is only 11.5 m away from the brick and concrete building. Based on the geological and hydrological conditions, this connecting passage is presented in a plane skew state, which is a unique channel constructed using artificial ground freezing technology.

Fig. 3
figure 3

Aerial photograph of Fuzhou Metro Line 5 and section connecting channel.

Full size image

The strata where the connecting channel is located are muddy soil, silty clay (including gravel), completely weathered granite porphyry, and strongly weathered granite porphyry (liking sandy soil) from top to bottom, shown in Fig. 4. The distribution depth of these strata ranges from − 23.36 m to − 9.57 m, and they are rich in water and soft texture, which exhibits the characteristics of “soft, rotten, and deep”.

Fig. 4
figure 4

Geological distribution map of section connecting channel of Fuzhou Metro Line 5.

Full size image

Based on the above conditions, the artificial ground freezing technology is used to resist groundwater. The design scheme for the freezing pipes of the connecting channel is shown in Fig. 5.

Fig. 5
figure 5

Design scheme for the frozen pipes of the connecting channel.

Full size image

The freezing pipe is made of seamless low carbon steel with an outer diameter of 89 mm and a wall thickness of 8 mm. The design positive freezing time is 45 days, and after freezing for 45 days, the frozen wall has completely formed with a closed shape and a certain thickness. The design thickness of the frozen wall is ≥ 2.15 m for the opening section of the channel horn mouth, and it is ≥ 2.4 m for the normal section of the channel. The average temperature of frozen soil is ≤ − 13℃. The salt water temperature is − 18℃ after positive freezing for 7 days, and it is − 21℃ after positive freezing for 15 days, and it is − 28℃ during tunnel excavation. The temperature difference inside the inlet and outlet pipes is less than 2℃.

Acquisition of artificial frozen soil parameters

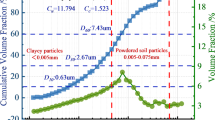
Four types of soil samples (muddy soil, silty clay, completely weathered granite porphyry, and strongly weathered granite porphyry) are achieved using hole–drilling method, and the soil sampling results are shown in Table 1.

Table 1 Soil sampling results.
Full size table

Subsequently, these four soil samples are used for density and moisture content measurements, freezing temperature measurement, thermal conductivity measurement, frost heave and thaw settlement coefficient measurements, and elastic modulus and Poisson’s ratio measurements according to China’s geotechnical engineering investigation standard (GB50021–2001), and China’s artificial frozen soil physical and mechanical properties test procedures (MT/T593–1996), and the experimental process is shown in Fig. 6.

Fig. 6
figure 6

Experimental process.

Full size image

The results of soils’ density and moisture content are shown in Table 2, the freezing temperature is shown in Table 3, the specific heat and latent heat of phase transformation is shown in Table 4, the thermal conductivity is shown in Table 5, the frost heave and thaw settlement coefficients are shown in Table 6, and the elastic modulus and Poisson’s ratio are shown in Table 7.

Table 2 Density and moisture content of soil (Average).
Full size table
Table 3 Freezing temperature of soil (Average).
Full size table
Table 4 Specific heat and latent heat of soil (Average, calculate by formula34.
Full size table
Table 5 Thermal conductivity of soil (Average).
Full size table
Table 6 Frost heave and thaw settlement coefficients of soil (Average).
Full size table
Table 7 Elastic modulus and poisson’s ratio of soil (Average).
Full size table
Table 8 Parameters of concrete.
Full size table

Above data are all necessary conditions for the Establishment of the numerical simulations.

Establishment of finite element model

A three–dimensional frozen model is established with a length of 40 m, a width of 20 m, and a height of 31 m according to the engineering design parameters of the planar skew connecting channel in Fuzhou Metro Line 5.

Fig. 7
figure 7

Finite element model.

Full size image

In Fig. 7, the element type of the three–dimensional frozen model is C3D8T, and the total number of it is 243,470. According to the geological exploration results, the soil layers in the numerical model from bottom to top are strongly weathered granite porphyry (liking sandy soil), completely weathered granite porphyry, silty clay (including gravel), and muddy soil, with the average thickness of 11 m, 5 m, 5 m, 10 m. The material of tunnel and connecting channel is concrete with strength level of 50 (parameters in Table 8), and the thickness of the structure is 300 mm, while the material parameters of each layer of soil are derived from the experimental data in above tables.

During the freezing process, frozen soil is treated as a heterogeneous elastic body, while thawed soil is treated as an isotropic elastic–plastic body, and the strength criterion follows the Mohr Coulomb yield condition. Therefore, the calculation of this model satisfies three–dimensional thermodynamic coupling equation, while this coupling equation has been compiled into FORTRAN files called by ABAQUS software35. Considering the orthogonal anisotropic deformation characteristics of frozen soil, here the deformation characteristic coefficient η = 0.936.

Besides, the initial temperature of the soil is set as 20℃, the outer wall temperature of the freezing pipe is set as − 21℃ during freezing period, while it is set as − 28℃ during excavation period, and the atmospheric temperature is set as 15℃. Furthermore, the convective heat transfer coefficient between the surface and the air is set as 175 kcal/(m2·d·℃)37. After the lining construction, the convective heat transfer coefficient between the inner surface of the structure and the air is set as 222 kcal/(m2·d·℃)38.

According to the Saint Venant principle, the frost heave and thaw settlement displacement at the far end of the frozen zone is relatively small. Therefore, setting free boundary conditions on the upper surface of the model, that is, not constrained by displacement in any direction and not subjected to any load; Setting rolling boundary conditions on the front and rear surfaces (x–z plane) of the model, that is, restricts the horizontal displacement in the y–direction of the surface; Setting rolling boundary conditions on the left and right surfaces (y–z plane) of the model, that is, restricts the horizontal displacement in the x–direction of the surface; Setting fixed boundary conditions on the lower surface of the model, that is, restricts the displacement in the x–, y–, and z–directions of the surface.

The calculation model sets up 5 analysis steps, namely geostatic stress balance (step 1), excavation and lining of left and right tunnel (step 2), freezing of connecting channel (step 3), excavation and lining of connecting channel (step 4), and natural thawing of connecting channel (step 5). After all program settings are completed, submit the model to the software for calculation.

Analysis of calculation results

Analysis of temperature field

Three–dimensional temperature models for freezing 5 days, 25 days, 45 days, thawing for 10 days, 40 days, and 68 days are generated by setting the temperature of element within − 21℃ to 0℃ in the post–processing module of the software, as shown in Fig. 8.

Fig. 8
figure 8

Evolution law of three–dimensional temperature field.

Full size image

In Fig. 8, each freezing pipe forms an independent frozen soil column around it after freezing for 5 days, and then these frozen soil columns continue to grow, intersecting initially after freezing for 25 days. Finally, a closed frozen soil wall is formed between the left and right tunnels after freezing for 45 days, which is consistent with the freezing design scheme. Subsequently, the frozen soil wall will be frozen deeply due to the loss of temperature during the excavation of the connecting channel by setting the freezing temperature as − 28℃. After the construction of the connecting channel structure, the freezing pipe stops supplying cooling and then the frozen soil wall enters the natural thawing period. The volume of the frozen soil wall rapidly shrinks due to temperature interactions between the frozen and unfrozen soil on the outer of the frozen soil wall, as well as between the inner wall of the frozen soil wall and the outer wall of the connecting channel. The surface of the frozen soil wall becomes smooth after thawing for 10 days, which is like to the melting of ice cubes. Furthermore, the left and right sides of the frozen soil wall completely melted through after thawing for 40 days. Finally, the frozen soil wall almost disappeared after thawing for 68 days.

To quantitatively evaluate the quality of temperature field evolution, temperature cloud map of the connecting channel’s mid span section is selected for analysis, shown in Fig. 9.

Fig. 9
figure 9

Evolution law of temperature field at the mid span of the connecting channel.

Full size image

In Fig. 9, after freezing for 5 days, a double row of frozen soil columns with freezing pipes as the center are formed at the top of the middle span of the connecting channel, and the frozen soil columns are independent of each other. While a single row frozen soil wall divided with three section is formed at the bottom of the middle span of the connecting channel. And the frozen soil walls on both sides of the middle span of the connecting channel have also begun to take shape. After freezing for 25 days, all frozen soil columns grown from freezing pipes intersect, and a closed frozen soil wall is initially formed. However, the development of the bottom of the frozen soil walls on the left and right sides of the connecting channel are relatively weak, and the frozen soil walls on the up and down sides of the connecting channel are still under strengthened freezing. Besides, at this period, the average thickness of the frozen soil wall is 2.13 m and the average temperature is − 5.1℃ by using the element statistical method. After freezing for 45 days, the closed frozen soil wall is fully developed, and the average thickness of the frozen soil wall is 2.95 m and the average temperature is − 13.4℃, which is satisfied with the required design.

After completion of the connecting channel structure, the frozen soil enters the natural thawing period. The melting process of frozen soil wall is relatively simple, which manifests as the low temperature points inside the frozen soil wall disappear due to the temperature transfer between soil particles, and the temperature distributed within the frozen soil wall tends to consistency. The temperature distribution range inside the frozen soil wall is from − 15℃ to − 1.1℃ after thawing 10 days, and it is from − 5.1℃ to − 1.1℃ after thawing 40 days, and it is − 1.1℃ after thawing 68 days. From this, the frozen soil has basically returned to normal temperature.

Analysis of displacement field

Under the influence of temperature and structural forces, the strata undergo varying degrees of vertical and horizontal deformation during the construction period. For the convenience of analysis, the right part of the model that divided by cut plane Ⅰ is selected for analysis the strata deformation law. Besides, the up surface of the model that divided by cut plan Ⅱ is selected for analysis the ground surface deformation law, shown in Fig. 10.

Fig. 10
figure 10

Schematic diagram of cutting plane.

Full size image

The three–dimensional vertical displacement cloud map of the right part of the model is shown in Fig. 11.

Fig. 11
figure 11

Evolution law of three–dimensional vertical displacement field.

Full size image

In Fig. 11, there is an upward frost heave displacement at the top of the plane skew connecting channel, while a downward frost heave displacement at the bottom of the plane skew connecting channel during the active freezing period. However, it exhibits the opposite rule during the natural thawing period. Comparing the three–dimensional cloud maps of these two periods, it can be found that the density of frost heave displacement evolution is higher than that of thaw settlement displacement evolution. Specifically, the maximum vertical frost heave displacement of the strata is 23.3, 60.6, and 74.9 mm, and the minimum vertical frost heave displacement is − 9.5, − 27.6, and − 32.5 mm, after freezing for 5, 25, and 45 days, respectively. Furthermore, the maximum vertical thaw settlement displacement of the strata is 3.8, 10.7, and 13.6 mm, and the minimum vertical thaw settlement displacement is − 7.4, − 26.1, and − 33.7 mm, after thawing for 10, 40, and 68 days, respectively.

In practical engineering, measuring ground surface vertical displacement is easy. Therefore, the ground surface displacement cloud maps are formed by extracting displacement data from the model surface, shown in Fig. 12.

Fig. 12
figure 12

Evolution law of ground surface vertical displacement.

Full size image

In Fig. 12, the cloud map of ground surface vertical frost heave displacement shows the shape of an eye, while the cloud map of ground surface vertical thaw settlement displacement shows the shape of a river. Specifically, the maximum ground surface vertical frost heave displacement is 14.0, 40.6, and 53.0 mm, and the minimum ground surface vertical frost heave displacement is 10.9, 36.0, and 46.6 mm, after freezing for 5, 25, and 45 days, respectively. Furthermore, the maximum ground surface vertical thaw settlement displacement is − 4.2, − 18.1, and − 24.1 mm, and the minimum ground surface vertical thaw settlement displacement is − 2.2, − 10.0, and − 13.5 mm, after thawing for 10, 40, and 68 days, respectively.

The three–dimensional horizontal displacement cloud map of the right part of the model is shown in Fig. 13.

Fig. 13
figure 13

Evolution law of three–dimensional horizontal displacement field.

Full size image

In Fig. 13, the maximum and minimum horizontal frost heave and thaw settlement displacements of the soil in the model occur respectively in the lower part of the left and right tunnel lines. However, there has been almost no horizontal movement of the soil on and below the connecting channel, which is because the existence of double–line tunnel provides certain protection for the soil and structure in the middle. Specifically, the maximum horizontal frost heave displacement of the strata is 12.3, 42.1, and 52.5 mm, after freezing for 5, 25, and 45 days, respectively. Furthermore, the maximum horizontal thaw settlement displacement of the strata is − 4.6, − 11.4, and − 16.1 mm, after thawing for 10, 40, and 68 days, respectively.

Demonstration of calculation results

Four ground surface displacement monitoring paths are set up on the construction site, where are distributed with 17 observation points uniformly. Among these four paths, one path is parallel to the connecting channel, located at the longitudinal centerline of the connecting channel. Meanwhile, the other three paths are perpendicular to the connecting passage, and the distance between the two adjacent paths is 4.721 m, while the middle path is in the middle of the connecting channel. The observation points on the parallel line are numbered V1 ~ V5, and the observation points on the vertical lines are numbered L1 ~ L12. The specific distances between the observation points are shown in Fig. 14.

Fig. 14
figure 14

Layout of on–site displacement monitoring points.

Full size image

The on–site measured data from three representative observation points are selected to verify the accuracy of the numerical calculation model results, namely V2, V3, and L6. V2 is located at the upstream of the connecting channel, and V3 is located at the midpoint of the connecting channel, and L6 is located at the edge of the middle span of the connecting channel.

Fig. 15
figure 15

Variation law of frost heave displacement with time.

Full size image

In Fig. 15, after freezing for 45 days, the on–site measured values of ground surface frost heave displacement at observation points V2, V3, and L6 are 48.46 mm, 49.58 mm, and 45.52 mm, respectively, while the numerical simulation values are 52.70 mm, 52.43 mm, and 52.39 mm, respectively, with errors of 4.24 mm, 2.85 mm, and 6.87 mm, respectively. After thawing for 68 days, the on–site measured values of ground surface thaw settlement displacement at observation points V2, V3, and L6 are − 24.11 mm, − 24.02 mm, and − 22.99 mm, respectively, while the numerical simulation values are − 23.15 mm, − 23.77 mm, and − 23.81 mm, respectively, with errors of 0.96 mm, 0.25 mm, and 0.82 mm, respectively.

The duration curves of ground surface frost heave displacement at the three observation points all follow an ascending power function, while the duration functions of ground surface thaw settlement displacement all follow a descending power function, and the on–site measured curve and numerical simulation curve show consistent patterns. Here, the three sets of data for frost heave and thaw settlement are fitted using power functions39, and the fitting results are shown in Table 9.

Table 9 Fitting curve of frost heave and thaw settlement displacement.
Full size table

In Table 9, at three observation points, the correlation coefficients of the power function fitting curves for on–site measured frost heave displacement are 0.95, 0.97, and 0.99, respectively, while the correlation coefficients for numerical simulation results are 0.96, 0.96, and 0.96, respectively. Furthermore, the correlation coefficients of the power function fitting curves for on–site measured thaw settlement displacement are 0.91, 0.94, and 0.91, respectively, while the correlation coefficients for numerical simulation results are 0.90, 0.90, and 0.90, respectively, showing a high degree of agreement.

Besides, at three observation points, the constant coefficients of the on–site measured frost heave fitting curve are 7.23, 7.66, and 7.00, while they are 7.69, 7.68, and 7.67 for numerical simulation results, with the errors of 0.46, 0.02, and 0.67. Furthermore, the constant coefficients of the on–site measured thaw settlement fitting curve are − 2.76, − 2.82, and − 2.69, while they are − 2.38, − 2.44, and − 2.45 for numerical simulation results, with the errors of 0.38, 0.38, and 0.24.

In summary, the consistency between the variation patterns of on–site measured data and numerical simulation is high, and the error between on–site measured values and numerical simulation predicted values is small. All these demonstrate that the established three–dimensional numerical simulation method for frost heave and thaw settlement has high accuracy.

Conclusions

In this paper, a three–dimensional thermodynamic coupling method for simulating the freeze–thaw soil is derived based on the secondary development platform of ABAQUS finite element software, and then applied to predict the ground deformation for the construction of a connecting channel using artificial ground freezing technology. The relevant conclusions are as follows.

  1. (1)

    Considering the phase transition process of freeze–thaw soil, the finite element calculation formula for the freeze–thaw temperature field is derived using the Galerkin weighted residual method. Then, considering the anisotropic characteristics of freeze–thaw soil, the strain equation of freeze–thaw soil caused by temperature at any position in space is derived through rotational matrix. Finally, an incremental matrix equation that can be compiled into FORTRAN language is obtained combining the constitutive equation of soil, which realizes the thermodynamic coupling of freeze–thaw soil in ABAQUS finite element software.

  2. (2)

    Based on above numerical simulation method, it is the first time to realize the entire process simulation of a connecting channel using artificial ground freezing technology. It has two significant characteristics of this freezing engineering that the characteristic of the construction strata is “soft, rotten, and deep” and the location distribution of the connecting channel and tunnel is skew in a plane.

  3. (3)

    The evolution process of the freezing temperature field and thawing temperature field in numerical simulation is consistent with the theoretical design. After freezing for 45 days, the average thickness of the frozen soil wall in the middle span of the connecting channel is 2.95 m, which is greater than the theoretical design value of 2.4 m, and the average temperature is − 13.4℃, which is lower than the theoretical design value of − 13℃. It basically returns to normal temperature after thawing for 68 days. Thus, the natural thawing time is about 1.5 times of the positive freezing time.

  4. (4)

    The evolution law of ground surface displacement in numerical simulation is consistent with the field measurement, and their displacement–time curves conform to the power function fitting relationship, and the correlation coefficients are all greater than 0.9. After freezing for 45 days, the ground surface frost heave displacement at the midpoint of the connecting channel in numerical simulation is 52.43 mm, while the measured value on site is 49.58 mm, with an error of only 2.85 mm. After thawing for 68 days, the ground surface thaw settlement displacement at the midpoint of the connecting channel in numerical simulation is − 23.77 mm, while the measured value on site is − 24.02 mm, with an error of only 0.25 mm. All these indicate the accuracy of the established numerical simulation prediction method.