Mechanical analysis and application of floor failure mechanism under repeated mining in close-distance coal seams

Abstract

The stress state of primary rocks is redistributed during coal mining, which leads to deformation and failure of the floor strata. Coal seam floor experiences repeated additional stress from the mining of two overlying seams in close-distance mining. An assessment of floor stability is required in the presence of a confined aquifer within the floor strata. The failure characteristics of floor rock strata are crucial for analyzing water inrush from floor. This mechanical response of floor deformation and failure becomes particularly pronounced when the roof is treated using the full caving method. Floor strata were analyzed for the 220,105 working face at Xinji 2^# Coal Mine, with an elastic half‑plane theory established. The stress distribution characteristics of the floor were investigated using software MATLAB. The width of the plastic zone and the maximum failure depth of floor were determined based on the slip line field theory of floor rock mass. A reference was provided for water damage control during repeated mining of the 1^# coal seam. Continuous field observation of floor failure was performed through drilling combined with the network parallel electrical method. Apparent resistivity at the depth of 19.6 m below floor was approximately twice the background resistivity of the corresponding stratum. The apparent resistivity of rock strata below 19.6 m remained constant, indicating a protective zone. These results confirm the reliability of the theoretical analysis and provide a technical foundation for safe mining in the working face.

Introduction

Coal remains the dominant energy source in China, constituting approximately 97% of the nation’s total proven fossil fuel reserves¹. This coal-oriented fundamental reality ensures that coal serves as the cornerstone of China’s energy security for the foreseeable future². As coal resource extraction continues to deepen and intensify, challenges (e.g., mine water inrush, gas outbursts, and rockbursts) have become prominent³. These issues pose significant threats to mining safety⁴. The water inrush of coal mine floor represents a potential risk in China’s coal mining industry^5,6. The frequency and severity of water inrush accidents have escalated markedly as mining depth increases^7,8.

Researchers have studied the failure mechanisms and depth of floor strata under repeated mining. Qian et al.⁹ developed a layered semi‑infinite medium wave calculation model grounded in classical mechanics and failure criterion, which treats deep rock mass as a semi-infinite body for mechanical analysis. This model elucidates the propagation, attenuation, and energy dissipation of stress waves within semi-infinite media, offering key theoretical foundations for deep rock mass mechanics. Zhang et al.¹⁰ applied semi-infinite theory to investigate the distribution and zoning of surrounding rock pressure in working faces. A calculation formula is established for the maximum failure depth of the floor strata by analyzing the extent of the plastic zone at the mining area ends. Sun et al.¹¹ and Zhang et al.¹² determined a criterion for floor instability through mechanical analysis, deriving calculation formulas for the floor‑heave amount. High stress, elevated lateral pressure, and the lithology of the floor roadway are the primary factors of severe floor heave in deep roadways. Meng et al.¹³ analyzed the distribution regularities of abutment pressure in the coal wall ahead of the working face during mining. Based on their analysis, a stress calculation model for the floor strata is developed. Besides, a failure criterion for floor rock mass is established using the Mohr-Coulomb strength criterion. Kang et al.¹⁴ analyzed field measurement data from roadway 1021 in the Xinwen mining area, revealing the evolution of floor stress in deep roadways with increased mining depth. Lu et al.¹⁵ constructed a floor stress model to analyze the mechanism of water pressure on the stress distribution patterns in the floor strata. Based on elastic mechanics theory, Liang et al.¹⁶ analyzed stress distribution in the floor strata during periodic weighting. They established a mechanical model for the floor strata and a stability analysis model for key aquicludes. Li et al.¹⁷ developed a 3D parallel electrical-method monitoring system, enabling real-time imaging of the evolution process of water-flowing fracture zones. Song¹⁸ revealed the correlation between the slip line field pattern and the roof weighting step by simulating with a mining dynamics test system. In summary, the existing research findings provide essential technical support for the safe and efficient extraction of coal resources. An elastic half-plane theory model for floor rock mass is constructed by focusing on the deformation and failure characteristics of the floor strata in extremely close-distance coal seams under repeated mining stress.

The 220,105 working face of Xinji 2^# Coal Mine is located below the 1^# coal seam, with an average distance of 1 m between the two seams. The 1^# coal seam has already been fully extracted, which affects the floor strata of the 220,105 working face. When the 220,105 working face is mined, its floor strata are subjected to additional mining-induced stresses once again. Given that the floor strata of the 220,105 working face contain an aquifer, the failure characteristics of these strata shall be studied. The work focused on the influence of repeated mining on the floor strata of the 220,105 working face. MATLAB was employed for a quantitative analysis of the stress distribution characteristics in the floor strata following mining activities. Furthermore, the slip line field theory was applied to determine the width of the plastic zone and the maximum depth of floor rock mass failure. The evolution mechanism of floor failure in the working face was revealed. On-site drilling was carried out to verify the reliability of the theoretical calculations. Also, the network parallel electrical method was employed for the on-site detection of the floor failure of the working face. The results provide a reference for analyzing floor deformation in close-distance coal seam mining.

Project background

Xinji 2^# Coal Mine is situated within Huainan Coalfield on the southern margin of the North China Plate. It extends approximately 180 km from east to west and 15–25 km from north to south, covering an area of about 3,600 km². The 220,105 working face has the upper and lower elevations of -526.8 and − 542.1 m, respectively. The mining of the 1^# upper coal seam has been largely completed, while the 1^# coal seam has been partially extracted. The stratigraphic vertical separation between the 1^# coal seam and the overlying 1^# upper coal seam within the working face ranges from 0 to 2.5 m, averaging 1.0 m. The distance from the 1^# coal seam to the underlying 1^# limestone stratum of the Taiyuan Formation varies between 20 and 28 m, with an average of 25 m. The floor of the 1^# coal seam is affected by repeated mining from both the 1^# upper coal seam and the 1^# coal seam.

The extraction of the 220,105 working face poses a potential risk of water inrush due to an aquifer in the floor rock mass. The 220,105 working face of the 1^# coal seam group in Xinji 2^# Coal Mine was taken as the research background. The work investigated the failure characteristics of the floor strata under repeated mining in extremely close-distance coal seams. The roof and floor strata of the 220,105 working face predominantly consist of quartz sandstone, sandy mudstone, and siltstone. Table 1 lists the mechanical parameters of these rock strata.

Table 1 Mechanical parameters of the rock strata in the working face.

Failure mechanisms and analysis of floor strata

Failure mechanism of floor strata

The progressive advancement of the working face results in gradual caving or suspension of the overlying strata in the goaf during coal seam extraction (Fig. 1). This redistributes the stress in the roof and floor strata. An advanced abutment pressure forms ahead of the working face within the coal pillar. The pressure subjects underlying floor and the area ahead of the working face to compression (Fig. 1a).

As the strata above floor in the delamination zone are not yet compacted, the stress acting on floor diminishes. Floor enters a pressure-unloading state characterized by stress release, which leads to expansion or heave in this region (Fig. 1b). As the working face advances, the overlying strata above the goaf undergo re-compaction, with floor compressed (Fig. 1c). Each section of floor experiences a deformation process during advancement, characterized by initial compression, subsequent expansion, and final re-compression.

The stress field within rock mass is redistributed under the coupling of mining-induced stress and confined water pressure. This redistribution results in deformation and failure of the floor strata and the formation of fractures. Confined water in floor generates vertical seepage flow under the pressure gradient. The seepage penetrating the plastic zone of floor establishes a conduit for water inrush. A mine water inrush disaster is triggered subsequently, posing a serious threat to safe production.

Fig. 1

Force on floor with the advanced working face.

Semi-infinite plane stress model

A vertical stress of intensity (q) is distributed along a segment of the boundary of a semi-infinite plane (Fig. 2). Arbitrary point M is located within the half-plane. A 2D rectangular coordinate system is established to determine the stresses in all directions at M. The spatial position of M is described by coordinates (x, y)¹⁹.

Fig. 2

Concentrated force model in a semi-infinite plane.

Differentiation element $d\zeta$ is selected within the neighborhood of the origin of coordinates on the y-axis (Fig. 2). The force acting on this element is defined by $dF=qd\zeta$. The component of the stress¹⁹ field generated at M in space by the point load is expressed by

$$d{\sigma _x}= - \frac{{2qd\zeta }}{\pi }\frac{{{x^3}}}{{{{\left[ {{x^2}+{{(y - \zeta )}^2}} \right]}^2}}}$$

(1)

$$d{\sigma _{\text{y}}}= - \frac{{2qd\zeta }}{\pi }\frac{{x{{(y - \zeta )}^2}}}{{{{\left[ {{x^2}+{{(y - \zeta )}^2}} \right]}^2}}}$$

(2)

$$d{\tau _{{\text{xy}}}}= - \frac{{2qd\zeta }}{\pi }\frac{{{x^2}{{(y - \zeta )}^{}}}}{{{{\left[ {{x^2}+{{(y - \zeta )}^2}} \right]}^2}}}$$

(3)

where x is the vertical dimension between M and point O, m; y is the horizontal distance between M and O, m; $\tau _{{{\text{xy}}}}$, $\sigma _{{\text{y}}}$, and $\tau _{{{\text{xy}}}}$ are the vertical, horizontal, and shear stress components at M induced by concentrated force dF, respectively, MPa.

The stress components in all directions at M can be determined by superimposing the stresses contributed by each infinitesimal element along AB¹⁹.

$${\sigma _x}= - \frac{2}{\pi }\smallint _{{ - b}}^{a}\frac{{q{x^3}d\zeta }}{{{{\left[ {{x^2}+{{(y - \zeta )}^2}} \right]}^2}}}$$

(4)

$${\tau _{{\text{xy}}}}= - \frac{2}{\pi }\smallint _{{ - b}}^{a}\frac{{q{x^2}(y - \zeta )d\zeta }}{{{{\left[ {{x^2}+{{(y - \zeta )}^2}} \right]}^2}}}$$

(5)

$${\sigma _{\text{y}}}= - \frac{2}{\pi }\smallint _{{ - b}}^{a}\frac{{qx{{(y - \zeta )}^2}d\zeta }}{{{{\left[ {{x^2}+{{(y - \zeta )}^2}} \right]}^2}}}$$

(6)

Floor stress distribution

Floor failure is primarily caused by the abutment pressure, according to mine ground pressure and strata control²⁰. Coal pillars induce abutment pressure as a result of stress redistribution in the surrounding rocks during mining. Therefore, an investigation into the failure mechanisms of floor should commence with floor stress distribution.

Stress of the floor strata

The floor strata can be subdivided into three distinct zones in the direction of the working face advance (Fig. 3). Zone I exhibits characteristics of stress release, forming a pressure-relief zone. Zone II demonstrates stress concentration, constituting a pressure-increase zone. Zone III remains unaffected by mining disturbances and represents the protolith stress zone²⁰.

Fig. 3

Force on floor.

The exposed roof area increases as the working face advances. Main roof rotates and fractures, while the immediate roof in the goaf collapses. The hydraulic support applies compressive force to the underlying floor, which makes the floor ahead of the working face in compression. Meanwhile, the stress on floor decreases because the rock strata above floor in the bed separation zone have not undergone compaction. Floor in this area enters a pressure-unloading state, which leads to expansion. The overlying rock strata behind the goaf collapse. The overlying strata recompact as the collapse height increases, which compresses floor. According to the theory of mine ground pressure and strata control, the floor of the mining area is primarily subjected to the advanced abutment pressure, the primary rock stress from the compacted zone, and the water pressure from the confined water in floor.

Based on an investigation into the floor failure mechanism under periodic weighting in the mining area, an elastic mechanics analytical approach is employed. This model establishes a theoretical model for the failure characteristics along the direction. An equivalent mechanical model is established for coal and rock mass in the front abutment pressure zone and the rear pressure-unloading zone ahead of the working face (Fig. 4). Stress distribution is assumed to be linear, and the water pressure from the artesian aquifer is modeled as a uniformly distributed load to simplify the analysis. A mechanical analysis coordinate system is established according to field conditions to characterize the direction of the working face. The coal wall serves as the coordinate reference point (O). The positive x-axis orients vertically downward along the normal direction of floor, while the y-axis orients toward the rear of the goaf.

Fig. 4

Mechanical model of floor.

Stress calculation of floor strata

The stress zoning model of the mining area floor is divided into four stressed zones along the coal seam strike (Fig. 4). c is the stress-affected width in the elastic deformation zone (CO); b-c is the distribution range of the plastic yield zone (BC); a-b is the width of the virgin rock stress zone (AB); d is the length of the roof control distance (OD); e-d is the range of the goaf pressure relief zone (DE); the influence zone of the confined aquifer (FG) has a width of a + e. γH is the fiducial value of the protolith stress. The peak of the front abutment pressure ahead of the coal wall reaches kγH, where k represents the stress concentration coefficient. The stress components in each zone satisfy the following equations²¹ according to the semi-infinite plane theory of elastic mechanics.

Stress components generated in the floor rock mass of the mining area by the load from the AB¹⁹ section are defined by

$${\sigma _{{\text{x}}1}}=\frac{{\gamma H}}{\pi }\left[ {\arctan \frac{{y+a}}{x} - \arctan \frac{{y+b}}{x}+\frac{{x\left( {y+a} \right)}}{{{x^2}+{{\left( {y+a} \right)}^2}}} - \frac{{x\left( {y+b} \right)}}{{{x^2}+{{\left( {y+b} \right)}^2}}}} \right]$$

(7)

$${\sigma _{{\text{y}}1}}=\frac{{\gamma H}}{\pi }\left[ {\arctan \frac{{y+a}}{x} - \arctan \frac{{y+b}}{x} - \frac{{x\left( {y+a} \right)}}{{{x^2}+{{\left( {y+a} \right)}^2}}}+\frac{{x\left( {y+b} \right)}}{{{x^2}+{{\left( {y+b} \right)}^2}}}} \right]$$

(8)

$${\tau _{{\text{xy}}1}}= - \frac{{\gamma H}}{\pi }\left[ {\frac{{{x^2}}}{{{x^2}+{{\left( {y+a} \right)}^2}}} - \frac{{{x^2}}}{{{x^2}+{{\left( {y+b} \right)}^2}}}} \right]$$

(9)

where γ is the average unit weight of the overlying strata, kN/m³; h is the vertical distance between the top of the aquifer and mining area floor, m; H is the burial depth of the coal seam, m; P is the pressure of the confined aquifer, MPa.

Stress components generated in the floor rock mass of the mining area by the load from the BC¹⁹ section are defined by

$${\sigma _{{\text{x}}2}}=\frac{{\gamma H}}{{\pi \left( {b - c} \right)}}\left\{ \begin{gathered} \frac{{\left( {k - 1} \right){x^3}+x\left( {y+b} \right)\left[ {\left( {k - 1} \right)y+\left( {kb - c} \right)} \right]}}{{{x^2}+{{\left( {y+b} \right)}^2}}} - \frac{{\left( {k - 1} \right){x^3}+x\left( {y+c} \right)\left[ {\left( {k - 1} \right)y+\left( {kb - c} \right)} \right]}}{{{x^2}+{{\left( {y+c} \right)}^2}}} \hfill \\ +\left[ {\left( {k+1} \right)y+\left( {kb - c} \right)} \right]\left( {\arctan \frac{{y+b}}{x} - \arctan \frac{{y+c}}{x}} \right) \hfill \\ \end{gathered} \right\}$$

(10)

$${\sigma _{{\text{y}}2}}=\frac{{\gamma H}}{{\pi \left( {c - b} \right)}}\left\{ \begin{gathered} \frac{{\left( {k - 1} \right){x^3}+x\left( {y+b} \right)\left[ {\left( {k - 1} \right)y+\left( {kb - c} \right)} \right]}}{{{x^2}+{{\left( {y+b} \right)}^2}}} - \frac{{\left( {k - 1} \right){x^3}+x\left( {y+c} \right)\left[ {\left( {k - 1} \right)y+\left( {kb - c} \right)} \right]}}{{{x^2}+{{\left( {y+c} \right)}^2}}} \hfill \\ - \left[ {\left( {k - 1} \right)y+\left( {kb - c} \right)} \right]\left( {\arctan \frac{{y+b}}{x} - \arctan \frac{{y+c}}{x}} \right)+\left( {k - 1} \right)x\ln \frac{{{x^2}+{{\left( {y+b} \right)}^2}}}{{{x^2}+{{\left( {y+c} \right)}^2}}} \hfill \\ \end{gathered} \right\}$$

(11)

$${\tau _{{\text{xy}}2}}=\frac{{\gamma H}}{{\pi \left( {c - b} \right)}}\left\{ {\frac{{\left( {b - c} \right){x^2}}}{{{x^2}+{{\left( {y+b} \right)}^2}}} - \frac{{\left( {b - c} \right)k{x^2}}}{{{x^2}+{{\left( {y+c} \right)}^2}}}+\left( {k - 1} \right)x\left( {\arctan \frac{{y+b}}{x} - \arctan \frac{{y+c}}{x}} \right)} \right\}$$

(12)

where k is the stress concentration coefficient of coal mass.

Stress components generated in the floor rock mass of the mining area by the load from the CO¹⁹ section are defined by

$${\sigma _{x3}}= - \frac{{k\gamma H}}{{\pi c}}\left[ {\frac{{{x^3}+xy\left( {y+c} \right)}}{{{x^2}+{{\left( {y+c} \right)}^2}}} - \frac{{{x^3}+x{y^2}}}{{{x^2}+{y^2}}}+y\left( {\arctan \frac{{y+c}}{x} - \arctan \frac{y}{x}} \right)} \right]$$

(13)

$${\sigma _{x3}}= - \frac{{k\gamma H}}{{\pi c}}\left[ \begin{gathered} \frac{{{x^3}+x{y^2}}}{{{x^2}+{y^2}}} - \frac{{{x^3}+xy\left( {y+c} \right)}}{{{x^2}+{{\left( {y+c} \right)}^2}}} - y\left( { - \arctan \frac{{y+c}}{x}+\arctan \frac{y}{x}} \right) \hfill \\ - x\ln \frac{{{x^2}+{{\left( {y+c} \right)}^2}}}{{{x^2}+{y^2}}} \hfill \\ \end{gathered} \right]$$

(14)

$${\sigma _{x3}}=\frac{{k\gamma H}}{{\pi c}}\left[ {x\left( {\arctan \frac{{y+c}}{x} - \arctan \frac{y}{x}} \right) - \frac{{c{x^2}}}{{{x^2}+{{\left( {y+c} \right)}^2}}}} \right]$$

(15)

Stress components generated in the floor rock mass of the mining area by the load from the DE¹⁹ section are defined by

$${\sigma _{{\text{x}}4}}=\frac{{k\gamma H}}{{\pi \left( {d - e} \right)}}\left[ {\left( {y - d} \right)\left( {\arctan \frac{{y - e}}{x} - \arctan \frac{{y - d}}{x}} \right)+\frac{{{x^3}+x\left( {y - d} \right)\left( {y - e} \right)}}{{{x^2}+{{\left( {y - e} \right)}^2}}} - \frac{{{x^3}+x{{\left( {y - d} \right)}^2}}}{{{x^2}+{{\left( {y - d} \right)}^2}}}} \right]$$

(16)

$${\sigma _{{\text{y}}4}}=\frac{{k\gamma H}}{{\pi \left( {d - e} \right)}}\left[ \begin{gathered} \left( {y - d} \right)\left( {\arctan \frac{{y - e}}{x} - \arctan \frac{{y - d}}{x}} \right) - \frac{{{x^3}+x\left( {y - d} \right)\left( {y - e} \right)}}{{{x^2}+{{\left( {y - e} \right)}^2}}}+\frac{{{x^3}+x{{\left( {y - d} \right)}^2}}}{{{x^2}+{{\left( {y - d} \right)}^2}}} \hfill \\ - x\ln \frac{{{x^2}+{{\left( {y - e} \right)}^2}}}{{{x^2}+{{\left( {y - d} \right)}^2}}} \hfill \\ \end{gathered} \right]$$

(17)

$${\tau _{xy4}}=\frac{{k\gamma H}}{{\pi \left( {d - e} \right)}}\left[ {x\left( {\arctan \frac{{y - d}}{x} - \arctan \frac{{y - e}}{x}} \right)+\frac{{{x^2}\left( {d - e} \right)}}{{{x^2}+{{\left( {y - e} \right)}^2}}}} \right]$$

(18)

Stress components generated in the floor rock mass of the mining area by the load from the FG¹⁹ section are defined by

$${\sigma _{x5}}=\frac{p}{\pi }\left[ {\arctan \frac{{y+a}}{x} - \arctan \frac{{y - e}}{x}+\frac{{x(y+a)}}{{{x^2}+{{\left( {y+a} \right)}^2}}} - \frac{{x\left( {y - e} \right)}}{{{x^2}+{{\left( {y - e} \right)}^2}}}} \right]$$

(19)

$${\sigma _{y5}}=\frac{p}{\pi }\left[ {\arctan \frac{{y+a}}{x} - \arctan \frac{{y - e}}{x} - \frac{{x(y+a)}}{{{x^2}+{{\left( {y+a} \right)}^2}}}+\frac{{x\left( {y - e} \right)}}{{{x^2}+{{\left( {y - e} \right)}^2}}}} \right]$$

(20)

$${\tau _{xy5}}= - \frac{p}{\pi }\left[ {\frac{{{x^2}}}{{{x^2}+{{\left( {y+a} \right)}^2}}} - \frac{{{x^2}}}{{{x^2}+{{\left( {y - e} \right)}^2}}}} \right]$$

(21)

Based on the principle of superposition, the stress components induced by the aforementioned segmented loads can be summed. The stress tensor components²² can be obtained at any point (x, y) within the floor rock mass of the mining area.

$$\left\{ {\begin{array}{*{20}{c}} {{\sigma _x}={\sigma _{x1}}+{\sigma _{x2}}+{\sigma _{x3}}+{\sigma _{x4}}} \\ {{\sigma _y}={\sigma _{y1}}+{\sigma _{y2}}+{\sigma _{y3}}+{\sigma _{y4}}} \\ {{\tau _{xy}}={\tau _{xy1}}+{\tau _{xy2}}+{\tau _{xy3}}+{\tau _{xy4}}} \end{array}} \right.$$

(22)

Based on the periodic weighting pattern in the 220,105 working face of Xinji 2^# Coal Mine, field surveys and laboratory rock mechanics tests²³ are analyzed. Stress concentration factor k is 2.3, with a rock mass unit weight of 25 kN/m³ and mining depth H of 540 m. Hydrogeological survey data reveal hydrostatic pressure P of 4.2 MPa. Rock mechanics tests indicate an internal frictional angle φ of 22° and cohesion c of 5.4 MPa for coal mass. Face width d of the hydraulic support is set at 10 m in the periodic weighting stage. The lengths of the plastic zone, elastic zone, and pressure-unloading zone ahead of the face are 15, 16, and 85 m, respectively. The relevant parameters and equations are compiled into code and processed using MATLAB. These results generate a contour distribution figure of the vertical, horizontal, and shear stresses on floor under periodic weighting.

The contour diagram of vertical stress in floor rock mass reveals a significant stress change at the coal wall of the working face (Fig. 5). A pronounced concentration of vertical stress occurs within 0–15 m beneath coal pillar floor ahead of the working face. This phenomenon reaches a peak of 40 MPa. The stress gradually diminishes with the increased depth of floor.

Fig. 5

Contour of the vertical stress in the floor rock mass.

The distribution of horizontal stress resembles that of vertical stress, characterized by stress concentration occurring in floor ahead of the working face (Fig. 6). Stress distribution exhibits an elliptical contour pattern, where the stress decreases as floor depth increases. The horizontal stress in goaf floor is significantly lower than that in floor ahead of the working face. The stress contours display a bulb-shaped distribution that attenuates with increased floor depth, while the affected area progressively contracts.

Fig. 6

Contour of the horizontal stress in floor rock mass.

The floor shear stress displays a clear demarcation line in the working face (Fig. 7). The shear stress in the floor ahead of and behind the working face exhibits approximately symmetrical bulb-shaped distribution, with opposing directions of action. Both regions form stress concentration zones in the working face. Floor rock mass is susceptible to deformation and failure under shear stress.

Fig. 7

Contour of the shear stress in floor rock mass.

Slip line field theory of floor rock mass

The theory of the three belts in floor was first proposed by Tianquan Liu. It has evolved into a more comprehensive framework with the continuous accumulation and advancement of theoretical and practical experience in mining above confined water. Mining-induced stress redistributes the rock pressure during the coal seam mining process. Three distinct zones form from top to bottom in the floor strata, including the bottom plastic zone, aquiclude, and bottom rising zone (Fig. 8)²⁴.

Bottom plastic zone

Stress redistribution in the floor strata induces the formation of a fracture development zone under mining-induced disturbance. The original water-resisting capability of this zone is compromised, transforming it into a conduit for upward permeation of confined water.

Aquiclude

This zone is the intact rock formation located beneath the water-conducting failure zone, which remains unaffected by mining activities. Its primary function is to prevent confined water inrush by virtue of its inherent mechanical strength and low permeability.

Bottom rising zone

This zone represents the height to which confined water rises through natural fractures or mining-induced fractures.

Fig. 8

Lower three zones structure in the floor strata.

Floor failure depth

The concentrated stress ahead of the coal wall increases during the coal seam mining and eventually exceeds the ultimate strength of floor rock mass. Floor experiences plastic deformation, which forms a bottom plastic zone²⁵. Based on field studies of floor failure and guided by computational theories of foundation mechanics in soil mechanics, floor can be divided into distinct zones according to its mechanical state and the range of limit equilibrium (Fig. 9).

Fig. 9

Floor failure depth and extent.

The zones include active limit stress zone Ⅰ (oab section), transition zone II (obc section), and passive limit zone III (ocd section). o is the location of the open-off cut or the coal wall; a is the position in floor where the maximum advanced abutment pressure occurs; b is a point on the floor slip line, with angle ∠bao measuring φ/2 + 45° from the horizontal direction; e is the point of maximum floor failure depth; d is the furthest point of floor failure into the goaf from the coal wall, with angle ∠cdo measuring -φ/2 + 45° from the horizontal direction; φ is the internal friction angle of floor rock mass²⁶.

The goaf expands as the working face advances and mining-induced stress is redistributed, which leads to stress concentration in the coal pillar ahead of the working face. The compressed floor strata expand, i.e., the active limit stress zone (zone I) horizontally compresses goaf floor. The goaf, losing the pressure from the overlying strata, expands. This expansion zone is the transition zone (zone II). Floor failure consequently exhibits a spoon shape (Fig. 9). The collapsed strata behind the goaf undergo re-compaction as the working face advances. Fractures gradually close, and the extent of failure diminishes. The deformation observed in this section is characterized by passive compressional deformation; therefore, this section is designated as the passive zone (zone III).

In ∆aob (Fig. 9),

$$ob={r_1}=\frac{{{l_1}}}{{2\cos \left( {{\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi 4}}\right.\kern-0pt}\!\lower0.7ex\hbox{$4$}}+{\raise0.7ex\hbox{$\phi $} \!\mathord{\left/ {\vphantom {\phi 2}}\right.\kern-0pt}\!\lower0.7ex\hbox{$2$}}} \right)}}$$

(23)

where φ is the average internal friction angle of floor rocks; l₁ is the yield width of the coal wall, defined as the distance from the coal wall to the point of maximum advanced abutment pressure in floor.

${\text{h}}={r_2}\sin \theta$ in ∆oef.

$$\theta =\frac{\pi }{2} - \left( {\frac{\pi }{4}+\frac{\phi }{2}} \right) - \partial$$

(24)

where θ is the angle between r₂ and floor; $\partial$ is the angle between r₁ and r₂.

Then,

$${\text{h}}={r_1}{e^{\partial \tan \phi }}\cos \left( {\partial +\frac{\phi }{2} - \frac{\pi }{4}} \right)$$

(25)

According to Eq. (25), floor failure depth varies with changes in $\partial$.

$\partial$ is derived using Eq. (25). Floor failure depth reaches its maximum when $\frac{{dh}}{{d\partial }}=0$.

$$\begin{gathered} \frac{{{\text{d}}h}}{{d\partial }}={r_1}\tan \phi {e^{\partial \tan \phi }}\cos \left( {\partial +\frac{\phi }{2} - \frac{\pi }{4}} \right) - {r_1}{e^{\partial \tan \phi }}\sin \left( {\partial +\frac{\phi }{2} - \frac{\pi }{4}} \right)=0 \hfill \\ {\text{tan}}\phi ={\text{tan}}\left( {\partial +\frac{\phi }{2} - \frac{\pi }{4}} \right) \hfill \\ \partial =\frac{\pi }{4}+\frac{\phi }{2} \hfill \\ \end{gathered}$$

(26)

Equations (23) and (26) are substituted into Eq. (25) to yield the maximum depth of floor failure.

$${\text{h}}=\frac{{{l_1}\cos \phi }}{{2\cos \left( {\frac{\pi }{4}+\frac{\phi }{2}} \right)}}{e^{\left( {\frac{\pi }{4}+\frac{\phi }{2}} \right)\tan \phi }}$$

(27)

Horizontal distance l₂ from the maximum failure depth of floor rock mass to the coal wall is defined by

$${l_2}=h\tan \phi =\frac{{{l_1}\sin \phi }}{{2\cos \left( {\frac{\pi }{4}+\frac{\phi }{2}} \right)}}{e^{\left( {\frac{\pi }{4}+\frac{\phi }{2}} \right)\tan \phi }}$$

(28)

Plastic zone width

The plastic zone width at the coal mass edge of the working face should be accounted for when the fracture depth of the coal-seam floor strata is calculated. This value can be determined through field measurements or computational analysis²⁷. According to the masonry beam theory proposed by Qian’s research team, yield width l₁ of the coal wall ahead of the working face is defined by

$${l_1}=\frac{M}{{2n\tan {\phi _0}}}\ln \left( {\frac{{K\gamma H+\frac{c}{{\tan {\phi _0}}}}}{{\frac{{nc}}{{\tan {\phi _0}}}}}} \right)$$

(29)

$$n=\frac{{1+\sin {\phi _0}}}{{1 - \sin {\phi _0}}}$$

(30)

where M is the thickness of the coal seam, m; $\varphi _{0}$ is the internal friction angle of the coal seam, °; K is the stress concentration factor; γ is the average unit weight of the overlying strata, kN/m³; H is mining depth, m; C is cohesion at the coal seam interface, MPa.

Floor failure depth calculation based on the slip line field theory

The 1^# coal seam in Xinji 2^# Mine has the thickness of 4 m and the burial depth of 540 m. γ is 25 kN/m³; C of the 1^# coal seam is 5.4 MPa; φ₀ is 22°; K is 2.3; the stress measurement coefficient is 0.3.

Equations (29) and (30) are substituted to obtain plastic failure width l₁ of the coal wall.

$$K=\frac{{1+\sin {{22}^\circ }}}{{1 - \sin {{22}^\circ }}}=2.198$$

$${l_1}=\frac{4}{{2 \times \frac{{1+\sin 22^\circ }}{{1 - \sin 22^\circ }} \times \tan 22^\circ }} \times \ln \frac{{2.3 \times 25 \times 540+5.4 \times \cot 22^\circ }}{{\frac{{1+\sin 22^\circ }}{{1 - \sin 22^\circ }} \times 5.4 \times \cot 22^\circ }}=15.67 \left( {\text{m}} \right)$$

l₁ and the average internal friction angle φ of floor rock mass are substituted into Eq. (27) to obtain.

$${\text{h}}=\frac{{15.67\cos 23^\circ }}{{2\cos \left( {\frac{\pi }{4}+\frac{{23^\circ }}{2}} \right)}}{e^{\left( {\frac{\pi }{4}+\frac{{23^\circ }}{2}} \right)\tan 23^\circ }}=19.55 \left( {\text{m}} \right)$$

Based on the slip line field theory of floor rock mass, the plastic zone width is 15.67 m at the coal mass edge of the 220,105 working face in Xinji 2^# Mine. Besides, maximum floor failure depth is 19.55 m.

Verification of floor failure depth based on empirical formulas

Floor failure depth is affected by various factors, necessitating a comprehensive evaluation. Numerous empirical formulas for estimating floor failure depth^28,29 are provided in the Code for Coal Pillar Retention and Coal‑Pressure Mining of Buildings, Water Bodies, Railways, and Main Working Faces and Design Code for Water Prevention and Control in Coal Mines. Floor failure depth h is determined using Eq. (31) when inclined length L of the working face is only considered.

$$h=3.2+0.085L$$

(31)

Based on the actual geological conditions of the 220,105 working face, floor failure depth is 18.075 m when L = 175 m. Equation (32) is used for calculating floor failure depth by incorporating L, mining depth H, and coal-seam inclination angle α.

$$h=0.0085H+0.1079L+0.1665\alpha - 4.3579$$

(32)

Based on the actual geological conditions of the 220,105 working face, H is 540 m, with the coal-seam inclination angle of 4°, and L of 175 m. The depth of the mining-induced failure zone is 19.77 m based on Eq. (32). Maximum floor failure depth can be estimated with the following empirical formula based on the mining width (L), mining depth (H), and mining height (M).

$$h=0.0113H+6.25\ln \frac{{{L_{}}}}{{40}}+2.52\ln \frac{M}{{1.48}}$$

(33)

Based on the actual geological conditions of the 220,105 working face, H is 540 m, with a coal seam inclination angle of 4°, a working face width of 175 m, and a mining height of 4 m. The calculated depth of the mining-induced failure zone is 17.824 m. The results obtained from Eq. (33) are in close agreement with the predictions of the floor plastic failure theory.

Field measurement of floor failure depth under repeated mining

Previous studies focused on the floor failure mechanism in the 220,105 working face through theoretical analysis. Substantial discrepancies persist between actual working conditions and laboratory settings due to the complexity and variability of the underground environment. The network parallel electrical method is employed to assess the in-situ failure conditions. It is determined through a comprehensive integration of multiple factors from the 220,105 working face in Xinji 2^# Coal Mine, e.g., field survey data, theoretical research results, workload, detection intensity, and cost. This method facilitates the precise characterization of the development features of the floor failure zone. The reliability of preliminary studies is validated.

Principle of the network parallel electrical method

The network parallel electrical method is a variant of the traditional high-density resistivity method and shares the same fundamental principles. There is an essential difference in the measurement mode between the network parallel electrical method and the traditional high-density electrical method. The traditional high-density electrical method adopts a point-by-point measurement, while the network parallel electrical method achieves an array-based measurement. As the working face advances, stress redistribution occurs in the surrounding rocks when this method is applied to coal mining. Fractures and failure generate within rock mass, altering its electrical properties. The electrical resistivity of rock mass increases following failure caused by mining activities. Their resistivity becomes conversely lower compared to that of dry strata when the rock strata contain water. Therefore, the failure characteristics of rock mass can be interpreted by monitoring variations in the geoelectric field³⁰.

The WBD series parallel electrical system (Fig. 10) is used on-site. This system employs a distributed, parallel intelligent method for acquiring electrode potential difference signals, enabling broad application in engineering geological surveys and dynamic groundwater monitoring.

Fig. 10

Parallel electrical testing equipment.

• (1) An intrinsically safe network parallel electrical instrument for mining is responsible for signal acquisition and processing.

• (2) A distributed network parallel electrical base station is used for receiving and transmitting signals. It works with the host instrument to form a distributed or centralized electrical system.

• (3) Two sets of specialized cables for electrical resistivity tomography signals include signal transmission cables and power cables. They are used to connect the main unit, base stations, and electrodes.

• (4) Grounding electrodes are used for measuring potential differences, typically including multiple grounding electrodes.

The deployment of several dozen to hundreds of electrodes allows for the configuration of various array types in network parallel electrical resistivity tomography systems. The general electrode arrangement typically adopts the pole-pole method, which operates on a relatively simple principle. Specifically, when current is supplied to one electrode, the remaining electrodes measure the potential differences. Acquired data are then converted according to specific requirements.

Field layout plan

Observation plan considerations

Based on the actual conditions of the 220,105 working face in Xinji 2^# Coal Mine, monitoring boreholes should be positioned in areas with simple geological structures and stable coal seams. This selection is intended to minimize the influences of coal seam instability and structural complexity on test results. The placement of observation position and the layout of monitoring boreholes should satisfy the following requirements.

(1) The observation position should be situated at a sufficient distance from the mining boundary. This placement enables the installation of boreholes with a depression angle that complies with observational requirements. (2) The strata at the observation site should be relatively planar, as undulations may introduce distortions in the observational data. (3) The geological conditions at the observation position should be simple. Besides, monitoring boreholes should be avoided in structurally complex zones.

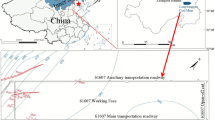
Based on the actual field construction conditions, one monitoring borehole is arranged in the airway of the 220,105 working face at this monitoring section. This borehole is designed to monitor the development characteristics and patterns of the mining-induced failure zone.

Observation plan and borehole parameters

Observation boreholes were arranged at the drilling site located at point L17 in the return airway of the 220,105 working face. The final hole positions of the boreholes were approximately 300 m in a straight line from the cutting hole. A total of two boreholes were arranged for this detection. The boreholes were oriented at 10° to the roadway, directed toward the inner side of the working face. Table 2 lists specific borehole parameters.

Table 2 Borehole parameters.

The resistivity measurement was conducted in two stages. The first stage occurred before the mining face entered the observation area, with data collected every 3–5 days. The second stage was initiated once the mining face entered the observation area. Data were collected every 48 h to capture the dynamic evolution process of the stress-strain field in the surrounding rocks.

Data acquisition

Following the installation of the borehole monitoring cable, the cable connectors were protected against dust and water. Background resistivity was measured. For each measurement, an infinite remote electrode was first inserted at a sufficient distance from the borehole mouth (generally greater than 250 m). The cable connector at the borehole collar was connected to the resistivity base station, which was linked to the main resistivity meter. Rock resistivity was measured after setting the parameters. As the coal mining face gradually advanced close to the borehole mouth, the cable was damaged and severed due to mining-induced effects. Then, the monitoring operation terminated. Figure 11 presents the field implementation.

Fig. 11

Field data collection. (a) Electrode installation, (b) Data acquisition.

Original data were processed using the high-density Wenner three-pole resistivity method after data acquisition. The calculation results were imported into software Surfer to generate inversion maps. These resulting inversion maps were then compared with geological profile maps to observe the resistivity of rock strata at different locations.

Electrical prospecting results

Figure 12a shows the scenario when the working face has advanced to a position 201 m from the borehole collar. Based on a comprehensive analysis of mining-induced stress propagation characteristics and field measurement data, mining activities have not affected the floor strata within the borehole monitoring zone. Measured apparent resistivity ranges from 800 to 1,000 Ω·m, serving as a baseline reference. This profile provides a reliable background value for the entire detection process.

Anomalous electrical characteristics appear when the working face advances to a position 97 m from the borehole collar in the profile. These anomalies are observed in the lower and middle sections at the periphery of the borehole control zone, specifically 10 to 15 m below floor. Apparent resistivity increases to 1200-1500 Ω·m (Fig. 12b). This increase is attributed to the accumulation of rock mass damage and the expansion of fracture networks caused by the advanced mining-induced stress.

Figure 12c reveals the resistivity response characteristics when the working face is 65 m away from the borehole collar. Apparent resistivity reaches 2500-3000 Ω·m at the mid-lower edge of the borehole control range. The floor strata experience tensile-shear coupled fracturing under mining, forming a distinct fracture zone³¹.

Fig. 12

Resistivity observation results.

The resistivity of the rock strata increased beneath the coal seam floor within the depth of 0–14 m when the working face is 36 m away from the borehole (Fig. 12d, e). Resistivity surges to 4,100 Ω·m in localized areas. Rock mass in this zone experiences extensive fracturing due to mining-induced stress, which develops a dense fracture network. Resistivity ranges from 1,600 to 3,000 Ω·m within the depth of 14–19.6 m. Fractures within the rock strata are widespread, yet remain largely unconnected.

Rock mass exhibits a significant anomalous zone as the working face advances to a position 16 m from the borehole collar (Fig. 12f). This area is induced by mining disturbance and occurs at the depth of 0–19.6 m below working face floor. This electrical response characteristic is consistent with the development of mining-induced fractures in floor rock mass. This area can be classified as a floor failure zone. Rock strata beneath the working face stabilize after initial failure during the later stages of coal seam extraction. The apparent resistivity profiles exhibit certain similarities.

Based on the apparent resistivity profiles in different stages, floor within the monitoring range is affected by advanced abutment pressure when the working face advances to about 140 m from the borehole collar. The electrical resistivity of the shallow rock strata in floor increases, accompanied by the development of fractures. The resistivity of the deeper rock strata in floor continues to rise as the working face advances. Resistivity reaches approximately twice the background value at the depth of 19.6 m below floor, confirming the maximum depth of floor failure.

Conclusion

• (1) Based on the theory of ground pressure and strata control, the failure mechanism of the floor strata was analyzed under caving gangue and the abutment pressure ahead of the working face. The failure of the floor strata was driven by the cyclic loading and unloading inherent to the compression-dilation-compression cycle.

• (2) According to the theory of an elastic half-plane, stress distribution within the floor strata exhibited significant non-uniformity. This failure was mainly induced by shear stress, with concentrated stress zones predominantly located near the working face.

• (3) The theoretical model based on the plastic slip line field in the floor strata yielded a plastic zone width of 15.67 m at the coal edge and the maximum failure depth of 19.55 m. This theoretical depth was closely matched by the in-situ parallel electrical survey result of 19.6 m, validating the reliability of the theoretical analysis.