Research on the performance inspection of large-span cable-stayed bridges under multi-physics field information guidance

Abstract

The temporal degradation of mechanical performance in large-span bridges necessitates the precise updating of Finite Element model parameters to guarantee accurate safety assessments and service life predictions. However, existing deep learning-based updating methodologies predominantly rely on single-physical-field inputs and assume homogeneous data topologies, thereby failing to capture complex, high-order mechanical interactions across heterogeneous physical domains. To overcome these limitations, this study proposes the Integrating Multi-Physical-Field Encoding Heterogeneous Graph Neural Network (IMPFE-HGNN). This novel architecture explicitly models the heterogeneous topology among strain, deflection, temperature, cable force, and acceleration sensors via meta-path subgraphs and relationship-aware encodings, enabling the extraction of high-order multi-physics semantics inaccessible to traditional architectures. Validated through a case study on a long-span cable-stayed bridge, the IMPFE-HGNN demonstrates substantial efficacy in parameter identification, yielding maximum correction rates of 43.33% for Poisson’s ratio and 10.20% for elastic modulus. Consequently, the predictive fidelity of the updated FE model is significantly enhanced: strain prediction error is reduced by a median of 61.4% (peaking at 77%), while deflection prediction accuracy improves by a median of 72.8% (peaking at 87%). Ablation studies substantiate the critical contributions of meta-path subgraphs and relationship encoding mechanisms, while sensitivity analyses determine optimal hyperparameters, identifying a meta-path length of 5 and a feature-mapping dimension of 128. Overall, this study presents a physically interpretable heterogeneous GNN paradigm for multi-source data fusion, offering a robust and precise framework for the structural performance assessment of long-span cable-stayed bridges.

Introduction

The American Society of Civil Engineers’ 2021 Report Card for America’s Infrastructure¹ assigned a grade of C to bridges, indicating that over 42% of bridges in the United States have surpassed their intended service life of 50 years, with 7.5% categorized as structurally deficient. Bridges, as critical components of transportation infrastructure, support economic activities and ensure public safety by continually bearing traffic loads during operation. This continuous loading makes them vulnerable to performance degradation and fatigue damage². Degradation and fatigue damage in bridges pose significant challenges, potentially resulting in service interruptions, increased maintenance costs, and catastrophic failures. Accurately identifying the actual stress state of bridge structures is fundamental for further analyses. A precise evaluation of their operational condition is crucial for ensuring safety and longevity. Regular performance assessments offer essential scientific and engineering insights for safety evaluations, life-cycle analysis, maintenance decision-making, and optimized design³.

Cable-stayed bridges are a prevalent type of long-span bridge and are central to major infrastructure projects globally. Due to the substantial traffic loads and complex environmental conditions endured during operation, cable-stayed bridges are prone to damage accumulation, which can lead to significant safety risks⁴. Currently, the primary methods for assessing the operational state of cable-stayed bridges include^5,6,7,8: visual inspection, structural inspection based on design codes, load testing, reliability-based analytical hierarchy process (AHP), and computer simulation combined with expert system evaluation. The visual inspection method is straightforward and cost-effective, allowing for the identification of visible defects. The structural inspection method based on design codes ensures adherence to engineering standards. Load testing provides direct insights into bridge performance under actual conditions. The Analytical Hierarchy Process (AHP) based on reliability theory integrates expert judgment with quantitative data. Computer simulation and expert system evaluation offer advanced analytical capabilities for a comprehensive assessment. These traditional methods often encounter challenges such as high labor intensity and subjectivity, making it difficult to detect internal or latent damage. Additionally, they typically lack real-time monitoring and comprehensive analysis capabilities, which are essential for addressing the dynamic and complex nature of cable-stayed bridges.

Finite element models (FEMs) of bridges are commonly used in computer simulations⁷. Despite their widespread application, these models often suffer from inaccuracies due to simplifications and assumptions. To address these inaccuracies, matrix correction and element correction techniques have been proposed⁹. Finite element model updating techniques, developed in the late 1970s, aim to minimize error functions through optimization, thereby reducing the discrepancy between model outputs and measured data¹⁰. In 1983, Berman et al.¹¹ introduced the matrix correction method, which focuses on adjusting the global structural matrix. However, this method can result in ill-conditioned solutions due to modifications made to the overall matrix. In 1985, Kabe¹² proposed the element correction method, which uses element correlations to adjust matrix elements or design parameters, addressing the limitations of matrix correction. While matrix correction may lead to ill-conditioned solutions and element correction remains complex and computationally intensive, artificial neural networks (ANNs) have emerged as a promising approach that combines the benefits of both techniques¹³. Despite this advancement, achieving high accuracy and robustness remains challenging. Deep learning algorithms, such as Long Short-Term Memory (LSTM) networks, Convolutional Neural Networks (CNNs), and Gated Recurrent Units (GRUs), have demonstrated potential in updating FEMs for bridges^14,15,16,17. Recent efforts have further explored advanced AI integration, including Genetic Algorithm-Based model updating within real-time digital twin environments¹⁸, and machine learning approaches leveraging Ground Vibration Test data for FEM correction¹⁹. In addition to model updating, machine learning methods are increasingly being deployed for direct structural capacity assessment, such as the prediction of the shear capacity of hollow-core RC piers²⁰, demonstrating their wide utility in structural engineering and performance evaluation. These models are adept at handling large datasets and capturing complex nonlinear relationships. However, current research often focuses on single-physical field information, which limits the comprehensiveness and accuracy of updates. There is a need for methods that integrate multi-physical field data to more accurately capture the complex behavior of bridge structures.

To address these challenges, this study proposes the Integrating Multi-Physical Field Encoding Heterogeneous Graph Neural Network (IMPFE-HGNN). The novelty of the proposed IMPFE-HGNN lies in its ability to explicitly model the multi-physical-field correlations and heterogeneous structural relationships that cannot be represented by traditional deep learning architectures such as ANN, CNN, LSTM, or Transformer-based FE updating models. Conventional neural networks treat monitoring data as uniformly structured inputs—typically vectors, images, or sequences—and thus implicitly assume homogeneous data topology. This assumption fails for long-span cable-stayed bridges, where strain, deflection, temperature, cable force, and acceleration sensors form a heterogeneous, relation-rich measurement network governed by distinct mechanical mechanisms. In contrast, the IMPFE-HGNN introduces three innovations: (1) Heterogeneous graph representation of multi-physics fields. While ANN/CNN/LSTM/Transformer models learn only from numerical sequences or grids, IMPFE-HGNN embeds structural mechanical properties and diverse sensor types into a heterogeneous graph. Each edge type encodes a physical relationship (static, dynamic, thermal, or force-related), allowing the model to preserve the underlying mechanical topology that cannot be captured by traditional architectures. (2) Meta-path subgraph encoding to capture cross-field semantic dependencies. Existing FE updating models rely on single-field input (e.g., only strain, only vibration, or only deflection) and therefore treat correlations across physical fields as noise. The proposed meta-path subgraphs explicitly aggregate higher-order mechanical interactions. This enables IMPFE-HGNN to learn how physical fields jointly influence FE parameters, rather than fitting isolated sensor responses. (3) Relationship-aware encoding to distinguish heterogeneous mechanical mechanisms. Traditional models conflate multiple physical processes into a single latent vector. The relationship encoder in IMPFE-HGNN assigns unique learnable vectors to different physical-field pathways, preventing semantic mixing between thermal, elastic, dynamic, and geometric influences. This directly improves parameter identifiability and avoids the information loss that plagues single-field or homogeneous-network models. These innovations collectively allow the IMPFE-HGNN to integrate multi-source sensing data while maintaining the physical meaning of structural interactions.

  Problem statement

Throughout a bridge’s service lifecycle, performance detection and monitoring involve the use of various types of sensors. Even though each sensor operates within different physical fields, they are closely related to the structural mechanical properties. This relationship creates connections between sensors across various physical fields, forming a complex network of physical field interactions. This network encompasses multiple types of nodes and edges, and even within the same pair of nodes, multiple types of interactions may coexist simultaneously. As illustrated in Fig. 1, the force field and strain field are directly related to structural static properties such as the elastic modulus and Poisson’s ratio of materials. The temperature field is related to structural static properties such as thermal conductivity and also affects the distribution of the strain field. The displacement field and acceleration field, on the other hand, are associated with structural dynamic properties such as mass, stiffness, and damping. Furthermore, the force field, strain field, temperature field, displacement field, and acceleration field interact with each other, forming a multi-layer heterogeneous network.

Fig. 1

Heterograph relationship between different sensors and structural mechanical properties.

This paper precisely captures the specific relationships between different sensors and structural mechanical properties, which can be represented through the edges of a graph neural network. These edges possess clear directionality, signifying that different sensors function solely within specific physical fields and are directed towards particular mechanical properties of the material or structure. Nonetheless, due to the numerous mechanical indicators employed to describe materials or structures and the coupling effects between physical fields, accurately capturing these interactions remains challenging. For instance, the uneven distribution of the temperature field can result in changes to properties such as the elastic modulus and Poisson’s ratio of materials, which in turn can impact the measurement of force and strain fields. These alterations can further influence material properties like stiffness and damping, ultimately impacting the measurement of displacement and acceleration fields. These coupling effects can be described through the edges of a graph neural network and the multi-layer heterogeneous network. Consequently, this paper proposes an Integrating Multi-Physical Field Encoding Heterogeneous Graph Neural Network (IMPFE-HGNN) for more accurate updating of finite element models.

This paper takes a cable-stayed bridge as a case study, a structure that has undergone long-term health monitoring. Due to the extended service life of the bridge, its mechanical properties have degraded, necessitating a performance assessment through load testing and the concurrent updating of its finite element model to more accurately monitor the bridge’s health status. By proposing an Integrating Multi-Physical Field Encoding Heterogeneous Graph Neural Network (IMPFE-HGNN), this paper corrects the finite element model parameters, including the elastic modulus and Poisson’s ratio of the concrete, the elastic modulus and Poisson’s ratio of the main girder steel, and the elastic modulus of the stay cables. This approach enables more precise monitoring of the bridge’s structural health.

Methodology

  Preliminaries

• (1) Heterogeneous Graph²¹: A heterogeneous graph is a graph =(,,,,,) composed of multiple types of nodes and edges, where V and A are the sets of nodes and node types, respectively, and :→ is the mapping function from nodes to their types. E and R represent the sets of edges and edge types, respectively, and :→ is the mapping function from edges to their types, with ||+||>2. Figure 2a illustrates the multi-physical field information network represented by the monitoring data of the long-span cable-stayed bridge used in this study. Essentially, this network is a heterogeneous graph that includes nodes representing structural static properties, structural dynamic properties, cable force sensors, stress sensors, strain sensors, displacement sensors, and acceleration sensors. There are various relationships among these nodes. For instance, there are static relationships between cable force sensors, stress sensors, strain sensors and structural properties, as well as dynamic relationships between displacement sensors, acceleration sensors and structural properties.

• (2) Meta-Path: The meta-paths typically capture the rich physical field semantics of a heterogeneous graph. A meta-path P can represent a composite relationship that connects multiple types of nodes²². For example, for $\:{c}_{1}\underrightarrow{{e}_{1}}{c}_{2}\underrightarrow{{e}_{2}}\cdots\:\underrightarrow{{e}_{l}}{c}_{l+1}$, the composite relationship between node types $\:{\text{c}}_{\text{1}}$ and $\:{\text{c}}_{\text{l}\text{+1}}$ can be denoted as $\:e={e}_{1}\circ\:{e}_{2}\circ\:\cdots\:\circ\:{e}_{l}$. Figure 2b shows the meta-path CSS, which indicates that different types of sensors (cable force sensors, strain sensors) are controlled by the same structural static property (elastic modulus). A meta-path instance is an actual continuous sequence of nodes extracted from the heterogeneous graph, defined according to the meta-path.

• (3) Meta-Path Subgraph: For a node v in a heterogeneous graph, $\:{P}_{\varphi\:\left(v\right)}$ denotes the set of meta-paths originating from the node type $\:\varphi\:\left(\nu\:\right)$. Given a meta-path $\:P\in\:{P}_{\varphi\:\left(v\right)}$, the meta-path subgraph of node v can be defined as $\:G=({V}_{v}^{P},{E}_{v}^{P},\varphi\:,\phi\:)$, which represents the local graph structure comprised of all meta-path instances corresponding to P. Essentially, a meta-path subgraph extracts substructures from the heterogeneous network to more comprehensively capture the network’s rich physical field semantic information. Figure 2c illustrates the subgraph corresponding to the meta-path SCSSD, with structural static properties (elastic modulus) as the starting point. This subgraph represents the structural static properties (elastic modulus, Poisson’s ratio) obtained through the involvement of different sensor types (cable force, strain, displacement, stress sensors). Compared to repetitively mining multiple meta-paths, the subgraph captures complete structural static information while reducing information redundancy.

• (4) Heterogeneous Graph Embedding: Given a heterogeneous graph G, the purpose of heterogeneous graph representation learning is to learn a mapping function $\:V\to\:{\mathbb{R}}^{d},d\ll\:\left|V\right|$ that maps different types of nodes into a low-dimensional vector space, enabling different network analysis tasks to be completed based on these low-dimensional dense vectors.

Fig. 2

Multi physical field heterogeneous graph and meta-path examples.

Integrating multi physical field encoding heterogeneous graph neural network

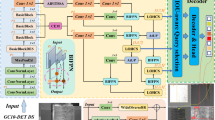
This paper proposes Integrating Multi Physical Field Encoding Heterogeneous Graph Neural Network (IMPFE-HGNN). The model framework is shown in Fig. 3. Specifically, firstly, node feature transformation is performed through a linear layer. According to the predefined fixed length, all meta-paths corresponding to the target node type are selected, and subgraphs are constructed respectively to perform feature propagation. A lightweight mean aggregator is used to obtain the physical field semantic representations under different meta-path subgraphs. Relationship encodings are learned for each meta-path and added to the physical field semantic representation of the target node. Feature mapping transformation of node representations is performed through a multilayer perceptron to enhance the expressive ability. Finally, the target node representations under different physical field semantic views are fused to obtain the node embedding vector applied to downstream tasks.

Fig. 3

Integrating multi physical field encoding heterogeneous graph neural network.

Model explanation

• (1) Node Feature Transformation.

In a heterogeneous graph G, attributes of different node types have different characteristics. For example, in a physical field network, different physical field types are used to describe physical field nodes, and elastic modulus, Poisson’s ratio, mass, stiffness, damping, etc. are used to describe structural mechanical property nodes. In addition, different node types may have different feature vector dimensions. To eliminate the heterogeneity of attribute information, it is necessary to perform linear transformation on node feature vectors to project them into the same vector space and maintain the same vector dimension. The feature vector of node v of type $\:\varphi\:\left(\nu\:\right)$ after projection is represented as:

$${h^{\prime}_v}={W_{\phi (v)}} \cdot {h_v}$$

(1)

Where $\:{h}_{v}^{{\prime\:}}\in\:{\mathbb{R}}^{d}$, $\:{h}_{v}\in\:{\mathbb{R}}^{{d}_{\varphi\:\left(\nu\:\right)}}$ is the original feature, and $\:{W}_{\varphi\:\left(\nu\:\right)}\in\:{\mathbb{R}}^{d\times\:{d}_{\varphi\:\left(\nu\:\right)}}$ is a learnable parameterized weight matrix corresponding to the node type.

• (2) Meta-Path Subgraph Construction.

According to the meta-path $\:P\in\:{P}_{\varphi\:\left(v\right)}$ corresponding to the node type $\:\varphi\:\left(\nu\:\right)$, this paper constructs the meta-path subgraph $\:{G}_{v}^{P}$ centered on the target node v. It describes the local graph structure connected to the target node through all meta-path instances corresponding to the meta-path P. Meta-paths of different types and lengths express different physical field semantic information. All meta-paths shorter than a specific length are used to extract information, but this approach may have the problem of physical field semantic overlap²³. Therefore, in order to reduce the redundant computation of information caused by short meta-paths being covered by long meta-paths and avoid the dependence of meta-path selection on human prior knowledge, this paper selects all meta-paths of a predefined fixed length²⁴. Taking the data set in this paper as an example, some representative meta-paths under the target type nodes are shown in Table 1.

Table 1 Part of the path statistics for partial length elements.

• (3) Lightweight Mean Aggregator.

In order to achieve multi-path message passing in the meta-path subgraph $\:{G}_{v}^{P}$, it is necessary to calculate and aggregate node features according to different meta-path relationships. To reduce computational overhead, this paper avoids complex attention operations and adopts an efficient mean calculation method²⁵ to fuse features of different physical field semantic relationships. It gradually aggregates all node features in the subgraph layer by layer from the end of the meta-path in the subgraph to the target node, more comprehensively retaining the structure and physical field semantic relationships between nodes. To strengthen the interaction between nodes of different meta-paths, the feature transfer between nodes of the same relationship type in the subgraph is carried out simultaneously. In this way, information loss caused by only aggregating neighborhood nodes of the same type as the target node can be avoided²⁶, feature interaction between meta-path nodes is carried out in advance, and the message passing process is accelerated. Finally, the feature information in the subgraph is transmitted to the target node along the meta-path, and the node representation is updated according to the aggregated result and its own features. For node v at layer l, the node representation based on meta-path P is:

$$h_{{v,P}}^{l}=MEAN(G_{v}^{P},\left\{ {h_{t}^{{l - 1}},\forall t \in G_{v}^{P}} \right\})$$

(2)

where each $\:{h}_{v,P}^{l}$ contains the physical field semantic feature information of the target node v under the corresponding subgraph $\:{G}_{v}^{P}$ of the meta-path $\:P\in\:{P}_{\varphi\:\left(v\right)}.$

• (4) Meta-Path Relationship Encoder.

The method of obtaining node representations using a lightweight mean aggregator greatly reduces computational overhead but may eliminate the distinct features of nodes. At the same time, as the network depth and the length and type of meta-paths increase, repeated aggregation of neighborhood features by the target node may lead to physical field semantic confusion, making it difficult to distinguish different nodes. Therefore, after feature aggregation of the meta-path subgraph, this paper designs a set of relationship-aware encoders to learn relationship encodings $\:\left\{{R}_{P}^{Enc},P\in\:{P}_{\varphi\:\left(v\right)}\right\}$ for the meta-paths corresponding to the target node and combine them into the target node representation, which can be expressed as:

$$h_{{v,P}}^{{l^{\prime}}}=h_{{v,P}}^{l} \oplus R_{P}^{{Enc}}$$

(3)

where $\:{R}_{P}^{Enc}\in\:{\mathbb{R}}^{d}`$, ⊕ indicates adding the relationship encoding to the target node representation. Different from learning encoding representations for each type of relationship in the meta-path separately²⁷, in order to integrate the global features of meta-path nodes and reduce the computation amount, this paper learns relationship encodings for the entire meta-path and combines it with the target node representation under the corresponding meta-path.

• (5) Feature Mapping.

The physical field semantic vectors under different meta-paths may have different dimensions or be located in different data spaces. This paper uses a Multi-Layer Perceptron (MLP) to design the corresponding feature mapping layer to learn the mapping transformation relationship for the physical field semantic representation under the meta-path P corresponding to the target node v, and map the physical field semantic vector fused with the relationship encoding to the same feature space. Specifically, this paper first uses a fully connected feedforward neural network for linear transformation, followed by a LeakyReLU activation function layer and a Dropout layer to improve the nonlinear expression and generalization ability of the model, and then connects a fully connected layer to transform the output into the target dimension. The feature mapping layer can be expressed as:

$$\tilde {h}_{{v,P}}^{l}=MLP(h_{{v,P}}^{{l^{\prime}}})$$

(4)

• (6) Physical Field Semantic Fusion.

Through the previous steps, the target node v obtains a set of vector representations under different meta-path physical field semantic views $\:\left\{{\stackrel{\sim}{h}}_{v,P}^{l},\forall\:P\in\:{P}_{\varphi\:\left(v\right)}\right\}$. The meta-path-based method needs to fuse these vectors to obtain the final representation of the node. In order to adaptively distinguish the importance of different meta-path relationships, this paper multiplies the learnable weight parameters with the node representation under the corresponding meta-path subgraph and adds the results correspondingly to perform linear fusion of the node representation, which is expressed as:

$$\tilde {h}_{{v,{P_{\phi (v)}}}}^{l}=\sum\limits_{{P \in {P_{\phi (v)}}}} {{W_P} \cdot } \tilde {h}_{{v,P}}^{l}$$

(5)

where $\:{W}_{P}\in\:{\mathbb{R}}^{d}$ is a learnable weight parameter that reflects the degree of influence of the physical field semantic relationship of the corresponding meta-path on the final node representation.

  Experimental dataset

Basic information

The experimental data set in this paper comes from a cable-stayed bridge with a hybrid structure of steel box girder and P.C. box girder. The bridge is 3,500 m long and 30 m wide, with six lanes in both directions. There are sightseeing sidewalks on both sides of the main bridge, and the main span has a navigation clearance of 38 m. The main bridge of the bridge is a cable-stayed bridge with a hybrid structure of orthotropic plate steel box girder and P.C. box girder in a high-stress amplitude tension-anchored semi-floating system with a double tower and double cable planes. The span combination is: 47 m (P.C. box girder) + 47 m (P.C. box girder) + 100 m (steel box girder) + 518 m (steel box girder) + 100 m (steel box girder) + 47 m (P.C. box girder) + 47 m (P.C. box girder). The main bridge is 2,940.724 m long, of which the cable-stayed bridge is 906 m long, the north main approach bridge is 880.95 m long, and the south main approach bridge is 615.15 m long.

Monitoring dataset

This cable-stayed bridge leverages intelligent sensing, the internet of things, cloud computing, and big data to oversee the structural health. Employing cloud computing and big data analytics alongside internet connectivity and data management protocols, the system provides real-time surveillance of critical bridge components and their health, promptly identifying hazardous states and issuing alerts. Integrating real-time data analysis with routine inspections shifts monitoring from a reactive to a proactive stance, thereby enhancing operational precision and elevating the standardization and intelligent management of bridge infrastructure. The bridge’s structural safety and operation monitoring system encompasses several key components.

• (1) Environmental temperature: The system facilitates temperature measurement across diverse operational environments by tracking the distribution of various thermometers and the variance in temperature and humidity. This methodology enables continuous temperature monitoring throughout different seasons and time frames. Parameters including temperature, humidity, thermal stress, water quality, and soil conditions are monitored in real time. Such comprehensive surveillance aids in forecasting the implications of climate change on the mechanical integrity of bridge structures.

• (2) Vehicle load: Including vehicle load, vehicle usage load, and traffic flow. Buried piezoelectric sensing devices are used to obtain the time history of traffic loads, and cameras and flashing devices are set up to monitor vehicle driving speed, flow, and emergencies.

• (3) Bridge structure response: Seismic response analysis of piers is carried out to study aspects such as pier displacement, deformation, and dynamic response. Displacement and deformation monitoring is applied to the lateral and longitudinal displacement, inclination, and structural deformation monitoring of important bridge components. Sensors used include displacement meters, inclinometers, electronic imagers, and electronic rangefinders. In the dynamic response of bridge structures, it involves the force distribution and changes of members, the dynamic deformation and dynamic rotation of the structure, the acceleration value of structural response, the dynamic relative displacement of expansion devices or supports, and other contents. The sensors mainly used include force measuring elements (such as force rings, magnetoelastic elements, etc.), strain elements, and acceleration elements.

Finite element modeling and load test dataset

• (1) Finite Element Model Description.

The finite element model of the cable-stayed bridge was developed in SAP2000 v15, employing specific element formulations to ensure structural fidelity. The main girder was simulated using frame elements based on Timoshenko beam theory to account for shear lag and warping in the orthotropic steel box, while the towers utilized variable-section frame elements to reflect their tapered reinforced concrete geometry. The stay cables were modeled as tension-only truss elements, with the P.C. approach spans represented by shell elements to handle membrane-bending coupling. To authentically replicate the structural boundary conditions, the tower bases were fully fixed, and the girder-tower connection was modeled as a semi-floating system constrained vertically and laterally but free to slide longitudinally. Side-span bearings were configured with appropriate longitudinal sliding and transverse guidance, and the full-bridge model was employed without symmetry constraints to address asymmetric stiffness distributions.

Regarding the analysis settings, while material nonlinearity was excluded due to the elastic nature of the load tests, geometric nonlinearity was rigorously incorporated. The analysis utilized SAP2000 P-Δ formulation under nonlinear static load cases to capture large displacement effects and the stress-stiffening of the stay cables. This configuration ensures that the simulation accurately reproduces both the global geometric stiffness changes and the local deformation behaviors observed during testing, providing a reliable baseline for the IMPFE-HGNN updating process.

• (2) Load Test Dataset

This cable-stayed bridge has been under long-term health monitoring. Due to the relatively long working time of the bridge, the mechanical properties of the structure have degraded. Therefore, load tests are needed to conduct performance detection on the bridge and simultaneously update the finite element model to more accurately monitor the health of the bridge. The bridge space structure finite element analysis software SAP2000 V15 is used for modeling and analysis. The main girder of the whole bridge is simulated by beam elements, and the stay cables are simulated by truss elements. The model has a total of 1205 nodes and 751 elements. For long-span cable-stayed bridges, deformation-sensitive parts such as the main girder, main tower, stay cables, and main span should be observed emphatically. According to the live load internal force and displacement envelope diagram of the bridge span structure, the test sections such as the maximum bending moment, maximum deflection section of the main girder structure, and the maximum bending moment and maximum longitudinal displacement of the main tower are determined. From this, the strain (stress) and displacement test sections are determined. According to the actual engineering situation of the bridge and the analysis results of the most dangerous sections of the finite element, combined with the requirements of relevant bridge test specifications, 13 × 2 test sections are selected for testing, show in Fig. 4. The specific test parameters include: the maximum positive bending moment and deflection of the main girder of the 1# side span (section I-I), the maximum negative bending moment of the main girder at the top of the 1# auxiliary pier (section II-II), the maximum positive bending moment and deflection of the main girder of the 2# side span (section III-III), the maximum negative bending moment of the main girder at the top of the 2# auxiliary pier (section IV-IV), the maximum positive bending moment and deflection of the main girder of the 3# side span (section V-V), the maximum negative bending moment of the main girder at the top of the 3# auxiliary pier (section VI-VI), the maximum positive bending moment and deflection of the main girder at 1/4 span of the middle span (section VII-VII), the maximum positive bending moment and deflection of the main girder at 1/2 span of the middle span (section VIII-VIII), the negative bending moment of the main girder near pier RZ4# in the middle span (section X-X), the most unfavorable bending moment of the 1# main tower (section XI-XI), the maximum offset of the top of the 1# main tower (section XII-XII), and the maximum cable tension under live load of the stay cables.

Fig. 4

Schematic diagram of the arrangement of important sensors.

• (1) Layout of strain sensor measuring points for the main girder.

  The strain of a bridge structure reflects its overall and local safety status. Each component directly bears the action of vehicle loads. Under the action of vehicle loads, local stresses will occur in each component of the bridge. Therefore, dynamic monitoring of relevant sections of the bridge deck is needed. According to the results of finite element model analysis, measuring points are set at 1/4 span, mid-span, 3/4 span of the main span, and mid-span of the auxiliary span. The strain monitoring of the main girder is shown in Fig. 4.

• (2) Layout of measuring points for main girder deflection and tower displacement.

  The change in the position of the tower top can reflect the deformation of the structure under the action of live loads and wind loads. The change in the height of the tower top can reflect the change in the settlement of the foundation at the lower layer of the structure. The height of the main girder and the transverse and longitudinal displacements of the bridge play an important role in the stress analysis of the bridge. On this basis, GNSS technology is used to conduct dynamic three-dimensional displacement monitoring of the top of the main tower. Through finite element model analysis, it is found that the maximum deflection value of the main girder appears at the mid-span position. Therefore, 12 measuring points are arranged at the main span to measure the deflection of the main girder, and 14 measuring points are arranged at the side span. One measuring point is arranged on each bridge tower. The layout diagram of measuring points for main girder deflection and bridge tower displacement is shown in Fig. 4.

• (3) Layout of vibration measuring points.

  As can be seen from the calculation results of the finite element model, the instability of the steel cable will cause the instability of the natural vibration frequency of the bridge, and the instability of some structures will cause the destruction of the bridge. By monitoring the vibration status and dynamic characteristics of the bridge, the overall health status of the bridge can be understood macroscopically. This load test uses a force-balanced accelerometer that can monitor the vertical vibration of the bridge in real time. Therefore, a total of 9 measuring points are arranged at the mid-span of the side span, mid-span of the main span, and 1/4 span of the main span, as shown in Fig. 4.

• (4) Layout of cable force sensors.

  Stay cables are important carriers of cable-stayed bridges and play an important role in the main girder and tower of cable-stayed bridges, and at the same time bear static loads. When there is a difference between the actual bearing capacity of the stay cable and the preset bearing capacity, an interrelated force will be formed between the cable-stayed bridge and the tower, and this force will directly affect the deformation of the superstructure. The cable force of stay cables is the internal force of cable-stayed bridges under various working conditions and is an important index for evaluating its safety and bearing capacity. Through the cable force detection of the whole bridge, this load test can effectively evaluate the durability of steel cables. According to finite element model analysis, a total of 12 measuring points are determined to be arranged on the outermost, innermost, and eighth cables of the bridge tower, as shown in detail in Fig. 4.

Sensor data preprocessing

To ensure data quality and temporal consistency across the multi-physical field inputs, the following preprocessing protocols were strictly applied:

• (1) Time synchronization of raw monitoring data. To strictly enforce temporal consistency across heterogeneous data streams, the bridge is equipped with a unified data acquisition platform synchronized by a GPS-disciplined clock. All sensor inputs—spanning strain, acceleration, GNSS displacement, cable force, and temperature—are tagged with absolute timestamps. These multi-rate data streams were subsequently aligned to a unified temporal grid via linear interpolation. Furthermore, high-frequency dynamic signals (e.g., 100–200 Hz acceleration data) were downsampled to match the sampling rate of low-frequency static sensors (e.g., 1 Hz GNSS data). This process ensures that all modalities share synchronized time indices, which is foundational for capturing meaningful physical correlations via meta-path subgraphs in the IMPFE-HGNN.

• (2) Noise filtering and preprocessing. Noise removal was applied to both monitoring and load-test datasets prior to being fed into the IMPFE-HGNN. For strain and cable-force data, a zero-phase 4th-order Butterworth low-pass filter was used to eliminate high-frequency electrical noise and short-term spikes. Acceleration signals were denoised using a band-pass filter (0.1–20 Hz) corresponding to the structural vibration bandwidth. For GNSS displacement data, a moving-average smoothing window (3–5 s) was applied to reduce multipath interference. Temperature readings, which naturally exhibit slow variations, were processed using an outlier-removal step based on median absolute deviation (MAD). After filtering, all signals were normalized using z-score scaling to ensure uniform magnitude across physical fields.

  Finite element model correction based on IMPFE-HGNN

This paper employs bridge monitoring and load test data as inputs for the model, which uses the elastic modulus E₁ and Poisson’s ratio µ₁ of C50 concrete, as well as the elastic modulus E₂ and Poisson’s ratio µ₂ of main girder steel D345, and the elastic modulus E₃ of the stay cables as the target outputs. The model is developed utilizing the PyTorch framework. To mitigate overfitting, early stopping with a patience of 50 epochs is employed, alongside a learning rate of 0.005 and a dropout rate of 0.5. To ensure a level playing field for comparison, all models are configured with identical hyperparameters, and the preprocessing of input data adheres to a uniform format. The reported experimental outcomes are averages derived from multiple iterations.

Parameter correction

• (1) Parameter selection.

There are many factors that affect the calculation results of the finite element model. Through the empirical method and sensitivity analysis, five parameters that need to be corrected are selected: concrete elastic modulus E₁, concrete Poisson’s ratio µ₁, main girder steel elastic modulus E₂, main girder steel Poisson’s ratio µ₂, and stay cable elastic modulus E₃. The finite element model parameters and parameter values are shown in Table 2. In order to obtain a considerable number of training samples, according to design data and specifications, in this test, the values of each parameter are limited to a certain interval range and 10 value levels are set within the interval range. According to the uniform design rule, this test can be regarded as a uniform design table with 5 factors and 10 levels. Performing 20 finite element model calculations can obtain the required training samples. The finite element model is shown in Fig. 5 and (Table 2).

Fig. 5

Finite element model of cable-stayed bridge.

Table 2 Main parameters of sap 2000 fe model information

• (2) Implementation Details and Model Training.

To ensure reproducibility and a rigorous evaluation of the proposed IMPFE-HGNN method, the entire implementation and training protocol were standardized. The model was developed using the PyTorch 1.13 framework and executed on an NVIDIA RTX 3090 GPU. Training utilized the Adam optimizer ($\:\eta\:$ =0.005, β₁ = 0.9, β₂ = 0.999), with a consistent batch size of 32 maintained across all experiments. The dataset, comprising FE-generated samples and field-measured responses, was partitioned into three mutually exclusive subsets: 70% for training, 15% for validation, and 15% for independent testing. To effectively mitigate overfitting, the model was trained for a maximum of 5,000 epochs, incorporating an early-stopping mechanism with a patience window of 50 epochs based on the validation loss. Crucially, the test set was strictly held out and specifically included field data from loading conditions not present in the training subset, thereby enabling an objective assessment of the model’s generalization capability. To ensure robust performance reporting, all configurations were executed through five independent runs with different random seeds, and the average results are reported in this study, with all prediction accuracy metrics derived solely from the outcomes of this independent test set.

• (3) Parameter correction.

Input the actual stress, strain, and main girder deflection obtained from the load test into the IMPFE-HGNN neural network algorithm trained by multiple training samples to calculate the improved values of the parameters to be corrected in the SAP2000 model, and compare before and after correction. The parameter correction results are shown in Table 3.

Table 3 Parameter modification results.

The parameter optimization outcomes reveal that in the SAP2000 finite element model, the parameter values significantly affect the model’s computational outcomes. Specifically, the Poisson’s ratio exhibits a notably larger error, with a maximum relative error of 43.33%. In contrast, the elastic modulus displays a comparatively minor error, with a maximum relative error of 10.20%. It is crucial to address the physical interpretation of the updated main girder steel Poisson’s ratio (µ₂), which reached a value of 0.43. The updated value here represents an effective global parameter rather than a pure material constant. The substantial deviation associated with the Poisson’s ratio is primarily attributed to the idealization of the complex material distribution and geometry during the finite element modeling. Specifically, the actual bridge utilizes an orthotropic plate steel box girder design, characterized by complex anisotropic stiffness behavior. However, the finite element model employed in this study simplifies the main girder using beam elements. Beam elements cannot fully capture the transverse stiffness, shear lag effects, and local deformation characteristics of a wide orthotropic box girder. Consequently, the IMPFE-HGNN algorithm compensates for these geometric simplifications and the unmodeled composite action by adjusting µ₂ to a higher “equivalent” value. This allows the simplified global model to accurately reproduce the transverse deformation and strain coupling observed in the multi-physics field sensor data.

• (4) Robustness analysis across varied span regions.

In the prediction of bridge deflection and strain, the application of the IMPFE-HGNN algorithm not only mitigates errors introduced by parameter selection but also demonstrates significant robustness across heterogeneous structural regions. This study compares the discrepancies between the finite element model’s predictions and the actual load test measurements for both main girder strain and deflection. To verify the model’s generalizability, the comparative analysis is structured to juxtapose the pre-correction errors with those post-correction by the IMPFE-HGNN algorithm, specifically categorizing the results into distinct span regions governed by different material properties and mechanical behaviors. The graphical representation of this comparative analysis for the main girder strain error is presented in Fig. 6, while Fig. 7 illustrates the comparative analysis of the main girder deflection error across these varied regions.

Fig. 6

Correction of four representative cross-sectional strain values.

In this paper, the strain values of four representative sections are taken as the analysis objects to evaluate the model’s performance under different structural characteristics. Specifically, Section I-I (1# side span) and Section III-III (2# side span) represent the Prestressed Concrete (P.C.) box girder segments, characterized by high stiffness and linear behavior; whereas Section V-V (3# side span) and Section VIII-VIII (mid-span) represent the orthotropic steel box girder segments, which exhibit greater flexibility and geometric nonlinearity. As can be seen from Fig. 6, there is a certain error in calculating the bridge deformation value by using the SAP2000 finite element modeling method, particularly due to the difficulty in simultaneously capturing the stiffness of both concrete and steel components. Before parameter correction, the difference between the bridge slab strain obtained by finite element calculation and the actual bridge load test is relatively large, reaching a maximum of 124.84 × 10^− 6; after parameter correction, the difference between the two is significantly reduced across both material types, as shown by the red solid line in the figure. At the same time, this paper compares the strain difference before and after parameter correction and finds that among the measuring points arranged at the sections, the bottom plate is more sensitive to parameter correction than the inclined bottom plate, with a maximum correction reaching 77%. This indicates that the IMPFE-HGNN is particularly effective in correcting the simulation of the bottom plate, which often experiences high strain levels and pronounced nonlinear mechanical behavior in both the P.C. and steel box girder regions.

.

Fig. 7

Correction of bridge deflection.

Through finite element model analysis, it is found that the maximum deflection value appears at the mid-span position dominated by the steel structure. Therefore, the analysis is stratified into two groups: 14 measuring points arranged at the side spans (P.C. box girders) and 12 measuring points arranged at the main span (steel box girder). This paper takes these 26 measuring points as the object to analyze the calculation error of bridge deflection under material heterogeneity. As can be seen from Fig. 7, before parameter correction, the difference between the FEM calculation and the actual load test is relatively large, reaching a maximum of 164.86 mm at 1/4 of the main span; after parameter correction, the difference is significantly reduced, as shown by the red solid line. As shown in the figure, the difference in bridge deflection measured at the side span (concrete) is smaller than that in the main span (steel) regardless of correction. This is because the steel box girder in the main span is more likely to exhibit strong geometric nonlinear characteristics in actual operation compared to the rigid concrete side spans. At the same time, this paper compares the deflection difference before and after parameter correction and finds that the proposed algorithm maintains high correction accuracy for the side span (P.C. region) while effectively handling the large deformations in the main span. It is mainly manifested in a greater difference before and after correction in the transition zones, and the maximum correction can reach 87%. This analysis demonstrates that while the main span presents greater challenges due to its flexibility, the IMPFE-HGNN algorithm shows strong robustness in coordinating the stiffness updates for both concrete and steel structural systems.

To provide a more rigorous evaluation of the model’s performance beyond peak values, we analyzed the error distribution across all sensor locations. Table 4 summarizes the global performance metrics, contrasting the maximum improvements with median values and error variance.

Table 4 Statistical evaluation of model prediction accuracy.

For strain (Fig. 6), while the maximum correction reached 77% at the bottom plate of the main girder where nonlinear effects are strongest, the median improvement across all monitored sections was 61.4%. The significant reduction in the Interquartile Range (IQR) of the error (from 45.20 to 12.15 µ_ε) indicates that the IMPFE-HGNN model effectively stabilizes prediction accuracy across different structural components. For deflection (Fig. 7), the analysis of 26 measuring points reveals consistent performance. Although the maximum correction of 87% was observed in the side span, the median improvement for the entire bridge was 72.8%. The post-correction RMSE dropped to 24.18 mm, demonstrating that the algorithm provides robust corrections not only for the highly nonlinear main span but also for the side spans, reducing the overall variability of the prediction errors.

• (5) Different Load Scenarios.

To rigorously validate the generalization capability of the proposed IMPFE-HGNN framework beyond standard operational conditions, a granular performance evaluation was conducted under two distinct load test scenarios: Symmetrical Loading and Asymmetrical Loading. These scenarios were specifically selected to impose fundamentally different mechanical states on the structure, ranging from global longitudinal bending dominated by vertical stiffness to complex localized torsional-flexural coupling induced by eccentric loads. The quantitative comparison between the field-measured responses, the initial finite element predictions, and the IMPFE-HGNN updated results is detailed in Tables 5, 6 and 7. This comparative analysis serves to verify the model’s fidelity in accurately capturing both the global deformation modes and local stress concentrations under heterogeneous load distributions.

The Symmetrical Loading scenario was designed to primarily investigate the global flexural stiffness of the main girder. Under this condition, the vehicular test loads were positioned symmetrically around the mid-span of the main cable-stayed section. This specific configuration induces the theoretical maximum positive bending moment within the girder, making it the most stringent test for evaluating the accuracy of the model’s assigned equivalent axial stiffness and flexural rigidity after initial parameter estimation. The primary focus of the evaluation in this scenario is the vertical deflection of critical cross-sections, particularly the mid-span.

Table 5 Deformation under symmetrical loading and the corresponding correction results.

As shown in Table 5, the analysis focuses on the mid-span deflection (Section VIII-VIII), where the maximum vertical displacement occurs under symmetrical loading. The field measurement recorded a deflection of -171.00 mm. The initial finite element model, suffering from inaccurate stiffness parameters, significantly overestimated the structural flexibility with a prediction of -251.50 mm. Following the parameter correction via IMPFE-HGNN, the predicted deflection converged to -180.44 mm, resulting in a relative error of only 5.52%. This validates the model’s accuracy in capturing global vertical stiffness under large-deformation symmetrical conditions.

The Asymmetrical Loading scenario was designed to impose a complex, coupled stress state, testing the model’s ability to handle localized and non-uniform structural responses. In this test, eccentric vehicular loads were specifically applied near Pier RZ4#, a region critical for generating maximum negative bending moments over the auxiliary pier and simultaneously inducing significant torsional coupling in the main girder section. Unlike the symmetrical case, this scenario demands that the IMPFE-HGNN accurately capture localized stiffness variations and the three-dimensional interaction between the girder and the auxiliary support.

Table 6 Deformation under asymmetrical loading and the corresponding correction results.

Table 7 Strain within the negative moment region under asymmetrical loading and the corresponding correction results.

Table 6 presents the results for the asymmetrical loading case, where loads were applied eccentrically near Pier RZ4#. This scenario induces complex coupling between bending and torsion. The critical observation point near the pier (Section X-X) recorded a measured deflection of -96.00 mm. The updated model predicted a value of -100.90 mm, corresponding to a relative error of 5.10%. To further verify the model’s fidelity under this complex stress state, the strain in the negative moment region of the auxiliary pier was analyzed show in Table 7. The corrected model achieved a high precision with a relative error of 4.77%, demonstrating the robustness of the IMPFE-HGNN in reproducing local mechanical behaviors under non-symmetrical loading.

Ablation experiment

To ascertain the efficacy of the IMPFE-HGNN algorithm, this paper performs ablation studies on node classification and link prediction tasks, introducing three modified versions: (1) IMPFE-HGNN without meta-path subgraphs (w/o MS), which omits the use of meta-path subgraphs and indiscriminately aggregates all node types within a specified proximity to the target node; (2) IMPFE-HGNN without relationship encoding (w/o RE), which excludes the encoding of relational information from the model; (3) IMPFE-HGNN without feature projection (w/o FP), which eliminates the feature mapping component of the original model. Concurrently, this study employs the Probability Density Function (PDF) to characterize the outcomes of the ablation experiments.

$$\:{\pi}_{\text{i}}\text{=PDF}\left\{\frac{{\text{y}}_{\text{i}}^{\text{ture}}\text{-}{\text{y}}_{\text{i}}^{\text{pred}}}{\text{max}\left(\left|{\text{y}}_{\text{i}}^{\text{ture}}\right|\right)}\right\}\:\:$$

(6)

Fig. 8

Evaluation of ablation experiments of IMPFE-HGNN on different datasets. (a) Monitoring-only dataset, (b) Load test-only dataset, (c) Monitoring and load test datasets.

Ablation experiments were conducted on the node prediction tasks for deflection and strain on the monitoring-only dataset, the load test-only dataset, and the monitoring and load test datasets. The experimental results are shown in Fig. 8. When randomly selecting nodes to aggregate features on the monitoring-only dataset and the load test-only dataset, the model effect drops significantly, which illustrates the effectiveness of obtaining physical field semantic information using meta-path subgraphs. The method proposed in this paper can avoid physical field semantic confusion when aggregating node features. After removing the feature mapping and relationship encoding, the model effect also decreases to different degrees.

Sensitivity analysis

This paper conducts parameter sensitivity analysis on the node classification task of IMPFE-HGNN on the monitoring and load test datasets, and studies the influence of meta-path length, feature mapping layer dimension, and model network layer number on node representation. To evaluate parameter sensitivity, this paper uses the cumulative probability value (PA) of the prediction error within the 90% confidence interval within − 0.1 to 0.1 as the evaluation index.

Fig. 9

Sensitivity analysis of different parameters in IMPFE-HGNN model. (a) Meta-path length sensitivity, (b) Encoding dimension sensitivity, (c) Network layer sensitivity.

• (1) Meta-path length.

  IMPFE-HGNN selects all meta-paths of fixed length to construct subgraphs to extract physical field semantic information. Shorter meta-paths can capture the direct correlation between nodes, and longer meta-paths can expand the information propagation range. Therefore, the selection of meta-path length has an important influence on node representation performance. Figure 9a shows the experimental results of selecting different meta-path lengths. It can be seen that on the monitoring and load test datasets, the cumulative probability value first increases and then decreases with the increase of the original path, and reaches the highest cumulative probability when the meta-path length is 5. When the meta-path length is further increased, the extracted subgraph structure and features are more complex. Different nodes may be connected to the same meta-path, which means that the meta-path subgraph cannot capture meaningful features for each node and contains more noise and redundant information, resulting in a decrease in node representation performance.

• (2) Dimension of feature mapping layer.

  To project node vectors from disparate physical field semantic spaces into a unified feature space and to bolster the model’s expressive capacity, the IMPFE-HGNN algorithm integrates a feature mapping layer that receives node representations. An elevated dimensionality within this mapping layer is conducive to capturing the nuances of input features, thereby enhancing the model’s learning efficacy. Nevertheless, an excessively high dimension may precipitate overfitting and concurrently escalate computational complexity. Figure 9b illustrates the experimental outcomes associated with varying the dimensions of the relationship encoding. The findings indicate that an optimal mapping layer dimension is 128, beyond which any further increase in dimension leads to a near-linear degradation in model performance.

• (3) Number of network layers.

  The network layer of the IMPFE-HGNN model contains different operations such as subgraph construction, relationship encoding, and feature mapping. A deep network can usually better capture the complex patterns and structures in the data, thereby improving the feature extraction ability. However, the complexity of the model also increases accordingly, increasing the training difficulty and computational cost. Due to the data distribution and class imbalance of different datasets, the optimal number of network layers is often different. Figure 9c shows the experimental results of different numbers of network layers. The results show that the optimal number of network layers of the model in the node classification task on the monitoring and load test datasets is 2. As the number of network layers further increases, the learned node representations are more difficult to distinguish, resulting in a significant decrease in the model effect.

Conclusion

This paper introduces an Integrating Multi Physical Field Encoding Heterogeneous Graph Neural Network (IMPFE-HGNN) approach. This methodology integrates multi-physical field data gleaned from an array of sensor types. Employing a lightweight mean aggregator, it derives node representations within meta-path subgraphs that connect various sensor types and structural mechanical attributes. The model develops tailored relationship encodings for each meta-path category. Post feature mapping, it amalgamates node features across different physical field semantic perspectives, thereby assembling a proxy model capable of encapsulating the intricate interplay among diverse physical field data. The application of the IMPFE-HGNN algorithm to a cable-stayed bridge load test scenario underscores its capacity to markedly enhance bridge performance diagnostics. The ensuing conclusions are drawn from this study:

• (1) The algorithm significantly improves the accuracy in multiple parameter corrections of the bridge finite element model. In terms of structural mechanical property parameters, the maximum correction of Poisson’s ratio parameter can reach 43.33%, and the maximum correction of elastic modulus parameter is 10.20%.

• (2) The algorithm improves the accuracy of the predicted value of the finite element correction model. For strain predictions, the model achieved a median accuracy improvement of 61.4%, with a maximum localized correction of 77%. For deflection predictions, the median improvement was 72.8%, and the RMSE was reduced by approximately 78%. The maximum correction reached 87%. These statistics confirm that the IMPFE-HGNN offers a generalized improvement in structural health monitoring fidelity, rather than improving only specific isolated points.

• (3) To substantiate the efficacy of the IMPFE-HGNN, this paper undertakes ablation studies focused on node classification and link prediction. The findings validate the approach’s capability to effectively harness physical field semantic information through the utilization of meta-path subgraphs. The proposed methodology adeptly circumvents the potential for semantic conflation during the aggregation of node features from disparate physical domains.

• (4) This paper conducts parameter sensitivity analysis on the node classification task of IMPFE-HGNN on the monitoring and load test datasets, and studies the influence of meta-path length, feature mapping layer dimension and model network layer number on node representation. The results indicate that the optimal meta-path length is 5, the optimal dimension for the feature mapping layer is 128, and the optimal number of model network layers is 2.

The primary objective of this research is to employ a heterogeneous graph neural network incorporating multi-physical field encoding for the parameter refinement of finite element models for long-span cable-stayed bridges. This is achieved by leveraging service status data collected from various sensors, thereby offering a robust method for the performance monitoring of such bridges. By integrating multi-physical field data with sophisticated deep learning techniques, the proposed approach aims to enhance the precision of bridge performance assessments, thereby fostering safer and more efficient infrastructure management.