Introduction

The rapid expansion of the global population and the corresponding surge in energy consumption have intensified the search for clean, renewable, and sustainable energy sources1,2. Among the various emerging energy alternatives, hydrogen has gained exceptional attention due to its extremely high gravimetric energy density, environmental friendliness, and potential to reduce dependence on fossil fuels. Despite these advantages, practical hydrogen utilization still faces major challenges related to safe and efficient storage and transportation. Conventional storage methods—such as compression and liquefaction—suffer from high cost, operational complexity, and safety concerns, thereby limiting their large-scale deployment3. Consequently, the development of advanced solid-state hydrogen storage materials has become a critical research priority.

Metal hydride perovskites have emerged as one of the most promising candidates for hydrogen storage. These materials reversibly absorb hydrogen via chemical reactions and are known to release hydrogen at relatively low temperatures while achieving moderate storage densities4. Beyond energy storage, metal hydrides are also attractive because they offer advantages over nuclear, solar, and wind-based systems—most notably the absence of radioactive waste, climatic/geographical dependence, and noise generation5. Hydrogen, being non-toxic, abundant, and producing only water upon combustion, is particularly suitable for powering household systems, automobiles, and electronic devices. However, key bottlenecks remain in hydrogen production, transportation, and storage technologies6. Solid-state storage materials are considered superior to liquefaction-based approaches in terms of efficiency and safety, motivating increasing research activity on perovskite hydrides (ABH₃)7.

The ABH₃ hydride family exhibits notable hydrogen storage potential with gravimetric hydrogen densities ranging between 1.2 wt% and 6 wt%8. Recent studies emphasize the tunable storage behavior arising from the interplay between alkaline and alkali metal atoms within these materials. Compared with compressed hydrogen gas and cryogenic liquid storage systems, perovskite metal hydrides demonstrate enhanced safety, higher density storage, and reduced energy loss9. Achieving efficient hydrogen storage ultimately depends on identifying compounds with optimal structural and thermodynamic behavior. In this context, density functional theory (DFT) has become an indispensable tool for predicting structural, thermodynamic, mechanical, and electronic properties prior to experimental synthesis10.

With global energy demand projected to increase by approximately 25% by 204011, the shift from non-renewable fossil fuels toward sustainable alternatives is unavoidable. Due to its natural abundance, sustainability, and eco-friendly combustion process, hydrogen stands out as a leading candidate for future energy systems. Its mass-energy density is nearly three times higher than gasoline, further reinforcing the motivation for a hydrogen-based economy12.

Substantial progress has been made in the theoretical and experimental exploration of hydrogen perovskite hydrides. In ABH₃ hydrides, hydrogen behaves as an anion, whereas A and B correspond to monovalent and divalent cations, respectively13. Shakoor et al. reported the hydrogen storage capacities of LiPdH₃, NaPdH₃, and KPdH₃ as 2.59 wt%, 2.23 wt%, and 2.035 wt%14. Tahir et al. investigated XSnH₃ (X = Li, K), revealing hydrogen gravimetric densities of 2.35 wt% and 1.88 wt%15. CaNiH₃ exhibited ~ 3 wt% hydrogen storage, while decomposing at 773 K and 3 MPa into CaH₂ and Ni16. Rehman et al. employed DFT to analyze cubic MgXH₃ (X = Cr, Fe, Mn) and confirmed their mechanical stability along with favorable electronic, vibrational, and thermodynamic behavior17. Muhammad et al. combined DFT and the CASTEP framework to examine XGaH₃ (X = Li, K), reporting hydrogen densities of 1.86 wt% and 0.89 wt%18. Abdullah et al. further demonstrated the structural, elastic, phonon, mechanical, and thermodynamic stability of MgFeH₃ and MgCoH₃19. Remarkably, Rkhis et al. enhanced the hydrogen storage capacity of ZrNiH₃ through transition-metal substitution and strain engineering20. Xu et al. provided comprehensive studies of XVH₃ (X = Na, K, Rb, Cs), XAlH₃ (X = Na, K), and XTiH₃ (X = K, Rb, Cs), confirming their mechanical, thermodynamic, and dynamical stabilities via DFT calculations21,22,23.

In light of these advances, our study introduces, for the first time, a comprehensive investigation of the newly proposed boron-based perovskite hydrides XBH₃ (X = Ba and Sr). To the best of our knowledge, no prior theoretical or experimental research exists on these compounds. Using first-principles density functional theory calculations, we thoroughly examine their structural, electronic, magnetic, optical, mechanical, thermal, vibrational, and hydrogen storage properties within the GGA-PBE framework. The results reveal that both BaBH₃ and SrBH₃ possess robust structural frameworks, mechanical stability, favorable electronic characteristics, and notable thermal durability. Most importantly, the computed gravimetric hydrogen storage values indicate that these compounds have promising hydrogen absorption capability, positioning them as strong candidates for solid-state hydrogen storage systems.

Therefore, this work provides the first systematic analysis of BaBH₃ and SrBH₃, offering new insights into boron-derived hydride perovskites. The findings not only contribute to the existing body of knowledge on metal hydride perovskites but also lay a solid foundation for future theoretical and experimental research aimed at developing next-generation hydrogen storage materials.

Computational methodology

We used the WIEN2K simulation program24 to do first-principles computational studies based on DFT to look into the physical features of boron-based hydrides XBH₃ (X = Ba, Sr). For single-point calculations and structural optimization procedures, the Perdew-Burke-Ernzerhof (PBE) exchange-correlation function and the Generalized Gradient Approximation (GGA) were combined. The present study was performed exclusively using the WIEN2k code based on the full-potential linearized augmented plane wave (FP-LAPW) all-electron method and K-point mesh that was evenly spaced across the first Brillouin zone to make sure the findings were accurate. We got the best crystal structure using XCrySDen software, which is based on calculated electronic wave functions and charge densities25. The space group Pm-3 m-221 for XBH3 (X = Ba and Sr) is a boron-based perovskite hydride. The following are the pseudo-atomic electrical configurations for the elements: Barium (Ba): 5s² 5p⁶ 6s², Strontium (Sr): 4s² 4p⁶ 5s², Boron (B): 2s² 2p¹, and Hydrogen (H): 1s¹. We meticulously computed the complex dielectric constant, denoted by the symbol ε(ω), which is the sum of its imaginary component ε₂(ω) and real component ε₁(ω). This provided us with a strong foundation upon which to calculate several other optical characteristics, including the loss function L(ω), the optical conductivity σ(ω), and the refractive index n(ω).

Additional calculations were performed to determine the optical reflectivity R(ω) and the absorption coefficient α(ω), using the refractive index calculations as a starting point. This improved our understanding of the material’s light-interaction properties. The parameters were set to 2 × 10− 5 eV for energy difference per atom, 0.05 eV/Å for ionic Hellmann-Feynman force, and 2 × 10− 3 Å for maximal ionic displacement26. Additionally, the mechanical elastic constants of these perovskite hydrides for the optimal geometry model were determined using the stress-strain technique. Four distinct cycles were needed for each strain, which was thoroughly examined and assessed. To ensure that the process was carried out correctly, the maximum amplitude was meticulously set to a very tiny value of 0.003 Å during these cycles. Following this intricate procedure, a more thorough calculation of the elastic constants was performed using the Voigt Reuss Hill (V) averaging approach. This improved the accuracy of the results from the earlier strains.

Results and discussion

Structural properties

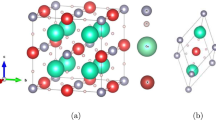
The structural characteristics of XBH3 (X = Ba, Sr) boron-based perovskite hydrides were examined using first-principles simulations. These calculations confirmed the cubic crystal structure in the Pm-3 m (221) space group. The ideal crystal structure produced by the XCrySDen program is shown in Fig. 1. Hydrogen (H) atoms are found in the octahedral face-centered positions (0.5, 0, 0), (0, 0.5, 0), and (0, 0, 0.5); X-cations (Ba and Sr) are found in the unit cell vertices (0,0,0); and boron (B) atoms are found in the central position (0.5, 0.5, 0.5).

Fig. 1
figure 1

The optimized crystal structure of (a) BaBH3, (b) SrBH3 boron-based hydrides.

Full size image

The Generalized Gradient Approximation (GGA-PBE) functional method is used in the optimization process. This ensures that the structure is refined accurately. These results provide us a lot of information on how atoms are arranged and how stable XBH3 hydrides are. They also show that these compounds might be used to store hydrogen27,28. Through structural optimization techniques, we found the lattice parameters, unit cell volumes, formation enthalpies, and gravimetric hydrogen storage capacities (Cwt%) of XBH₃ hydrides (X = Ba, Sr), which are shown in Table 1. The measured lattice constants for BaBH3 and SrBH3 are 3.71 Å and 3.52 Å, respectively. The two structures being studied, XBH3 (X = Ba, Sr), have unit volumes of 51.06 Å3 and 43.76 Å3, respectively. It has been shown that BaBH3 has a bigger lattice parameter and unit cell volume than SrBH3. This is mostly because Ba has a larger ionic radius (0.19 nm) than Sr (0.13 nm). In addition, the study of these new perovskite hydrides, which are being looked at for the first time without any previous theoretical frameworks or experimental datasets, has shown that they have many benefits and possible uses in the field of materials that are used to store hydrogen in a safe and efficient way. We find out whether the XBH3 (X = Ba and Sr) molecules are thermodynamically stable by calculating their formation energy (Eform). Formation energy is the amount of energy required to put the molecules of a composite in order. The equation below29 is used to get the formation energy:

Table 1 The computed lattice constants (Å), volume (Å3), band gap (Eg in eV), density (in.
Full size table
$$\:{E}_{Form}={E}_{XB{H}_{3}}^{Total}-\left({E}_{X}^{Bulk}+{E}_{B}^{Bulk}+3{E}_{H}^{Bulk}\right)$$
(1)

The overall ground state energy of the XBH3 complex is \(\:{E}_{XB{H}_{3}}^{Total}\). The ground state energy of the atoms in their bulk form is given by \(\:{E}_{X}^{Bulk}\), \(\:{E}_{B}^{Bulk}\), and \(\:{E}_{H}^{Bulk}\). The calculated values of for BaBH3 and SrBH3 are – 17.30 eV/atom and – 17.39 eV/atom, respectively. Both materials are thermodynamically stable, according to the investigation; however, Table 1’s data indicates that SrBH3 is more stable than BaBH3. Both materials are thermodynamically stable, according to the investigation; however, Table 1 data indicates that SrBH3 is more stable than BaBH3. For the cubic structures of XBH3 (where X = Ba and Sr), the negative formation energy (EForm) values demonstrate the stability and ease of synthesis of these compounds.

Electronic properties

The electronic characteristics of XBH₃ (X = Ba, Sr) perovskite hydrides were systematically examined through band structure (Eg), total density of states (TDOS), and partial density of states (PDOS). In Fig. 2 (a) and 2 (b), the band structure was evaluated along the major high-symmetry points (Γ, X, R, and M) of the Brillouin zone within an energy range of − 10 eV to 10 eV. Hydrogen adsorption on material surfaces occurs either via chemisorption, where hydrogen forms strong chemical bonds with the host lattice, or via physisorption, where hydrogen interacts weakly with the surface. Since the strength of hydrogen–material interaction largely dictates reversible hydrogen storage behavior, the analysis of electronic properties becomes essential30. Materials that exhibit a high density of electronic states at the Fermi level and possess accessible states near this energy are more likely to demonstrate enhanced hydrogen adsorption energies.

Fig. 2
figure 2

Calculated electronic band structures of (a) BaBH3, (b) SrBH3 boron-based hydrides.

Full size image

The electronic band structures of BaBH₃ and SrBH₃ computed using the GGA-PBE approach (Fig. 3) show that the valence band crosses the Fermi level without any visible band gap, confirming their metallic nature. The coincidence of the valence band maximum and conduction band minimum at the high-symmetry points (X, R, M, Γ) further supports this property31. The zero-band-gap energy indicates that electron excitation from the valence band to the conduction band does not require external input, leading to high electrical conductivity. The presence of free charge carriers accelerates kinetic pathways for hydrogen absorption and desorption, which is why metallic compounds frequently display reversible hydride formation. Consequently, both BaBH₃ and SrBH₃ possess advantageous electronic traits for hydrogen storage applications.

Fig. 3
figure 3

Calculated spin polarized band structure of (a) BaBH3, (b) SrBH3 boron-based hydrides, where black and red lines represented spin-up and spin-down states.

Full size image

The TDOS plots of XBH₃ (X = Ba, Sr), calculated across − 10 eV to 10 eV (Fig. 4), provide further evidence of metallic behavior. The continuous spread of density of states at the Fermi level implies that electrons can migrate freely between energy levels, a defining characteristic of metallic systems32. This facilitates enhanced charge mobility and supports reversible hydrogen storage processes. The high number of accessible states across the energy range strengthens the classification of BaBH₃ and SrBH₃ as potential hydrogen storage materials.

Fig. 4
figure 4

Total density of state of XBH3 (X = Ba, Sr) hydrides.

Full size image

PDOS analysis (Fig. 5) provides deeper orbital-level insight into the electronic structure. Notable s-state peaks arise around − 7.89 eV for BaBH₃ and − 8.95 eV for SrBH₃, revealing their significant role in shaping the valence band. The conduction band, however, is largely influenced by d-state contributions, confirming the hybridized nature of electronic interactions within the lattice. The H 1 s, B 2p, and X-site 5s/6s states (for Ba and Sr) contribute prominently to the total electronic configuration across the examined energy range33. For BaBH₃, H 1 s states dominate from − 10 eV to slightly above the Fermi level, whereas B 2p states primarily contribute between − 8 eV and the Fermi level, strongly influencing the conduction process. In SrBH₃, similar coupling trends are observed, although the Fermi level shifts slightly upward relative to BaBH₃, indicating subtle differences in electronic interactions despite overall similar metallic characteristics.

Fig. 5
figure 5

Calculated partial density of state of (a) BaBH3, (b) SrBH3 boron-based hydrides.

Full size image

The PDOS results strengthen the conclusions drawn from TDOS and band structure, revealing that the interplay of s, p, and d orbitals yields an uninterrupted set of electronic states across the Fermi level. This confirms the metallic nature of both compounds and reinforces the proposition that BaBH₃ and SrBH₃ are promising candidates for hydrogen storage34. Their zero-band-gap electronic structure, continuous DOS at the Fermi level, and high conductivity collectively support efficient and reversible hydride formation, establishing these boron-based perovskite hydrides as strong contenders for optoelectronic and next-generation hydrogen storage materials.

Magnetic properties

The magnetic properties of XBH3 (X = Ba, Sr) perovskite hydrides were analyzed using Density Functional Theory (DFT) to assess the influence of spin polarization on their electronic structure. The calculated spin-polarized total density of states (TDOS) and partial density of states (PDOS) are shown in Figs. 6(a, b) and 7(a, b), respectively. These analyses provide critical insights into the contribution of spin states to the overall electronic structure. The spinpolarized band structures were analyzed at high-symmetry points (X, R, Γ, M, and R) throughout the first Brillouin zone, providing a detailed understanding of the magnetic interactions and electronic transitions in the studied materials35. By meticulously assessing and calculating the band gaps within a material, we are able to provide a comprehensive and insightful explanation regarding how the electronic states are distributed throughout the entirety of its electronic structure. As depicted in Figs. 6(a, b), the Fermi level (EF) is referenced at zero energy. The black and red lines correspond to the spin-up and spin-down states, respectively. There is a complete overlapping of spin-down and spin-up states in the bandgap plots, which indicates that the net magnetic moment of the material is zero. This exact correspondence among the spin-up and spin-down states indicates that any magnetic interactions present in the system will cancel out each other, which ultimately supports the fact that the system is non-magnetic. A comprehensive understanding of the parameters is essential for understanding the electronic applications of materials, specifically in those applications where we need non-magnetic behavior. This non-magnetic behavior is important for various applications to avoid scatterings, which can occur due to spins associated with the electronic states, as these scatterings can affect the conductivity and efficiency of the devices.

Fig. 6
figure 6

Calculated spin polarized total density of state of (a) BaBH3, (b) SrBH3 boron-based hydrides.

Full size image

Additionally, we also determined the spin-polarized partial density of states (PDOS) to analyze how the spin-polarized total density of state (TDOS) of each atom is affected by the magnetization. As depicted in Fig. 7(a, b), the spin-up configurations for H s, B s, p, Ba s, and Sr-s, p states are symmetrical to the spin-down states, with no observable deviation in spin characteristics among these states. Therefore, the non-magnetic nature of the studied materials is confirmed by these results. Non-magnetic perovskite hydrides have low magnetic interactions and greater stability, which makes them suitable for use in H2 storage devices. Furthermore, these materials exhibit an outstanding capacity for reversible absorption and desorption under moderate temperature and pressure conditions36. The ongoing investigations and studies pertaining to boron-based hydrides are primarily concentrated on the improvement and optimization of their chemical compositions as well as their molecular structures, with the ultimate goal of attaining significantly higher levels of efficiency, thereby establishing them as the most viable and promising contenders in the race for sustainable and environmentally friendly energy solutions that can meet the growing demands of our modern world.

Fig. 7
figure 7

Calculated spin polarized partial density of state of (a) BaBH3, (b) SrBH3 boron-based hydrides.

Full size image

Optical properties

The optical properties of materials are critical for understanding their interaction with electromagnetic radiation, which directly impacts their applicability in various advanced technologies. Key parameters for determining the material’s applicability in hydrogen storage, photo catalysis, coatings, solar cells and optoelectronic devices, are absorption coefficient α(ω), reflection R(ω), optical conductivity σ(ω), energy loss function L(ω), refractive index n(ω), and complex dielectric functions ε(ω). We have conducted a thorough investigation into the optical properties of perovskite-type hydrides XBH3 (X = Ba, Sr) to measure their response to light energy. The absorption coefficient serves as a crucial parameter that effectively quantifies the inherent capability of a specific material to absorb electromagnetic radiant energy, particularly at a designated wavelength, measured per unit length, which in turn stimulates and excites the electrons within the material on an electronic level. The expression given below was used to calculate the absorption coefficient α(ω)37.

$$\:\alpha\:\left(\omega\:\right)=\frac{4\pi\:k}{\lambda\:}$$
(2)

The maximum absorption coefficient values were determined as 40.53 × 104 cm-1 at 23.37 eV for BaBH3 and 35.18 × 104 cm-1 at 25.57 eV for SrBH3, as illustrated in Fig. 8(a). These remarkably high absorption coefficient values confirm the suitability of BaBH3 for photodetectors, solar cells, sensors, energy storage, and optoelectronic applications.

Fig. 8
figure 8

The calculated optical parameters; (a) absorption coefficient α(ω), (b) conductivity σ(ω), (c) real dielectric function ε1(ω), and (d) imaginary dielectric function ε2(ω) for XBH3 (X = Ba, Sr) hydrides.

Full size image

The optical conductivity σ(ω) explains the mechanism of conduction of photo-excited electrons within the material. The below expression was used to evaluate the material’s optical conductivity σ(ω)38:

$$\:\delta\:\left(\omega\:\right)=\frac{\alpha\:\left(\omega\:\right)n\left(\omega\:\right)c}{4\pi\:}$$
(3)

The calculated optical conductivity for BaBH3 and SrBH3 reveals that BaBH3 has higher values, with a peak of 5.92 1/fs at 22.87 eV. SrBH3 shows high peaks of 4.77 1/fs at 5.18 eV and 4.46 1/fs at 24.34 eV. The enhanced optical conductivity, as shown in Fig. 8(b), implies that BaBH3 possesses more vacant states and a higher density of states, making it advantageous for energy storage and optoelectronic device applications. The dielectric function ε(ω) is the most fundamental parameter in the study of an electrically or optically active material. It regulates how materials interact with electromagnetic radiation and influences both the propagation of light and the movement of electrons. The real part of this function ε1(ω) is due to dispersion and polarization effects and the imaginary part ε2(ω) corresponds to absorption characteristics. The Kramers-Kronig transformation was used to obtain the dielectric function ε(ω) using momentum matrix elements between wave functions. The real component of the dielectric constant ε1(ω) can be determined using the following equation:

$$\:{\epsilon\:}_{1}\left(\omega\:\right)=1+\frac{2}{\pi\:}M{\int\:}_{0}^{\infty\:}\frac{{\epsilon\:}_{2}\left({\omega\:}^{{\prime\:}}\right){\omega\:}^{{\prime\:}}}{{\omega\:}^{{\prime\:}2}-{\omega\:}^{2}}d\omega\:$$
(4)

The real component of the dielectric constant ε1(ω) relates to the light energy polarization at the resonance frequency. The imaginary component ε2(ω) of the dielectric function was evaluated using the following expression:

$$\:{\epsilon\:}_{2}\left(\omega\:\right)=\frac{2{e}^{2}\pi\:}{{\Omega\:}{\epsilon\:}_{0}}\sum\:_{k,v,c}\left|{\psi\:}_{k}^{c}\right|u.r{\left|{\psi\:}_{k}^{v}\right|}^{2}\delta\:\left({E}_{k}^{c}-{\psi\:}_{k}^{v}-E\right)$$
(5)

Here, u denotes the polarization direction, e represents electronic charge, ω stands for the light frequency, and \(\:{\psi\:}_{k}^{v}\) and \(\:{\psi\:}_{k}^{c}\) are the wave functions of the valence and conduction bands, respectively. The real part ε1(ω) and the imaginary part ε2(ω) were employed to compute the complex dielectric function39:

$$\:\epsilon\:\left(\omega\:\right)={\epsilon\:}_{1}\left(\omega\:\right)+{\epsilon\:}_{2}\left(\omega\:\right)$$
(6)

Figure 8(c-d) shows the real and imaginary dielectric functions of XBH₃ (X = Ba and Sr), highlighting significant polarization and dispersion, which are typical characteristics of materials with high light absorption. Contrarily, SrBH3 exhibits a more gradual decrease in ε1(ω) as compared to BaBH3. The imaginary part ε2(ω) reaches its highest peaks at 1.6 eV for BaBH3, with a maximum of 13.84, and at 2.2 eV for SrBH3, with a peak of 12.27, indicating considerable absorption at these energy levels.

The loss function L(ω), which quantifies the amount of energy lost due to scattering and photon dispersion, was also calculated. The loss function, L(ω), of the materials was was determined using the equation below:

$$\:L\left(\omega\:\right)=\frac{{\epsilon\:}_{2}\left(\omega\:\right)}{{\epsilon\:}_{1}^{2}\left(\omega\:\right)+{\epsilon\:}_{2}^{2}\left(\omega\:\right)}$$
(7)

The loss function shows its maximum peaks at 12.14 for BaBH3 at 27.35 eV and 6.52 for SrBH3 at 29.05 eV, as depicted in Fig. 9(a). This suggests that BaBH3 experiences greater photon energy losses. The reflectivity R(ω) of XBH3 (X = Ba and Sr) hydrides was determined by using the following equation40:

Fig. 9
figure 9

The calculated graphs of optical parameters; (a) optical loss function L(ω), (b) reflectivity R(ω), (c) refractive index n(ω), and (d) extension coefficient K(ω), for XBH3 (X = Ba, Sr) hydrides.

Full size image
Fig. 10
figure 10

Calculated directional dependent of (a) Young’s modulus, (b) linear.

Full size image
$$\:R\left(\omega\:\right)=\frac{{(n-1)}^{2}+{k}^{2}}{{(n+1)}^{2}+{k}^{2}}$$
(8)

The reflectivity results, which are illustrated in the detailed graphical representation found in Fig. 9(b), reveal static values that stand at 0.42 for the compound known as BaBH3 and a slightly higher value of 0.52 for the compound referred to as SrBH3. Both BaBH3 and SrBH3 demonstrate a notable peak reflectance of 0.53, occurring at an energy level of 26.87 eV, while SrBH3 shows a peak reflectance of 0.35 at a higher energy level of 28.26 eV, indicating distinct optical properties between the two materials. These significant results clearly illustrate that BaBH₃ possesses a remarkable suitability for various applications that necessitate high reflectance capabilities, such as the production of solar cells and the development of architectural coatings aimed at achieving efficient management of both heat and light.

The refractive index n(ω) and the extinction coefficient k(ω) are key parameters to analyze the interaction of light with these materials. These parameters are determined using the following expressions41:

$$\:n\left(\omega\:\right)=\frac{{\left[{\left\{{\epsilon\:}_{1}^{2}\left(\omega\:\right)+{\epsilon\:}_{2}^{2}\left(\omega\:\right)\right\}}^{1/2}+{\epsilon\:}_{1}\left(\omega\:\right)\right]}^{1/2}}{\sqrt{2}}$$
(9)
$$\:K\left(\omega\:\right)=\frac{{\left[{\left\{{\epsilon\:}_{1}^{2}\left(\omega\:\right)+{\epsilon\:}_{2}^{2}\left(\omega\:\right)\right\}}^{1/2}-{\epsilon\:}_{1}\left(\omega\:\right)\right]}^{1/2}}{\sqrt{2}}$$
(10)

The peak values of the real component of the refractive index n(ω) of BaBH3 and SrBH3 are 4.4 and 6.1, respectively, and with increasing photon energy it decreases gradually. Peak values of extinction coefficient k(ω) of 2.15 at 1.9 eV for BaBH3 and 1.98 at 2.5 eV for SrBH3 are shown. Figure 9 (c-d) show that SrBH3 has a greater atomic number and electron density, resulting in a higher refractive index. The findings presented herein serve to substantiate the assertion that XBH3 (where X = Ba, Sr), demonstrates remarkable and outstanding optical properties that encompass a wide range of critical parameters, such as the dielectric function that describes how the material responds to electric fields, the refractive index which indicates how light is bent when it passes through the substance, the absorption coefficient that quantifies how much light is absorbed by the material, reflectivity which determines the fraction of light that is reflected off its surface, optical conductivity that reveals how well the material conducts light, and finally, the energy loss function that illustrates the energy dissipation mechanisms occurring within the system. Detailed evaluation of these attributes reveals that XBH3 (X = Ba, Sr) is a very promising material for solar cell and energy storage applications, photonics, photodetectors, and optoelectronic technologies.

Mechanical properties

Hydrogen storage materials are essential for the efficient storage and release of hydrogen, serving key applications such as fuel cells, hydrogen-fueled vehicles, and energy storage solutions. Of all the key criteria, mechanical stability remains a core aspect as it defines the material’s ability to remain strong and safe from deformation when subjected to mechanical stress or strain42. In hydrogen storage, mechanical stability deals with pressure resistance in the system, temperature change, and cyclic hydrogen storage and release. These properties are improved by reinforcing materials such as metal hydrides, which have high hydrogen absorption capacity in order to increase the material’s strength, toughness fatigue, and corrosion resistance. The potential mechanical properties of boron-based perovskite hydrides XBH3 (X = Ba, Sr) can be analyzed in terms of their elastic constants, which are essential for determining the material staking mechanism and nature of bonding. The various characteristics of elasticity provide insightful and invaluable information regarding the material in question, specifically detailing how this material reacts and responds to applied stress, as well as its remarkable capacity to recover and regain its original form once the applied stress is no longer present, in addition to shedding light on its inherent structure and overall strength. Both structural and elastic properties are of significant importance in application due to their direct relationship with the stability, mechanical stiffness, and tolerance to longitudinal and shear stresses, which are fundamental parameters used for hydrogen storage. The Chapin method was utilized for the analysis of cubic symmetry in these perovskite hydrides, which employs just three constants (C11, C12, and C44) to report the elastic and thermodynamic properties of the perovskite-type hydrides. These constants were derived from the second-order derivative of energy concerning volume E(V)43. The computed elastic constants, summarized in Table 2, are analyzed using Born stability criteria to

Table 2 The calculated elastic constants Cij (GPa), and born stability criterion; cauchy pressure (C11-C12) for XBH3 (X = Ba and Sr) compounds.
Full size table

assess the elastic stability of XBH3 (X = Ba and Sr) perovskite hydrides44. :

$$\:{C}_{11}-{C}_{12}>0,\:{C}_{11}+2{C}_{12}>0,\:{C}_{11}>0\:and\:{C}_{44}>0$$
(11)

The above criteria have been confirmed by the studied material, which indicates mechanical stability of the perovskite material. Table 3 explains the elastic constants (B, G, E, Poisson’s ratio, B/G, and AU) which give important information on the bulk modulus (B), the shear modulus (G), Young’s modulus (E), Poisson ratio, B/G, and anisotropy factor (AU) of the studied sandwich. The Voigt-Reuss-Hill (VRH) approximations are utilized for calculation of the bulk modulus (B).

Table 3 The computed bulk modulus B (GPa), shear modulus G (GPa), young’s modulus E (GPa), pugh’s index ratio B/G, poisson’s ratio (υ), G/B ratio, vicker’s hardness Hv (GPa), Poisson ratio, Vickers hardness (Hv in GPa) and anisotropic index AU for XBH3 (X = Ba and Sr) compounds.
Full size table
$$\:{B}_{v}=\frac{{C}_{11}+2{C}_{12}}{3}$$
(12)
$$\:{B}_{R}=\frac{{C}_{11}+2{C}_{12}}{3}$$
(13)
$$\:B=\frac{{B}_{v}+{B}_{R}}{2}$$
(14)

The shear modulus (G) is calculated as follows:

$$\:G=\frac{{G}_{v}+{G}_{R}}{2}$$
(15)
$$\:{G}_{v}=\frac{{3{C}_{44}+C}_{11}-{C}_{12}}{3}$$
(16)
$$\:{G}_{R}=\frac{{5(C}_{11}-{C}_{12}){C}_{44}}{{3(C}_{11}-{C}_{12})+4{C}_{44}}$$
(17)

Young’s modulus (E) and Poisson ratio () are calculated through the following relation45:

$$\:E=\frac{9BG}{3B+G}$$
(18)
$$\:v=\frac{3B-2G}{3(3B+G)}$$
(19)

The computed elastic constants validate the mechanical stability of XBH₃ (X = Ba, Sr) perovskite hydrides, offering crucial insights into their structural integrity. Poisson’s ratio (ν) and Pugh’s ratio (B/G) are critical parameters for assessing the ductility or brittleness of the materials. A material is classified as ductile if Poisson’s ratio (ν) > 0.26 and Pugh’s ratio (B/G) > 1.75; otherwise, it exhibits brittle behavior. The computed elastic constants are useful in confirming the mechanical stability of perovskite hydrides XBH₃ (X = Ba, Sr) which contribute necessary information of their structural integrity. The two critical parameters determining the ductility or brittleness of the material are Poisson’s ratio (ν) and Pugh’s ratio (B/G). If Poisson’s ratio ν > 0.26 and Pugh’s ratio B/G > 1.75 then a material is classified as ductile, while for B/G ≤ 1.75 it exhibits brittle behavior. The Poisson’s ratios calculated for BaBH3 and SrBH3 are 0.23 and 0.25, respectively, below the ductility threshold confirming that both systems are brittle. This state is corroborated by the computed Pugh’s ratio values of 1.51 for BaBH3 and 1.72 for SrBH3 which resemble brittle behavior. Furthermore, Young’s modulus (E), Bulk modulus (B), and Shear modulus (G), listed in Table 3, also validate their mechanical properties. Since these parameters are important in determining the material response to stress, deformation, and structural bonding, the results unequivocally establish that XBH3 (X = Ba, Sr) perovskite hydrides are mechanically stable and intrinsically brittle, which makes them ideal for hydrogen storage applications. The anisotropic factor of XBH3 (X = Ba and Sr) perovskite hydrides is calculated using the equation46.

$$\:{A}^{U}=\frac{2{C}_{44}}{{C}_{11}-{C}_{12}}$$
(20)

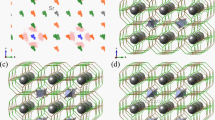
In order to conduct a more in-depth examination of the intricate phenomenon of elastic anisotropy, the sophisticated and highly regarded ELATE software was employed to meticulously extract an abundance of valuable information pertaining to the directional characteristics of the mechanical properties, all of which are fundamentally influenced by the specific orientation of the crystal structure47 shown in figure-10 (a-d). True color maps for Young’s modulus, shear modulus, Poisson’s ratio, and linear compressibility are depicted in Fig. 9, where the blue color corresponds to the minimum value. In contrast, the green color corresponds to the maximum value. A spherical shape in these visualizations indicates isotropic behavior, whereas deviations suggest anisotropy. These results validate that Poisson’s ratio, Young’s modulus, and shear modulus are anisotropic characteristics while linear compressibility is isotropic. The highest and lowest computed values for these parameters are presented in Table 4. The anisotropic nature of Poisson’s ratio, Young’s modulus, bulk modulus, and shear modulus highlights the material’s structural stability across different crystallographic directions. These findings underscore the presence of an optimized crystal structure, balanced exchange interactions, and a homogeneous microstructure, making XBH3 (X = Ba and Sr) perovskite hydrides highly suitable for hydrogen storage and optoelectronic applications where directional stability is a critical performance factor.

Table 4 The computed values of maximum and minimum values of young’s modulus (E), linear compressibility (β), shear modulus (G), and poisson’s ratio (υ) for XBH3 (X = Ba and Sr) compounds.
Full size table

Thermal and vibrational properties

To examine and understand the structural stability of XBH3 (X = Ba and Sr) boron-based hydrides, dynamic stability and thermodynamic properties were analyzed. The phonon dispersion curves, as shown in Fig. 11(a-b), enable a better understanding of the vibrational characteristics of these materials in a system. Due to the five atoms per unit cell, there are 15 phonon branches, of which 12 are optical, and three are acoustic48. The sign of the phonon frequencies usually defines the stability of these compounds. If the frequencies are negative, then the compound is unstable, whereas positive values mean that the compound is stable. For BaBH3 and SrBH3, the phonon frequencies range from 0 to 40 THz at high-symmetry points, with all frequencies being real, thereby confirming their dynamical stability.

Fig. 11
figure 11

The phonon dispersion curves of (a) BaBH3, (b) SrBH3 boron-based hydrides.

Full size image

The Debye temperature (θD) quantifies the mean vibrational energy of the constituent atoms within a solid. It bears a correlation to the propagation velocity of sound as well as various thermodynamic characteristics. The Debye temperature of perovskite depends on the compositional elements and the crystal structure of the composure perovskite material. Normally, perovskites with higher atomic number masses or stiffer interatomic potentials and covalent bonds have higher Debye temperatures. From the subsequent equation, one can obtain the Debye temperature49,50:

$$\:{\theta\:}_{D}=\frac{h}{{k}_{B}}{\left[\frac{3n}{4\pi\:}\left(\frac{{N}_{a}\rho\:}{M}\right)\right]}^{1/3}\times\:{v}_{m}$$
(21)

Where Na refers to Avogadro’s number, kB corresponds to Boltzmann’s constant, and h is recognized as Planck’s constant. The average sound velocity in polycrystalline materials is as follows51:

$$\:{v}_{m}={\left[\frac{1}{3}\left(\frac{2}{{v}_{t}^{3}}+\frac{1}{{v}_{i}^{3}}\right)\right]}^{-1/3}$$
(22)

In Eq. (22), vi refers to the longitudinal sound velocity, and it corresponds to the transverse sound velocity. The shear modulus (G) and bulk modulus (B) values were used to obtain these velocities through the given expressions:

$$\:{v}_{i}=\sqrt{\frac{B+\frac{4G}{3}}{\rho\:}}$$
(23)
$$\:{v}_{t}=\sqrt{\frac{G}{\rho\:}}$$
(24)

The calculated values of sound velocities, Debye, and melting temperatures of the perovskite compounds BaBH3 and SrBH3 are given below in Table 5. It is important to note that SrBH3 has greater interatomic forces than BaBH3, which is supported by a higher bulk modulus. This is further substantiated by the high Debye temperature of SrBH3, implying that the atomic contact and lattice structure of the compound are more rigid. The Melting temperature () is a very important parameter of materials which are used for hydrogen storage and it is used to define the thermal stability of the material. An equation incorporating elastic constants is used to evaluate the melting temperatures of differing perovskites to determine their sensitivity to high temperature conditions as follows:

$$\:{T}_{m}=553+5.91{C}_{11}$$
(25)

Table 5 shows that SrBH3 has a higher melting temperature compared to BaBH3. This further indicates that SrBH3 has stronger bonds, which is essential for preserving structural integrity at the high temperatures often encountered in hydrogen storage applications. The Debye frequency (ωD), detailed as the highest vibration frequency allowed for phonons during heat transfer, can be estimated by:

$$\:{\omega\:}_{D}=\frac{{k}_{B}\times\:{\theta\:}_{D}}{h}$$
(26)
Table 5 The computed values of longitudinal sound velocity Vl (ms−1), transverse sound velocity Vt (ms−1), average sound velocity Vm (ms−1), melting temperature Tm (K) and Debye temperature θD(K) for XBH3 (X = Ba and Sr) compounds.
Full size table

Furthermore, hardness (Hv) for these materials is determined using:

$$\:{H}_{v}=0.92\times\:{\left(\frac{B}{G}\right)}^{1.137}\times\:{G}^{0.708}$$
(27)

This analysis is shown to confirm that the Debye temperatures, melting points, and hardness values so obtained are suitable for hydrogen storage in high temperature conditions. Thus, it gives essential information on how to increase the efficiency and reliability of hydrogen storage systems subjected to thermal stress. The elastic constants, along with the sound velocities, provide significant insight into the ways in which the intrinsic material parameters contribute to enhancing the overall stability and operational efficiency of materials specifically designed for hydrogen storage applications, while the Debye temperatures (θD) that are derived from these analyses are discovered to hold a central position of great importance in this context. Utilizing phonon data within the framework of the quasi-harmonic Debye model, the thermodynamic properties of XBH3 (X = Ba, Sr) hydrides were systematically analyzed, as illustrated in Fig. 12(a, b). The calculated and analyzed important properties are the Internal energy (E), Entropy (S), Helmholtz free energy (F), and Heat capacity at constant volume (Cv), these characteristics were determined within a reference temperature range spanning from 0 to 1000 K and these parameters were evaluated using the following expressions:

Fig. 12
figure 12

The temperature-dependent functions: enthalpy, free energy and entropy for XBH3 (X = Ba and Sr) hydrides.

Full size image
$$\:S\left(T\right)={k}_{B}\left(\int\:\frac{\frac{\hslash\:\omega\:}{{k}_{B}T}}{\text{exp}{\left(\frac{\hslash\:\omega\:}{{k}_{B}T}\right)}^{-1}}F\left(\omega\:\right)d\omega\:-\int\:F\left(\omega\:\right)\text{l}\text{n}[1-exp\left(\frac{\hslash\:\omega\:}{{k}_{B}T}\right)d\omega\:]\right)$$
(28)
$$\:{C}_{v}\left(T\right)=\frac{{k}_{B}\int\:{\left(\frac{\hslash\:\omega\:}{{k}_{B}T}\right)}^{2}exp\left(\frac{\hslash\:\omega\:}{{k}_{B}T}\right)F\left(\omega\:\right)d\omega\:}{{\left[exp\left(\frac{\hslash\:\omega\:}{{k}_{B}T}\right)-1\right]}^{2}}$$
(29)
$$\:E\left(T\right)={E}_{tot}-{E}_{zp}+\int\:\frac{\hslash\:\omega\:}{exp\left(\frac{\hslash\:\omega\:}{{k}_{B}T}\right)}F\left(\omega\:\right)d\omega\:$$
(30)
$$\:T\left(T\right)={E}_{tot}-{E}_{zp}+{k}_{B}T\int\:F\left(\omega\:\right)ln\left[1-exp\left(\frac{\hslash\:\omega\:}{{k}_{B}T}\right)\right]d\omega\:$$
(31)

Here, kB stands for Boltzmann’s constant, ℏ represents Planck’s constant, F(ω) signifies the phonon density of states, and T denotes the temperature. The total energy Etot and zero-point energy Ezp were evaluated as 0.47 eV for BaBH3 and 0.50 eV for SrBH3. The results reveal that both entropy and internal energy rise as temperature increases, while free energy experiences a decline. This trend aligns with the expected thermodynamic properties of stable materials. At room temperature, the CV values for BaBH3 and SrBH3 are calculated as 12.53 J/mol K and 12.05 J/mol K, respectively. Figure 13 highlights the temperature-dependent variation in heat capacity (Cₚ), providing insights into the phonon contributions to the thermal properties of these hydrides. Additionally, Fig. 12 demonstrates a linear increase in enthalpy with temperature, while entropy and free energy exhibit non-linear trends. The exponential rise in entropy, driven by increased thermal agitation, reflects greater atomic disorder, whereas free energy decreases with rising temperature. These findings underscore the thermodynamic stability of XBH3 (X = Ba, Sr) hydrides, reinforcing their potential for advanced applications, particularly in hydrogen storage.

Fig. 13
figure 13

Heat capacity of (a) BaBH3, (b) SrBH3 boron-based hydrides.

Full size image

Hydrogen storage

The gravimetric hydrogen storage capacity is a fundamental parameter for assessing a material’s suitability for solid-state hydrogen storage. It quantifies the amount of hydrogen stored per unit mass of the material, typically expressed in weight% (wt%)52. A higher gravimetric value indicates that a smaller quantity of material can store a greater amount of hydrogen, which is highly advantageous for portable and mobile energy applications.

This parameter is influenced by several factors, including the intrinsic composition of the material, operating temperature and pressure conditions, and the underlying hydrogen absorption–desorption mechanisms. Among the various solid-state storage media, metal hydrides, complex hydrides, and porous adsorption-based materials are widely recognized as leading candidates due to their favorable hydrogen uptake characteristics and potential for reversible storage.

In the present investigation, the gravimetric hydrogen storage capacities of XBH₃ (X = Ba, Sr) boron-based perovskite hydrides were calculated using the gravimetric ratio, which measures the mass fraction of hydrogen relative to the total mass of the host material. The calculation incorporates three parameters:

  • mH — molar mass of hydrogen,

  • mHost — molar mass of the host hydride material, and.

  • H/M — the hydrogen-to-material atomic ratio.

The obtained values, summarized in Table 1, reveal that BaBH₃ exhibits a gravimetric capacity of 1.96 wt%, whereas SrBH₃ shows a significantly higher capacity of 2.89 wt%. The notably superior value for SrBH₃ indicates that it can store a greater proportion of hydrogen per unit mass than BaBH₃, highlighting its enhanced promise for high-performance hydrogen storage systems. This capacity is determined through the subsequent equation:

$$\:{C}_{wt}\%=\left(\frac{\frac{H}{M}{m}_{H}}{{m}_{Host}+\frac{H}{M}{m}_{H}}\times\:100\right)\%$$
(32)

Overall, the results confirm that although both boron-derived perovskites demonstrate potential for hydrogen storage applications, SrBH₃ possesses a more favorable hydrogen-to-mass ratio, making it a more efficient candidate for practical solid-state storage compared to BaBH₃.

Conclusion

In this study, we employed Density Functional Theory (DFT) with the WIEN2K code to assess the structural, electrical, optical, mechanical, magnetic, thermal, and hydrogen storage characteristics of XBH₃ (X = B, Sr) boron-based hydrides, highlighting their significant potential for hydrogen storage applications. Notably, the gravimetric hydrogen storage capacities of 1.96 wt% for BaBH₃, and 2.89 wt% for SrBH₃ highlight their strong performance as hydrogen storage materials. The analysis of optoelectronic parameters highlights their metallic nature, high dielectric response in the visible spectrum, and efficient thermal conductivity. The XBH₃ (X = Ba, Sr) boron-based hydrides exhibit cubic structures and are thermodynamically, mechanically, and dynamically stable, with negative formation energies confirming their stability. Mechanical stability is confirmed by their Pugh’s ratio and Cauchy pressure, while their optical properties, including high dielectric functions and ultraviolet absorption peaks, enhance their potential for optoelectronic applications. These findings collectively suggest that XBH₃ (X = Ba, Sr) boron-based hydrides are highly suitable candidates for advancing hydrogen storage technologies, contributing to the development of sustainable and efficient energy solutions.