Synergistic augmentation of BDS PPP-B2b: integrating LEO constellations and wide-lane ambiguity resolution for instantaneous convergence

Abstract

To address the slow convergence issue of PPP-B2b, this paper proposes a positioning method that integrates wide-lane ambiguity resolution (WAR) with low earth orbit (LEO) synergistic enhancement. First, based on an uncombined precise point positioning (PPP) model that accounts for the clock constant bias (CCB), the extra-wide lane (EWL) and wide-lane (WL) fractional cycle biases (FCBs) for GPS/BDS-3 were extracted. Subsequently, two hybrid LEO constellations with scales of 96 and 144 satellites were designed, and multi-frequency observations were simulated. Finally, four sets of progressive experiments (float solution, wide-lane fixed solution, LEO-enhanced float solution, and synergistic enhanced solution) were designed to evaluate the enhancement performance. The results demonstrate that both WAR and LEO enhancement can improve the accuracy and convergence performance of PPP-B2b, with temporal complementarity during the convergence stage. Specifically, WAR enhancement improves the initial epoch accuracy to decimeter-level and reduces the average convergence time by over 30%, while LEO enhancement requires multiple epoch accumulations but achieves or even surpasses the WAR enhancement within a short time (e.g., 20–40 s) due to its rapid geometric variation advantage, reducing the average convergence time from approximately 20 min to 1–2 min. The synergistic enhancement of both methods balances the initial epoch parameter estimation accuracy and rapid convergence advantage, achieving improvements in average accuracy and convergence time of over 70% and 90%, respectively.

Introduction

The Beidou Navigation Satellite System (BDS) is a Global Navigation Satellite System (GNSS) independently developed by China. The BDS-3 constellation completed its global deployment in July 2020 and has since officially provided global Positioning, Navigation, and Timing (PNT) services¹. Its service quality and signal availability in the Asia–Pacific region, a primary coverage area for services like PPP-B2b, have been positively evaluated in various studies, including performance analyses from India^2,3. Compared with previous generations, BDS-3 features a more comprehensive signal architecture while retaining distinctive functions like short-message communication. New signals such as B1C, B2a, and B2b have been added, enhancing its compatibility and interoperability with other systems like GPS and Galileo⁴. Notably, BDS-3 utilizes the PPP-B2b signal as a data broadcast channel. Correction parameters, such as GNSS precise orbits and clock errors, are transmitted via its Geostationary Earth Orbit (GEO) satellites to provide augmentation services for users in China and surrounding regions⁵. As the PPP-B2b service operates independently of ground communication networks, it supports real-time PPP applications in areas with poor communication connectivity, such as deserts and offshore regions.

Currently, the PPP-B2b service primarily covers China and its neighboring areas, with availability exceeding 80%^6,7. Applying PPP-B2b corrections to broadcast ephemerides significantly mitigates orbit discontinuity during ephemeris updates, improving radial accuracy to several centimeters, while clock accuracy reaches the sub-nanosecond level, meeting the requirements for real-time PPP⁷. Further enhancement of PPP-B2b product performance can be achieved by parameterizing residual orbit and clock errors through functional or stochastic models^8,9,10,11. Typically, the standard PPP-B2b service achieves static centimeter-level and kinematic decimeter-level positioning accuracy, but this requires approximately 10–20 min of convergence time^12,13,14. This significantly limits its application in high real-time scenarios and represents a critical technical bottleneck in the field. The underlying reason lies in the inherent weakness of the PPP model and the strong correlation among parameters, necessitating extended filtering time for precise parameter separation.

To improve the real-time performance of PPP-B2b, researchers worldwide have conducted numerous valuable studies focusing on multi-frequency multi-system integration, undifferenced ambiguity resolution, regional atmospheric augmentation, and Low Earth Orbit (LEO) enhancement. From the perspective of multi-frequency multi-system performance enhancement, the PPP-B2b service, by fully leveraging its multi-frequency signals (e.g., B1I, B1C, B2a, B3I) and integrating with multi-system like GPS, achieves comprehensive optimization of real-time precise point positioning performance. Compared to using BDS-3 alone, adopting a GPS/BDS-3 dual-system configuration reduces convergence time by approximately 30%¹⁵. Based on BDS-3 five-frequency PPP-B2b, the convergence time can be controlled within 15 min, representing a 29% reduction compared to the dual-frequency model¹⁶. Implementing multi-frequency undifferenced ambiguity resolution fundamentally mitigates its correlation with parameters like coordinates and is a key technical pathway for achieving rapid and precise coordinate estimation. In BDS triple-frequency PPP research, Li et al. shortened the convergence time by about 18% through ambiguity resolution¹⁷. Constructed based on multi-frequency combination theory, Extra-Wide-Lane (EWL) and Wide-Lane (WL) ambiguities can typically be fixed within one minute or even instantaneously owing to their longer wavelengths and stronger resistance to residual errors, enabling rapid decimeter-level convergence^{18,19,20,21,22}. Furthermore, utilizing the constraints from fixed EWL/WL ambiguities can also shorten the initialization time of Narrow-Lane (NL) ambiguities^21,22,23. For real-time PPP-B2b applications, Tao et al. extracted compatible Observable-Specific Bias (OSB) products and broadcast them at 90-s intervals. Through ambiguity resolution, positioning accuracy improved by over 60%, and convergence time was reduced to within 5 min²⁴. Yuan et al. proposed a single-station State-Space Representation (SSR) augmentation method for PPP-B2b ambiguity resolution. Its performance correlates with baseline length, achieving ambiguity resolution within tens of seconds for short to medium baselines, while requiring about 10 min for convergence in long-baseline scenarios²⁵.

Drawing on the technical approach of Network Real-Time Kinematic (NRTK), another focal technique in recent years is PPP-RTK. This involves extracting high-precision atmospheric delays, performing regional modeling, and applying regional atmospheric constraints to achieve rapid centimeter-level positioning comparable to NRTK, building upon ambiguity resolution^26,27,28. However, its performance is limited by the scale of reference network and atmospheric activity. Centimeter-level atmospheric modeling over large areas remains challenging, and the service is unavailable in regions without reference station coverage, such as deserts^29,30,31. Additionally, high-precision atmospheric extraction often relies on the correct fixing of NL ambiguities. Considering the current lack of publicly available phase bias products suitable for PPP-B2b, Zhao et al. explored the feasibility of PPP-RTK based on PPP-B2b float solutions. By optimizing the stochastic model for atmospheric augmentation information, they achieved horizontal positioning accuracy better than 10 cm within 1 min³².

Exploring how to extend instantaneous high-precision positioning capability from regional augmentation to any location globally has become a highly worthwhile topic. LEO constellations, with their unique advantages of global coverage and rapid geometric changes, present a highly feasible solution. Su et al. investigated LEO-augmented BDS-only PPP, reducing the convergence time from 30 min to about 1 min³³. Li et al. conducted experiments based on multiple LEO constellations of different scales, reporting reductions of over 90% in both the convergence time of float solutions and the initialization time of fixed solutions^34,35. In obstructed environments, introducing LEO satellites can also improve PPP convergence time and ambiguity fixing rate to varying degrees³⁶. Hong et al. studied LEO-augmented PPP-RTK, demonstrating a significant reduction in the Time To First Fix (TTFF) of ambiguities³⁷. Integrating LEO constellations into PPP-B2b, when more than three LEO satellites are available, the average convergence time can be reduced to within 1 min³⁸. Furthermore, combining multiple augmentation methods, such as jointly using LEO and atmospheric enhancements, can yield better performance than any single method alone³⁹. Beyond theoretical simulation studies, the practical impetus for LEO-augmented PPP is strengthening rapidly with the large-scale deployment of global LEO constellations. Internationally, mega-constellations like SpaceX’s Starlink (with over 6,000 satellites launched as of early 2025) are primarily for broadband communication, yet their sheer scale offers inherent potential for geometric diversity in positioning. Concurrently, dedicated commercial PNT constellations are emerging, such as Xona Space Systems and TrustPoint, which are developing LEO satellites explicitly designed to provide alternative, robust PNT services. Domestically, China is also advancing its LEO infrastructure through national projects and commercial initiatives like the CENTISPACE™ constellation, which is designed to provide PPP enhancement services⁴⁰. This global trend underscores the timeliness and practical significance of researching LEO-augmented PPP algorithms, particularly for integration with existing systems like PPP-B2b.

Previous studies have made significant progress in either LEO-augmented PPP or ambiguity-resolved PPP independently, often utilizing post-processed precise products. However, a systematic investigation that integrates these two techniques within the real-time PPP-B2b service framework has been lacking. Crucially, the temporal complementarity between instantaneous ambiguity resolution and geometry-driven convergence, as well as their potential synergistic effect, has not been quantitatively explored for PPP-B2b. This study fills this gap by proposing and evaluating a combined WAR + LEO enhancement scheme specifically designed for PPP-B2b, with a novel focus on dissecting their complementary roles and quantifying the resulting synergy in accelerating convergence.

The structure of this paper is as follows: Section "Models and methodology" systematically elaborates the research methodology, including the multi-frequency uncombined PPP model considering the PPP-B2b clock constant bias (CCB), the wide-lane ambiguity solution (WAR) enhancement strategy, and the LEO constellation augmentation scheme. Section "Experimental results and analysis" presents the experimental analysis, sequentially evaluating the characteristics of EWL/WL FCBs, and comprehensively comparing the positioning performance of various enhancement strategies. Section "Discussion" provides an in-depth discussion of the mechanisms and implications of the research findings. Section "Conclusions" summarizes the main conclusions of the study. Through this research framework, the synergistic mechanism of LEO augmentation and ambiguity resolution in enhancing PPP-B2b service performance is systematically investigated.

Models and methodology

Multi-frequency uncombined PPP model accounting for PPP-B2b clock constant bias

The message types of the PPP-B2b augmentation service are listed in Table 1. Currently, it primarily broadcasts corrections for the dual-system (GPS/BDS-3), including orbits, clock, and Differential Code Biases (DCBs), to China and surrounding regions. The orbit corrections comprise Radial (R), Along-track (T), and Cross-track (N) components. Specifically, the orbit and clock corrections are used to rectify errors in the broadcast ephemeris, while the DCB corrections are used to unify the multi-frequency pseudorange reference⁴¹.

Table 1 PPP-B2b message type definitions.

The method for applying the PPP-B2b corrections is as follows ⁴¹:

$$\left\{ \begin{gathered} X_{{{\text{B2b}}}}^{{s,{\text{Q}}}} = X_{{{\text{brd}}}}^{{s,{\text{Q}}}} - \left[ {e_{{\text{r}}} \, e_{{\text{a}}} \, e_{{\text{c}}} } \right] \cdot \Delta O \hfill \\ t_{{{\text{B2b}}}}^{{s{\text{,Q}}}} = t_{{{\text{brd}}}}^{{s{\text{,Q}}}} - \frac{{C_{0} }}{c} \hfill \\ \tilde{P}_{{{\text{signal}}}} = P_{{_{{{\text{signal}}}} }} - {\text{DCB}}_{{{\text{signal}}}} \hfill \\ \end{gathered} \right.$$

(1)

where the superscript $s$ denotes different satellites; the superscript ${\text{Q}}$ denotes different constellations (Q = G for GPS, Q = C for BDS-3); the subscript ${\text{signal}}$ denotes a specific signal frequency; $c$ is the speed of light in vacuum; $X_{{{\text{brd}}}}^{{s,{\text{Q}}}}$ and $t_{{{\text{brd}}}}^{{s{\text{,Q}}}}$ are the satellite position and clock bias calculated from the broadcast ephemeris (using LNAV for GPS and CNAV1 for BDS-3, respectively); $\Delta O$, $C_{0}$, and ${\text{DCB}}_{{{\text{signal}}}}$ are the orbit, clock, and DCB corrections broadcast by PPP-B2b (in meters); $e_{{\text{r}}}$, $e_{{\text{a}}}$, $e_{{\text{c}}}$ are the unit vectors in the radial, along-track, and cross-track directions, respectively; $X_{{{\text{B2b}}}}^{{s,{\text{Q}}}}$ and $t_{{{\text{B2b}}}}^{{s{\text{,Q}}}}$ are the corrected satellite position and clock bias; $P_{{_{{{\text{signal}}}} }}$ and $\tilde{P}_{{{\text{signal}}}}$ are the pseudorange observations before and after DCB correction, respectively.

Compared to conventional multi-frequency uncombined PPP, the PPP-B2b-based model must address two key aspects. First, the clock references differ between GPS and BDS-3 broadcast ephemerides; for instance, GPS uses an L1/L2 ionosphere-free combination, whereas BDS-3 uses the B6I frequency. The model must unify them to a dual-frequency ionosphere-free combination reference, which also aligns with the widely adopted International GNSS Service (IGS) data processing standards. Second, a significant satellite-dependent Clock Constant Bias (CCB) is present in PPP-B2b clock corrections and must be compensated for in the model.

Considering the above two factors, the multi-frequency uncombined PPP model accounting for CCB can be constructed as follows³²:

$$\left\{ \begin{gathered} P_{r,1}^{{s,{\text{Q}}}} = \rho_{r}^{{s,{\text{Q}}}} + c \cdot \tilde{t}_{{r,{\text{IF}}}}^{{\text{Q}}} - c \cdot t_{{{\text{B2b}}}}^{{s{\text{,Q}}}} { + }M_{r}^{{s,{\text{Q}}}} \cdot T_{r} { + }\gamma_{1} \cdot \tilde{I}_{r,1}^{{s,{\text{Q}}}} { + }b^{{s,{\text{Q}}}} - D^{{s,{\text{Q}}}} + e_{r,1}^{{s,{\text{Q}}}} \hfill \\ P_{r,2}^{{s,{\text{Q}}}} = \rho_{r}^{{s,{\text{Q}}}} + c \cdot \tilde{t}_{{r,{\text{IF}}}}^{{\text{Q}}} - c \cdot t_{{{\text{B2b}}}}^{{s{\text{,Q}}}} { + }M_{r}^{{s,{\text{Q}}}} \cdot T_{r} { + }\gamma_{2} \cdot \tilde{I}_{r,1}^{{s,{\text{Q}}}} { + }b^{{s,{\text{Q}}}} - D^{{s,{\text{Q}}}} + e_{r,2}^{{s,{\text{Q}}}} \hfill \\ \vdots \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \vdots \hfill \\ P_{r,i}^{{s,{\text{Q}}}} = \rho_{r}^{{s,{\text{Q}}}} + c \cdot \tilde{t}_{{r,{\text{IF}}}}^{{\text{Q}}} - c \cdot t_{{{\text{B2b}}}}^{{s{\text{,Q}}}} { + }M_{r}^{{s,{\text{Q}}}} \cdot T_{r} { + }\gamma_{i} \cdot \tilde{I}_{r,1}^{{s,{\text{Q}}}} { + }b^{{s,{\text{Q}}}} - D^{{s,{\text{Q}}}} + \psi_{r,i}^{{\text{Q}}} - \psi_{i}^{{s,{\text{Q}}}} + e_{r,i}^{{s,{\text{Q}}}} \hfill \\ L_{r,1}^{{s,{\text{Q}}}} = \rho_{r}^{{s,{\text{Q}}}} + c \cdot \tilde{t}_{{r,{\text{IF}}}}^{{\text{Q}}} - c \cdot t_{{{\text{B2b}}}}^{{s{\text{,Q}}}} { + }M_{r}^{{s,{\text{Q}}}} \cdot T_{r} - \gamma_{1} \cdot \tilde{I}_{r,1}^{{s,{\text{Q}}}} { + }b^{{s,{\text{Q}}}} - D^{{s,{\text{Q}}}} + \lambda_{1} \cdot \overline{N}_{r,1}^{{s,{\text{Q}}}} + \varepsilon_{r,1}^{{s,{\text{Q}}}} \hfill \\ L_{r,2}^{{s,{\text{Q}}}} = \rho_{r}^{{s,{\text{Q}}}} + c \cdot \tilde{t}_{{r,{\text{IF}}}}^{{\text{Q}}} - c \cdot t_{{{\text{B2b}}}}^{{s{\text{,Q}}}} { + }M_{r}^{{s,{\text{Q}}}} \cdot T_{r} - \gamma_{2} \cdot \tilde{I}_{r,1}^{{s,{\text{Q}}}} { + }b^{{s,{\text{Q}}}} - D^{{s,{\text{Q}}}} + \lambda_{2} \cdot \overline{N}_{r,2}^{{s,{\text{Q}}}} + \varepsilon_{r,2}^{{s,{\text{Q}}}} \hfill \\ \vdots \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \vdots \hfill \\ L_{r,i}^{{s,{\text{Q}}}} = \rho_{r}^{{s,{\text{Q}}}} + c \cdot \tilde{t}_{{r,{\text{IF}}}}^{{\text{Q}}} - c \cdot t_{{{\text{B2b}}}}^{{s{\text{,Q}}}} { + }M_{r}^{{s,{\text{Q}}}} \cdot T_{r} - \gamma_{i} \cdot \tilde{I}_{r,1}^{{s,{\text{Q}}}} { + }b^{{s,{\text{Q}}}} - D^{{s,{\text{Q}}}} + \lambda_{i} \cdot \overline{N}_{r,i}^{{s,{\text{Q}}}} + \varepsilon_{r,i}^{{s,{\text{Q}}}} \hfill \\ \hat{b}^{{s,{\text{Q}}}} = b^{{s,{\text{Q}}}} \hfill \\ \end{gathered} \right.$$

(2)

where the subscripts $r$ and $i$ denote the receiver and frequency, respectively; $P_{r,i}^{{s,{\text{Q}}}}$ and $L_{r,i}^{{s,{\text{Q}}}}$ represent the pseudorange and carrier-phase observations in units of length; $\rho_{r}^{{s,{\text{Q}}}}$ is the geometric distance from the receiver to the satellite; $T_{r}$ is the zenith wet delay (ZWD) and $M_{r}^{{s,{\text{Q}}}}$ is its corresponding mapping function; $\tilde{t}_{{r,{\text{IF}}}}^{{\text{Q}}}$ is the re-parameterized receiver clock error; $\tilde{I}_{r,1}^{{s,{\text{Q}}}}$ is the re-parameterized ionospheric delay at the first frequency; $\gamma_{i}$ is the ionospheric scale factor ($\gamma_{i} = {{f_{1}^{2} } \mathord{\left/ {\vphantom {{f_{1}^{2} } {f_{i}^{2} }}} \right. \kern-0pt} {f_{i}^{2} }}$); $\lambda_{i}$ and $\overline{N}_{r,i}^{{s,{\text{Q}}}}$ are the wavelength and float ambiguity parameter, respectively; $\psi_{r,i}^{{\text{Q}}}$ and $\psi_{i}^{{s,{\text{Q}}}}$ are the receiver-end and satellite-end Inter-Frequency Bias (IFB) parameters introduced by multi-frequency pseudoranges; $\hat{b}^{{s,{\text{Q}}}}$ is the a priori CCB constraint value extracted from the reference network; $D^{{s,{\text{Q}}}}$ is the clock reference transformation parameter for BDS-3 (not required for GPS); $e_{r,i}^{s}$ and $\varepsilon_{r,i}^{s}$ represent the observation noise for pseudorange and carrier-phase, respectively.

In the aforementioned model, the receiver-end IFBs are estimated as constants. The satellite-end IFBs are not explicitly estimated as parameters but are effectively corrected using the DCB products from PPP-B2b or Chinese Academy of Sciences (CAS) analysis center. Fundamentally, the IFB parameters represent specific linear combinations of DCBs⁴². Taking the new BDS-3 signals B1c/B2a and the GPS L5 signal as examples, the relationship between the pseudorange IFB and the DCBs can be expressed as:

$$\left\{ \begin{gathered} \psi_{{\text{B1c/B2a}}}^{{s,{\text{C}}}} = \frac{{1 - \gamma_{\text{B1c/B2a}} }}{{\gamma_{2} - 1}} \cdot \left( {{\text{DCB}}_{{{\text{B6I}}}} {\text{ - DCB}}_{{{\text{B2I}}}} } \right) + \left( {{\text{DCB}}_{{\text{B1c/B2a}}} {\text{ - DCB}}_{{{\text{B2I}}}} } \right) \hfill \\ \psi_{{{\text{L5}}}}^{{s,{\text{G}}}} = \frac{{ 1-\gamma_{\text{L5}}}}{{\gamma_{2} - 1}} \cdot \left( {{\text{DCB}}_{{{\text{L2}}}} {\text{ - DCB}}_{{{\text{L1}}}} } \right) + \left( {{\text{DCB}}_{{{\text{L5}}}} {\text{ - DCB}}_{{{\text{L1}}}} } \right) \hfill \\ \end{gathered} \right.$$

(3)

Similarly, the BDS-3 clock reference transformation parameter can also be calculated using the corresponding DCB information:

$$D^{{s,{\text{C}}}} = \frac{{f_{{{\text{B2I}}}}^{2} }}{{f_{{{\text{B2I}}}}^{2} - f_{{{\text{B6I}}}}^{2} }} \cdot {\text{DCB}}_{{{\text{B2I}}}}$$

(4)

where $f_{{{\text{B2I}}}}$ and $f_{{{\text{B6I}}}}$ are the frequencies of the B2I and B6I signals, respectively; ${\text{DCB}}_{{{\text{B2I}}}}$ is the DCB correction for the B2I frequency broadcast by PPP-B2b.

The parameters to be estimated in the model described by Eq. (2) include non-ambiguity parameters such as receiver position, receiver clock error, and ZWD, as well as multi-frequency float ambiguity parameters for each satellite.

$$X = \left[ {\underbrace {{x,\tilde{t}_{{r,{\text{IF}}}}^{{\text{Q}}} ,T_{r} ,\tilde{I}_{r,1}^{{s,{\text{Q}}}} ,\psi_{r,i}^{{\text{Q}}} ,b^{{s,{\text{Q}}}} }}_{{\text{Non - Ambiguity}}},\underbrace {{\overline{N}_{r,1}^{{s,{\text{Q}}}} ,\overline{N}_{r,2}^{{s,{\text{Q}}}} , \cdots ,\overline{N}_{r,i}^{{s,{\text{Q}}}} }}_{{\text{Multi - Frequency Raw Ambiguity}}}} \right]$$

(5)

where $x$ represents the receiver position; for convenience in subsequent description, the non-ambiguity parameters are denoted by $a = \left[ {x,\tilde{t}_{{r,{\text{IF}}}}^{{\text{Q}}} ,T_{r} ,\tilde{I}_{r,1}^{{s,{\text{Q}}}} ,\psi_{r,i}^{{\text{Q}}} ,b^{{s,{\text{Q}}}} } \right]$.

For instance, when processing BDS-3 quad-frequency data (B1c/B2I/B2a/B6I), the parameter vector $X$ consists of the following: the non-ambiguity part includes 3 coordinates, 1 receiver clock, 1 ZWD, and 2 receiver IFB parameters (for the B1c and B2a signals). Additionally, for each of the $m$ observed satellites, one ionospheric delay parameter and one CCB parameter are estimated. The ambiguity part contains 4 float ambiguity parameters per satellite. Thus, the total dimension of $X$ is 7 + 2 m + 4 m.

Regarding the estimation strategy: coordinate parameters are treated as constants for static processing or white noise for kinematic processing; the receiver clock bias is typically estimated as white noise; atmospheric parameters (e.g., ionospheric delay, ZWD) exhibit strong temporal correlation and are therefore modeled as random-walk processes; ambiguities and associated hardware biases (e.g., receiver-end IFB) are estimated as constants for a given continuous arc.

PPP-B2b enhanced by wide-lane ambiguity resolution (WAR)

The reliability of PPP positioning can be improved through the integer constraints imposed by ambiguity resolution. Given the limited accuracy of PPP-B2b orbit and clock corrections, reliably fixing narrow-lane ambiguities directly remains challenging. Therefore, this paper primarily focuses on fixing Extra-Wide-Lane (EWL) and Wide-Lane (WL) ambiguities. Importantly, a wide-lane fixed solution is considered successfully achieved only when both the EWL and WL ambiguities are fixed simultaneously.

EWL/WL FCB estimation methodology

In undifferenced data processing, float ambiguity parameters lose their integer nature because they absorb hardware delay biases. Consequently, high-precision Fractional Cycle Bias (FCB) must be estimated prior to ambiguity resolution to restore this integer characteristic. Without loss of generality, any float ambiguity can be expressed as the sum of an integer component and a combination of receiver-end and satellite-end FCB:

$$\overline{N}_{r}^{s} = N_{r}^{s} + d_{r} - d^{s}$$

(6)

where $N_{r}^{s}$ is the integer ambiguity; $d_{r}$ and $d^{s}$ are the receiver-end and satellite-end FCB, respectively.

Theoretically, FCB estimation is possible using data from a single reference station. However, in practice, a global or regional network of reference stations is typically employed to ensure the accuracy and reliability of the estimated FCB. For instance, for a network comprising $m$ reference stations simultaneously observing $n$ satellites, the undifferenced ambiguities for all station-satellite pairs can be combined into the following system of equations⁴³:

$$\left[ {\begin{array}{*{20}c} {V_{1} } \\ {V_{2} } \\ \vdots \\ {V_{m} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {R_{1} } \hfill & {S^{1} } \hfill \\ {R_{2} } \hfill & {S^{2} } \hfill \\ \vdots \hfill & \vdots \hfill \\ {R_{m} } \hfill & {S^{m} } \hfill \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}l} {d_{1} } \hfill \\ {d_{2} } \hfill \\ \vdots \hfill \\ {d_{m} } \hfill \\ {d^{1} } \hfill \\ {d^{2} } \hfill \\ \vdots \hfill \\ {d^{n} } \hfill \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} {L_{1} } \\ {L_{2} } \\ \vdots \\ {L_{m} } \\ \end{array} } \right]$$

(7)

where $d_{j} (j = 1,2, \cdots ,m)$ represents the receiver-end FCB parameters; $d^{j} (j = 1,2, \cdots ,n)$ represents the satellite-end FCB parameters; $L_{j} (j = 1,2, \cdots ,m)$ is the observation vector from all stations; $R_{j}$ and $S^{j} (j = 1,2, \cdots ,m)$ are the design matrices corresponding to the stations, with dimensions of $n \times m$ and $n \times n$ respectively. In matrix $R_{j}$, all elements in the j-th column are 1 while all other elements are 0. In matrix $S^{j}$, all diagonal elements are -1 while all off-diagonal elements are 0. $V_{j} (j = 1,2, \cdots ,m)$ represents the residual vector of the stations. Meanwhile, the specific form of $L_{j} (j = 1,2, \cdots ,m)$ is given by:

$$L_{j} = \left[ {\begin{array}{*{20}c} {\overline{N}_{j}^{1} - N_{j}^{1} } \\ {\overline{N}_{j}^{2} - N_{j}^{2} } \\ \vdots \\ {\overline{N}_{j}^{n} - N_{j}^{n} } \\ \end{array} } \right]$$

(8)

It is important to note that the receiver and satellite FCBs are linearly dependent; the model described by Eq. (7) has a rank deficiency of 1. This is typically resolved by applying a pseudo-observation constraint to the FCB of one chosen satellite or receiver to achieve a full-rank model:

$$C = d^{{{\text{ref}}}}$$

(9)

where ${\text{ref}}$ represents the selected reference satellite, and the constraint value $C$ is theoretically arbitrary (often set to 0).

Combining Eqs. (7) and (9), the receiver and satellite FCBs are estimated using an iterative least-squares algorithm. To improve the performance of the FCB estimation, ambiguities with post-fit residuals exceeding a predefined threshold (e.g., 0.3 cycles) can be down-weighted or eliminated during the iterative process⁴³.

Since the regional reference network cannot guarantee continuous tracking of a single satellite, the reference satellite used in the solution may change across epochs. To ensure the continuity and stability of the FCB time series, the following strategy is adopted: For each epoch, the satellite with the highest number of continuous tracking records within the regional network is selected as the current reference. For the first epoch, its FCB constraint value can be set arbitrarily (typically to zero); for all subsequent epochs, the FCB constraint value for the current reference satellite is set to its estimated value from the immediately preceding epoch. This method, through constraint transfer between adjacent epochs, effectively prevents datum jumps caused by reference satellite changes and ensures the temporal continuity of the FCB products.

For uncombined PPP, theoretically, the float ambiguities of the raw frequencies can be used directly as observations in the aforementioned iterative least-squares model to obtain the FCBs for the respective frequencies. However, in practice, the raw frequencies have short wavelengths, making them sensitive to residual ionospheric delays, multipath, and unmodeled errors. Consequently, they might be down-weighted or rejected as outliers during the quality control of the iterative estimation, adversely affecting the FCB estimation performance. Therefore, a common strategy in practical data processing is to perform a linear transformation of the raw ambiguities to form combined ambiguities with long-wavelength characteristics, such as EWL and WL combinations, before estimating the FCBs. Based on existing research, Table 2 lists the EWL and WL combinations adopted in this paper³¹.

Table 2 EWL/WL ambiguity combinations used for FCB estimation.

Sequential EWL/WL resolution with PAR strategy

Based on the PPP-B2b float solution $(X,Q_{XX} )$, the satellite with the highest elevation angle is selected as the reference satellite. Between-satellite single-differences and transformation matrices for EWL/WL combinations are then constructed. This process eliminates the influence of receiver-end FCBs and yields a float solution that simultaneously includes EWL ambiguities, WL ambiguities, and other non-ambiguity parameters (such as position and tropospheric delay), along with their complete variance–covariance matrix³¹.

$$\left\{ \begin{gathered} X_{{{\text{LC}}}} = D \cdot X = \left[ {a,\underbrace {{\overline{N}_{{r,{\text{WL}}}}^{{s,{\text{Q}}}} ,\overline{N}_{{r,{\text{EWL}}}}^{{s,{\text{Q}}}} }}_{{\text{WL/EWL Ambiguity}}}} \right] \hfill \\ Q_{{XX,{\text{LC}}}} = D \cdot Q_{XX} \cdot D^{{\text{T}}} \hfill \\ \end{gathered} \right.$$

(10)

where $D$ represents the between-satellite single-differenced EWL and WL transformation matrix; $\overline{N}_{{r,{\text{WL}}}}^{{s,{\text{Q}}}}$ and $\overline{N}_{{r,{\text{EWL}}}}^{{s,{\text{Q}}}}$ denote the vectors of WL and EWL float ambiguities for each satellite, respectively.

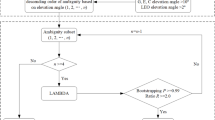
The satellite-end FCBs of the single-differenced ambiguities are corrected to restore their integer nature. Sequential fixing of EWL and WL ambiguities is then performed in order of decreasing wavelength. Specifically: The LAMBDA method is first used to search for and fix the EWL ambiguities. The fixed EWL ambiguities are then imposed as strong constraints to update the float solutions of the WL ambiguities and other parameters, along with their variance–covariance matrix⁴⁴. Subsequently, the updated WL ambiguities are searched and fixed. In this study, a valid WL fixed solution at a given epoch is considered successfully achieved only when both the EWL and WL ambiguities are fixed for that same epoch.

To further enhance the efficiency and reliability of ambiguity resolution, a Partial Ambiguity Resolution (PAR) strategy is incorporated into the aforementioned sequential fixing process. By applying elevation masks with progressively increasing cutoff angles, a subset of ambiguities is selected for fixing. This helps avoid fixing failures caused by poor-quality observations from low-elevation satellites (e.g., those severely affected by multipath errors), thereby improving the success rate of EWL/WL ambiguity fixing^45,46.

PPP-B2b enhanced by LEO constellations

Given the current limited number of LEO satellites carrying navigation payloads, this paper employs simulated LEO constellations for analysis. First, the design scheme of the LEO constellations is introduced, followed by an explanation of the simulation strategy for LEO pseudorange and carrier phase observations.

Design of multi-scale LEO constellations

To evaluate the enhancement effect of LEO constellation scale on the PPP-B2b service, this study designed two LEO constellation schemes with hybrid orbit configurations using the STK software; the detailed parameters are listed in Table 3. Both schemes adopt an orbital altitude of 1000 km. Scheme 1 consists of 96 LEO satellites, employing a “polar orbit + dual-inclination” configuration, with the inclinations of the two orbital planes being 40° and 55° respectively. The polar-orbiting satellites ensure basic global coverage capability, while the inclined satellites provide targeted coverage over most core areas of China. Scheme 2 consists of 144 LEO satellites, utilizing a “polar orbit + triple-inclination” configuration. The three orbital planes with inclinations of 35°, 50°, and 65° theoretically enable effective coverage of the Asia–Pacific region from low to high latitudes. The configurations of the two schemes are shown in Fig. 1, and their ground tracks over a single day are shown in Fig. 2. For comparison, the GNSS (GPS and BDS-3) constellation structures are also displayed in the figures, where the GNSS orbit information is derived from the real-tracked Two-Line Element (TLE) files provided by North American Aerospace Defense Command (NORAD). It can be observed that due to the high velocity and shorter orbital period of LEO satellites, their ground track coverage within a single day is significantly denser.

Table 3 Design parameters of LEO constellations with different scales.

Fig. 1

Schematic diagram of the GNSS and LEO constellations (Left: BDS-3 in blue, GPS in green; Middle: Scheme 1 with 96 LEO satellites; Right: Scheme 2 with 144 LEO satellites).

Fig. 2

Ground tracks of the GNSS and LEO constellations.

Simulation of LEO observations

The pseudorange and carrier phase observation equations describe the functional relationship between the station-satellite geometric range and various error sources. Observation simulation can be regarded as the inverse process of precise positioning solution, i.e., based on the true geometric range, various errors such as atmospheric delays, clock errors, and tidal effects are synthetically added. For a specific frequency, the pseudorange and carrier phase observation equations can be expressed as:

$$\left\{ \begin{gathered} P_{r,i}^{{s,{\text{L}}}} = \rho_{r}^{{s,{\text{L}}}} + c \cdot t_{r}^{{\text{L}}} - c \cdot t^{{s,{\text{L}}}} { + }T_{r}^{{s,{\text{L}}}} { + }\gamma_{i} \cdot I_{r,1}^{{s,{\text{L}}}} + e_{r,i}^{{s,{\text{L}}}} \hfill \\ L_{r,i}^{{s,{\text{L}}}} = \rho_{r}^{{s,{\text{L}}}} + c \cdot t_{r}^{{\text{L}}} - c \cdot t^{{s,{\text{L}}}} { + }T_{r}^{{s,{\text{L}}}} - \gamma_{i} \cdot I_{r,1}^{{s,{\text{L}}}} + \lambda_{i} \cdot N_{r,i}^{{s,{\text{L}}}} + \varepsilon_{r,i}^{{s,{\text{L}}}} \hfill \\ \end{gathered} \right.$$

(11)

where the superscript ${\text{L}}$ denotes parameters related to the LEO constellation; $t_{r}^{{\text{L}}}$ and $t^{{s,{\text{L}}}}$ represent the receiver and satellite clock errors for the LEO constellation, respectively; $T_{r}^{{s,{\text{L}}}}$ denotes the slant tropospheric delay; $I_{r,1}^{{s,{\text{L}}}}$ is the slant ionospheric delay for the LEO satellite at the first frequency; and $N_{r,i}^{{s,{\text{L}}}}$ is the corresponding integer ambiguity.

This paper simulates L1/L2/L5/L6 four-frequency LEO observation data. Considering the relatively short orbital period of LEO satellites, the sampling rate is set to 1 s. The simulation strategies for the main error terms involved in Eq. (11) are listed in Table 4. Notably, for the tropospheric delay, to ensure the consistency of the common ZWD parameter during the subsequent combined processing of the simulated LEO data and the real-tracked GNSS data, the ZWD estimates obtained from the static PPP solution of the reference stations were used in the simulation of the tropospheric error term. To make the observations more realistic, an elevation-dependent stochastic model was used to calculate the random noise for different observations, with the standard deviations for zenith pseudorange and carrier phase observations set to 0.3 m and 3 mm, respectively. Furthermore, for errors not listed in the table, such as phase wind-up⁴⁷, relativistic effects, and tidal effects, established error models were used for computation.

Table 4 Simulation strategy for main error terms of LEO observations.

It is crucial to emphasize that the research focus of this paper is on utilizing the rapid geometric changes of LEO satellites to enhance the convergence performance of PPP-B2b, rather than achieving ambiguity resolution for the LEO system itself. Therefore, in the subsequent data processing strategy, the carrier phase observations from LEO satellites will always be processed as float solutions, without attempting to fix their ambiguities. Based on this core data processing strategy, no additional FCBs were simulated for the LEO carrier phase observations during the simulation stage. Furthermore, as the simulated LEO satellite constellations do not correspond to real physical satellite platforms and their antenna designs, precise satellite antenna Phase Center Offsets (PCO) and Phase Center Variations (PCV) values cannot be obtained. Consequently, reasonable simplifications were made in this paper, and LEO satellite-related antenna corrections were not simulated.

By combining Formulas (2) and (11), the LEO/GNSS fused PPP model is obtained.

$$\left\{ \begin{gathered} P_{r,1}^{{s,{\text{Q}}}} = \rho_{r}^{{s,{\text{Q}}}} + c \cdot \tilde{t}_{{r,{\text{IF}}}}^{{\text{Q}}} - c \cdot t_{{{\text{B2b}}}}^{{s{\text{,Q}}}} { + }M_{r}^{{s,{\text{Q}}}} \cdot T_{r} { + }\gamma_{1} \cdot \tilde{I}_{r,1}^{{s,{\text{Q}}}} { + }b^{{s,{\text{Q}}}} - D^{{s,{\text{Q}}}} + e_{r,1}^{{s,{\text{Q}}}} \hfill \\ P_{r,2}^{{s,{\text{Q}}}} = \rho_{r}^{{s,{\text{Q}}}} + c \cdot \tilde{t}_{{r,{\text{IF}}}}^{{\text{Q}}} - c \cdot t_{{{\text{B2b}}}}^{{s{\text{,Q}}}} { + }M_{r}^{{s,{\text{Q}}}} \cdot T_{r} { + }\gamma_{2} \cdot \tilde{I}_{r,1}^{{s,{\text{Q}}}} { + }b^{{s,{\text{Q}}}} - D^{{s,{\text{Q}}}} + e_{r,2}^{{s,{\text{Q}}}} \hfill \\ \, \vdots \, \vdots \hfill \\ P_{r,i}^{{s,{\text{Q}}}} = \rho_{r}^{{s,{\text{Q}}}} + c \cdot \tilde{t}_{{r,{\text{IF}}}}^{{\text{Q}}} - c \cdot t_{{{\text{B2b}}}}^{{s{\text{,Q}}}} { + }M_{r}^{{s,{\text{Q}}}} \cdot T_{r} { + }\gamma_{i} \cdot \tilde{I}_{r,1}^{{s,{\text{Q}}}} { + }b^{{s,{\text{Q}}}} - D^{{s,{\text{Q}}}} + \psi_{r,i}^{{\text{Q}}} - \psi_{i}^{{s,{\text{Q}}}} + e_{r,i}^{{s,{\text{Q}}}} \hfill \\ L_{r,1}^{{s,{\text{Q}}}} = \rho_{r}^{{s,{\text{Q}}}} + c \cdot \tilde{t}_{{r,{\text{IF}}}}^{{\text{Q}}} - c \cdot t_{{{\text{B2b}}}}^{{s{\text{,Q}}}} { + }M_{r}^{{s,{\text{Q}}}} \cdot T_{r} - \gamma_{1} \cdot \tilde{I}_{r,1}^{{s,{\text{Q}}}} { + }b^{{s,{\text{Q}}}} - D^{{s,{\text{Q}}}} + \lambda_{1} \cdot \overline{N}_{r,1}^{{s,{\text{Q}}}} + \varepsilon_{r,1}^{{s,{\text{Q}}}} \hfill \\ L_{r,2}^{{s,{\text{Q}}}} = \rho_{r}^{{s,{\text{Q}}}} + c \cdot \tilde{t}_{{r,{\text{IF}}}}^{{\text{Q}}} - c \cdot t_{{{\text{B2b}}}}^{{s{\text{,Q}}}} { + }M_{r}^{{s,{\text{Q}}}} \cdot T_{r} - \gamma_{2} \cdot \tilde{I}_{r,1}^{{s,{\text{Q}}}} { + }b^{{s,{\text{Q}}}} - D^{{s,{\text{Q}}}} + \lambda_{2} \cdot \overline{N}_{r,2}^{{s,{\text{Q}}}} + \varepsilon_{r,2}^{{s,{\text{Q}}}} \hfill \\ \, \vdots \, \vdots \hfill \\ L_{r,i}^{{s,{\text{Q}}}} = \rho_{r}^{{s,{\text{Q}}}} + c \cdot \tilde{t}_{{r,{\text{IF}}}}^{{\text{Q}}} - c \cdot t_{{{\text{B2b}}}}^{{s{\text{,Q}}}} { + }M_{r}^{{s,{\text{Q}}}} \cdot T_{r} - \gamma_{i} \cdot \tilde{I}_{r,1}^{{s,{\text{Q}}}} { + }b^{{s,{\text{Q}}}} - D^{{s,{\text{Q}}}} + \lambda_{i} \cdot \overline{N}_{r,i}^{{s,{\text{Q}}}} + \varepsilon_{r,i}^{{s,{\text{Q}}}} \hfill \\ \hat{b}^{{s,{\text{Q}}}} = b^{{s,{\text{Q}}}} \hfill \\ P_{r,i}^{{s,{\text{L}}}} = \rho_{r}^{{s,{\text{L}}}} + c \cdot t_{r}^{{\text{L}}} - c \cdot t^{{s,{\text{L}}}} { + }M_{r}^{{s,{\text{L}}}} \cdot T_{r} { + }\gamma_{i} \cdot I_{r,1}^{{s,{\text{L}}}} + e_{r,i}^{{s,{\text{L}}}} \hfill \\ L_{r,i}^{{s,{\text{L}}}} = \rho_{r}^{{s,{\text{L}}}} + c \cdot t_{r}^{{\text{L}}} - c \cdot t^{{s,{\text{L}}}} { + }M_{r}^{{s,{\text{L}}}} \cdot T_{r} - \gamma_{i} \cdot I_{r,1}^{{s,{\text{L}}}} + \lambda_{i} \cdot N_{r,i}^{{s,{\text{L}}}} + \varepsilon_{r,i}^{{s,{\text{L}}}} \hfill \\ \end{gathered} \right.$$

(12)

The corresponding parameters to be estimated are:

$$X_{{\text{LEO/GNSS}}} = \left[ {\underbrace {{x,\tilde{t}_{{r,{\text{IF}}}}^{{\text{Q}}} ,t_{r}^{{\text{L}}} ,T_{r} ,\tilde{I}_{r,1}^{{s,{\text{Q}}}} ,I_{r,1}^{{s,{\text{L}}}} ,\psi_{r,i}^{{\text{Q}}} ,b^{{s,{\text{Q}}}} }}_{{\text{Non - Ambiguity}}},\underbrace {{\overline{N}_{r,1}^{{s,{\text{Q}}}} ,N_{r,1}^{{s,{\text{L}}}} ,\overline{N}_{r,2}^{{s,{\text{Q}}}} ,N_{{r,{2}}}^{{s,{\text{L}}}} , \cdots ,\overline{N}_{r,i}^{{s,{\text{Q}}}} ,N_{r,i}^{{s,{\text{L}}}} }}_{{\text{LEO/GNSS Multi - Frequency Raw Ambiguity}}}} \right]$$

(13)

Experimental results and analysis

Given that the PPP-B2b signal is broadcast by three BDS-3 GEO satellites and its current effective service area primarily covers China and its surrounding regions, the experimental data selected for this study consists of reference station network data covering the Asia–Pacific region on July 21, 2025. The distribution of these stations is shown in Fig. 3. The reference stations marked in blue are used to extract FCB products for GPS and BDS-3 satellites, providing prior information for subsequent EWL/WL ambiguity resolution. The stations marked in red (GAMG, YAYC, WUH2) serve as user stations. On one hand, their precisely known coordinates are used to simulate LEO pseudorange and carrier phase observations. On the other hand, they serve as user stations for performance verification of all subsequent positioning schemes. These user stations are equipped with high-precision receivers capable of receiving multi-frequency signals from GPS (L1/L2/L5) and BDS-3 (B1c/B2I/B2a/B6I), with a data sampling rate of 1 s.

Fig. 3

Distribution of the selected reference station network in the Asia–Pacific region.

For the GPS system, observations from satellites such as those of BLOCK IIF are known to be affected by significant Inter-Frequency Clock Bias (IFCB)⁴⁸. To ensure the rigor of the multi-frequency uncombined model, the corresponding IFCB corrections were extracted and applied in the data preprocessing stage. Specifically, an epoch-differencing method based on the regional reference network was applied to the geometry-free linear combinations of L1/L2 and L1/L5. The derived corrections were then applied to the raw observations on the respective frequencies⁴⁹. This step removes the potential influence of IFCB on the integer nature of ambiguities and the estimation of other parameters, thereby enhancing the internal consistency of the GPS data processing.

The data processing in this study adopts a strategy that fuses “simulated LEO observations” with “measured GNSS observations”. Regarding ambiguity resolution, the process first simultaneously fixes three types of EWL ambiguities: GPS (L2-L5) and BDS-3 (B1c-B2I, B6I-B2a). After successfully fixing the EWL ambiguities and applying them as constraints, the process proceeds to resolve the shorter-wavelength WL ambiguities: GPS (L1-L2) and BDS-3 (B2I-B6I). Throughout the fixing process, a Ratio test threshold of 2.0 is set as the criterion for successful ambiguity resolution.

In the subsequent experiments, based on the analysis of EWL/WL FCB characteristics, the individual contributions of wide-lane ambiguity resolution (WAR) and LEO augmentation, as well as their synergistic enhancement effects, are systematically evaluated. Accordingly, the following four sets of progressive comparative experimental schemes are specifically designed for this purpose:

• (1) PPP-B2b Float Solution: Standard GPS/BDS-3 uncombined PPP float solution utilizing only PPP-B2b corrections, serving as the baseline for evaluating enhancement effects. Denoted as “PPP-B2b”.

• (2) WAR-Augmented PPP-B2b: Building on Scheme 1, introduces the aforementioned stepwise fixing strategy to resolve EWL/WL ambiguities for GPS and BDS-3. Used to assess the enhancement effect of WAR on PPP-B2b. Denoted as “PPP-B2b + AR”.

• (3) LEO-Augmented PPP-B2b Float Solution: Building on Scheme 1, integrates simulated observations from either the 96 or 144-satellite LEO constellations (while maintaining float ambiguities for LEO observations). Used to evaluate the enhancement benefit independently provided by the rapid geometric changes of LEO satellites. Denoted as “PPP-B2b + LEO96” or “PPP-B2b + LEO144”.

• (4) PPP-B2b with Combined WAR and LEO Augmentation: Integrates simulated observations from both the 96 and 144-satellite LEO constellations and fixes the EWL/WL ambiguities for GPS and BDS-3. Aims to verify the enhancement effect achievable through the synergy of both augmentation methods. Denoted as “PPP-B2b + AR + LEO96” or “PPP-B2b + AR + LEO144”.

Stability analysis of EWL/WL FCB

High-quality FCB estimates are a prerequisite for successful ambiguity resolution. Figures 4 and 5 present the EWL/WL FCB results for each GPS and BDS-3 satellites, respectively. Limited by the regional distribution of the reference network and the availability of PPP-B2b corrections, the daily FCB series for some satellites contain gaps. However, within continuous arcs, the FCBs generally demonstrate high stability. Visually, stability improves with longer wavelengths; consequently, EWL FCBs, benefiting from their significantly longer wavelengths, exhibit markedly better stability than WL FCBs. An interesting finding concerns the BDS-3 B1c-B2I EWL FCBs: the values for all satellites cluster around ± 0.5 cycles. Consequently, if one satellite is chosen as a reference, the between-satellite single-differenced FCBs cluster near 0 or 1 cycle. This phenomenon is likely attributable to the very close frequencies of B1c and B2I. Furthermore, a preliminary comparison of the WL FCB series between GPS and BDS-3 suggests that BDS-3 WL FCBs exhibit smaller fluctuations.

Fig. 4

EWL/WL FCBs for individual GPS satellites.

Fig. 5

EWL/WL FCBs for each BDS-3 satellites.

Figure 6 shows the daily standard deviation (STD) of the EWL/WL FCBs for each satellite. The STD values for EWL FCBs are all below 0.01 cycles. While the STD values for WL FCBs vary among different satellites, none exceed 0.05 cycles overall. For BDS-3, the average daily STDs for the (B1c-B2I, B6I-B2a, B2I-B6I) EWL/WL FCBs are (0.001, 0.005, 0.015) cycles, respectively. For GPS, the average daily STDs for the (L2-L5, L1-L2) EWL/WL FCBs are (0.003, 0.019) cycles, respectively. The stability of EWL FCBs is generally comparable between GPS and BDS-3, but BDS-3 demonstrates better stability for its WL FCBs.

Fig. 6

Standard deviations of EWL/WL FCBs for each GPS/BDS-3 satellites.

To comprehensively assess the quality and goodness-of-fit of the FCB estimation, the distribution of the posterior residuals from the network adjustment is further analyzed. Figures 7 and 8 presents the statistical histograms of the posterior residuals for various EWL/WL combinations of GPS and BDS-3. The analysis shows that the posterior residuals for all EWL combinations are within ± 0.1 cycles. For the wide-lane combinations, 87.92% and 99.13% of the GPS L1-L2 residuals fall within ± 0.1 cycles and ± 0.2 cycles, respectively. For BDS-3 B2I-B6I, the corresponding proportions are significantly higher, at 97.82% and 99.98%, respectively. All residuals are tightly clustered around zero with no evident systematic bias. This result, from the perspective of the internal consistency of the estimation process, further confirms the high reliability of the FCB products generated by the proposed method.

Fig. 7

Distribution of ambiguity posterior residuals from GPS EWL/WL FCB estimation (left: L2-L5 extra-wide-lane, right: L1-L2 wide-lane).

Fig. 8

Distribution of ambiguity posterior residuals from BDS-3 EWL/WL FCB estimation (left: B1c-B2I extra-wide-lane, middle: B6I-B2a extra-wide-lane, right: B2I-B6I wide-lane).

Comprehensive positioning performance evaluation

To systematically evaluate the improvement of WAR and LEO augmentation on the PPP-B2b service, this study conducted segmented batch processing for three user stations (GAMG, YAYC, WUH2) based on the aforementioned FCB products and simulated LEO data. To obtain more statistical samples while considering the convergence accuracy of the FCB products, data from 01:00 to 23:00 were divided into 1-h intervals. A kinematic PPP mode was adopted, resulting in 66 positioning solution segments from the three stations for subsequent analysis. This setup avoids the potential impacts of satellite constellation transitions and truncated observation arcs at the daily boundary (00:00 UTC) on geometric completeness. It also ensures that the network solutions used to generate the FCB products are beyond their initial convergence phase, thereby guaranteeing the stability of the products used in the subsequent positioning experiments.

Due to the substantial wavelengths of the chosen EWL/WL combinations (e.g., 20.93 m for B1c-B2I), reliable single-epoch ambiguity resolution is inherently achievable. Consequently, the Time-To-First-Fix (TTFF) is consistently 1 epoch, and the fixing rate approaches 100% across all experimental schemes, even without LEO augmentation. Therefore, LEO integration does not yield a statistically significant improvement in these particular metrics, as its primary role is to accelerate the convergence of other tightly coupled parameters (e.g., coordinates, tropospheric delay) by rapidly changing the geometric diversity, rather than to aid the fixing of the already easily resolvable long-wavelength ambiguities.

Consequently, this section will sequentially analyze the impact of WAR and different scales of LEO constellation augmentation on PPP-B2b positioning performance (particularly convergence time and positioning accuracy), further dissect the advantageous characteristics of the two enhancement methods during different convergence stages, and finally validate the comprehensive performance improvement through the synergistic enhancement scheme.

Contribution of WAR to PPP-B2b performance

Taking station GAMG as an example, Fig. 9 shows a comparison of the positioning results before and after WAR. Visually, each segment starts with the typical convergence trend of the PPP-B2b service, and the positioning error during the convergence stage is significantly smaller after WAR is applied. Figure 10 shows the average positioning error comparison across all 66 segments. Through WAR, both the positioning accuracy and convergence performance of PPP-B2b are improved. The horizontal and vertical positioning accuracies within the 1-h interval improved from (0.166, 0.257) m to (0.125, 0.190) m, representing improvements of 24.4% and 26.1%, respectively. Notably, the accuracy at the very first epoch was significantly enhanced, improving from (0.491, 0.925) m to (0.329, 0.559) m. As the filtering progressed, the results from the two methods tended to become consistent. Using thresholds of 15 cm horizontally and 30 cm vertically⁴, the convergence times after applying WAR were shortened from (1261, 472) s to (827, 290) s, representing reductions of 34.4% and 38.6%, respectively.

Fig. 9

Positioning error at station GAMG before and after WAR.

Fig. 10

Average positioning error over 1-h intervals before and after WAR.

Impact of LEO constellations on PPP-B2b performance

Generally, integrating LEO constellations offers two main advantages: firstly, the increased number of available satellites optimizes the station-satellite geometry; secondly, the fast motion of LEO satellites accelerates parameter convergence. Figure 11 first presents the sky plots of GNSS satellites (GPS/BDS-3) and LEO constellations of different scales over a 1-h period at station GAMG. The GNSS satellite tracks change slowly in the sky, with a relatively fixed distribution over short periods, resulting in sparse and slowly varying sky plots. This implies that in GNSS-only mode, the PPP solution must rely on extended observation periods to accumulate sufficient geometric diversity for adequate parameter decorrelation, consequently resulting in prolonged convergence times. In stark contrast, due to their low orbital altitude (~ 1000 km) and high velocity, the LEO satellites exhibit highly dynamic and densely covered tracks in their sky plots. Within the same period, numerous LEO satellite tracks cover almost all azimuths from low to high elevation angles, nearly uniformly covering the entire sky plot. This rapid, globally covering geometry provided by the LEO constellations means that at any given moment, the receiver can receive signals from diverse directions in space. This greatly enhances the observability of the model and is key to rapidly separating coupled parameters such as receiver position, clock errors, tropospheric delays, and ambiguities. Figure 12 compares the number of available satellites at this station after adding LEO constellations. Under the 96- and 144-LEO constellation scenarios, the average number of available satellites increased from 14.2 to 17.9 and 19.4, respectively.

Fig. 11

Comparison of LEO/GNSS sky plots at station GAMG during 05:00–06:00.

Fig. 12

Comparison of available satellite numbers under LEO96 and LEO144 constellations.

Figure 13 shows the PPP-B2b positioning results enhanced by the two different scales of LEO constellations. It can be observed that after integrating LEO constellations, the positioning errors in the N, E, and U directions converge rapidly. Furthermore, benefiting from the increased number of visible satellites, the positioning results after convergence are also more stable. Figure 14 presents the average positioning results across all segments. It can be seen that LEO constellation augmentation also improves the accuracy and convergence performance of PPP-B2b. With the 96-LEO constellation enhancement, the average horizontal and vertical accuracies improved from (0.166, 0.257) m to (0.061, 0.095) m, representing improvements of 63.2% and 63.0%, respectively. When the constellation scale was expanded to 144 satellites, the accuracy further improved to (0.047, 0.075) m, representing improvements of 71.6% and 70.6%. Using the same convergence thresholds of 15 cm horizontally and 30 cm vertically⁴, after introducing the 96- and 144-LEO constellations, the average convergence times were shortened from (1261, 472) s to (153, 78) s and (82, 55) s, respectively. These correspond to reductions of (87.9%, 83.5%) and (93.5%, 88.3%). Evidently, with the enhancement from the rapid geometric changes of LEO constellations, the PPP-B2b convergence time can be reduced from about 20 min to 1–2 min.

Fig. 13

Comparison of positioning results at station GAMG enhanced by LEO96 and LEO144 constellations, respectively.

Fig. 14

Average positioning error over 1-h intervals enhanced by LEO96 and LEO144 constellations, respectively.

Comparative analysis of enhancement strategies and synergistic effects

The preceding analyses have separately verified the effectiveness of both WAR and LEO constellation augmentation in improving PPP-B2b performance. This section provides a systematic and comprehensive comparison of the characteristics and synergistic performance of the different enhancement strategies. As shown in Fig. 15, the results indicate that WAR and LEO augmentation accelerate positioning convergence via two distinct pathways, each possessing unique advantages. The core strength of WAR lies in its instantaneity. By fixing the ambiguity parameters to integer values, it eliminates a major error source starting from the very first epoch. This leads to a stepwise improvement in positioning accuracy during the initialization phase, directly achieving approximately decimeter-level precision. In contrast, LEO augmentation still relies on the accumulation of several epochs to adequately separate parameters. However, benefiting from the rapid geometric changes introduced by their high velocity, the positioning accuracy improves swiftly over time, typically surpassing the accuracy achieved by WAR alone within 20 to 40 s. Consequently, the two enhancement strategies exhibit significant temporal complementarity during the convergence process: WAR provides superior initial parameter estimation accuracy, while LEO augmentation ensures sustained rapid convergence capability.

Fig. 15

Comparison of positioning errors during the initial 2 min under WAR, LEO96/LEO144, and combined WAR & LEO96/LEO144 augmentation schemes.

Based on the above analysis, this study further investigated a synergistic strategy that integrates the advantages of both enhancement methods. As shown in Fig. 15, this combined scheme leverages WAR to achieve decimeter-level positioning at the first epoch. Subsequently, driven by LEO augmentation, it maintains the same rapid convergence trend observed in the “PPP-B2b + LEO” solution. Ultimately, the synergistic strategy demonstrates the best overall performance among all compared schemes. It not only achieves the fastest convergence speed but also delivers optimal positioning accuracy throughout the entire convergence process, thanks to its superb initial accuracy.

To quantitatively evaluate the performance of the different enhancement strategies, Figs. 16 and 17 present statistics on the average positioning accuracy over 1-h arcs and the average time required for each scheme to reach predefined convergence thresholds (e.g., 15 cm horizontally and 30 cm vertically). The results show that under the synergistic enhancement: for the 96-LEO scenario, the average horizontal and vertical accuracies improved from (0.166, 0.257) m to (0.053, 0.073) m, representing improvements of (71.7%, 68.1%); for the 144-LEO scenario, the accuracies improved to (0.040, 0.058) m, representing improvements of (77.4%, 75.7%); the average convergence times were reduced from (1261, 472) s to (123, 47) s for the 96-LEO scenario (reductions of 90.2%, 90.0%) and to (63, 34) s for the 144-LEO scenario (reductions of 94.9%, 92.8%).

Fig. 16

Comparison of positioning accuracy under WAR, LEO96/LEO144, and combined WAR & LEO96/LEO144 augmentation schemes.

Fig. 17

Comparison of convergence time under WAR, LEO96/LEO144, and combined WAR & LEO96/LEO144 augmentation schemes.

Furthermore, compared to using either WAR or LEO augmentation alone, the synergistic strategy shows varying degrees of performance improvement. Overall, WAR and LEO constellation augmentation are complementary and synergistic technical pathways.

To further investigate the LEO augmentation mechanism, a comparison of the ambiguity resolution Ratio values was conducted (as shown in Fig. 18). The inclusion of LEO observations strengthens the ambiguity resolution model, resulting in a notable increase in the Ratio values, particularly during the convergence phase.

Fig. 18

Comparison of Ratio values for PPP-B2b EWL/WL ambiguity resolution with LEO144 augmentation.

Discussion

This study advances the field by moving beyond the independent application of either technique. While prior work has demonstrated that LEO improves float solution convergence or that ambiguity fixing enhances precision, our contribution lies in the first systematic demonstration that these methods are temporally complementary and synergistic within the PPP-B2b context. We quantitatively show that WAR provides superior initial accuracy, while LEO enables sustained rapid convergence, and that their combination yields gains greater than the sum of individual parts. This mechanistic insight addresses the core convergence bottleneck of PPP-B2b in a novel and effective manner.

It must be emphasized that the conclusions of this study are primarily derived from simulated LEO data. Although major error sources were incorporated during simulation to ensure result reliability, a gap remains between the simulation environment and the complexity of the real world. It is important to acknowledge the limitations inherent in our simulation-based analysis, which may lead to optimistic performance estimates. First, the LEO observations were simulated without accounting for satellite-specific antenna phase center offsets and variations (PCO/PCV), which, in a real system, would introduce unmodeled ranging errors and could affect ambiguity resolution reliability. Second, the LEO satellite clock errors were simulated by recycling high-quality GPS precise clock products. In reality, the stability and the precision of real-time orbit and clock determination for LEO satellites remain a significant challenge and would directly impact convergence performance. Third, LEO-specific hardware biases (e.g., inter-frequency biases) were not simulated, as this study primarily focused on the contribution of rapid geometry change to float solution convergence. These simplifications were made to isolate and demonstrate the potential geometric benefit of LEO augmentation. Therefore, while the results compellingly demonstrate the synergistic mechanism and substantial potential of combining WAR with LEO geometry, the reported convergence times should be interpreted as a lower bound under controlled conditions. Future work necessitates validation using real LEO navigation signals and addressing the practical challenges of LEO precise orbit and clock determination, antenna calibration, and hardware bias handling.

Furthermore, while this study focused on fixing EWL and WL ambiguities, which indeed brings significant initial performance improvement to the PPP-B2b service, achieving reliable narrow-lane ambiguity resolution remains the ultimate goal for attaining instantaneous and stable centimeter-level positioning in the long run. However, narrow-lane ambiguity fixing faces severe challenges, including shorter wavelengths, higher sensitivity to unmodeled errors, and the need for higher-precision FCB products. Consequently, the exploration of precise Narrow-Lane FCB estimation techniques and robust ambiguity resolution strategies applicable to the PPP-B2b service constitutes another critical research topic for future work.

Conclusions

This paper proposed and validated a solution integrating WAR with LEO constellation synergistic augmentation to address the technical bottleneck of slow convergence in the PPP-B2b service. By constructing a complete technical chain encompassing FCB product generation, LEO constellation design, and multi-system integrated processing, this study achieved stable extraction of GPS/BDS-3 EWL/WL FCBs based on an uncombined PPP model accounting for CCB. The BDS-3 WL FCBs demonstrated superior stability (STD better than 0.02 cycles). Regarding constellation design, targeting China and its surrounding regions, hybrid-orbit LEO constellations with scales of 96 and 144 satellites were constructed using optimized orbital configurations involving multiple inclinations (40°/55° and 35°/50°/65°, respectively). The proposed enhancement algorithms were validated using real-tracked reference station network data from the Asia–Pacific region.

Experimental results demonstrate that both WAR and LEO augmentation improve PPP-B2b accuracy and convergence performance through different mechanisms. Utilizing the integer nature of ambiguities, WAR improved the horizontal and vertical positioning accuracy at the first epoch from (0.491, 0.925) m to (0.329, 0.559) m, and reduced the horizontal and vertical convergence times by 34.4% and 38.6%, respectively. In contrast, LEO augmentation offered limited improvement to the initial epoch accuracy; its primary contribution lies in utilizing rapid geometric changes to achieve superior accuracy within 20–40 s. Augmentation with the 144-LEO constellation shortened the horizontal and vertical convergence times from 1261 and 472 s to 82 s and 55 s, representing improvements of 93.5% and 88.3%, respectively. Particularly noteworthy is the synergistic enhancement strategy, which fully leverages the temporal complementary advantages of both methods during convergence. It balances the initial epoch parameter estimation accuracy with rapid convergence capability, improving horizontal and vertical positioning accuracy by 71.7–77.4% and 68.1–75.7%, respectively. Simultaneously, it reduced the convergence time from nearly 20 min for conventional PPP-B2b to 63 s (horizontal) and 34 s (vertical), representing a reduction exceeding 90%.

The results fully confirm that the synergistic approach combining WAR and LEO constellation augmentation can effectively resolve the convergence bottleneck of the PPP-B2b service, providing a reliable technical pathway towards achieving instantaneous high-precision positioning over wide areas. Future research efforts will focus on exploring reliable methods for narrow-lane ambiguity resolution and seeking further validation using real in-orbit LEO navigation signals.