Introduction

Cities, as complex systems, face short-term shocks and long-term changes during development1. Climate crisis is one of the 21 st century’s most severe global challenges, marked by escalating compound disasters and rising uncertainty risks2. From 2000 to 2019, the United Nations Office for Disaster Risk Reduction reported 7,348 major natural disasters globally, and it affected 4.2 billion people and caused $2.97 trillion in economic losses. These disasters repeatedly threaten urban infrastructure and disrupted city operations and citizens’ lives. Over half of the global population currently lives in urban areas3, and this proportion is expected to reach 70% by 2050.

Urbanisation has led to ecological imbalances, resource supply-demand conflicts and increased strain on municipal facilities, which hinder sustainable development4. In response, resilience has emerged as a strategy to enhancing cities’ capability to withstand shocks and pressures, which reduces vulnerability5. Ayyub6 noted that resilient infrastructure mitigates disturbances effectively, which also elaborated by Dhakal and Zhang7. Enhancement of infrastructure resilience is critical and requires immediate attention. Infrastructure is divided into two categories: engineering and social. Engineering infrastructure includes roads, railways, bridges, power supplies and water supplies8. Urban infrastructure encompasses water supply, drainage, transportation, energy supply and telecommunication systems, a definition widely accepted by scholars9,10. Accurate quantification of urban resilience aids in gaining insights into urban development dynamics and supports decision making. Scholars have developed various methods to assess urban resilience, with the indicator approach being widely used due to its convenience for city comparisons11,12. Complex system resilience assessment involves decomposing it into aspects and forming an indicator tree13. Multi-objective decision methods, such as Technique for Order Preference by Similarity to Ideal Solution (TOPSIS)14, AHP15 and VIKOR16, are often combined with indicator systems. Some scholars use neural networks to evaluate resilience levels17.

A scientific evaluation framework must be built to ensure result accuracy and reliability. Scholars have developed frameworks from various perspectives. Some focused on resilience characteristics, such as absorption, adaptation and recovery13,18, and others, like Sun and Cui19, emphasised economic, social and environmental benefits of urban infrastructure. However, few studies considered the operational mechanism of resilience enhancement. This study proposes an urban infrastructure resilience (UIR) evaluation system based on the pressure-state-response (PSR) model. Initially introduced by Papport and Friend20 in 1979 and later refined by OECD and UNEP21 for ecological research, the model’s three layers—pressure, state and response—capture the interconnected operational mechanisms of resilience. This causal framework addresses causes, current states and strategies to enhance resilience. The PSR model has been widely applied in ecological environment assessment22, urban and public management23, risk assessment24, sustainable development25, and so on.

Assessing urban resilience in isolation is insufficient, especially for urban agglomerations. The development of a city not only depends on itself but is also influenced by other cities. Regional integration has intensified flows of capital and technology, which not only enhanced coordinated development but also spread risks. Some scholar explored the co-evolution and resilience propagation throughout urban systems over time with the help of data-driven methods26. However, most existing studies overlooked city interactions and regional characteristics in resilience construction. Complex networks are a commonly used for building relationships among objects. Complex networks model systems as sets of nodes and edges to uncover the topology emerging from their interactions. Recent studies adopted network models and used topology metrics (degree, betweenness, clustering, modularity and efficiency) together with cascading failure to quantify robustness and recovery. Zhang et al.27 introduced a novel resilience assessment framework based on complex network theory by modelling urban infrastructure as an interconnected network of nodes (buildings) and edges (roads). Some network metrics are used to characterise resilience level, such as the global efficiency of a network. Ashja-Ardalan et al.28 proposed an integrated approach utilising complex network theory, topological metrics and spatial climate data to assess the resilience of road networks under various climate change scenarios. Zhang et al.29 used financial companies of various sizes in the YRD as research data combined with complex network models to explore the connection strength and resilience of the urban network.

Network analysis is typically used to quantify the resilience level. Meanwhile, this study integrated resilience levels with network analysis. By integrating PSR framework and complex network, the analysis not only evaluated individual city resilience but also further explored the relationships among cities in the development and construction of resilience. This study constructed an evaluation index system based on the PSR framework to quantify the infrastructure resilience level of each city. However, the evaluation framework alone cannot capture the interconnections among cities within urban agglomerations. In short, complex network analysis adds the missing regional view by (i) representing intercity linkages within each dimension (pressure/state/response), (ii) having an understanding of risk and coordination in the region resilience construction with the help of network attribute metrics (e.g. degree centrality, betweenness centrality and clustering coefficient); (iii) being able to identify and prioritise the critical node cities to guide targeted interventions.

This paper provides several key contributions. Firstly, it combines the PSR model with complex network theory to create a replicable multiscale assessment tool, applicable domestically and internationally. Secondly, by quantifying the infrastructure resilience levels, it uncovers the resilience development pattern in Yangtze River Delta (YRD) and identifies two critical cities requiring urgent attention, specifically Huainan and Huaibei. Thirdly, with the help of network metrics, such as degree centrality, betweenness centrality and clustering coefficient, the topological evolution of the resilience network can be explored. Finally, critical vulnerable nodes are identified as those whose degree centrality and betweenness centrality both rank above the 90th percentile, providing a scientific basis for targeted interventions. These findings aim to inform resilient city construction, regional governance and urban planning.

Study area

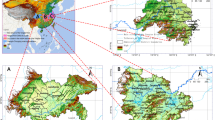
The Yangtze River Delta (YRD), located near the Yellow and East China Seas, is a flat terrain area covering 41 cities in Shanghai, Jiangsu, Zhejiang, and Anhui. With a population of 227 million and an urbanization rate over 60%, it generates nearly one-quarter of China’s GDP and one-third of its import/export volume despite occupying less than 4% of China’s land area30. The region has a subtropical monsoon climate and the highest river network density in China, making it highly vulnerable to floods. Global warming has caused significant increases in annual average temperatures, including both maximum and minimum values. In 2020, heavy rainfall during the flood season resulted in once-in-50-year floods affecting over 10 million people. As one of the six major global urban agglomerations, the YRD plays a key role in China’s economic transformation, technological innovation, and regional development31. However, rapid urbanization, excessive resource use, intensifying climate change, and high population density pose significant challenges. Therefore, studying urban infrastructure resilience in the YRD is crucial.

Materials and methods

Conceptual framework

The PSR model, valued for its logicality, flexibility and comprehensiveness, has been applied in urban resilience assessment32, land quality evaluation33 and ecological environment analysis34. Its three dimensions—pressure, state and response—highlight the relationships among causes, systems and human actions35. Pressure stems from natural disasters and human activities, which affects infrastructure. State reflects a system’s stability and resistance to disturbances. Response involves measures, which are informed by past experiences, implemented by governments and residents to address these effects36.

This study integrated the PSR model with complex network theory to construct a PSR-complex network framework. With 41 YRD cities as nodes, the edges of the network were determined based on differences in resilience levels. Cities with higher resilience outperformed those with lower resilience in terms of economic development, infrastructure construction and science and technology and attracted more resources. In addition, they were expected to play a radiating role in driving the development of surrounding cities and those with lower resilience levels. Therefore, the greater the development gap between cities, the more likely they are to depend on and receive support from other cities, which led to closer interactions and strengthened intercity connections37. Three interrelated networks were formed: pressure resilience, state resilience and response resilience networks. These networks revealed city interdependencies, identified critical cities and explored regional dynamics. The pressure resilience network examined how pressures propagate across urban infrastructure. The state resilience network showed how resource sharing affects neighbouring cities. The response resilience network highlighted the flows of capital and technology and risk response collaboration. Critical cities’ actions can significantly affect surrounding areas.

Figure 1 outlines the research framework. This study consisted of four sequential stages. Construction of the indicator system: This stage ensured the systematicity and comprehensiveness of the assessment, which translated the abstract concept of urban resilience into quantifiable measurement dimensions. Quantification of resilience levels: Raw data were collected for each tertiary indicator, and the entropy-weighted TOPSIS method was employed to calculate a comprehensive UIR score for each city annually. The scores range between 0 and 1, which enabled the comparability of resilience levels across different cities and years and formed the foundation for all subsequent analyses. Analysis of spatiotemporal evolution of UIR: Geographic Information System (GIS) visualisation and geostatistical trend analysis were used to reveal the spatiotemporal patterns and evolutionary trends of resilience. Analysis of resilience network structure evolution and critical node identification: Based on the constructed urban networks and with the help of complex network metrics (e.g. degree centrality, betweenness centrality and clustering coefficient), the evolutionary characteristics of the urban resilience network structure and can be analysed. Cities that ranked within the top five in degree centrality and betweenness centrality were identified as key vulnerable node cities.

Fig. 1
figure 1

Depiction of the research content framework (UIR: urban infrastructure resilience).

Full size image

Data source

Our data is primarily sourced from authoritative publications, such as the “China Statistical Yearbook,” “China City Statistical Yearbook,” “China Urban Construction Statistical Yearbook,” “China Environment Statistical Yearbook,” “Shanghai Statistical Yearbook,” “Jiangsu Statistical Yearbook,” “Zhejiang Statistical Yearbook,” and “Anhui Statistical Yearbook.” We also rely on the National Centers for Environmental Information (NCEI) and National Meteorological Science Data Center. These sources are carefully selected for their credibility, ensuring the authenticity and effectiveness of the data we analyze. However, during the collection process, there may be occasional gaps in data for specific years or indicators. Excluding such data outright would result in potential information loss, compromising the precision of our analysis. Given the low data missing fraction of the used dataset, this study utilizes two primary methods for imputing missing values: mean imputation method and growth rate imputation method.

UIR index system

The selection of quantitative indicators that can reflect the risks faced by the urban infrastructure system, functional status and the response measures implemented by various entities is the key to measuring its resilience level. As a causal framework, the interrelationship among pressure, state and response can affect UIR. On the one hand, stress factors can disrupt the stable operation of infrastructure, and changes in the infrastructure state convey crucial information to relevant responding entities. Implementation of correct and effective response measures can mitigate the effect of stress to some extent. On the other hand, stress signals guide responding entities to take appropriate measures. The effective implementation of these measures can enhance the functional state of infrastructure and strengthen its capability to withstand external disturbances. Based on references and the theoretical connotations of the PSR model and adhering to the principles of systematicity and data availability, we selected 10 secondary and 36 tertiary indicators. Notably, we innovatively introduced indicators for high-temperature days, low-temperature days, torrential rain days and days above strong gale (Table 1). Two types of indicator attributes, namely, positive and negative, were considered. Positive indicators imply that high values enhance urban infrastructure UIR, and negative indicators mean that high values exert pressure and may undermine resilience.

Table 1 UIR evaluation index system.
Full size table

TOPSIS-based comprehensive evaluation method

Initially introduced by Hwang et al.60, the TOPSIS ranks the second most favoured approach in multicriteria decision making61. It has found extensive application in different research fields, such as urban resilience62,63, flood resilience64, water resource carrying capacity65, supplier selection66, priority ranking67, and so on. By fully utilising the original data, TOPSIS constructs positive and negative ideal solutions and computes the Euclidean distances from each evaluated entity to these points, which effectively highlights the disparities among them68. In this research, we integrated the TOPSIS evaluation framework with entropy weight method to assess the UIR in YRD. The TOPSIS method was employed to integrate the multiple PSR indicators into a comprehensive resilience score for each city. This technique identified the best and poorest performance across all indicators and ranked cities based on their relative closeness to the ideal solution. This approach is particularly suited for our study as it provides a clear and comparable metric for ranking urban resilience, which formed the basis for subsequent spatiotemporal and network analyses. The specific calculation steps are shown in the appendix.

Quantitative analysis of network structure characteristics

For the annual network of each index (pressure, state, response), the degree centrality \(\:{C}_{D}\left(v\right)\) and betweenness centrality \(\:{C}_{B}\left(v\right)\) were calculated for all nodes. The top five nodes were selected using \(\:{C}_{D}\left(v\right)\) and \(\:{C}_{B}\left(v\right)\) in descending order. Degree centrality measures the number of connections of a node in a network. For an undirected graph \(\:G=(V,E)\), where \(\:V\) is a set of nodes, \(\:E\) is a set of edges, and the calculation formula of degree centrality \(\:{C}_{D}\left(v\right)\) of node \(\:\text{v}\) is as follows:

$$\:{C}_{D}\left(v\right)=\frac{d\left(v\right)}{\left[\left|V\right|-1\right]}$$
(1)

where \(\:d\left(v\right)\) refers to the degree of the node \(\:\text{v}\) (i.e. the number of edges connected to the node \(\:v\)), and \(\:\left|V\right|\) is the total number of nodes in the network. Betweenness centrality is used to measure the extent to which a node mediates the shortest path between other nodes in the network. The formula below is used to calculate for intermediate centrality \(\:{C}_{B}\left(v\right)\) of node \(\:\text{v}\):

$$\:{C}_{B}\left(v\right)=\frac{\sum\:_{s\ne\:v\ne\:t}\:{\sigma\:}_{st}\left(v\right)}{{\sigma\:}_{st}}$$
(2)

where \(\:{\sigma\:}_{st}\) denotes the number of shortest paths from node \(\:s\) to node \(\:t\), and \(\:{\sigma\:}_{st}\left(v\right)\) refers to the number of nodes \(\:\text{v}\) in the shortest path from node \(\:s\) to node \(\:t\). The clustering coefficient measures the proximity of nodes to each other. For node \(\:v\), the clustering coefficient \(\:C\left(v\right)\) is calculated as follows:

$$\:C\left(v\right)=\frac{2{e}_{v}}{\left[{k}_{v}\left({k}_{v}-1\right)\right]}$$
(3)

where \(\:{e}_{v}\) denotes the number of edges actually present between the neighbor nodes of node \(\:v\), and \(\:{k}_{v}\) indicates the degree of node \(\:v\). The average clustering coefficient of the network is the average of the clustering coefficient of all nodes. Table 2 provides further explanation of the meaning of the higher and lower values of the three network attribute metrics.

Table 2 Interpretation of network attribute metrics.
Full size table

Identification of key node cities

For each dimension and annual network, we set the identification threshold using the 90% quantiles of degree centrality and betweenness centrality across all years and dimensions69. In mathematics, for each node \(\:\text{v}\) in the node set \(\:V\), we calculated its degree centrality \(\:{C}_{D}\left(v\right)\) and betweenness centrality \(\:{C}_{B}\left(v\right)\). A node was identified as critical for a given year only if it simultaneously satisfied the condition that it ranked among the top five nodes for degree centrality and betweenness centrality. The two metrics effectively identified nodes that were most critical in terms of connectivity (degree centrality) and flow control (betweenness centrality). The failure of such nodes would, from a topological perspective, most severely disrupt network connectivity and efficiency. A city possessing high ‘connectivity’ and ‘control’ within the urban network inherently bears significant hub and coordination responsibilities in regional integration. Consequently, its vulnerability poses the highest systemic risk to the entire network.

Coregulation threshold calculations were performed, that is, through the calculation of the 90% quantile of degree centrality and betweenness centrality across all years and for all metrics. Let \(\:X=\left\{{x}_{1},{x}_{2},\cdots\:,{x}_{n}\right\}\) be the set of values of all degree centrality or intermediate betweenness centrality and order \(\:X\) in ascending order to obtain \(\:{X}^{{\prime\:}}=\left\{{x}_{\left(1\right)},{x}_{\left(2\right)},\cdots\:,{x}_{\left(n\right)}\right\}\). The calculation formula of \(\:p\) quantile \(\:{Q}_{p}\) is as follows:

$$\:\left\{\begin{array}{c}{Q}_{p}=\frac{{x}_{\left(np\right)}+{x}_{\left(np+1\right)}}{2},\:np\:is\:an\:integer\:\\\:k=\lfloor{np}\rfloor\left(\text{T}\text{a}\text{k}\text{e}\:\text{t}\text{h}\text{e}\:\text{w}\text{h}\text{o}\text{l}\text{e}\:\text{d}\text{o}\text{w}\text{n}\right),{Q}_{p}={x}_{\left(k+1\right)},\:np\:is\:not\:an\:integer\end{array}\right.$$
(4)

Results and analysis

Overall characteristics of UIR

We developed a PSR framework and applied the entropy-weighted TOPSIS method to evaluate the resilience of urban infrastructure in 41 YRD cities from 2013 to 2022. SPSS27 software analysis revealed the key points summarised in Table 3: (1) The mean value increased from 0.1102 to 0.1496, which indicates a relatively low improvement. (2) The maximum and minimum values rose, with a more pronounced increase in the former, which highlights the need to focus on lower-resilience cities. (3) Standard deviation increased from 0.091 to 0.130, which indicates greater variability among cities. (4) Kurtosis initially increased and then decreased, which reflects a more balanced development; skewness decreased, which suggests more symmetrical resilience levels. (5) The coefficient of variation peaked in 2019 but slightly declined by 2022, which indicates persistent spatial disparities. Despite positive trends, efforts should continue to promote integration and reduce disparities in the YRD region.

Table 3 Descriptive statistical analysis of UIR in the YRD.
Full size table

Spatial evolution of UIR

Using ArcGIS, we created a three-dimensional resilience development trend chart that includes pressure, state and response (Fig. 2). The black bars show each city’s resilience magnitude and position. The green curve represents the east–west best-fit projection for UIR, and the blue curve shows the north–south best-fit projection. Resilience trends revealed significant regional disparities. State and response resilience levels were higher in the east and lower in the west, with an inverted U-shape in the north and south. Pressure resilience was higher in the east and south but lower in the west and north. From 2013 to 2022, the north–south trend line shifted from parabolic to linear, which indicates an improved pressure resilience in central areas. Table 4 shows some major cities in different directions.

Fig. 2
figure 2

Trend line of the UIR level in the YRD from 2013 to 2022.

Full size image
Table 4 Major cities in different directions.
Full size table

We selected the years 2013, 2016, 2019 and 2022 to illustrate the spatial distribution and evolution of infrastructure resilience in the YRD urban agglomeration. Using the natural breakpoint method, resilience levels were categorised into five groups: I (low), II (relatively low), III (medium), IV (relatively high) and V (high)70. Maps were created using ArcGIS (Fig. 3). From 2013 to 2022, the region developed a central–peripheral structure centred around provincial capitals. Key cities, including Shanghai, Suzhou, Nanjing, Hangzhou, Ningbo and Hefei, formed the core, and surrounding areas showed lower resilience. In 2013, fifteen cities had low resilience, but by 2022, only Huainan and Huaibei remained in this category. This trend highlights the positive influence of provincial capitals on regional development. Special attention is needed for Huainan and Huaibei, which still exhibit insufficient resilience and require targeted measures. Meanwhile, the number of high-resilience cities increased from one to six. Throughout this period, Shanghai maintained its leadership, and Hefei and Ningbo improved from moderate to high resilience. Second- and third-tier cities, such as Suqian, Yangzhou, Taizhou, Wenzhou, Jinhua and Lishui, maintained relatively stable resilience levels.

Fig. 3
figure 3

Spatial distribution of UIR in YRD.

Full size image

Urban network analysis in YRD

The entropy-based TOPSIS method offers an effective quantitative tool for the accurate evaluation of the level of independent resilience in each city. This method clearly delineates the resilience performance of a city across various dimensions by comprehensively considering multiple indicators of the city. As a key node in a regional system, the resilience of cities is influenced not only by their own factors but also by those of surrounding cities. As illustrated in Fig. 3, cities with high resilience drive neighbouring cities to exhibit greater resilience, whereas cities with low resilience evolve more slowly. Certain cities and their interconnections play a crucial role in the resilience of the entire network. With the aid of network analysis methods, this section identifies these key nodes and important connections. Through urban dynamic network analysis across different years, the calculation of several key network properties, such as degree centrality, betweenness centrality and clustering coefficient, these indicators provide valuable insights into the evolution of network structure and the changing relationships between cities over time.

Analysis of UIR network

As illustrated in Fig. 4, the average degree centrality and the average clustering coefficient of urban networks exhibited an upward trend in their fluctuations. This finding suggests that the synergistic effect of urban networks and the close local cooperation within the region intensified and evolved towards greater regional integration. The average betweenness centrality remained highly stable, with variations not exceeding 0.002.

Fig. 4
figure 4

Temporal variation of the UIR network attributes from 2013 to 2022.

Full size image

Analysis of urban pressure, state and response network

The analysis of the three key indicators—pressure resilience, state resilience, and response resilience—is based on annual average degree centrality, average betweenness centrality, and average clustering coefficient. Their temporal evolution is shown in Fig. 5, with numerical values provided in Table 5. Degree centrality represents the number of direct connections a node maintains within a network and serves as an indicator of a city’s level of network engagement. A high degree centrality value (> 0.5), such as that observed in the stress system in 2019 (0.628), corresponds to a densely connected network, in which disturbances in one city may propagate rapidly to others and coordinated responses across multiple locations are enabled. An intermediate degree centrality (0.2–0.5), as seen in the response system in 2020 (0.362), indicates maintained intercity connectivity alongside a more decentralized network structure, which may support localized risk mitigation.

Fig. 5
figure 5

Temporal variation of subnetwork attributes from 2013 to 2022.

Full size image
Fig. 6
figure 6

Topological Evolution of the pressure resilience network, 2013–2022 (Note: the size of the nodes represents the degree centrality, and node colour signifies the betweenness centrality).

Full size image

Betweenness centrality measures a node’s role in mediating network connectivity by indicating how often it lies on shortest paths between other nodes. In urban networks, values above 0.015 suggest a city functions as a structural bridge—such as the state-level system in 2022 (0.021), highlighting key intermediary roles, particularly in the Yangtze River Delta transportation network. These nodes may influence overall network efficiency if disrupted. A median range (0.01–0.015), as seen in the 2019 pressure system (0.01), indicates moderate routing involvement, reflecting multiple alternative pathways and enhanced redundancy. Values below 0.01 suggest limited intermediary function, typical of decentralized networks with prevalent direct connections.

Fig. 7
figure 7

Topological evolution of the state resilience network, 2013–2022 (Note: the size of the nodes represents the degree centrality, and the node colour signifies the betweenness centrality).

Full size image

The clustering coefficient measures local connectivity density in urban networks. A value above 0.6 indicates a tightly connected structure (e.g., 0.691 in 2013 for the state system), reflecting high intraregional coordination but potential systemic vulnerability. Values between 0.4 and 0.6 suggest moderate connectivity (e.g., 0.514 in 2015 for the stress system), balancing regional integration and external linkage. A coefficient below 0.4 (e.g., 0.360 in 2021) indicates reduced cohesion, potentially affecting resource flow efficiency.

Fig. 8
figure 8

Topological evolution of the response resilience network, 2013–2022 (Note: the size of the nodes represents the degree centrality, and node colour represents the betweenness centrality).

Full size image

Some key network metrics are summarised in Table 5. In 2019, degree centrality of the state system peaked, reflecting enhanced infrastructure connectivity under the new urbanisation policy and improved network efficiency. By 2021, the pressure system’s degree centrality declined to its minimum (0.436), while betweenness centrality reached its maximum (0.015), coinciding with structural changes from the ‘two-carbon’ initiative and the emergence of specific cities as transmission hubs. In 2017, the response system’s clustering coefficient peaked at 0.738, associated with knowledge exchange through sponge city pilot programmes. These trends indicate how policy measures have influenced urban network configurations over time.

Table 5 Network attribute index values of the pressure, state and response network.
Full size table

The figure displays the visual analysis of UIR networks from 2013 to 2022. Node sizes reflect degree centrality and show city connections and importance. Based on the visual comparisons presented in Figs. 6, 7 and 8, the pressure resilience network (Fig. 6) displays a distinct structural pattern, characterized by a higher prevalence of direct connections among cities. In contrast, the topological structures of the state resilience network (Fig. 7) and the response resilience network (Fig. 8) exhibit a notable similarity, revealing a clearer dependence on core cities. Shanghai, acting as a core hub in the network, consistently ranked highest in betweenness centrality. The network’s bridge roles shifted from a single core to multiple cores, which reduced reliance on individual cities. More cities now serve as bridges and play key roles in resource, information or traffic flow control. In 2013, the network was unbalanced, and by 2020 to 2022, it became closer and more balanced.

Identification of critical node cities

For each annual network, nodes are ranked in descending order by degree and betweenness centrality. To identify critical vulnerable cities, a threshold selects those within the top five for both measures. This cutoff reflects a noticeable decline in centrality scores after rank five, indicating a distinct group of high-influence nodes. Given the size of the Yangtze River Delta urban agglomeration, focusing on the top five balances comprehensiveness and relevance. In the urban pressure resilience network, Taizhou and Zhoushan are consistently identified as key vulnerable nodes. Between 2013 and 2022, Suzhou and Xuzhou emerge as newly vulnerable, replacing Wenzhou. In both state and response resilience networks, Shanghai, Hangzhou, Nanjing, and Suzhou remain central vulnerable nodes. Since 2017, Ningbo replaces Anqing in these positions. The state and response networks show similar patterns. Targeting these priority cities for intervention supports network optimization, promotes balanced intercity linkages, reduces overreliance on critical hubs, and lowers systemic risk (Fig. 9).

In Fig. 9, \(\:p=0.9\), threshold \(\:={Q}_{0.9}=\text{i}\text{n}\text{f}\{x\in\:\mathbb{R}\mid\:F(x)\ge\:0.9\}\), where \(\:F\left(x\right)\) is the cumulative distribution function of the data. Each column represents the top five node cities for every year.

Fig. 9
figure 9

Critical Vulnerable Nodes (2013–2022). Note: The coregulation threshold for degree centrality is 0.868, and for betweenness centrality, it is 0.050. Nodes exceeding these thresholds are considered critical vulnerable nodes.

Full size image

Discussion

Applicability of the PSR-complex network dynamic evaluation framework

The enhancement of resilience constitutes a dynamic process, and the causal relationships inherent in the PSR framework offer a scientific explanation for this phenomenon, thereby establishing it as a robust framework for resilience measurement. Resilience enhancement manifests as a feedback effect arising from the mutual coupling among pressure, state, and response. Exogenous and endogenous pressures, such as climate hazards or economic shocks, act to degrade the infrastructure state. The observed state conditions, in turn, shape the formulation and implementation of government responses. Crucially, these responses generate a feedback loop that exerts influence on both future pressures (through mitigation and risk governance strategies) and the subsequent state (through adaptation measures).

At the urban agglomeration scale, the PSR-complex network dynamic evaluation framework demonstrates superior comprehensiveness and applicability compared to frameworks designed for individual cities. A key distinction lies in its approach to evaluating city resilience by conceptualizing and visualizing urban agglomerations as networks. This network perspective places emphasis on intercity connections, particularly concerning pressure transmission and resource flows, thereby enhancing the understanding of resilience at both the city and regional levels. The study integrated resilience data into the model to explore evolving regional development patterns over time, with explicit consideration of inter-city linkages. Over the past decade, observed increases in degree and betweenness centrality metrics have indicated a trend towards growing regional integration. This integration has been characterized by a shift from a single-core dominance model to one of multicentre collaboration, effectively reducing reliance on any single city. Within the pressure network, a process of decentralization has occurred, with direct urban connections increasingly replacing the previously dominant single-hub radiation model. In contrast, the state and response networks have exhibited the formation of tightly interconnected group structures at the local level, which maintain reliance on key cities. These empirical observations collectively validate the framework’s value and highlight its extensibility for application across various models according to specific research or practical needs.

The analytical framework developed in this study exhibits strong potential for migration and application to other urban agglomerations. Its application adheres to a standardized process: (1) the collection of local data in accordance with the established PSR indicator system; (2) the quantification of urban resilience scores based on this data; and (3) the construction of an urban resilience network, wherein cities serve as nodes and the differences in resilience scores between cities act as edge weights. The utilization of consistent network metrics across different applications facilitates meaningful cross-regional comparisons. This replicable approach significantly enhances the framework’s practical value for urban planners and policymakers. Furthermore, while the core methodology remains consistent to ensure reliability and comparability, the framework also possesses inherent flexibility. When applied to regions with distinct geographical contexts (for example, seismic zones or arid regions), researchers can contextualize the framework by substituting or adjusting specific indicators within the PSR layer, all without necessitating changes to the overall analytical structure. This adaptability ensures the framework’s relevance and utility across diverse environmental and developmental settings.

Resilience development analysis in YRD

Siphon and spillover effects

The first finding shows that the Yangtze River Delta (YRD) development model prioritizes provincial capitals as growth engines for surrounding cities (Fig. 3). This strategy enhances regional resilience by balancing agglomeration in core cities with spillover effects in peripheral areas. While it strengthens core cities and supports peripheral development through inter-city cooperation and resource sharing, it may also worsen regional imbalances at certain stages.

In the early-middle phases of YRD regional integration, the “siphon effect” dominated71,72,73. In line with prior studies on regional development dynamics—such as those by Fujita and Thisse74on economic geography and Gu et al.75 on urban hierarchy in China’s mega-city regions—our findings reaffirm the role of core cities as primary engines of growth through their advantages in infrastructure, market maturity, and concentration of high-value-added industries. The observed pattern of resource agglomeration in Shanghai, Hangzhou, and Nanjing echoes the “core-periphery” model proposed by Krugman76, where central nodes attract capital, skilled labor, and innovation-intensive firms from surrounding areas, thereby reinforcing their own resilience and competitiveness.

Our results reveal a key limitation of the classical model: while core cities accelerate resource concentration, spillovers—such as industrial relocation, technology diffusion, and knowledge exchange—are delayed in peripheral regions. This delay reflects the absorptive capacity framework77, increasingly used in regional studies78. Effective spillovers require peripheral cities to have advanced enabling conditions—not just basic infrastructure, but also skilled labor and institutions capable of adopting new knowledge and technologies.

Network analysis shows that while inter-city collaboration in the Yangtze River Delta (YRD) is growing—consistent with Li and Wu’s79 findings on regional integration—the development remains uneven. Core cities like Shanghai, Nanjing, and Hangzhou dominate as hubs with most partnerships, whereas peripheral cities have weaker connectivity and fewer collaborative links. This gap in centrality suggests that despite rising network density, benefits are not equally shared. Sectoral differences further reveal that knowledge-intensive industries such as IT and advanced manufacturing lead cross-city cooperation, while traditional sectors remain less involved. These patterns underscore how economic specialization and institutional capacity shape regional innovation networks.

Risk resistance capacity and risk exposure level

The spatial variation in resilience across regions aligns with earlier findings on regional vulnerability and adaptive capacity58. The link between higher risk resistance and higher risk exposure supports the theory that areas under greater external pressure develop stronger resilience over time, provided they have adequate resources and institutional support80. In southern cities, strong pressure resilience coexists with weak state and response resilience. Regions facing less stress may underinvest in adaptive infrastructure and emergency systems due to low immediate needs, suggesting that comprehensive resilience is limited more by perceived necessity than by capability.

Central cities show lower pressure resilience but higher state and response resilience, indicating a development path influenced by frequent or intense external shocks that strengthen monitoring, governance, and recovery systems81,82. This pattern suggests repeated risk exposure can drive institutional learning and systemic adaptation when feedback between risks and policy responses remains effective. In the Yangtze River Delta (YRD)—including Shanghai, Jiangsu, Zhejiang, and parts of Anhui—economic activity has grown steadily in recent years. A dense network of highways, railways, and waterways supports regional connectivity. Industrial output, technological innovation, and foreign trade play key roles in the national economy. Ongoing investments in public services and urban planning drive urban expansion, while environmental measures address air and water quality issues.

Driving mechanism of the Temporal changes of network indicators

The temporal progression of network indicators within the Yangtze River Delta (YRD) resilience network corresponds with the dynamics of the regional urban network. This progression signifies a transition from a singularly centralized, imbalanced structure to a multi-centered, interconnected configuration. Concurrently, the escalating centrality of Hangzhou, Hefei, and Ningbo indicates a growing functional differentiation within the region, corroborating the hypothesis that specialized industry and knowledge-based strategies can enhance the significance of secondary cities83,84. The augmentation of these cities’ node centrality suggests that urban functional diversification fosters a more equitable and resilient spatial structure.

Improved transportation connectivity, particularly through expanded high-speed rail and intercity expressways, has strengthened urban linkages in the Yangtze River Delta. This infrastructure supports the efficient movement of goods, services, and people, enhancing integration among urban centers. Upgraded transport systems are linked to higher network density and reduced spatial disparities in large metropolitan regions. The reinforcement of secondary nodes and closer inter-node connections reflect a shift toward a more distributed and adaptive network structure, potentially improving regional resilience by enhancing shock absorption and redistribution capacity85. Similar patterns appear in other polycentric regions such as the Pearl River Delta and Rhine-Ruhr area, where coordinated infrastructure investment and functional complementarity have boosted network adaptability. Meanwhile, the gradual decentralization of network flows—while preserving Shanghai’s centrality—suggests a hybrid urban model that combines hierarchical organization with horizontal connectivity.

Changes in critical node cities

In examining the structural dynamics of urban networks within the context of environmental risk management, this study identifies critical node cities based on thresholds in degree and betweenness centrality. These centrality measures serve as indicators of high connectivity and intermediary positioning, both of which can influence the propagation of risks across the network. As illustrated in Fig. 9, the evolution of centrality among critical cities has been analyzed over time, differentiated by pressure, state, and response dimensions.

The analysis reveals that cities identified as critical within the pressure network exhibit lower stability compared to those in the state and response networks. This variability is attributed to the inherent uncertainty associated with risk-shock events, which may lead to shifting patterns of influence. The observed rotation of central nodes in the pressure dimension suggests a distributed pattern of influence, potentially reducing dependence on any single hub. However, this dynamism may also pose challenges for consistent risk monitoring and intervention targeting.

In contrast, the state and response networks show more consistency in core structure. Shanghai, Hangzhou, Nanjing, and Suzhou remain central nodes over time. This centrality supports efficient resource and information diffusion, reflecting functional integration. However, it also means high systemic reliance on a few urban centers. A disruption in a key city may impede data transmission or delay coordinated responses. The structural stability aids long-term planning and intercity coordination, but emphasizes the need to safeguard central nodes for network resilience. These findings match prior observations on well-connected hubs facilitating network coherence, and highlight potential vulnerabilities under stress.

Policy recommendations from empirical findings

Policy recommendations based on the Spatiotemporal evolution of resilience

An analysis of infrastructure resilience in YRD cities from 2013 to 2022 shows an overall improvement, though disparities have slightly widened. A core-periphery pattern has emerged, centered on Shanghai, Nanjing, Hangzhou, Hefei, and Ningbo, reflecting the leading role of core cities and ongoing challenges in regional coordination. To promote balanced development, policies should strengthen the radiation and driving effects of core cities through targeted cooperation with peripheral regions, especially in critical infrastructure and industrial development. For low-resilience cities like Huainan and Huaibei, which lag behind the regional average, precise assessments and tailored strategies—such as “one city, one policy” support—are needed86. Meanwhile, medium-resilience cities showing steady progress offer valuable governance models and policy practices. Their successful experiences should be identified and shared to accelerate regional resilience building.

Policy recommendations based on resilience network analysis results

Strategies for different network characteristics

First, the observed decentralization trend in the pressure network leads to a more even stress distribution across cities, reducing over-reliance on a few cities. This dispersion can enhance system-wide resilience by reducing local overload. However, the low clustering coefficient indicates limited local connectivity among neighbouring cities, which may delay emergency coordinated responses. To address this, designating central nodes as regional hubs and allocating more emergency resources can enable rapid resource redistribution. Second, for the interconnected group structure in the state and response network, two key aspects are intra-cluster coordination and inter-cluster connectivity. Strengthening internal cluster linkages supports infrastructure monitoring, data exchange, and unified emergency protocols, improving local response efficiency. Meanwhile, maintaining inter-cluster connections is crucial to prevent overall network failure during large-scale disruptions.

Navigating the trade-off between cooperative efficiency and systemic vulnerability

The high clustering coefficient in the UIR network reveals a key trade-off in regional integration: increased collaborative efficiency comes with greater systemic vulnerability. Dense cluster structures, as seen in state and response networks, enable rapid sharing of resources, information, and response capabilities, reducing coordination costs and achieving economies of scale. However, this tight coupling also enables cascading failures—a local disruption in one city can quickly spread through dense connections, triggering a regional crisis. Therefore, policymakers should aim not for maximum connectivity, but for robust interconnectivity87. This requires introducing buffers and circuit breakers—risk isolation mechanisms at critical points to contain failures; strengthening bridge connections between clusters to ensure support flows when one is compromised; and encouraging cities to develop unique, redundant emergency functions, preserving local diversity and alternative solutions to avoid vulnerabilities from over-standardization.

Similarities and differences with existing research

Firstly, in overall trend development, this paper reached the same conclusion as other studies, showing that urban resilience in the YRD region has generally risen, and the same result was found in UIR. However, there are differences. Ecological resilience inequity first increased then declined fluctuantly, and in urban infrastructure resilience, inter-city disparities slightly widened, indicating the siphon effect outweighs the spillover effect38,39. In spatial distribution, eastern YRD cities had higher resilience than western ones, and this study reached the same conclusion at the urban infrastructure level88. By using trend line analysis in ArcGIS and examining three dimensions separately, this work offers more detailed conclusions and intuitive visualizations.

Secondly, the economic resilience of the YRD urban agglomeration has a significant correlation with network structure, which suggests that the economic resilience of a city can be influenced by its neighbouring cities37. Similarly, the clustering coefficient and degree centrality of the UIR network in YRD showed an upward trend from 2013 to 2022, which indicates that intercity connections was strengthened. However, differences were also observed in the conclusions. Yang et al.37 discovered that Shanghai does not play a bridging role in the economic resilience network, which contrasts with its role in the UIR network. By integrating the complex network approach with the PSR framework, several new conclusions have been derived in this study.

Conclusion

This study proposes an innovative evaluation framework based on the PSR-complex network model to assess infrastructure resilience in 41 prefecture-level cities in the YRD region from 2013 to 2022. Using metrics such as degree centrality, betweenness centrality, and clustering coefficients, it reveals the correlation and dynamic evolution of the multidimensional resilience network. A quantile threshold mechanism identifies critical vulnerable nodes. The proposed dynamic network analysis framework supports scientific decision-making for urban agglomeration resilience governance. Key findings are as follows:

The infrastructure resilience of cities in the Yangtze River Delta region generally improved, though disparities between cities slightly increased. Spatially, differences were evident across the pressure, state, and response subsystems. Pressure levels were higher in the east and south, lower in the west and north. The state and response subsystems showed similar patterns: a north–south inverted U-shape and an east-high–west-low distribution, likely due to regional economic structures, resource allocation, and geography. In the pressure network, decentralization increased, suggesting a more even or complex distribution of pressures. In contrast, the state and response networks developed tightly connected clusters but followed different trajectories. Both networks saw rising clustering coefficients, yet their centrality trends diverged: the state network had declining degree centrality but rising betweenness centrality, while the opposite occurred in the response network. The response network is reducing reliance on hub cities, whereas the state network remains dependent on core cities due to geographical constraints.

In the pressure network, Taizhou, Zhoushan, Suzhou, Xuzhou, and Wenzhou were identified as critical vulnerable nodes due to their geography, industrial structure, or resources. In contrast, Shanghai, Hangzhou, Ningbo, Nanjing, and Suzhou emerged as key vulnerable nodes in the state and response networks, indicating that these core cities face higher risks despite their significant roles. These insights highlight priorities for enhancing resilience. This study enriches urban resilience research and offers new perspectives for future work by using complex network models to capture city interactions, enabling a more comprehensive, long-term understanding of regional resilience beyond individual cities.

Several key research directions have been identified. First, the analytical framework can be extended to other resilience indicators—such as urban ecological and economic resilience—and applied in comparative studies across major urban agglomerations to identify common patterns and unique features. Second, spatial and geographical factors should be integrated into network models to better reflect how physical distance and location influence city relationships. Third, policy text analysis, case studies, and expert interviews should be used to validate links between observed network changes over time and specific policy implementations. Fourth, targeted intervention strategies should be designed and simulated for critical vulnerable nodes, such as by creating redundant connections, to assess their effectiveness in reducing systemic risks and improving network robustness. These directions can help policymakers and urban planners build more sustainable and resilient cities.

Endnote

1Case source: For example, in July 2023, the Beijing-Tianjin-Hebei region of China experienced severe rainstorms, with localized torrential rainfall exceeding historical records. Over 5 million people were affected by the disaster, leading to significant disruptions in railway, aviation, and urban transportation systems. Trains experienced varying degrees of delays and cancellations, with three trains detained, signal interruptions and shortages of essential supplies. [https://news.cctv.com/2023/08/09/ARTI1UsG9kgAKrlposnROJTY230809.shtml]

2Case source: In July 2021, a heavy rainstorm occurred in north-central Henan province, according to a press conference in Henan province, the flood affected 14.814 million people in 150 counties and 1,664 townships, with 1,221 residential in the main urban areas experiencing water outages and 102 km of the Beijing-Guangzhou railway line being destroyed, disrupting train operations for 18 days and affecting transportation for 48 days. [https://www.henan.gov.cn/2021/07-21/2186301.html]

3Data source “Human cost of disasters: an overview of the last 20 years (2000–2019)”.

4Data source: https://data.worldbank.org/.