Significance of Marangoni convection in ethylene glycol base hybrid nanofluid flow with viscous dissipation through a porous medium

Abstract

The current research deals with analytical analysis of Marangoni convection on ethylene glycol base hybrid nanofluid two-dimension flow with viscous dissipation through a porous medium, which have some important application in mechanical, civil, electronics, and chemical engineering. Two types of nanoparticles one is sliver and other is graphene oxide and ethylene glycol is used as base fluid in this research work. The authors applied appropriate transformations to convert a collection of dimension form of nonlinear partial differential equations to dimensionless form of nonlinear ordinary differential equations. The transformed nonlinear ordinary differential equations are solved with the help of an approximate analytical method known as the homotopy analysis method. The effects of various parameters, including nanoparticle volume fraction, porosity parameter, Marangoni convection, and Eckert number, on energy and momentum profiles are analyzed, with the results illustrated using graphs. A physical explanation is provided to simulate and evaluate the behavior of nanofluid structures, such as temperature and velocity, in response to changes in these influencing factors.

Introduction

An advanced kind of nanofluid known as a hybrid nanofluid is made up of a base fluid (such as water, ethylene glycol, or oil) that has two or more different kinds of nanoparticles mixed into it. These nanoparticles may consist of metallic, non-metallic, or composite materials like graphene, copper, titanium dioxide, aluminium oxide, or carbon nanotubes (CNTs). In contrast to traditional nanofluids, which only contain one kind of nanoparticle, the mixture of several nanoparticles offers improved thermal and physical properties.To enhance the synergistic effects on stability, viscosity, and thermal conductivity, two or more kinds of nanoparticles are employed.utilised in heat exchangers, solar energy systems, thermal management systems, electronic device cooling, and other industrial settings where improved heat transmission is required. Marangoni convection is produced due to gradient in surface tension with boundary of a fluids, this impact also occurred due to differences in temperature of a surface. Marangoni convection has some important application in engineering and industries, such is boiling and evaporation, surfactant driven flows, semiconductor manufacturing, material coating and deposition the defined and some other important uses the researchers and engineering study Marangoni convection to expand their strategies and controlled the related flow problem, different scientists investigate the features of Marangoni convection in the occurrence of numerous impacts recently. Khan et al.¹ examined Marangoni convection and shown that the fluid particles’ velocity is increased by the Marangoni convection parameter. Sadiq et al.² investigated Marangoni forced convection in Casson nanoliquid flow and show that both velocity and temperature filed have inverses relation to Marangoni convection parameter. Rashid et al.³ investigated Marangoni convection numerically by using ND Solve method of Mathematica 10.3 software. Qayyum et al.⁴ investigated Marangoni convection in hybrid nanofluid flow submerged in ethylene glycol and water base fluids. Khashi et al. ⁵ investigated thermal Marangoni convection and stability analysis of hybrid nanofluid flow past a permeable stretching/shrinking surface. Rehman et al. ⁶ investigated consequence of the Marangoni convection CNT nanofluids and show that Marangoni convection has double impact on velocity filed. Rasool et al.⁷ investigated Marangoni convective nanofluid flow and show that temperature filed is decreasing with the increasing of Marangoni convection parameter. Rehman et al.⁸ investigated the influence of Marangoni convection in hybrid nanofluids for enhancing the heat transfer rate. Rehman et al.⁹ investigated the influence of Marangoni convection on MHD hybrid nanofluids and discussed the impact of various parameters on both the velocity and temperature profiles. Rehman et al.¹⁰ examined how the magnetic field and Marangoni convection affected the erratic flow of nanofluids past an extended sheet. AlQdah et al.¹¹ investigated Marangoni convection and show that this investigation changes the thermal conductivity with the change of surface tension parameter. Lin et al.¹² investigate the Marangoni convection flow and heat transfer characteristics of power-law nanofluids influenced by a temperature gradient, incorporating the effects of the modified Fourier’s law.. Magyari et al.¹³ investigate thermosolutal Marangoni convection in the presence of heat and mass generation or consumption. Mahanthesh et al.¹⁴ investigate Marangoni convection on MHD nanoliquids flow past a to a disk source. To further enhance heat transfer efficiency, the scientists introduced a novel kind of nanofluid name is hybrid nanofluid. Hybrid nanofluids are the extension of conventional nanofluid, where two or more metals are combined to create different chemical bonds, leading to unique properties. When more than one nanoparticles mixed in the Casson fluid such a fluid is called Casson hybrid nanofluid. This hybrid combination has proven to be advantageous in various applications such as power systems, welding, vehicle thermal coordination, lubrication, and more. The concept of hybrid nanofluid was first introduced by. Venkitaraj et al.¹⁵. Subsequently. Devi et al.^16,17 investigated MHD hybrid nanofluid flow using movable surfaces to gain further insights into this intriguing phenomenon. Tayebi and Chamkha¹⁸ conducted a numerical study on $\text{Cu}-{\text{Al}}_{2}{\text{O}}_{3}-Water$ hybrid nanofluid, while Ghadikolaei et al.¹⁹ investigated ${\text{TiO}}_{2}-\text{Cu}/{\text{H}}_{2}\text{O}$ hybrid nanofluid with inclusion of Lorentz force. Hayat et al.²⁰ examined the behavior of Ag-CuO/water hybrid nanofluid near a rotating surface, while Yousefi et al.²¹ utilized a stretching cylinder to analyze the characteristics of hybrid nanofluid. Subhani et al.²² employed a stretching surface to study the behavior of ${\text{Cu}-\text{TiO}}_{2} /{\text{H}}_{2}\text{O}$ hybrid nanofluid. Jan et al.²³ examine how varying thermal conductivity affects the flow of a trihybrid nanofluid past an extended surface. Waqas et al.²⁴ investigate the thermal analysis of hybrid nanofluids based on blood that flow magnetically through a revolving channel. Hussain et al.²⁵ study entropy analysis in hybrid nanofluid mixed convective flow affected by chemical reactions and melting heat. Hassan et al.²⁶ study heat transport analysis of the flow of a hybrid nanofluid (ag-cuo) in a porous medium. on heat transfer. From the above published research work and up to authors knowledge no one investigate analytical analysis of Marangoni convection on ethylene glycol base hybrid nanofluid two-dimension flow with viscous dissipation through a porous medium, for the first time this model is study analytically with the influence of viscous dissipation and Marangoni convection on ethylene glycol base hybrid nanofluid, the consider flow problem is examined by using the fundamental principles of fluid dynamics and thermodynamics. The using the similarity variables in leading equations of energy and momentum, along with integration of thermo physical properties of hybrid nanofluid, resulted a coupled NLODEs. To solve NLODEs, the HAM, is used along with MATHEMATICA software. Due to its consequences for heat and mass transfer, fluid dynamics, and material processing, analysing the impact of Marangoni convection on hybrid nanofluid flow has important applications in a range of industries and research domains. Here are a few of the more important uses. Devices such as LEDs and microchips can effectively drain heat thanks to hybrid nanofluids with improved thermal characteristics. Through improved localised heat transfer at the fluid interface, Marangoni convection enhances cooling. Hybrid nanofluids with Marangoni-driven flow enhance heat dissipation in applications where good thermal performance is essential. Marangoni convection is essential for controlling fluid flow and particle movement in microscale systems. These effects can be amplified by hybrid nanofluids, which increases the accuracy and effectiveness of such systems for chemical and biological applications.

Flow problem formulation.

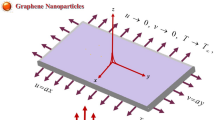
Consider 2D, incompressible, steady, laminar, viscous flow of,$Ag + GO + EG$, ethylene glycol base hybrid nanofluid past a stretching porous medium. The x axis is considering parallel to the surface in the direction of fluid particles and y axis is consider vertical to the surface. $T_{w} = T_{\infty } + \frac{{T_{0} a^{2} }}{{l^{2} }}$, is the reference temperature, where a is any positive constant,$l$, is the length of the surface and $T_{\infty }$, $T_{0}$, are the reference temperature. To model the consider flow problem, the continuity, momentum, and energy equations are used according to Madhukesh et al.²⁷ as:

$$\frac{{\partial \hat{u}}}{\partial x} + \frac{\partial v}{{\partial y}} = 0,$$

(1)

$$\hat{u}\frac{{\partial \hat{u}}}{\partial x} + v\frac{{\partial \hat{u}}}{\partial y} = \frac{{\mu_{hnf} }}{{\rho_{hnf} }}\frac{{\partial^{2} \hat{u}}}{{\partial y^{2} }} - \nu_{hnf} \frac{{\hat{u}}}{K},$$

(2)

$$\hat{u}\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} = \frac{{k_{hnf} }}{{\left( {\rho c_{p} } \right)_{hnf} }}\frac{{\partial^{2} T}}{{\partial y^{2} }} - \frac{1}{{\left( {\rho c_{p} } \right)_{hnf} }}\frac{{\partial q_{r} }}{\partial y} + \mu_{hnf} \left( {\frac{{\partial \hat{u}}}{\partial y}} \right)^{2} ,$$

(3)

where, $\rho_{hnf}$ is hybrid nanofluid density, $T$ represents fluid temperature, $k_{hnf}$ represents fluid thermal conductivity $\left( {\rho \;c_{p} } \right)_{hnf},$ signifies the heat capacity, ${\rm K},$ is the dimension porosity parameter and $\mu_{hnf},$ denotes hybrid nanofluid viscosity.

The BCs for the given flow problem are

$$\begin{aligned} & \mu_{nf} \frac{{\partial \hat{u}}}{\partial y} = \frac{\partial \sigma }{{\partial T}}\frac{\partial T}{{\partial x}},v = 0,T = T_{w} ,\,\,at\,y = 0 \\ & \hat{u} \to 0,T \to T_{\infty } \,at\,y \to \infty \\ \end{aligned}$$

(4)

In Eq. 3, $q_{r}$, represent the heat flux and defined according to Rosseland assumption as;

$$q_{r} = \frac{{\partial T^{4} }}{\partial y}\frac{4}{3}\frac{{\sigma^{*} }}{{k^{*} }}$$

(5)

where the surface tension $\sigma$, is the linear function of temperature and is defined as;

$$\sigma = \sigma_{0} \left( {1 - \gamma T\left( {T - T_{\infty } } \right)} \right)$$

(6)

where $\gamma T = - \frac{1}{{\sigma_{0} }}\left( {\frac{\partial \sigma }{{\partial T}}} \right)_{{T = T_{\infty } }}$,

Thermophysical properties of hybrid nanofluid

$$\begin{aligned} & \rho_{hnf} = \left[ {\left( {1 - \phi_{2} } \right)\left( {1 - \phi_{1} } \right)\rho_{bf} + \phi_{1} \rho_{{p_{1} }} } \right] + \phi_{2} \rho_{{p_{2} }} , \\ & \left( {\rho c_{p} } \right)_{hnf} = \left[ {\left( {1 - \phi_{2} } \right)\left( {1 - \phi_{1} } \right)\left( {\rho c_{p} } \right)_{bf} + \phi_{1} \left( {\rho c_{p} } \right)_{{p_{1} }} } \right] + \phi_{2} \left( {\rho c_{p} } \right)_{{p_{2} }} , \\ & \mu_{hnf} = \frac{{\mu_{bf} }}{{\left( {1 - \phi_{1} } \right)^{2.5} \left( {1 - \phi_{2} } \right)^{2.5} }}, \\ &\frac{{ k_{hnf} }}{{ k_{bf} }} = \frac{{k_{{p_{2} }} + \left( {n - 1} \right)k_{bf} - \left( {n - 1} \right)\phi_{2} \left( {k_{bf} - k_{{p_{2} }} } \right)}}{{k_{{p_{2} }} + \left( {n - 1} \right)k_{bf} + \left( {n - 1} \right)\phi_{2} \left( {k_{bf} - k_{{p_{2} }} } \right)}}, \\ \end{aligned}$$

(7)

The similarity transformations for the defined flow problem is;

$$\begin{aligned} \psi & = x\sqrt {av_{hnf} } f\left( \eta \right),\eta = \sqrt {\frac{a}{{\nu_{hnf} }}} y,\hat{u} = axf^{\prime}\left( \eta \right),v = \sqrt {a\nu_{hnf} } f\left( \eta \right) \\ T & = T_{\infty } + \left( {T_{w} - T_{\infty } } \right)\theta \left( \eta \right), \\ \end{aligned}$$

(8)

The similarity transformations in Eq. (8) and the thermophysical properties of the hybrid nanofluid in Eq. (7) are applied to convert the basic flow Eqs. (1)–(3) from their dimensional form to a dimensionless form. The continuity equation is satisfied when Eq. (8) is used, and Eqs. (2)–(4) are expressed as follows.

$$\begin{gathered} \frac{1}{{\left( {1 - \phi_{1} } \right)^{2.5} \left( {1 - \phi_{2} } \right)^{2.5} \left[ {\left\{ {\left( {1 - \phi_{2} } \right)\left( {1 - \phi_{1} + \phi_{1} \frac{{\left( {\rho C_{p} } \right)_{{s_{1} }} }}{{\left( {\rho C_{p} } \right)_{f} }}} \right)} \right\} + \phi_{2} \frac{{\left( {\rho C_{p} } \right)_{{s_{2} }} }}{{\left( {\rho C_{p} } \right)_{f} }}} \right]}}f^{\prime\prime\prime} + \lambda f^{\prime} - \left( {f^{\prime}} \right)^{2} - ff^{\prime\prime} = 0, \hfill \\ \hfill \\ \end{gathered}$$

(9)

$$\begin{aligned} & \frac{{k_{nf} }}{{k_{s} }}\left( {1 + \frac{4}{3}Rd} \right) \\ & \quad \frac{1}{{\left( {1 - \phi_{1} } \right)^{2.5} \left( {1 - \phi_{2} } \right)^{2.5} \left[ {\left\{ {\left( {1 - \phi_{2} } \right)\left( {1 - \phi_{1} + \phi_{1} \frac{{\left( {\rho C_{p} } \right)_{{s_{1} }} }}{{\left( {\rho C_{p} } \right)_{f} }}} \right)} \right\} + \phi_{2} \frac{{\left( {\rho C_{p} } \right)_{{s_{2} }} }}{{\left( {\rho C_{p} } \right)_{f} }}} \right]}}\theta^{\prime\prime} \\ & \quad + \Pr \left( {f\theta^{\prime} - 2f^{\prime}\theta } \right) + Ec\left( {f^{\prime\prime}} \right)^{2} = 0, \\ \end{aligned}$$

(10)

With the transform boundary condition;

$$\begin{aligned} f\left( 0 \right) & = 0,f^{\prime}\left( 0 \right) = - 2Ma,\theta \left( 0 \right) = 1,\, \\ \theta \left( \infty \right) & = 0,f^{\prime}\left( \infty \right) = 1, \\ \end{aligned}$$

(11)

where $\lambda = \frac{{\nu_{hnf} }}{Ka}$ , is porosity parameter ,$Ma = \frac{{\sigma_{0} \gamma TT_{0} }}{{l^{2} a\sqrt {a\mu_{nf} \rho_{nf} } }}$, is marangoni convection parameter $Rd = \frac{{4T_{0}^{3} \sigma^{*} }}{{{\rm K}^{*} k_{hnf} }}$, is radiation parameter, $\delta = \frac{{T_{w} - T_{\infty } }}{{T_{\infty } }}$, is the temperaturere diffrence, $Ec = \frac{{\left( {u_{w} (x)} \right)^{2} }}{{C_{p} (T_{w} - T_{\infty } )}}$ , is the eckert number and $\Pr = \frac{{\mu_{hnf} \left( {\rho C_{p} } \right)_{hnf} }}{{k_{hnf} }}$, is the prandtl number.

The key physical quantities in this research are the skin friction coefficient and the Nusselt number, which are defined as follows

$$C_{fx} = \frac{{\tau_{wx} }}{{\rho u_{w}^{2} }},Nu = k_{hnf}^{ - 1} \frac{{q_{w} }}{{l\left( {T_{w} - T_{\infty } } \right)}}$$

(12)

$$\,\tau_{wx} \,\, = \left( {\mu_{hnf} \frac{\partial u}{{\partial y}}} \right)_{y = 0} \,\,\,\,\,\,\,,\,q_{w} = - k_{hnf} \frac{1}{l}\left( {\frac{\partial T}{{\partial y}}} \right)_{y = 0}$$

(13)

In Eq. (13), $\tau_{wx} \,and\,\tau_{wy} \,$ is the shear stress on the surface in the x and y directions. Using Eq. (15) in Eq. (14), the non- dimension form of skin friction and nusselt number is as follow;

$$\,\sqrt {{\text{Re}} x} C_{fx} \,\, = \frac{{f^{\prime\prime}\left( 0 \right)}}{{\left( {1 - \phi_{1} } \right)^{2.5} \left( {1 - \phi_{2} } \right)^{2.5} }}\,\,\,\,,\,\frac{Nu}{{\sqrt {{\text{Re}} x} }} = - \frac{1}{l}\frac{{k_{hnf} }}{{k_{f} }}\left( {\theta^{\prime}\left( 0 \right)} \right)$$

(14)

Solution by HAM

One analytical method for resolving nonlinear differential equations is the Homotopy Analysis Method (HAM). Shijun Liao created it in the 1990s as a substitute for conventional perturbation techniques, which frequently call for tiny parameters or other constrictive requirements. HAM is extensively used in applied mathematics, physics, and engineering and offers a comprehensive framework for estimating solutions to nonlinear problems.With HAM, the user can begin with a solution estimate that does not have to meet any beginning or boundary criteria.The technique links the initial nonlinear problem to a more straightforward, solvable problem by creating a “homotopy” (a continuous deformation). An auxiliary parameter controls this deformation. The authors utilize the homotopy analysis method, an approximate analytical technique, to solve the system of nonlinear ordinary differential Eqs. (9–10) along with the transformed boundary condition (11). An important factor in guaranteeing the convergence of the approximate analytical solution is the introduction of an auxiliary parameter.

The initial solution is found using the following technique.

$$f_{0} (\eta ) = 1 - e^{ - \eta } ,\theta_{0} (\eta ) = e^{ - \eta } { ,}$$

(15)

The linear operators in the above-mentioned situation are defined as;

$$L_{{f_{1} }} (f_{1} ) = f_{1}^{\prime \prime \prime } - f^{\prime\prime}_{1} ,\,\,{\text{L}}_{\theta } {(}\theta {) = }\theta \,{^{\prime\prime}}\,,$$

(16)

They possess the subsequent characteristics;

$$L_{{f_{1} }} (D_{1} + D_{2} \eta + D_{3} \eta^{2} ) = 0\,\,and\,{\text{L}}_{\theta } (D_{4} + D_{5} \eta ) = 0{,}$$

(17)

The whole solutions, contains the constants, the nonlinear operators $N_{\theta } \,and\,N_{{f_{1} }} \,$, are given as.

$$\frac{{d^{3} f_{1} (\eta ,r)}}{{d\eta^{3} }} + \lambda \left( {\frac{{df_{1} (\eta ,r)}}{d\eta }} \right) - \left( {\frac{{df_{1} (\eta ,r)}}{d\eta }} \right)^{2} - f_{1} (\eta ,r)\frac{{d^{2} f_{1} (\eta ,r)}}{{d\eta^{2} }} = 0,$$

(18)

$$\left( {1 + \frac{4}{3}Rd} \right)\frac{{d^{2} \theta (\eta ,r)}}{{d\eta^{2} }} + \Pr \left( {f_{1} (\eta ,r)\frac{d\theta (\eta ,r)}{{d\eta }} - 2\theta (\eta ,r)\frac{{f_{1} \theta (\eta ,r)}}{d\eta }} \right) + Ec\left( {\frac{{d^{2} f_{1} (\eta ,r)}}{{d\eta^{2} }}} \right)^{2} = 0,$$

(19)

The fundamental idea of HAM as described by^28,29,30,31 for Eqs. (18–19) as;

$$\left[ {1 - r} \right]L_{{f_{1} }} \left[ {f_{1} (\eta ,r) - f_{0} (r)} \right] = rh_{{f_{1} }} N_{{f_{1} }} \left[ {f_{0} (\eta ,r)} \right],$$

(20)

$$\left[ {1 - r} \right]L_{\theta } \left[ {\theta (\eta ,r) - \theta_{0} (r)} \right] = rh_{\theta } N_{\theta } \left[ {f_{1} (\eta ,r),\theta (\eta ,r)} \right],$$

(21)

The leading factor, when $r = 1{\text{ and r}} = 0$, is

$$f_{1} (\eta ,1) = f_{1} (\eta )\,and \, \theta (\eta ,1) = \theta (\eta ), \,$$

(22)

such that $r \in [0,1]$, is we take:

about $r = 0$ of $\theta (\eta ,r)\, \, and \, f_{1} (\eta ,r) \,$, the Taylor’s series expansion, are

$$\begin{aligned} f_{1} (\eta ,r) & = f_{0} (\eta ) + \sum\limits_{e = 0}^{\infty } {f_{e} (\eta )r^{e} } , \, \\ \theta (\eta ,r) & = \theta_{0} (\eta ) + \sum\limits_{e = 0}^{\infty } {\theta_{e} (\eta )r^{e} } , \, \\ \end{aligned}$$

(23)

The secondary limitations $h_{{f_{1} }} {\text{and }}h_{\theta } \,$ are selected as, the Eq. (23) converges if $r = 1$, substituting $r = 1$, we gain:

$$\begin{aligned} f_{1} (\eta ) & = f_{0} (\eta ) + \sum\limits_{n = 1}^{\infty } {f_{n} (\eta )} , \, \\ \theta (\eta ) & = \theta_{0} (\eta ) + \sum\limits_{n = 1}^{\infty } {\theta_{n} (\eta )} , \\ \end{aligned}$$

(24)

Results

Table 1 show the impact of, $\lambda ,\phi_{1} ,\phi_{2}$ on surface resistance, according to table one we see that the enhancing value of $\lambda ,\phi_{1} ,\phi_{2}$, additionally raising the skin friction; in fact, as these parameters increase in magnitude, additional friction forces are created, which leads to an increase in skin friction.

Table 1 Skin friction via $\lambda ,\phi_{1} ,\phi_{2}$.

Table 2 shows the effects of $Ec,\delta ,Rd$ on the Nusselt number, Table 2, display that the enchasing value of $Ec,\delta ,Rd$ , increases the Nusselt number.

Table 2 The impact of $Ec,\delta ,Rd$ on Nusselt number via.

Table 3 presents the residual errors for the momentum and energy equations, providing a basis for a robust convergence conclusion.

Table 3 Show Convergence of the method for, $\theta \left( \eta \right)$ and $f^{\prime}\left( \eta \right)$.

Discussion

This subsection examines the impact of various dimensionless parameters on velocity and temperature profiles, highlighting their significance. The geometry of the problem is given in Fig. 1. This section focuses on key flow characteristics and examines the influence of dimensionless parameters on critical entities to better understand the underlying physics of the scenario. Schematic representations in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 illustrate the dynamics of velocity and temperature profiles, as derived from the analytical solution (HAM), under varying values of specific model parameter while keeping other factors constant. This study focuses on the analytical investigation of two-dimensional ethylene glycol-based hybrid nanofluid flow, incorporating the effects of viscous dissipation and Marangoni convection over a porous surface. By employing the Homotopy Analysis Method (HAM), the nonlinear model equations were effectively solved using the BVP2 solver in Mathematica (Wolfram Language), which is specifically designed for handling boundary value problems for differential equations. The geometric configuration of the problem is illustrated in Fig. 1. The impact of various parameters on fluid temperature and velocity is illustrated using graphs and tables. Figure 2 shows the effect of nanoparticle volume fraction on the velocity field, with all other parameters kept constant. As shown in the figure, the fluid velocity field decreases as the volume fractions of both nanoparticles increase at the same rate. The way that variations in the concentration of nanoparticles in a base fluid affect the flow velocity is known as the effect of nanoparticle volume fraction on the velocity field. Because of changes in the fluid’s density, viscosity, and thermal conductivity, increasing the volume fraction of nanoparticles generally has an impact on the velocity field. The hybrid nanofluid’s effective viscosity usually rises with an increase in the volume fraction of nanoparticles, increasing flow resistance. The velocity field decreases as a result. Because of the fluid’s increased density and viscosity, the addition of nanoparticles accelerates momentum diffusion, which further slows the flow. Because it takes more energy for the fluid to overcome viscous forces, a higher volume percentage of nanoparticles may result in a thicker momentum barrier layer.

Fig. 1

Geometry of the problem.

Fig. 2

Fluid velocity via nanoparticles volume friction.

Fig. 3

Fluid velocity via porosity parameter.

Fig. 4

Fluid velocity via Marangoni convection parameter.

Fig. 5

Fluid temperature via thermal radiation parameter.

Fig. 6

Fluid temperature via Eckert number.

Fig. 7

Fluid temperature via nanoparticles volume friction.

Fig. 8

Porosity parameter via skin friction.

Fig. 9

Marangoni convection via skin friction.

Fig. 10

Thermal radiation via Nusselt number.

Fig. 11

Eckert number via Nusselt number.

Fig. 12

Compression of current work with Abbas et al.³².

The effect of the porosity parameter is illustrated in Fig. 3, where all other parameters are held constant. As shown in Fig. 3, the fluid velocity field decreases as the porosity parameter increases. A crucial factor in fluid flow analysis in porous media is porosity, which has a big impact on the fluid velocity field. The percentage of a porous medium’s volume that is made up of void areas that allow fluid to pass through is known as the porosity parameter. Resistance rises when porosity falls because less area is available for fluid flow. Lower velocities result from this, and the flow may become more confined or irregular. Variations in porosity can have a substantial impact on the velocity distribution at the microscopic level by causing local eddies, preferred flow routes, and stagnation zones. The impact of Marangoni convection parameter is presented in Fig. 4, when other parameters are fixed. Figure 4, shows fluid velocity filed is increasing as the values of Marangoni convection parameter enhancing. Physically when we increase the value of Marangoni convection parameter the place of the fluids particles change rapidly which provide more space to the fluids particles for moment and fluids velocity increasing by increasing Marangoni convection parameter. The impact of surface tension gradients on fluid motion, usually at fluid–fluid interfaces or between a liquid and a gas, is described by the Marangoni convection parameter. It is essential to a fluid’s velocity field, especially in systems where temperature or concentration gradients cause surface tension to fluctuate. When a gradient in surface tension develops at a fluid interface as a result of either concentration (solutal Marangoni effect) or non-uniform temperature (thermal Marangoni effect), Marangoni convection takes place. The dynamics of the molten pool during welding or crystal formation are impacted by Marangoni convection. In spaceship experiments, fluid motion is dominated by Marangoni convection when gravity is absent. Figure 5, show the impact of thermal radiation parameter on temperature distribution, when the other parameters are fixed. Figure 5 illustrates the direct relationship between thermal radiation and temperature distribution. As the value of the thermal radiation parameter increases, the temperature distribution also rises. The temperature field in heat transfer systems is greatly influenced by the thermal radiation parameter, especially when radiative heat exchange is present in high-temperature settings or in optically thick media.The relative significance of radiative heat transmission in relation to other heat transfer modes, such conduction or convection, is measured by the thermal radiation parameter. The Rosseland approximation for radiative heat flux in an optically thick medium is frequently used to introduce it into models. The temperature distribution is greatly impacted by radiation, which takes over as the primary heat transmission mechanism. Because radiative heat transmission is long-range and energy is efficiently transported even over greater distances, the temperature field tends to flatten out. Figure 6 examines the impact of the Eckert number on the temperature distribution while keeping other parameters constant. It indicates a direct relationship between the Eckert number and the temperature field, showing that an increase in the Eckert number leads to a corresponding rise in the fluid temperature field. The relative significance of heat conduction against viscous dissipation (the conversion of mechanical energy into heat) in a fluid flow is measured by Ec. The flow’s K.E (kinetic energy) contribution to the temperature field through viscous dissipation is described by the Eckert number. The transformation of kinetic energy into thermal energy has a significant impact on the temperature field. As the heat produced by viscous forces contributes to the external heat input, the temperature field as a whole rises. Because of increasing viscous dissipation, fluid temperatures rise with higher Eckert number values. The temperature field differs greatly from the situation without dissipation at high Eckert numbers because the heat produced internally redistributes the energy throughout the flow. Figure 7 displays the inspiration of nanoparticles volume friction via temperature filed on. Figure 7, show that temperature distribution is increasing with the increasing of nanoparticles. The percentage of nanoparticles in a nanofluid is indicated by the nanoparticle volume fraction. It is essential for figuring out the fluid’s thermal characteristics, which include its heat capacity, viscosity, and effective thermal conductivity. These factors all have a direct impact on the temperature field in heat transfer systems. The thermal conductivity of the nanofluid significantly enhances with an increase in the nanoparticle volume fraction. Better heat conduction throughout the fluid is made possible by this improvement, resulting in more consistent and effective heat transfer. Additionally, adding nanoparticles raises the nanofluid’s effective viscosity, especially at high volume fractions. This may reduce convective heat transmission by slowing down fluid velocity. As heat dissipation is enhanced by the greater thermal conductivity, the temperature field starts to exhibit discernible variations. Figure 8, show the impact of porosity parameter on skin friction, which shows that the enhancing value of porosity parameter, also increasing the skin friction. Skin friction in flows through or over porous materials is greatly influenced by the porosity parameter, which quantifies the percentage of a porous medium that is made up of void spaces. The tangential force per unit area applied to a surface as a result of fluid viscous shear stresses is known as skin friction. There is less room for fluid flow in high-porosity materials because the solid matrix takes up the majority of the volume. Higher flow resistance and greater fluid–solid surface interaction result from this. Figure 9, show the impact of Marangoni convection parameter on skin friction, which shows that the enhancing value of Marangoni convection parameter, decreases the skin friction. In fluid flow systems with surface tension-driven convection, skin friction is significantly influenced by the Marangoni convection parameter. The tangential force per unit area caused by viscous shear stresses at a surface is referred to as skin friction. By intensifying velocity gradients close to the surface, the generated flow raises viscous shear stresses and, as a result, skin friction. In boundary layers close to hot or concentration-varying surfaces, this is especially apparent. The effects of Eckert number on the Nusselt number are discussed Fig. 10. The findings show that the Nusselt number is increasing with the increasing of Eckert number. By taking into consideration how heat transport is impacted by viscous dissipation, the Eckert number affects the Nusselt number. How viscous dissipation impacts the thermal energy in the system determines how the Nusselt number, which shows the ratio of convective to conductive heat transfer, varies with the Eckert number. The fluid’s temperature near the surface rises as the Eckert number rises because the fluid’s kinetic energy produces heat through viscous dissipation. The thermal boundary layer is altered by this extra heating, which improves convective heat transfer. The effects of thermal radiation parameter on the Nusselt number are discussed Fig. 11. The findings show that the Nusselt number is increasing with the increasing of thermal radiation parameter. The ratio of convective to conductive heat transfer, or the Nusselt number, is determined in large part by the thermal radiation parameter. When describing the efficiency of heat transmission in a fluid flow system, the Nusselt number is crucial. By adjusting the heat transmission processes, the thermal radiation parameter affects the Nusselt number, especially when radiation starts to matter more than conduction and convection. The fluid’s temperature gradients lessen in this regime, and radiation-induced heat transfer works more effectively. The dominance of radiation is shown in the Nusselt number, which rises strongly with the thermal radiation parameter.

Conclusions

This research work explained the significance of marangoni convection in ethylene glycol base hybrid nanofluid flow with viscous dissipation through a porous medium, that contains $GO,Ag$ nanoparticles with ethylene glycol as base fluid. The system of partial differential equations is converted into a set of nonlinear ordinary differential equations by using similarity transformations. These resulting temperature and velocity equations are then analytically solved using the semi-numerical Homotopy Analysis Method (HAM). The impact of significant criterion on the results is shown graphically. The main findings of the study are summarized below.

• (i) Raising the values of porosity parameter and nanoparticles volume friction decrees fluid velocity filed.

• (ii) Fluid velocity filed growing with growing of Marangoni convection parameter

• (iii) Raising the values of Eckert number, nanoparticles volume friction and thermal radiation parameter, improve the temperature distribution.

• (iv) Raising the values of porosity parameter improve the fluid skin friction.

• (v) Raising the values of Marangoni convection, the skin friction is decreasing.

• (vi) By increasing the values of the Eckert number, improvement in the Nusselt number.

• (vii) Growing the values of the thermal radiation parameter, improvement in the Nusselt number.

• (viii) The residual error decreases with an increasing number of iterations.