Introduction

As the main working mechanism of coal mines, the performance of the drum is the key to affecting the safety and efficiency of coal mining. Especially in coal seams with complex mining conditions, higher requirements are put forward for the performance of drums. Studying the cutting and loading performance of the drum under complex coal seams, and understanding the impact of drum structural parameters on its performance, is of great significance for improving drum performance and structural evolution. As early as the 1870s, scholars began to study the working performance of shearer drums. Brooke1 studied the loading performance of helical drum under different structural and kinematic parameters. Becker2 analyzed the influence of mining parameters on linear cutting noise, load, productivity and specific energy consumption. Hurt3 pointed out that coal baffle structural parameters, working face arrangement relationship, and blade depth are the key factors affecting the loading performance of the helical drum. Mazurkiewicz4 analyzed the influence of the arrangement, size and form of pick on the process of helical drum cutting coal-rock. Jaszczuk5 explored the relationship between the dynamic load of pick and the structural design, kinematic parameters and body position of helical drum. Ayhan et al.6 analyzed the load characteristics of different shaped drums through underground tests, and found that the load-bearing performance of conical drum is better than that of cylindrical drum. Gao et al.7 conducted a large number of cutting experiments using helical drums with different structures and proposed an empirical model of the drum cutting torque. Abu et al.8 studied the axial and radial cutting resistance of dry and wet coal wall through experiments. Luo et al.9 experimentally studied the load characteristics of helical drum cutting coal-rock and coal-rock mixture, and analyzed the influence of cone angle, cutting distance, helix angle, pick arrangement and traction speed on the axial force of helical drum. Dewangan et al.10 studied the influence of installation angle and coal-rock conditions on pick wear by performing cutting experiments with WC–Co material pick. Li et al.11,12 established a mathematical model of cutting thickness and cutting resistance by judging the cutting conditions in the process of oblique cutting, and conducted an experimental study on the cutting load characteristics of helical drum. Eshaghian et al.13 used laser cladding technology to deposit nickel-based superfine coatings NiBSiFeWC to improve the wear resistance and mechanical properties of coal mining cutter bits.

However, the interaction between helical drum and coal-rock is strongly coupled and nonlinear. Theoretical analysis and physical experiments cannot be fully applied to the study of drum cutting process under complex coal seam conditions. With the development of finite element and discrete element technology, it is widely used in the simulation analysis of helical drum cutting and loading process. Based on the virtual simulation, Bo14 determined the main failure forms of coal-rock fragmentation by LS-DYNA finite element simulation method. John15 obtained the temperature transfer law of pick cutting coal-rock by using the finite element method. Through finite element simulations and an automated rotating coal mine simulation platform, Brijes16 verified the effect of the size and shape of the pick tip on the cutting performance of the cutting system. Mikl et al.17 analyzed the load and stress states of picks with different geometries by using ABAQUS. Wyk et al.18 performed numerical simulations of pick forces in rock cutting tests by using the discrete element method. Tribological interactions such as contact, shear, fracture, friction and wear were used in these cutting tests. Fu19 established a discrete element model for single pick cutting coal-rock, and analyzed the load characteristics of pick during the cutting process. Liu and Chen et al.20,21 studied the wear characteristics of pick and blade in the process of drum cutting coal-rock by using finite element method and discrete element method. Also using the finite element method and discrete element method, Carlos22 analyzed the cutting theory and stress distribution of the pick. Zhao and Tian et al.23,24 conducted a systematic and in-depth study of the dynamic characteristics and the coal loading rate of drum by using EDEM. In addition, Zhao et al.25,26,27 simulated the drum cutting process of coal-rock containing gangue by the discrete element method, and analyzed the influence trend of coal-rock strength, traction speed and drum rotation speed on drum wear. In order to investigate the influence of hub form on the coal loading rate of the drum, Gao et al.28 designed seven drums with different hub forms and structures, and studied the influence of the complexity of hub structures on the coal loading performance by discrete element method simulation. The change curves with the research object of different drums, such as coal loading rate, velocity field distribution, and contact force between fallen coal particles, were obtained. Wan et al.29 analyzed the dynamic response of cutting equipment using the finite element method. The relationship between the performance of the cutter bits and their vibration characteristics was examined, providing methodologies to enhance the stability of cutting equipment. Liu et al.30 used the Archard model in EDEM software to study the wear patterns of shearer drum blades and developed a multi-objective optimization model based on blade wear to improve blade life. The mentioned research results have laid the foundation for analyzing the working performance of the drum, but there are fewer studies related to the construction of a comprehensive performance evaluation model of drums including load characteristics and coal loading performance.

With the development of research on the working performance of drums, scholars have increasingly realized that in order to adapt to harsh underground environments and meet the needs of coal production, designing and manufacturing efficient and sturdy drums has become an urgent need. So far, many methods have been proposed to optimize the structural parameters of the drum and achieve structural evolution of the drum. Yu et al.31 used a genetic algorithm (GA) to optimize the structural and kinematic parameters of the drum at different cutting impedances. In order to improve the coal loading performance, lump coal rate and coal economic efficiency. However, when dealing with multi-objective optimization, there may be issues with slow convergence speed, which provides a direction for improvement in future research. Li et al.32 optimized the outer edge diameter and helix angle of the blade, drum rotation speed and traction speed by means of particle swarm optimization algorithm and ant colony algorithm (PSO-GACA). Wu and Li et al.33,34 optimized the drum structural parameters to reduce the load fluctuation coefficient and cutting specific energy consumption. Taking the coal loading rate, cutting specific energy consumption and load fluctuation as the optimization objectives. However, the study lacks a systematic analysis of the impact of different mining environment conditions. Mao et al.35 optimized the blade thickness, spiral angle, head number, pick number on the same section and pick installation angle by using the NSGA-III algorithm. Based on the discrete element method, Zhao et al.36,37 developed a multi-objective optimization model of drum, and obtained the optimal structural parameters by using GA. However, the applicability of the model still requires further validation in practical applications. Ding and Wang et al.38,39 studied the optimization of drum structure, and the relevant results can provide a reference for improving the drum performance. Duan et al.40 used the parameters of the cutting teeth and drum as design variables and established the response function of the design variables based on the central composite experimental method. The optimal structural and working parameters of the cutting teeth and drum of the coal mining machine were obtained through multi-objective bat algorithm and grid based multi-objective bat algorithm. This provides some theoretical references for the design and production of rollers, and has certain guiding significance for the design and production of rollers. The successful application of intelligent optimization algorithms in drum structure optimization not only significantly improves the design level, but also greatly shortens the design cycle. It is an important method for drum structure optimization.

In view of the above, this study aims to investigate the relationship between the influence of the structural parameters of the drum on its working performance by means of virtual prototyping technology, and to realize the structural optimization of the drum in order to improve its reliability and working performance. Taking MG400/951-WD shearer drum as the research object, this study explores the influence of spiral angle, installation angle and cutting distance on average cutting resistance, load fluctuation coefficient, cutting specific energy consumption and coal loading rate when the drum cuts in complex coal seams. The comprehensive performance evaluation function of the drum was fitted, and the optimal parameters were obtained using the NSGA-II algorithm. Virtual prototyping technology provides methodological guidance for the design and development of high-performance and high-strength drums.

Theoretical foundations and numerical models

During the cutting process, there are contact, compression, collision, and friction behaviors between the drum and coal rock materials. In this study, based on the coal rock cutting theory and with the help of discrete element theory, a numerical model of drum cutting complex coal seams is established in order to explore the complex coupling interaction relationship between the drum and coal rock materials. In this section, the mechanical model of drum cutting, the mathematical model of drum loading coal rock materials, and the discrete element bonding contact model are introduced. Additionally, a detailed introduction is given to the testing and discretization of coal rock material properties.

Mechanical model of drum cutting

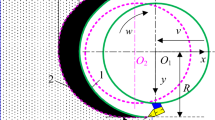
In the complex coal seam containing gangue layer, when the drum cuts at a traction speed v and a rotation speed n, the force on the drum will also change when the cutting object changes. As shown in Fig. 1, when the drum cuts pure coal, the cutting resistance Yj, traction resistance Yj, and lateral force Xj of a single pick can be described as41,42:

$$Z_{j} = 10\overline{{A_{p} }} \frac{{0.35b_{p} + 0.3}}{{b_{p} + K_{\psi } \left( {h_{\max } \sin \theta } \right)^{0.5} }}h_{\max } \sin \theta \cdot t_{cp} K_{z} K_{y} K_{\phi } K_{C} K_{ot} \frac{1}{\cos \beta ^{\prime}}$$
(1)
$$Y_{j} = \left( {0.5{{\sim }}0.8} \right)Z_{j}$$
(2)
$$X_{j} = 0.2Z_{j}$$
(3)
Fig. 1
figure 1

Schematic diagram of the pick force.

Full size image

When θ meets the formula (4), the shearer drum is in a state of cutting gangue, and the cutting resistance Zj′, traction resistance Yj′, and lateral force Xj′ of a single pick can be described as43:

$$\sin \theta \ge \sin \angle ACB = \frac{AB}{{AC}} = \frac{{\sqrt {AC^{2} - BC^{2} } }}{AC} = \frac{{\sqrt {R^{2} - (0.5\delta )^{2} } }}{{R^{2} }}$$
(4)
$$Z_{j}^{\prime} = P_{K} \left[ {k_{T} k_{\psi } {k}^{\prime}_{\psi } k_{d} {k}^{\prime}_{y} \left( {0.25 + 1.8h_{\max } \sin \theta \cdot t_{cp} } \right) + 0.1S_{j} } \right]$$
(5)
$$Y_{j}^{\prime} = \frac{{0.25Z_{j}^{\prime} \left( {0.15 + 0.00056P_{K} } \right)}}{{\left( {10h_{\max } \sin \theta } \right)^{0.4} }}$$
(6)
$$X_{j}^{\prime} = Z_{j}^{\prime} \left( {\frac{{C_{1} }}{{C_{2} + 10h_{\max } \sin \theta }} + C_{3} } \right)\frac{{h_{\max } \sin \theta }}{{t_{cp} }}$$
(7)

where \(\overline{{A_{p} }}\) is the average value of cutting impedance of coal seam in the non-ground pressure affected area, N/mm; \(b_{p}\) is the calculated width for the working part of the pick, mm; \(t_{cp}\) is the cutting width of pick, mm; \(K_{z}\) is the exposed free surface coefficient. \(K_{y}\) is the influence coefficient of cutting angle. \(K_{\phi }\) is the influence coefficient of the front edge shape of pick. \(K_{C}\) is the influence coefficient of pick arrangement. \(K_{ot}\) is the influence coefficient of ground pressure on coal wall. \({\beta ^{\prime}}\) is the deflection angle of pick, °; \(K_{\psi }\) is the brittleness coefficient of coal. \(\theta\) is the position angle of pick, °; R is drum radius, mm. \(P_{K}\) is the contact strength of rock, MPa; \(k_{T}\) is the type coefficient of pick. \(k_{\psi }\) is the shape coefficient of cemented carbide head. \(k`_{\psi }\) is the shape coefficient of pick head. \(k_{d}\) is the diameter coefficient of cemented carbide head. \(k`_{y}\) is the influence coefficient of cutting angle of pick. \(S_{j}\) is the projected area of wear surface of blunt pick on cutting plane, mm2. C1, C2 and C3 are related to the arrangement of the picks.

By decomposing the cutting resistance and traction resistance of the picks based on the coordinate system, the combined forces in the X, Y, and Z directions on each cutting line are obtained:

$$\left\{ {\begin{array}{*{20}c} {F_{{{\text{X}}i}} = \sum\limits_{j = 1}^{n} {(Y_{ij} \cos \theta - Z_{ij} \sin \theta )} } \\ {F_{{{\text{Y}}i}} = \sum\limits_{j = 1}^{n} {( - Y_{ij} \sin \theta - Z_{ij} \cos \theta )} } \\ {F_{{{\text{Z}}i}} = \sum\limits_{j = 1}^{n} {X_{ij} \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } & {} & {} \\ \end{array} } & {} & {} \\ \end{array} } } \\ \end{array} } \right.$$
(8)

By translating the force on each cutting line to the center of mass of the drum, as shown in Fig. 2, the X-, Y-, and Z-directional forces of the drum are obtained:

$$\left\{ {\begin{array}{*{20}c} {F_{{\text{X}}} = \sum\limits_{j = 1}^{N} {F_{{{\text{X}}i}} } } \\ {F_{{\text{Y}}} = \sum\limits_{j = 1}^{N} {F_{{{\text{Y}}i}} } } \\ {F_{{\text{Z}}} = \sum\limits_{j = 1}^{n} {F_{{{\text{Z}}i}} } } \\ \end{array} } \right.$$
(9)
Fig. 2
figure 2

The synthesis and transformation of force.

Full size image

In addition, considering that the spiral blades will be subjected to coal loading counterforce RS and additional axial force Xq during the cutting process, the Z-direction combined force of the drum should be:

$$F_{{\text{Z}}} = \sum\limits_{i = 1}^{N} {F_{{{\text{Z}}i}} } - R_{S} + X_{q}$$
(10)

in where, \(R_{{\text{S}}} = \frac{\pi }{4}(D_{sr}^{2} - D_{g}^{2} )(1 - \frac{{\delta^{\prime} }}{{L\cos \alpha^{\prime} }})BW_{Z} \psi \gamma_{S}\), \(X_{q} = \frac{{\pi RL_{2} \sin \alpha_{0} }}{{2L_{1} B}}F_{Y} K_{2}\).

where Dsr is effective diameter, m. \(\delta ^{\prime }\) is spiral blade thickness, m. L is spiral blade lead, m. \(\alpha ^{\prime}\) is cutting angle, °. WZ is resistance coefficient of pushing raw coal. \(\psi\) is drum filling coefficient. \(\gamma_{s}\) is loose coal bulk density, t/mm3. L1 is distance between guide shoes, m. L2 is distance from the center of the rear sliding shoe to the end face of the coal wall of the front drum, m. \(\alpha_{0}\) is the maximum rotation angle of the shearer when cutting into the coal wall, °. K2 is cutting force increase coefficient.

Mathematical model for coal loading rate of drum

Coal rock is crushed by the drum and then conveyed to the scraper conveyor under the action of spiral blades. However, only part of the broken coal rock will be directly conveyed to the scraper conveyor in this process, so the coal loading rate is used to evaluate the coal loading capacity of the drum. Based on the bulk mechanics theory, the motion state of coal rock during drum loading is shown in Fig. 3.

Fig. 3
figure 3

The movement of coal rock mass.

Full size image

Here, V1 and V2 are the circumferential velocity and relative sliding velocity of coal rock particles, respectively, obtained by the pushing action of the spiral blades. According to the velocity projection theorem, V1 and V2 are projected onto the N–N direction:

$$V_{{2}} = V_{{1}} \frac{\sin \beta }{{\cos \rho_{m} }}$$
(11)

where \(\beta\) is helix angle, °. \(\rho_{m}\) is friction angle, °. V1 = \(2\pi nR\).

Therefore, the coal flow axial velocity Vn is:

$$V_{n} = V_{2} \cos (\beta + \rho_{m} ) = 2\pi nR\frac{{\sin \beta \cos (\beta + \rho_{m} )}}{{\cos \rho_{m} }}$$
(12)

Based on the structural characteristics of the drum, we can know that the maximum possible coal flow cross-sectional area Smax of the single head spiral blade drum is:

$$S_{\max } = \frac{\pi }{4}(D_{y}^{2} - D_{g}^{2} )\left(1 - \frac{{\delta^{\prime} }}{L\cos \beta }\right)$$
(13)

The relationship between the theoretical coal loading mass QZ of the drum and the coal flow axial velocity Vn and the the maximum possible coal flow cross-sectional area Smax can be described as:

$$Q_{Z} = S_{\max } V_{n} \psi$$
(14)

By organizing Eqs. (12) and (13), the theoretical coal loading mass of the multi-head helical drum is obtained as follows:

$$Q_{Z} = \frac{{\pi^{2} }}{2}(D_{y}^{2} - D_{g}^{2} )\left(1 - \frac{{Z\delta^{\prime} }}{L\cos \beta }\right)L\psi nR\frac{{\sin \beta \cos (\beta + \rho_{m} )}}{{\cos \rho_{m} }}$$
(15)

The theoretical coal falling mass of the drum is:

$$Q_{L} = 2RBv\lambda$$
(16)

Therefore, the coal loading rate of the drum is obtained as:

$$\eta = \frac{{Q_{Z} }}{{Q_{L} }}$$
(17)

where Dy is spiral blade diameter, mm. Dg is hub diameter, mm. Z is number of spiral blade heads. B is drum cutting depth, mm. \(\lambda\) is loose coefficient of coal rock.

Discrete element bonding contact model

In the DEM, the object is considered as a discontinuous discrete medium: a collection of several particles with size, mass and contact parameters. When particles are in contact with each other, interactions will occur at the point of contact. The particle–particle and particle-boundary contact can be described by the vibrational equations of motion44, as shown in Fig. 4.

Fig. 4
figure 4

The Hertz-Mindlin with bonding model.

Full size image

where r1, r2 are radius of particles 1 and 2; r1n, r2n are contact radius of particles 1 and 2; Un is normal overlap between particles; Cn, Ct are normal and tangential damping; Sn, St are normal contact stiffness and tangential contact stiffness between particles.

Their relations are obtained:

$$S_{n} = 2E^{*} \sqrt {r^{*} U_{n} }$$
(18)
$$S_{t} = 8G^{*} \sqrt {r^{*} U_{n} }$$
(19)
$$C_{n} = 2\ln e\sqrt {\frac{{S_{n} m^{*} }}{{\pi^{2} + \ln^{2} e}}}$$
(20)
$$C_{t} = 2\ln e\sqrt {\frac{{S_{t} m^{*} }}{{\pi^{2} + \ln^{2} e}}}$$
(21)

where \(E^{*}\) is equivalent elastic modulus, and 1/E* = (1 − u1)/E1 + (1 − u2)/E2; E1, E2 are macroscopic elastic modulus of coal particles 1 and 2; u1, u2 are macroscopic Poisson ratio of particles 1 and 2; G* is equivalent elastic modulus, and 1/G* = (2 − u1)/G1 + (2 − u2)/G2; G1, G2 are macroscopic shear modulus of particles 1 and 2; r* is equivalent radius of particles, and 1/r* = 1/r1 + 1/r2; m* is equivalent mass of particles, and 1/m* = 1/m1 + 1/m2; m1, m2 are mass of particles 1 and 2; e is restitution coefficient of particles.

The motion of the particle follows Newton’s second law, so that the motion equation of the particles can be obtained:

$$\left. {\begin{array}{*{20}c} {m\ddot{u} = \sum F } \\ {I\ddot{\varpi } = \sum M } \\ \end{array} } \right\}$$
(22)
$$\left. \begin{gathered} \ddot{u}(t) = \frac{{v{(}t +\Delta t) - v(t)}}{{\Delta t}} \hfill \\ \ddot{\varpi }(t) = \frac{{\omega {(}t +\Delta t) - \omega (t)}}{{\Delta t}} \hfill \\ \end{gathered} \right\}$$
(23)

where \(\ddot{u}\), \(\ddot{\varpi }\) are acceleration and angular acceleration of particle; \(v(t)\) and \(\omega (t)\) are the velocity and angular velocity of particles at time t, respectively, and \(\Delta t \to 0\); m, I are mass and rotational inertia of particle; \(\sum F\), \(\sum M\) are resultant force and resultant moment of particle’s centroid.

By integrating Eq. (22), the particle displacement can be described as follows:

$$\left. {\begin{array}{*{20}c} {(u)_{n + 1} = (u)_{n} + (\dot{u})_{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \Delta t} \\ {(\varpi )_{n + 1} = (\varpi )_{n} + (\dot{\varpi })_{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \Delta t} \\ \end{array} } \right\}$$
(24)

Therefore, the new displacement value of the particle is obtained according to Eq. (24), which is substituted into the force–displacement relationship to calculate the new force, and so on in a cycle to achieve tracking the motion of each particle at any moment.

Drum model

In this study, the MG400/951-WD coal mining machine is selected as a prototype, as shown in Fig. 5. It adopts the method of front drum cutting at the bottom and rear drum cutting at the top, which is suitable for thin coal seam working faces containing gangue. During the operation of the coal mining machine, the drum is responsible for crushing and loading coal and rock materials. It is the core working mechanism of the cutting unit of the coal mining machine, assembled from picks, blades, end plate, and hub. The picks are arranged in a spiral on the blades. In drum design, its structural parameters are very important, including drum diameter, drum width, number of heads, blade diameter, blade thickness, spiral angle, installation angle, cutting distance, etc. The selection of structural parameters and correct design will directly affect the performance of the drum, such as cutting force, coal loading capacity, etc., and also affect the reliability of other parts. The initial structural and material parameters of the drum of this type of coal mining machine are shown in Table 1.

Fig. 5
figure 5

Model of shearer drum.

Full size image
Table 1 Initial structural parameters and material parameters.
Full size table

Virtual model of coal wall

The property parameters of coal-rock materials and discretization are the key to establish the coal wall model. Based on the engineering application background of this type of coal mining machine, the coal rock samples were selected from the Wenyu Coal Mine in Ordos, Yanzhou Coal Industry, and the standard samples with 50 mm × 50 mm × l00 mm were obtained using the DQ-1 rock cutting machine. Then, a series of physical experiments, such as density test and loading test, were conducted, as shown in Fig. 6. The relevant parameters of the coal-rock materials were obtained, as shown in Table 2.

Fig. 6
figure 6

Coal rock property testing.

Full size image
Table 2 Physical and mechanical parameters of coal-rock materials.
Full size table

Due to the existence of coal seam cracks and the fact that the coal and rock will be broken into randomly shaped and sized blocks during the drum cutting process, reasonable discretization is necessary to ensure the scientific nature of the coal wall numerical simulation model. Through statistical analysis of the shape and size of coal and rock in typical working faces, this study sets the particle virtual model as spherical and blocky, where the blocky particle model is composed of 10 particle units with different positional information.

According to the coal seam structure of the working face, there is a layer of gangue distributed inside the coal seam in this study, which is located in the middle and lower part of the coal seam, with a thickness of 50 mm. The number of particles is the key factor affecting the simulation speed. The more particle number, the longer the simulation time. Therefore, in order to reduce the amount of computer calculation and improve the simulation efficiency, the following assumptions were made in the process of establishing the coal wall model: ① reduction and simplification of the size of the coal wall model, in which the height of the coal wall is 2500 mm, the width is 1200 mm, and the length is 2050 mm; ② The coal mining machine is used for mining in nearly horizontal coal seams, thus ignoring the influence of coal seam dip angle. Based on the relative position relationship between the drum and the coal wall, a particle factory was established and filled (Fig. 7A, B). Among them, there are approximately 62,000 coal particles and about 9500 gangue particles. The contact model between particles is set as Hertz Mindlin with bonding model. The contact parameters and bonding parameters between particles were set by referring to Table 1 and Eqs. (1)–(4). Finally, the coal wall model was completed, as shown in Fig. 8.

Fig. 7
figure 7

The particle filling process.

Full size image
Fig. 8
figure 8

Numerical simulation model of drum cutting coal-rock.

Full size image

The coal wall is anisotropic and has a complex internal structure. Therefore, it is crucial to verify the accuracy of the coal wall discrete element model. The compressive strengths of the virtual coal rock samples were obtained by carrying out uniaxial compression virtual simulation experiments, as shown in Fig. 9. The simulation results show that the compressive strength of the virtual coal rock is 18.24 MPa and 37.65 MPa, respectively, with an error of only 2.99% and 5.85% compared to the physical experimental results (Table 1), which confirms the correctness of the discrete element model of the coal wall.

Fig. 9
figure 9

Comparison curves of coal rock compressive strength: (a) compressive strength of coal; (b) compressive strength of gangue.

Full size image

Verification and discussion

Experimental verification

Through simulation, the dynamic cutting process of the drum was obtained under the working conditions of traction speed of 10 m/min and drum rotation speed of 58 r/min, as shown in Fig. 10, the cutting load of the drum as shown in Fig. 11.

Fig. 10
figure 10

The dynamic cutting process of drum: (a) drum cutting state at t = 3.5 s; (b) drum cutting state at t = 6.65 s; (c) drum cutting state at t = 7.5 s; (d) cloud diagram of coal-rock particle velocity at t = 3.5 s; (e) cloud diagram of coal-rock particle velocity at t = 6.65 s; (f) cloud diagram of coal-rock particle velocity at t = 7.5 s.

Full size image
Fig. 11
figure 11

The cutting force of the drum.

Full size image

From Fig. 10, it can be seen that the coal wall is broken by the cutting action of drum. Firstly, the broken particles inside the coal wall enter the drum envelope area, and are then moved by the combined action of blade extrusion and gravity. Some particles in the drum envelope area flow along the drum axis to one side of the scraper conveyor, and some particles are thrown into the area behind the drum. According to the relative position relation between drum and scraper conveyor, the number of particles flowing into the gap between coal wall and conveyor increases gradually as the drum cuts continuously, and eventually forming a circulating coal pile. When the height of the circulating coal pile is high enough to reach the height of the conveyor side chute, the particles will flow into the conveyor and be transported out. In addition, the particle velocity is higher during the initial cutting, with a maximum velocity of 9.53 m/s, and then the particle velocity decreases relatively.

From Fig. 11, we can know that the cutting force of drum increases with the number of picks involved in the cutting process from 0 to 1.5 s. The dynamic force of drum presents a significant nonlinear fluctuation. The maximum cutting force is 351.5301 kN, the average value is 207.4116 kN.

In order to determine the coal loading rate of the drum, based on the actual cutting and loading of coal and rock by the underground coal mining machine, the coal falling area was divided into loading area and goaf area, that is, statistical area I and II, and the number of particles in each area was counted. Therefore, according to the definition of coal loading rate: the percentage of the particle mass in the the coal loading area (Area I) to the total mass of all broken particles, the variation curve of coal loading rate was obtained, as shown in Fig. 12.

Fig. 12
figure 12

The variation curve of particle number and coal loading rate: (a) regional division; (b) number of particles in each statistical area; (c) coal loading rate.

Full size image

From Fig. 12, it can be seen that the total number of particles falling into statistical area I and II increases linearly during the cutting process, but the coal particles entering statistical area I are significantly more than that in statistical area II. During the initial cutting process, almost all of the broken particles enter the area I. Therefore, the coal loading rate is close to 100%. With the continuous cutting, the number of broken particles in area II increases gradually, and the coal loading rate of the drum decreases accordingly. When the helical drum is in a stable cutting state, the particles-drum system is approximate to a dynamic balance process, so the coal loading rate gradually tends to be stable and basically maintained at about 61%.

In order to verify the correctness of the numerical simulation results, with the help of the experimental conditions in the Liaoning Province Key Laboratory of Large-scale Industrial and Mining Equipment, cutting experiments under the same working conditions were carried out by manufacturing the physical models artificial coal wall and drum, and the drum force curve was obtained through noise reduction, as shown in Fig. 13.

Fig. 13
figure 13

Cutting experiment and experimental load: (a) experimental platform; (b) drum force.

Full size image

From Fig. 13, it can be known that maximum cutting force is 366.1334 kN, the average value is 205.5418 kN. The errors between the simulation results and the experimental results are 4.15% and 0.9%, respectively, which proves the accuracy of the simulation results and indicates that the numerical model used in this paper can be used to study the process of drum cutting coal-rock.

Performance analysis and structural optimization

The above analysis shows that during the process of cutting coal-rock materials, the drum is subjected to harsh loads, and the coal loading effect is not ideal. The overall performance of the drum needs to be improved. The structural parameters have a significant impact on the reliability and performance of the drum. However, blindly changing structural parameters cannot achieve the goal of optimizing the comprehensive performance of the drum. Therefore, the helix angle, pick installation angle, and cutting distance are selected as optimization parameters. Based on discrete element numerical simulation, the influence of each parameter on the load characteristics and coal loading performance of the drum is analyzed. A comprehensive performance evaluation model for the drum is established, and the NSGA-II algorithm was used for optimization and solution.

Various performances of drum under different helix angles

Based on the numerical simulation results, the performance of drum under different helix angles are obtained, as shown in Table 3. and the variation curves of the average cutting resistance, load fluctuation coefficient, cutting specific energy consumption and coal loading rate are obtained, as shown in Fig. 14.

Table 3 Various performances of drum under different helix angles.
Full size table
Fig. 14
figure 14

Variation performance curves of drum under different helix angles: (a) load fluctuation coefficient and average cutting resistance; (b) cutting specific energy consumption and coal loading rate.

Full size image

From Fig. 14, it can be known that when the helix angle increases from 9° to 21°, the average cutting resistance presents an irregular trend of decrease–increase–decrease; and the load fluctuation coefficient first increases and then decreases. While, the cutting specific energy consumption and coal loading rate increase gradually. Moreover, based on the data in Table 3, the fitted functions of the average cutting resistance, load fluctuation coefficient, cutting specific energy consumption and coal loading rate are obtained, as shown in Eq. (25)–(28).

$$f_{1} (\beta ) = - 0.003601\beta^{3} + 0.1578\beta^{2} - 2.169\beta + 112.3$$
(25)
$$f_{2} (\beta ) = - 2.354e^{ - 4} \beta^{3} + 8.9e^{ - 3} \beta^{2} - 0.1011\beta + 0.9727$$
(26)
$$f_{3} (\beta ) = 1.448e^{ - 4} \beta^{3} - 5.275e^{ - 3} \beta^{2} + 0.06996\beta + 0.6138$$
(27)
$$f_{4} (\beta ) = 5.035e^{ - 3} \beta^{3} - 0.2322\beta^{2} + 3.742\beta + 40.66$$
(28)

Various performance of drum under different installation angles

The performance of drum under different installation angles are shown in Table 4. Similarly, the variation curves of the average cutting resistance, load fluctuation coefficient, cutting specific energy consumption and coal loading rate are obtained, as shown in Fig. 15.

Table 4 Various performances of drum under different installation angles.
Full size table
Fig. 15
figure 15

Variation performance curves of drum under different installation angles: (a) load fluctuation coefficient and average cutting resistance; (b) cutting specific energy consumption and coal loading rate.

Full size image

From Fig. 15, it can be known that when the installation angle increases from 32° to 56°, the average cutting resistance, load fluctuation coefficient and cutting specific energy consumption increase first and then decrease, while the change of coal loading rate is just the opposite. Moreover, the fitted functions of the average cutting resistance, load fluctuation coefficient, cutting specific energy consumption and coal loading rate are obtained, as shown in Eqs. (29)–(32).

$$f_{1} (\alpha ) = 7.747e^{ - 4} \alpha^{3} - 0.07785\alpha^{2} + 2.214\alpha + 90.01$$
(29)
$$f_{2} (\alpha ) = 1.102e^{ - 5} \alpha^{3} - 1.173e^{ - 3} \alpha^{2} + 0.03651\alpha + 0.3652$$
(30)
$$f_{3} (\alpha ) = 1.02e^{ - 5} \alpha^{3} - 7.31e^{ - 4} \alpha^{2} + 2.484e^{ - 3} \alpha + 1.382$$
(31)
$$f_{4} (\alpha ) = - 1.044e^{ - 4} \alpha^{3} + 5.91e^{ - 3} \alpha^{2} + 0.1745\alpha + 50.68$$
(32)

Various performance of drum under different cutting distances

The performance of drum under different cutting distances are shown in Table 5. Similarly, in order to analyze the influence of cutting distance on the cutting and loading performance of the drum more visually, the variation curves of the average cutting resistance, load fluctuation coefficient, cutting specific energy consumption and coal loading rate are obtained, as shown in Fig. 16.

Table 5 Various performances of drum under different cutting distances.
Full size table
Fig. 16
figure 16

Variation performance curves of drum under different cutting distances: (a) load fluctuation coefficient and average cutting resistance; (b) cutting specific energy consumption and coal loading rate.

Full size image

From Fig. 16, it can be known that when the cutting distance increases from 54 to 70 mm, the average cutting resistance and cutting specific energy consumption decrease gradually. While, the load fluctuation coefficient and coal loading rate increase gradually. However, when the cutting distance continues to increase, the cutting specific energy consumption increases, and the coal loading rate decreases. Moreover, the fitted functions of the average cutting resistance, load fluctuation coefficient, cutting specific energy consumption and coal loading rate are obtained, as shown in Eqs. (33)–(36).

$$f_{1} (t) = - 6.235e^{ - 4} t^{3} + 0.1334t^{2} - 9.503t + 328.5$$
(33)
$$f_{2} (t) = 1.431e^{ - 4} t^{3} - 0.02935t^{2} + 2.001t - 44.71$$
(34)
$$f_{3} (t) = 8.488e^{ - 5} t^{3} - 0.0151t^{2} + 0.8656t - 14.79$$
(35)
$$f_{4} (t) = - 1.286e^{ - 3} t^{3} + 0.2367t^{2} - 14.18t + 334.5$$
(36)

Multi-objective optimization model

On the basis of multi-objective optimization theory, the evaluation functions of the average cutting resistance, load fluctuation coefficient, cutting specific energy consumption and coal loading rate are obtained according to Eqs. (33)–(36), which are described as Fi(X), where i = 1,2,3,4, X = (\(\beta\), \(\alpha\), t).

$$\begin{aligned} F_{1} (\beta ,\alpha ,t) & = - 0.0012\beta ^{3} + 0.0526\beta ^{2} - 0.7228\beta \\ & \quad + 2.5794e^{{ - 4}} \alpha ^{3} - 0.0259\alpha ^{2} + 0.738\alpha \\ & \quad - 2.078e^{{ - 4}} t^{3} + 0.0445t^{2} - 3.1677t + 176.9367 \\ \end{aligned}$$
(37)
$$\begin{aligned} F_{2} (\beta ,\alpha ,t) & = - 9.8083e^{{ - 5}} \beta ^{3} + 3.708e^{{ - 3}} \beta ^{2} - 0.04213\beta \\ & \quad + 5.51e^{{ - 6}} \alpha ^{3} - 5.865e^{{ - 4}} \alpha ^{2} + 0.01826\alpha \\ & \quad + 1.1925e^{{ - 5}} t^{3} - 2.446e^{{ - 3}} t^{2} + 0.1668t - 3.1379 \\ \end{aligned}$$
(38)
$$\begin{aligned} F_{3} (\beta ,\alpha ,t) & = 4.8267e^{{ - 5}} \beta ^{3} - 1.758e^{{ - 3}} \beta ^{2} + 0.02332\beta \\ & \quad + 3.4e^{{ - 6}} \alpha ^{3} - 2.437e^{{ - 4}} \alpha ^{2} + 8.28e^{{ - 4}} \alpha \\ & \quad + 2.8293e^{{ - 5}} t^{3} - 5.033e^{{ - 3}} t^{2} + 0.2885t - 3.7258 \\ \end{aligned}$$
(39)
$$\begin{aligned} F_{4} (\beta ,\alpha ,t) & = 1.741e^{{ - 3}} \beta ^{3} - 0.0803\beta ^{2} + 1.2938\beta \\ & \quad - 3.443e^{{ - 5}} \alpha ^{3} + 1.949e^{{ - 3}} \alpha ^{2} + 0.05755\alpha \\ & \quad - 4.173e^{{ - 4}} t^{3} + 0.0768t^{2} - 4.6009t + 139.3062 \\ \end{aligned}$$
(40)

In the optimization process, minimizing the average cutting resistance, load fluctuation coefficient and cutting ratio energy consumption and maximizing the coal loading rate are the optimization objectives, and helix angle, installation angle and cutting distance are the optimization variables. It is assumed that all the performance indicators are of equal importance. That is, the weight coefficient of each optimization index is 0.25. Therefore, the multi-objective optimization model can be described as Eq. (41).

$$\left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {{\text{min}}} & {F{(}X{)} = \left[ {\begin{array}{*{20}c} {F_{1} (X)} & {F_{2} (X)} & {F_{3} (X)} & {F_{4} (X)} \\ \end{array} } \right]} \\ \end{array} } \\ {\begin{array}{*{20}l} {{\text{s}}{\text{.t}}.} & {F_{1} (X) \ge 0,F_{2} (X) \ge 0,F_{3} (X) \ge 0,F_{4} (X) \ge 0} \\ \end{array} } \\ {8 \le X_{1} \le 22} \\ {30 \le X_{2} \le 60} \\ {20 \le X_{31} \le 80} \\ \end{array} } \right.$$
(41)

In this study, the NSGA-II algorithm is used to solve the multi-objective optimisation problem. Table 6 gives the detailed setting information of NSGA-II algorithm required in the modefront (esteco, Inc, Trieste, Italy) software, and the computational model is shown in Fig. 17.

Table 6 Calculation settings of the NSGA-II algorithm.
Full size table
Fig. 17
figure 17

The computational model.

Full size image

Optimization results

Figure 18a shows the optimization results for the average cutting resistance, load fluctuation coefficient and cutting specific energy consumption, and Fig. 18b shows the optimization results for the load fluctuation coefficient, cutting specific energy consumption and coal loading rate. The available solutions are marked with a solid green circle, the unavailable solutions with a solid yellow circle, and the Pareto Frontier with red circle. We can know that most of the solutions are available, and the Pareto Frontier is at the top of the solution space, which indicates that the NSGA-II algorithm worked as expected and made a clear trade-off between the average cutting resistance, load fluctuation coefficient, cutting specific energy consumption and coal loading rate.

Fig. 18
figure 18

Optimization Results: (a) Pareto citizens; (b) the selected designs of the optimization.

Full size image

Figure 19 shows the parallel coordinates chart. We can know that among the best designs of Pareto Frontier, X1 is basically between 16.5° and 20°, most of X2 is between 42° and 48°, X3 is between 69.5 mm and 74 mm. In addition, there are a small number of optimal designs with X2 between 35° and 40°, X3 between 63.5 mm and 66 mm. Theoretically, as the number of iterations increases, the results obtained become more and more accurate. Thus, the design with the highest number of iterations in the Pareto Frontier is chosen as the optimal solution for this optimization. Eventually, Table 7 presents the selected optimal design. And according to the technical and economic aspects of the processing, the parameters were rounded off. Through simulation analysis and theoretical calculation of the optimized drum performance, we compared the performance parameters of the drum before and after optimization (Table 7), and found that the average cutting resistance of the drum after optimization decreased by 12.75%, the load fluctuation coefficient decreased by 10.13%, the cutting specific energy consumption decreased by 2.34%, and the coal loading rate increased by 10.57%. By monitoring the performance of the optimized drum after being put into operation (Fig. 20), we found that the drum had good performance, reliable operation, and ideal coal loading effect during service, indicating a significant improvement in drum performance after optimization.

Fig. 19
figure 19

The parallel coordinates chart of the optimization.

Full size image
Table 7 Comparison of drum performance before and after optimization.
Full size table
Fig. 20
figure 20

Industrial test.

Full size image

Conclusions

A numerical model of drum cutting coal and rock was established using discrete element theory. The influence of drum structural parameters on its working performance was studied through numerical simulation, and the fitting function between cutting characteristics and coal loading rate was reconstructed. Based on the fitting function and NSGA-II algorithm, the optimization design of drum structural parameters was determined. The main contributions are as follows:

  1. 1.

    The influence of structural parameters on the cutting characteristics and coal loading performance is obtained: the cutting specific energy consumption and coal loading rate increase with the helix angle; the average cutting resistance, load fluctuation coefficient and cutting specific energy consumption increase first and then decrease with the installation angle, while the change of coal loading rate is just the opposite.

  2. 2.

    A successful optimization model is implemented to seek for optimum drum structural parameters by minimizing the average cutting resistance, load fluctuation coefficient and cutting ratio energy consumption and maximizing the coal loading rate. Taking into account both technical and economic factors, the optimal helix angle is determined to be 18°, the optimal installation angle is 45°, and the optimal cutting distance is 71 mm.

  3. 3.

    The average cutting resistance, load fluctuation coefficient, and cutting specific energy consumption of the optimized drum are reduced by 12.72%, 9.81%, and 2.85%, respectively, and the coal loading rate is increased by 9.59%. The underground test shows that the performance of the drum has been significantly improved.