Introduction

The impact of laser radiation on metallic materials is used in a wide range of technological applications. The technologies that involve laser heating to generate a local molten zone (MZ), that then undergoes rapid solidification, deserve of particular attention. This principle underlies in additive manufacturing of parts by selective laser melting (SLM)1,2,3, directed energy deposition (DED)4,5,6, as well as laser beam welding (LBW)7,8. In these methods, a small dimension of the molten zone and large temperature gradients are typical. As a result, the primary microstructure with long columnar grains is frequently formed. This feature can induce anisotropy in structural characteristics within local domains inside the finished product or weld1,4,7,8,9. In that context, one of the most significant research problems is an analysis of mechanisms that affect the solidification path. The practical goal is elaborating on the required microstructure characteristics, such as the shape and size of grains and sub-grains.

The solidification process can be altered by employing different physical mechanisms. In earlier studies10,11,12,13,14,15,16,17, the analysis of variable electromagnetic fields and constant magnetic fields has been conducted. The influence of electromagnetic fields on crystallization under typical for SLM conditions has been studied in17. It was revealed that a significant impact can only be achieved under high magnetic field strength. Additionally, the MZ size should be larger than the typical for SLM and DED values of between 0.2 and 1 mm. It is desired that the MZ size is above 1 mm, as in LBW processing. Another method of influencing the crystallization process is the ultrasonic (US) treatment, which is widely used in casting18,19. The recent experiments20,21 have shown some promising results in LBW and prospects in DED22,23,24,25,26,27 and SLM28. The different materials such as Ti–6Al–4 V22, Inconel 62522, stainless steel 316 L23, Al–12Si24, and Ti–TiB composites25 were tested to investigate the effect of US. As reported in25,26,27,29, the ultrasound treatment results in reduced porosity, improves reinforcement, and leads to a refined grain structure.

There is no comprehensive description in literature regarding the exact influence of US on the primary crystal structure. However, most researchers associate this phenomenon with the effect of acoustic cavitation of vapor-gas bubbles20,21,22,23,24,25,26,27. The bubble growth and collapse in molten metal alloys can occur rapidly in \(\sim 30~{\text{\varvec{\upmu}s}}\)30, as revealed by in situ synchrotron X-ray visualization31. The acoustically induced cavitation creates intense energy-material interactions inside the bubbles with hotspots up to \(\sim 5000\)  °C and pressure up to \(\sim {10^3}{\text{~~bar}}\). The heating and cooling rates are as high as \(\sim {10^{10}}~{\text{K}}/{\text{s}}\). These physical effects result in grain refinement18,32,33,34 through fragmentation35 of dendrites and additional nucleation36,37.

The LBW process, as well as DED and SLM, consistently shows the existence of a noteworthy quantity of vapor-gas bubbles, which can be observed through the formation of pores in the solidified material38,39,40,41,42,43,44,45,46,47,48. The pores can be classified into three distinct types38,39,40,41. Type 1 pores are characterized by their substantial size (over 100 microns) and irregular shape (sphericity is less than 0.6)39. These defects occur due to an incomplete material fusion, which leads to empty spaces between the powder particles that were not melted. The presence of these defects is also connected to a phenomenon known as the balling effect, wherein the powder particles coalesce into globular spherical particles, hindering the deposition of a metal onto the substrate. Alternatively, the excessive laser energy density can cause formation of deep, narrow melting channels, known as keyholes. The gas or vapor inside the keyhole could be trapped by the liquid phase and kept inside until crystallization. It results in the second type of pores. The size of these pores is relatively large, up to 100 microns41, and their shape is roundish with a sphericity of above 0.742.

The third type of pores has nearly a perfect spherical shape and a small size43. These pores are typically referred to as the gas pores, and they are attributed to inert gases (argon, helium) trapped within the powder during the atomization process39,42. Gas atomization leads to the higher porosity comparing to that got by other methods, such as rotating electrode plasma spheroidization44. Other mechanisms of gas pore formation include: (1) bubbles formed by metals with low boiling points, like in Al and Mg alloys45, and (2) gas dissolved between powder particles that does not escape from the melt pool during rapid cooling46. Some of these defects can be mitigated through post-processing techniques, such as hot isostatic pressing, which can remove nearly all pores and reduce the porosity from 0.35 to 0.01%48. However, this method does not eliminate gas pores completely, despite their relatively small size, which is significant in some application.

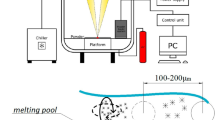
This article calculates the ultrasonic threshold characteristics required to activate the cavitation collapse process of vapor-gas bubbles within the radius range \({R_0} \in \left[ {1;100} \right]~\;{\text{\varvec{\upmu}m}}\) under processing conditions typical for DED, SLM, and LBW. The generation of US during laser processing requires special attention. Two approaches21,22,23,24 exist to generate US inside MZ. In US welding, a piezoelectric transducer should be placed in MZ, as described in21. However, this method is only suitable for MZ of large sizes. In DED, additive processing occurs directly on the surface of the sonotrode, similar to the studies22,23,24. However, there are limitations to this technique because of the sound attenuation as the component increases in size and the reflections of waves with interference patterns near the surface occur. The sonotrode method is not technologically suitable for the SLM process because the high intensity of ultrasonic waves may cause damage to the deposited powder layer.

Let us further consider the technology of US generation based on the optoacoustic effect using laser radiation in a highly absorbing medium26,27,28,49,50,51. This method offers a benefit of producing localized US vibrations while circumventing the constraints related to a sonotrode scheme. There are two primary mechanisms for optoacoustic sound generation. (1) Thermoelastic mechanism. In order for this mechanism to function, it is required for the rate of thermal expansion to surpass the speed of sound in the medium, which is usually between 4 and 5 km/s in metals. (2) Mechanism of ablation and intensive evaporation. It is governed by the reactive pressure exerted by the material escaping from the surface, leading to the generation of an elastic wave50,51.

Ultrashort laser pulses with a high power density can cause significant values of the acoustic pressure amplitude51. Within this mode, it is possible to implement heating comprised two distinct temperatures. Within this process, the temperature of the electrons exceeds that of the ionic subsystem, causing the supersonic expansion within the system and the subsequent separation of a surface layer of material (known as ablation)52,53. The threshold pulse duration is determined by the strength of the solid phase. In54,55,56,57, the ablation of gold, tin, iron, tantalum, and molybdenum using ultrashort laser pulses was studied. Based on these studies, it can be concluded that the pulse duration should not exceed \({10^{ - 12}}\)s. The duration of exposure is not sufficient for the cavitation collapse of vapor-gas bubbles within the melt. This paper is focused on pulses with the duration of \({\text{\varvec{\Delta}}}\tau ~\sim ~[{10^{ - 7}};{10^{ - 4}}]s\) which coincides with the characteristic time of subsonic heat expansion and intense surface evaporation51. Hence, the objective of this study is the examination of physical parameters and the assessment of technical viability in utilization of the optoacoustic method in SLM, DED, and LBW processing for inducing the cavitation collapse of dissolved bubbles.

Model of the bubble collapse by cavitation

A gas bubble may change its size under ultrasonic (US) exposure. Upon reaching a US threshold, two scenarios are possible where the bubble either deflates or inflates58. The latter case is possible if a reduced pressure front exists in the acoustic wave. Such conditions are generated, for example, by a piezoelectric transducer or under laser ablation with ultrashort (\({\text{\varvec{\Delta}}}\tau <{10^{ - 12}}\) s) pulses. In the present study, US is caused by intensive evaporation of the material, hence only a compression phase is conceivable which always leads to the bubble’s deflation.

At the initial phase of cavitation, the peer interaction of bubbles is negligible. Thus, the question about the threshold US intensity required for the cavitation initiation is reduced to a problem for a single bubble. A classic approach is the Neppiras-Noltingk model59, which shows fair accuracy in the description of vapor bubbles under the US action. The governing equation is

$$R\ddot{R} + \frac{3}{2}\dot{R}^{2} = \frac{1}{\rho }\left( {\left( {P_{h} + \frac{{2\sigma }}{{R_{0} }} - P_{v} } \right)\left( {\frac{{R_{0} }}{R}} \right)^{{3K}} - \frac{{2\sigma }}{R} - 4\eta \frac{{\dot{R}}}{R} - (P_{h} + P)} \right)$$
(1)

where \(R=R\left( t \right)\) is the time-dependent bubble radius, the dots above \(R\left( t \right)\) correspond to its time derivatives as \(\dot {R}=\frac{{dR\left( t \right)}}{{dt}}\), \(\:\ddot{R}=\frac{{d}^{2}R\left(t\right)}{d{t}^{2}}\), \({P_v}\) is the vapor pressure of the liquid,\({\text{~}}{P_h}\) is the hydrostatic pressure. Here \(P=P\left( t \right)\) is the imposed acoustic pressure induced by the US wave with \(P>0\) under compression by the external medium, \(\sigma\) is the surface tension at the liquid /gas interface,\(~\eta\) is the viscosity of the liquid, \(\:K\) is the polytropic coefficient of gas.

Equation (1) is the confluent equation derived from the Navier-Stokes equations in spherical coordinates, with the origin at the center of a spherical bubble. The chosen approximation reduces the equation of state to a 1D problem, where the bubble size is determined only by the function \(R\left( t \right)\). On one hand, Eq. (1) is suitable for both numerical solution and its analytic evaluation. On the other hand, the obtained solution does not give an exact information on the immediate moment of the cavitation process because of the used approximations.

The moment of collapse can be determined from Eq. (1) using an indirect criterion. In synchrotron radiation experiments, the cavitation collapse of a gas-vapor bubble is phenomenologically connected with its maximal size during the expansion phase. In31, the authors studied cavitation phenomena in the Bi-8 wt.%Zn melt at 427°С. During the inflation of bubbles, their linear size increased by a factor of 2.8. Then, the bubbles collapsed in the compression phase of the acoustic cycle. Simultaneously, tiny bubbles are generated and they act as the new centers of cavitation. The similar estimates of the size increase were reported in60 and for the Al–10 wt% Cu melt in61. Alternatively, in studies62,63, a collapse event in the melt was registered once the radius increased by the factors of \(1.6\) in Bi-8 wt.%Zn and by \(1.4\) in Al–10 wt% Cu, respectively. This variance reported in the literature may be caused by the absence of an accurate analysis of the threshold size, which was considered as an auxiliary parameter. It is possible that the factor of about \(\:3\) corresponds to intensive cavitation, whereas the threshold value is close to the factor in the range \(1.4 \div 1.6\) reported in62,63.

In the model, a vapor-gas bubble can be considered as an oscillatory system that moves under the influence of an external force, such as US vibrations. If the US frequency coincides with the natural frequency, then the bubble oscillates in a resonant mode. This can be easily shown by using Eq. (1) after certain reductions. Let us assume that the hydrostatic pressure \({P_h}\) remains constant while the acoustic pressure \(P=P\left( t \right)\) represents the pressure of a plane harmonic wave affecting the bubble as:

$$P\left( t \right)=\frac{{{P_A}}}{2}\left( {1 - \cos wt} \right)=\frac{{{P_A}}}{2}\left( {1 - \cos 2\pi \nu t} \right),$$
(2)

where \({P_A}\) is the amplitude of the acoustic wave generated in MZ by an external US source with the cyclic and linear frequencies \(\:w\) and \(\nu\), respectively. Equation (2) describes a wave with only a compression phase, corresponding to the mechanism of US generation through intense evaporation. Since the wavelength is significantly larger than a characteristic size of bubbles, \(P\left( t \right)\) can be assumed equal over the entire bubble surface. To simplify the calculations, we define the function \(r\left( t \right)\) that represents the deviation of the radius from its initial value \({R_0}\) as

$$r\left( t \right)=R\left( t \right) - {R_0}.$$
(3)

Assuming that \({R_0} \gg \left| r \right|\), the following expression is received from Eq. (2)

$$\frac{{{d^2}r}}{{d{t^2}}}+w_{r}^{2}r=\frac{{{P_A}}}{{2\rho {R_0}}}\left( {1 - \cos wt} \right),$$
(4)

Equation (4) describes the forced oscillations of a system, whose natural frequency \({w_r}\) is given by

$$w_{r} = \frac{1}{{R_{0} }}\sqrt {\frac{1}{\rho }\left( {3K\left( {P_{h} + \frac{{2\sigma }}{{R_{0} }} - P_{v} } \right) - \frac{{2\sigma }}{{R_{0} }}} \right)} .$$
(5)

For bubbles with a radius \({R_0}={10^{ - 6}}\)m immersed in metallic melts, the natural frequency is \({\nu _r}=\frac{{{w_r}}}{{2\pi }} \approx {10^6}~{\text{Hz}}\). The viscous effects have been neglected during deriving Eqs. (5) and (6). This approximation is valid according to the analysis of the Reynolds number. For our case, \({\text{Re}} \approx \frac{{2\rho ~}}{{\pi \eta }}\nu {r_{max}}{~^2}\), where \({r_{max}}\) is the oscillation amplitude of \(r\left( t \right)\), \(\frac{2}{\pi }\nu {r_{max}}\) is the characteristic velocity of the liquid near the bubble surface. Here the velocity is expressed via the displacement and frequency. The coefficient \(2/\pi\) follows from time averaging of the harmonic function \(r\left( t \right)\). By substituting the values of viscosity and density in Table 1, we can derive an estimate of \({\text{Re}} \leqslant 6 \times {10^5}\nu {r_{max}}{~^2}\). Thus, in the ranges of \(\nu\) and \({R_0}\) that were examined, the condition \({R_0} \gg \left| r \right|\) ensures that \({\text{Re}} \ll 1\), thereby the viscous effects can be neglected.

Next, the US acoustic pressure can be seen as an external force. Equation (4) shows that two types of cavitation collapse are possible. The resonant mode occurs if \(\:w\) is approximately equal to \({w_r}\), while the non-resonant mode occurs if \(\:w\) is significantly less than \({w_r}\). Let us first consider the non-resonant collapse model. It is possible to receive from Eq. (4) a simplified expression to estimate the threshold value of the acoustic pressure amplitude \(P_{A}^{{th}}\)

$$P_{A}^{{th}} ~ = \rho R_{0}^{2} w_{r}^{2} = 3KP_{h} + \left( {3K - 1} \right)\frac{{2\sigma }}{{R_{0} }}.$$
(6)

In this approximation, the threshold amplitude \(P_{A}^{{th}}\) of the acoustic pressure does not depend on the frequency of acoustic oscillations. This mathematical finding has a physical meaning that the bubble collapses during the first period of exposure to the acoustic wave in the non-resonant mode. The only importance is the magnitude of the pressure. The non-resonant mode is achieved experimentally by utilization of a piezoelectric transducer with a sonotrode, which generates the high-intensity US (\(I \approx {10^8}{\text{W}}{{\text{m}}^{ - 2}}\)) typically within the frequency range of \(\nu \in \left[ {20;100} \right]\) kHz22,23,24. In the approximation of a plane acoustic wave, this corresponds to the amplitude of acoustic pressure \({P_A} \approx 4 \times {10^7}\) Pa. This pressure level suffices for the collapse of bubbles during the first exposure period to the US wave. Alternatively, the resonant US mode facilitates a notable decrease in the threshold intensity that is sufficient for triggering the cavitation collapse. In the next section, this resonant US threshold is evaluated and the laser power required for US cavitation is derived.

Calculation of the ultrasound cavitation threshold

The threshold US characteristics under the resonance conditions have been determined by solving Eq. (1) numerically using Wolfram Mathematica. The calculations were performed for two metallic alloys, including the stainless 316 L steel and titanium Ti-6Al-4 V alloy (Table 1). Some listed characteristics depend on temperature. However, accounting for these dependencies would significantly complicate Eq. (1) with no substantial gain in the accuracy of calculus. For this reason, most parameters in Table 1 are taken at the boiling temperature at standard atmospheric pressure.

Table 1 Thermophysical properties of the 316 L and Ti-6Al-4 V melts used in the calculations.
Full size table

Figure 1 shows the results of numerical calculations of the dimensionless bubble radius \(R\left( t \right)/{R_0}\) over time, denoted by the orange line. The bubble undergoes the influence of a planar acoustic wave with the dimensionless pressure \(~P\left( t \right)/{P_A}\) modulated along with the black dashed line. These data have been obtained by solving Eq. (1) for a bubble with the initial radius of \({R_0}={10^{ - 5}}~\)m inside the 316 L melt. The size oscillations depicted in Fig. 1 occur under resonance conditions at the acoustic wave frequency of \(\nu ={\nu _r}=220~\)kHz.

The plot \(R\left( t \right)/{R_0}\) in Fig. 1 is interrupted at the moment of time, which is defined by the following criteria of the bubble collapse under resonance conditions. (1) The linear size of the bubble doubles relatively to its initial state, i.e. \(R\left( t \right)/{R_0} \geqslant 2\) before the final stage of compression. (2) During the compression, the bubble size rapidly reduces in size by a factor of 3, i.e. \(R\left( t \right)/{R_0} \leqslant 1/3.\) These criteria are based on the analysis of previous studies31,60,61,62,63 and they naturally correspond to experimental and theoretical tests.

Figure 1 further illustrates how the bubble size increases under the diminishing pressure and it decreases under elevating the compressive pressure. Thus, the amplitude of the radius oscillations \({\text{max}}\left| {R\left( t \right) - {R_0}} \right|\) increases over time and the bubble collapses completely during the fifth oscillation of the ultrasonic wave. An expansion of the time range in the numerical solution of Eq. (1) leads to the evolution of a bubble size as follows. After an initial increase of the oscillation amplitude, there is a subsequent slight decrease. This is followed by another cycle of the amplitude increase, and so on. If the bubble does not collapse during the contraction phase, this behavior preserves in time and the bubble oscillated with periodic decays.

Equation (6) provides the expression for the threshold (minimum) value of the acoustic pressure amplitude \(P_{A}^{{th}}\) at which the bubble collapse should occur during the first period of the acoustic excitation. Now the concept of the resonant threshold amplitude \(P_{A}^{{rth}}\) of acoustic pressure has to be introduced at this point. This is the minimum pressure level at which the bubble collapse during several vibrations of the acoustic wave. At any values of the US frequency \(\nu\) in Eq. (2), the inequality \(P_{A}^{{rth}}<P_{A}^{{th}}\) holds true. However, if the bubble is in a state of resonant oscillations, \(P_{A}^{{rth}}\) can be significantly less than \(P_{A}^{{th}}\). Figure 2 presents the results of numerical calculations of \(P_{A}^{{rth}}\) for a bubble with a radius of \({R_0}={10^{ - 5}}\)m in the 316 L (orange) and titanium Ti-6Al-4 V (blue) melts at various ultrasound frequencies \(\nu\). The calculated values are marked by squares for 316 L and by circles for Ti-6Al-4 V that are then connected by the straight segments. The minimum frequencies in the graphs correspond to the resonance conditions of bubble collapse. In other words, they correspond to the frequency of acoustic oscillations equal the natural frequency of the bubble \(\nu ={\nu _r}\). The natural frequencies are\(~{\nu _r}=330~\) kHz and \(220~\)kHz for Ti-6Al-4 V and 316 L correspondingly. The black diamond in Fig. 2 corresponds to the resonant frequency of the acoustic wave \(\nu ={\nu _r}=220~\) kHz at the resonant threshold amplitude \(P_{A}^{{rth}}=2 \times {10^5}~{\text{Pa}}\) of acoustic pressure. Hence, the results calculated in Fig. 1 correspond to the diamond point in Fig. 2.

Fig. 1
figure 1

Results of numerical calculations of Eq. (1) illustrating the change of the dimensionless bubble radius \(R\left( t \right)/{R_0}\) over time (orange line) influenced by a planar acoustic wave with the instantaneous acoustic pressure \(P\left( t \right)/{P_A}\) (black dashed line). The plots are calculated for a bubble with \({R_0}={10^{ - 5}}\) m immersed into the 316 L melt. The oscillations occur in the resonant mode with the pressure amplitude \(P_{A}^{{rth}}=2 \times {10^5}\) Pa of the acoustic wave at the natural frequency \(\nu =220~{\text{kHz}}\) which correspond to the black diamond marker in Fig. 2.

Full size image
Fig. 2
figure 2

Summary plot of a series of numerical calculations for the threshold amplitude \(P_{A}^{{rth}}\) of acoustic pressure as a function of an ultrasound frequency \(\nu\). The initial bubble radius is \({R_0}={10^{ - 5}}\) m. The orange and blue curves correspond to the 316 L and Ti-6Al-4 V melts. The calculated values are connected by straight segments for ease of perception. The black diamond point marks the resonant conditions for 316 L.

Full size image

The data in Fig. 2 reveal how \(P_{A}^{{rth}}\) depends on a frequency\(~\nu\) of an external acoustic wave. If the wave frequency shifts to the left relatively to the resonant frequency \({\nu _r}\), it leads to an abrupt deviation of the bubble from its resonant oscillations. As a result, a sharp jump of \(P_{A}^{{rth}}\) by a factor between 4 and 5 occurs in Fig. 2. The shift of \(\nu\) to the right from \({\nu _r}\) yields a smooth increase in \(P_{A}^{{rth}}\) Here the dependence of \(P_{A}^{{rth}}\) on the frequency \(\nu\) is close to a linear function and it can be expressed by the following regression relationship:

$$\frac{{P_{A}^{{rth}}\left( \nu \right)}}{{P_{A}^{{rth}}\left( {{\nu _r}} \right)}} \approx \alpha \frac{\nu }{{{\nu _r}}}~{\text{if}}~\nu >~{\nu _r},$$
(7)

where α is a constant specific to a bubble size and melt properties. The general form of the graphs presented in Fig. 2 is typical for bubbles with radii in the range \({R_0} \in \left[ {{{10}^{ - 6}};{{10}^{ - 4}}} \right]~\)m, although the value of the coefficient α varies slightly. For bubble size \({R_0} \in \left[ {{{10}^{ - 5}};{{10}^{ - 4}}} \right]\)m it was found \(\alpha \in [0.4;0.5\)] while for smaller bubbles with \({R_0} \approx {10^{ - 6}}{\text{m}}\) the coefficient increases up to \(\alpha \approx 0.7\).

Few series of simulations similar to those presented in Fig. 2 have been conducted for bubbles with different initial radii \({R_0}\). Based on these calculations, the resonance frequencies \({\nu _r}\left( {{R_0}} \right)\) and the resonant threshold amplitudes \(P_{A}^{{rth}}\left( {{R_0}} \right)\) of acoustic pressure were determined for bubbles of various sizes. The results are presented in Table 2, as well as in Figs. 3 and 4 for Ti-6Al-4 V and 316 L. Using the data provided in Table 2 and the method of least squares, two phenomenological formulae were derived within the range \({R_0} \in \left[ {1,100} \right]~\)µm to calculate the resonance frequency as a function of the radius

$$\:{\nu\:}_{r}\left({R}_{0}\right)=\left\{\begin{array}{cc}27.89\times\:{10}^{3}+\frac{6.77\times\:{10}^{-3}}{{R}_{0}^{1.52275}}\:\text{H}\text{z}\:&\:\left(\text{f}\text{o}\text{r}\:\text{T}\text{i}-6\text{A}\text{l}-4\text{V}\right),\:\\\:16.64\times\:{10}^{3}\text{\hspace{0.05em}}+\frac{4.38\times\:{10}^{-3}}{{R}_{0}^{1.52729}}\:\text{H}\text{z}\:&\:\left(\text{f}\text{o}\text{r}\:316\text{L}\right),\:\end{array}\right.$$
(8)

and the resonant threshold amplitude of acoustic pressure

$$\:{P}_{A}^{rth}\left({R}_{0}\right)=\left\{\begin{array}{cc}66.30\times\:{10}^{3}+\frac{0.2581}{{R}_{0}^{1.1592}}\:\text{P}\text{a}&\:\left(\text{f}\text{o}\text{r}\:\text{T}\text{i}-6\text{A}\text{l}-4\text{V}\right),\\\:\:42.19\times\:{10}^{3}\text{\hspace{0.05em}}+\frac{0.2431}{{R}_{0}^{1.16774}}\:\text{P}\text{a}&\:\left(\text{f}\text{o}\text{r}\:316\text{L}\right),\end{array}\right.$$
(9)
Table 2 Resonant frequencies \({\nu _r}\left( {{R_0}} \right)\) and the resonant threshold amplitudes \(P_{A}^{{rth}}\left( {{R_0}} \right)~\)of acoustic pressure obtained from the series of numerical calculations based on Eq. (1).
Full size table

The interpolation functions (8) and (9) are depicted in Figs. 3 and 4 respectively by solid lines in the logarithmic scale. The Ti-6Al-4 V data are represented in blue, while the 316 L data are given in orange. Within the range \({R_0} \in \left[ {1;22} \right]{\text{~\varvec{\upmu}m}}\), the calculated points fit well the solid lines. However, a deviation between the interpolation functions (8) and (9) and the calculated points listed in Table 2 occurs at \({R_0} \geqslant 22~{\text{\varvec{\upmu}m}}\). It can be explained by two reasons. First, the terms in Eq. (1) associated with the surface energy become comparable to those describing the hydrostatic \({P_h}\) and vapor \({P_\nu }~\)pressures in the interval \({R_0} \geqslant 22~\)µm. As a result, the slightly different dependencies \({\nu _r}\left( {{R_0}} \right)\) and \(P_{A}^{{rth}}\left( {{R_0}} \right)\) are expected in the domain \({R_0} \geqslant 22~{\text{\varvec{\upmu}m}}\) compared to the range \({R_0} \in \left[ {1;22} \right]~{\text{\varvec{\upmu}m}}\). Second, any discrepancy in the logarithmic scale in the lower part of the plot appears visually more pronounced than in the upper part.

Fig. 3
figure 3

Numerically calculated natural frequency \({\nu _r}\left( {{R_0}} \right)\) as a function of a bubble radius. The Ti-6Al-4 V and 316 L melts are presented by the blue and orange graphs, respectively. The calculated points correspond to Table 2, while the solid lines represent the interpolation functions given by Eq. (8).

Full size image
Fig. 4
figure 4

Numerically calculated resonant threshold amplitude \(P_{A}^{{rth}}\left( {{R_0}} \right)~\)(solid lines, Eq. (9)) of acoustic pressure and threshold acoustic pressure \(P_{A}^{{th}}\left( {{R_0}} \right)\) (dashed lines, Eq. (6)) as a function of a bubble radius. The Ti-6Al-4 V and 316 L melts are presented by the blue and orange graphs, respectively, where the calculated points correspond to Table 2.

Full size image

For quantitative analysis, the dashed lines in Fig. 4 display the amplitude \(P_{A}^{{rth}}\) of the acoustic pressure obtained from Eq. (6). By comparing the dashed (\(P_{A}^{{th}}\)) and solid lines (\(P_{A}^{{rth}}\)), it becomes clear that adjusting the frequency of acoustic oscillations according to Eq. (8) significantly decreases the threshold acoustic amplitude sufficient to initiate the cavitation process of the vapor-gas bubbles with the initial radius \({R_0}\).

Estimation for the threshold laser power intensity

As shown in Fig. 3, the frequency range for achieving the resonant cavitation collapse of bubbles with radii \({R_0} \in \left[ {1,100} \right]{\text{~\varvec{\upmu}m}}\) lies within the interval \({\nu _A} \in \left[ {{{10}^4};{{10}^7}} \right]{\text{~Hz}}\). The lower frequencies \({\nu _r}\) and threshold amplitudes \(P_{A}^{{rth}}\) of acoustic pressure correspond to larger bubbles. The US vibrations in this frequency range can be generated by piezoelectric transducers. However, as mentioned earlier, this technology has significant limitations for practical implementation during SLM and DED. This section determines the laser power intensity needed to produce US of a specific amplitude.

As shown above, we are interested in elaborating on the optoacoustic method of US generation through the process of intense material evaporation. Heating of the sample surface to the temperature \({T_s}\) results in intense substance evaporation. Thus, the reactive pressure \({P_r}\) generated at the surface of MZ is

$$~{P_r}=\left( {1 - \frac{\phi }{2}} \right){P_{vap}}=\left( {1 - \frac{\phi }{2}} \right){P_0}{e^{{A_{Me}} - \frac{{{B_{Me}}}}{T}}}~,$$
(10)

where \({P_{vap}}\) is the equilibrium vapor pressure above MZ, \(\phi\) is a coefficient characterizing the material fraction that leaves MZ after evaporation. With laser processing of metallic materials, the coefficient \(\phi\) varies in the range \(\phi \in \left[ {0;0.82} \right]{\text{~}}\)and it increases if the vapor pressure of the material is high. The function of the saturated vapor pressure \({P_{vap}}\) on temperature is further considered within an exponent approximation. Hence, in Eq. (10) \({P_0}\) is the pressure of 1 Pa, \({A_{Me}},~{B_{Me}}\) are the phenomenological material-dependent constants.

Only a fraction of the laser power is absorbed by the surface and that results in heating of the material. Another fraction is employed for substance evaporation from the surface. For accurate estimations, the following physical approximation is used. It is assumed that the layer of MZ heated by a laser pulse of duration \({\text{\varvec{\Delta}}}t\) has a characteristic depth \({h_T} \approx \sqrt {{\alpha _T}{\text{\varvec{\Delta}}}t} ,~\)where \({\alpha _T}~\)is the thermal diffusivity of the material. Then the temperature in this layer varies with depth \(\:z\) in the following manner

$$T\left( {z,t} \right) \approx {T_s}\left( t \right){\left( {\frac{{{T_0}}}{{{T_s}\left( t \right)}}} \right)^{\frac{z}{{{h_T}}}}},$$
(11)

where \(\:z\) is the coordinate calibrated as \(z=0\) at the target surface, and the Oz axis is directed downwards, i.e. deep into the substrate. Here \({T_s}\left( t \right)\) is the surface temperature which increases over time and \({T_0}\) is the initial temperature of the layer close to the surface just before the laser pulse at \(t=0~\). The heat-propagation velocity can be estimated as \({v_T} \approx \sqrt {\frac{{{\alpha _T}}}{{{\text{\varvec{\Delta}}}t}}}\), while the velocity \({v_b}\) of the evaporation front is determined by the surface temperature \({T_s}\left( t \right)\) as follows

$${v_b}=\frac{\phi }{{\left( {2 - \phi } \right)\rho {v_{vap}}}}{P_r}.$$
(12)

By solving the inverse problem using these approximations, an expression for the laser power density I in a laser pulse of duration \({\text{\varvec{\Delta}}}t\) is derived. This pulse should be strong enough to produce a reactive pressure \({P_r}\) of a specific magnitude on the target surface:

$$I\left( {{P_r}} \right)=\frac{1}{{{\kappa _{abs}}}}\left( {\frac{{\phi {L_{vap}}}}{{\left( {2 - \phi } \right){v_{vap}}}}{P_r}+\frac{{{c_{Me}}\rho {v_T}\left( {2{T_s} - {T_0}} \right)\left( {{T_s} - {T_0}} \right)}}{{\left( {3{T_s} - {T_0}} \right){\xi ^{}}}}} \right),~$$
(13)

where \({c_{Me}}\) is the specific heat capacity, \(\rho\) is the density, \({L_{vap}}\) is the heat of vaporization, \({\kappa _{abs}}\). is the absorption coefficient, and \({v_{vap}}\) is the average velocity z-component of an arbitrary molecule evaporating the MZ surface determined as:

$${v_{vap}}=\sqrt {\frac{{{k_B}{T_s}}}{{{\mu _{Me}}}}} .$$
(14)

Here \({k_B}\) is the Boltzmann constant, and \({\mu _{Me}}\)is the molar mass. The reactive pressure \({P_r}\) is also linked to the surface temperature \({T_s}\) from Eq. (11) by

$${T_s}\left( {{P_r}} \right)=\frac{{{B_{Me}}}}{{{A_{Me}} - ln\left( {\frac{{2{P_r}}}{{\left( {2 - \phi } \right){P_0}}}} \right)}}.~~~$$
(15)

The coefficient ξ is determined by the relative movement of the heating and boiling fronts as

$$\xi =\frac{{{v_T}\left( {1 - \frac{{{T_0}}}{{{T_s}}}} \right)}}{{{v_T}\left( {1 - \frac{{{T_0}}}{{{T_s}}}} \right)+{v_b}\left( {\frac{{{T_0}~ - ~{T_s}}}{{{T_0}~ - ~3{T_s}}}} \right)}}~$$
(16)

with \(\xi \in \left[ {0;1} \right]\). In case of laser pulses of about \({\text{\varvec{\Delta}}}t \approx {10^{ - 6}}\) s, the initial temperature \({T_0}<{T_{BOIL}}\), and pressure \({P_r}=1~\)bar, the asymptotics \(\xi \to 1\) is correct. The first term in brackets in Eq. (13) determines the fraction of absorbed laser energy got used on evaporation, while the second term determines the energy fraction spent on heating the MZ domain.

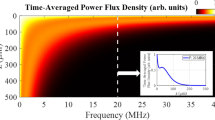
Figure 5 depicts the calculated results got via Eqs. (13)–(16) for Ti-6Al-4 V (blue) and steel 316 L (orange), according to the data provided in Table 1. The auxiliary parameters are selected with the absorption coefficient \({\kappa _{abs}}=0.3\) typical for smooth mirror surfaces of most metals and the evaporation parameter \(\phi =0.82\) adequate for substance evaporation in vacuum72. The temperature \({T_0}\) depends on MZ and laser processing regimes. In what follows, a typical for SLM and DED case is selected where the surface layer is overheated to \({T_0}={T_L}+1000\) K before the laser pulse, where \({T_L}\) is given in Table 1. These estimates are valid for laser 3D machines that combine processing using both the continuous and pulse lasers simultaneously. An example of such a machine is earlier presented in our works26,27. Then the laser radiation intensity needed to achieve the specified reactive pressure on the target surface within a characteristic time interval \({\text{\varvec{\Delta}}}t \approx {10^{ - 6}}\) s is presented in Fig. 5.

Based on the provided estimates under typical SLM and DED conditions, it is found that the surface temperature reverts to its initial value \({T_0}\) within a characteristic cooling time of approximately \({\text{\varvec{\Delta}}}t \approx {10^{ - 7}} \div {10^{ - 6}}\) s. It means that generation of US waves in the frequency range \({\nu _A} \in \left[ {{{10}^4};{{10}^7}} \right]~\)Hz is theoretically workable via intense evaporation from the annealed surface using a pulsed laser.

Next, the threshold value of laser radiation power \({P_r}\) required to activate the cavitation process was evaluated. Let us consider a case of pulsed laser annealing of the target surface, which generates the reactive vapor pressure described by a periodic law similar to Eq. (2). Then the maximum value of reactive pressure \({P_r}~\)determines the amplitude \({P_A}\) of acoustic vibrations in Eq. (2), and near the target surface \({P_r} \approx {P_A}\).

The power of the laser radiation is related to the radiation intensity as

$${p_l}=\pi r_{l}^{2}I,~$$
(17)

where \({r_l}\) is the radius of the laser spot. The analysis of the threshold power \({p_l}\) of pulsed laser radiation required to activate the cavitation process of a bubble with the initial radius \({R_0}\) is presented in Fig. 6; Table 2. The calculations were performed based on Eqs. (13)–(17) with the data from Table 1 and the laser spot radius \({r_l}=50{\text{\varvec{\upmu}m}}\) which is typical for SLM machines. The \({p_l}\) values in Table 2 are determined based on the calculated points \(P_{A}^{{rth}}\left( {{R_0}} \right)\) given in the same Table 2, whereas the solid lines in Fig. 6 are obtained from Eq. (9).

Fig. 5
figure 5

Calculated radiation intensity I within a laser pulse of duration \({\text{\varvec{\Delta}}}t \approx {10^{ - 6}}\) s required to generate the reactive vapor pressure \({P_r}\) sufficient for cavitation. The blue and orange lines correspond to the titanium Ti-6Al-4 V alloy and 316 L steel.

Full size image
Fig. 6
figure 6

Threshold power \({p_l}\) of pulsed laser radiation required to activate the cavitation process in a bubble with the initial radius \({R_0}\) calculated using Eqs. (8) and (9) for Ti-6Al-4 V (blue) and 316 L steel (orange). The calculated \({p_l}~\)values are provided in Table 2 and are denoted by circles for Ti-6Al-4 V and squares for 316 L.

Full size image

Discussion and summary

The data analysis of Table 2; Fig. 6 yields the expected laser power \({p_l}~\)required to achieve the ultrasonic (US) cavitation. For bubbles with the radius \({R_0} \in \left[ {1,100} \right]\) µm, the regime of cavitation collapse occurs if \({p_l} \in \left[ {117;1540} \right]~\)W w th the lower value of \({p_l}\) for larger bubbles. Such regimes of pulse laser processing are readily accessible at laboratory conditions and in production lines. The laser pulse frequency suitable for US cavitation is determined by Eq. (8). The pulse relative duration should be sufficiently large for the temperature-time profile closely resembling a sinusoid at the surface layer. It has been shown in73 that the desired conditions can be accomplished by modulating the power of a fiber laser. A practical example of implementation of a pulsed laser inside of the laser DED system has been suggested earlier in26,27. Thus, the practical way to activate the optoacoustic cavitation of vapor-gas bubbles is feasible based on the performed here analysis.

The present study has examined the range of processing regimes to employ the optoacoustic effects for US cavitation in selective laser melting, directed energy deposition, and laser welding processes. It is concluded that the pulsed laser radiation can generate US vibrations in the molten zone through the intense material evaporation from the surface.

  1. 1.

    As shown, it is possible to reduce significantly the threshold amplitude of acoustic vibrations required to activate the cavitation collapse by proper selection the US frequency near the natural frequency of dissolved bubbles. In this study, the phenomenological formulae Eqs. (8) and (9) are derived for selecting the optimal regime of US vibrations in laser processing of 316 L stainless steel and Ti-6Al-4 V melts. The analytical formulae Eqs. (13) and (17) are also derived for the laser pulse power required to generate a specified US wave caused by intensive material evaporation from the surface.

  2. 2.

    From technological prospectives, the vapor-gas bubbles can be formed as defects of consolidation and solidification in the SLM/DED/LBW processes. In this case, relatively large bubbles are observed and US processing helps demolish such defects. Alternatively, gas bubbles of small size, which are always present in the molten zone, may affect the solidification path and microstructure via cavitation. Hence, analysis of such bubbles is also required in practical applications.

  3. 3.

    For large vapor-gas bubbles with the radius \(10<{R_0}<100~\) µm, formed because of boiling or keyhole effects, the resonant frequencies belong to the range \(\nu \in \left[ {14;320} \right]~\)kHz. The resonant threshold amplitude of acoustic pressure ranges as \(P_{A}^{{rth}} \in \left[ {0.6;2.4} \right]~\)bar, corresponding to a threshold power of pulsed laser radiation in the range \({p_l} \in \left[ {117;331} \right]\) W.

  4. 4.

    For small bubbles with a radius \({R_0} \leqslant ~10~\;{\text{\varvec{\upmu}m}}\), which are always present in the molten zone during SLM, DED, and LBW processes, the resonant frequencies are in the range \({\nu _A} \geqslant 220\)\({\text{kHz}}\). The resonant threshold amplitude of acoustic pressure ranges as \(P_{A}^{{rth}} \geqslant 2\) bar, corresponding to the threshold laser power \({p_l} \geqslant 209\) W.