Introduction

The artificial ground freezing method is extensively recognized and utilized in geotechnical engineering domains such as subway construction, tunnel engineering, bridge construction, and shaft sinking in specialized strata1,2,3. This technique not only enhances the mechanical strength and water resistance of soil layers but also ensures safety and stability under complex geological conditions. However, in practical engineering applications, the method frequently encounters technical challenges, notably the misalignment of freezing holes and the fracturing of freezing pipes4,5. In the Quaternary loose strata of the Huainan-Huaibei mining area, an expansive calcareous clay layer is prevalent. Given its intricate mineral composition, pronounced stratification, variable thickness, and propensity to swell upon water exposure, this layer is prone to frequent freezing pipe fracture incidents during construction. Statistics indicate that most fractures occur at the interface between the calcareous clay and sand layers. This primarily results from the delayed freezing process of the calcareous clay, leading to a slower development and reduced strength of the frozen wall, which presents a distinct weakness compared to other strata. As excavation progresses into this area, radial force unloading generates dislocation forces at the interface, triggering the fractures in freezing pipes.

To optimize the performance of the artificial ground freezing method, it is crucial to ensure that the frozen soil curtain’s strength and water-sealing capabilities align with design specifications. The strength and water-sealing properties of frozen soil are affected by multiple factors6,7, including soil properties (such as soil types, dry density7, and water content8,9), freezing conditions (temperature10,11,12,13), overlying loads, and horizontal stresses14,15. Soil properties are considered internal factors, whereas freezing conditions, overlying loads, and horizontal stresses serve as external factors. These factors interact intricately rather than existing in isolation, collectively influencing the physical and mechanical response mechanisms of calcareous clay16,17,18. Consequently, profound research and understanding of the mechanical properties of calcareous clay under multifactorial interactions19,20,21 are vital for optimizing the artificial ground freezing method in shaft sinking, thereby improving construction quality and safety22,23. Such insights will not only address practical challenges in current projects but also furnish robust technical support for future underground space development and utilization24,25,26.

Furthermore, current research predominantly focuses on analyzing frozen soil’s mechanical characteristics and deformation behavior. According to thermodynamic theory, material failure mechanisms essentially represent system instability phenomena driven by energy shifts. This encompasses not only energy accumulation but also its subsequent dissipation and transformation—core dynamics underlying material deformation or failure under complex stress conditions27,28. Thus, deeply investigating the energy evolution laws of frozen soil under complex conditions and their intrinsic links to failure behavior from a thermodynamic perspective is imperative. Numerous studies affirm energy’s substantial role throughout the deformation, damage accumulation, and final failure stages in geotechnical materials29,30. Energy accumulation signifies continuous external impacts on specimens’ internal structures, while energy dissipation and transformation correlate directly with microstructural adjustments, damage accrual, and macroscopic material failures31. Therefore, mastering the intricate relationship between energy conversion mechanisms and structural failure is essential. Research on energy storage and dissipation capabilities offers valuable insights for practical engineering applications involving frozen soil.

In conclusion, previous studies have illuminated frozen soil’s mechanical characteristics under singular or limited independent variable changes. Yet, comprehensive research on energy evolution mechanisms during deformation processes—and especially on frozen calcareous clay under multifactorial interactions—is scarce. Given the intricate mechanical properties of frozen soil in dynamic natural environments, the prevalent practice of isolating each factor’s influence via the control variable method possesses inherent limitations32. Such approaches fall short of providing a holistic understanding of frozen soil’s mechanical properties and energy evolution laws under multifactorial interactions.

This study aims to elucidate the complex mechanical properties and energy evolution mechanisms of frozen calcareous clay through experimental analysis of multifactorial interactions, thereby laying a robust theoretical foundation and offering technical support for applying the artificial ground freezing method in calcareous clay contexts. To achieve this, an orthogonal experiment encompassing four factors and four levels—considering temperature, confining pressure, dry density, and water content—was conducted to systematically explore the mechanical property evolution laws of frozen calcareous clay across diverse interaction levels. By examining energy density dynamics, we analyze the conversion processes among input energy, elastic strain energy, and dissipated energy, further assessing how these transformations impact specimens’ microscopic crack structures. This affords novel insights into understanding frozen soil’s mechanical behavior under complex environmental conditions.

Materials and methods

Experimental materials

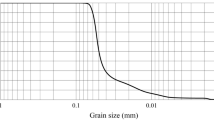
The calcareous clay (CC) employed in the test was retrieved from the deep layer of a coal mine situated in the Huainan-Huaibei mining area in the northern region of Anhui Province, China (with a burial depth ranging from 420 to 430 m), and was conveyed back to the test laboratory following sealed packaging. The fundamental physico-mechanical properties of the in-situ soil samples are presented in (Table 1). In accordance with the standard33, if the remolded soil test is to be conducted, the in-situ soil should initially be dried naturally. Upon completing the drying procedure, the in-situ soil should be placed in an oven at 105 °C for 12 h. After crushing, the lump of soil was crushed by a soil crusher for primary comminution. At this juncture, the particle size of the soil particles is difficult to fulfill the requirements necessary for the test, thus it is necessary to employ a mill for secondary comminution. After crushing, the soil particles were screened using a 0.5 mm sieve mesh, and soil samples with the requisite particle size for the experiment could be acquired. The process of crushing soil is shown in (Fig. 1). The sieved soil samples underwent particle size distribution testing using a laser particle size distribution meter (BT-2001)34, and the test results are presented in (Fig. 2). The test results reveal that the particle size of calcareous clay is predominantly distributed within the range of 0.5–450 μm, with the 25–180 μm particle size being dominant. From the cumulative content curve of the particle size distribution of calcareous clay, it can be noted that the slope of the curve is relatively stable, signifying that the texture of calcareous clay is homogeneous, and the fluctuation of the particle size range is relatively minor. This is conducive to ensuring that the fabricated specimens are homogeneous and isotropic.

Table 1 Properties of deeply buried calcareous clay.
Full size table
Fig. 1
figure 1

Broken soil flow chart.

Full size image
Fig. 2
figure 2

Particle size distribution of calcareous clay.

Full size image

Test scheme

Orthogonal design

Orthogonal experiment is a widely adopted methodology for investigating problems with multiple factors at various levels. It utilizes orthogonal arrays to organize and analyze multi-factor studies, aiming to identify representative combinations of experimental conditions from a vast array of possibilities. This approach provides a comprehensive understanding of the influence of each factor on the experimental outcomes. Compared to full factorial experiments, orthogonal experiments offer significant advantages; they substantially reduce the number of required experiments while maintaining comprehensive and reliable results, thereby enhancing research efficiency.

In this study, the orthogonal experimental design strictly adheres to established protocols. Four influencing factors—temperature, confining pressure, water content, and dry density—are selected, each examined at four levels, resulting in 16 distinct experimental schemes, as illustrated in (Table 2). The objective of these schemes is to thoroughly investigate the impact of each factor and their interactions on the mechanical properties and energy evolution mechanism of frozen calcareous clay.

During the soil sample preparation, the calculation method of dry density is as the following equation35:

$${\rho _d}=\frac{{{m_1}}}{v}$$
(1)
$$m={m_1}+{m_1} \times \omega$$
(2)

where, m1 is the mass of the dry soil of a single sample; \({\rho _d}\) is the dry density of soil; v is the sample volume; m is the sample mass; \(\omega\) is water content.

Table 2 Orthogonal experimental design table.
Full size table

Specimen preparation

The mass of dry soil and water required for each group of specimens was calculated based on Eqs. (1) and (2). The two were thoroughly mixed and placed in a sealed bag for 24 h, so that the water was completely blended with the soil to ensure that the water content of the soil samples was uniform. The prepared soil is sequentially filled into a mold with internal dimensions of 50 mm × 100 mm, in five installments. Compaction was performed at each stage. During the first to fourth compaction stages, a moderate compaction strategy was employed to prevent over-compaction, ensuring adequate space for subsequent soil layers. Additionally, the surface of each layer was intentionally scratched to improve adhesion between layers. This method is designed to physically encourage interlocking among soil particles, thereby enhancing the specimen’s overall stability36. After the specimens were compacted, the specimens, along with the molds, were sealed with cling film and placed in a -20 °C cryostat for 1 h before being demolded. After demolding, the specimens continued to be sealed with cling film and frozen in a cryostat at −20 °C for 24 h, and finally they were placed in a cryostat at the target temperature for an additional 24 h. Prior to preparing each specimen, it is essential to clean the mold thoroughly to eliminate any impurities that could compromise the specimen’s quality. Following this, an even coating of petrolatum should be applied to the mold’s inner surface. This coating helps establish a smooth and uniform contact interface between the specimen’s outer surface and the mold’s inner surface. According to tribological principles, petrolatum effectively reduces both static and dynamic friction coefficients during the demolding process. This reduction in friction facilitates the damage-free and smooth separation of the specimen from the mold. Furthermore, petrolatum exhibits excellent chemical stability, minimizing the risk of chemical reactions with the specimen during testing. This ensures the preservation of the specimen’s purity.

Test procedures

The test apparatus employs the low-temperature geotechnical triaxial test system (ZTCR-2000, Changchun Development Test Instrument Co., Ltd., China) shown in (Fig. 3a), which comprises five components: a computer processing system, a low-temperature geotechnical triaxial test control system, a low-temperature geotechnical triaxial testing machine, a hydraulic oil circulating pump, and an alcohol refrigerant circulating pump. The schematic diagram illustrating the principle of the triaxial test system is presented in (Fig. 3b). It reveals that the computer processing system controls the low-temperature geotechnical triaxial test system. This system can adjust the hydraulic oil circulating pump to deliver the necessary axial and confining pressures for the testing machine. An independent control switch allows users to operate the alcohol refrigerant circulating pump according to specific requirements. The test chamber is equipped with both axial and circumferential strain gauges, and a geotechnical sensor positioned above the chamber measures axial pressure. During testing, data on axial pressure and the resulting axial and circumferential strains are transmitted in real time to the computer system, which displays them as stress-strain curves. This feature significantly aids testers in monitoring and analyzing the specimen’s current condition.

Prior to initiating the test, it is essential to regulate the temperature within the test chamber to achieve the predetermined target temperature. This involves a pre-cooling treatment lasting 2 h. Upon completion of the pre-cooling phase, the specimen is loaded immediately. Following this, a prestress of 100 N is applied to secure the specimen firmly. Subsequently, the specimen must undergo an additional freezing period of 6 h to ensure it attains the target temperature state by the commencement of the test. The stress path of the specimen during the triaxial test is shown in Fig. 4, beginning at the pre-loading stage. Throughout this stage and the entirety of the freezing period, only the prestress of 100 N is maintained on the specimen. Upon conclusion of the freezing stage, hydrostatic pressure loading is applied according to the specified target confining pressure value. During this operation, both axial and confining pressures should be maintained at equilibrium to ensure the deviatoric stress remains at 0 MPa. After achieving the target confining pressure, a stabilization period of 30 min is required to permit complete consolidation of the specimen under these conditions. Finally, an axial load is applied at a constant rate of 0.3 mm/min until specimen failure occurs37. In Fig. 5, the comparison of the specimens before and after the test reveals significant axial compression, leading to an hourglass-shaped deformation characterized by larger ends and a narrower middle section. This morphological change is accompanied by the appearance of pronounced wrinkles.

Fig. 3
figure 3

Configuration of low temperature geotechnical triaxial test system. (a) Physical diagram of triaxial test system. (b) Principle diagram of triaxial test system.

Full size image
Fig. 4
figure 4

The stress path diagram of the specimen during the triaxial test.

Full size image
Fig. 5
figure 5

Comparing samples before and after test.

Full size image

Analysis of mechanical properties of frozen calcareous clay

The strength and deformation characteristics of frozen soil are key parameters for assessing the mechanical responses of soil masses and have long been central areas of investigation for numerous scholars38,39,40. Deviatoric stress provides an intuitive measure of the shear stress state in materials, making it crucial for predicting the failure trends and ultimate load-bearing capacity of frozen calcareous clay under complex stress conditions41,42. Conversely, volumetric strain indicates changes in the volume of frozen calcareous clay during stress application and serves as a critical metric for evaluating the overall stability of engineering structures. Therefore, using sensitivity analysis to prioritize the influence of various factors on the volumetric strain of frozen calcareous clay helps engineers strategically control these key factors in real-world engineering projects. This approach enables the flexible adjustment of construction plans, effective prediction and prevention of potential engineering problems, and ultimately ensures the safety and stability of the projects43,44.

Table 3 lists the failure stress information of specimens of frozen calcareous clay under 16 interaction levels. For each interaction level, three specimens were prefabricated to determine the discreteness of the experimental results. As shown in Table 3, there is minimal variation in the failure stress across the specimen groups under different interaction levels, indicating high stability and reliability of the experimental results. Notably, specimens with failure stresses closest to the average values are marked with an asterisk (*). These specimens have been selected for subsequent in-depth analysis to ensure representativeness and accuracy of the findings.

Table 3 The failure stress information of test specimens under different interaction levels.
Full size table

Relationship between deviatoric stress and axial strain

The deviatoric stress-axial strain curves of frozen calcareous clay at each temperature are presented in (Fig. 6). It can be observed from the figure that the deviatoric stress-axial strain curves at different interaction levels exhibit strain hardening characteristics. At −5 and −10 °C, the curves are of the weak hardening type45, and at −15 and −20 °C, the curves are of the general hardening type. As the temperature decreases, the hardening degree of the curve gradually increases. This was analyzed to be attributed to the following reasons: with the decrease in temperature, the liquid water in the soil was gradually transformed into solid ice crystal particles, and the cementing effect of the ice crystal particles enhanced both the strength and the strain-hardening characteristic of the soil body46.

The microstructure of frozen calcareous clay and its mechanical behavior are schematically presented in Fig. 7, whence it can be observed that the frozen calcareous clay generates extrusion and friction among the soil particles under axial and circumferential pressure. During the freezing process, liquid water is converted into ice, and its lubricating effect is attenuated or even vanishes. The formation of cementing ice firmly bonds the neighboring soil particles together and yields a fully constrained cementation on the cementation surface, thereby augmenting the cohesion of calcareous clay. The presence of pore ice is analogous to the addition of sand, gravel, and other aggregates to cement, which plays a sort of ‘replacement’ role and significantly enhances the strength of calcareous clay.

The deviatoric stress-axial strain curves of frozen calcareous clay can be categorized into elastic and elasto-plastic stages, and this phenomenon can be accounted for by the following analysis: Under the hydrostatic pressure for 30 min, the pore space of the specimen is compacted. Owing to the formation of cemented ice, the soil particles form a close cemented structure with one another. At this juncture, the deformation modulus of the specimen is considerable. The deviatoric stress increases rapidly with the axial strain in a linear manner. The cemented ice and pore ice have not yet been melted, which is elastic in nature. With the continuous increment of axial strain, the deviatoric stress and axial strain exhibit non-linear growth. The slope of the curve, that is, the deformation modulus, gradually reduces and tends to stabilize. There is no distinct peak point in the entire curve. At this stage, the internal cemented ice and pore ice of the specimen seemed to be melted or even crushed. The internal cracks gradually formed and expanded. The specimen was damaged. The deformation modulus gradually declined, and the resistance to deformation was weakened.

In conjunction with Fig. 6, it is discerned that in the elastic phase, the slope and the stress value at the inflection point exhibit an ascending trend as the temperature drops and the peripheral pressure rises. The cause of this phenomenon is as follows: Firstly, as the temperature declines, the content of unfrozen water reduces, giving rise to an increase in cemented ice and pore ice. At this juncture, the cementation and ‘replacement’ effects augment, which leads to an increase in the deformation modulus of the specimen. Secondly, the augmentation in confining pressure leads to an increase in the external load on the specimen. At the microscopic level, the pore space is further compacted by the high confining pressure, resulting in closer contact between soil particles and increased compression and friction. At the macroscopic level, the specimens were subjected to greater circumferential pressures, which resulted in increased confinement and thereby enhanced their ability to resist deformation.

Fig. 6
figure 6

Curve of relation between deviational stress and axial strain.

Full size image
Fig. 7
figure 7

Microstructure and mechanical behavior of frozen calcareous clay.

Full size image

Relationship between volume strain and axial strain

Volume strain, serving as a comprehensive index for gauging the deformation characteristics of the specimen, can furnish a comprehensive reflection of the deformation characteristics of the material in the process of force application. As illustrated in Fig. 8, the figure portrays the influence of multiple factor interactions on the volume strain of frozen calcareous clay. As evinced by the figure, the volume strain of frozen calcareous clay manifests a marked volume shrinkage deformation with the augmentation of axial strain at diverse interaction levels, and the deformation intensifies with the escalation of axial strain.

Further analysis disclosed a negative correlation between the dry density of the specimen and its peak shrinkage deformation under a constant negative temperature. This implies that as the dry density of the specimen diminishes, the peak shrinkage deformation escalates. This phenomenon can be ascribed to a direct association between the reduction in dry density and the decrease in the number of soil particles, accompanied by an increment in porosity. During the loading process, the gradual closure of pores under external force resulted in a reduction in the distance between particles, thereby augmenting the shrinkage deformation of the specimen.

It is also crucial to contemplate the influence of confining pressure on volume shrinkage deformation. In the context of a constant negative temperature, a positive correlation prevails between confining pressure and the peak of volume shrinkage deformation. This correlation is manifested as follows: an augmentation in confining pressure leads to an increase in the peak of volume shrinkage deformation. This is attributed to the fact that an increase in confining pressure boosts the compaction effect of the specimen during the loading process, which is directly manifested in the aggravation of volume shrinkage deformation. Secondly, an increase in circumferential pressure effectively constrained the circumferential deformation of the specimen and precluded the possibility of volume expansion. Ultimately, the increase in peripheral pressure also facilitates the disruption of the cementation between soil particles and ice crystal particles, intensifies particle fragmentation, and subsequently curtails the rolling behavior between particles, thereby attenuating or even eliminating the potential for shear uplift. The combined effect of these factors constitutes a stress-strain curve that displays strain hardening, whilst the volume strain exhibits shear contraction characteristics.

Fig. 8
figure 8

Curve of relation between volume strain and axial strain.

Full size image

Sensitivity analysis of the effect of factors on peak volume strain

The analysis of orthogonal test results47 primarily employs two methodologies: intuitive analysis and variance analysis. Intuitive analysis is renowned for its simplicity. By accurately calculating the mean values of test indices for each factor at various levels, it swiftly identifies the optimal combination of factor levels that maximize the indices. In contrast, variance analysis offers a more precise evaluation method. It quantifies the significance of each factor’s influence on the test indices, thereby revealing the interaction relationships among various factors in a more comprehensive manner. In this study, we utilized the variance analysis approach to perform sensitivity analysis. Specifically, we conducted an average range analysis on the target values—defined here as the peak volumetric strain values at each interaction level—under the influence of each factor. By calculating the difference between the maximum and minimum average test values48, we identified the main factors affecting the target values. Furthermore, in this investigation, peak volumetric strain values were selected from specimens closest to the mean value to mitigate the impact of random errors on the analysis outcomes. Consequently, we contend that our analysis results are both representative and accurate.

The sensitivity analysis derived from the test results is presented in (Table 4). The data indicate that dry density exerts the most significant influence on peak volumetric strain, with a range value of 5.03%, whereas water content has the least influence, with a range value of 1.05%. The ranking of factors influencing peak volumetric strain is as follows: dry density > confining pressure > temperature > water content. Notably, the effects of dry density and confining pressure on peak volumetric strain are substantially greater than those of temperature and water content, further corroborating the rationality of the observed phenomenon.

Table 4 Sensitivity analysis of peak volume strain.
Full size table

Analysis of energy evolution mechanisms in frozen calcareous clays

Theoretical analysis

The deformation of an object under the influence of an external force leads to the displacement of the deformation point in the direction of the force. This process is characterized by the transfer of work to the system from the external force. During the deformation process, the internal microstructure of frozen calcareous clay undergoes substantial evolution and transformation, accompanied by a coupling of energy dissipation and damage mechanisms. In a triaxial test, the specimen and the test system jointly constitute a closed system. It can be assumed that there is no energy exchange between the system and the external environment during the test. Therefore, the total energy input to the test loading system ought to be equal to the elastic strain energy plus the energy dissipated due to plastic deformation of frozen calcareous clay.

Specifically, the energy input from an external force to a frozen calcareous clay specimen can be divided into two distinct components. The first component is the work accomplished by the axial force during the axial deformation of the specimen. The second component is the work accomplished by the peripheral pressure during the circumferential deformation of the specimen. In contrast, the elastic strain energy can be defined as the energy that is accumulated and stored within the frozen calcareous clay specimen during the elastic deformation stage. The dissipated energy is a complex and diverse set of energy forms, primarily consisting of the plastic strain energy dissipated during the irreversible plastic deformation of the specimen, the thermal energy generated by frictional slip between soil and ice crystal particles, and other potential forms of radiant energy.

It is noteworthy that the process of energy dissipation is intimately associated with the occurrence of plastic deformation. As a direct consequence of energy dissipation, it is inclined to lead to the gradual deterioration of material strength49,50,51. On the other hand, when the elastic energy stored in frozen calcareous clay attains a certain level and is abruptly released, it may give rise to the destruction of the structure. Therefore, investigating the impacts of diverse interactions on the mechanical properties of frozen calcareous clay not only facilitates a profound understanding of its deformation and damage mechanisms but also offers an important theoretical foundation for relevant engineering practice. The above energy relationship can be expressed as:

$${U_F}={U_E}+{U_D}$$
(3)

where, UF, UE, UD are the input energy density, elastic strain energy density and dissipated energy density, respectively.

The input energy density and elastic strain energy density can be expressed as:

$$\left\{ \begin{gathered} {U_F}=\int_{0}^{{{\varepsilon _1}}} {{\sigma _1}{\text{d}}{\varepsilon _1}+\int_{0}^{{{\varepsilon _2}}} {{\sigma _2}{\text{d}}{\varepsilon _2}+\int_{0}^{{{\varepsilon _3}}} {{\sigma _3}{\text{d}}{\varepsilon _3}} } } \hfill \\ {U_E}=\frac{1}{2}{\sigma _1}{\varepsilon _1}^{{\text{e}}}+\frac{1}{2}{\sigma _2}{\varepsilon _2}^{{\text{e}}}+\frac{1}{2}{\sigma _3}{\varepsilon _3}^{{\text{e}}} \hfill \\ \varepsilon _{i}^{{\text{e}}}=\frac{1}{E}\left[ {{\sigma _i} - v({\sigma _j}+{\sigma _k})} \right] \hfill \\ \end{gathered} \right.$$
(4)

where, \({\sigma _1}\), \({\sigma _2}\), \({\sigma _3}\) are the first, second and third principal stresses, respectively; \({\varepsilon _i}\), \({\varepsilon _i}^{{\text{e}}}\) are the strain in the direction of the principal stress and the elastic strain, respectively; E is the modulus of elasticity; v is the Poisson’s ratio; i, j, k are the subscripts of the variables, i, j, k = 1,2,3.

In conventional triaxial compression experiments \({\sigma _2}={\sigma _3}\), Eq. (4) is brought into Eq. (3) to obtain the elastic strain energy density and dissipated strain energy density as:

$$\left\{ \begin{gathered} {U_E}=\frac{1}{{2E}}\left[ {{\sigma _1}^{2}+2(1 - v)} \right.{\sigma _3}^{2} - \left. {4v{\sigma _1}{\sigma _3}} \right] \hfill \\ {U_D}=\int_{0}^{{{\varepsilon _1}}} {{\sigma _1}{\text{d}}{\varepsilon _1}+2\int_{0}^{{{\varepsilon _3}}} {{\sigma _3}{\text{d}}{\varepsilon _3} - \frac{1}{{2E}}\left[ {{\sigma _1}^{2}+2(1 - v)} \right.{\sigma _3}^{2} - \left. {4v{\sigma _1}{\sigma _3}} \right]} } \hfill \\ \end{gathered} \right.$$
(5)

Analysis of energy evolution mechanisms

Relationship between energy density and axial strain

The mechanical parameters of frozen calcareous clay were derived based on the results of conventional triaxial compression tests, as shown in (Table 5). The variation curves of input energy density, elastic strain energy density, and dissipation energy density of frozen calcareous clay with axial strain under different interaction levels were obtained in accordance with Table 5 and Eqs. (4) and (5). The results are presented in (Fig. 9).

Table 5 Mechanical parameters of frozen calcareous clay.
Full size table
Fig. 9
figure 9

Curve of relation between energy density and axial strain.

Full size image

As shown in Fig. 9, the energy densities (including input energy density, elastic strain energy density, and dissipation energy density) of frozen calcareous clay increased with the increase in axial strain throughout the test at any interaction level. At the initial stage of the test, the elastic strain energy density increased rapidly with the increase in axial strain. Subsequently, when the specimen entered the elastic-plastic phase, its growth rate decelerated significantly. This implies that in the elastic phase, the storage of elastic strain energy is predominantly dominant. After entering the elastic-plastic stage, the elastic strain energy transformed by the work done by the external force gradually diminishes or even ceases to be transformed.

The trend of elastic strain energy density in relation to axial strain is akin to the evolution of the stress-strain curve. At the initial stage of loading, the micropores and micro-fissures within frozen calcareous clay were gradually compacted and closed under external load. The elastic strain energy density curve essentially coincided with the input energy density curve and exhibited a nearly linear growth tendency. Moreover, the dissipated energy at this stage was nearly negligible. As the test proceeds, the specimen enters the elastic-plastic stage. In this stage, the elastic strain energy density curve gradually tends to flatten and may even cease to increase, indicating that the elastic strain energy in the specimen at this moment has nearly reached the storage limit. Under external loading, new cracks form within the specimen, dissipating a portion of the surface energy. The stress concentration at the crack tip generates acoustic emission energy, along with irreversible plastic strain energy and various forms of radiation energy. Consequently, the energy dissipation density curve progressively increases with axial strain during this stage.

The electron microscope scanning image of the specimen obtained after the test is presented in (Fig. 10). From the figure, it can be observed that the specimen exhibits a reticulated crack structure. This indicates that during the test process, microcracks within the specimen germinated and then gradually expanded and extended, ultimately intersecting with one another52,53. Owing to the plastic nature of the soil, despite the specimen undergoing substantial compression deformation, no penetrating cracks were formed. This prevented the generation of fracture surfaces, which also explains why the elastic strain energy within the specimen has not been released.

Fig. 10
figure 10

Scanning electron microscope image of crack after specimen test.

Full size image

Peak energy density evolution law

The variation patterns of the peak input energy density (UFm) and peak dissipation energy density (UDm) under different interaction levels are shown in (Figs. 11 and 12). According to Figs. 11 and 12, it can be visualized that UFm and UDm of frozen calcareous clay generally increase with the augmentation of peripheral pressure under the condition of constant temperature. However, both UFm and UDm of sample C-3 are lower than those of C-2 at −15 ℃. This phenomenon might be attributed to the small volume shrinkage deformation of the specimen at this interaction level. The specific reasons are as follows: In conjunction with Fig. 8c, it can be observed that the volume shrinkage deformation of the specimen increases with the increase in axial strain during the test. In the middle and late stages of the test, dilation occurred, causing the confining pressure to perform negative work, which offset part of the positive work done by the axial stress. This resulted in a decrease in the growth rate of input energy for C-3 (as shown in Fig. 9c). At this point, the growth of elastic strain energy plateaued with no significant increase. Consequently, under the influence of input energy, the growth rate of dissipated energy also slowed, ultimately resulting in both UFm and UDm of the C-3 sample being slightly lower than those of C-2.

Additionally, it can be observed from the figure that under the same temperature condition, as the peripheral pressure increases from 0.5 MPa to 2 MPa, the UFm and UDm of frozen calcareous clay at different temperatures exhibit different increments with the increase in peripheral pressure. At −5 ℃, the increments of UFm and UDm were 173.84 and 164.29%, respectively. At −10 ℃, the increments of UFm and UDm were 95.12 and 86.01%, respectively. At −15 ℃, the increments of UFm and UDm were 30.07 and 23.60%, respectively. At −20 ℃, the increments of UFm and UDm were 72.54 and 67.58%, respectively. This is attributed to the fact that the higher the circumferential pressure, the higher the compressive strength of frozen calcareous clay, and the more energy is introduced into the test system during the test. At the same time, the greater the irrecoverable deformation of the specimen, and the dissipated energy also increases correspondingly.

Fig. 11
figure 11

The relationship between UFm and different interaction levels.

Full size image
Fig. 12
figure 12

The relationship between UDm and different interaction levels.

Full size image

The sensitivity analysis of the peak elastic strain energy density (UEm) was conducted, and the results are presented in (Table 6). From the analysis results, it can be distinctly observed that the effect of temperature on UEm is the most prominent, with an extreme difference value of 0.1315%. In contrast, the effect of water content on UEm is comparatively minor, with an extreme difference of merely 0.0113%. The sensitivity of each influencing factor on UEm was ranked as follows: temperature > pressure > dry density > water content. This ranking indicates that the influence of temperature and pressure on UEm is considerably higher than that of dry density and water content.

The influence of temperature as a crucial factor in the mechanical properties of materials has been demonstrated in numerous studies. For instance, Ouhadi54 discovered that temperature variations can significantly modify the microstructure of a material, thus affecting its mechanical properties. Additionally, confining pressure has also been recognized as an important factor influencing the mechanical behavior of materials. Huang55 in his study emphasized the effect of confining pressure on the mechanical properties of rock in compression shear fracture.

Although the impacts of dry density and water content on UEm are relatively minor, they may still play a non-negligible role under certain working circumstances. Chen56 demonstrated that the variation in dry density can affect the modulus of elasticity of the material to a certain extent, while the variation in water content influences the strength properties of the material. Therefore, although the sensitivity of these two factors is relatively low in this study, they still merit attention in further research.

Table 6 Sensitivity analysis of peak elastic strain energy density.
Full size table

Sensitivity analyses disclosed the significant impacts of temperature and confinement pressure on the UEm of frozen calcareous clay. The experimental results indicated that as the confining pressure increased and the temperature decreased, the UEm increased correspondingly. Under the same conditions of confining pressure or temperature, even though the dry density and water content of frozen calcareous clay were different, there still existed an obvious linear relationship between the UEm and the confining pressure and temperature. This was visually manifested by the plotted relationship curves, as shown in (Fig. 13). The data in the figure demonstrate that the relationship between the UEm of frozen calcareous clay and the ambient pressure and temperature is highly correlated. The correlation coefficients, R2, are all greater than 0.93, a result that strengthens the reliability of the linear relationship. The relationship satisfies the following equation:

$${U_{Em}}=a{\sigma _3}+b$$
(6)
$${U_{Em}}=cT+d$$
(7)

where, T is the temperature of frozen calcareous clay; a is the growth rate of elastic strain energy density with respect to peripheral pressure when frozen calcareous clay is destroyed at constant temperature; b is the elastic strain energy density when frozen calcareous clay is destroyed under uniaxial compression; c is the growth rate of elastic strain energy density with decreasing temperature when frozen calcareous clay is destroyed under constant peripheral pressure; d is the elastic strain energy density of calcareous clay at 0 °C when fractured at a given peripheral pressure.

From Fig. 13 and Eqs. (6) and (7), it can be observed that under the conditions of higher peripheral pressure and lower temperature, the deformation resistance of frozen calcareous clay is enhanced, its strength is increased, and the density of internal elastic strain energy increases markedly when the specimen is damaged. This implies that the effects of temperature and peripheral pressure should be given special attention in practical applications, especially at the design and material selection stages.

Fig. 13
figure 13

The relationship curve of UEm with confining pressure and temperature. (a) Fitted curve of frozen calcareous clay UEm versus confining pressure. (b) Fitted curve of frozen calcareous clay UEm versus confining pressure.

Full size image

Conclusion

In this paper, conventional triaxial tests on frozen calcareous clay were conducted by designing a four-factor, four-level orthogonal test incorporating temperature, confining pressure, water content, and dry density. The complex nonlinear relationship between deviatoric stress, volume strain, and axial strain of frozen calcareous clay under different interaction levels was systematically analyzed. The sensitivity ranking of each factor to the peak volume strain was investigated. Moreover, the energy evolution mechanism of frozen calcareous clay in triaxial compression was dissected. The main conclusions are as follows:

  1. (1)

    The deviatoric stress-axial strain curves consistently exhibit strain hardening characteristics in the frozen calcareous clay specimens. As the temperature decreases, the degree of hardening progressively increases.

  2. (2)

    All four factors—dry density, confining pressure, temperature, and water content—affect volumetric strain. Sensitivity analysis reveals that the influence of these factors on peak volumetric strain ranks as follows: dry density > confining pressure > temperature > water content. Under different combinations of the four factors, specimens exhibit significant volumetric shrinkage deformation. At a constant temperature, peak volumetric strain is negatively correlated with dry density and positively correlated with confining pressure.

  3. (3)

    The input energy density, elastic strain energy density, and dissipated energy density increase with rising axial strain. However, the growth rate of elastic strain energy density is relatively high at the initial loading stage but slows or halts once the specimens reach the elastoplastic stage.

  4. (4)

    At a constant temperature, the peak input energy density and peak dissipated energy density increase with higher confining pressure. Moreover, the peak elastic strain energy density shows a clear linear increase with rising confining pressure and decreasing temperature.