Energy feature extraction and visualization of voltage sags using wavelet packet analysis for enhanced power quality monitoring

Abstract

Power quality (PQ) disturbances, such as voltage sags, are significant issues that can lead to damage in electrical equipment and system downtime. Detecting and classifying these disturbances accurately is essential for maintaining reliable power systems. This paper introduces a novel approach to voltage sag analysis by employing wavelet packet analysis combined with energy-based feature extraction to enhance PQ monitoring. The study decomposes voltage sag signals into different frequency bands to extract key features for disturbance detection. We compare six commonly used mother wavelets (db1, db4, db10, dmey, sym5, and coif5) to identify the most suitable wavelet for voltage sag detection. The energy distribution curve analysis is used to evaluate the energy characteristics of each wavelet’s decomposition, with a focus on identifying the most effective signal features for PQ monitoring. The paper presents a thorough error analysis and compares the energy values extracted by different wavelet functions to demonstrate the reliability and accuracy of the proposed method. The results show that wavelet packet analysis significantly improves the detection and classification of voltage sag disturbances, providing a robust and efficient tool for real-time PQ monitoring. This study contributes to the development of advanced PQ monitoring systems by offering a more precise and computationally efficient method for voltage sag analysis, ultimately helping to protect electrical systems from potential damage and reducing operational costs. Wavelet packet analysis is applied as a novel feature extraction method for voltage sag detection by offering improved time-frequency analysis over traditional methods. Energy features are extracted from wavelet packet coefficients for sag identification. This work utilizes wavelet packet analysis to extract energy-based features for voltage sag detection.

Introduction

The generated electrical energy must meet the continuous power requirements of consumers without any disturbances. These disturbances, such as fluctuations in voltage or current, can affect the performance and safety of electrical systems. To evaluate the effect of these variations, it is necessary to monitor the quality of power supplied. Power quality refers to the condition of the electrical supply, ensuring that voltage, current, and frequency remain within acceptable limits. Power quality disturbances are defined as deviations in voltage, current, or frequency from their desired values, which can lead to equipment malfunction or failure. As defined in¹, power quality issues arise when problems in voltage, current, or frequency cause the misoperation or failure of electrical equipment. These disturbances can include voltage sags, swells, harmonics, and transients, each of which can have detrimental effects on both the power system and the connected loads.

Fig. 1

Different types of real time signal which require signal processing.

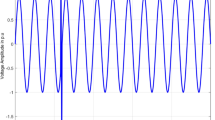
To assess the impact of these disturbances, real-time signals such as those shown in Fig. 1 are analyzed using advanced signal processing methods. These techniques allow for the extraction of meaningful information from raw data, helping to detect and characterize power quality disturbances. This monitoring is essential for maintaining the reliability and longevity of electrical systems and preventing damage to sensitive equipment. Voltage and current quality are termed combinedly as “power quality”¹. Characterization of any signal refers to the description of the features of signals that make them different from the required signal. Figure 2 shows the different disturbances considered for analysis for which different mathematical transforms can be applied to extract information in different domains, resulting in evaluation of power quality.

Fig. 2

Power quality disturbance signals and their description with respect to reference sinusoidal voltage.

This provides complete information about the signal to design or to take preventive measures for overcoming the adverse effects of deviation from ideal values. In¹ the term “characterization” is process of extraction of useful measurement data to describe the event so that there is no necessity of retaining all information of the event. To initiate action of mitigation of the disturbances, they must be recognised properly and causes also must be known. Voltage supplied by electric power utilities is subjected to undesirable variations due to different conditions and faults. The quality of voltage supplied will be affected as constant voltage is to be supplied and hence all the variations remain under the broad category of power quality disturbances. It shows representation of considered signals i.e. variation in the signals with reference to pure sine voltage.

Analysis of disturbance signals to take suitable preventive measures results in improvement of power quality^2,3. Generation of voltage signals can be done in MATLAB using command line and graphical user interfaces. An attempt is made to obtain useful information in identification of sag using wavelet packet transform techniques.

Reasons for increased emphasis on power quality are:

• Less tolerance of equipment when subjected to disturbances.

• Increase in harmonic distortion to the types of loads like A.C motor drives, adjustable speed drives, arc welding and electric heating-based applications.

• Necessity for quality indicators to serve as a reference.

• Using renewable energy sources as a part of integrated generation of electric power.

• Effect of power electronic semiconductor drives and lighting loads for illumination.

• Environmental and economic issues.

According to¹, power quality and voltage quality can be synonymously used as control is possible on the quality of voltage and current control is based on connected load. To characterise PQ disturbances and measurement of voltage and current forms the first step. The variations are to be recorded to have information about changes on the power system. The two conditions for power supply are supply must be free of interruption and the voltage is to be maintained within tolerance limits.

While voltage sag detection and power quality (PQ) monitoring have been extensively studied, existing methods often fall short in addressing the complexities inherent in real-world systems^4,5,6,7. Traditional approaches, such as Fourier analysis and time-domain analysis, provide useful insights but struggle with the non-stationary and transient nature of voltage sag signals. These methods often assume that the signals are stationary or periodic, limiting their effectiveness in detecting and classifying disturbances that vary in duration, amplitude, and frequency. Moreover, many conventional techniques lack the ability to perform multi-scale analysis of voltage sag signals, which are crucial for identifying transient disturbances that may not be captured adequately at a single resolution. As a result, these methods can struggle with real-time detection, especially in the presence of noise or complex signal characteristics that often occur in modern power systems. Despite the widespread use of wavelet transforms, which are capable of analyzing non-stationary signals at multiple scales, there is still a lack of comprehensive studies comparing the effectiveness of different mother wavelets for voltage sag detection^8,9. Furthermore, the use of energy-based features to enhance the accuracy of classification and improve real-time PQ monitoring has not been fully explored. This gap in the literature highlights the need for a more robust, efficient, and accurate approach to voltage sag detection that can overcome the limitations of existing methods.

The primary aim of this study is to propose and validate an innovative methodology for the accurate detection and analysis of voltage sags in power systems, utilizing wavelet packet analysis in conjunction with energy-based feature extraction. The study seeks to address key challenges in power quality (PQ) monitoring by leveraging advanced signal processing techniques to enhance the reliability and efficiency of disturbance detection. The specific objectives are detailed below:

• To design a novel framework combining wavelet packet analysis with energy-based feature extraction to address the limitations of traditional PQ monitoring methods, such as Fourier transforms and time-domain techniques.

• To evaluate six widely used mother wavelets (db1, db4, db10, dmey, sym5, and coif5) and determine their effectiveness in decomposing voltage sag signals for accurate classification of disturbances.

• To enhance detection accuracy and robustness by incorporating energy-based feature extraction, enabling reliable classification of voltage sag disturbances even in noisy environments.

• To implement multi-scale wavelet packet decomposition for real-time detection and classification of voltage sags across varying signal frequencies, overcoming challenges associated with transient and non-stationary disturbances.

• To conduct a detailed error analysis of energy values extracted by different wavelets, validating the reliability and efficiency of the proposed method and comparing it against traditional approaches.

• To demonstrate the practical implications of the proposed methodology by providing a computationally efficient tool for real-time PQ monitoring, contributing to improved system reliability and reduced operational costs.

• To address real-world challenges in power systems by offering a scalable solution for voltage sag detection, applicable across various industrial and commercial environments.

Time-domain methods lack the resolution to capture the intricate frequency-domain changes introduced by sags. While wavelet analysis has been used, few studies explore its full potential, such as wavelet packet decomposition, for precise sag detection. Research gap emphasize that the approach using wavelet packet energy features, offers improved sensitivity and robustness to noise, addressing the limitations of both time-domain and basic wavelet methods. In remainder of the paper, Sect. 2 discusses the role of signal processing in power quality analysis and literature review about power quality, different transforms and feature extraction. Section 3 elaborates signal processing using wavelet packet transform. Section 4 discusses energy for wavelet packet transform based calculations and finally, paper is concluded in Sect. 5.

Role of signal processing in power quality

Analysis is based on signal processing methods and proper understanding of the signals can be possible by using mathematical transforms which represents the signals into different domains^10,11. Transforms are applied for certain information extraction from the signal which is to be processed, termed as ‘raw’ signal. Changes due to deviations exceeding acceptable range from ideal signal are analyzed. In terms of supply voltage, a pure sinusoidal signal is considered as reference and ideal waveform.

In¹² an attempt is made to bridge the gap between the areas of signal processing and power quality by consolidating various signal processing methods for various power system applications. The term event can be assigned to power quality disturbances that have a beginning and an ending.

Power quality monitors record events within the process of:

• Determination of voltage magnitude.

• Comparison with threshold values and.

• Defining characteristics of the event.

This involves measurement of voltage or current as waveform data and further processing of variations and events¹². By signal processing, data is to be extracted that is not direct for understanding and interpretation.

For an analysis and interpretation, obtained data is converted into useful information by signal processing. For enhanced automatic control, artificial intelligence-based methods can be accompanied. The term ‘power quality’ is self-explanatory in terms of quality power to be supplied for consumers. The disturbances should not affect the sensitive equipment. The signals considered for analysis are sine signal for reference and sag signal.

Power quality

Electric power is generated and loads receive electricity supplied continuously. Power quality is defined by C. Sankaran¹³ in a broad sense as a set of boundaries of electrical systems to work with desired performance. All the power quality disturbances and their organization into different categories is explained in¹⁴. Power disturbances with possible solutions and causes are summarized by J. Seymour¹⁵. Mathematically generated rms voltage signals of sine and sag in time domain are shown in Fig. 3 (a) and (b) with voltage magnitude in per unit in time domain. Figure 3(b) depicts decrease in voltage from reference value of 1 p.u for a duration of 0.05 to 0.15 msec. According to¹⁴, sag is decrease in rms voltage from 0.1 pu and 0.9 pu for duration of 0.5 cycles to 1 min.

Fig. 3

(a) Sine signal in time domain.

(b) Voltage sag signal in time domain.

Out of all power quality disturbances, sag is considered for analysis in this work which can be extended to other power quality disturbances and any other real-time relevant signals not only confined to electrical supply voltage. Focus on voltage sags for power quality analysis has direct impact on equipment functionality and voltage supply as explained below:

• 1. High occurrence and sensitivity: Voltage sags occur frequently in power systems and can cause problems for sensitive equipment, like control systems, medical devices, and information technology. These types of devices often cannot handle even short drops in voltage, leading to system errors or unexpected shutdowns.

• 2. Economic importance: In industries that rely on uninterrupted power supply, such as manufacturing or data processing, sags can result in financial loss by interrupting operations or damaging products in production. By studying and addressing voltage sags, companies can reduce these risks and prevent productivity losses.

• 3. Unique source of power quality issues: Voltage sags are not typically caused by complete system failures but by specific situations like motor startups, faults in the utility grid or switching large equipment. These factors make voltage sags different from other disturbances, meaning they need unique analysis methods and mitigation strategies.

Reasons for occurrence of voltage sags in supply voltage supplied by utilities to load:

• 1. Utility or External Faults: Short circuits, lightning strikes, or damage to distribution lines can cause temporary drops in voltage. These faults affect not just the source area but can ripple through the grid, leading to sags for other connected users.

• 2. Large Inrush Currents: When equipment such as motors or transformers starts up, it draws a high surge of current, reducing the overall voltage level temporarily. This impact is felt across connected equipment and leads to a sag.

• 3. Switching of Loads: When large loads are connected or disconnected from the system, they can create sudden shifts in voltage. Similarly, capacitor bank switching can cause temporary voltage drops.

• 4. Poor Connections: Loose connections within the power distribution network can lead to sags, especially when large currents pass through these areas, adding resistance and causing voltage drops.

• 5. Weather Conditions: Extreme weather, particularly thunderstorms or high winds, often damages power lines or equipment, leading to faults that cause sags in the voltage supply across a large area.

Choosing voltage sags for analysis highlights their role in system efficiency and reliability, making it a valuable focus for enhancing both equipment protection and overall power quality. The same analysis can be extended for any other type of signals for extracting useful information consisting of deviation present with respect to ideal values.

Application of transforms to signals results in information that is not directly available. A signal that has been transformed is termed as processed signal. Analysis, diagnosis and detection of power quality disturbances can be done using transforms which include wavelet transform and S-Transform⁸. In¹⁶, to classify disturbances, data is partitioned and signal processing techniques are focussed. According to A. W. Galli et al.¹⁷identification relates to categories of signals, their decomposition and representation as sum of basic functions. In¹⁸, it was reviewed that some transforms can be used for classification of power quality disturbances.

Role of different transforms in power quality evaluation

Fourier transform (FT), short time Fourier transform (STFT) and wavelet transform (WT) are widely used for PQ analysis¹⁹. “Phase shift and missing voltage” are examined in²⁰ to find information about disturbances. The fundamental voltage component is used in²¹. In ²² it is analyzed that dilation of single prototype function results in different scales and levels of resolutions. An algorithm is implemented in²³ for estimation of voltage sag. In²⁴. disturbance is evaluated by the difference between transient and sine waveforms taken as ideal value. The transients are localized in the analysis presented in²⁵. Singh et al.²⁶ demonstrated the effectiveness of using Fourier transform-derived discriminant (FTDD) features for robust detection of power quality disturbances in real-time applications. Their work underscores the necessity of advanced feature extraction techniques to improve the reliability of PQ monitoring systems in noisy environments. The system stated in²⁷ is able to find disturbances in noise which is a random signal. Method proposed method in²⁸ is for identifying the start and stop time of disturbances. High-frequency contents of the original signal are obtained through a “succession of convolution process”²⁹. The term “detail-spectrum-energy” is used in³⁰ for detection and classification. In³¹, it is shown that transients are located in the width of the signal and sag is analyzed.

In³², limitations of ‘complex wavelet transform’ are explained. In³³, ‘first level wavelet coefficient energies’ are used to detect very short duration components. Voltage sag is characterized in³⁴. It is stated in³⁵ that ‘wavelets’ is a powerful tool for PQ analysis.

Feature extraction of power quality disturbance signals

A wavelet-based energy content method is given in³⁶. Wavelet-based methods are elaborated in³⁷. The importance of correct ‘detection and description’ of PQ events is stated in³⁸. H. Y. Zhu et al.³⁹ recognized strength of wavelets in transient analysis due to good time-frequency characteristics. The Institute of Electrical and Electronics Engineers (IEEE) dictionary⁴⁰ defined power quality in terms of ‘powering and grounding of equipment’. The International Electrotechnical Commission (IEC)⁴¹, defined power quality in terms of “characteristics of electricity evaluated against a set of reference parameters”.

In⁴² importance of choice of scales is explained. In⁴³ “fully scalable window” concept is explained. In⁴⁴, wavelet packet transform is used for three levels with monitoring by obtained feature vectors. Input in⁴⁴ refers to PQ signals and output obtained is the type of disturbance and is shown that there is an increased potential of “wavelet packet energy”. In⁴⁵, testing samples are generated using equations.

The advantages of using equations for signal generation are:

• Easy adjustment of signal noise content.

• Different signal parameters can be used. For example, harmonic frequency content for harmonics, duration of disturbances, magnitude of voltages etc. are different parameters.

In⁴⁶, a unit is designed for wavelet transform is used for capturing high frequency noise due to fault initiation by presenting detail coefficients. Shannon entropy-based algorithms are proposed in⁴⁷, for obtaining the orthogonal best basis with a library of “predefined modulated waveforms” indexed by position, frequency and scale parameters. Suitable mother wavelet is selected in⁴⁸ based on level one detail coefficients magnitudes for high-impedance fault detection and classification between healthy and fault phases. A term called “fault criterion” in fault detection algorithm is proposed in⁴⁸ which acts as a threshold value for sum of level one detail coefficients.

The advantages of transient analysis are explained in ⁴⁹ with two examples of application of wavelet analysis to current drawn by an arc furnace and to the generator turbine vibration waveforms. The plots for standard deviation for each resolution level termed as standard MRA curves⁵⁰ are obtained showing deviation in energy content for sag, swell and frequency content for harmonics. For similar features, the difference between standard deviations of disturbances and pure sine wave are calculated. Wavelet analysis of PQ signals is carried out in⁵¹ using ‘coif5’ as mother wavelet for wavelet analysis by comparing with S-transform in terms of time for computation. F.B. Costa et al.⁵² used normalized wavelet coefficient energies to analyze oscillographic data with transients by considering pre-fault transients. The main characteristics of voltage sag are obtained using MATLAB/ Simulink in⁵³. E. Perez et al.⁵⁴ proposed after a comparison analysis, wavelet analysis combined with Kalman filtering is best for characterization of voltage events. Reference⁵⁵ deals with voltage sag detection, harmonic current detection by taking an arc furnace system and switching transient. In⁵⁶, it is mentioned that narrow wavelets have high frequency short term effects.

The term “PQ data analytics” has been used in⁵⁷ and it is examined in⁵⁸ that daub4 and daub6 are mentioned to be suitable for detecting disturbances and choice of wavelet basis function plays an important role. An energy function is proposed in⁵⁹ for detecting disturbances and stator current is used to get energy of level 7 details and comparison is done with a threshold. In⁶⁰ for identification of non-stationary signals, energy is used for transform coefficients to extract features. In method proposed in⁶¹ for feature extraction, wavelet transform is used with wavelet coefficient energies. It is mentioned in⁶² that by using wavelet packets, transient features can be obtained under ‘more comprehensive scale’ than wavelet transforms. In⁶², wavelet energy of $\:j$ decomposition scale is given by $\:\sum\:_{k}{\left|{D}_{j}\left(k\right)\right|}^{2}$ with $\:{D}_{j}\left(k\right)$represents elements of each decomposed signal. Wavelet entropy is effectively employed in⁶³ for detecting changes in non-stationary signals. Different wavelet entropy measures, definitions and their calculation methods are presented in⁶⁴. For identification of many power quality disturbances, ‘energy method’ is an effective feature extraction technique for transform coefficients⁶⁵. In the method proposed in⁶⁶, in feature extraction stage, wavelet transform is used along with energy features. Continuous wavelet transform applications are discussed in^67,68,69. In⁷⁰, voltage variations existing for a short duration are be analyzed using signal processing methods and classification of signals using wavelet transform based low frequency representation of the signals. Reference⁷¹ is about how voltage variations are corrected by using devices like static var compensator and explains the role of thyristor-controlled reactor and thyristor switched capacitors. Importance of filters in reduction of harmonics is explained in^72,73,74. References^{75,76,77,78,79,80} provide additional information about the emphasis of various terms of entropy, energy, discrete wavelet and wavelet packet analysis in diagnosis of power quality events. Different examples are illustrated for equipment condition monitoring, home appliances and load monitoring⁸¹. The aim of this paper is to apply wavelet packet transform to the generated sag signal and extract of ‘energy’ feature of the signals. A suitable mother wavelet is selected for signal analysis using ‘energy’ of signals. To accomplish formulated objectives, contributions in this paper are as follows.

• Emphasis on importance of power quality and necessity for signal processing.

• Wavelet packet-based analysis of sag signal.

• Comparison with respect to an ideal sine signal by evaluation of energy values of sag signal for different levels.

• Wavelet packet transform for finer resolution, different suitable mother wavelets, evaluation of the strength of the signals using “energy” feature are presented.

Signal processing of power quality disturbances using wavelet packet transform

In⁸², design of prototype model is proposed resulting in saving of electrical power. The purpose of study of all power quality disturbances using different techniques is also to save electric power supplied by utilities to consumers⁸³, Continuous Wavelet Transform is used to visualize transient and short duration voltage variations. In⁸⁴, discrete wavelet transform is applied and then few statistical features are extracted. Perception of power quality disturbances is carried out in⁸⁵ by using Fourier Transform, Short-Time Fourier Transform, Continuous transform and Discrete Wavelet Transforms to extract and compare information in different domains. In⁸⁶ the percentage ratios of the energies of the disturbances to that of reference are calculated. Breaking up of a signal is termed as ‘decomposition’. Wavelet packet transform (WPT) is used for processing of PQ signals.

Next level approximations and details are obtained in ‘wavelet packet analysis’ by splitting present level approximations and details starting from original signal. Next level approximations and details are obtained in ‘wavelet analysis’ by splitting the present level approximations only starting from original signal. Wavelet packet transform coefficients $\:{C}_{p}^{n,j}\:$are given by the Eq. (1).

$$\:{C}_{p}^{n,j}={\int\:}_{-\infty\:}^{\infty\:}x\left(t\right){\psi\:}_{n}\left({2}^{-j}t-p\right)dt$$

(1)

The terms $\:\psi\:,$$\:j,p$ and $\:n$ in Eq. (1) represent wavelet function, number of decomposition level, position parameter and channel number defining position in tree⁸⁷. The features of ‘energy’ indicating strength of signals and ‘entropy’ indicating disorderly states of the signals are used for classifying signals. In order to visualize the sag signal, MATLAB environment is used.

Wavelet packet analysis

Test signals for wavelet packet analysis are generated in MATLAB for 0.4 s and sag with magnitude of 0.5 pu is initiated from 0.05 to 0.15 s with a frequency of 50 Hz.

Time is taken as a row vector containing 4001 elements from 0 to 0.4 s (400msec) in steps of 0.1 msec (first element 0 + (400msec/0.1msec = 1 + 4000 = 4001 elements) in MATLAB environment. Figure 4 (a) and (b) shows the wavelet tree and wavelet packet tree depicting the difference between both of them for four level decomposition.

Fig. 4

Wavelet and Wavelet Packet Tree representation.

Next level approximations and details are obtained in ‘wavelet packet analysis’ by splitting present level approximations and details starting from original signal. Corresponding signal for each node label can be visualized in MATLAB. The first numbers in node labels indicate level of decomposition. Second terms in node labels have zero and even numbers indicating approximations and odd numbers indicating details. Precise mother wavelet is to be selected out of available large number of wavelet families. Figure 4 (b) shows the numbering of indices of wavelet packet tree and in all the node labels first term ‘4’ indicate fourth level decomposition with 16 terminal nodes. Color maps are used to observe the deviation in coefficients upon changing the level of wavelet packer decomposition. Figure 5 lists out different types of mother wavelets used in this analysis. The tree diagrams of wavelet and wavelet packet trees, visually represent how the signal is decomposed:

• Wavelet Tree shows the hierarchical decomposition of the signal into approximation and detail coefficients across levels.

• Each split indicates a breakdown of the signal into lower-frequency approximations and higher-frequency details.

• Wavelet Packet Tree provides a more detailed breakdown, as both approximation and detail components are further decomposed into sub-bands at each level.

• This tree is richer in information and shows a finer time-frequency structure of the signal.

Fig. 5

Different Mother wavelets that used for sag signal analysis.

Wavelet packet analysis is an effective tool for analyzing non-stationary signals like voltage sags because it provides a detailed time-frequency representation. The choice of wavelet functions plays a critical role in this process. The specific wavelets mentioned in Fig. 5 are selected due to the following reasons:

• 1. Smoothness and Transient Sensitivity: Wavelets like Daubechies (db4, db6, etc.) or Symlets are commonly used because their compact support and smooth structure which make them ideal for capturing abrupt changes in signals, such as voltage sags.

• 2. Vanishing Moments: Higher vanishing moments allow these wavelets to represent transient signal features efficiently, which is crucial for detecting sags.

• 3. Energy Distribution: The wavelets chosen ensures that most of the energy during a sag is concentrated in a few coefficients, improving feature extraction accuracy.

• 4. Empirical Validation: Using MATLAB, different wavelets are tested to compare their performance in terms of energy feature clarity and discrimination between sags and ideal sine signals. The wavelets that performed best in these tests were selected.

For detailed analysis, level four decomposition is considered. In wavelet analysis, only approximations are decomposed and details are not split. Each level of approximations and details are split into approximation and detail of next level in wavelet packet analysis. This results in finer resolution of signals. The variation in terms of colored coefficients is shown in Fig. 6 (a) along with labels for nodes with corresponding colormap illustrated in Fig. 6(b). Different coefficients obtained by wavelet packet transform for four level wavelet packet decomposition of voltage sag signal are depicted. Color map indicates scale of colors from minimum to maximum with colored coefficients of terminal nodes. For fourth level decomposition, each row of 16 rows represents terminal nodes 15 to 0 from top to bottom as shown in Fig. 6 (a).

Fig. 6

(a) Terminal node coefficients (b) Scale of colors from minimum to maximum with colored coefficients of terminal nodes.

Each ‘packet’ with its node label from 0 to 15 respectively are indicated from (a) to (p) in Fig. 7 with normalized magnitude on y-axis and time in seconds on x-axis. It is seen that the packet (4,0) is representing low frequency representation of original sag signal. Whichever packets have significant variation in magnitude, is giving its contribution in terms of deviation present in the signal.

Fig. 7

(a) to (p) Level four wavelet packet decomposition coefficients of terminal nodes of sag signal.

Different terminal coefficients of node labels of 0 to 15 for voltage sag signal after four level wavelet packet decomposition are depicted in Fig. 7 using Daubechies wavelet of order 4 (db4) as mother wavelet. The deviation in coefficients changes upon changing the type of wavelet used. Different terminal coefficients of node labels of 0 to 1, 0 to 3, 0 to 7 and 0 to 31 for voltage sag signal for first, second, third and fifth level wavelet packet decomposition respectively are depicted in Fig. 8 (a) to (d) with following information:

• For first level decomposition, each row of 2 rows represents terminal nodes 1 and 0 from top to bottom.

• For second level decomposition, each row of 4 rows represents terminal nodes 3 to 0 from top to bottom.

• For third level decomposition, each row of 8 rows represents terminal nodes 7 to 0 from top to bottom.

• For fifth level decomposition, each row of 32 rows represents terminal nodes 31 to 0 from top to bottom.

Fig. 8

Terminal node coefficients of Sag after wavelet packet decomposition (WPD) (a) First level (b) Second level (c) Third level (d) Fifth level.

For wavelet packet decomposition of sag signal, the following conclusions are drawn:

• Unlike standard wavelet decomposition, wavelet packet decomposition is more flexible as it decomposes both approximation and detail coefficients, offering a richer set of frequency sub-bands.

• In wavelet packet decomposition, the best wavelet is chosen focusing on maximizing the preservation of signal details. This can lead to better frequency resolution since the decomposition explores a finer grid of the time-frequency space.

• This is useful for detecting subtle changes, like those in voltage sag signals.

• The colored coefficients typically represent the amplitude or energy of the signal across different scales and time intervals for each node in the decomposition:

• As shown in colormap, high magnitude colors indicate higher amplitude or energy components, suggesting strong activity or significant features in that frequency range.

• Low magnitude colors represent lower amplitude components, which may be noise or less significant information in the signal.

• The “best wavelet” refers to the wavelet function that most effectively captures the relevant features of voltage sag signal.

• The colored coefficients illustrate how the signal’s energy and characteristics are distributed across frequency bands and time intervals, helping to analyze the dynamics of the voltage sag.

• Information about the most relevant nodes for capturing the primary characteristics of the signal, such as the main frequency components and transient events in a voltage sag signal can be obtained.

• Nodes having less significant information are effectively considered less significant for the representation, analysis, or compression of the signal.

• Nodes having ‘zero’ energy are omitted.

Figure 9 depicts the bandwidth information for wavelet packet terminal nodes for all levels 1 to 5 respectively from (a) to (e) for a sampling frequency of 10,000 Hz. The colormap indicates the node indices of 2, 4, 8, 16 and 32 for levels 1 to 5 wavelet packet decomposition. The frequency information of the wavelet packet terminal nodes can be obtained directly in MATLAB.

Fig. 9

Frequency ranges for (a) First (b) Second (c) Third (d) fourth (e) Fifth level terminal nodes.

In wavelet packet decomposition, the rows of the colored coefficient matrix are not uniform due to the differing energy values which indicate the strength of the signal, captured in each node at different levels of decomposition. Energy features extracted from wavelet packet coefficients are highly sensitive to the unique characteristics of voltage sags compared to the traditional methods of Root Mean Square (RMS) voltage and Total Harmonic Distortion (THD) due to the following reasons:

• 1. Abrupt amplitude changes: Voltage sags involve sudden drops in amplitude. These changes cause distinct variations in the wavelet packet coefficients, leading to a noticeable shift in energy at specific decomposition levels.

• 2. Frequency Analysis: Sags introduce distortions or harmonics, which appear as energy changes in specific frequency bands isolated by wavelet packet analysis.

• 3. Noise Robustness: Energy features in the wavelet domain are less affected by noise compared to time-domain features like RMS voltage or Total Harmonic Distortion THD allowing for more reliable detection.

• 4. Superiority over traditional features:

• RMS Voltage: RMS can fail to detect short-duration sags or shallow sags.

• THD: THD measures harmonic content but might not fully capture transient events.

• Wavelet Energy: Captures both magnitude and frequency domain changes, providing a comprehensive characterization of the sag.

Due to the above reasons, preference is given for energy features for detecting sags.

Each node in the wavelet packet tree represents a distinct frequency band and time interval, capturing the energy of the signal in that specific sub-band. This results in variations in the amplitude or energy density represented by each node, which is then visually represented by the varying colors in the coefficient matrix with specific nodes explanation as below:

Energy distribution across nodes.

In 5-level wavelet packet decomposition, each node captures a different frequency band of the signal. The energy distribution affects the visual representation as below:

• 1. Node-Specific Frequency Bands:

• Each terminal node corresponds to a specific frequency range. For example:

  • 5,0 might capture the lowest frequency sub-band within the decomposition at level 5.

  • 5,1, 5,2, and 5,3 capture progressively higher frequency sub-bands.

  • Voltage sags often involve specific low or mid-frequency ranges, which may lead to higher energy concentration in certain nodes. This means nodes associated with these significant frequencies will show higher energy, resulting in different colors (often warmer colors) in the matrix.

• 2. Non-Uniform Energy Levels:

• Different nodes can capture varying amounts of signal energy. Nodes with a higher energy concentration (typically from significant features of the signal) will display brighter or warmer colors, while nodes with lower energy concentrations (often representing noise or less important details) will appear cooler.

• For instance, if 5,0 and 5,1 capture the main components of the voltage sag, these rows in the colored coefficient matrix will display higher intensities (warmer colors) compared to 5,2 or 5,3, where the energy might be lower due to their higher frequency range and less relevance to the sag characteristics.

Resolution difference due to node depth

• At level 5 of decomposition, each node represents a finer time-frequency resolution. The depth and specificity of each node mean that each captures a smaller frequency band with varying energy. As a result, nodes like 5,0 and 5,1 might have more uniform or prominent energy (if they capture core features), while nodes 5,2 and 5,3 could show scattered or lower intensity.

The non-uniformity across rows is a visual manifestation of how energy is distributed unevenly across the terminal nodes:

• High Energy Nodes: Nodes that capture the main features of the voltage sag will show higher intensity. For instance, 5,0 and 5,1 might capture a significant portion of the sag’s main oscillatory behaviour, giving them a consistently high energy and, therefore, a warmer color.

• Lower Energy Nodes: Nodes like 5,2 and 5,3 might capture high-frequency components, which may contain less relevant information or noise. These nodes will have lower energy, resulting in cooler colors and less intensity.

In summary, the non-uniform rows in the wavelet packet color coefficient matrix reflect how different nodes capture distinct energy levels due to the frequency characteristics of the voltage sag signal. This is why higher energy (warmer colors) in specific rows corresponding to nodes like 5,0 and 5,1 and lower energy (cooler colors) in other rows is observed.

Level wavelet packet decomposition for voltage sag signal

In a 4-level decomposition:

• The signal is decomposed into 16 terminal nodes, from 4,0 to 4,15, each representing a specific sub-band.

• Voltage sags often contain more energy in the lower frequency bands, as sags involve a sustained drop in voltage rather than high-frequency transients.

• Nodes 4,0 to 4,3 likely capture the lower frequencies, containing significant signal energy if the sag mainly affects the low-frequency components.

• Higher Nodes 4,12 to 4,15 represent higher frequency bands. If the sag signal has a sharp transition or brief oscillations, some energy might appear in higher nodes, but typically, they carry less energy and are often less significant for sags.

Thus, nodes 4,0, 4,1, 4,2, and 4,3 can be emphasized if they capture the bulk of the sag signal’s energy.

To consolidate the information:

• The signal is decomposed into 32 terminal nodes, from 5,0 to 5,31, providing an even finer time-frequency grid than the 4-level decomposition.

• For voltage sags, the additional level allows for better isolation of the low- and mid-frequency bands, which may be particularly useful if there are subtle frequency components or harmonic effects within the sag signal.

• Nodes 5,0 to 5,7 represent the lowest frequency bands and often capture the primary energy of a sag signal, as sags generally impact the lower frequency spectrum.

• If the sag includes low-frequency oscillations or a mild transient, some of the energy might be distributed across these mid-frequency nodes 5,8 to 5,15 making them potentially relevant.

• Higher Nodes 5,16 to 5,31 represent the highest frequencies and are often less relevant in the context of voltage sags, unless the sag is accompanied by high-frequency noise or switching transients.

Thus, nodes like 5,0 through 5,7 (and possibly some in 5,8 to 5,15), capturing the main low-frequency components and any significant mid-frequency details.

In all the figures of colored coefficients for terminal nodes, obtained by wavelet packet tree one to five levels of decomposition, variations are more in bottom row as it represents low frequency content of the signal with more strength and resembling to original signal but with reduced time interval. The scale of colors shown in each figure is from minimum to maximum value. Each row in the figures represent from down to up the coefficients corresponding to left to right nodes of tree. This is called natural order. The percentage ratios of the energies of the disturbances to that of reference can also be calculated. The selection can be based upon factors like nature of the signal whether the signal has abrupt or smooth changes, sharp edges and information to be obtained from the signal. If ‘n’ is the level of decomposition, $\:{2}^{n}$terminal nodes are obtained. References^74,75,76,89 provide mathematical basics involved and provide an in-depth approach for exploring wavelet packet transform applications and wavelet packet analysis. For example, for the practical modular unit implemented in⁹⁰ for reliable operation of an asynchronous machine, application of wavelet packet transform can be incorporated for extracting information from the voltage signals in the monitoring section. This ensures prevention of emergency failures as information about poor power quality can be obtained. Figure 10 gives pictorial representation of the mother wavelets from (a) to (f) used in this wavelet packet analysis with normalized magnitude on y-axis and time on x-axis.

Fig. 10

Different Mother wavelets (a) db4 wavelet (b) db1 wavelet (c) dmey wavelet (d) sym5 wavelet (e) coif5 wavelet (f) db10 wavelet.

Level one, two, three, four and five decomposition levels have 2, 4, 8, 16 and 32 terminal nodes respectively. ‘Best Wavelet Packet Tree’ can be obtained which indicates the significant nodes contributing to the structure of the signal. The variation present in the time domain signal can be visualized in best tree representation also with a reduction in terminal nodes.

Best wavelet packet tree

For a voltage sag signal, selecting the best wavelet packet tree means identifying the nodes in a wavelet packet decomposition that best capture the signal’s significant features, usually in terms of energy concentration in certain frequency bands relevant to the sag.

In wavelet packet decomposition:

• Both approximation and detail coefficients are decomposed at each level, providing a much finer time-frequency resolution than standard wavelet decomposition.

• Each terminal node represents a unique frequency band. Since voltage sags typically affect specific frequency components, certain nodes (frequency bands) may carry higher energy, making them more relevant for analysis.

For best wavelet packet tree, 1, 2 and 3 do not make significant difference from wavelet packet tree. For a sag signal, the best wavelet packet tree selection for 4 and 5 levels is based on the energy or information criterion. The following information can be obtained from Fig. 11(a) to 11(d).

• High energy concentration in nodes relevant to the frequency characteristics of the sag.

• Entropy or other threshold criteria that highlight nodes where significant signal information resides.

• For voltage sag signals, the best wavelet packet tree will typically include nodes that capture the main frequency bands where the energy is most concentrated.

Fig. 11

(a) Best Tree representation for four level wavelet packet decomposition (b) Colored coefficients for four level best wavelet packet tree (c) Best Tree representation for five level wavelet packet decomposition (d) Colored coefficients for five level best wavelet packet tree.

• Voltage sags often contain more energy in the lower frequency bands, as sags involve a sustained drop in voltage rather than high-frequency transients.

• Best wavelet packet tree at 4 levels will likely emphasize nodes that capture the bulk of the sag signal’s energy.

• Best wavelet packet tree at 5 levels for a sag signal focus on nodes capturing the main low-frequency components and any significant mid-frequency details.

The selection of the best packet tree nodes is based on:

• Energy Concentration: For a voltage sag, the energy is concentrated in the low-frequency nodes, as sags are usually low-frequency phenomena. Nodes with high energy contain the essential characteristics of the sag.

• Frequency Band Relevance: By focusing on nodes that capture the low- and mid-frequency bands relevant to the sag, core impact of the sag is captured without including unnecessary high-frequency noise.

For a voltage sag:

• 4-Level Best wavelet Packet Tree focuses on nodes which capture the low-frequency characteristics of the sag.

• 5-Level Best wavelet Packet Tree focuses on nodes providing a finer resolution and more accurate representation of the sag’s primary frequency bands.

By selecting the best packet tree, a focused, efficient representation of the sag signal, preserving the primary information while minimizing unnecessary details is achieved.

Significance of different nodes

• 1. Energy Concentration: In wavelet analysis, the signal’s energy is often concentrated in a few nodes that capture the main features of interest (like sudden voltage drops or oscillations). Nodes that capture minimal energy or detail can be considered negligible since they don’t contribute much to the core characteristics of the signal. This is why certain nodes emerge as terminal nodes.

• 2. Thresholding and Pruning: The concept of terminal nodes arises because wavelet analysis aims to simplify the data while retaining key features. By pruning nodes with low energy or those representing less important frequency bands, we reduce complexity. This is particularly beneficial for noise reduction and data compression.

• 3. Time-Frequency Resolution Trade-off: In wavelet packet analysis, decomposition is exhaustive, splitting the signal into many more sub-bands compared to standard wavelet analysis. By focusing on only a subset of these nodes, specific time-frequency regions that reveal the core features of the voltage sag are prioritized. Nodes with low energy or that don’t represent unique signal characteristics become less relevant, essentially because they offer redundant or non-critical information.

• 4. Simplification for Interpretation: For practical analysis, interpreting an entire decomposition tree (especially in wavelet packet decomposition) can become overwhelming. By selecting only, the best wavelet and the most relevant terminal nodes, focus is laid on the information that best represents the signal. This simplifies the analysis without compromising on accuracy, allowing to retain the primary features while discarding background noise or redundant details.

While some detailed frequency components or minor variations are omitted, the main idea is that this data isn’t crucial for understanding the signal’s primary features. Thus:

• Important Patterns are retained: The significant nodes retain the essential features like the sudden drop and oscillations associated with a voltage sag.

• Noise and Minor Details are reduced: Non-critical nodes are pruned, which can help remove minor noise and enhance the clarity of the signal features relevant to analysis.

In essence, omitting non-significant nodes doesn’t mean losing critical information—it means focusing on the signal’s core characteristics by isolating the most informative parts of the time-frequency representation.

Energy for wavelet packet decomposition

The number of terminal nodes for level one, two, three, four and five decompositions are 2, 4, 8, 16 and 32 respectively. Wavelet packet decomposition is used for processing of the signals. For all the five levels of decomposition using ‘db4’, ‘db1’, ‘sym5’, ‘dmey’, ‘coif5’ and ‘db10’ wavelets, values of energy are obtained. Energy values for terminal node coefficients obtained after wavelet packet decomposition of all signals are listed.

Program code

This program is executed in MATLAB. T is wavelet packet tree and E represents the energy values. Level of decompositions are 1, 2 3, 4 and 5.

Syntax used for energy values.

T = wpdec (signal, level of decomposition, ‘mother wavelet’, ’entropy’, ’parameter’).

E = wenergy (T).

The objective is to apply wavelet packet transform for voltage sag signal and to obtain information about disturbance in signal using features of energy by using ‘entropy’. The sudden changes in signals can be observed by combining wavelet packet decomposition with a criterion called “entropy”. Measure of disorderly states is termed as entropy and gives ordering of non-stationary signals⁷⁷. In⁷⁰, comparison is done between entropy values of approximations of disturbance signals and reference sinusoidal signal. Performance comparison is evaluated in⁷⁸ and entropy is defined as, “measure of imbalance and uncertainty”. Based on features of maximum gradient, entropy, variance, kurtosis, skewness etc. signals are classified by proposed decision tree in⁷⁹ using 3-D feature plots. The features of level 1 detail coefficients which include peak, variance, and skewness of level 7 approximations, mean deviation of level 6 details are extracted using wavelet transform in⁸⁰ and Table 1 gives different definitions of entropy used in various fields.

Table 1 Definitions of entropy in various fields.

In MATLAB environment, if the type of entropy is not specified, ‘Shannon; entropy is considered as default. In the present work, for extracting energy features, Shannon entropy is used.

In all the tables from 2 to 6, the calculated energy values are listed for levels one to five for six types of mother wavelets considered for analysis. Level one, two, three, four and five decomposition levels have 2, 4, 8, 16 and 32 terminal nodes respectively. Using ‘db4’, ‘db1’, ‘sym5’, ‘dmey’, ‘coif5’ and ‘db10’ wavelets, energy values are obtained for one to five levels of decomposition. The nodes which are not indicated represent energy value as 0. To avoid redundancy, nodes having zero energy values are omitted. Energy values are shown with terminal node representation with ‘N’ representing node label or node index for different levels of decomposition. Tables 2, 3, 4, 5 and 6 show the energy values for wavelet packet decomposition corresponding to the terminal nodes (1, 0) to (1,1) of first level, (2, 0) to (2, 3) of second level, (3, 0) to (3, 7) of third level, (4, 0) to (4,15) of fourth level and (5, 0) to (5, 31) of fifth level using six types of mother wavelets.

Table 2 Energy values with node labels for level 1 terminal nodes.

Table 3 Energy values with node labels for level 2 terminal nodes.

Table 4 Energy values with node labels for level 3 terminal nodes.

Table 5 Energy values with node labels for level 4 terminal nodes.

Table 6 Energy values with node labels for level 5 terminal nodes.

Description based on node structure:

The data provided for wavelet packet decomposition has a distinct node structure for each level:

• Level 1: 2 nodes (0, 1).

• Level 2: 4 nodes (0, 1, 2, 3).

• Level 3: 8 nodes (0, 1, 2, …, 7).

• Level 4: 16 nodes (0, 1, 2, …, 15).

• Level 5: 32 nodes (0, 1, 2, …, 31).

For each level, energy values are calculated for both sine and sag signals using different wavelets like db4, db1, sym5, db10, dmey, sym5 and coif5. The terminal nodes for each level give insight into how the energy of the signal is distributed across different frequency bands.

Summary:

• 1. Level 1 (2 nodes):

• For wavelets like db4, sym5, coif5, dmey, and db10, almost 100% of the energy is concentrated in node 0.

• In contrast, db1 splits energy between nodes 0 and 1 (99.9754% and 0.0246%, respectively). This indicates that db1 captures more details in the signal, even at this early stage of decomposition.

• 2. Level 2 (4 nodes):

• For most wavelets, the energy is concentrated mostly in node 0 with a very small percentage in node (1) For example, db4 has 99.9948% in node 0 and 0.0002% in node 1.

• However, db1 spreads the energy further, with 99.876% in node 0, 0.0984% in node 1, and 0.0246% in node (2) This suggests that db1 captures more variation across nodes as compared to other wavelets.

• 3. Level 3 (8 nodes):

• Wavelets like db4, sym5, and coif5 concentrate energy around node 0 with minimal energy in other nodes (e.g., db4 shows 99.9978% at node 0, with tiny values at nodes 1, 2, and 3).

• Again, db1 shows a more distributed energy spread, with 99.484% at node 0, but significant portions in nodes 1 to 5 (e.g., 0.393% at node 1 and 0.0981% at node 2).

• 4. Level 4 (16 nodes):

• For wavelets like db4, sym5, coif5, and db10, most energy is still in node 0, with minor spreads across nodes 1 to 7.

• db1 continues to capture more detail, with 97.9245% at node 0, but also energy spread across nodes 1 to 10 (e.g., 1.5595% at node 1, 0.3868% at node 2, etc.).

• 5. Level 5 (32 nodes):

• Even at this level, wavelets like db4, sym5, coif5, and dmey have most of the energy in node 0, while db1 has 91.8815% in node 0, but energy spread across nodes 1 to 31. This wide distribution shows that db1 is sensitive to small signal variations and captures a broader range of frequency components.

• Wavelets like db4, sym5, coif5, and db10 concentrate energy in a small number of nodes across all levels, meaning they are better suited for signals where the main information is captured in large-scale structures (like periodic or smooth signals).

• Wavelet db1, on the other hand, spreads the energy more evenly across nodes, capturing finer details and higher frequencies in the signal. This can be useful for more complex signals where subtle variations are important (such as detecting sag events or other transient phenomena).

Figure 12 shows energy values of terminal node coefficients of sine and sag signals for ‘db10’ mother wavelet for five level decomposition excluding first terminal node as it is capturing whole of the signal information and the purpose is to analyze the deviation present in the signal with respect to the desired signal. Figure 12 depicts comparison of energy values of sag signals with reference sine signal using ‘db10’ mother wavelet.

Fig. 12

Comparison of energy values sag signal with reference sine signal using ‘db10’ mother wavelet.

Energy values for terminal node coefficients (excluding node 0) of sine and power quality disturbance signals using ‘db1’, db4’, ‘dmey’, ‘sym5’, ‘coif5’ and ‘db10’ mother wavelets for five level decomposition are shown in Fig. 13.

Fig. 13

Error in energy values for sag signal with respect to sine signal.

Node 0 represents low frequency resolution of signals representing ‘approximation’ with large energy value compared to other terminal nodes as listed in different tables. All the calculations are done using Shannon entropy. Maximum values are chosen from error values. 2 terminal nodes are present termed as 0 and 1 for 1st level decomposition. 4 terminal nodes are present termed as 0 to 3 for 2nd level decomposition. 8 terminal nodes are present termed as 0 to 7 for 3rd level decomposition. 16 terminal nodes are present termed as 0 to 15 for 4th level decomposition. 32 terminal nodes are present termed as 0 to 31 for 5th level decomposition. Energy values are obtained and the difference in energy values are obtained calculated by considering the difference of energy values of sine signal taken as reference and energy values of sag signal. The nodes of terminal nodes are 2, 4, 8, 16 and 32 for levels 1 to 5 decomposition. For all levels, error values are as shown in Table 7.

Table 7 Error values for different levels of decomposition.

Information about type of wavelet suitable for sag signal is obtained. By using wavelet packet transform, sag disturbance can be identified. By decomposing signal into finer levels, information about changes in the signal can be obtained. From all obtained values, coif5 wavelet gives high values for sag. So mother wavelet can be selected based upon large difference values of energy of terminal nodes as shown in Table 8. Energy values are obtained for all 1st, 2nd, 3rd, 4th and 5th levels of decomposition using six wavelets. The maximum energy values for wavelet packet decomposition corresponding to the terminal nodes of first to fifth level using all six mother wavelets obtained are listed in Table 8. For each node, for each level, difference in energy values of both disturbance and reference sine signal are calculated. The term ‘error’ value is assigned for the difference in energy.

Table 8 Maximum error values from first to fifth level decomposition using different mother wavelets.

Each signal is decomposed to five levels and energy values are calculated using entropy types. Comparison with energy values is done with that of reference sinusoidal signal. Calculations are performed for error in the energy values for each level and for large error values mother wavelet is identified. Energy values are obtained for terminal nodes and are compared with that of sinusoidal voltage signal. The change in values is noted and based upon the error values, mother wavelet is identified.

The energy distribution curve gives information about the variation of strength of signal after applying wavelet packet decomposition. Large error value indicates that the mother wavelet is effective in identifying the correlation obtained by comparison of the disturbance signals with shifted and dilated mother wavelets. The functions ‘wenergy’ is described as energy for wavelet packet decomposition under wavelet packet algorithms. This analysis is carried out sung the functions of ‘wenergy’ and ‘wpdec’ related to wavelet packet tree in MATLAB,

Though the potential for online or real-time application of this method is directly not addressed, wavelet packet analysis can be adapted for real-time monitoring by addressing the few challenges and can be made feasible with the following considerations:

• 1. Computational Challenges:

• Wavelet Packet Analysis involves multiple levels of decomposition, which can be computationally intensive.

• Solutions:

  • Optimized MATLAB functions for decomposition can be used.

  • Exploration of real-time hardware acceleration (e.g., GPUs or FPGAs) for faster processing.

  • Focus on fewer decomposition levels or specific frequency bands critical to sag detection.

  • 2. Latency:

• Real-time systems require minimal delay. Testing the method on MATLAB Real-Time or Simulink can help measure and optimize latency.

Dynamic thresholds

Testing the method on MATLAB’s real-time platforms and reporting results on processing time and detection latency would demonstrate feasibility for online applications. This explains the real-time applicability of wavelet packet analysis.

Conclusion and future research directions

Signal processing techniques are necessary to apply for power quality disturbance signals in order to extract information that is not available in time domain. Wavelet packet analysis is performed using wavelet packet transform and terminal node coefficients are obtained. A feature ‘energy’ for wavelet packet decomposition is extracted with the energy distribution curves providing information about the change in signal strength of signals. Signals considered for analysis is sag by taking a pure sinusoidal signal as reference. Energy values for levels one to five terminal nodes are obtained in MATLAB environment. Energy differences termed as error values are calculated as a difference between sine and sag signals are obtained. For each signal and each mother wavelet used, maximum error values are obtained for 1st to 5th levels. Six mother wavelets are used to carry out the analysis. Mother wavelet is identified producing large error in energy values and concludes about the correlation obtained by comparison of the disturbance signal with shifted and dilated mother wavelets. Maximum error values are obtained for fifth level decomposition. It is observed from wavelet packet analysis that the coefficients display the underlying nature of the signal in a different perspective resulting in more information retrieval about the disturbance signals.

Future study could look into utilizing sophisticated machine learning methods like deep learning and reinforcement learning to automatically detect, classify, and forecast power quality issues, building on the knowledge obtained from wavelet packet analysis. Exploring the combination of real-time monitoring systems with intelligent algorithms for proactive power quality management and developing adaptive signal processing techniques for dynamic power grid environments are important areas for further research. Moreover, investigating the possible synergies between wavelet packet analysis and other signal processing techniques like empirical mode decomposition (EMD) or singular spectrum analysis (SSA) might improve the strength and effectiveness of power quality monitoring systems. Exploring new research pathways in the subject should focus on the influence of integrating renewable energy and emerging technologies like electric vehicles and smart grids on power quality dynamics, and developing innovative solutions to tackle associated challenges and this concept can be applied for any other signals to derive useful information and visualization of the deviation in different perspectives.

Detailed breakdown of false positives and false negatives will result in understanding the reliability of this method in practical applications. False positives and false negatives can act as key metrics to evaluate the reliability of voltage sag detection method as discussed below:

• 1. False Positives:

• These occur when the algorithm incorrectly identifies a normal signal as a voltage sag.

• Causes: Noise, transient events (e.g., switching operations), or minor distortions mistaken as sags.

• Impact: Leads to unnecessary interventions, wasting resources and potentially causing disruptions.

• 2. False Negatives:

• These occur when the algorithm fails to detect an actual voltage sag.

• Causes: Shallow sags (small magnitude reduction) or sags masked by noise or other overlapping phenomena.

• Impact: Can result in equipment malfunction or process interruptions, making them more critical than false positives.

These issues can be addressed for wavelet packet analysis-based voltage sag detection using energy as a feature.:

• A confusion matrix can be included, which provides a breakdown of:

  • True Positives: Correctly detected sags.

  • True Negatives: Correctly identified normal signals.

  • False Positives: Misclassified normal signals.

  • False Negatives: Missed sags.

• Metrics such as precision, recall, and F1-score to quantify detection performance can be calculated.

• Fine-tune thresholds can be used in energy feature analysis to minimize false positives and negatives.

Following statistical analysis for performance comparison can be done for adding credibility to results.:

• Standard Deviation: The variability in detection accuracy across multiple trials or datasets can be reported.

• Confidence Intervals: Intervals that indicate the range within which the true accuracy likely falls can be provided.

• Significance Testing: Hypothesis testing like t-tests can be conducted to compare method with traditional techniques. This shows whether performance improvements are statistically significant.

By including these metrics, comparisons can be more robust and substantial.