Information theory and thermodynamic properties for a combined potential model

Abstract

Yukawa potential and Hulthẻn potential are very useful potential models with applications in different areas of physics. The present study examined theoretic measure and thermodynamic properties of energy levels and wave functions for a combination of these two potentials. The effect of screening parameter on Fisher information and Shannon entropy as well as the effect of temperature on the various thermodynamic properties of the combined potentials and its subsets potentials are well studied. The effects of screening parameter on the thermodynamic properties of the combined potentials are also studied. This study shows equivalence of temperature effect on the combined potential and Hulthẻn potential but a different effect on Yukawa potential. Fisher information and the Shannon entropy for both position and momentum spaces as a function of the screening parameter obey Heisenberg principle, satisfy Cramer-Rao inequality and Bialynick-Birula, Mycielski inequality. The Shannon entropy shows the stability of the system for low screening parameter. It is also shown that the strength of Hulthẻn potential outweighed the strength of Yukawa potential in their combination for thermodynamic properties.

Introduction

The exact solutions of both relativistic wave equations and non-relativistic wave equation in quantum mechanics are very useful since wave function and eigenvalues of a system can describe a system completely. The relativistic wave equations (which includes Dirac equation, Klein Gordon equation and Duffin-Kemmer-Petiau equations) are used to analyze spin zero particles, spin half particles and spin one particles. However, non-relativistic wave equation (Schrödinger equation) is used to describe non-relativistic spinless particles. This non-relativistic wave equation has drawn numerous attentions over the years due to its applications in different fields. Authors have examined and reported solutions of the Schrödinger equation with different physical potential terms of interest in various areas of sciences and engineering. Eyube et al.¹, for instance, reported potential parameters of improved scarf II potential energy function. The original scarf II potential model was transformed to its improved form and was used to study spectra of some molecules. Sun et al.², studied exact solutions of an asymmetric double wall potential. These authors examined the effects of the potential parameters on wave function with respect to origin. Barakat³ critically studied anharmonic oscillator potential and found out that his adopted method gives exact results over full range of potential parameters. Das and Arda⁴, reported exact solution of non-relativistic wave equation for a pseudoharmonic potential for N-dimensions. These authors deduced bound states and special cases of the potential. The variation of energy eigenvalue as a function of dimensions were fully studied. Ejere and Ebomwonyi⁵, calculated energy band gap of Cu₂ZnSnS₄ quaternary semiconductor alloy for a Hylleraas potential in the presence of magnetic field. The author reported that the energy band gap of Hylleraas potential depends on the presence of the magnetic field and the confining potential. Dong et al.⁶, reported exact solutions of the sine hyperbolic type potential and analyzed various energy levels of the potential. Falaye et al.⁷, studied shifted Tietz-Wei oscillator. They calculated energy spectrum for shifted Tietz-Wei oscillator and applied their result to some diatomic molecules. In another article, Falaye and his group⁸, studied Schrödinger equation for Tietz-Wei diatomic potential model. They obtained eigensolution techniques and their applications. The study was also applied to Fisher information entropy. Wei et al.⁹, obtained solutions of Dirac equation for a Coulomb potential in 2 + 1 dimensional systems. The authors examined degeneracies occurring in both spin symmetry and pseudospin symmetry. Taseli¹⁰, studied Morse potential in non-relativistic domain and obtained exact solutions for vibrational levels of Morse potential. Sun et al.¹¹, calculated quantum information entropies for an asymmetric trigonometric Rosen–Morse potential and verified BBM relation that proves the correctness of their results. Emeje et al.¹², recently obtained thermodynamic properties of standard Coulombic potential. These authors’ examined thermodynamics and its relationship with the potential parameters. They also examined special cases of their potential function. In ref^13,14. respectively, temperature effect on thermodynamic behaviour has been reported. Their result shows principle to diffusion-controlled phase transformations in Fe-C-X alloys. Khordad and Ghanbari¹⁵, studied thermodynamic properties of potassium molecule for generalized Mobius square potential and reported the highest deviation of their predicted result from experimental result as 0.01139 at 800 K for heat capacity, 0.07486 at 4000 K for entropy, 0.10017 at 6000 K for enthalpy and 0.09112 at 5000 K for Gibbs free energy. Their model performed perfectly for these thermal properties of potassium molecule. Onate et al.¹⁶, reported molar entropy for iodine molecule, silicon carbide, and carbon phosphide. Their results agreed with experimental data. Their model was tested by calculating average absolute deviation from experimental data that varies from molecule to molecule. Habibinejad et al.¹⁷ calculated thermal properties of boron nitride for a q-deformed exponential-type potential. Their model reproduces experimental data with higher deviation compared to other models. Their deviations are recorded as 3.9716% for heat capacity, 2.3567% for Gibbs free energy and 8.5868% for enthalpy. Buchowiecki¹⁸ investigated BBr molecule at high temperature in classical approach. In his study, it was discovered that entropy is least sensitive to the approximations in the ro-vibrational coupling while heat capacity is the most sensitive. Eyube et al.¹⁹ reported molar Gibbs free energy and molar heat capacity at constant pressure of chlorine molecule, carbon monoxide and bromine molecule for improved generalized Pὂschl-Teller (IGPT) oscillator. Their predicted results were compared with experimental data to verify their calculated result. The model shows a good representation of thermodynamic properties of different molecules. Jia et al.²⁰, calculated thermodynamic properties of nitrogen dimer. Their results perfectly agreed with experimental values at all temperatures. Their model executes complete perfection for thermal calculation of different molecules. Nath²¹, obtained exact solutions of the time-dependent Schrödinger equation in presence of time- dependent potential. This author carefully calculated analytical forms of the partition function and the corresponding thermodynamic quantities at high temperature using Euler–Maclaurin summation formula over a finite. Nath and Roy²², study energy level and thermodynamic properties such as vibrational mean energy, vibrational entropy, vibrational free energy and vibrational heat capacity for hydrogen molecule and lithium hydride. The effect of temperature parameter on various thermodynamic properties was examined.

It is on record that thermodynamic properties have many useful applications in the human environment. For example, entropy has applications in dissolution, adsorption, phase transition, fluorescence microscopy, material synthesis as well as protein activity^{23,24,25,26,27,28,29,30,31,32,33}, enthalpy on the other hand is very important in adsorption, thermochemical modeling of biomass conversion systems, plasma gasification, and phase transition. Motivated by the usefulness and applications of theoretic measure and thermodynamic properties from the wave functions and energy levels of the Schrödinger equation, Hulthẻn and Yukawa potentials, this study wants to examine some theoretic measure and thermodynamic properties from energy levels of a combination of Yukawa and Hulthẻn potentials. These two potentials are important potentials that are very useful in science. The combination of the Yukawa potential and Hulthẻn potential is given as

$$V(r)= - \frac{{{\lambda _0}{e^{ - \delta r}}}}{r} - \frac{{{\lambda _1}{e^{ - \delta r}}}}{{1 - {e^{ - \delta r}}}}$$

(1)

where ${\lambda _0}$and ${\lambda _1}$are the strengths of Yukawa potential and Hulthẻn potential respectively. A combination of Hulthẻn potential is studied for Klein-Gordon equation by Ahmadov et al.³⁴ where the relativistic effect of the this combination was analysed. These potentials are active potentials in physics. Yukawa potential can be viewed as a screened Coulomb potential, where the exponential term effectively screens the interaction at larger distances. In nuclear physics, Yukawa potential provides a good approximation for the strong nuclear force that binds protons and neutrons together in the nucleus. It is also used in particle physics and condensed matter physics, to describe interactions mediated by massive particles. It is also used as a tensor term to remove energy degeneracies to attain atomic stability. The Hulthẻn potential³⁵ is another potential model used in quantum mechanics to describe interactions between particles. It is often used as an approximation to Yukawa potential and is particularly useful in the study of certain problems in atomic, molecular, and nuclear physics. Their usefulness and applications lead to their choice in this study. The theoretic measure such as the Fisher information and Shannon entropy are used to determine the localization of a particle in a system. They measure the uncertainty of a system through the probability density.

The parametric Nikiforov-Uvarov method

The energy levels of the potential (1) will be obtained using the parametric Nikiforov-Uvarov method. Following the work of Tezcan and Sever³⁶, the standard/reference equation for the parametric Nikifov-Uvarov method is given by

$$\frac{{{d^2}\psi (y)}}{{d{y^2}}}+\frac{{{w_1} - {w_2}y}}{{y(1 - {w_3}y)}}\frac{{d\psi (y)}}{{dy}}+\frac{{ - {\rho _0}{y^2}+{\rho _1}y - {\rho _2}}}{{{y^2}{{(1 - {w_3}y)}^2}}}\psi (y)=0$$

(2)

According to Tezcan and Sever³⁶, the conditions to obtain the energy equation and its corresponding radial wave function are

$${w_2}n - (2n+1){w_5}+n(n - 1){w_3}+{w_7}+2{w_2}{w_8}+\left( {2n+1} \right)\left( {\sqrt {{w_9}} +{w_3}\sqrt {{w_8}} } \right)+2\sqrt {{w_8}{w_9}} =0$$

(3)

$$\psi (y)={y^{{w_{12}}}}{(1 - {w_3}y)^{ - {w_{12}} - \frac{{{w_{13}}}}{{{w_3}}}}}P_{n}^{{\left( {{w_{10}} - 1,\frac{{{w_{11}}}}{{{w_3}}} - {w_{10}} - 1} \right)}}(2{w_3}y)$$

(4)

The values of the parametric constants in Eqs. (3) and (4) are obtained as follows:

$$\left. \begin{gathered} {w_4}=0.5(1 - {w_1}),{w_5}=0.5({w_2} - 2{w_3}),{w_6}=w_{5}^{2}+{\rho _0},{c_7}=2{w_4}{w_5} - {\rho _1},{w_8}=w_{4}^{2}+{\rho _2}, \hfill \\ {w_9}={w_3}({w_7}+{w_3}{w_8})+{w_6},{w_{10}}=1+2{w_4}+2\sqrt {{w_8}} ,{w_{11}}={w_2} - 2{w_5}+2\left( {\sqrt {{w_9}} +{w_3}\sqrt {{w_8}} } \right), \hfill \\ {w_{12}}={w_4}+\sqrt {{w_8}} ,{w_{13}}={w_5} - \left( {\sqrt {{w_9}} +{w_3}\sqrt {{w_8}} } \right) \hfill \\ \end{gathered} \right\}$$

(5)

Bound state solutions

In this section, the bound state of the interacting potential will be calculated. To obtain the solution of the radial potential for any quantum system, the radial Schrödinger equation for the non-relativistic energy ${E_{n,\ell }}$ is given by^37,38

$$- \frac{{{\hbar ^2}}}{{2\mu }}\frac{{{d^2}{R_{n,\ell }}(r)}}{{d{r^2}}}+\left[ {V(r) - {E_{n,\ell }}+\frac{{{\hbar ^2}}}{{2\mu }}\frac{{\ell (\ell +1)}}{{{r^2}}}} \right]{R_{n,\ell }}(r)=0$$

(6)

where $\hbar$ is the reduced Planck’s constant, $\mu$ is the reduced mass of the particle, $\ell$is the angular quantum number, n is the quantum number and ${R_{n,\ell }}(r)$ is the wave function. The centrifugal term in Eq. (6) can be approximated using the formula^39,40

$$\frac{{\ell (\ell +1)}}{{{r^2}}} \approx \frac{{\ell (\ell +1){\delta ^2}}}{{{{(1 - {e^{ - \delta r}})}^2}}}$$

(7)

Substituting Eq. (1) and Eq. (7) into Eq. (6) and by defining a transformation of the form $y={e^{ - \delta r}},$and inserting it into Eq. (6), we have

$$\frac{{{d^2}{R_{n,\ell }}(y)}}{{d{y^2}}}+\frac{{1(1 - y)}}{{y(1 - y)}}\frac{{d{R_{n,\ell }}(y)}}{{dy}}+\left[ {\frac{{\frac{{2\mu ({E_{n,\ell }} - {V_\lambda })}}{{{\delta ^2}{\hbar ^2}}}{y^2}+\frac{{2\mu ({V_\lambda } - 2{E_{n,\ell }})}}{{{\delta ^2}{\hbar ^2}}}y+\frac{{2\mu {E_{n,\ell }}}}{{{\delta ^2}{\hbar ^2}}} - \ell (\ell +1)}}{{{y^2}{{(1 - y)}^2}}}} \right]{R_{n,\ell }}(y)=0$$

(8)

$${V_\lambda }=\delta {\lambda _0}+{\lambda _1}$$

(9)

Comparing Eq. (8) with Eq. (2), the parameters in Eq. (5) become

$$\left. \begin{gathered} {w_1}={w_2}={w_3}=1,{w_4}=0,{w_5}= - \frac{1}{2},{w_6}=\frac{1}{4}+\frac{{2\mu {V_\lambda } - {E_{n,\ell }}}}{{{\delta ^2}{\hbar ^2}}},{c_7}=\frac{{ - 2\mu {V_\lambda }+2{E_{n,\ell }}}}{{{\delta ^2}{\hbar ^2}}}, \hfill \\ {w_8}=\ell (\ell +1) - \frac{{2\mu {E_{n,\ell }}}}{{{\delta ^2}{\hbar ^2}}},{w_9}=\ell (\ell +1)+\frac{1}{4},{w_{10}}=1+2\sqrt {\ell (\ell +1) - \frac{{2\mu {E_{n,\ell }}}}{{{\delta ^2}{\hbar ^2}}}} , \hfill \\ {w_{11}}=3+2\ell +2\sqrt {\ell (\ell +1) - \frac{{2\mu {E_{n,\ell }}}}{{{\delta ^2}{\hbar ^2}}}} ,{w_{12}}=\sqrt {\ell (\ell +1) - \frac{{2\mu {E_{n,\ell }}}}{{{\delta ^2}{\hbar ^2}}}} ,{w_{13}}= - 1 - \ell - \sqrt {\ell (\ell +1) - \frac{{2\mu {E_{n,\ell }}}}{{{\delta ^2}{\hbar ^2}}}} \hfill \\ \end{gathered} \right\}$$

(10)

Substituting Eq. (10) into Eq. (3) and Eq. (4) respectively, the solution of the radial Schrödinger equation for the potential (1) gives energy levels and wave function respectively as

$${E_{n,\ell }}=\frac{{\ell (\ell +1){\delta ^2}{\hbar ^2}}}{{2\mu }} - \frac{{{\delta ^2}{\hbar ^2}}}{{8\mu }}{\left( {\frac{{\frac{{2\mu (\delta {\lambda _0}+{\lambda _1})}}{{{\delta^2}{\hbar ^2}}} - \ell (\ell +1) - {{(\ell +n+1)}^2}}}{{n+\ell +1}}} \right)^2}$$

(11)

$${R_{n,\ell }}(y)=N{y^{\sqrt {\ell (\ell +1) - \frac{{2\mu {E_{n,\ell }}}}{{{\delta ^2}{\hbar ^2}}}} }}{(1 - y)^{1+\ell }}P_{n}^{{\left( {2\sqrt {\ell (\ell +1) - \frac{{2\mu {E_{n,\ell }}}}{{{\delta ^2}{\hbar ^2}}}} ,2(0.5+\ell )} \right)}}(1 - 2y)$$

(12)

Theoretic measure

The theoretic quantity that determines the uncertainty in a random variable as it measures the content of an information produced^41,42,43,44. To calculate any theoretic quantity, first the normalization constant will be calculated using normalization condition. Thus,

$$\int\limits_{{ - \infty }}^{\infty } {{{\left| {{R_{n,\ell }}(y)} \right|}^2}} dy=1$$

(13)

After some simplifications, the normalization constant is obtained as

$${N^2}=\frac{{(2n)!\delta \eta \Gamma (2\eta +2\ell +2n+3)\Gamma (2\eta +2\ell +n+3)}}{{(2\ell +2n+3)\Gamma (2\ell +n+3)\Gamma (2\eta +n+1)}}$$

(14)

where

$$\eta =\sqrt {\ell (\ell +1) - \frac{{2\mu {E_{n,\ell }}}}{{{\delta ^2}{\hbar ^2}}}}$$

(15)

Substituting Eq. (14) into Eq. (12), the complete wave function for quantum state becomes

$${R_{n,\ell }}(y)=\sqrt {\frac{{(2n)!\delta \eta \Gamma (2\eta +2\ell +2n+3)\Gamma (2\eta +2\ell +n+3)}}{{(2\ell +2n+3)\Gamma (2\ell +n+3)\Gamma (2\eta +n+1)}}} {y^\eta }{(1 - y)^{1+\ell }}P_{n}^{{\left( {2\eta ,2(0.5+\ell )} \right)}}(1 - 2y)$$

(16)

At the ground state, $n=0,$

$${R_{0,\ell }}(y)=\sqrt {\frac{{\delta \eta \Gamma (2\eta +2\ell +3)\Gamma (2\eta +2\ell +3)}}{{(2\ell +3)\Gamma (2\ell +3)\Gamma (2\eta +1)}}} {y^\eta }{(1 - y)^{1+\ell }}P_{n}^{{\left( {2\eta ,2(0.5+\ell )} \right)}}(1 - 2y)$$

(17)

At the first excited state, $n=1,$

$${R_{1,\ell }}(y)=\sqrt {\frac{{2\delta \eta \Gamma (2\eta +2\ell +5)\Gamma (2\eta +2\ell +4)}}{{(2\ell +5)\Gamma (2\ell +4)\Gamma (2\eta +2)}}} {y^\eta }{(1 - y)^{1+\ell }}P_{n}^{{\left( {2\eta ,2(0.5+\ell )} \right)}}(1 - 2y)$$

(18)

At the second excited state, $n=2,$

$${R_{2,\ell }}(y)=\sqrt {\frac{{24\delta \eta \Gamma (2\eta +2\ell +7)\Gamma (2\eta +2\ell +5)}}{{(2\ell +7)\Gamma (2\ell +5)\Gamma (2\eta +3)}}} {y^\eta }{(1 - y)^{1+\ell }}P_{n}^{{\left( {2\eta ,2(0.5+\ell )} \right)}}(1 - 2y)$$

(19)

The momentum space wave function is obtained using Fourier transform. The momentum wave function at the ground state is

$${R_{0,\ell }}(p)=\sqrt {\frac{{2\alpha !\eta \Gamma (2\eta +2\ell +3)\Gamma (2\eta +2\ell +3)}}{{(\ell +2)\Gamma (2\ell +3)\Gamma (2\eta +1)}}} \times \frac{{\Gamma (\eta )\Gamma \left( {\ell +2+\frac{{ip}}{{2\alpha }}} \right)}}{{2\alpha \sqrt {2\pi } \Gamma \left( {\eta +\ell +3+\frac{{ip}}{{2\alpha }}} \right)}}$$

(20)

$${R_{1,\ell }}(p)=\frac{{4\alpha !\eta \Gamma (2\eta +2\ell +3)\Gamma (2\eta +2\ell +2)}}{{(\ell +2)\Gamma (2\ell +2)\Gamma (2\eta +2)}} \times \frac{{\left[ {\alpha \left( {2\ell +\eta +1} \right) - ip\eta } \right]\Gamma (\eta )\Gamma \left( {\ell +2+\frac{{ip}}{{2\alpha }}} \right)}}{{2{\alpha ^2}\sqrt {2\pi } \Gamma \left( {\eta +\ell +3+\frac{{ip}}{{2\alpha }}} \right)}}$$

(21)

Fisher information

Fisher information measures the narrowness and the oscillatory nature of the probability distribution. Fisher information for position space and momentum space respectively are given as^45,46

$$\:I\left(\rho\:\right)=\int\:\frac{{\left[\nabla\:\rho\:\left(\varvec{r}\right)\right]}^{2}}{\rho\:\left(\varvec{r}\right)}d\varvec{r}$$

(22)

$$\:I\left(\gamma\:\right)=\int\:\frac{{\left[\nabla\:\gamma\:\left(\varvec{p}\right)\right]}^{2}}{\gamma\:\left(\varvec{p}\right)}d\varvec{p}$$

(23)

.

Shannon entropy

Shannon entropy determines the uncertainty in a random variable as it measures the content of an information produced. The Shannon entropy for position space and momentum space respectively are written as^45,46

$$\:S\left(\rho\:\right)=-\int\:\rho\:\left(\varvec{r}\right)ln\rho\:\left(\varvec{r}\right)d\varvec{r}$$

(24)

,

$$\:S\left(\gamma\:\right)=-\int\:\gamma\:\left(\varvec{p}\right)ln\gamma\:\left(\varvec{p}\right)d\varvec{p}$$

(25)

.

The probability density is the square of the wave function generally written in the form $\:\rho\:\left(r\right)={\left|R\left(y\right)\right|}^{2}$ and $\:\gamma\:\left(p\right)={\left|R\left(p\right)\right|}^{2}$ for position and momentum spaces.

The pure vibrational partition function and the thermodynamic properties

To calculate a pure vibrational partition from the energy levels, the energy levels in Eq. (11) must be a pure vibrational energy level. For pure vibrational state $\ell =0,$then, Eq. (11) becomes

$${E_n}= - \frac{{{\delta ^2}{\hbar ^2}}}{{8\mu }}{\left( {\frac{{\frac{{2\mu (\delta {\lambda _0}+{\lambda _1})}}{{{\delta ^2}{\hbar ^2}}} - {{(n+1)}^2}}}{{n+1}}} \right)^2}$$

(26)

After obtaining the pure vibrational energy levels of the combined potentials, then, the pure vibrational partition function can be calculated. To calculate the pure vibrational partition function, the energy level in Eq. (26) is re-written as

$${E_n}= - \lambda _{2}^{2}{\left( {\frac{{{\lambda _3} - {{(n+1)}^2}}}{{n+1}}} \right)^2}$$

(27)

where

$$\lambda _{2}^{2}=~\frac{{{\delta ^2}{\hbar ^2}}}{{8\mu }},{\lambda _3}=\frac{{2\mu (\delta {\lambda _0}+{\lambda _1})}}{{{\delta ^2}{\hbar ^2}}}$$

(28)

The partition function from any energy level is given as^{47,48,49,50,51}

$$Z=\mathop \sum \limits_{{n=0}}^{{{n_{\hbox{max} }}}} {e^{\beta {E_n}}}$$

(29)

where $\beta ={({k_\beta }T)^{ - 1}},$${k_\beta }$is the Boltzmann constant, T is the absolute temperature and ${n_{\hbox{max} }}$is the maximum quantum state obtained from the solution of ${{d{E_n}} \mathord{\left/ {\vphantom {{d{E_n}} {dn.}}} \right. \kern-0pt} {dn.}}$ This maximum quantum state is essentially positive and is given as

$${n_{\hbox{max} }}=2+{(\delta \hbar )^{ - 1}}\sqrt {{\delta ^2}{\hbar ^2} - 2\mu (\delta {\lambda _0}+{\lambda _1})}$$

(30)

This study will adopt the lower-order Poisson summation formula⁵² that gives an approximate value of a summation to an accurate value to calculate the vibrational partition function. Thus, Eq. (29) becomes^15,16,17,52

$$Z=\mathop \sum \limits_{{n=0}}^{{{n_{\hbox{max} }}}} {e^{\beta {E_n}}}=\frac{1}{2}\left[ {f(0) - f({n_{\hbox{max} }}+1)} \right]+\int\limits_{0}^{{{n_{\hbox{max} }}+1}} {f(x)dx}$$

(31)

Substituting Eq. (27) into Eq. (31), the partition function turns to be

$$Z=\frac{1}{2}\left[ {{e^{\lambda _{2}^{2}\lambda _{4}^{2}}} - {e^{\lambda _{2}^{2}\lambda _{5}^{5}}}} \right]+\int\limits_{0}^{{{n_{\hbox{max} }}+1}} {{e^{\lambda _{2}^{2}{{\left( {\frac{{{\lambda _3} - {{(x+1)}^2}}}{{x+1}}} \right)}^2}}}dx}$$

(32)

where.

$$\lambda _{4} = \lambda _{3} - 1,\,\lambda _{5} = \frac{{\lambda _{3} - (n_{{\max }} + 2)^{2} }}{{n_{{\max }} + 2}}$$

(33)

Defining ${\lambda _6}={\lambda _2}\left( {\frac{{{\lambda _3} - {{(x+1)}^2}}}{{x+1}}} \right)$ Eq. (32) becomes

$$Z=\frac{1}{2}\left[ {{e^{\lambda _{2}^{2}\lambda _{4}^{2}}} - {e^{\lambda _{2}^{2}\lambda _{5}^{5}}}} \right]+\int\limits_{{{\lambda _7}}}^{{{\lambda _8}}} {\left[ {\frac{{{\lambda _2}{\lambda _6} - \sqrt {{{\left( {2+\lambda {}_{6}\lambda _{2}^{{ - 1}}} \right)}^2}+4\left( {{\lambda _3} - \lambda {}_{6}\lambda _{2}^{{ - 1}} - 1} \right)} }}{{2{\lambda _2}\sqrt {{{\left( {2+\lambda {}_{6}\lambda _{2}^{{ - 1}}} \right)}^2}+4\left( {{\lambda _3} - \lambda {}_{6}\lambda _{2}^{{ - 1}} - 1} \right)} }}} \right]{e^{\lambda _{6}^{2}}}d{\lambda _6}}$$

(34)

where.

$$\lambda _{7} = \lambda _{2} \lambda _{4} ,\,\lambda _{8} = \lambda _{2} \lambda _{5}$$

(35)

Using maple software, Eq. (34) can be evaluated to give the complete pure vibrational partition function as

$$Z=\frac{1}{2}\left[ {{e^{\frac{{\beta {\delta ^2}{\hbar ^2}\lambda _{4}^{2}}}{{8\mu }}}} - {e^{\frac{{\beta {\delta ^2}{\hbar ^2}\lambda _{5}^{2}}}{{8\mu }}}}+\frac{{\sqrt \pi \left\{ {erfii\left( {\frac{{\delta \hbar {\lambda _5}}}{2}\sqrt {\frac{\beta }{{2\mu }}} } \right) - erfi\left( {\frac{{\delta \hbar {\lambda _4}}}{2}\sqrt {\frac{\beta }{{2\mu }}} } \right)} \right\}}}{{\delta \hbar \sqrt {\frac{\beta }{{2\mu }}} }}} \right]$$

(36)

The factor ${e^{ - 4{\lambda _3}\lambda _{4}^{2}}}$ is infinitesimally small and thus, equivalent to zero. With Eq. (36), the various thermodynamic properties can be calculated as follows.

(i). Enthalpy H. The enthalpy of a system can be calculated using the formula

$$H=R{T^2}\frac{{\partial \ln Z}}{{\partial T}}$$

(37)

$$H=R{T^2}\frac{{\partial \ln \left( {\frac{{{e^{\frac{{{\delta ^2}{\hbar ^2}\lambda _{4}^{2}}}{{8\mu {k_\beta }T}}}}}}{2} - \frac{{{e^{\frac{{{\delta ^2}{\hbar ^2}\lambda _{5}^{2}}}{{8\mu {k_\beta }T}}}}}}{2}+\frac{{\sqrt \pi \left\{ {erfii\left( {\frac{{\delta \hbar {\lambda _5}}}{2}\sqrt {\frac{1}{{2\mu {k_\beta }T}}} } \right) - erfi\left( {\frac{{\delta \hbar {\lambda _4}}}{2}\sqrt {\frac{1}{{2\mu {k_\beta }T}}} } \right)} \right\}}}{{\delta \hbar \sqrt {\frac{2}{{{k_\beta }T\mu }}} }}} \right)}}{{\partial T}}$$

(38)

where R is a gas constant with numerical value of 8.314 J mol^− 1 K^− 1.

(ii). Gibbs free energy G. The Gibbs free energy is calculated using the formula

$$G= - RT\ln Z$$

(39)

$$G= - RT\ln \left[ {\frac{{{e^{\frac{{{\delta ^2}{\hbar ^2}\lambda _{4}^{2}}}{{8\mu {k_\beta }T}}}}}}{2} - \frac{{{e^{\frac{{{\delta ^2}{\hbar ^2}\lambda _{5}^{2}}}{{8\mu {k_\beta }T}}}}}}{2}+\frac{{\sqrt \pi \left\{ {erfii\left( {\frac{{\delta \hbar {\lambda _5}}}{2}\sqrt {\frac{1}{{2\mu {k_\beta }T}}} } \right) - erfi\left( {\frac{{\delta \hbar {\lambda _4}}}{2}\sqrt {\frac{1}{{2\mu {k_\beta }T}}} } \right)} \right\}}}{{\delta \hbar \sqrt {\frac{2}{{{k_\beta }T\mu }}} }}} \right]$$

(40)

(iii). Entropy S. Entropy is calculated using the formula

$$S=R\ln Z+RT\frac{{\partial \ln Z}}{{\partial T}}$$

(41)

$$S=\frac{{H - G}}{T}$$

(42)

(iv). Heat capacity at constant pressure ${C_p}$ Heat capacity at constant pressure is calculated using the formula

$${C_p}=\frac{{\partial H}}{{\partial T}}$$

(43)

$${C_p}=\frac{\partial }{{\partial T}}\left( {R{T^2}\frac{{\partial \ln \left( {\frac{{{e^{\frac{{{\delta ^2}{\hbar ^2}\lambda _{4}^{2}}}{{8\mu {k_\beta }T}}}}}}{2} - \frac{{{e^{\frac{{{\delta ^2}{\hbar ^2}\lambda _{5}^{2}}}{{8\mu {k_\beta }T}}}}}}{2}+\frac{{\sqrt \pi \left\{ {erfii\left( {\frac{{\delta \hbar {\lambda _5}}}{2}\sqrt {\frac{1}{{2\mu {k_\beta }T}}} } \right) - erfi\left( {\frac{{\delta \hbar {\lambda _4}}}{2}\sqrt {\frac{1}{{2\mu {k_\beta }T}}} } \right)} \right\}}}{{\delta \hbar \sqrt {\frac{2}{{{k_\beta }T\mu }}} }}} \right)}}{{\partial T}}} \right)$$

(44)

Table 1 Energies of the Hulthẻn-Yukawa potential as a function of screening parameter with $\mu =\hbar =1,$${\lambda _=}=0.5,$and ${\lambda _1}=0.3.$

Table 2 Fisher information for position space and momentum space as a function of the screening parameter at the ground state and first excited state.

Table 3 Shannon Entropy for position space and momentum space as a function of the screening parameter at the ground state and first excited state.

Table 4 Vibrational enthalpy (H) and Gibbs free energy (-G) of a combination of Yukawa and Hulthẻn (YHP), Yukawa (YP), and Hulthẻn (HP) potentials as a function of temperature with $\mu =\hbar =1,$$\alpha =0.05,$${\lambda _0}= - 2$ and ${\lambda _1}= - 3.$

Table 5 Vibrational entropy (S) and Gibbs free energy (cp) of a combination of Yukawa and Hulthẻn (YHP), Yukawa (YP), and Hulthẻn (HP) potentials as a function of temperature with$\mu =\hbar =1,$$\alpha =0.05,$${\lambda _0}= - 2$ and ${\lambda _1}= - 3.$

Table 6 Vibrational enthalpy, Gibbs free energy, entropy and heat capacity of a combination of Yukawa and Hulthẻn (YH) potentials as a function of the screening parameter with$\mu =\hbar =1,$$T=100,$${\lambda _0}= - 2$ and ${\lambda _1}= - 3.$

Discussion

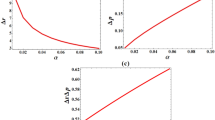
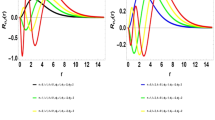
Table 1 presents energy eigenvalues of the interacting potential as a function of screening parameter for the ground state and first excited state with $\ell =0$ and $\ell =1.$ For $\ell =0,$ the energies are completely bounded both at ground and at first excited state. For $\ell =1,$the energies are positive as the screening parameter goes above 0.2. Table 2 shows Fisher information for position space and momentum space as a function of the screening parameter at ground state and first excited state. As the screening parameter increases, Fisher information for position space and momentum space varies inversely with each other. At every value of the screening parameter, Fisher information for position space at the ground state are lesser than their counter path at first excited state but Fisher information for momentum space at ground state are higher than their counter path at first excited state. There is a diffused density distribution in momentum space at ground state and at excited states. This correspond to a localized density distribution in position space at both the ground state and excited state. Thus, there is more uncertainty in momentum space as the screening parameter increases. The results obey Heisenberg principle and satisfied Cramer-Rao inequality for one dimensional case with minimum bound of 4.56264314 at ground state and 4.98409273 at excited. Table 3 shows Shannon entropy for both position space and momentum space as a function of the screening parameter at ground state and first excited state. In both cases, the Shannon entropy in momentum space are bounded at lower screening parameter with entropy squeezing. For negative entropy, a moving particle becomes condensed so that it does not move at all. The system becomes more stable at this moment. It is therefore noted that with increasing $S(\gamma ),$$S(\rho )$ decreases but only to the extent that their sum stays above the stipulated lower bound of the value (1 + ln) to obey and satisfied the Bialynick-Birula, Mycielski inequality for one dimensional case. Table 4 presents enthalpy and Gibbs free energy respectively as a function of temperature for a combination of Yukawa and Hulthẻn potential (YHP), Yukawa potential (YP) and Hulthẻn potential (HP). A rise in temperature leads to a rise in enthalpy for the three potentials but, the enthalpy for YHP and that of HP are closer both at lower temperatures and higher temperatures while enthalpy for YP at different temperatures are very far apart from those of YHP and HP. At the lowest temperature, YHP and HP system respectively has enthalpy less than 1JMol^− 1K⁻¹ but, YP system has higher enthalpy at all temperatures. This could probably be due to the screening parameter that multiplied the strength of the potential. However, it is observed that the enthalpy for the combined potential is less than the enthalpy of the individual subset potentials at both lower and higher temperatures. The change in enthalpy at higher temperatures are higher than the change in enthalpy at lower temperatures for all the potentials. The temperature and Gibbs free energy varies inversely with each other. It is also shown here that Gibbs free energy of YHP and HP are closer compared to the Gibbs free energy of YP. Again, the Gibbs free energy of YP are higher than the Gibbs free energy of YHP and HP at both lower and higher temperatures. Similarly, the Gibbs free energy of the combined potential is less than the Gibbs free energy of individual subset potentials. The Gibbs free energy at all temperatures for all potentials are less than 1JMol^− 1K⁻¹. Table 5 shows entropy and heat capacity respectively for YHP, YP and HP as a function of temperature. An increase in temperature from 200 K to 1200 K decreases the entropy of YHP but increases as the temperature rises above 1200 K. For HP, entropy decreases as temperature rises from 200 K to 1000 K but, increases as temperature rises above 1000 K. However, for YP, entropy increases as temperature rises for all temperature range studied. This behaviour is contrary to the behaviour exhibited by YHP and HP respectively. Except at 200 K, the entropy of YP is higher than the entropy of YHP and HP respectively for the temperature range studied. However, temperature and heat capacity vary inversely with each other for YHP and HP respectively but, for YP, the temperature and the heat capacity vary directly with each other. The entropy for YHP and HP respectively, are very high at every temperature while the entropy for YP remains between 15JMol^− 1K⁻¹ and 15.3JMol^− 1K⁻¹ for the temperature range studied. At every 200 K change in temperature, there is a minute rise in the entropy of the YP while a significant decrease in entropy is observed for the YHP and HP respectively. Table 6 presents the various thermodynamic properties as a function of the screening parameter at low temperature for YHP. The various thermodynamic properties except the heat capacity increases as the screening parameter goes up. However, between the value of 0.15 and 0.25, the entropy deceases but increases as the screening parameter increases from 0.25.

Conclusion

The energy and thermal properties of a combined Yukawa and Hulthẻn potential are fully studied in the absence of the rotational quantum number. The Fisher information and Shannon entropy obeyed and satisfied their condition of reality. The Shannon entropy exhibit squeezing effect and stability at low screening parameter for the momentum space. The thermodynamic properties of the two subset potentials exhibit different features. However, the thermodynamic properties of the Hulthẻn potential and the thermodynamic properties of the mother potential exhibit similar beheviours. For most thermodynamic properties, the result of the mother potential is also less than the result of each of the sunset potentials. This study shows that even though YP and HP look alike, their results are never closer. In our next study, we will examine the vibrational mean energy and vibrational free energy using both Possion summation formula and the use of classical limit at high temperature.