Thermal performance of Falkner Skan model (FSM) for (GOMoS₂)/(C₂H₆O₂-H₂O) 50:50% nanofluid under radiation heating source

Abstract

The hybrid base solvent water (H₂O) and ethylene glycol (C₂H₆O₂) are highly use in industrial applications due to excellent solvability. Addition of hybrid nanoparticles (GO-MoS₂) augments the thermal conductivity of these fluids which ultimately make them very productive. Hence, the current study aims to develop and investigate the novel hybrid nanofluid model (GO-MoS₂)/(C₂H₆O₂-H₂O) through MRW (moving riga wedge) and SRW (static riga wedge) cases. The traditional Falkner Skan Model (FSM) is modified using the novel effects of solar radiations, internal heating source and fixed magnets which is associated to the concept of Riga wedge. Further, the improved thermal-physical characteristics of hybrid nanofluids will use to enhance the thermal productivity. A mathematical model is developed for the flow situation of (GO-MoS₂)/(C₂H₆O₂-H₂O) and treated numerically. The results furnished through graphical way and comprehensive discussion provided. It is examined that the movement of (GO-MoS₂)/(C₂H₆O₂-H₂O) reduced for MRW and observed the rapid velocity near the surface. The heat generating source and solar radiations number enhanced the performance of (GO-MoS₂)/(C₂H₆O₂-H₂O) and better predicted ranges for these parameters are observed from $\:Q=\text{0.1,0.2,0.3,0.4}$ and $\:Rd=\text{1.0,2.0,3.0,4.0}$. Moreover, the boundary layer region becomes thin for heating source and it increased for stronger solar radiation effects. The nanoparticle amount of GO and MoS₂ enhanced the model utilization while higher magnetic number and MRW number $\:\lambda\:$ controlled the thermal boundary layer. The results for the model dynamics are noticed dominant for MRW case as compared to SRW case.

Introduction

Heat transport phenomena in fluids are a significant research motive in numerous engineering systems and industries. These include, but are not limited to, heating and cooling of buildings, chemical engineering, applied and mechanical engineering, etc. Although conventional fluids (water, EG, kerosene oil, etc.) have excellent solvability characteristics but low thermal conductivity, due to which these fluids have a weak heat transfer rate. Therefore, the heat transfer performance of common fluids can be enhanced by dispersing nanometer-sized particles. The resultant fluid, commonly known as nanofluid, has better heat transfer possibilities than common fluids. Researchers from different fields put their efforts into the formulation of efficient nanofluid models from different physical aspects.

Nanofluid is simply a uniform mixture of one type of nanoparticle and the base fluid. In 2021, Madhukesh et al.¹ conducted a comprehensive study on hybrid nanofluid by considering AA7072 and AA7075 alloys. The authors formulated the problem of stretching surfaces under the innovative effects of resistive heating and non-fourier heat flux. The outcomes revealed that aluminum alloys-based hybrid nanofluids have good heat transfer rate than water. Animasaun et al.² were inspired by the joint thermal conductivity of ternary nanoparticles and investigated the effects of an unsteady parameter on the model dynamics through a convective surface. They observed that when the surface angle approaches to $\:{90}^{o}$, the unsteady acceleration decreases while convective acceleration enhances. The thermal radiative aspects of Casson nanofluid in the presence of internal heat absorption/generation sources have been discussed by Saeed et al.³. It was concluded that the energy transport enhanced with an increase in the thermal radiative source and the boundary layer thickness decreased for larger values of the rotating parameter.

The static or moving wedge conditions extensively alter the motion and thermal behaviour of the fluids. Hence, Mahanthesh et al.⁴ extended the work for moving case for heat transfer enhancement. The authors considered ZnO-EG as working fluid and performed sensitivity analysis if the model. The significant effects of wedge movement are examined on the velocity and heat transport rate. Another study regarding the Falkner Skan flow under the impacts of freezing temperature and molecular diameter effects were examine in⁵. Vahedi et al.⁶ focused on the characteristics of wedge flow for electrically conducted Cu/water. They found that the thermal and hydrodynamic boundary layers depreciated for stronger magnetic number and smaller wedge angle. Among the nanomaterials, ferromagnetic material has their own significance due to their structure and magnetic properties. Therefore, Gowda et al.⁷ explored the impacts of magnetic dipoles on the functionality of nanofluid comprising ferromagnetic nanoparticles. Further, the effects of Stefan heating also included in the model and handled the nanofluid model numerically. It was concluded that convective thermal condition has tendency to enhance the heat transfer rate in nanofluid.

Use of MHD, heating source and radiations are of larger interest in various disciplines particularly in thermal engineering. Implications of these phenomenon contribute effectively in transport mechanism of hybrid nanofluids. Kumar et al.⁸ used radiations effects for thermal applications of hybrid nanofluids. The analysis carried for radiated wedge and examined thermal enhancement due to strengthening the radiation source. The obtained data compared with previous once and validated the study. Sajjan et al.⁹ and Raju et al.¹⁰ extended the concept of nonlinear radiations, nanomaterials shape, and Darcy effects for boundary layer and permeable channel, respectively. The hybrid nanofluids are taken under the effects of shapes and varying thermal conductivities. They found that role of nonlinear radiations is crucial for thermal applications while Darcy phenomena opposes the hybrid nanofluid motion. The study of quadratic and linear convection on the transport mechanism of multiple nanoparticles based model have been discussed in¹¹. The efficiency of hybrid nanofluid is observed high than that conventional nanofluids and suggested that modified nanofluids are reliable for thermal applications.

Recently, Goud et al.¹² and Mahmood et al.¹³ reported the numerical analysis of Newtonian and non-Newtonian nanofluid models under varying physical conditions. The results validated with open literature and examined that (Al₂O₃-Cu)/H₂O hybrid nanofluid has excellent thermal characteristics. Insertion of unsteady effects in the nanofluid modelling highly affect the model performance. Keeping in mind the significance of unsteady phenomena, Alghamdi et al.¹⁴, Fwaz et al.¹⁵, Khadija et al.¹⁶ and Adnan et al.¹⁷ investigated different nanoliquid problems for heat transfer applications. The authors accommodated important physical phenomena and found excellent outcomes for nanofluids. They recommended that nanofluids have better momentum and heat transfer abilities which are important form industrial applications. The CNTs termed as carbon nanotubes obtained much interest of the researchers in the last few decades. This is heat transfer nanomaterial having fascinating structure. Different studies (see Refs^18,19,20,21). on the performance of CNTs based fluid dynamics models have been discussed by various experts in the field and agreed that the CNTs have excellent heat transmission ability under laminar flow regimes.

Reddy et al.²² investigated hydromagnetic based (Ag-CuO)/H₂O model and performed sensitivity analysis under thermal radiation impacts. The problem is associated to the convective surface and found that the efficiency of hybrid nanofluid enhanced as the convection effects increases. Shamshuddin et al.^{23,24] and [25}, provided deep analysis of nanofluids and checked the thermal progress through different methodologies. Impacts of ferromagnetic, MHD and resistive heating are observed. The studies explored that nanofluids are innovative class which have considerable thermal efficiency compared to simple fluids.

The study of hybrid and ternary nanofluids for heat transfer applications cannot be ignored because these fluids providing an excellent enhanced properties like thermal conductivity, heat capacity, electrical conductivity and dynamic viscosity etc. In recent years, researchers turned towards thermal investigation in advanced nanofluids by engaging variety of nanomaterials. A study for hybrid nanofluid under solar thermal radiative effects has been reported by Waqas et al.²⁶ and Ferdows et al.²⁷ performed numerical simulation for heat and mass transport in nanofluids using single and two phase models. The authors used Al₂O₃, Cu and GO nanoparticles²⁸ to enhance the characteristics of conventional fluids. The studies revealed that velocity enhanced with increasing Deborah effects while higher Schmidt number values encouraged the mass transfer. Further, the authors suggested that hybrid nanoliquids have enhanced heat and mass transport rate and recommended better for practical applications. Further, comprehensive literature and key findings of the studies are given in Table 1.

Table 1 Literature review for boundary layer flows under different physical circumstances.

In the view of above reported studies, it is noticed that although numerous attempts have been made for the thermal analysis in common, nano and hybrid nanofluids through wedge under different physical circumstances. However, there are still some openings for mathematical modelling and analysis of heat transfer for advanced nanoliquids through Riga wedge. The novelty of the hybrid nanofluid problem will enhance by including the influences of fixed magnets due to Riga case, solar radiations, nanoparticle’s concentrations and internal heating species. Thus, the key objectives of the research are:

• To introduce the concept of Riga wedge and how it alter the flow dynamics and heat transfer rate.

• To develop the heat transfer problem for hybrid nanofluid using effective characteristics with special emphasize on moving and static wedge cases.

• To investigate the influences of solar radiations and internal heating source on the overall performance of the model.

• To estimate the comparative results for fluid movement and thermal transport through static and moving wedges.

Model development

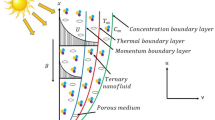
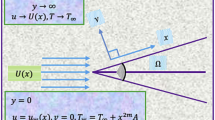
In this study, consider Falkner Skan flow (FSF) of ternary nanofluid under steady state condition. To enhance the functionality of water, the hybrid nanoparticles (Go-MoS₂) are used with uniform dispersion characteristics. The base liquid is taken as water due to excellent solvability. The coordinates are designated in such a way that the $\:x$-component is in the direction of wedge. The wedge surface is made by alternating arrangements of magnets due to which is called Riga wedge. The temperature near the working surface and at ambient locations are taken as $\:{T}_{w}$ and $\:{T}_{\infty\:}$, respectively. Further, the accelerating wedge and free stream velocities are $\:{u}_{w}={x}^{m}{U}_{w}$ and $\:{u}_{e}={x}^{m}{U}_{\infty\:}$ ($\:0.0\le\:m\le\:1$ and $\:{U}_{w},\:{U}_{\infty\:}$). The hybrid nanofluid components are demonstrated in Fig. 1. Further restrictions for the model formulation are as under:

• The functional ternary fluid possesses incompressibitly characteristics and there is no chemical species present therein.

• The hybrid nanoparticles (Go-MoS₂) and primary solvent are thermally in equilibrium.

Fig. 1

The hybrid nanofluid (GO-MoS₂)/(C₂H₆O₂-H₂O) components.

The primary physical laws which possesses the BLF of ternary nanoliquid through a Riga wedge are described in the subsequent mathematical expressions^34,35.

$$\:{u}_{x}+{v}_{y}=0$$

(1)

$$\:{u}_{x}u+{u}_{y}v={u}_{e}{u}_{e}^{{\prime\:}}+\frac{{\mu\:}_{hybridnano}}{{\rho\:}_{hybridnano}}{u}_{yy}+\frac{{M}_{o}{J}_{o}\pi\:}{8{\rho\:}_{hybridnano}}{e}^{(-\frac{\pi\:}{a}y)}$$

(2)

$$\:{T}_{x}u+{T}_{y}v=\frac{{k}_{hybridnano}}{{\left(\rho\:{c}_{p}\right)}_{hybridnano}}{T}_{yy}+\frac{16{\sigma\:}^{*}{T}_{\infty\:}^{3}}{3{k}^{*}{\left(\rho\:{c}_{p}\right)}_{hybridnano}}{T}_{yy}+\frac{Q}{{\left(\rho\:{c}_{p}\right)}_{hybridnano}}({T}_{w}-{T}_{\infty\:})$$

(3)

The fluid flow is subject to the subsequent conditions at the RWS (Riga wedge surface) and at free stream positions. Further the similarity transformative functions for the present investigation are described in Eq. (5). The term $\:\chi\:$ represents the stream function and the velocity components are obtained using $\:u={\chi\:}_{y}$ and $\:v=-{\chi\:}_{x}$ which satisfy the law of conservation of mass.

$$\:u={u}_{w}{\downarrow\:}_{y=0},\:T={T}_{w}{\downarrow\:}_{y=0},\:v=0,\:u\to\:{u}_{e}{\downarrow\:}_{y\to\:\infty\:},\:T\to\:{T}_{\infty\:}{\downarrow\:}_{y\to\:\infty\:}$$

(4)

$$\:\eta\:={\left(\frac{{u}_{e}\left(x\right)\left(m+1\right)}{2x{\nu\:}_{f}}\right)}^{0.5}y,\:\beta\:\left(\eta\:\right)=\frac{T-{T}_{\infty\:}}{{T}_{w}-{T}_{\infty\:}},\:\chi\:={\left(\frac{2x{u}_{e}\left(x\right){\nu\:}_{f}}{m+1}\right)}^{0.5}F\left(\eta\:\right)$$

(5)

The formulas for significant factors for the present ternary nanofluid model are given in Eqs. (6, 7), respectively.

$$\:{C}_{skinfric}=\frac{{\mu\:}_{hybridnano}}{{u}_{e}^{2}{\rho\:}_{f}}{u}_{y}{\downarrow\:}_{y=0}$$

(6)

$$\:Nu=-x\left[\frac{{k}_{hybridnano}+{q}_{y}}{{k}_{f}\left({T}_{w}-{T}_{\infty\:}\right)}\right]{T}_{y}{\downarrow\:}_{y=0}$$

(7)

Further, the effective formulas for ternary nanofluid properties like electrical conductivity, thermal conductivity, heat capacity and dynamic viscosity are expressed in Table 2 (see Refs^36,37,38). where, $\:\:{\widehat{\mathfrak{H}}}_{2}={\varphi\:}_{2}$and $\:{\widehat{\mathfrak{H}}}_{1}={\varphi\:}_{1}$ are the nanoparticles concentrations. Moreover, the values of nanoparticles and their response on the ternary nanofluid characteristics³⁹ are furnished in Figs. 2 and 3, respectively.

Table 2 Influential characteristics of ternary nanofluids for the current designed model.

Fig. 2

The nanoparticles and hybrid base fluid properties.

Fig. 3

The variations in nano and hybrid nanofluids with increasing nanoparticles amount.

Now, by practicing the similarity rules and the characteristics of hybrid nanofluids, the following nonlinear mathematical model is obtained which possesses the laminar steady flow through a Riga wedge under solar radiations and heating source effects. Further, the reduced form of the flow conditions are given in Eq. (10).

$$\:\frac{\frac{{\mu\:}_{hybridnano}}{{\mu\:}_{pf}}}{\frac{{\rho\:}_{hybridnano}}{{\rho\:}_{pf}}}{F}^{{\prime\:}{\prime\:}{\prime\:}}+F{F}^{{\prime\:}{\prime\:}}+\frac{2m}{1+m}\left[1-{F}^{{\prime\:}2}\right]+\frac{{\sigma\:}_{hybridnano}}{{\sigma\:}_{pf}}M{e}^{-\alpha\:\eta\:}=0$$

(8)

$$\:\left(\frac{{k}_{hybridnano}}{{k}_{pf}}+\frac{4}{3}Rd\right){\beta\:}^{{\prime\:}{\prime\:}}+\frac{{\text{Pr}\left(\rho\:{c}_{p}\right)}_{hybridnano}}{{\left(\rho\:{c}_{p}\right)}_{pf}}\left[F{\beta\:}^{{\prime\:}}+Q\beta\:\right]=0$$

(9)

$$\:F\left(0\right)=0,\:{F}^{{\prime\:}}\left(0\right)=\lambda\:,\:{F}^{{\prime\:}}\left(\infty\:\right)=1,\:\beta\:\left(0\right)=1,\:\beta\:\left(\infty\:\right)=0$$

(10)

The Eqs. (11–12) are obtained with appropriate differentiation and effective properties of nanofluids in Eqs. (6–7).

$$\:{\left(\frac{2R{e}_{x}}{1+m}\right)}^{1/2}{C}_{skinfric}=\frac{{\mu\:}_{hybridnano}}{{\mu\:}_{pf}}F{\prime\:}{\prime\:}\left(0\right)$$

(11)

$$\:{\left(\frac{2}{\left(1+m\right)R{e}_{x}}\right)}^{1/2}Nu=-\left(\frac{{k}_{hybridnano}}{{k}_{pf}}+Rd\right)\beta\:{\prime\:}\left(0\right)$$

(12)

The physical constraints embedded in the hybrid nanofluid model are wedge moving parameter ($\:\lambda\:=\frac{{U}_{w}}{{U}_{\infty\:}}$), Prandtl number ($\:Pr=\frac{{\mu\:}_{pf}{\left({c}_{p}\right)}_{pf}}{{k}_{pf}}$), radiation number ($\:Rd=\frac{16{\sigma\:}^{*}{T}_{\infty\:}^{3}}{3{k}_{pf}{k}^{*}}$).

Mathematical analysis

Mathematical treatment of the model performed via numerical scheme usually termed as RK⁴⁰ scheme. After reducing the higher model problem into IVP⁴¹, the propose scheme implemented successfully according to their standard procedure and executed the results for velocity and temperature fields for MRW (moving riga wedge) and SRW (static riga wedge) cases. The optimum values of $\:\eta\:$ is considered $\:5$ which represents the upper boundary limit. The numerical results for the velocity $\:F{\prime\:}\left(\eta\:\right)$ excellently fulfill the boundary conditions $\:{F}^{{\prime\:}}\left(0\right)=\lambda\:=0.3$ (MRW), $\:{F}^{{\prime\:}}\left(0\right)=\lambda\:=0.0$ (SRW), and upper boundary $\:{F}^{{\prime\:}}\left(\infty\:\right)={F}^{{\prime\:}}\left(5\right)=1.0$. Similarly, the temperature solutions for MRW and SRW showing good agreement with the boundary conditions. In both the cases, the temperature is examined as $\:\beta\:\left(0\right)=1.0$ (at the surface) and asymptotic behaviour of the temperature starts beyond $\:\eta\:=3.3$ which tells about the validity of the temperature condition $\:\beta\:\left(\infty\:\right)=0$. These results are given in Table 3.

Stage I: At the first stage, the transformations associated to the problem are expressed as the following form.

$$\:{\models\:}_{1}=F,\:{\models\:}_{2}={F}^{{\prime\:}},\:{\models\:}_{3}={F}^{{\prime\:}{\prime\:}},\:{\models\:{\prime\:}}_{3}=F{\prime\:}{\prime\:}{\prime\:}$$

(13)

$$\:{\models\:}_{4}=\beta\:,\:{\models\:}_{5}={\beta\:}^{{\prime\:}},\:{\models\:{\prime\:}}_{5}=\beta\:{\prime\:}{\prime\:}$$

(14)

Stage II: Arrange the obtained higher order problem into simplified form for both temperature and velocity.

$$\:{F}^{{\prime\:}{\prime\:}{\prime\:}}=\frac{{\mu\:}_{hybridnano}}{{\mu\:}_{pf}}\frac{{\rho\:}_{pf}}{{\rho\:}_{hybridnano}}\left[-F{F}^{{\prime\:}{\prime\:}}-\frac{2m}{1+m}\left[1-{F}^{{\prime\:}2}\right]-\frac{{\sigma\:}_{hybridnano}}{{\sigma\:}_{pf}}M{e}^{-\alpha\:\eta\:}\right]$$

(15)

$$\:{\beta\:}^{{\prime\:}{\prime\:}}=-{\left(\frac{{k}_{hybridnano}}{{k}_{pf}}+\frac{4}{3}Rd\right)}^{-1}\:\left[\frac{{{Pr}\left(\rho\:{c}_{p}\right)}_{hybridnano}}{{\left(\rho\:{c}_{p}\right)}_{pf}}\left[F{\beta\:}^{{\prime\:}}+Q\beta\:\right]\right]$$

(16)

Stage III: At this stage, the Eqs. (15–16) will transform in to the first order form using the associated functions from Eqs. (13–14).

$$\:{\models\:{\prime\:}}_{3}=\frac{{\mu\:}_{hybridnano}}{{\mu\:}_{pf}}\frac{{\rho\:}_{pf}}{{\rho\:}_{hybridnano}}\left[-{\models\:}_{1}{\models\:}_{3}-\frac{2m}{1+m}\left[1-{\left({\models\:}_{2}\right)}^{2}\right]-\frac{{\sigma\:}_{hybridnano}}{{\sigma\:}_{pf}}M{e}^{-\alpha\:\eta\:}\right]$$

(17)

$$\:{\models\:{\prime\:}}_{5}=-{\left(\frac{{k}_{hybridnano}}{{k}_{pf}}+\frac{4}{3}Rd\right)}^{-1}\:\left[\frac{{{Pr}\left(\rho\:{c}_{p}\right)}_{hybridnano}}{{\left(\rho\:{c}_{p}\right)}_{pf}}\left[{\models\:}_{1}{\models\:}_{5}+Q{\models\:}_{4}\right]\right]$$

(18)

Stage IV: The associated conditions and the transformed problem is then operated through coding in MATHEMATICA 13.0 and achieved the solutions and results due to varying parameters.

Table 3 Solutions of hybrid nanofluid model for the velocity and temperature for MRW and SRW cases.

The present extended model is compared (Table 4) with the outcomes of Watanbe⁴² under $\:Rd=0,\:\varphi\:=0$ and $\:\lambda\:=\frac{2m}{m+1}$. The output computed for skin friction and observed that the present results are well aligned with previous once and proves the reliability.

Table 4 Validation of the problem results.

Results interpretation

A detailed investigation of the velocity, temperature, shear drag and Nusselt number for hybrid nanofluid under varying ranges of the physical parameters are demonstrated in this section. The results are interpreted for MRW and SRW cases for both the temperature and velocity fields.

Figure 4a-d presenting the velocity $\:F{\prime\:}$ of hybrid nanofluid for multiple ranges of $\:\lambda\:$, $\:M$, $\:{\varphi\:}_{1}$ and $\:{\varphi\:}_{2}$, respectively. The results reveal that the nanoliquid movement reduces for variable movement of the wedge ($\:\lambda\:$) and higher magnetic number values $\:M$. However, for accelerating RW, the particles movement is rapid than that of SRW. Physically, the fluid particles at the surface gain extra momentum due to the wedge movement which results increase in the velocity field. At the free stream, the fluid velocity is observed stable and no fluctuations are examined. This behaviour of the velocity represents that the imposed physical condition fulfilled. The next subset of Fig. 4c-d indicates the velocity variations when the nanoparticles amount augmented form $\:0.01$ to $\:0.04$. Higher dispersion of nanoparticles (GO-MoS₂) provided that the movement depreciates. Physically, high number of nanoparticles occupy space between the molecules and enhance the fluid’s density. As a consequence the intermolecular forces disturbed and bind the fluid particles tightly and the fluid motions drops. This means lessen the nanoparticles concentration lead to quite slow decrease in the movement.

Fig. 4

The velocity distribution of hybrid nanofluid for (a) $\:\lambda\:$, (b) $\:M$, (c) $\:{\varphi\:}_{1}$ and (d) $\:{\varphi\:}_{2}$.

The physical effects like heating source present in the fluid, solar thermal radiations, amount of nanoparticles, magnetic and moving surface aspects highly impact the temperature of hybrid nanofluids. Hence, the Fig. 5a-f designates to analyze the temperature performance of hybrid nanofluid under aforementioned physical phenomena. The heating source and solar radiations effectively enhanced the performance of (GO-MoS₂)/(C₂H₆O₂-H₂O) in the range of $\:\text{0.1,0.2,0.3,0.4}$ and $\:\text{1.0,2.0,3.0,4.0}$, respectively. However, the fluid under stronger radiation effects is examined more efficient than heating source. Physically, the particles become more radiated due to externally applied thermal radiations which boosts the model performance. The surface layer particles absorb heat and transfer it to the very next later which lead to augmentation in overall temperature performance. Further, the TBL over the surface is observed from $\:\eta\:=0.0$ to $\:\eta\:\approx\:2.0$ for heating source variations and $\:\eta\:=0.0$ to $\:\eta\:\approx\:3.5$ for radiations effects. This shows that for higher heating source number, the TBL reduced and the temperature asymptotically vanishes towards the ambient portion over the surface. The temperature approaches to $\:1$ at $\:\eta\:=0.0$.

Figure 5c-d and e-f highlighting the temperature performance for $\:{\varphi\:}_{1},\:{\varphi\:}_{2},\:\lambda\:$ and $\:M$, respectively. It is observable that when the nanoparticles enhanced from $\:0.01$ to $\:0.04$, the temperature augmented. Physically, the thermal conductivity of the hybrid nanoliquid enhanced due to increasing number of nanoparticles and thermal conductivity of these particles. As a consequence, the whole thermal conductivity of the hybrid fluidic system enhanced due to which the temperature increase significantly. On the contrary, the moving parameter $\:\lambda\:$ and magnetic number $\:M$ controlled the temperature as mentioned in Fig. 5e-f. Hence, these two factors are observed excellent for the temperature reduction.

Fig. 5

The temperature distributions of hybrid nanoliquid for (a) $\:Q$, (b) $\:Rd$, (c) $\:{\varphi\:}_{1}$, (d) $\:{\varphi\:}_{2}$, (e) $\:\lambda\:$, and (f) $\:M$.

Figure 6a-b presenting the estimations for shear drag while Fig. 6c demonstrates the changes for heat transfer rate under augmented radiation number. It is obvious that the shear drag at the surface increases by strengthening the magnetic field effects. Physically, sophisticated magnetic field effects produces stronger Lorentz forces in the hybrid fluidic system which directly reduce the fluid movement. Due to this reason, the shear drag at the surface enhanced. Further, the skin friction declines for larger moving wedge number from $\:0.0$ to $\:1.5$. Physically, when the wedge movement increases the particles stuck at the surface get momentum and moves freely. This phenomena lead to drops in the shear drag for rapid RWG inside the fluid system. In the particular case, the heat transport rate reduces when radiation effects enhanced and these influences are demonstrated in Fig. 6c for simple, nano and hybrid nanofluidic systems.

The streamlines and isotherms variations for different default parametric values are furnished in Fig. 7a-h. The concentration of streamlines increases for stronger magnetic effects. When the strength of magnetic field increases, it shows resistance in the flow of nanofluid. Hence, the intensity of streamlines enhances towards the surface. Similarly, the heatlines are decorated for $\:Rd=0.3$ and $\:Rd=3.0$ with other default parameters values. The heatlines intensifies as the effects of radiation number changes from 0.3 to 3.0. Physically, the higher intensification of this phenomena is associated to the external energy provided by the radiations to the fluidic system. As a consequence, the heatlines increases.

Fig. 6

The SF and Nu behaviour for higher parametric values.

Fig. 7

The streamlines and heat lines trends for parametric values.

Conclusions

The performance of hybrid nanomaterial (GO-MoS₂) suspended in hybrid base solvent (C₂H₆O₂-H₂O) is conducted in this research. The problem formulation was done via hybrid models for nanofluids and appropriate mathematical rules. The important physical aspects on the hybrid nanofluids for MRW and SRW are deeply discussed and concluded that:

• The hybrid functional liquid (GO-MoS₂)/(C₂H₆O₂-H₂O) achieved optimum velocity for MRW case while it reaches to $\:1$ towards free stream.

• The volume concentration of MoS₂ in the range of $\:0.01$ to $\:0.04$ highly resists the movement due to higher density and the intermolecular forces.

• The heat generating source and solar radiations number enhanced the performance of (GO-MoS₂)/(C₂H₆O₂-H₂O) and better predicted ranges for these parameters are observed from $\:Q=\text{0.1,0.2,0.3,0.4}$ and $\:Rd=\text{1.0,2.0,3.0,4.0}$.

• The thin thermal boundary layer is examined for higher heat generating effects while it enlarges for the solar radiation effects.

• The increase in the amount of GO and MoS₂ nanoparticles from $\:0.01$ to $\:0.04$, result the thermal augmentation of (GO-MoS₂)/(C₂H₆O₂-H₂O).

• The higher magnetic effects and MRW number $\:\lambda\:$ controlled the thermal transport and thermal boundary layer.