Introduction

Understanding the phenology of species — the study of periodic events in biological life cycles shaped by seasonal and annual climate fluctuations — is essential across fields like agriculture (e.g., crop yield forecasting1), nature conservation (e.g., assessing species responses to global changes2), and public health (e.g., managing allergens and emerging infectious diseases carried by arthropod vectors3). Ecologists have therefore developed and tested several modelling approaches, i.e. the mechanistic and correlative approaches, to infer the phenology of species and how it varies over space and time. The mechanistic approach employs laboratory or field observations about the influence of biotic or abiotic factors on the targeted life history traits (e.g. the effect of temperature on a juvenile form development rate) to parametrise mathematical models inferring the life cycle of the species of interest (e.g4,5,6,7). Although generally accurate, mechanistic models often require estimating multiple parameters and are therefore constrained by the availability of ecological observations in the scientific literature7,8. As an alternative, ecologists frequently turn to correlative models, which establish statistical relationships between a response variable (e.g., species abundance or presence-absence) and a set of mostly abiotic covariates9,10.

Despite the utility of correlative models, their outputs are subject to various sources of variability, such as sampling location bias and model tuning11,12,13,14. The choice of the modelling method, in addition, has proven influential, as different models applied to the same dataset can yield distinct results15,16,17. This inter-model variability has prompted the use of ensemble modelling techniques, also called consensus modelling, which involves fitting multiple independent algorithms on the same input data and then aggregating the individual models’ outputs to produce a final prediction, reducing the risk of overfitting and extrapolation issues17. While simple aggregation methods like averages and weighted averages have been traditionally used17,18, more advanced ensemble techniques, such as stacking or stacked generalisation19, have recently demonstrated superior performance20,21,22,23. In stacked ensemble modelling, multiple base models’ predictions serve as inputs for a meta-learner, which learns from these predictions and generates the ultimate prediction by combining information from all the base models.

Leveraging the strengths of spatio-temporal stacked modeling in capturing complex dynamic ecological processes, we applied this approach to infer the weekly egg abundance of the invasive mosquito Aedes albopictus in Southern Europe from 2010 to 2022. The ‘Asian tiger mosquito’ (Aedes (Stegomyia) albopictus), with its rapid expansion24,25 and critical role as a vector for outbreaks of vector-borne diseases26,27,28,29, presents a compelling case study for evaluating the model’s capability to accurately forecast spatio-temporal patterns of egg-laying activity and abundance, enabling targeted public health interventions.

Local public health authorities have established surveillance and monitoring initiatives to better understand the distribution, abundance, and seasonality of Ae. albopictus, supporting the development of proactive strategies for population and disease control. However, these efforts require significant economic and personnel resources. As a result, the implementation of passive surveillance systems — such as modeling techniques that reliably predict vector abundance and seasonal patterns — has been advocated to provide invaluable support to local public health agencies30. Although correlative models are commonly used to infer the geographic distribution of Ae. albopictus31, this study is, to our knowledge, the first to apply a stacked spatio-temporal model for this species, generating weekly maps of egg abundance that highlight the length and peak of the oviposition activity. The model enables the inference of seasonal egg abundance even in areas lacking active surveillance, providing crucial support for resource allocation in monitoring and surveillance efforts. These results lay a robust methodological foundation for forecasting the spatio-temporal abundance of Ae. albopictus and offer a flexible framework adaptable to specific public health needs associated with this species.

Methods

Biological observations and area of interest

We used Ae. albopictus’ egg counts obtained from monitoring activities conducted with ovitraps as the response variable in our models. Ovitraps are cheap and efficient monitoring tools consisting of a dark container filled with water and a substrate, usually a masonite stick, where container-breeding mosquitoes can lay their eggs. The egg-laying substrate is collected on a weekly or biweekly basis, depending on the local protocol adopted by the stakeholders, and the number of eggs laid on the egg-laying substrate counted.

We used the VectAbundance v0.15 database, which contains ovitrap observations from four European countries (Albania, France, Italy, and Switzerland) with active monitoring and surveillance programs for Ae. albopictus between 2010 and 202232. In VectAbundance, individual ovitrap observations were processed such that, if the monitoring period exceeded one week, egg counts were randomly distributed across the active weeks. Additionally, to account for microclimatic variability and sampling differences, the data were aggregated using the median within a 9 × 9 km grid (see Da Re et al.32 for a detailed description of the sampling protocols and data preprocessing).

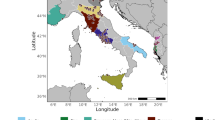
The observations available in VectAbundance v0.15 are located in a geographical extent spanning from 6° to 21° E and from 36° to 47° N (Fig. 1). According to Cervellini et al.33, this area is characterised by three main biogeographical regions, namely Alpine, Continental, and Mediterranean (Fig. 1). Since the location of the ovitraps well represents these three biogeographical regions, we decided to limit the geographical area of extrapolation of the model to the abovementioned geographical extent and these biogeographical regions only.

Fig. 1
figure 1

Biogeographical regions of Europe according to Cervellini et al.33 and the location (green dots) of the egg observations available in VectAbundance v0.15. The black lines represent the borders of the administrative areas of the countries of interest at the NUTS2 level. The map was created using R v4.334.

Full size image

Modelling

Stacked generalisation is a technique that combines predictions from multiple individual models, known as base learners or base models, to make a final prediction19,20,23,35. In stacked generalisation, the outputs of individual base learners serve as inputs to a meta-learner, which is another model that learns from the predictions of the individual models. The meta-learner then generates the final prediction by combining and synthesising the information from the individual models (Fig. 2a). Stacking has the potential to improve the accuracy and robustness of ecological models by leveraging the strengths of different models and effectively capturing complex relationships in the data20. However, it is important to remark that while stacking can reduce model variance and improve predictions, it comes with trade-offs as it increases model complexity, reduces interpretability, and augments the computational time compared to individual models36.

Fig. 2
figure 2

(a) A conceptual representation of the stacking approach; (b) Framework of the modelling approach presented in the study.

Full size image

Model formulation

As with all correlative models, stacked models require providing each base learner with a response variable and a set of covariates. We used as a response variable the weekly egg observations described in Sect. 2.1. As covariates, we selected three main environmental drivers that significantly influence the behaviour and development of mosquitoes, namely temperature, photoperiod (i.e., duration of daylight in 24 h) and precipitation37,38,39,40,41,42,43. Covariate preprocessing, including details on each variable’s ecological significance and specific preprocessing steps, is described in SM1.1 and omitted here for brevity. For each of these three covariates, we considered also their lagged values, since the mosquito life cycle can take several days or weeks to complete38,40. The lagged temperatures and photoperiod were calculated as the median value between the observations recorded in the current week (t), the previous week (t-1), and the week before that (t-2), whilst the lagged precipitation was computed as the cumulative weekly value between the precipitation recorded in the current week (t), the previous week (t-1), and the week before that (t-2). We similarly processed these covariates also for lag t-3.

In addition to the environmental covariates, which we include as distributed lags, we considered seasonal and cyclical components. Specifically, we used the Fourier series, with sine and cosine harmonic waves, to accommodate the yearly pattern and shorter-term seasonality. For these calendar effects the Fourier terms offer a more parsimonious representation than dummy variables, in particular when the frequency of the data is large (see Hyndman and Athanasopoulos44, Ch. 7 Sect. 4). We selected four relevant harmonic: one pair of harmonics is used for describing the yearly evolution, whereas another pair of harmonics is needed to capture some seasonal patterns. The four trigonometric waves were added to the other environmental predictors and provided a significant contribution to describing the cyclic patterns and fluctuations in the median weekly number of eggs.

Based on the results of the explorative modelling (SM1.2), which suggested excluding lag-1 variables, and preliminary collinearity analysis (SM1.3), we designed two distinct but complementary models. The regression model infers the number of eggs as a function of temperature, photoperiod, and precipitation, all lagged by -2 and − 3 weeks, and the four Fourier’s harmonics (Eq. 1).

$$\begin{gathered} {\text{Regression model:}}Egg{\text{ }}count \sim Temperature.lag2 + Temperature.lag3{\text{ }} \hfill \\ \quad + Photoperiod.lag2 + Photoperiod.lag3{\text{ }} \hfill \\ \quad + CumulativePrec.lag2 + CumulativePrec.lag3{\text{ }} \hfill \\ \quad + SineYear + CosineYear + SineSeasonal + CosineSeasonal \hfill \\ \end{gathered}$$
(1)

The autoregressive model (Eq. 2) adds to the predictors considered in the Regression model (Eq. 1) an autoregressive component based on the number of eggs observed at week t-1 (Egg count.lag1).

$$\begin{gathered} {\text{Autoregressive model:}}\,Egg{\text{ }}count \sim Egg{\text{ }}count.lag1 + Temperature.lag2 + Temperature.lag3{\text{ }} \hfill \\ \quad + Photoperiod.lag2 + Photoperiod.lag3{\text{ }} \hfill \\ \quad + CumulativePrec.lag2 + CumulativePrec.lag3{\text{ }} \hfill \\ \quad + SineYear + CosineYear + SineSeasonal + CosineSeasonal \hfill \\ \end{gathered}$$
(2)

Stacked model

Each model formulation was applied to four individual base algorithms, namely extreme gradient boosting (xgBoost), boosted regression trees (BRT), random forest (RF) and cubist (Fig. 2b).

Extreme gradient boosting (xgBoost) is a powerful gradient boosting algorithm based on the concept of boosting, where weak models (typically decision trees) are sequentially trained to correct the mistakes made by the previous models45. The algorithm optimises an objective function by iteratively adding models to the ensemble, minimising the loss. xgBoost employs a gradient-based approach to improve the performance of the weak models and handle complex interactions among variables. Boosted regression trees (BRT) is a boosting algorithm that combines multiple decision trees to form an ensemble model46. Similar to xgBoost, BRT sequentially trains decision trees, with each subsequent tree focusing on correcting the errors made by the previous trees. The algorithm optimises an objective function by iteratively adding trees, and the final prediction is a weighted sum of the predictions from all the trees. Random Forest is an ensemble learning method that constructs a collection of decision trees and combines their predictions to make accurate predictions47. Each tree in the RF is built on a randomly sampled subset of the data and a randomly selected subset of features. This randomness helps to reduce overfitting and increase the diversity among the trees, and the final prediction is determined by averaging or voting the predictions from all the trees in the forest. Finally, cubist is a rule-based algorithm that combines decision trees with linear models. It creates a set of rules by recursively partitioning the data based on the predictor variables48. Each rule corresponds to a specific region of the feature space and predicts the response variable using a linear model. The algorithm iteratively builds a series of decision trees and linear models, optimising an objective function that balances accuracy and complexity.

We tuned the hyperparameters of each of the four machine-learning algorithms for both model formulations (Eqs. 1–2; Table 2.1). Then, for each model formulation separately, we combined the predictions of each tuned algorithm into the meta-learner, defined as a linear regression of the egg count (response variable) and the four algorithms’ predictions (covariates). Both meta-learners were used to predict the abundance of Ae. albopictus eggs over the period 2010–2022 on the training and validation datasets. The meta-learner trained with the four algorithms having as model formulation Eq. 1, i.e. the regression model, was also used to predict, and thus extrapolate, over the whole area of interest for the period 2010–2022.

Model validation

The egg observations were partitioned into one training and two testing datasets for the external and internal validation; (Fig. 2b). To conduct the external validation, i.e. using observations not used to train the models, we employed a random selection process choosing two VectAbundance’s ovitraps within each distinct NUTS2 level for every biogeographical region. This selection was limited to VectAbundance’s ovitraps with a minimum of three years’ worth of observations, guaranteeing the presence of a robust time series for validation. These observations were excluded from the training dataset allowing for an exhaustive coverage of the longitudinal and latitudinal gradient of the area of interest. We excluded Sicily from the external validation dataset because it hosts only one ovitrap and represents the southernmost observation in the area of interest (see Fig. S3.1 for the locations of the ovitraps used for the external validation). After excluding these stations, we defined the training dataset as all the observations spanning from 2010 to 2021 and the internal validation dataset as all the observations gathered in 2022.

As an additional validation, we also performed a 10-fold cross-validation on the training dataset by retaining, for each fold, 70% of the observations to train the model. The class of models used is either regression or autoregression, so the standard k-fold cross-validation can be implemented, as suggested by Hyndman and Athanasopoulos44 (Ch 5. Section 10). To estimate the model’s predictive error we estimated, for each station and validation dataset, the root mean squared error (RMSE) and the mean absolute error (MAE).

Deriving pseudo-phenological indexes: introducing the period-over-threshold

In addition to utilising the regression stacked model for predicting the average number of eggs for each week within a given year across the area of interest, we also aimed to derive estimates about the predicted seasonality of Ae. albopictus’ egg-laying activity. Different approaches have been proposed to compute seasonal indexes of mosquitoes like onset (i.e. beginning of the season), peak, and offset (i.e., end of the season49,50). However, these approaches assume a repeated and even sampling of the species of interest, which, unfortunately, is not the case across the sampling locations of our dataset. Therefore, here we propose and define a pseudo-seasonal index that we call the period-over-threshold (POT).

The POT represents the period in which the variable of interest, i.e. the average number of eggs, is above a certain threshold. Here, we define the POT as the number of weeks in which the weekly average number of eggs is equal to or higher than 55 eggs, the spatially and weekly aggregated average median number of eggs (excluding zeros) observed over the whole area of interest during the period 2010–2022. We acknowledge that the POT, as defined here, is a heuristic approach, and therefore we performed a sensitivity analysis varying the threshold to 20 and 125, defined by the average interquartile range (IQR) of the observed distribution.

Finally, we investigated if the observed and predicted POT have varied in time and space among the different biogeographical regions over the 2010–2022 period. We tested whether the length of the observed and estimated POT is affected by the year (quantitative) and the biogeographical regions (qualitative: Alpine/Continental/Mediterranean) and their interaction, using Generalised Linear Mixed Models (GLMMs) with Poisson error distribution and log link function, considering the ID of the VectAbundance’s ovitraps as a random factor. The same GLMM was applied to both the observational dataset used to train the regression-stacked model and a dataset of predictions for the period 2010–2022, generated by the regression-stacked model itself.

Results

Ovitraps dataset descriptive statistics

The 149 VectAbundance’s ovitraps are located in four European countries (Albania, France, Italy and Switzerland). Overall, 30 aggregated ovitraps were located in the Alpine biogeographical region, while 48 and 71 were located in the Continental and Mediterranean biogeographical regions, respectively. Most of the ovitraps were active during the period 2020–2022, with only a few stations that were monitored for more than three seasons32. 120 aggregate ovitraps were used to train the models, whilst 19 were retained for the external validation.

Model outputs

The random forest algorithm showed the highest regression coefficient in the regression stacked model and so resulted as the most important algorithm (Table S2.2), while the most important environmental predictors were the 3-week-lagged temperature and photoperiod (Fig. S2.3A). On the other hand, cubist was the most important algorithm for the stacked autoregressive model, with the 1-week-lagged value of observed eggs being the most important predictor (Fig. S.2.3B).

Both stacked models were able to capture the seasonal and interannual variability of the ovitraps time series in the training dataset and both validation datasets (Figs. 3, S3.2). A detailed representation of the external validations for both models, broken down at the location level, is available in SM3 in Figs. S3.3–S3.4 for the regression and autoregressive models respectively. The predicted values for both the internal and external validation matched the observation patterns in the three biogeographical regions, with the autoregressive model showing, in general, a closer association with the observations. The autoregressive model showed overall a higher R2 and lower RMSE and MAE compared to the regression model in the training and both validation datasets (Table 1; Fig. S3.5). For both model formulations, both RMSE and MAE are lower in the Alpine biogeographical region compared to the Continental and Mediterranean regions; however, RMSE and MAE values within the Continental and Mediterranean regions show no significant differences between their respective training and testing datasets (Fig. S3.6).

Table 1 Stacked model validation metrics from the 10-fold cross-validation made on the training dataset.
Full size table
Fig. 3
figure 3

Median and interquartile range of the number of eggs observed (grey lines) and predicted by the regression model in both the internal and external validation. Both the observed and predicted values were aggregated over the three biogeographical regions to allow an easier representation.

Full size image
Fig. 4
figure 4

Median number of eggs predicted weekly by the regression model in the area of interest for the year 2022. The black lines represent the borders of the administrative areas of the countries of interest at the NUTS2 level. The grey areas are outside the area of interest. The map was created using R v4.334.

Full size image

Spatial predictions

The spatio-temporal predictions of the stacked regression model for 2022 reveal seasonal and latitudinal variation in egg abundance across the study area (Fig. 4). Egg-laying activity begins in early spring, with the median number of eggs exceeding 50 from week 20 (mid-May) onwards. The peak of the season is estimated around week 30 (end of July), particularly in the Po and Rhone valleys and along the Adriatic, Ionian, and Tyrrhenian coasts. Egg abundance decreases after week 35 (end of August), but this decline follows a latitudinal and geographical gradient. In southern and coastal areas, predicted egg numbers remain above 100 through week 40 (early October), dropping below 50 only after week 45 (November). In alpine regions, egg-laying activity is restricted to warmer months, while in coastal areas, predictions indicate prolonged activity into late autumn.

Period-over-threshold

On average, the observed POT spans 7 (6–9 IQR) weeks for the Alpine biogeographical region, 20 (19–22 IQR) and 15 (14–16 IQR) weeks for the Continental and Mediterranean biogeographical regions, respectively. The predicted POT shows generally a shorter length, with 4 (3–5 IQR) weeks for the Alpine biogeographical region, and 17 (16–18 IQR) and 11 (9–12 IQR) weeks for the Continental and Mediterranean biogeographical regions respectively. The spatial representation of the predicted POT for the year 2022 (Fig. 5; POT IQR displayed in Fig. S3.7) shows a longer length of the POT in the Po Valley and coastal zones of the area of interest (POT > 20 weeks). Mountainous and foothills areas show, on average, short (POT < = 5 ) or absent POT.

The Poisson GLMMs investigating the effect of the interaction between the year and the biogeographical regions on the POT show significant effects for all the explanatory variables and their interactions, except for the Alpine biogeographical region in the observed dataset (Table S3.8). The predicted values of the models trained on the observed and estimated POT showed a positive increase, independent from the reference year, for all the biogeographical regions but the Alpine in the observed dataset over the period 2010–2022 (Fig. 6).

Fig. 5
figure 5

Spatial representation of the predicted critical period-over-threshold (POT) for the year 2022 in the area of interest. White pixels are characterised by an average median weekly number of eggs always lower than 55. The black lines represent the borders of the administrative areas of the countries of interest at the NUTS2 level. The map was created using R v4.334.

Full size image
Fig. 6
figure 6

Modelled relationships between the Period-over-threshold and the interaction between the year and biogeographical regions using a Poisson GLMM.

Full size image

Discussion

Ensemble modelling is a popular technique to mitigate the artefacts or errors that may arise from individual algorithm predictions. Among the different ensemble techniques available, stacking has recently risen as one of the approaches leading to a more robust and accurate final prediction20,21,22,23,51. In this study, we proposed a reproducible application of a stacked model to infer the spatio-temporal egg abundance of a species of interest, the Tiger mosquito Ae. albopictus. We stress that our approach can be replicated and applied to different case studies and species, as recently shown by Bonannella and colleagues20,21, if longitudinal observations on their abundance and phenology are available. The application of a stacked model on both regression and autoregressive model formulations resulted in reliable estimates of mosquito egg abundance, providing an important to support local public health authorities to better allocate monitoring and surveillance resources.

Predictive accuracy of the models

The performance metrics of the regression and autoregressive models indicated a consistently strong predictive accuracy throughout the entire time series. Furthermore, the values of RMSE and MAE displayed similarities between the internal and external validation datasets. The autoregressive model showed generally higher predictive performance than the regression model, having the lagged number of eggs observed as the most important predictive variable. This was not unexpected, since the preliminary exploratory analysis (SM 1.2), made with genuine regression models, displayed strong empirical autocorrelation, of order one, in the residuals. However, the high predictive accuracy of the autoregressive model has the drawback of not being able to spatially extrapolate its predictions outside the training dataset. Whilst this can be seen as a limitation, it offers the opportunity of having accurate estimates and forecasts in specific locations, allowing the model to be informed with local and high-quality environmental information, using e.g. weather station observations. On the contrary, the regression model allowed us to spatially extrapolate the predictions in areas that were not previously sampled. The median number of eggs predicted over the study area for the year 2022 matches the expected seasonal dynamic of the species. Though egg-laying activity might occur in March and April, it increases around week 20 (mid-May) and ends in early October following elevational and latitudinal gradients43,50,52. In the alpine areas, our spatial estimates resembled those obtained using different modelling techniques and training datasets (e.g53). Previous dynamical distribution modelling approach forecasting Ae. albopictus eggs abundance at high spatial (0.01 latitudinal and longitudinal degrees) and temporal (weekly) resolution over ten Balkan countries projected annual peaks in egg abundance between the summer months of August and September i.e. approximately from weeks 32 to 3854. The field investigation in Albania in 2023 has shown the peak of the season in July (weeks 28-29-30) and another peak at the end of August and beginning of September (weeks 35–36; personal communication of E. Velo). For the coastal areas of the Tyrrhenian Sea, the spatio-temporal prediction of the stacked regression model confirms the results of previous studies carried out in central Italy, where the peak of activity and the end of the season is expected at the end of August and November, respectively (Fig. 4;42,50). Interestingly, these estimates based on ovitrap data (i.e. collection of eggs) comply with independent estimates obtained from data acquired collecting a different life stage of the mosquito (i.e., host-seeking females) at the two opposite ends of Italy (Trentino and Sicily) that identified the beginning of the season in mid-June and mid-March and the peak of the season in early August and August-September, respectively55,56.

Period-over-threshold

The pseudo-phenological index POT computed for Ae. albopictus during the year 2022 also showed latitudinal and elevational gradients, with the Po Valley and coastal areas having generally longer POT than mountainous areas. In the coastal areas of the Tyrrhenian Sea, the estimated POT is between 15 and 20, decreasing to 5 weeks in low mountain areas and to zero in high mountain peaks, similar to what was described in previous studies42,50. The spatial pattern depicted in Fig. 5 resembles those representing the estimates Ae. albopictus seasonal length presented by Petrić et al.57. However, the estimates of Petrić et al.57, based on multiple conditional statements of temperature and photoperiod, show a generally longer period of activity of the species compared to the estimated POT. This is not unexpected, because the two outputs are intrinsically different: the POT measures the length of the period over a user-defined threshold, whilst Petrić et al.57 have estimated the length of the period of activity of the mosquito considering the environmental conditions triggering eggs hatching, which in Mediterranean areas can begin in early March though at low density57.

In both the Continental and Mediterranean biogeographical regions, both observed and estimated POT durations have been increasing by approximately one week every year. This trend suggests a potential direct impact of global warming on the abundance of this species, as discussed in previous studies50,58,59,60,61. However, it is also essential to consider that the prolonged POT duration might be influenced by other factors, such as the increased monitoring efforts and the expanding range of the insect, leading to higher observed counts and longer POT periods.

Other threshold-based indexes have been proposed specifically for Ae. albopictus, but those are mostly epidemiological indexes (e.g62,63). We believe that the strength of the POT method lies in its broad interpretability and applicability. This approach can be employed not only in spatial epidemiology applications, as demonstrated in our case study but also in monitoring other alien species or supporting biological conservation efforts. It enables the identification of locations and periods when a particular population falls below or surpasses a defined threshold, signalling the need for targeted local interventions.

Limitations and future perspectives

As for most ecological models, one of the main limitations of these results relies on the quantity and quality of the training dataset64. First of all, egg observations were pooled from ovitraps having different volumes, shapes, oviposition substrates, revisiting times, etc32. This, unfortunately, is a limitation related to the different sampling and monitoring schemes employed by the different institutions32. Despite the preprocessing operation on the observations collected by the ovitraps, some of these sources of variability have likely influenced our results and therefore should be taken into account while interpreting them. Therefore, we want to highlight the importance of carrying out reproducible and comparable sampling schemes following the most updated standards for ovitraps monitoring, as those presented as the outcome of the AIM-COST cost action by Miranda et al.65.

Our dataset is also spatially biased because most of the observations are spatially clustered in north-central Italy, especially in the Emilia-Romagna region, where one of the most consistent and long-lasting surveillance programs has been carried out since 2010. The observations coming from this region had likely the highest quality, having been sampled continuously every two weeks from 2010 onwards. Spatial clustering is known to bias the models’ estimates and predictions66 and therefore has likely produced sub-optimal predictions in the southern part of the area of interest. This detrimental aspect of our outputs can only be resolved by increasing the sampling effort in the southern part of the study area.

Another potential source of variability in the training dataset is the effect of vector control practices affecting the abundance of collected eggs. Pest control agencies act to limit the abundance of the species and reduce the nuisance the bites are causing to the population67. Unfortunately, this is an effect that we cannot control, as we do not have access to the location and period of each pest containment treatment carried out in the area and period of interest. In addition to the coarse resolution of the climatic predictors, which may not fully capture fine-scale climatic variations influencing the mosquito life-cycle, we acknowledge the potential value of other relevant predictors not included in this study, such as land use/land cover and human population density. However, the exclusive placement of ovitraps in urban areas limits the availability of contrasting data needed to effectively incorporate these variables.

Despite these limitations, the proposed framework seems feasible to be implemented to produce both local and continental scale predictions and forecasts, contributing to supporting the stakeholders in their effort against Ae. albopictus. Using e.g. regional circulation models and/or weather generators, the methodology presented here can be used to produce estimates for the next seasons under different climatic scenarios. Interestingly, the presented methodology can be implemented and corrected during the season by including the results of the monitoring activities in the training dataset. The estimates of these models can also be compared to estimates produced by other correlative models (e.g68). , or mechanistic models such as albopictus69 and dynamAedes7, producing a plethora of models’ estimates accounting for different aspects of the biological system studied.

By employing the results of our modelling approach, public health authorities can make informed decisions regarding the implementation of control measures, allocation of resources, and targeted interventions to mitigate the risks posed by invasive mosquitoes and safeguard human and animal health. The latter aspect has gained particular interest during the past two decades when the impact of invasive species on public health has become more evident (e.g.,70,71). Apart from the public health aspect, we believe our work has a broader scope, providing a tool that can be adapted to infer the spatio-temporal abundance and seasonality of different species of interest.