Introduction

The rapid growth of urban traffic demand has further aggravated the problems of traffic congestion, air pollution and traffic accidents. As an important part of intelligent transportation system, accurate and efficient traffic flow prediction method can not only support more scientific road design and land use planning, but also effectively reduce congestion and carbon emissions and promote the realization of green travel. In addition, the results of traffic flow prediction can optimize the operation of urban logistics and public transportation, reduce costs and improve resource utilization efficiency. Therefore, accurate prediction and effective management of traffic flow has become an urgent challenge for urban traffic managers and researchers.

With the development of deep learning, convolutional neural network-based traffic flow prediction algorithm introduces spatial features, but only realizes grid-based road network representation. Then, the graph neural network is introduced to improve the spatial feature extraction significantly, and the prediction accuracy is also greatly improved. However, current traffic flow prediction algorithms still face some limitations. On the one hand, they still have shortcomings in learning nonlinear transformation features, mainly focusing on short-term features of traffic flow data, and lacking long-term trend extraction and cycle analysis. On the other hand, the future state of traffic depends not only on the historical state, but also on various external factors, including static factors such as street restaurants, schools, bus stops, and dynamic factors such as weather conditions and traffic control. To solve these problems, this paper proposes a multi-information fusion prediction network (MIFPN) for traffic flow prediction. This method takes into account the short-term characteristics, long-term trends and periodic characteristics of historical traffic flow data, and combines external static and dynamic information. The main innovations of this paper include:

  • The proposed MIFPN model integrates external road information. Static information is used to learn node traffic features under different spatial attributes, while dynamic information captures flow transformation features under various weather conditions. A feature-enhancement unit is designed to collect the dynamic D and static S attributes of road sections, which fuses the traffic feature matrix X and the attribute matrix \(K=(S,D)\) into an expanded matrix \({X_{long}}\).

  • A long-term trend extractor is designed based on a subsequence transformer, enabling the MIFPN model to capture the long-term characteristics of traffic flow data. By leveraging a masked subsequence Transformer, compressed and contextually rich subsequences are generated, and a long-term trend extractor is obtained using stacked one-dimensional dilated convolution layers on these subsequences.

  • A cycle extractor is designed to capture the periodic characteristics within a week and a day. A graph convolutional module is employed to combine the spatial dependencies of the traffic graph and the hidden spatial dependencies within the graph, resulting in a cycle extractor.

The proposed multi-information fusion traffic flow forecasting method synthesizes external road information, static and dynamic characteristics, and temporal and spatial relations, and has a positive impact on urban planning, environmental sustainability and economic benefits. By learning spatial attribute characteristics and traffic changes under dynamic conditions, combined with long-term trend and periodic feature extractor, the method enhances the predictability of traffic flow prediction, optimizes intelligent traffic signal control and route planning, and strongly supports the development of smart cities.

The remainder of the paper is structured as follows: the second section reviews related work and trends in traffic flow prediction. Section III presents the details of the proposed method in this paper. In Section IV, experiments based on real datasets are conducted to evaluate the performance of the proposed method in comparison with the baseline method, and perturbation analysis is performed to test the robustness of the model. Section V summarises the work of this paper and gives an outlook.

Related work

Earlier, traffic flow prediction1,2,3 was mainly based on mathematical and statistical models. Autoregressive Integral Moving Average (ARIMA)4 and its variants are classical methods5 and are widely used in traffic prediction problems. However, these methods are mainly for small datasets and are not suitable for dealing with complex and dynamic time series data. With the development of machine learning6,7,8, it is possible to model more complex time series data, including feature models9, Gaussian process models and state space models Such models are capable of handling non-linear time series features but are poor for modelling complex road networks and dynamic traffic data. Deep learning models with more feature layers and more complex architectures have better results for modelling spatio-temporal correlation of traffic flow with large sample data processing For example, Convolutional Neural Networks (CNNs) are effective in modelling spatial relationships of traffic data constructed in the form of road networks, but lack the construction of road topological relationships. However, road networks can be naturally represented as graphs, where distances between roads can be expressed as weights of edges, and the modelling problem of non-Euclidean data structures can be effectively solved by graph neural networks (GNN)10,11,12.

GNNs can be classified into two categories, spectrum-based GNNs and space-based GNNs .Bruna et al. first proposed spectral CNNs to generalise CNNs to non-Euclidean spaces, but the spectral decomposition process for Laplace matrices has excessive computational complexity. ChebNet13 applies Chebyshev polynomials to approximate complex spectral convolutions, which effectively reduces the complexity of spectral convolutions and reduces the number of parameters, and is therefore less likely to overfit the data. GCN14,15 can be regarded as a first-order ChebNet with regularisation, which is computationally efficient and easy to stack in multiple layers. Space-based GNN describes the process of graph convolution as an aggregation of information from the central node and its neighbouring nodes from the point of view of local spatial associations between nodes. Glimer16 summarised the operations of aggregation, readout and so on for spatially-based GNNs and generalised one-class message-passing neural networks (MPNNs). The GCN can also be viewed as a spatial-based message-passing neural network, where the weights of messages from neighbouring nodes during aggregation are fixed and determined by the degree of the node. GAT17 introduced a multi-head self-attention mechanism in graph neural networks to dynamically assign weights to messages from neighbouring nodes during aggregation. Therefore, GAT can better focus on information from important nodes compared to GCN.

Based on GNNs, modelling of temporal correlation in traffic flow has been further introduced and many spatio-temporal graphical neural network models have been proposed for traffic prediction tasks18,19,20. Based on the time-dependent modelling, STGNNs are classified into RNN-based, CNN-based and Transformer-based STGNNs. The RNN-based STGNN is represented by the DCRNN21,22,23, which uses gated recurrent units (GRUs), extracts temporal features from the data, and employs a diffusive convolutional neural network (DCNN) to simulate the effects of spatio-temporal variations from one node to the others in the traffic network. The CNN-based STGNN is ASTGCN24,25,26, which introduces a spatio-temporal attention mechanism to capture long-range temporal dependencies and implicit spatial connectivity in road networks and combines it with spatial graph convolution and temporal one-dimensional convolution in order to model the spatio-temporal dynamics in traffic data. The transformer-based STGNN is STTN27,28,29, which integrates a graphical convolution process into a spatial Transformer, and together with a temporal Transformer, STTN can capture long-term dependencies from traffic data.

However, the traffic forecasting task not only relies on historical traffic information and spatial relationships, but is also influenced by various external factors, such as weather conditions and the distribution of surrounding POIs. How to integrate information from external influences into the model is a major issue in current transport work. For example, Liaoetal integrated an LSTM-based encoder to encode external information and modelled multimodal data as sequential inputs. Zhangetal implemented a traffic prediction task with external weather information by feature fusion of input features and weather information, mainly based on the GRU model .In summary, this paper exploits the long-term trend and periodicity of historical traffic data and incorporates information external to the road to improve the accuracy and robustness of traffic flow prediction.

Methodology

Relevant definition

Definition 1

Road network \(G=(V,E)\) to represent the connectivity about road segments. \(V={v_1},{v_2}, \ldots ,{v_n}\) denotes the set of road segments, n is the number of road segments, \(E={e_1},{e_2}, \ldots ,{e_m}\) is the set of edges indicating connectivity between two road segments, and m denotes the number of edges. In general, the adjacency matrix A is used to illustrate the connectivity of a road network. When G is an unweighted network, A is a matrix of 0 and 1, which 1 indicates a connection to the corresponding road segment, and 0 otherwise.

Definition 2

Traffic speed is regarded as an intrinsic attribute of each node on the urban road network, which is represented by a traffic characterization matrix X, and denotes the traffic speed on the i-th road segment at time t as matrix \(\chi _{i}^{t}\).

Definition 3

External factors affecting traffic conditions are used as auxiliary attributes of online sections of urban roads, which can form the attribute matrix \(K=\{ {K_1},{K_2}, \ldots ,{K_l}\}\), as l is the category number of the auxiliary information. The set of auxiliary information of type j, is denoted as \({K_j}=\{ {j^1},{j^2}, \ldots ,{j^t}\}\), which is the j-th auxiliary information of the i-th road segment at time t.

In summary, the traffic prediction problem can be seem as learning a function f on the basic road network G, feature matrix X and attribute matrix K to obtain the traffic information for the future time period T, as shown in Eq. (1):

$$[{x_{t+1}},{x_{t+2}}, \ldots ,{x_{t+T}}]=f(G,X|K)$$
(1)

MIFPN framework

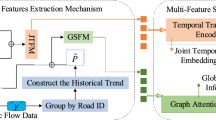
The entire MIFPN framework is shown in Fig. 1. Firstly, external information is fused into the traffic data. Secondly, a subsequence level time series representation is extracted from the long term series based on a subsequence learner, and long term and short term time features are obtained from the subsequence by means of a trend extractor, a period extractor and a feature fusion. Finally, the obtained temporal features are combined with short-term feature data fused with external information for traffic flow prediction.

Fig. 1
figure 1

MIFPN model diagram.

Full size image

External information

This paper analyzes the influence of external factors on traffic states from both static and dynamic perspectives. The external factors are defined as dynamic D and static S attributes of road segments in the road network. Then, the traffic characteristic matrix X and the attribute matrix \(K=(S,D)\) are synthesized into an expansion matrix \({X_{long}}\).

Static factors

Primarily refers to static geographic information that does not change over time, but still has an impact on the state of traffic. For example, the distribution of POIs around a road section can determine people’s access patterns and the attractiveness of the road section, which in turn is reflected in its traffic state.

Fig. 2
figure 2

POI speed distribution graph.

Full size image

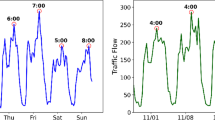
Figure 2 shows the average traffic performance for Shenzhen taxis at different types of nodes over the course of a day. After analysing the data, different types of nodes have different behavioural characteristics, and the surrounding buildings and environment of a road node can have an impact on traffic flow. For example, morning and evening flows would be higher in residential areas than at other times of the day, while midday and evening flows would be significantly higher in catering areas. Therefore, classifying the architectural attributes of the road nodes themselves as points of interest and incorporating them into the data stream will help to improve the accuracy of the traffic flow data.

\(S \in {R^{n \times p}}\) is a collection of p distinct static attributes \(\{ \overrightarrow {{s_1}} ,\overrightarrow {{s_2}} , \ldots ,\overrightarrow {{s_p}} \}\). As the attribute values don’t change by time, the matrix S is always used, and only the corresponding columns of the feature matrix X is extracted during the generation of the augmented matrix at each timestamp. The extended matrix \(E_{s}^{t}\) with static properties is formed at timet, as shown in Eq. (2):

$$E_{s}^{t}=[{X^t},S]$$
(2)

Dynamic factor

Weather information is an important factor affecting traffic flow and is selected as a dynamic feature. Traffic peaks and flow characteristics have different manifestations under varying weather conditions. Figure 3 shows 10 nodes selected from the Shenzhen taxi dataset and analysed for their speed averages under different weather conditions. It can be clearly seen that the speed behaviour of the vehicles changes significantly in different weather conditions, with the lowest speeds in foggy weather and the highest mean speeds on sunny days.

Fig. 3
figure 3

Speed conditions in different weather.

Full size image

\(D \in {R^{n \times (w * t)}}\), unlike S, is W different dynamic properties. It is noteworthy to consider that traffic states are cumulatively affected by dynamic factors over time. We extend the size of the selection window to \(m+1\) when forming \({E^t}\), So choose \(D_{W}^{{t - m,t}}=[D_{W}^{{t - m}},D_{W}^{{t - m - 1}}, \ldots ,D_{W}^{t}]\). Finally, through the Attribute Enhancement Cell (A-Cell), the augmented matrix containing information about static and dynamic external attributes and traffic characteristics at time t is formed as \({E^t} \in {R^{n \times (p+w * (m+1))}}\). \({E^t}\) shown in Eq. (3)

$${E^t}=[{X^t},S,D_{1}^{{t - m,t}},D_{2}^{{t - m,t}}, \ldots ,D_{w}^{{t - m,t}}]$$
(3)

Subsequence learner

Masked Subsequence Transformer (MST) is to infer the contents of masked subsequences from a small number of subsequences and their temporal contexts, allowing the model to efficiently learn compressed, contextually informative subsequence representations from long time sequences. The design of the MST consists of two fundamental issues: (1) masking strategies and (2) models for learning the representations.

(1) Masking strategy. There are two important factors to be considered in the MST masking strategy, the basic unit of masking and the masking ratio. Existing methods usually use a 5-minute time step as the basic unit of input data, which does not capture the trend of long time series well. Inspired by27, long sequences are divided into equal-length subsequences containing multiple time steps, and use these subsequences as the basic unit of model input. Both BERT30 and MAE use template reconstruction to learn the basic semantic information in the data. The information density of image data is relatively low and the pixel points have spatial continuity, so even if the MAE masks out 75% of the pixels, the main content of the image can still be inferred. Long-term traffic flow data is similar to images with temporal continuity and low information density. Thus requires a relatively high masking rate 75% random masking.

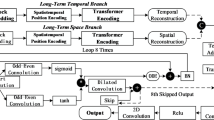
(2) Model for learning the representation. For time series, the difference between Transformer and temporal models such as RNN and 1DCNN is that the inputs of each time step in Transformer are directly connected to each other. Regardless of the increase in time step length, Transformer considers the representation of previous temporal features. In this paper, the Transformer encoder is used as the STRL, as shown in Fig. 4. The MST consists of two parts, the STRL and the self-supervised task head. The STRL learns the temporal representations of the subsequences, and the self-supervised task head reconstructs the complete long sequence based on the temporal representations of the unmasked subsequences and the masking tokens.

Fig. 4
figure 4

Schematic diagram of the mask subsequence model.

Full size image

Specifically, long history sequences are partitioned into non-overlapping subsequences \({X_{long}}=[{X_{t-L}},{X_{t-L+1}}, \ldots ,{X_{t-1}}]\). Then, randomly mask 75% of the subsequences, and marked as the masked subsequence. The remaining unmasked subsequences serve as input to STRL, as shown in Eq. (4):

$${S_{unmasked}}=STRL({X_{unmasked}})$$
(4)

where, \({S_{unmasked}}\) represents the STRL processed output of \({X_{unmasked}}\). The self-supervised task header consists of a Transformer layer and a linear output layer, which can reconstruct the given unmasked mask and the complete long sequence \({S_{[MASK]}}\) of learnable mask tokens, as shown in Eq. (5):

$$\left[ {{{\hat {X}}_{masked}},{{\hat {X}}_{unmasked}}} \right]=TaskHead(\left[ {{S_{unmasked}},{S_{[MASK]}}} \right])$$
(5)

The goal of pre-training is to minimize the error between the reconstructed mask value and the mask true value. Hence, only masked subsequences are considered in calculating losses, as shown in Eq. (6):

$${\mathcal{L}_{pretrain}}({\hat {X}_{masked}},{X_{masked}};{\Theta _T})=\left\| {{{\hat {X}}_{masked}} - {X_{masked}}} \right\|$$
(6)

where, \({\Theta _{\text{T}}}\) is the learnable parameters of the whole Transformer.

Trend extractor

The relatively small amount of information in the short-term historical series is insufficient to infer complex future traffic flow changes, whereas the long-term historical series can help the model to determine traffic flow fluctuations at future moments. For this purpose, a long-term trend extractor is designed to extract the long-term trend characteristics of the traffic flow from the temporal representation of the subsequence.

Commonly used basic structures for temporal feature extraction include RNNs and 1D CNNs. However, it is difficult for RNNs to handle long sequences because they cannot process features at each time step in parallel and are prone to the problems of gradient vanishing and gradient explosion. Ordinary one-dimensional CNNs have a limited receptive field, and increasing that receptive field requires stacking multiple CNN layers, which leads to a significant increase in the number of model parameters as the depth of the model increases. As shown in Fig. 5, a stacked one-dimensional dilated convolutional layer is used as the long-term trend extractor.

Fig. 5
figure 5

Schematic diagram of the trend extractor model.

Full size image

The sensory field of this module grows exponentially with the number of 1-dimensional dilated convolutional layers, which allows for efficient capture of trending features while avoiding problems such as gradient vanishing. The dilation convolution operation is expressed as shown in Eq. (7):

$$x{*_d}C(m)=\mathop \sum \limits_{{k - 1}}^{{j=0}} C(m)x(m - d \times j)$$
(7)

where, m denotes the m-th element in the sequence x, \({\mathbf{C}} \in {{\mathbb{R}}^k}\) denotes the convolution kernel, and d denotes the expansion rate. In this paper, the convolutional layer can be represented as follows in Eq. (8):

$${D_i}=Con{v_i}({D_{i - 1}})=MaxPool(gelu({D_{i - 1}}{*_d}{C_i}))$$
(8)

where the maximum pooling operation is used to reduce the dimensionality. The dilated rate d of i-th layer is set to \({2^i}\). When \(i=1\), the input to the module is the set of subsequence time S, \({D_1}=S=[{S_1},{S_2}, \ldots ,{S_N}]\). The output of the last convolutional layer is considered as a long-term trend feature \({H_{long}}\).

Cycle extractor

Traffic flows are usually cyclical, with similar spatial and temporal patterns for the same time periods on different dates and days of the week. In this paper, a periodicity extractor is built, a module that extracts the spatial dependence of input features across nodes with different time steps while preserving the temporal information of the subsequence. Suppose that the duration of a day corresponds to a time period, denoted by l. Then, the representation of the corresponding moments of the previous week and the previous day can be expressed as respectively: \({S_{week}}={S_{N - 7*l}}\) and \({S_{day}}={S_{N - l}}\) (N denotes the number of subsequences and is equal to \(N=S/l\)). As shown in Fig. 6, passing \({S_{week}}\) and \({S_{day}}\) to the spatial-based graphical convolution module to obtain \({H_{week}}\) and \({H_{day}}\) for periodic temporal features. This module is similar to the one proposed in [30], where the graph convolution module combines the spatial dependencies of the flow graph and the spatial dependencies hidden in the graph.

Fig. 6
figure 6

Schematic diagram of the cycle extractor.

Full size image

Specifically as shown in Eqs. (9) and (10).

$${H_{week}}=\mathop \sum \limits_{K}^{{k=0}} P_{f}^{k}{S_{week}}{W_{k1}}+P_{b}^{k}{S_{week}}{W_{k2}}+A_{{adp}}^{k}{S_{week}}{W_{k3}}$$
(9)
$${H_{day}}=\mathop \sum \limits_{K}^{{k=0}} P_{f}^{k}{S_{day}}{W_{k4}}+P_{b}^{k}{S_{day}}{W_{k5}}+A_{{adp}}^{k}{S_{day}}{W_{k6}}$$
(10)

where, \({P_f}=\frac{A}{{\Sigma _{{j=1}}^{n}{A_{ij}}}}\) and \({P_b}=\frac{{{A^T}}}{{\Sigma _{{j=1}}^{n}A_{{ij}}^{T}}}\) matrices correspond to the forward and backward diffusion of the graphical signals, respectively, and denote the corresponding transfer matrices. The power k of the matrix represents the number of steps in the diffusion process. W denotes the weight matrix and Aadp is an adaptive neighbourhood matrix which is considered as the transfer matrix for the hidden diffusion process. \({A_{adp}}=Softmax\left( {\operatorname{Re} LU({E_1}E_{2}^{T})} \right)\), \({E_1}\) and \({E_2}\) denote the source and target node embeddings, respectively, and the spatial dependency weights between the source and target nodes are derived by multiplying \({E_1}\) and \({E_2}\) together. \(\operatorname{Re} LU()\) is used to remove weak dependencies and \(Soft\hbox{max} ()\) is used for normalisation.

Fusion module

There is a strong temporal correlation between future short-term traffic flows and historical short-term traffic flows, so short-term trends need to be modelled separately.

It has been widely demonstrated that STGNN excels at capturing fine-grained features from short-term sequences [5, 34]. Firstly, spatial and temporal features are learnt through spatial and temporal learning networks respectively. Then, the two features are fused by a certain spatio-temporal fusion neural network structure. In this paper, an existing STGNN such as Graph WaveNet is used as a short-term trend extractor to obtain a finer-grained short-term trend map, as shown in Eq. (11):

$${H_{short}}=STGNN(A,X)$$
(11)

where the short sequence denotes the last subsequence in the long sequence, and A is the neighbourhood matrix. \(STGNN()\) denotes the STGNN model used.

In order to comprehensively consider the long and short-term features in the long historical series, the previously obtained long-term trend features, cyclical features and short-term trend features are fused to obtain the final prediction results Y, as shown in Eq. (12):

$$\hat {Y}=MLP(MLP({H_{long}}||{H_{week}}||{H_{day}})||{H_{short}})$$
(12)

where the symbol || denotes a join operation. The goal of the traffic flow prediction task is to make the output of the model as close as possible to the true value, so L1 loss is chosen as the objective function. This is expressed in the following Eq. (13), where\(Y=[{X_t},{X_{t+1}},\ldots,{X_{t+F - 1}}]\)indicates the actual value.

$${\mathcal{L}_{forecast}}(\hat {Y},Y;\Theta )=\left\| {\hat {Y} - Y} \right\|$$
(13)

Experiments and analyses

Experimental setup

The runtime environment used in the experiments of this paper is shown in Table 1.

Table 1 Experimental environment.
Full size table

Before model training, the original data set needs to be preprocessed. Firstly, the graph structure representation of the road network is constructed according to the address information of the sensor, which is mainly used to calculate the adjacency matrix. In this paper, it is defined by the sensor distance and the connectivity property between nodes. Then, the data set is divided into the training set, the validation set, and the test set in a ratio of 7:2:1, and the data is shred in a way that predicts the data of the next hour based on the historical data of 1 h. Based on the premise of external information fusion, and facilitate data management, this paper splices time, POI and weather attributes on the basis of historical sequences and corresponds to each other in the time dimension. The usable data for training and testing is finally obtained.

In the experiments, each Batch is set to have a size of 64, with a total of 100 epochs, and the decay rate of course learning is updated every 2000 rounds. The length of data input and output is 12, the data dimension is 4, and the hidden dimension of long-term trend extractor and periodic extractor is set to 4. The STGNN used in the experimental part of this paper is Graph WaveNet [33]. During the training process, the initial learning rate is set to 0.01, the decay rate is 0.1, and the optimizer is trained using Adam, and the training model is validated every 5 epoch. The whole model training time is about 6 h, and each epoch takes about 4 min.

Data set

SZ-taxi dataset: It was collected from the taxi operation data system in Shenzhen and first used in the T-GCN network by Ling et[16]. The time span of the dataset is from 1st January 2015 to 31st January 2015, with a 15-minute interval, and includes speed values for 156 road nodes, as well as an adjacency matrix representing connections between nodes.

SZ_POI: This dataset provides information about POIs around the selected road section. POI categories can be classified into 9 types, food and beverage services, businesses, shopping services, transport facilities, educational services, living services, medical services, accommodation and others. Calculating the distribution of POIs on each road segment, the POI type with the largest percentage is used as the characteristic of the road segment. Thus, the size of the obtained static attribute matrix is 156*1.

SZ_Weather: The auxiliary information contains the weather conditions of the study area recorded in January 2015 every 15 min. The weather conditions were classified into five categories, sunny, cloudy, foggy, light rain and heavy rain. Using the time-varying weather information, a 156*2976 dynamic attribute matrix was constructed.

Evaluation indicators

The traffic flow prediction task is essentially a large-scale, characterised data regression simulation problem. In this paper, mean absolute error (MAE), root mean square error (RMSE), and mean absolute percentage error (MAPE) are used to evaluate the accuracy of prediction results. As shown in Eqs. (14–16)

$$MAE=\frac{1}{n}\mathop \sum \limits_{n}^{{i=1}} \left| {{{\hat {y}}_i} - {y_i}} \right|$$
(14)
$$RMSE=\sqrt {\frac{1}{n}\mathop \sum \limits_{n}^{{i=1}} {{\left( {{{\hat {y}}_i} - {y_i}} \right)}^2}}$$
(15)
$$MAPE=\frac{{100\% }}{n}\mathop \sum \limits_{{i=1}}^{n} \left| {\frac{{{{\hat {y}}_i} - {y_i}}}{{{y_i}}}} \right|$$
(16)

where n is the number of samples, the \({\hat {y}_i}\) and \({y_i}\) are the predicted and true values of the i-th sample, respectively.

Analysis of experimental results

In order to test the effectiveness of the algorithm, nine representative algorithms were selected to compare the accuracy of the prediction results under different time steps. Among them, GWnet31, STSGCN32, AGCRN33 and DSTET34 are the newly published prediction methods, which have achieved better prediction accuracy in the original paper.

Table 2 Experimental results of each model on the SZ-TAXI dataset.
Full size table

As can be seen from the Table 2 data, the model proposed in this paper performs well on most of the indicators in the Shenzhen taxi dataset. Compared with the second best performing model, the prediction accuracy is improved in all the three prediction steps, and the MAE, RMSE, and MAPE are improved by 28%, 19.7%, and 28.5% on average, respectively. The effectiveness of the algorithm design proposed in this paper in reducing the relative error and the strong long-term prediction ability are demonstrated.

The STGCN and ASTGCN models perform well on the dataset, which is closely related to the characteristics of the dataset itself.The SZ dataset is collected in an area with high complexity of urban roads, which has a high degree of influence from external factors. The STGCN and ASTGCN models use multinomial Chebyshev map convolution, which can obtain richer feature information from the space. Although the algorithm designed in this paper does not use Chebyshev polynomials, it is better than the above models because it obtains the features of the high-order graph signal flow through the combination of graph convolution modules, and, at the same time, introduces the POI attribute, which enables the graph convolution process to make use of the hidden spatial features of the nodes.

Another noteworthy point is that out of the nine baseline models, DSTET is the only one that takes periodicity into account when predicting traffic flow and shows the best performance. This result proves the importance of periodicity.One of the main differences between DSTET and MIFPN models is that MIFPN models have the ability to capture long term trends, and the advantage of MIFPN models over DSTET may be attributed to their introduction of long term trends for forecasting.

DCRNN’s diffusion convolution and temporal codec structure based on graph network has a simpler structure, but adopting the principle of end-to-end sequence prediction makes the network structure enough to learn the transformed features of the traffic, so the effect is slightly better. In 30 min and 60 min, the RMSE value of MIFPN is slightly higher than that of GWnet model, and the reason for this is that GWnet model adopts the non-fixed structure of graph network, which can learn the hidden edge relationship between the nodes in the whole graph, which indicates that this model has something special in learning the relationship between the nodes. The subsequent algorithm design can pay more attention in this aspect.

In summary, the model proposed by the algorithm has improved its effect at most of the time points of the dataset. On the other hand, ASTGCN, due to the complexity of the model and the many parameters, although the attention network is used in both space and time, its prediction effect depends on the complexity of the road conditions, and the results are not obvious.The effect of adaptive neighbour matrix used by the two networks, Graph Wavenet and AGCRN, is also approaching the best in the dataset, which shows from the side that the relationship between the nodes is not static. How to extract the dynamically changing correlation between nodes, so that the model can improve the learning ability is also the main research direction of the subsequent research.

Ablation experiment

In order to verify the role of each module in the model in predicting the results, this section conducts an ablation experiment of the model on the SZ-taxi dataset. The degree of enhancement of each module on the prediction results and its theoretical basis is analysed by comparing the experiment with the complete model after module elimination and without elimination.

Firstly, all external information (POI & Weather) is ablated. The specific way of ablation is to use only the speed as an input based on the original model and will add only the vehicle speed as an input to the graph convolution layer for prediction.

Next, the components added to the model are ablated to validate the model. The trend extractor, specifically ablated by removing the trend extractor module from the base of the model and using external information and extracted cycle information as inputs to get the prediction results. The cycle extractor, specifically ablated by removing the cycle extractor module on top of the model and using only external information and the trend extractor as inputs to generate prediction results. The experimental results are shown in Table 3.

Table 3 Results of ablation experiments.
Full size table

The external information fusion model proposed by the algorithm improves the MAE metric by 4.81%, the RMSE by 3.3% and the MAPE by 1.51% on the SZ dataset, proving that the predictive ability of the model with the addition of the road information is by significantly improved. Long-term trend characteristics also improve the prediction effect on the dataset, in which MAE improves by 2.8%, RMSE improves by 2.15%, and MAPE improves by 0.86%. From the experimental results, it can be seen that the long-term trend characteristic effectively improves the prediction ability of the model. This is because in the long term, the data is showing a smooth upward and downward trend as well as staying constant. Cyclic characteristics are very obvious to improve the model prediction results, MAE improved by 3.8%, RMSE improved by 3.75%, and MAPE improved by 1.82%. Within urban roads, people and cars share lanes, resulting in a drastic degree of flow variation over time, and traffic flow information is highly cyclical within days and weeks.

Through the ablation experiments on the dataset, it can be concluded that in traffic flow prediction, the flow information of the road network itself is affected by other factors outside the road network, and by incorporating these factors into the prediction model, the effect of prediction and the speed of convergence are effectively improved. In addition, the cycle module and the long-term trend extraction module designed in this paper both help to improve the model, in which the cycle module is more useful than the long-term trend extraction module. In addition, through experimental validation of this paper, it is found that the cycle module is helpful for the traffic flow prediction algorithm when data is missing.

In order to demonstrate the role of the period module for the traffic flow prediction algorithm when data are missing, this paper selects the traffic flow prediction results of two nodes in the same time period in the SZ-taxi dataset for visualisation, as shown in Fig. Figure 7, (a) demonstrates the prediction of this paper’s traffic flow prediction algorithm in the normal situation, and (b) represents the prediction task under the premise of partial data missing, i.e., part of the short-term traffic flow data is missing. As can be seen from the comparison of the data results, even in the case of partial data missing reality. The model can also predict the values of traffic flow attributes based on the periodic characteristics of traffic flow data. It shows that the periodicity extractor can effectively enhance the robustness of the model.

Fig. 7
figure 7

Results comparison chart.

Full size image

Summary and outlook

The MIFPN traffic flow prediction algorithm proposed in this paper, the model model incorporates external information on the one hand, and on the other hand, the cycle extractor as well as the long-term trend extractor are designed. Through experimental verification, it is found that the proposed algorithm in this paper is greatly superior to machine learning algorithms, and compared with similar deep learning algorithms, there is also a great improvement. On the basis of enhancing the performance of the algorithm, this paper also explores the use of the period extractor to greatly improve the robustness of the model when part of the data is missing. For the case of missing data this paper explores the strength and depth of this paper is still to be explored, in addition to the long-term prediction of this paper is also to be studied in depth.