Introduction

The worldwide growth in energy requirement, due to increasing population, has factually depend on traditional fuels like coal, oil, and natural gas. As they are depleting rapidly and also environmental issues demands a paradigm shift to sustainable options1,2. Solar photovoltaic (PV) and wind energy have developed as suitable alternatives becuse to their accessibility and environmental profits3,4. Though they are having potential benefits, the intermittent behaviour of these sources, due to climate variations, poses issues for delivering consistent power supply5. To mitigate this, hybrid models integrating PV & wind power have been initiated. These systems combines the complementary features of both, offering reliable energy output, minimizing generation prices, and delivering extra energy export to the grid6.

While hybrid systems improve reliability, their integration with power networks introduces challenges such as harmonic distortions from power electronic devices, leading to issues like waveform distortion, low power factor, and load imbalances7. Addressing these power quality issues requires advanced mitigation strategies. Active filters, particularly DSTATCOMs8, are widely used for their ability to regulate voltage at the PCC, balance loads, and suppress harmonics9. Their effectiveness depends on the control strategies employed. Conventional methods like SRF10 & IRP theories are common but face limitations in handling non-linear loads and require precise filter tuning, resulting in delays and reduced harmonic mitigation efficiency11.

Adaptive techniques, such as LMS12, VLMS, and hybrid approaches, improve convergence and reduce computational demands but require careful parameter tuning12,13. Advanced methods like neuro-fuzzy systems offer potential but need refinement to ensure robust performance under dynamic conditions14,15. This study proposes an ANN-based DSTATCOM16 control for PV-wind hybrid systems using the Backpropagation algorithm. The ANN’s adaptive learning enables real-time harmonic reduction without prior knowledge of network parameters17. A 4-leg inverter, regulated via DC-DC and AC-DC converters, ensures balanced, sinusoidal GC under variable load conditions18. MATLAB simulations and hardware validation confirm the approach’s ability to enhance power quality and system reliability.

The layout of this paper configured as presented here, Section “Design of the XANN based model” reflects a comprehensive illustration of the developed ANN model for the DSTATCOM control. Section “XANN model outputs and description” states modelling results obtained using Simulink to test the defined appraoch. Section “Realtime set-up of proposed model” presents the realtime setup validation of the ANN based converter. At the end, Section “Conclusion” concludes the paper by projecting the significant highlights and upcoming research trends.

Design of the XANN based model

System methodology

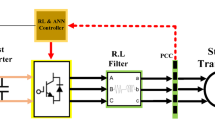
The architecture for evaluating the proposed DSTATCOM, controlled by an XANN algorithm, is presented in Fig. 1. The system integrates a grid-connected inverter with three inductors, which serve as coupling components linking the inverter to the grid at PCC. This topology allows the inverter to act as a DSTATCOM. The PV-wind power module produces DC voltage, then it is supplied to a DC link. The grid-tied inverter functions as a DSTATCOM receives that DC link voltage as the input. The primary objective of this converter is to reduce power quality (PQ) concerns created by power electronic un-balanced loads powered by the grid. These load demands reactive power while generating non-sinusoidal currents. The DSTATCOM, positioned at the PCC, injects the necessary compensatory current for the load and facilitates quadrature power circulation between itself and the load19. This makes the grid side current pure sinusoidal. The control strategy employed for the DSTATCOM leverages a ANN model, which computes precise RC for compensation20. Furthermore, a 4th leg in the DSTATCOM is implemented to address neutral imbalances caused by uneven load distribution. Central to the system’s operation is a hysteresis-based control scheme, which produces the switching pulses required for the DSTATCOM. This control approach ensures precise and dynamic compensation of harmonics and imbalances, thereby enhancing overall system stability and power quality.

Fig. 1
figure 1

Outline picture of the grid-connedted PV-Wind system.

Full size image

Control scheme

The DSTATCOM regulator employs an XANN based control approach to generate reference signals. Backpropagation, a fundamental technique for training neural network, evaluates the errors during forward flow and iteratively apprising the synaptic values of neural layer elements via backward flow. This method forms the foundation of XANN learning21. To enhance transparancy in neural outputs, different learning strategies can be employed, including structural, functional, and parameter-based adaptation methods22,23. Among these, parameter-based adaptation focuses on adjusting parameters like learning rate, bias and synaptic weights during the learning period24,25. This work is focused on a learning rate adaptation strategy to train the explainable neural model using the backpropagation algorithm.

The regulator is designed as a feed-forward neural network comprising three distinct layers, one is input, middle one is hidden and the final is output layer. Data enters through the input layer and is processed in the middle layer, here the learning scheme is executed26. The output layer completes the mechanism and generates the outputs of the controller. By employing the proposed algorithm, the model achieves improved learning and precision27. The training methodology and workflow are illustrated in Fig. 2, and the neural model structure, which determines the active and reactive RC values of the regulator, is presented in Fig. 3.

Fig. 2
figure 2

Elementary structure of the Neural model.

Full size image
Fig. 3
figure 3

XANN control of the DSTATCOM regulator.

Full size image

An illustrative flowchart outlining the new XANN-based regulator approach is provided in Fig. 4. This comprehensive framework ensures accurate computation of reference signals, thereby enhancing the performance and adaptability of the DSTATCOM28.

Fig. 4
figure 4

User Centric chart of the developed XANN model.

Full size image

The mathematical analysis of the XANN regulator’s approach of developing RC is presented here:

The base voltage (\({V}_{B}\)) at PCC is provided by below equation,

$${\text{V}}_{\text{B}}= \frac{2}{3}\times ({{\text{V}}_{\text{phR}}}^{2}+{{\text{V}}_{\text{phY}}}^{2}+{{\text{V}}_{\text{phB}}}^{2})$$

The regulated in-phase components on the source side are presented in (1),

$${\text{U}}_{{{\text{Rp}}}} = { }\frac{{{\text{V}}_{{{\text{phR}}}} }}{{{\text{V}}_{{\text{B}}} }},\quad {\text{u}}_{{{\text{Yp}}}} = { }\frac{{{\text{V}}_{{{\text{phY}}}} }}{{{\text{V}}_{{\text{B}}} }},\quad {\text{u}}_{{{\text{Bp}}}} = { }\frac{{{\text{V}}_{{{\text{phB}}}} }}{{{\text{V}}_{{\text{B}}} }}$$
(1)

A developed approach of XANN is accountable for adjusting the connected weights linked with the real-axis value (XAp) & the quadrature-axis value (XAq) of R-ph LC, as demonstrated by Eqs. (2) to (7). Employing data capturing tools, the currents of three phases of the loads (\({i}_{lR}\), \({i}_{lY}\), \({i}_{lB}\)) are obtained. On the input side of the XANN model, the Eqs. (2), (3), and (4) are applied to determine the reference components of current29.

$$I_{lRp} = X_{b} + i_{lR} u_{Rp} + i_{lR} u_{Yp} + i_{lR} u_{Bp}$$
(2)

where \({X}_{b}\) reflects the bias value, the LC RCs IlRp of R-ph is processed using an activation function, as presented in (4). Thereafter, these components are over operated to get the outcome of the feed-forward network30.

$${M}_{Rp }=f\left({i}_{lRp}\right)= \left(\frac{1}{1 + {e}^{{-i}_{lRp}}}\right)$$
(3)

The resultant \({M}_{Rp}\) from the input network acts as the source for the next network of the ANN model. The middle network gives an outcome, which is reflected in Eq. (5).

$${i}_{Rp1}= {X}_{ml}+ {X}_{Rp}{M}_{Rp} + {X}_{Yp}{M}_{Rp} + {X}_{Bp}{M}_{Rp}$$
(4)

where \({X}_{ml}\), \({X}_{Rp}\) reflects the basic weights of middle network, the attuned weight for phase R of the real axis component is obtained as given in (5).

$${X}_{Rp}\left(i\right)= {X}_{p}\left(i\right)+\eta \left\{{X}_{p}\left(i\right)-{X}_{Rp1}\left(i\right)\right\}{f}^{\prime}\left({i}_{Rp1}\right){M}_{Rp}\left(i\right)$$
(5)

In this background, \({X}_{p}\left(i\right)\) reflects the obsolute value of the real-axis weighted value of the currents at load, whereas \({X}_{Rp}\left(i\right)\) presents the attuned component of the weight for R-leg at the ith time intervel. \({X}_{Rp1}\left(i\right)\) and \({M}_{Rp}\left(i\right)\) presents the vital components of the active axis values of currents for R-leg connected load and the outcome correspondingly, at the ith time intervel of the feed-forward structure. \({f}^{\prime}\left({i}_{Rp1}\right)\) denotes the derivative of \({i}_{Rp1}\). The sign ‘η’ indicates the learning constant used by the developed XANN model of the structure. Likewise, the regulated vlaues of real-axis components of currents for loads at Y and B are obtained as shown in (5).

The obtained components of \({i}_{Rp1}, {i}_{Yp1}, {i}_{Bp1}\) are required to be processed through the activation function within the XANN structure. This dispensation gives the components of real-axis reference values at load end (\({X}_{Rp1}, {X}_{Yp1}, {X}_{Bp1}\)), as per (6).

$${X}_{Rp1 }=f\left({i}_{Rp1}\right)= \left(\frac{1}{1 + {e}^{{-i}_{Rp1}}}\right)$$
(6)

The average value of the reference active-axis \({X}_{p}\) is given as per (7).

$${X}_{p}= \frac{{W}_{Rp1}+ {W}_{Yp1}+{W}_{Bp1}}{3}$$
(7)

The outcome from this network is regulated using a LPF with an effective constant ξ to obtain the ultimate value of the real-axis component (\({X}_{lpt}\)) as given in (8).

$${X}_{lpt}=\upxi {X}_{p}$$
(8)

Correspondingly, the values related to the quadrature axis current values (\({X}_{q}\), \({X}_{Rq}\), \({X}_{Yq}\), \({X}_{Bq}\)) are obtained using Eqs. (9) to (15). These obtained components are then processed through a filter & regulated by a grading constant ‘α’ to get the final weight linked with the q-axis component \({X}_{lqt}\).

The Q-axis source voltages are determined as given in (10).

$${u}_{Rq}=\frac{{-u}_{Yp}+{u}_{Bp}}{\sqrt{3}},{u}_{Yq}=\frac{{3u}_{Rp}+{u}_{Yp}-{u}_{Bp}}{2\sqrt{3}}, {u}_{Bq}=\frac{{-3u}_{Rp}+{u}_{Yp}-{u}_{Bp}}{2\sqrt{3}}$$
(9)
$$I_{lRq} = X_{m} + i_{lR} u_{Rq} + i_{lR} u_{Yq} + i_{lR} u_{Bq}$$
(10)
$${X}_{Rq }=f\left({i}_{lRq}\right)=\left(\frac{1}{1 + {e}^{{-i}_{lRq}}}\right)$$
(11)

The results determined from the feed-forward structure (XRq, XYq, XBq) are considered as input to a middle network of the developed XANN structure. The results of the middle layer are obtained as per (12)

$${i}_{Rq1}={X}_{ml}+{X}_{Rq}{M}_{Rq}+{X}_{Yq}{M}_{Rq}+{X}_{Bq}{M}_{Rq}$$
(12)

The new value of spike q-axis value of the R-ph is obtained using (13) and (14).

$${X}_{Rq}\left(i\right)={X}_{q}\left(i\right)+\eta \left\{{X}_{q}\left(i\right)-{X}_{Rq1}\left(i\right)\right\}{f}^{\prime}\left({i}_{Rq1}\right){M}_{Rq}\left(i\right)$$
(13)
$${X}_{Rq1 }=f\left({i}_{Rq1}\right) =\left(\frac{1}{1 + {e}^{{-i}_{Rq1}}}\right)$$
(14)

The mean component of basic q-axis weight (Xq) is calculated using (15).

$${X}_{q}= \frac{{X}_{Rq1}+ {X}_{Yq1}+{X}_{Bq1}}{3}$$
(15)

The final component of reactive power value is given in (16)

$$X_{lqt} = \alpha X_{q}$$
(16)

The desired DC Value is compared with the actual value and the difference is fed to the PI controller, and obtained current ignites the production of bi-directional converter signals31. The error obtained in the DC link is calculated using (17) given by:

$${V}_{dcE}\left(i\right)= {V}_{dc}*\left(i\right)-{V}_{dc}\left(i\right)$$
(17)

One more PI regulator is used for defining the RC of the current at battery as presented in Fig. 5.

Fig. 5
figure 5

PI monitor for DC regulator.

Full size image

The outcome of the PI reguator is presented in (18).

$${I}_{PL}\left(i\right)= {I}_{PL}\left(i-1\right)+{K}_{if}\left\{{V}_{dcE}\left(i\right)- {V}_{dcE}\left(i-1\right)\right\}+{K}_{pf}{V}_{dcE}\left(i\right)$$
(18)

here kpf and kif are the P & I bock’s co-effecients projected in the inner block diagram of DC link. The value of the real-axis component of the reference GC (XFp) is given below,

$${X}_{Fp}={I}_{PL}\left(i\right)+{X}_{lpt}$$
(19)

At PCC, value of terminal voltage (VT) and its base (V*T) is compared to obtain the error, then it is processed via a PI regulator as given in (20–21),

$${V}_{TE}\left(i\right)= {V}_{T}*\left(i\right)-{V}_{T}\left(i\right)$$
(20)
$$V\left(i\right)=V\left(i-1\right)+{K}_{iv}\left\{{V}_{TE}\left(i\right)- {V}_{TE}\left(i-1\right)\right\}+{K}_{pv}{V}_{TE}\left(i\right)$$
(21)

The magnitude of the q-axis component of the grid RCs (XFq) is obtained as denoted by Eq. 22,

$${X}_{Fq}=V\left(i\right)+{X}_{lqt}$$
(22)

Using the obtained values for the d and q axes components, the reference components are computed using (23) and (24).

$${i}_{sRp}={X}_{Fp}{u}_{Rp},{i}_{sYp}={X}_{Fp}{u}_{Yp}, {i}_{sBp}={X}_{Fp}{u}_{Bp}$$
(23)
$${i}_{sRq}={X}_{Fq}{u}_{Rq}, {i}_{sYq}={X}_{Fq}{u}_{Yq}, {i}_{sBq}={X}_{Fq}{u}_{Bq}$$
(24)

The final RCs at grid side 3 lines are obtained as below.

$$i^{*}_{sR} = i_{sRp} + i_{sRq} ,\quad i^{*}_{sY} = i_{sYp} + i_{sYq} ,\quad i^{*}_{sB} = i_{sBp} + i_{sBq}$$
(25)

The obtained reference input values are cross verified with the active values. The changes detected in each leg are then transferred via the hysteresis controller for the production of switching pulses proposed for the specific phases of the converter. This DSTATCOM will make the system PF near to UPF, considering imaginary power manangement & mitigating harmonics at the source side. Consequently, it improves the quality of power substantially.

XANN model outputs and description

The developed XANN regulator is executed in MATLAB to produce IGBT pulses to the converter. The PV-Wind system manages a stiff DC bus voltage given as source to the converter. The configuration of the new XANN appraoch is presented in Fig. 6. The response investigation of the XANN regulator for converter in a PV wind power system is tested out for different loads like balanced & uneven nature.

Fig. 6
figure 6

Generating RC for DSTATCOM.

Full size image

Investigation of controller with balanced load

The XANN based converter is connected to the grid where a balanced load with non-linear in nature is also available. Load demands both imaginary power and non-linear current, DSTATCOM provides that non-linear current, acting as a grid-connected inverter. The controller is turned on at t = 0.05–0.1 s. The results of the GC, LC and controller current are presented in Figs. 7, 8 and 9. A model assessment in Fig. 8 reflects that prior to t = 0.1 s, the GC displays non-linear nature as it addresses the current requirement. When the controller is turned on at t = 0.1 s, it starts sharing the required reactive power & non-linear current to the load, ensuing in the conversion of the supply current into a actual sine format.

Fig. 7
figure 7

GC results before and later control.

Full size image
Fig. 8
figure 8

Load Current results.

Full size image
Fig. 9
figure 9

Compensator currents by DSTATCOM.

Full size image

The production of IGBT pulses for the grid-tied converter, which acts as a controller, is accomplished using the developed XANN approach. In distinction to providing uneven currents from 3 legs, only one balanced 3-leg current is given as source for the XANN model. The LC’s harmonic profile is evaluated early & later control, as presented in Fig. 10. The outcomes reflect an enrichment in results afrer control action. The THD value early to control is lmost 26%, while later control action is notably reduced to 4%. These values authorises that the system’s operation has been substantially enhanced via the control action.

Fig. 10
figure 10

THD (a) early to control (b) later control.

Full size image

Investigation of converter with uneven load

An uneven load with non-linear nature connected to grid along with an ANN-BP based DSTATCOM and is verified using the MATLAB outputs reflected in Fig. 11.

Fig. 11
figure 11

Output results at PCC: GCs, Currents at Load and Controller Current.

Full size image

These outputs exemplify the nature of 3-leg voltages & currents at source, which sustain an actual sinusoidal form. Contrarywise, the Fig. 11c reflects 3-leg LCs, with non-sinusoidal response. The Fig. 11d presents controlling currents, illustrate the required harmonic component for minimizing the effect of power electronic loads are injected at the PCC by the converter.

The outputs from the MATLAB displaying DC bus voltage, grid-side NC, the load NC, and the controller NC are shown in Fig. 12. The unevenness occuring due to the load is nullified by providing the required NC by using the converter’s fourth leg. As the NC at load is controlled by the converter, the NC of grid does not transfer any uneven current at the load, maintaining a balanced neutral at grid.The Fig. 13a,b projects 3-leg THD early and later control action for each phase respectively. It is resolved that THD later control is 2% for all 3 phases. Early to control, the power electronic uneven load values reflect THD approximately 20% in R-leg, 30% in Y-leg, & 6% in B-leg. Where as, the THD profile at the grid reaching near to 1%. These THD counts are available in Table 1.

Fig. 12
figure 12

DC link Voltage (Vdc), NC at Grid (ISryb), NC at Load (ILn) & Controller Current (IVSCn).

Full size image
Fig. 13
figure 13figure 13

(a) THD of 3-leg currents early to control (R-Y-B). (b) THD of 3-leg currents later control (R-Y-B).

Full size image
Table 1 THD assessment of 3 legs.
Full size table

Therefore, the developed XANN model perfectly follows the standard of IEEE 51918, it denotes that harmonic distrortion should not cross 5%. This performance substantially enhances the quality of power at the grid-tied solar-wind power system.

The comparison of the THD analysis of the DSTATCOM using PI Controller, Fuzzy Logic Controller and the ANN Controller is shown in the given below Table 2. It presents the improvement in the THD after the compensation and also shows that with ANN based DSTATCOM has been improved to 3.9% which is in the range of IEEE standard.

Table 2 THD Comparison for different controllers.
Full size table

Realtime set-up of proposed model

The developed inverter setup model is executed through the realtime setup projected in Fig. 14. The realtime setup of developed model using digital signal processing and control engineering (dSPACE) or even loading situation is executed and results obtained. The details of the realtime set-up are given in Table 3. The desired pulses for all 6 IGBTs of converter are generated by the DSP device to obtain the good performance.

Fig. 14
figure 14

Realtime setup of proposed Controller.

Full size image
Table 3 Details of the realtime setup.
Full size table

The setup made run for 10 µsec of sampling interval. Quartus tool is utilized to develop the model for the realization on the DSP controller. The MATLAB circuit developed is given to the dSPACE module via its integrated device. The data to be verified is shared with the dSPACE and DSP via a serial connector and the accomplished outputs are een using DSO.

The outputs of voltage and currents obtained using the realtime setup are taken by a DSO & are shown in Fig. 15. The outputs of GC demonstrated in Fig. 15. In this scenario, VS denotes pure voltage at grid , whereas IS reflects the current at grid. Before control action, the current at grid is full of harmonics, because power electronic load draws power from grid, till the converter is turned ON. Then, upon switching of the converter, it starts transferring the required imaginary power & compensating content to load, thereby making current at grid a perfect sinusoidal. Figure 15 demonstrates controller current (IC) and Volatge (VC), the converter’s current at PCC to address the power electronic load. Figure 16 representing the three currents of R-Y-B phases separately.

Fig. 15
figure 15

DSO values of current at grid, current at load & current and voltage of controller.

Full size image
Fig. 16
figure 16

DSO captured load side currents.

Full size image

LC’s harmonic profile with the balanced power electronic load is captures as 25.97% without control action. This value minimized nearly 4.17% as the developed ANN based model is turned-on. The harmonic profile after control action is presented in Fig. 17. The acquiescence to the IEEE 51918 is authorized, as the harmonic profile of GC reduced to less than 5%. An assessment of the harmonic content determined from SIMULINK and realtime outputs is projected in Table 4 and in Fig. 18 it is projected by a bar diagram. The orange one shows the harmonic profile using realtime setup & the blue one is harmonics representing the simulink value.

Fig. 17
figure 17

Harmonic profile of the grid-tied converter.

Full size image
Table 4 Evaluation of the harmonics obtained from simulink & realtime setup.
Full size table
Fig. 18
figure 18

Chart of harmonic profile projecting simulink and realtime outputs.

Full size image

To illustrate the performance of developed ANN based model is compared to PI based model and the investigations are projected in Table 5. From the results it is conditional that the developed ANN approach marks in mitigation of harmonics to 3.7% as related to traditional PI based approach whose harmonic profile stands at 6.4%.

Table 5 Assessment of the harmonic profile attained from developed ANN and PI approaches.
Full size table

Conclusion

The developed XANN based DSTATCOM is executed for power electronic based balanced & uneven loads in PV wind power system. The adoption of the XANN scheme, the grid-tied DSTATCOM perfectly addressed the imaginary power necessities of power electronic load and also alongside attaining a mitigation of harminics. The developed model projects a notable capacity to uphold a appropriate balance when challenged with uneven and non-sine load backgrounds. The matching of NC at the input side is attained when the uneven load’s ground creates issues at grid by using the fourth phase of the developed model. To authenticate its performance, the developed XANN based controller is executed on a realtime setup using dSPACE. The DSP controlled active filter is proficient in obtaining THD profile less than 5%, line-up with the IEEE 519 standards. A relative investigation is performed for the developed XANN based model and a converter with conventional PI control. The outputs authenticate the better outcomes of the developed model, beating the conventional PI method.

Future scope

  • In the further research work, multi-level inverters with the XANN-BP controller can be implemented for mitigating harmonics effectively.

  • Integrating real-time adaptive learning schemes to tune ANN parameters perfectly under dynamically changing environmental conditions.

  • Investigating hybrid control approaches integrating ANN with fuzzy logic or genetic algorithms for greater response.

  • Exploring the scalability of the control system to larger-scale renewable energy systems, including offshore wind farms and community solar setups.