Introduction

In recent years, the complexity and diversity of optimization problems in various domains-such as energy systems, communication networks, routing, and scheduling-have highlighted the limitations of traditional optimization methods1. These classical techniques struggle to address the increasingly intricate real-world challenges posed by large-scale and dynamic systems2. To overcome these challenges, meta-heuristic algorithms, inspired by intelligent behaviors of nature, have gained prominence as powerful tools to solve complex optimization problems.

Among these, Swarm Intelligence Optimization Algorithms (SIOAs)3, which mimic the collective behavior of biological systems such as birds flocking or ants foraging, have proven particularly effective4. These algorithms leverage the inherent mechanisms of exploration and exploitation of biological populations to navigate large and multidimensional solution spaces. In the last decade, a variety of bio-inspired algorithms have been proposed and refined, including the Tree Growth Algorithm (TGA)5, Forest Optimization Algorithm (FOA)6, the Cuckoo Search (CS)7, and the Grey Wolf Optimizer (GWO)8, which have been successfully applied to various problems in fields ranging from engineering design to path planning. According to various studies, dynamic storage9, workshop scheduling10, path planning11, and the travelling salesman problem12 can be solved using SIOAs.

Despite their successes, these algorithms face several challenges, particularly in addressing NP-hard problems (including job shop scheduling13, engineering design14and image processing15) that require finding near-optimal solutions in large and complex search spaces16,17. Traditional methods often fail to perform effectively, especially when dealing with problems involving high-dimensionality or dynamic environments. In response, researchers have turned to more flexible and reliable meta-heuristic approaches such as Naked Mole-Rat Algorithm (NMRA)18. NMRA, inspired by the mating and worker-breeder relationship of naked mole-rats, is a recent addition to the family of bio-inspired algorithms. NMRA has shown significant potential in solving optimization problems, particularly those in antenna design19, engineering design20, and image segmentation21. However, despite its strong exploitation phase, the algorithm tends to face challenges in its exploration phase, which limits its effectiveness in high-dimensional and multi-modal search spaces.

To address these challenges, this paper proposes an enhanced version of NMRA, referred to as Salp Swarm and Seagull Optimization-based Naked Mole-Rat Algorithm (SSNMRA). The main contribution of this work is two-fold:

  • Introducing a multi-algorithm strategy that integrates the Salp Swarm Algorithm (SSA)22and the Seagull Optimization Algorithm (SOA)23 into the exploration phase of NMRA, and

  • Incorporating a stagnation phase and a self-adaptive mutation operator to improve the algorithm’s ability to avoid local optima and enhance its performance in solving complex optimization problems.

The multi-algorithm strategy divides the exploration phase into three parts, each utilizing different search strategies from NMRA, SSA, and SOA. This approach significantly improves the exploration capability of the algorithm by enhancing its diversity in search. Additionally, the stagnation phase monitors the algorithm’s progress and triggers more aggressive exploration if no improvement is observed over a set number of iterations. Lastly, a simulated annealing (sa) based mutation operator24 is incorporated to further refine the initial search, making the algorithm self-adaptive and improving its robustness across various optimization problems.

Through extensive experimentation, the proposed SSNMRA is evaluated on several benchmark optimization problems. The results demonstrate that SSNMRA outperforms traditional NMRA and other state-of-the-art algorithms in terms of both solution quality and convergence speed. This paper provides valuable insights into the integration of multiple optimization strategies within a single framework, offering a more effective solution for tackling complex real-world problems.

The rest of the article is divided into different sections as follows, the need of the proposed algorithm along with the details of SSNMRA is detailed in Section 3. The experimental results are described and discussed in Section 4. Section 5 concludes the paper along with summary of future work.

Related work

Optimization algorithms inspired by natural systems have attracted significant attention due to their ability to solve complex real-world problems where traditional optimization methods fall short. Swarm Intelligence Algorithms are among the most popular approaches due to their simplicity and effectiveness in handling large, high-dimensional search spaces. These algorithms are widely used across different domains, from energy systems to engineering design and scheduling problems.

SIOAs, such as the Ant Colony Optimization (ACO)25, Particle Swarm Optimization (PSO)26, and Bat Algorithm (BA)27, have been successfully applied to a wide range of optimization problems. These algorithms mimic the collective behavior of swarms, such as ants finding food or birds flocking, to find optimal solutions through local interactions among individuals in a population. The fundamental advantage of SIOAs lies in their balance between exploration (searching for new areas of the solution space) and exploitation (refinement of solutions within a known region). Among the numerous SIOAs, the Grey Wolf Optimizer (GWO)8, Cuckoo Search (CS)7, and improved African Vultures Optimization (AVO)28 is particularly notable for their ability to balance exploration and exploitation. GWO mimics the hunting behavior of grey wolves, whereas CS is based on the brood parasitism behavior of cuckoos. AVO is inspired by the foraging and scavenging behaviors of African Vultures. These birds have developed sophisticated strategies to locate food, often relying on group dynamics and observing the behavior of other birds.

A recently proposed meta-heuristic, Manta Ray Foraging Optimization (MRFO)29, inspired by the foraging behavior of manta rays, has shown significant promise in handling complex optimization problems. MRFO has been widely used for various applications, including engineering optimization, where the need for balance between exploration and exploitation is critical. Another recent development is the Heterogeneous Comprehensive Learning Symbiotic Organism Search (HCL-SOS) algorithm30, which utilizes a comprehensive learning strategy to improve the algorithm’s performance in solving multi-modal optimization problems. This approach combines heterogeneous learning mechanisms to adaptively explore the solution space, significantly improving the algorithm’s robustness. In addition to these advances, algorithms based on chaotic behavior, such as the Chaotic Rime Optimization Algorithm (CROA)31 with adaptive mutualism, have been proposed to solve feature selection problems. These algorithms employ chaotic maps to enhance search diversity, thus preventing premature convergence and improving global search capability.

The naked mole-rat algorithm (NMRA) is a recent SIOA based on the natural mating behavior of naked mole-rats18. This algorithm and its variants are found to be suitable for solving different real optimization problems such as engineering design problems20, image segmentation21, and non uniform circular antenna array19. A group of 50 to 295 members of this species live in a worker-breeder relationship. The relationship between workers and breeders refers to the division of the population into workers and breeders categories. Performing labour and maintenance, providing assistance in the selection of new breeders, and other tasks are all concerns of the worker group. Breeders are nominated from the worker pool and specifically chosen to mate with the queen. It is not uncommon for workers to be moved from breeder pools to worker pools if a particular breeder is not up to snuff when compared to the others in the group. The process repeats iteratively, with the best workers becoming the new breeders and the best breeder mates with the queen.

The algorithm is divided into two phases, the worker and breeder phase. Using two random NMRs in close proximity, the worker phase is updated, while the breeder phase is controlled based on the best NMR. After the predetermined number of iterations, the best breeder is considered to be the solution to the problem. In both the phases, a simple random mating factor governs the outcome of the problem. A better exploitation operation is found in NMRA because the updated solution depends on both mating factor and the best solution in the breeder phase. In contrast, the exploration process relies simply on random solutions, and hence the quality of the solutions has lower improvement. In this step, the algorithm is susceptible to poor exploration because it falls into a local optimal solution.

As a result, NMRA’s exploitation operation is highly effective, but its exploration operation is relatively poor. Hence, to improve the exploration capability of NMRA, it needs to be improved. It is important to keep in mind that the worker phase focuses on the exploration characteristics of algorithm. So, a multi-algorithm strategy by grouping iterations has been employed in this work to improve NMRA’s performance. Here, the term multi-algorithm strategy means to improve the exploration process, multiple algorithms are used iteratively.

In the worker phase, different algorithms are used for a specific set of iterations. During the breeding phase, on the other hand, no modification has been introduced in the basic NMRA and is remains same. Stagnation has been added as a new phase to the algorithm to keep an eye on solutions that are becoming stagnant. There are three different search equations from three different algorithms used in the modified exploration phase, while the basic NMRA equations are used as it is in the exploitation phase. In addition, parametric enhancements have been employed in the algorithm to make it self-adaptive.

The worker phase is divided into three parts depending on the number of iterations, and the search equations of NMRA, salp swarm algorithm (SSA)22and seagull optimization algorithm (SOA)23have been incorporated, and hence named as salp swarm and seagull optimization based NMRA (SSNMRA). The basic NMRA search equations are used for the first third of iterations, the search equations for the second third, and the SOA equations are employed for the rest of the iterations. The stagnation phase (GWO-CS algorithm based search equations) is activated as soon as a certain threshold is not satisfied for the set of iterations for the updated solutions21. Following subsections provide a more in-depth explanation of why these algorithms were used.

A simulated annealing (sa) based mutation operator24 has also been added to the proposed algorithm’s initial parameter values, which improves the working of proposed algorithm. Since, no parametric adjustments (user-based) are required with this mutation operator, the algorithm becomes self-adaptive.

Despite the considerable success of various SIOAs, most existing techniques, including NMRA, struggle with poor exploration in complex optimization spaces, leading to local optima. The proposed SSNMRA aims to bridge this gap by introducing a multi-algorithm strategy during the worker phase and improving the exploration phase through the integration of SSA and SOA. To clarify the research gap further, a comparative table has been presented summarizing the key features of the reviewed algorithms, their strengths, weaknesses, and the contributions of the proposed SSNMRA.

Table 1 The comparative analysis of algorithms.
Full size table

The comparative analysis given in Table 1 clearly identifies the strengths and limitations of existing algorithms, highlighting the gap in exploration capability in many swarm-based algorithms. While NMRA excels in exploitation, its exploration is limited, especially in high-dimensional optimization tasks. The proposed SSNMRA algorithm overcomes this by incorporating multiple algorithms in the worker phase, introducing a stagnation phase, and making the algorithm self-adaptive with a mutation operator. These enhancements aim to improve both exploration and exploitation, offering a promising solution for solving complex optimization problems.

Proposed approach

NMRA is a recently developed optimization algorithm that produces consistent results for the optimization tasks. However, compared to advanced hybrid and adaptive algorithms, NMRA’s performance is less consistent. The main reason is NMRA’s poor exploration ability that causes the algorithm to get stuck in local optima. Additionally, tweaking the mating factor \((\lambda )\) and breeding probability (bp) parameters could make the algorithm more efficient at balancing exploration and exploitation (for controlling the extent of global and local search). This research examines these two aspects and develops a new NMRA variant called salp swarm and seagull optimization based NMRA (SSNMRA), with the following key features:

  • First, three distinct search equations are utilized for different iteration sets to enhance the worker phase’s capabilities.

  • The original NMRA equations are applied for the first third of iterations, SSA and SOA based equations for the second and third sets respectively.

  • A new stagnation detection phase based on GWO-CS algorithms is introduced to improve the balance between exploitation and exploration.

  • NMRA’s core parameter \(\lambda\) is united with a simulated annealing (sa) based mutation operator24 to make it self-adaptive without requiring user-based parameter customisation.

  • The original NMRA breeder phase structure is retained and applied with randomized techniques.

SSNMRA aims to improve NMRA’s exploration and provide a more adaptive and efficient optimization algorithm while preserving the original NMRA framework.

Need of this algorithm

With the development of new optimization algorithms, determining which one is best for a particular optimization problem is very challenging. The no-free-lunch theorem (NFL) has shown that relying on one optimization method is not sufficient for evaluating performance across all problem domains32. Therefore, novel optimization approaches based on modifications are needed to handle a variety of optimization problems. The main reason for altering the original method is that every problem domain is unique in terms of its nature (constrained or unconstrained), complexity, size and other factors. Due to high dimensionality and numerous local minima, it is difficult for researchers to develop improved versions that yield superior outcomes. The original NMRA has poor exploration capabilities, which reduces the overall efficiency of the algorithm. Thus, new worker phase equations are required to prevent getting stuck in local minima and ensure proper exploration is conducted. These additional equations need to be incorporated in a way that does not disrupt the fundamental structure of NMRA.

Proposed algorithm: SSNMRA

The proposed SSNMRA optimization technique merges the advantages of NMRA, SSA, and SOA. This algorithm consists of five phases. The initial phase involves initializing random solutions, followed by the worker phase, which integrates all enhancements to refine the exploration process. The third phase, known as the breeder phase, mirrors the basic NMRA approach, while the subsequent phase involves selection operations. The final phase is characterized as the stagnation phase, employing GWO-CS algorithms.

Initialization

The SSNMRA begins with the initialization of random search candidates within a defined range for a dimension (d), with the following expression:

$$\begin{aligned} SN_{i,j} = lb_{j} + rand(0,1) \times (ub_{j}-lb_{j}) \end{aligned}$$
(1)

where i \(\epsilon\) [1, 2, 3.... .N], N represents the population size of naked mole (number of search candidates), j \(\epsilon\) [1, 2, 3, . .d]. The optimization problem’s dimension is d, \(SN_{i,j}\) is the solution of the \(i^{th}\) search candidate for the \(j^{th}\) dimension, the test problem’s lower and upper boundaries are \(lb_j\) and \(ub_{j}\) respectively, and rand(0, 1) is distributed randomly in the range [0, 1].

Worker phase

The worker phase of the proposed optimization algorithm is derived from conventional NMRA, SSA, and SOA. As in the exploration phase, it has been observed that the worker phase is less reliable, necessitating further refinement to enhance its operational effectiveness. This worker phase consists of three algorithmic equations, and one of these equations is chosen for a particular set of iterations to update the new solution. The use of these equations are defined in three phases as:

a) Phase I:The maximum exploration is important in first one-third iterations and classical NMRA’s equation is used for these iterations18. This phase is mainly driven using two random solutions and an adaptive \(\lambda\) parameter using sa mutation operator as given in equation (3). The random solutions may move close together in this case, but the greater steps provided by employing \(\lambda\)make it more exploratory33. As a result, the solutions can search the entire search space. The following equation is considered for the generation of a new search candidate’s solution:

$$\begin{aligned} SN_{i}^{t+1}=SN_{i}^{t}+\lambda (SN_p^t-SN_q^t) \end{aligned}$$
(2)
$$\begin{aligned} \lambda =\gamma _{min}+(\gamma _{max}-\gamma _{min}) \times p^{(k-1)} \end{aligned}$$
(3)

where k, \(\gamma _{min}\) and \(\gamma _{max}\) are random numbers specified in the range [0, 1] and p is set to 0.95, \(SN_i^t\) is the solution of \(i^{th}\) worker for \(t^{th}\) iteration, \(SN_i^{t+1}\) represents the new solution generated by randomly choosing previous solutions \(SN_p^t\) and \(SN_q^t\) from the workers pool and are chosen such that new adaptive \(\lambda\) variable improves the search process and increasing the probability of exploration.

b) Phase II:During the second one third iterations, the exploration process of optimization algorithm begins to migrate towards the exploitation operation. As a result, both exploitation and exploration operations are important at this stage. The mathematical equations based on SSA was employed for this set of iterations due to its effective combined exploration and exploitation capabilities22. To track exploration and exploitation, \(c_1\) is one of the important parameter and need to be optimized. The generalized equations to implement this phase are given as:

$$\begin{aligned} SN_{i}^{t+1}= {\left\{ \begin{array}{ll} SN_{best}+c_1((ub_j-lb_j)c_2+lb_j) \hspace{5pt} z \ge 0 \\ SN_{best}-c_1((ub_j-lb_j)c_2+lb_j) \hspace{5pt} z \le 0 \end{array}\right. } \end{aligned}$$
(4)
$$\begin{aligned} c_1=2\hspace{2pt}e^{-(\frac{4t}{t_{max}})^2} \end{aligned}$$
(5)

where t denotes the current iteration value, \(t_{max}\) is maximum count of iterations, \(SN_{i}^{t+1}\) represents new solution of search candidate with respect to best solution \(SN_{best}\) and \(c_2\) is randomly distributed between 0 and 1.

c) Phase III:The optimization algorithm has to provide significant exploitation operations in the last one third set of iterations. The SOA method is well-known for its effectiveness in addressing optimization problems due to its attacking behaviour and makes the algorithm capable for better exploitation operations. This is because each seagull in SOA only updates its position in relation to best fittest seagull. As a result, each seagull is updated in each iteration, and when all of the seagulls have been updated, the seagulls are sorted by fitness. The algorithm is able to avoid local optima, resulting in improved exploitation operations23. This phase’s general equations are as follows:

$$\begin{aligned} SN_i^{t+1}=(SN_d \times x_1 \times x_2 \times x_3) + SN_{best} \end{aligned}$$
(6)
$$\begin{aligned} SN_d = |SN_c + SN_m| \end{aligned}$$
(7)
$$\begin{aligned} SN_c = SN_a \times SN_i^t \end{aligned}$$
(8)
$$\begin{aligned} SN_a= f_c - \left( t \times (\frac{f_c}{t_{max}})\right) \end{aligned}$$
(9)
$$\begin{aligned} SN_m = SN_b \times (SN_{best}- SN_i^t) \end{aligned}$$
(10)
$$\begin{aligned} SN_b = 2 \times SN_a \times r_1 \end{aligned}$$
(11)
$$\begin{aligned} x_1 = rad \times cos (p) \end{aligned}$$
(12)
$$\begin{aligned} x_2 = rad \times sin (p) \end{aligned}$$
(13)
$$\begin{aligned} x_3 = rad \times p \end{aligned}$$
(14)
$$\begin{aligned} rad = u \times e^{pv} \end{aligned}$$
(15)

where \(SN_i^t\) is the search candidate solution for the current iteration t, \(SN_a\) defines search candidate’s movement behaviour in the search space, \(f_c\) is used to control the frequency with \(SN_a\) which decreases from \(f_c\) to 0 linearly and value of \(f_c\) is set to 2. The solution of search agent \(SN_i^t\) in relation to the best-fit search candidate \(SN_{best}\) is defined by \(SN_m\) with a random parameter \(SN_b\). The parameter \(SN_b\) is accountable for correct balance between exploitation and exploration operations. \(SN_c\) is the position of search candidate that does not collide with other search candidates. The distance between search candidate and the best fit search candidate is defined by \(SN_d\). Finally, spiral turn’s radius is denoted by rad, p is defined in range \([0,2\pi ]\), constants u and v represents shape of spiral and e is natural logarithm.

Breeder phase

In the proposed SSNMRA algorithm, this particular phase is executed employing the original structure of NMRA. Here, breeder rats are restricted and are tasked to mating with the queen (global optima). Consequently, the breeding period predominantly aligns with the exploitation phase. This exploitation phase is leveraged in the global search phase, aiming to attain a global solution as the termination criteria near completion by seeking a solution closer to the current best solution. The breeder phase of the new SSNMRA algorithm remains unaltered from that of the original NMRA and is implemented as follows:

$$\begin{aligned} SN_i^{t+1}=(1-\lambda )SN_i^t+\lambda (SN_{best}-SN_i^t) \end{aligned}$$
(16)

where mating parameter \(\lambda\) is based on sa mutation operator and rest of the parameters are same as defined in the worker phase.

Selection operation

The selection phase of SSNMRA is deemed the most critical. This optimization technique adopts a greedy selection approach, where the new solution is treated as the current local best solution and is updated if the newly generated solutions surpass the performance of the previous generation’s solution. The selection method for the minimization process, utilizing the fitness \(f(SN_i^t)\) for the \(SN_i^t\) solution, is described as follows:

$$\begin{aligned} SN_{new}^{t+1}= {\left\{ \begin{array}{ll} SN_{new} \hspace{20pt}if f(SN_{new})<f(SN_i^t)\\ SN_i^t \hspace{35pt} otherwise \end{array}\right. } \end{aligned}$$
(17)

Stagnation phase

GWO and CS emerge as two successful algorithms effectively addressing numerous real-world optimization challenges. They demonstrate exceptional capabilities in both exploration and exploitation. These attributes are further enhanced when the GWO algorithm is integrated with the CS algorithm, fostering a balance between exploitation and exploration operations34. To begin, averaging three random solutions from the entire search group improves the search. The updated solutions are based on previous ones and are expressed as

$$\begin{aligned} SN_1=SN_i-P_1(Q_1.SN_{new}-SN_i^t) \end{aligned}$$
(18)
$$\begin{aligned} SN_2=SN_i-P_2(Q_2.SN_{new}-SN_i^t) \end{aligned}$$
(19)
$$\begin{aligned} SN_3=SN_i-P_3(Q_3.SN_{new}-SN_i^t)P \end{aligned}$$
(20)
$$\begin{aligned} SN_{new}^{t+1}=\frac{SN_1+SN_2+SN_3}{3} \end{aligned}$$
(21)

where \(Q=2a.r_1-a\) and \(P=2.r_2\) provides \(Q_1, Q_2, Q_3\) and \(P_1, P_2, P_3\), which are produced from Q and P, respectively. The random integers \(r_1\) and \(r_2\) are evenly distributed, however the variable a is linearly decreasing. In this case, equation (21) provides solutions, which are subsequently subjected to a CS-based search equation. The new solution is generated via Cauchy randomization given as:

$$\begin{aligned} f_{Cauchy(0,h)}(\delta )=\frac{1}{\pi } \frac{h}{({h^2}+{\delta ^2})} \end{aligned}$$
(22)

The Cauchy distribution function is calculated as follows:

$$\begin{aligned} w=\frac{1}{2}+\frac{1}{\pi }arctan(\frac{\delta }{h}) \end{aligned}$$
(23)

The value of \(\delta\) can be found by solving the equation (23) and described as:

$$\begin{aligned} \delta =tan(\pi (w-\frac{1}{2})) \end{aligned}$$
(24)

Here, final search equation inspired by CS is described as:

$$\begin{aligned} SN_i^{t+1}=SN_i^t+\alpha \otimes {Cauchy(\delta )}(SN_{best}-SN_i^t) \end{aligned}$$
(25)

Here, scaling factor is h and the Cauchy random number is \(\delta\). Utilizing a Cauchy-based distribution offers a key advantage due to its thicker tail, allowing for larger steps that facilitate better exploration of the search space and help avoid local optima, ultimately enhancing search performance. However, solely relying on new solutions derived from the current best solution may limit exploration of the search space and potentially lead to premature convergence. Consequently, SSNMRA offers the added advantage of robust exploration operations and a balanced approach to exploration and exploitation. The flow chart illustrating the proposed SSNMRA is provided in Fig 1.

Fig. 1
figure 1

Flow chart of proposed SSNMRA.

Full size image

Results and analysis

The compatibility of the SSNMRA algorithm has been examined in the 100-digit challenge test suite (CEC 2019)35 as described in Table 2, designing of linear antenna array and E-shaped patch antenna in this section. The purpose of this performance assessment is to compare the proposed algorithm with other algorithms to determine its credibility. The first subsection assesses SSNMRA’s performance for CEC 2019 numerical test problems, while the second assesses SSNMRA’s working capability for linear antenna array design (LAA) and the third subsection deals with designing an E-shaped patch antenna. For experimental analysis, results are simulated on MATLAB version R2023b (https://in.mathworks.com/products/matlab-online.html) along with CST 2022 (Computer Simulation Technology; https://www.3ds.com/products/simulia/cst-studio-suite) simulation software on windows 11, intel i7 processor having a RAM of 8GB.

Table 2 100-digit challenge (CEC 2019) benchmark test suite.
Full size table

Performance analysis of SSNMRA for CEC 2019 test suite

The effectiveness of the proposed SSNMRA is evaluated on the ten most challenging 100-digit challenge (CEC 2019) numerical test suite35. The description of these test problems is detailed in Table 236. Here, the effectiveness of proposed SSNMRA is compared with other competitive algorithms such as winner of CEC 2019 competition (jDE100)37, differential evolution (DE)38, SSA22, NMRA18and SOA23 as shown in Table 3. The statistical outcomes are presented in terms of mean, worst, best, median and (Std) values with 50 population size and 500 iterations for 50 runs of each algorithm.

The findings presented in Table 3 shows that SSNMRA can outperform alternative algorithms for problem \(p_1\) for median, mean and std values. The results for problems \(p_2\) and \(p_3\) are comparable based on std values and SSNMRA is demonstrated to be the best among the other algorithms. The proposed SSNMRA findings are determined to be superior to other optimization strategies under consideration for problems \(p_4\), \(p_5\), \(p_6\), \(p_7\), \(p_9\), and \(p_{10}\). Finally, for the problem \(p_8\), the working efficiency of SSA is optimal in terms of best and median values.

Table 3 Statistical results for CEC 2019 problems.
Full size table
Table 4 The computation time(s) obtained by SSNMRA and simulated algorithms for CEC 2019 benchmark test suite.
Full size table

Apart from simulated results, two statistical tests namely Wilcoxon’s rank-sum (p-rank) test39and Friedman (f-rank) test40 have been employed to validate the efficiency of SSNMRA. Firstly, the analysis is done in terms of win(w)/loss(l)/tie(t) to determine p-rank. If the comparison optimization technique outperforms SSNMRA, the scenario is denoted by a “+” and is known as a “win(w)” situation. The “−” sign is utilised because the test algorithm performs worse than the SSNMRA in the loos(l) scenario. The “\(=\)” indication indicates that the competing algorithms are equally capable of solving the objective function in the case of tie(t). The suggested optimization technique SSNMRA outperforms in all test instances, as shown in the sixth row of each numerical problem in Table 3. Secondly, the f-rank is calculated and from the last two rows of Table 3, it is concluded that SSNMRA ranked first among all the algorithms considered.

The convergence graphs of DE, SSA, SOA, NMRA and the proposed SSNMRA for the numerical test problems are depicted in Fig. 2. These graphs provide a comprehensive comparison of the convergence behaviour of the algorithms across various test scenarios. From Fig. 2, it is evident that SSNMRA demonstrates a significantly faster convergence rate compared to SSA, DE, SOA, and NMRA for the majority of problems, specifically \(p_1\), \(p_2\), \(p_3\), \(p_4\), \(p_5\), \(p_6\), \(p_7\), \(p_8\) and \(p_{10}\). This rapid convergence indicates that SSNMRA is highly effective in navigating the solution space and quickly approaching optimal or near-optimal solutions. For problem \(p_9\), a slightly different trend is observed. The original SSA converges to the optimal solution relatively early in the iterative process, demonstrating strong performance for this particular problem. However, SSNMRA converges at a later stage, indicating that while it may not exhibit the fastest convergence in this specific instance, it still manages to achieve competitive results eventually. This suggests that SSNMRA maintains robustness and adaptability across diverse problems, even when it does not outperform SSA. Overall, compared to DE, SSA, SOA, and NMRA, SSNMRA exhibits a faster convergence rate in most scenarios, highlighting its efficiency and reliability as an optimization algorithm. Its ability to outperform existing methods in the majority of cases underscores its potential as a robust solution for complex optimization problems.

SSNMRA, being a hybrid optimization algorithm of SSA, SOA and NMRA along with its self-adaptive capabilities and local minima avoidance properties, achieved better results at the cost of higher computational cost. The average CPU times of the different algorithms, considering all cases, are provided in Table 4. As can be seen in the table, SSA and SOA each achieved the lowest computation time for most of the functions. NMRA also achieved optimal computation time for a small number of functions. DE performed a little poor in terms of computational time. SSNMRA achieved better results while maintaining the runtime at a reasonable cost.

Fig. 2
figure 2figure 2

Convergence profiles of DE, SSA, SOA, NMRA and SSNMRA for CEC 2019 problems.

Full size image

Analysis of SSNMRA on linear antenna array design

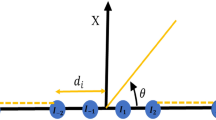
In this subsection, LAA designing parameters are optimized using the proposed SSNMRA. The aim is to find suitable antenna parameters so that it meets the required design criteria. A 2N-element LAA consists of 2N isotropic elements placed in a linear manner along the x-axis as shown in Fig 3. There are two sets of N elements on both sides of origin. The symmetry of geometry reduces the computational complexity to half. The array factor (AF) of the LAA array is a function of the spacing between the elements and element currents is given by:

$$\begin{aligned} AF\left( \phi \right) =2\sum _{n=1}^{N} I_n cos[k x_n cos(\phi )+ \phi _n] \end{aligned}$$
(26)

where \(I_n\), \(x_n\) and \(\phi _n\) represents the element amplitude excitation, the spacing between the elements and the phase of each element. If the spacing between the elements is fixed and is equal to \(0.5\lambda\), then these types of arrays are known as uniformly spaced LAAs. On the other hand, for unequally spaced arrays the element excitations are uniform but element locations are changed to get the required antenna radiation pattern. Here, in this paper, both equally spaced and non-uniform antenna arrays are optimized using the SSNMRA.

Fig. 3
figure 3

A 2N-element LAA along the x-axis.

Full size image

In antenna arrays, the energy is distributed between the main lobe and the number of side lobes. For a directional antenna, it is desired that the side lobe level (SLL) should be as minimum as possible to avoid interference from undesired directions. Moreover, sometimes it is required to jam a signal in a particular direction and can be achieved by aligning the null in that particular direction41. To achieve an antenna array with minimum possible SLL and nulls, a suitable fitness function is defined and is given below:

$$\begin{aligned} Fitness=k_1f_{SL}\left( \phi \right) +k_2f_{NS}(\phi ) \end{aligned}$$
(27)

Where \(k_1\) and \(k_2\) are the weights of the two objectives with \(k_1+k_2=1\), and SL is the side lobe region and \(\phi _k^{null}\) is \(k^{th}\) null direction. The AF here is in decibels and \(f_{SL}\left( \phi \right)\) and \(f_{NS}(\phi )\) are defined as:

$$\begin{aligned} f_{SL}\left( \phi \right) =max(AF\left( \phi \right) ) \end{aligned}$$
(28)
$$\begin{aligned} f_{NS}\left( \phi \right) =\max _{k=1\ldots ..K}{\left( AF\left( \phi _k^{null}\right) \right) } \end{aligned}$$
(29)

Unequally spaced arrays

In the first case, a 12-element non-uniform LAA excited with equal amplitude excitations is taken for optimization using SNMRA. The design of a non-uniform antenna is a classical antenna design problem that has been dealt various researches in the past. An aperiodic AF is obtained by the non-uniform spacing. The unequal spacing helps to obtain low SLL with less number of antennas for a fixed antenna length. The connection between AF and element placements is non-linear and non-convex, making the construction of a non-uniform array difficult and sophisticated. The AF for the non-uniform array with equal amplitude excitations is expressed as

$$\begin{aligned} AF\left( \phi \right) =2\sum _{n=1}^{N} cos[k x_n cos(\phi )] \end{aligned}$$
(30)

For proving the robustness and effectiveness of SNMRA, it is here applied to an antenna problem and its comparison is made with the other optimization techniques. A 12-element symmetric array design problem is considered using SSNMRA. The goal is to achieve the required radiation pattern by optimizing the positions of elements. Since it is a symmetric structure, only six elements are to be optimized to get the desired radiation pattern. The objective for this case is to minimize the maximum SLL and for that the fitness function given in equation 27 is used with the values \(k_1=1\) and \(k_2=0\). Along with SSNMRA, other algorithms namely SSA, SOA, and NMRA are used for optimization. The population is set at 60 with a maximum of 250 iterations. The SLL obtained by SSNMRA is \(-20.7\) dB which is least in contrast to other algorithms used here for antenna optimization. The value of SLL obtained by NMRA, SSA and SOA is \(-19.6\) dB, \(-19.1\) dB and \(-19.3\) dB respectively which is higher than SSNMRA optimized antenna. The optimized element positions using SNMRA are shown in Table 5. The comparison of convergence graphs shown in Fig 4 (a) also indicates the enhanced performance of the hybrid SSNMRA. The normalised array factor graph of the SSNMRA antenna along with the pattern of other optimized antennas is presented in Fig 4 (b).

Table 5 Optimum positions of \(2N (N=6)\) element Linear Antenna Array obtained using SSNMRA.
Full size table
Fig. 4
figure 4

(a) Convergence graph of different algorithms for 12-element LAA (b) Normalised Array factor graph of 12-element LAA (c) Normalised Array factor graph of 20-element LAA.

Full size image

Equally spaced arrays

In the second example, another example of linear antenna design is taken up for optimization. An equally spaced 20 elements is optimized for having a radiation pattern with reduced SLL and wide null in the required direction. The desired antenna radiation pattern is obtained by optimizing the antenna element amplitudes while keeping the positions and phases of antenna elements fixed. The spacing between antenna elements is fixed to \(\lambda /2\). The first element is placed, on both sides of origin, at a distance of \(\lambda /4\) so as to have \(\lambda /2\) spacing between the consecutive antenna elements. The phase of each antenna element is fixed to zero i.e. \(\phi =0\). The AF for the equally spaced case can be written as:

$$\begin{aligned} AF\left( \phi \right) =2\sum _{n=1}^{N} I_n cos[(n-0.5)\pi cos (\phi )] \end{aligned}$$
(31)

The optimization aims to reduce the maximum SLL but also place a wide null between \(120^{\circ }\) and \(130^{\circ }\). The fitness function considered is given in equation 27 with \(k_1=0.8\) and \(k_2=0.2\). Owing to the symmetry of LAA, the element amplitudes to be optimized are ten. The amplitude of the elements is varied between 0 and 1. For all the algorithms considered here, the number of iterations is taken as 250 and the population size is fixed to 100. The normalized array factor graph of the SSNMRA optimized antenna is presented in Fig 4 (c). The radiation patterns of antennas optimized using NMRA, SOA and SSA are also shown in the same figure. Clearly, it is observed that all the algorithms were able to attain the SLL below −30 dB but a deeper null of −58 dB is only provided by SSNMRA. The optimized antenna array amplitudes are given in Table 6.

Table 6 Optimum amplitudes of \(2N (N=10)\) element Linear Antenna Array obtained using SSNMRA.
Full size table

Analysis of SSNMRA on patch antenna design

The versatility of the proposed meta-heuristic algorithm on micro-strip patch antenna design is verified in this section. The antenna design consists of two metallic layers separated by an air substrate of 5.5 mm thickness. The bottom layer consists of a metallic square shaped ground of 60 mm in dimension. The top layer is chosen as E shaped patch for wideband wireless applications42. The E shape is designed by inserting two identical rectangular slots \(\left( S_L\times S_W\right)\) in the rectangular patch \(\left( L_P\times W_P\right)\) as illustrated in Fig 5. The slots are inserted in such a manner to maintain a central distance \(C_S\) from the horizontal axis. The antenna is fed using the coaxial feeding line at a location \(P_f\) from the origin.

Fig. 5
figure 5

Front view of the E shaped patch antenna.

Full size image
Fig. 6
figure 6

CST and MATLAB interfacing for antenna optimization.

Full size image

The proposed algorithm is utilized to determine the best-optimized dimensions of the E shaped patch for wideband applications. The verification for the performance parameters of the antenna is obtained using the CST simulator. The Electromagnetic simulator is linked with MATLAB to estimate the objective function as per the algorithm illustrated in Fig 6. The objective function of the antenna for return loss maximization and impedance bandwidth improvement is defined as:

$$\begin{aligned} f_{obj}=Minimize\ \left\{ \left[ min(S11)\right] _{f=5 \hspace{3pt} to \hspace{3pt} 5.5 GHz}\right\} \end{aligned}$$
(32)

The parameters to be optimized and their bounds to maintain the E shape geometry is summarized in Table 7.

Table 7 Antenna parameter optimization summary.
Full size table

The proposed algorithm is initialized for a maximum of 50 iterations with a population size of 60. The scattering parameter obtained for the optimized antenna parameters is presented in Fig 7. It is observed that the antenna is resonating for the required impedance bandwidth with a minimum S11 of −46.09 dB for the proposed SSNMRA in comparison to the −29.39 dB, −34.81 dB and −39.93 dB for NMRA, SOA and SSA algorithm respectively. On the other hand, the other reported algorithm provides a minimum S11 of −30.48dB for DE43, −34.06dB for SADE43, −31dB for WDO44, −37dB for SMO45and −34.59dB for GWO42 on the same problem. Thus, the proposed technique proves to be a good candidate as compared to the competitive algorithms.

Fig. 7
figure 7

S11 for the optimized E pattern antenna.

Full size image

Fig 8 illustrates the convergence behaviour of four algorithms-the SSNMRA being ahead of others. The curve of SSNMRA is the fastest and steadiest, with convergence to a score below −40 dB, while NMRA, SOA, and SSA come up with slower convergence, with higher scores stabilized, indicating less optimal results.

Fig. 8
figure 8

Convergence graph for E pattern antenna design.

Full size image

Apart from the scattering parameters the radiation pattern obtained at resonance frequency for the different technique is illustrated in Fig 9 (a) and (b). It can be observed from the normalized radiation pattern that the main beam of the pattern is orthogonal to the E plane with few minor lobes.

Fig. 9
figure 9

(a) Normalised radiation pattern in Polar plane (b) Normalised radiation pattern in Azimuth plane.

Full size image

SSNMRA does have certain limitations that need to be addressed. First, while the hybridization of SSA and SOA improves the exploration phase, it may still struggle with certain types of highly non-convex or dynamically changing optimization problems. The effectiveness of SSNMRA in real-time or adaptive systems, where the optimization problem evolves over time, is yet to be thoroughly tested. Additionally, the performance of SSNMRA is heavily dependent on the parameters used, and the self-adaptive mutation operator, while helpful, might require further tuning for specific problem sets to achieve optimal results. Finally, the computational complexity of SSNMRA increases due to the multiple algorithmic components involved, which may limit its scalability for large-scale optimization problems.

Conclusion and future work

This work proposed a novel hybrid optimization technique, namely SSNMRA, that combines the benefits of NMRA, SSA, and SOA. In addition to the benefits of these algorithms, the SSNMRA includes a stagnation phase based on GWO-CS algorithms to avoid trapping the algorithm in a local optimal solution. After the hybridization and incorporation of the stagnation phase, SSNMRA is made self-adaptive utilizing a simulated annealing (sa) based mutation operator. The extensive experimentation conducted on CEC 2019 benchmark optimization problems has demonstrated that SSNMRA outperforms traditional NMRA and other state-of-the-art optimization algorithms for all the 10 optimization problems and secured \(1^{st}\) rank validated by statistical f-rank test. Further, SSNMRA is applied to the synthesis of LAA with the goal of minimizing SLL and null placement. Additionally, the performance of the SSNMRA is validated for designing an E-shaped patch antenna and SSNMRA delivers very promising results at the cost of higher computational time.

As a future prespective, one can use SSNMRA in conjunction with machine learning to tackle more challenging real-world problems, because of the impressive results obtained on the benchmark test suite. The handling of dynamic landscapes, image segmentation and classification and/or image enhancement optimization problem may all be benefited from SSNMRA. There are numerous ways that the proposed method can be boosted from additional learning techniques, as well as it can be upgraded to many/multi-objective optimization algorithms.