A novel pythonic paradigm for image encryption using axis-aligned bounding boxes

Abstract

In the digital age, images permeate every facet of our lives, often carrying critical information for organizations, institutions, and even nation-states. Ensuring their security against unauthorized access is paramount. This research introduces a novel image encryption algorithm designed to safeguard the integrity and confidentiality of sensitive gray-scale digital images. The algorithm leverages the theory of axis-aligned bounding boxes, translating the input image into a 3D representation. Within this 3D space, two identically sized boxes are generated and assessed for overlap. If the boxes do not overlap, the pixels within them are swapped. This pixel-swapping process, guided by random numbers generated from a 5D multi-wing hyper-chaotic map, is repeated numerous times to infuse confusion into the image. To further enhance security, diffusion effects are introduced by performing an XoR operation between the confused image and random numbers provided by the piece-wise linear chaotic map. This study employs private key cryptography and utilizes four gray-scale images to validate the feasibility and effectiveness of the proposed method. Simulation has been carried out in the Pythonic ecosystem. So, the algorithms presented in this study are designed to closely resemble Python code. Comprehensive validation metrics attest to the robustness of the cipher, achieving an information entropy of 7.99985 and a computational speed of 0.3987 seconds. These results underscore the potential of this encryption approach for practical, real-world applications. These applications span military, diplomacy & government, commerce, showbiz, industry, and social life etc.

Introduction

In the contemporary era, the Internet has revolutionized the global landscape, intertwining advanced technologies such as cloud computing, big data, Internet of Things (IoT), data mining, and machine learning to craft diverse hardware and software products. A vast amount of data is generated daily across various facets of human life, including commerce, education, scientific research, e-government, weather forecasting, medicine, and personal matters. Predominantly, this data manifests in the form of images and pictures, stored on hard disks, cloud servers, flash drives, PDAs, and transmitted extensively over the public network, such as the Internet.

While routine storage and transmission of images may not concern third parties, certain images, like designs of new missiles, can be highly sensitive. Consequently, their storage and transmission carry significant implications and repercussions if not handled with extreme care. Malicious hackers and other adversaries are constantly seeking opportunities to compromise valuable images. Traditionally, image security has been achieved through encryption techniques that transform plain images into unrecognizable formats^1,2.

A plethora of image cryptosystems have been developed in the past, with the mathematical theory of chaos and chaotic maps serving as the backbone of these ciphers^3,4. Chaotic maps, essentially mathematical functions generating random data, play a pivotal role in encryption and decryption algorithms. Numerous ciphers have emerged using chaotic systems alone, others through the combination of chaotic systems and DNA computing, and some through the fusion of chaotic maps, DNA computing^5,6, and automatons^7,8,9. Hundreds of image encryption schemes have been developed in the past, employing various concepts of confusion and diffusion—principal operations behind any cryptographic product. For example, the work¹⁰ wrote an image encryption scheme in which the given image pixels were disarrayed. Further, diffusion operation was employed through the usage of the secret key. The said key was crafted through an amalgamation of varied chaotic systems. The reported scheme was demonstrated very robust against the avalanche attacks. Further, it proved very defiant to the varied attacks of statistical nature. Moreover, the computational time of the suggested scheme was very small. In an other project of image encryption¹¹, a 2D chaotic system termed as Salomon map was developed exploiting the notion of Salomon function. The newly developed Salomon map has greater Sample entropy, Kolmogorov entropy, Lyapunov exponent, and correlation dimension. A notable feature of this newly developed chaotic map was that its Lyapunov exponent could reach to the tune of 11 which demonstrates that the chaotic data spawned by the suggested map was furnished with great randomness. By using the newly developed map, an image cipher was written in which the low and high bits were exchanged with each other in a selective manner. Besides, varied measures were adopted to test the robustness of the proposed image encryption scheme like randomness tests, various simulated attack and decorrelation analysis.

Chaotic maps and systems are virtually the life blood of the image ciphers as described earlier. These maps exist in many flavors. For instance, there are low dimensional maps, high dimensional maps and hyper-chaotic systems/maps. Low dimensional maps consist of 1D or 2D. High dimensional maps consist of 3D. Lastly the maps which produce more than three streams of random numbers are called as hyper-chaotic maps. Image cryptographers use these maps depending upon the peculiar logic, they have conceived for their security products. The work¹², for instance, employed the 1D logistic chaotic map to come up with a speedy and efficient image cipher. In particular, the authors of the reported work demonstrated that an efficient scrambling was achieved through the usage of chaotic data for a square image with 3N pixels (Each color bit plain has N numbers of pixels). Apart from that, the algorithm developed used a key which comprising of 192 bits. The given image was broken down into many blocks and each block was selected in an arbitrary fashion for introducing the diffusion effects. Additionally, multiple XoR operations were carried out. A yet another work¹³ employed 2D logistic chaotic map to develop a novel image cipher. Besides, DNA technology was also used in the said work named as 2DNALM. This work was based on a three-pronged strategy. In the first stage, the pixels of the given plain-text image were permuted through the usage of position key-based scrambling operation. The second phase applied double DNA encoding to the scrambled images, utilizing different rules from DNA cryptography to generate an encoded image. In the final step, the encoded image was encrypted using an XoR operation with chaotic keys generated from a 2D logistic map. Entropy analysis and experimental results demonstrated that the proposed scheme offered strong encryption and effectively resisted various common attacks. An another work⁵ used the 3D intertwining logistic chaotic map. Using the 15-puzzle mathematical construct, the pixels of the given plain-text image were scrambled. Moreover, DNA strands were also used to heighten the security effects. Simulation and security analyses rendered very promising results. Besides, in a work¹⁴, a hyper-chaotic map has been used to spawn the streams of random numbers. In this particular scheme, multiple images were encrypted in one go. Several images were divided into columns, and a regular cube was formed by stacking multiple planes of a fixed size. Each plane in the stack was treated as a layer of the cube along the z-axis. Lastly, security analysis gave very nice results.

Cryptography is a dynamic field, with cryptographers continually striving to develop robust ciphers, while cryptanalysts employ their ingenuity to identify vulnerabilities, gaps, and weaknesses to break these ciphers. The perpetual threat posed by cryptanalysts tests the ambitions of cryptographers. Many image ciphers have been compromised in previous years due to various factors, including low key space, low plain-text sensitivity, and poor design principles^15,16. Design principles for image cryptography are plentiful in the literature, yet there is no universally agreed-upon best approach. A substantial number of ciphers have been developed following the confusion-diffusion architecture, a concept pioneered by Fridrich^17,18,19.

Many image ciphers have been successfully broken by identifying various loopholes and other lacunas in their design principles. For instance, the work²⁰ was broken by²¹. The authors of the work²⁰ contended that their work was secure and could withstand the cyber threats from the community of hackers and other adversaries. But the study²¹ demonstrated that their algorithm couldn’t withstand the chosen plain-text attack. According to the findings of the work²¹, the forward-diffusion and backward-diffusion of the original algorithm used two different diffusion keys and there was a cipher-text feedback mechanism, the analysis of the diffusion by iterative optimization showed that it could be equivalent to global diffusion. Moreover, the way, chaotic data was being spawned, was totally independent of the the given plain image, hence, corresponding permutation and diffusion key streams could be retrieved by adjusting the individual pixel values of the chosen plain-texts. In the same way, the work²² examined the image cipher given in²³ and found loopholes and other drawbacks. The work²³ employed DNA Coding, Lorenz Chaotic map and Quantum logistic map and dubbed their work as IEA-QCDC. Further, their contention was that their work was secured as well as reliable. However, the study²² launched a chosen-plaintext attack and obtained the equivalent diffusion and permutation keys. Apart from that, through the analysis of encryption effect of DNA encryption operations, various characteristics of DNA codes were summarized. Besides, it was also found that iterative sequences got by non-chaotic state was not defiant to the only-ciphertext attacks. Lastly, various suggestions were given to improve the security of IEA-QCDC. Additionally, many efforts have been made to come up with novel security algorithms in the varied domains^{24,25,26,27,28,29,30,31,32,33,34,35,36}.

Image encryption is essential to protect sensitive information from unauthorized access, particularly as image data becomes more prevalent in applications like medical imaging, surveillance, and secure communications. Traditional encryption methods can struggle with the unique structure and high data volume of images. Our proposed solution addresses these challenges by enhancing security through specialized techniques tailored for image characteristics, ensuring robustness while maintaining efficiency for real-time applications. This approach not only strengthens security but also provides adaptability for various image formats and sizes, addressing specific challenges of storage, transmission, and privacy.

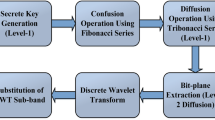
Motivated by the aforementioned discussion, this research study aims to develop a secure and novel image encryption scheme in which scrambling has been carried out in a 3D setting to heighten the security effects. As some gray scale image is input, it is converted into a 3D image. The mathematical construct of axis-aligned bounding boxes has been used³⁷. In particular, a pair of boxes with the same size is generated within the confines of the 3D image. A condition has been developed which checks whether the two boxes overlap/intersect with each other. In case, they do, no operation is carried out. Otherwise, the pixels surrounded by these two boxes are interchanged with each other. This operation is repeated multiple times to achieve the required level of confusion in the gray-scale image. 5D multi-wing hyper-chaotic³⁸ and piece wise linear chaotic maps³⁹ have been used in this work. Both the simulations and comprehensive security analysis yielded highly promising results.

The remainder of the paper is organized as follows. “Preliminaries” section discusses the axis aligned bounding boxes and theory of chaos. In particular, 5D multi-wing hyper-chaotic map and piece-wise linear chaotic maps have been discussed. In “Suggested image encryption scheme” section, two things have been described, i.e., the way initial values have been spawned for carrying out the diffusion and scrambling operations and the suggested image encryption scheme. Apart from that, the machine experimentation and simulation have been given in the “Suggested algorithm’s machine simulation” section. “Security/performance analyses” section provides a detailed security analysis by employing the different state of the art benchmarks in the community of cryptographers. Lastly, the “Conclusion and future work” section closes the paper by describing the concluding remarks, limitations of the suggested work and the possible future research directions.

Related work

Scrambling is one of the cardinal operations in the image encryption. A minute study of the related literature indicates that the image cryptographers have unlocked the inherent potential of various mathematical constructs to come up with a novel image cipher. Table 1 shows the list of few constructs employed in the past and the construct employed in this study.

Table 1 Comparison of the previous and the proposed work.

Preliminaries

Axis-aligned bounding boxes (AABBs)

Axis-Aligned Bounding Boxes (AABBs) are a simple and efficient way to represent the spatial extent of objects in a Cartesian coordinate system³⁷. These bounding boxes are “axis-aligned,” meaning their edges are parallel to the coordinate axes. This makes mathematical computations involving AABBs simpler and faster.

AABBs are computationally efficient for collision detection and spatial queries⁴⁴. Besides, since their edges are aligned with the coordinate axes, calculations involving AABBs are straightforward. Additionally, AABBs are often used in Bounding Volume Hierarchy (BVH), a tree structure that helps accelerate spatial queries⁴⁵. Besides, AABBs provides a simple yet powerful tool for spatial representation, gaming, and computational geometry. Their simplicity and efficiency make them ideal for many applications where fast and easy bounding volume calculations are required.

An AABB is usually defined by two points in some 3D space: the minimum corner (with the smallest x, y, and z coordinates) and the maximum corner (with the largest x, y, and z coordinates). These two points are often referred to as:

• min: $(x_{\text {min}}, y_{\text {min}}, z_{\text {min}})$

• max: $(x_{\text {max}}, y_{\text {max}}, z_{\text {max}})$

Given two points, the min point $(x_{\text {min}}, y_{\text {min}}, z_{\text {min}})$ and the max point $(x_{\text {max}}, y_{\text {max}}, z_{\text {max}})$, the volume of the AABB is given by:

$$\begin{aligned} Volume = (x_{\text {max}} - x_{\text {min}}) \cdot (y_{\text {max}} - y_{\text {min}}) \cdot (z_{\text {max}} - z_{\text {min}}) \end{aligned}$$

(1)

To determine if two AABBs intersect, we check for overlap in each dimension. Two AABBs intersect if and only if:

$$\begin{aligned} \begin{aligned} x_{\text {min}}^A&\le x_{\text {max}}^B \\ x_{\text {max}}^A&\ge x_{\text {min}}^B \\ y_{\text {min}}^A&\le y_{\text {max}}^B \\ y_{\text {max}}^A&\ge y_{\text {min}}^B \\ z_{\text {min}}^A&\le z_{\text {max}}^B \\ z_{\text {max}}^A&\ge z_{\text {min}}^B \\ \end{aligned} \end{aligned}$$

(2)

Where A and B are the two AABBs being tested for intersection.

In this study, the inherent potential of the notion of AABBs will be tapped. In particular, the given 2D image will be converted to a 3D image. After that, two boxes of the same size will be created randomly within the 3D image. In case, the formed boxes do not overlap with each other, the pixels contained by them will be swapped with each other. This process will be repeated multiple times to introduce confusion effects into the given plain image.

Chaotic systems/maps

Theory of chaos deals with those systems which are highly dynamic and render sea changes in their behaviour, the moment a very minor twist is made in their initial values. These values include the states and system parameters. Leveraging this ingenious concept, scientists and mathematicians have developed numerous chaotic maps and systems designed to generate streams of random numbers. These maps are widely utilized in image encryption to perform diffusion and confusion operations. The primary reason for their extensive use lies in their exceptional properties, including aperiodicity, pseudo-randomness, mixing, ergodicity, and unpredictability⁴⁶.

5D hyper-chaotic system

Following mathematical equations characterize the 5D hyper-chaotic map³⁸.

$$\begin{aligned} \begin{array}{lllll} \dot{x} = -ax + yz \\ \dot{y} = -by + fv \\ \dot{z} = -cz + gw + xy \\ \dot{w} = dw - hx \\ \dot{v} = ev - x^{2}y \\ \end{array} \end{aligned}$$

(3)

We descibe below the variables being used in this system.

• The list a, b, c, d, e, f, g, h depict the system parameters.

• x, y, z, w, v are the state variables.

• yz, xy and $x^{2}y$ are the nonlinear terms.

Apart from that, Periodic orbit, chaotic and hyper-chaotic and other dynamic behaviors of these systems can be seen here³⁸. Table 2 shows the values selected to draw the different attractors of this system. Additionally, the time step of the system’s solution is 0.001. Apart from that, the chaotic behavior of the System (3) has been depicted in the Fig. 1. Additionally, the Lyapunov exponents (Lyapunov exponents quantify how sensitive a dynamical system is to initial conditions by measuring the rate of separation between close trajectories. A positive Lyapunov exponent indicates chaotic behavior, where small differences in starting points grow exponentially over time. This metric helps determine system stability and predictability) have been calculated as $L_{1} = 9.979$, $L_{2} = 1.96$. $L_{3} = 0.005362$. $L_{4} = -19.13$. $L_{5} = -27.82$ as depicted in the Fig. 2. Higher values of entropy (Entropy is a measure of unpredictability and complexity in the system’s behavior over time. It reflects the rate at which the map produces new information as it evolves, with higher entropy indicating greater disorder and unpredictability in the map’s output. Entropy quantifies how sensitive a chaotic system is to initial conditions, meaning even small differences in starting points will lead to significantly divergent outcomes) of the data produced by the chaotic maps are always desirable.

Table 2 Initial values and system parameters of the chaotic map.

Fig. 1

Various attractors System (3) and projection on the planes: (a) xyz space (3D view); (b) xy plane (2D view); (c) xz plane (2D view); (d) yz plane (2D view); (e) xv plane (2D view); (f) zw plane (2D view).

Fig. 2

System (3) Lyapunov exponents.

Once, random data is generated, its randomness must be checked before we use it. Fortunately, there exists a suite called as NIST Test Suite⁴⁷. According to the study⁴⁸, the significance level p for the varied tests should be above from the threshold 0.01 for some random number to be accepted. Table 3 shows the test results against an array of security parameters.

Table 3 Test results of statistical randomness.

Piece-wise linear chaotic map

Piece-wise linear chaotic map (PWLCM) is a one-dimensional map. It is defined through the following mathematical equation³⁹. One can see the equation that, this map is recursive in character since it calls itself.

$$\begin{aligned} t_{i}=Q(t_{i-1},\eta )=\left\{ \begin{array}{ll} \frac{t_{i-1}}{\eta }, & \hbox {if 0 }< t_{i-1}< \eta \\ \frac{t_{i-1}-\eta }{2-\eta }, & \hbox {if } \eta \le t_{i-1}< 0.5\\ Q(1-t_{i-1},\eta ), & \hbox {if 0.5 } \le t_{i-1} < 1 \end{array} \right. \end{aligned}$$

(4)

For the value of $\eta$ lying in the range (0, 0.5), it shows a very nice chaotic behavior. Apart from that, this map is furnished with even distribution and nice ergodic properties. Moreover, this map is recursive in character.

Suggested image encryption scheme

The suggested image encryption scheme exploits the idea of axis-aligned bounding boxes which are created deep inside the 3D image. Let p be the gray scale image with the size of $m \times n$. This image is converted into the 3D image with the size of $(m \times n)^{1/3} \times (m \times n)^{1/3} \times (m \times n)^{1/3}$. Now two boxes with a minimum size of $1 \times 1 \times 1$ and a maximum size of $(m \times n)^{1/3} \times (m \times n)^{1/3} \times (m \times n)^{1/3}$ are spawned randomly within the 3D image. In case, these generated boxes overlap/intersect each other, no operation is carried out. In case, these boxes happen to be non-intersecting, the pixels encompassed by these two boxes are swapped with each other within the 3D image. This operation has been performed a large number of times to realize the effects of confusion in the given gray scale image (see Fig. 3). The random numbers given by the 5D multi-wing hyper-chaotic map have been utilized in this process. To get the diffusion effects in the scrambled image, piece-wise linear chaotic map has been used.

Engineering primary values of chaotic system

The family of chaotic maps requires some starting values so that it may spark it and required numbers of random data may be obtained. In the steps below, we will shed light on the way, the primary values have been obtained.

Step 1: Supply algorithm with the gray-scale image p of dimensions $m \times n$. To introduce plain-text sensitivity, determine average value avg of intensity values across all pixels. Subsequently, apply the following equation to modify the initial key $x_0$ of Chaotic System (3) currently in use.

$$\begin{aligned} x_0 = x_0 + \frac{avg}{2^{100}} \end{aligned}$$

(5)

The initial value $x_0$ is being updated in this equation.

Step 2: As the System (3) is iterated $(mn + n_{0})$ times, $\{x_t\}_{t=1}^{mn + n_{0}}$, $\{y_t\}_{t=1}^{mn+ n_{0}}$, $\{z_t\}_{t=1}^{mn+ n_{0}}$, $\{w_t\}_{t=1}^{mn+ n_{0}}$ and $\{v_t\}_{t=1}^{mn+ n_{0}}$ have been obtained. Moreover, value of $n_{0} \ge 500$. These initial $n_{0}$ values are typically regarded as unripe random data. To prevent any adverse impact, these values have been skipped.

Step 3: In the previous Step 2, the chaotic data deviates from the specific logic envisioned in this study. Consequently, the sequences x, y, z, w and v undergo set of Eq. (6). As a result, we obtain modified streams of arbitrary data referred to as $\{u1_{t}\}_{t=1}^{mn+ n_{0}}$, $\{v1_{t}\}_{t=1}^{mn+ n_{0}}$,$\{w1_{t}\}_{t=1}^{mn+ n_{0}}$,$\{u2_{t}\}_{t=1}^{mn+ n_{0}}$,$\{v2_{t}\}_{t=1}^{mn+ n_{0}}$,$\{w2_{t}\}_{t=1}^{mn+ n_{0}}$, and $\{s_{t}\}_{t=1}^{mn+ n_{0}}$.

$$\begin{aligned} \left\{ \begin{array}{llll} u1_{t} = floor(\mod (abs(x_t)-floor(abs(x_t)) \times 10^{14}, \lfloor \frac{(m \times n)^{1/3}}{\alpha }\rfloor ) + 1, & \\ v1_{t} = floor(\mod (abs(y_t)-floor(abs(y_t)) \times 10^{14}, \lfloor \frac{(m \times n)^{1/3}}{\beta }\rfloor ) + 1, & \\ w1_{t} = floor(\mod (abs(z_t)- floor(abs(z_t)) \times 10^{14}, \lfloor \frac{(m \times n)^{1/3}}{\gamma }\rfloor ) + 1 & \\ u2_{t} = floor(\mod (abs(w_t)-floor(abs(w_t)) \times 10^{14}, \lfloor \frac{(m \times n)^{1/3}}{\delta }\rfloor ) + 1 & \\ v2_{t} = floor(\mod (abs(v_t)-floor(abs(v_t)) \times 10^{14}, \lfloor \frac{(m \times n)^{1/3}}{\epsilon }\rfloor ) + 1 & \\ w2_{t} = \mod (u_{1t} + v1_{t}, \lfloor \frac{(m \times n)^{1/3}}{\phi }\rfloor ) + 1, & \\ s_{t} = \mod (v_{1t} + w1_{t}, \omega )+ 1, & \\ \end{array} \right. \end{aligned}$$

(6)

The values of these streams $\{u1_{t}\}_{t=1}^{mn+ n_{0}}$, $\{v1_{t}\}_{t=1}^{mn+ n_{0}}$, $\{w1_{t}\}_{t=1}^{mn+ n_{0}}$, $\{u2_{t}\}_{t=1}^{mn+ n_{0}}$, $\{v2_{t}\}_{t=1}^{mn+ n_{0}}$, and $\{w2_{t}\}_{t=1}^{mn+ n_{0}}$ $\{s_{t}\}_{t=1}^{mn+ n_{0}}$ range from 1 to $\lfloor \frac{(m \times n)^{1/3}}{\alpha }\rfloor$ + 1, $\lfloor \frac{(m \times n)^{1/3}}{\beta }\rfloor$ + 1,$\lfloor \frac{(m \times n)^{1/3}}{\gamma }\rfloor$ + 1,$\lfloor \frac{(m \times n)^{1/3}}{\delta }\rfloor$ + 1,$\lfloor \frac{(m \times n)^{1/3}}{\epsilon }\rfloor$ + 1,$\lfloor \frac{(m \times n)^{1/3}}{\phi }\rfloor$ + 1 and $\omega$ + 1 respectively. Moreover, $\alpha , \beta , \gamma , \delta , \epsilon , \phi \in [1, (m \times n)^{1/3})$. Besides, $[1, (m \times n)^{1/3})$ denotes a semi-closed (or half-open) interval where 1 is included, but $(m \times n)^{1/3}$ is not. The variables $\alpha$, $\beta$, $\gamma$, $\delta$, $\epsilon$, $\phi$ and $\omega$ would also serve as the key of the proposed image cipher. It will help defy the potential brute force threats. The symbol $\lfloor . \rfloor$ refers to the floor function.

Axis-aligned bounding boxes based image scrambler

Fig. 3

Axis-aligned bounding boxes based image scrambler.

Provide gray-scale image p with dimensions $m \times n$ as input. Invoke Algorithm (1) using the parameters p, u1, v1, w1, u2, v2, w2, s to achieve the objective of scrambling for the provided image p.

Algorithm 1

Bounding boxes based image scrambler.

Here the Algorithm (1) will be explained in details.

• Step 1: Line 1 finds the size of the given image p and stores it in the variables m and n.

• Step 2: Using the built-in Python function flatten, line 2 converts the given 2D image p into 1D image with size $1 \times mn$ and assigns it to the variable $image\_1d$.

• Step 3: Line 3 converts this 1D image into a 3D image with size $(m \times n)^{1/3}, (m \times n)^{1/3}, (m \times n)^{1/3} )$ and assigns to the variable $image\_3d$. It is to be noted that the number of pixels will remain same in the 2D, 1D and 3D images whatsoever since

  $$\begin{aligned} m \times n&= 1 \times mn \\&= (m \times n)^{\frac{1}{3}} \times (m \times n)^{\frac{1}{3}} \times (m \times n)^{\frac{1}{3}} \\&= (m \times n)^{\frac{1}{3} + \frac{1}{3} + \frac{1}{3}} \\&= m \times n \end{aligned}$$

• Step 4: The for loop spanning the lines (4-16) carries out the most important task of the confusion project of the proposed algorithm. This loop is iterating mn times. In each iteration of the loop, two boxes say Box 1 and Box 2 will be created. The random numbers given by the streams u1, v1, w1 and s are being used to generate the eight vertices for the Box 1. These eight vertices are getting assigned to the variable $box1\_vertices$. It is to be noted that u1, v1, w1 in each of the $i^{th}$ iteration of the for loop corresponds to the minX, minY and minZ vertex of the Box 1. The other seven vertices have been obtained by adding the value of stream s.

• Step 5: Similarly line 6 is populating the vertices of the Box 2 (denoted by $box2\_vertices$) by using the streams u2, v2, w2 and s.

• Step 6: In the if condition at line 7, the function CheckVerticesLimit is called with the parameters box1_vertices and $(m \times n)^{1/3}$. As the name suggests, this function checks whether all the vertices of the formed box fall within the limits of 1 to $(m \times n)^{1/3}$. If they do, the function returns true (line 5). However, if any vertex exceeds the limit, the function returns false (line 3) to the calling algorithm.

• Step 7: The same function, CheckVerticesLimit, is then called with the second box. If both function calls return true to the Algorithm 1, the logical and between them results in an overall true, which is then inverted by the tilde sign “” to false. Conversely, if either of the function calls returns false, the logical and results in an overall false, which the tilde sign inverts to true and the “continue” statement at line 8 shifts the control to the for loop header (line 4).

• Step 8: The if condition at the line 7 of Algorithm 1 calls the Algorithm DoBoxesIntersect with the parameters $box1\_vertices$ and $box2\_vertices$. This algorithm returns true if two boxes do intersect and false otherwise.

• Step 9: Line 1 of the Algorithm DoBoxesIntersect, in turn, calls the Algorithm GetAABB (Get Axis-Aligned Bounding Box) with the single parameter $box1\_vertices$ and returns the three tuples (minX1, maxX1), (minY1, maxY1), (minZ1, maxZ1) (Fig. 4).

• Step 10: Line 1 of the Algorithm GetAABB employs the notion of “list comprehension” using the Pythonic approach. The index point of the for loop takes the values of all eight tuples one by one, contained in the vertices variable and filling the list with the first value of the 3D point, i.e., $x-component$. The min function finds the minimum value from these eight values and assigns it to the variable minX. In the same fashion, other pertinent values have been extracted and assigned to the variables in the lines (2-6)

• Step 11: Lastly, line 7 returns the three tuples (minX, maxX), (minY, maxY), (minZ, maxZ) of the box with vertices to the Algorithm DoBoxesIntersect.

• Step 12: Line 2 of the Algorithm DoBoxesIntersect again calls the Algorithm GetAABB with the parameter $box2\_vertices$ and the results are assigned to the tuples (minX2, maxX2), (minY2, maxY2), (minZ2, maxZ2).

• Step 13: Lines (3-5) of the Algorithm DoBoxesIntersect carry out the necessary Boolean and operations to check any traces of the overlapping/intersection between the two boxes. Kindly refer to the set of Inequalities (2) for the conditions of the overlapping.

• Step 14: Line 6 returns the final result using the Boolean operator and to the Algorithm (1).

• Step 15: In case the Algorithm DoBoxesIntersect returns false, the tilde sign inverts it to true and the lines (11-14), of course, get executed. Line 11 extracts the three slices, i.e., $u1(index):u1(index)+s(index)$, $v1(index):v1(index)+s(index)$ and $w1(index):w1(index)+s(index)$ of the image $image\_3d$ and assigns this “mini box” to the variable box1 (see Fig. 5).

• Step 16: Similarly, line 12 extracts the second “mini box” and assigns it to the variable box2 (see Fig. 5).

• Step 17: Lines 13 and 14 assign these boxes to the $image\_3d$ in such a way that these extracted “mini boxes” are swapped within the $image\_3d$. (see Fig. 6).

• Step 18: Lastly, lines 17 and 18 convert the 3D image $image\_3d$ into the 2D image $image\_2d\_slice$.

• Step 19: Line 19 assigns the $image\_2d\_slice$ to the variable $p'$. Line 20 returns the confused and scrambled image $p'$.

• Step 20: Equation (7) performs the diffusion operation over the confused image $p'$.

  $$\begin{aligned} \left\{ \begin{aligned} q_j&= Q(q_{j-1}, \eta ) \\ f_j&= (q_j \times 10^{14}) \mod 256 \\ g_j&= p'_j \oplus f_j \oplus g_{j-1} \end{aligned} \right. \end{aligned}$$

  (7)

  where $1 \le j \le mn$ and $g_0$ is a given value which is a part of the key. Q refers to the PWLCM map; $q_0$ is the PWLCM map’s initial value and $\eta$ is the system parameter. $p'_j$ is the $j^{th}$ pixel of the permuted image with reading up to down and left to right. $g_j$ is the final encrypted image of the plain-text image $p_j$.

Fig. 4

A box with vertices.

Algorithm 2

Check vertices limit.

Fig. 5

Two randomly generated boxes (before swapping).

Fig. 6

Boxes after swapping.

Algorithm 3

Do boxes intersect.

Algorithm 4

Get AABB.

Procedure for image decryption

This research project has been carried out by applying the tenets of private/symmetric key cryptography. Just reversing the instructions of the encryption algorithm would yield the corresponding decryption algorithm.

Suggested algorithm’s machine simulation

To illustrate the proposed encryption framework, four grayscale images were selected from the USC-SIPI Image Database, accessible at http://sipi.usc.edu/database/. Machine simulation was conducted in Python 3 ecosystem. The chosen grayscale images include Clock, Moon, Resolution Chart, and Couple, each sized $512 \times 512$. Apart from that, random data was generated for suggested image security scheme using chaotic map/system of the 5D Hyperchaotic System. System parameters and initial values chosen are $x_0 = 1$, $y_0 = 1$, $z_0 = 1$, $w_0 = 1$, $v_0 = 1$, $a = 10$, $b = 60$, $c = 20$, $d = 15$, $e = 40$, $f = 1$, $g = 50$, and $h = 10$. Apart from that, the initial values selected for the piece-wise linear chaotic map are $t = 0.1$ and $\eta = 0.2$. One more key $g_0 = 95$ has been used (Eq. 7). Additionally, $\alpha = \beta = \gamma = \delta = \epsilon = \phi = 1$. Figure 7 illustrates plaintext images (Row 1), cipher/encrypted images (Row 2), and their corresponding decrypted versions (Row 3). These figures demonstrate the successful transformation of the original plain images into a noisy and blurry form, indicating the efficacy of cipher. Furthermore, the obtained cipher images have been successfully converted back to their initial forms after the application of decryption algorithm over them.

Fig. 7

Normal test images, cipher images and decrypted images: (a) Clock normal image; (b) Moon normal image; (c) Resolution Chart normal image; (d) Couple normal image; (e) Clock cipher image; (f) Moon cipher image; (g) Resolution Chart cipher image; (h) Couple cipher image; (i) Clock decrypted image; (j) Moon decrypted image; (k) Resolution Chart decrypted image; (l) Couple decrypted image. https://sipi.usc.edu/database/database.php?volume=misc.

Moreover, the color images have also been simulated using the suggested image encryption algorithm. One can see the Fig. 8 in which the first row represents the chosen color plain images; second and third row correspond to the cipher and decrypted images. One can notice that the algorithm has successfully worked for the color images as well.

Fig. 8

Normal test images, cipher images and decrypted images: (a) Pigeon normal image; (b) F16 normal image; (c) Female normal image; (d) Baboon normal image; (e) Pigeon cipher image; (f) F16 cipher image; (g) Female cipher image; (h) Baboon cipher image; (i) Pigeon decrypted image; (j) F16 decrypted image; (k) Female decrypted image; (l) Baboon decrypted image. https://sipi.usc.edu/database/database.php?volume=misc.

Security/performance analyses

Security analyses present a valuable chance for security engineers to substantiate the legitimacy of their work through utilization of diverse validation metrics. In this section, frequently used metrics will be employed over the suggested image cipher to prove its defiance from the varied assaults of the community of hackers and antagonists. For the purpose of comparison, we have selected relevant researches from the literature^14,49,50,51.

Key space

A robust encryption scheme is typically characterized by a substantial key space, acting as a deterrent against potential brute-force attacks. In such attacks, adversaries systematically attempt the entire key space to get an illegitimate access over plain image. In case, key space is sufficiently big, making it impractical to try all possible keys within a reasonable time-frame, the brute-force attack becomes infeasible.

The chaotic data in our proposed scheme is generated from the system parameters and the initial values of 5D hyper-chaotic map and piece-wise linear chaotic map. List of system parameters for the 5D hyper-chaotic map is a, b, c, d, e, f, g, h. Additionally, the list $x_0$, $y_0$, $z_0$, $w_0$, $v_0$ constitute the initial values. Moreover, for the diffusion, the chaotic data was obtained by the usage of piece-wise linear chaotic map with the parameters of $z_0$ and $\eta$. Additionally, one more key $g_0$ has also been used in combination of the PWLCM. The key space comes out to be $10^{14 \times 16} = 10^{224}$ which is better than the minimum key space $2^{100}$ required for the secured ciphers. It is to be noted that the machine precision is $10^{-14}$. If we include the variables $\alpha , \beta , \gamma , \delta , \epsilon , \phi$, the key space would be more than $10^{224}$. Table 4 shows key space of suggested cipher along with a comparison of the other related works. One can note that the proposed image cipher key space is better than the works^14,50.

Table 4 Key space of the proposed cipher and comparison with some other algorithms.

Analysis through pie chart diagram

In this section, an analysis based on mathematical instrument Pie will be carried out on the plain and cipher images’ pixels intensity values. Figure 9 shows the distribution of plain and cipher images’ pixels through the instrument of pie chart diagram. We have taken 12 bins for this purpose. One can notice that the slices of the pie are almost equal for the cipher image than those of the plain image. It signals towards the robustness of the proposed image cipher. Moreover, these results have also been shown in the Table 5. Additionally, variance has also been calculated against these values. We can see that the variance of the cipher image is 0.0522 which is far greater than 25.2239—the variance of plain image. This once again signals towards the strong cryptographic effects of the proposed image cipher.

Fig. 9

Analysis of pixels intensity values through pie chart: (a) Distribution of pixels intensities in plain image; (b) Distribution of pixels intensities in cipher image.

Table 5 Percentage of pixels’ intensity values in the bins.

Statistical analysis

Typically, two analyses are conducted within this category: namely, histogram and correlation analyses.

Drawing of cartesian histogram and its analysis

There exist 256 gray values for pixels of some image, and any image is a unique amalgamation of these intensity values. Histograms provide a visual representation of the intensity values within an image. When a histogram is constructed for a natural image, it exhibits fluctuating bars that convey the information encapsulated by the image. An effective image cryptosystem is anticipated to intricately manipulate pixel values in a manner that results in a histogram with uniformly distributed bars. This uniformity acts as a robust deterrent against potential hackers attempting a histogram attack.

Figure 10 illustrates the histograms for both the plain-text and cipher-text images of Clock. Noticeably, plain image histogram displays fluctuating bars, while histogram of the cipher image appears considerably smoother and more uniform. This uniformity serves as a significant impediment to success of some histogram attack.

Fig. 10

Histogram analysis of clock image: (a) Plain image; (b) Encrypted image.

Merely obtaining visual confirmation of uniformity of histogram bars is insufficient. Instead, variance will be employed for the quantification of variation within the histogram. Lesser variance values in the histograms of cipher images indicate higher levels of uniformity, and vice versa⁵². The variance values for the histograms of encrypted images of Clock, Moon, Resolution Chart, and Couple are presented in Table 6. Both the values for the Clock image and the average value for all the four selected images are better than the published work⁵³ which indicates that the proposed image cipher is equipped with enhanced security features.

Table 6 Findings of cipher image histogram variances.

Drawing of polar histogram and its analysis

The polar histogram of the plain gray-scale image likely shows smoother variations and specific peaks corresponding to the predominant intensity values in the image. This indicates that the image has areas with consistent brightness, such as regions with similar shading.

Uniform Distribution: The polar histogram of the ciphered image should ideally appear more uniform and less smooth, with a more even spread of intensity values. This is because encryption aims to randomize the pixel intensities, breaking any patterns that were present in the plain image.

Lack of Peaks: Unlike the plain image, the cipher image should lack distinct peaks, as the encryption process should distribute pixel values more uniformly across the entire range. This indicates a successful encryption, where the pixel intensities are randomized and do not reveal any discernible patterns from the original image.

Figure 11 shows that there is uniform distribution and lack of peaks for the cipher image (Fig. 11b) as compared to the plain image (Fig. 11a). This shows the nice security effects of the suggested work.

Fig. 11

Polar histogram analysis of Pigeon image: (a) Plain image; (b) Cipher image.

Correlation analysis

Most natural images inherently possess a certain coherence. This coherence arises from the tight and rigid correlationing between consecutive or adjacent pixels in these images. Adjacent pixels are those lying next to each other in three directions. They include diagonal, horizontal, or vertical. A proficient image encryption scheme is mandated to obfuscate and disperse the pixels data of given image in a manner that significantly mitigates the correlation among neighboring pixels, resulting in a noisy image that is challenging to recognize. In the ideal scenario, there should be no correlation among adjacent pixels.

For the correlation analysis, 3000 pairs of randomly selected adjacent pixels from both the plain and cipher images were chosen to evaluate the correlation using the formula (CC)⁵⁴:

$$\begin{aligned} CC=\frac{W\sum \limits _{d=1}^{W}(a_{d} \times b_{d})-\sum \limits _{d=1}^{W}a_{d} \times \sum \limits _{d=1}^{W}b_{d} }{\sqrt{\Bigg (W\sum \limits _{d=1}^{W}a_{d}^2-\bigg (\sum \limits _{d=1}^{W}a_{d}\bigg )^2\Bigg )\Bigg (W\sum \limits _{d=1}^{W}b_{d}^2-\bigg (\sum \limits _{d=1}^{W}b_{d}\bigg )^2\Bigg )}} \end{aligned}$$

(8)

In the provided equation, a and b represent the intensity values of two neighboring pixels in any direction, and W represents the total number of pixel data in the given image. Correlation coefficient distribution of contiguous pixels in directions of horizontal, vertical, and diagonal is visualized in Fig. 12. Numerically, the coefficient for the plain and cipher images of Clock is presented in Table 7. A noticeable trend is observed in this table: the coefficient is nearly 1 for the plain image, dropping to almost zero when the image is encrypted. The joint examination of Table 7 and Fig. 12 suggests a significant reduction in the relationship between adjacent pixels in the plain images. In simpler terms, it signifies a widespread breakdown of the strong correlation among pixels in the plain image. Table 8 provides a comparison of the correlation in the Clock cipher-text image with various related schemes. We can see that the findings of the suggested scheme and those of published ones are comparable in all the three directions.

Fig. 12

Calculated results of correlation distribution (Clock image): (a) For plain image in horizontal direction; (b) For plain image in vertical direction; (c) For plain image in diagonal direction; (d) For encrypted image in horizontal direction; (e) For encrypted image in vertical direction; (f) For encrypted image in diagonal direction.

Table 7 Correlation coefficient determined between the original Clock image and its corresponding encrypted image.

Table 8 Comparative analysis of correlation coefficients between adjacent pixels using different encryption techniques.

Information entropy analysis

Indubitably, inducing maximum disorder among the pixels in a given input image is a recurring objective in image encryption technology. Following the accomplishment of this task, there arises a natural need to quantify this disorder. The concept of information entropy, introduced by Shannon in 1949⁵⁵, can be employed for this purpose. In essence, entropy serves as a metric for measuring the degree of unpredictability and randomness inherent in the provided information source. Its mathematical formula is given by⁵⁶:

$$\begin{aligned} H(m) = \sum _{i=0}^{2^n-1}p(m_{i})log\frac{1}{p({m_i})} \end{aligned}$$

(9)

In the above mathematical equation, the function H(m) refers to the information entropy of m which is some information source. Additionally, $p(m_{i})$ denotes probability of the symbol $m_{i}$. Maximum entropy value is 8 for randomly rearranged pixels in any input image with $2^8$ gray values. To achieve heightened security effects, the entropy value for the provided input image should closely approach 8. The entropies for the chosen four images are detailed in Table 9. Noteworthy is the observation that this table illustrates an average entropy value very near the optimal 8, underscoring the resilience of our proposed scheme against entropy attacks. Furthermore, Table 9 provides a comparative analysis of the average entropy measure with some existing algorithms. The entropy value of 7.99985 for the proposed image encryption scheme applied to the Clock image is better than the one given in^49,50,51.

Table 9 Findings of entropy and comparison with other studies.

Differential attack

Differential attack is among the strategies employed by adversaries seeking access to the secret image. In this attack, the adversary makes subtle alterations to the input image, encrypts it, and attempts to discern a hidden relationship between the encrypted image with change of single bit value and an encrypted image without any change of single bit value. With clever manipulation of the situation, one can potentially ascertain the secret key of the encryption algorithm⁵⁷. In this attack dynamics, the hidden implications are investigated in cipher-text image, the moment a single bit is changed in plain-text image. Two commonly analyzed metrics for dealing with this attack are Unified Average Changing Intensity (UACI) and Number of Pixels Change Rate (NPCR). NPCR represents, as the name refers to, the number of pixel numbers change between plain-text and cipher-text images, whereas UACI is the average intensity of the differences between cipher-text and plain-text images. NPCR measures the percentage of pixels that change when a single pixel in the original (unencrypted) image is altered. High NPCR values mean that even a tiny change in the original image leads to widespread changes in the encrypted version, making it hard for attackers to trace or reverse the encryption. Whereas, UACI measures the average intensity difference between two encrypted images when the original image has a small change. High UACI values show that the encryption algorithm creates significant differences in pixel values, making it harder for attackers to guess patterns or identify image content.

Mathematical formulas corresponding to these notions are⁵⁸:

$$\begin{aligned} NPCR=\frac{\sum _{d,e}U(d,e)}{P\times Q}\times 100\% \end{aligned}$$

(10)

(P, Q) is the dimension of image in the provided equation. Besides, the piece-wise U(d, e) function is defined as:

$$\begin{aligned} U(d,e)=\left\{ \begin{array}{ll} 1, & \hbox {if }\, O(d,e)\ne O'(d,e) \\ 0, & \hbox {if }\, O(d,e)=O'(d,e) \end{array} \right. \end{aligned}$$

(11)

If the pixels at O(d, e) and $O'(d,e)$ are equal, U(d, e) is being assigned the value of 1, otherwise it is being assigned the value of 0.

$$\begin{aligned} UACI=\frac{1}{P \times Q}\left[ \sum _{d,e}\frac{|O(d,e)-O^{\prime }(d,e)|}{255}\right] \times 100\% \end{aligned}$$

(12)

Here, and $O^{\prime }$ refers to the cipher image when a single pixel is changed in the plain image. Additionally, O refers to the cipher image without any change. Table 10 displays both of these metrics (NPCR and UACI) for the selected four images.

The average values for NPCR and UACI across the images are $99.6122\%$ and $33.4512\%$ in a respective way. These values indicate that suggested cryptosystem is robust enough to withstand differential attacks taken by the hackers. Additionally, Table 11 provides a comparison of our NPCR and UACI values for the Clock image with some chosen works. Our method demonstrates that the NPCR value 99.6287% and the UACI 33.4876% are better than the ones in^14,49,50,51 which indicates that the proposed image cipher is furnished with the better security effects.

Table 10 Findings of NPCR and UACI security metrics.

Table 11 A comparative analysis of security metrics NPCR and UACI by various studies.

Tables 12 and 13 present critical values⁵⁹ related to the security parameters of NPCR and UACI respectively for images of sizes $64 \times 64$, $512 \times 512$, and $4096 \times 4096$. Specifically, critical values $N^*_{0.05}$, $N^*_{0.01}$, $N^*_{0.001}$ (three significance levels) are listed in Table 12. The interpretation is that if the NPCR results for two encrypted images are less than $N^*_{\alpha }$, these two encrypted images will not be randomized with a significance level of $\alpha$. As shown in Table 14, for the selected images processed by the proposed encryption scheme, NPCR values at all confidence levels exceed the critical (theoretical) benchmark for randomness across image sizes of $64 \times 64$, $512 \times 512$, and $4096 \times 4096$.

Regarding the UACI parameter, the critical value $U^*_\alpha$ is divided into two parts: $U^{*+}_\alpha$ and $U^{*-}_\alpha$ (see Table 13). The null hypothesis is rejected if the UACI value falls outside the interval ($U^{*-}_\alpha , U^{*+}_\alpha$). Table 15 demonstrates that, for various image sizes, UACI values meet the critical benchmarks established for the UACI randomness test. These results indicate the inherent robustness to the hackers’ attacks.

Table 12 Critical values (percentages) for NPCR randomness test.

Table 13 Theoretical results (percentages) for UACI randomness test.

Table 14 Critical values against NPCR randomness test for Clock image.

Table 15 Critical values against UACI randomness test for Clock image.

Chosen plaintext, known plaintext and ciphertext only attacks analyses

In cryptanalysis, attackers typically use plaintext and ciphertext attacks to attempt to break cryptosystems⁶⁰. In a ciphertext-only attack, the attacker has access to one or more ciphertexts without knowing the corresponding plaintexts. In a known plaintext attack, they possess pairs of plaintexts and their corresponding ciphertexts. In a chosen plaintext attack, the attacker has temporary access to the encryption mechanism, allowing them to generate as many ciphertexts as desired for selected plaintexts. If we can demonstrate that the proposed image cipher resists chosen plaintext attacks, then it is inherently resistant to known plaintext and ciphertext-only attacks, as these are subsets of the chosen plaintext attack.

In a chosen plaintext attack, the attacker gains temporary access to the encryption algorithm and may select a specific image, such as a black image (Fig. 13a), to encrypt in an attempt to uncover the secret key used. Upon encrypting this black image (Fig. 13b), the attacker obtains the chaotic data used within the encryption algorithm (the secret key). Next, they might attempt a known plaintext attack by selecting an arbitrary image, such as a pigeon (Fig. 13c), and encrypting it using the same key extracted from the black image encryption. However, to their frustration, the encrypted pigeon image cannot be correctly decrypted with this key (Fig. 13d). This process was repeated with a white image (Fig. 13e to h), further demonstrating the proposed cipher’s resilience to chosen plaintext, known plaintext, and ciphertext-only attacks.

Fig. 13

Chosen plaintext attack using Black and White images: (a) Original Black image; (b) Encrypted Black image; (c) Encrypted Pigeon image; (d) Attempted decryption of Pigeon image using the secret key derived from the Black image; (e) Original White image; (f) Encrypted White image; (g) Encrypted Pigeon image; (h) Attempted decryption of Pigeon image using the secret key derived from the White image.

Key sensitivity analysis

Key sensitivity describes the phenomenon where a very slight change in one of the cryptosystem’s keys leads to a significant difference in the output. The greater the key sensitivity of an encryption scheme, the stronger its security. During decryption, a minimal change in the input key set should prevent successful decryption of the encrypted image.

To illustrate key sensitivity, eight original images were encrypted using an initial key set, $U_{0} = \{x_{0}, y_{0}, z_{0}, w_{0}, v_{0}, a, b, c, d, e, f$, $g, h, t, \eta \}$. A tiny change, $\delta = 10^{-14}$, was then applied to each variable in the secret key individually, keeping other variables constant. The difference rates among pixels of the resulting cipher images were calculated between the images encrypted by $U_{0}$ and those encrypted by $U_{t}$ ($t = 1, 2, \ldots , 30$), where $U_{0}$ and $U_{t}$ differ only slightly in their values. The results, shown in Table 16, reveal an average key sensitivity of 99.61%, matching the level in⁶¹ and surpassing that in^62,63. These findings demonstrate that the proposed algorithm has a high level of key sensitivity.

Table 16 Difference rates between two images encrypted with minimally varied keys.

Peak signal-to-noise ratio analysis

A primary goal of an image cryptosystem is to increase the difference between the original plain-text image and the resulting cipher-text image. This difference is assessed using a metric known as the Peak Signal-to-Noise Ratio (PSNR), which quantifies the variance between the original image and its encrypted counterpart. Mathematically, it is defined as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} MSE = \frac{1}{M \times N}\sum _{b=1}^{M}\sum _{c=1}^{N}(P_{0}(b,c)-P_{1}(b,c))^ 2\\ PSNR = 20log_{10}({255}/{\sqrt{MSE}}) dB\\ \end{array}\right. } \end{aligned}$$

(13)

In the equation above, dimensions of the test image are denoted by M and N. Additionally, $P_{0}(b, c)$ and $P_{1}(b, c)$ denote the pixel values of original and encrypted images, respectively. MSE refers to the mean squared error. For optimal security effects, a larger MSE and a smaller PSNR are desirable.

Table 17 gives the results of the important metric PSNR obtained through various techniques. Notably, the PSNR values between decrypted image and original plain-text image consistently register as infinite ($\infty$), indicating that the decrypted image perfectly matches the original image (MSE = 0), highlighting the lossless nature of the proposed scheme. Additionally, concerning the similarity between the original image and the encrypted image, our algorithm exhibits the smallest PSNR value for the Clock image compared to other algorithms^64,65. Therefore, our algorithm demonstrates superior encryption effectiveness.

Table 17 PSNR findings between cipher-text and plain-text images. ‘P-C’ signifies the comparison between plain-text and cipher-text images, while ‘P-D’ denotes the comparison between plain-text and decrypted images.

Data crop and noise assaults

The real world is characterized by fuzziness and uncertainty. Images, when transmitted through channels, may encounter noise contamination or, at times, portions of the image may be inadvertently cropped. Effective image ciphers are expected to withstand such challenges posed by noise and data cropping. Figure 14c illustrates the encrypted image of Moon polluted by noise (Pepper & Salt) with density of 0.1. As we spark the decryption paraphernalia on it, the obtained image is drawn in Fig. 14d. One can notice that image concerned is easily recognizable after decryption.

Fig. 14

Defiance of suggested cipher against data loss and noise attacks: (c) Clock cipher image with 0.1 density of noise; (d) Decrypted image from (c); (a) Cipher image of Couple with 50% data loss; (b) Decrypted image from (a). https://sipi.usc.edu/database/database.php?volume=misc.

Moreover, Fig. 14a illustrates the cipher image of Couple with data loss to the tune of 50%. Subsequently, the decryption algorithm is applied to this encrypted image that underwent data loss. Corresponding decrypted image is presented in Fig. 14b. The image, after decryption, still preserves significant visual information, allowing for easy recognition. Consequently, the proposed scheme demonstrates its capability to counteract potential threats of data loss during image transmission.

Encryption throughput and speed analyses

Ensuring the security of any image cryptosystem is paramount during its development. Simultaneously, significant efforts should be dedicated to maintaining a reasonably fast execution speed for the cipher. Encryption schemes with nicer speed of execution are more promising in real-world scenarios. Suggested image security scheme was implemented and coded on an Intel(R) Core(TM) i5-4210U CPU @ 1.70 GHz 2.40 GHz, 8 GB memory system, running Windows 10 and Python 3. Encryption times for various images are presented in Table 18. Furthermore, our algorithm demonstrates efficiency compared to those in^14,49,50,51 in terms of speed (Table 19 and Fig. 15). The suggested algorithm beats the two studies^14,49.

Fig. 15

Comparison of computational time of algorithms.

Besides the analysis of speed, encryption throughput (ET) is also evaluated by some cryptographers sometimes. This analysis measures given image size that can be encrypted in a unit of time. Naturally, ciphers with larger ET values are considered superior. The notion of ET is expressed in the following mathematical equation⁶⁶.

$$\begin{aligned} ET=\frac{Image_{size} (Bit)}{Encryption_{time} (second)} \end{aligned}$$

(14)

Table 18 depicts ET of suggested scheme for chosen images of this research study. It is to be noted that $Image_{size} (Bit)$ corresponds to the number of bits in the given image.

Table 18 Encryption speed (sec) and throughput of suggested algorithm for security of digital images.

The encryption speed and hence encryption throughput will vary with different hardware configurations. We can’t say a priori that how they will vary. To actually see the difference, one will have to physically run the suggested image cipher upon the various hardware configurations.

Table 19 Comparison of the average speed by various encryption algorithms.

The proposed image encryption algorithm has been designed with scalability in mind, adapting efficiently to different image sizes by optimizing memory usage and computational steps. For larger images, the algorithm maintains a linear or near-linear time complexity, ensuring that encryption time grows proportionally with the image dimensions. Additionally, this approach is compatible with a variety of computing environments, from lightweight IoT devices to high-performance computing systems. Testing across different images has shown minimal latency, making the algorithm feasible for real-time applications in resource-constrained settings, such as mobile and embedded systems.

Computational complexity analysis

While analysis of speed in Subsection “Encryption throughput and speed analyses” addresses certain performance considerations, it is not without its shortcomings. Notably, speed metrics are influenced by factors such as specific platform, software, hardware, input image, etc. These variables make it challenging to provide an exact representation of the algorithm’s speed. To obtain a more intrinsic measure of speed and performance, theoretical analysis is typically employed. Asymptotics, a mathematical theory⁶⁷, is commonly used for this type of analysis.

Equation (6) calculates the streams of random numbers $\{u1_{t}\}_{t=1}^{mn}$, $\{v1_{t}\}_{t=1}^{mn}$, $\{w1_{t}\}_{t=1}^{mn}$, $\{u2_{t}\}_{t=1}^{mn}$, $\{v2_{t}\}_{t=1}^{mn}$, and $\{w2_{t}\}_{t=1}^{mn}$ $\{s_{t}\}_{t=1}^{mn}$. It takes $\Theta (7mn)$ steps. Algorithm 1 takes $\Theta (7mn + 7)$ steps. Algorithm 2 takes $\Theta (6)$ steps. Algorithm 3 takes $\Theta (49mn)$ steps. Equation (7) takes $\Theta (3mn)$ steps. The aggregate of these time complexities amounts to $\Theta (66mn)$ after we ignore the lower order terms.

Memory footprint

In this section, we analyze the memory footprint of the proposed image encryption algorithm. Memory efficiency is a crucial factor for encryption algorithms, especially for resource-constrained environments like IoT devices. The memory footprint encompasses all memory requirements, including the storage of input and output images, temporary buffers used in processing, and any additional data structures such as keys, lookup tables, or intermediate matrices. To provide a comprehensive analysis, we calculate the memory usage for each component involved in the encryption process, highlighting the efficiency and suitability of our algorithm for applications with limited memory resources.

Table 20 Memory footprint of the proposed algorithm.

Table 20 shows the memory consumed by each component of the proposed Algorithm 1. The total memory footprint of the proposed algorithm is 5(192) KB + 7(1792 KB) + 4(28) Bytes + 2(672) Bytes + 2(8 Bytes to 192 KB) = 13.1884 MB to 13.5638 MB. Since the proposed image cipher has been developed complying with the tenets of private key cryptography, so the decryption algorithm will also consume the same amount of memory.

The calculated memory footprint of the proposed image encryption algorithm is approximately 13 MB. This includes all necessary components, such as the original image data, intermediate buffers, and encryption keys. Given the complexity of the encryption process, this footprint demonstrates the algorithm’s efficiency, making it feasible for deployment in systems with moderate memory capacity. This level of memory consumption is especially suitable for applications in environments such as smart devices or IoT applications, where memory resources are often limited but security remains paramount.

In terms of real-world applicability, our algorithm demonstrates strong encryption performance with minimal computational overhead, making it feasible for real-time applications. Comparative tests on image processing times and memory usage have shown that our method maintains efficiency comparable to other leading algorithms, even under constrained environments.

Conclusion and future work

Image encryption is a hot research area in today’s digital images dominated world. This research project has presented a yet another image cipher in a 3D setting under the umbrella of Python ecosystem. The given gray scale image is converted into a 3D image. After that, a pair of the boxes (cubes) is generated within the premises of the 3D image. Each pair consists of eight vertices. The pixels covered by these pairs of boxes are swapped with each other numerous times to come up with the required confusion and scrambling. It has also been checked meticulously that the pairs so generated do not overlap with each other. In case, they overlap, no operation is carried out since some pixels will be lost. Two chaotic maps of 5D multi-wing hyper-chaotic and piece-wise linear chaotic map have been used in this study. These maps produce streams of random numbers. The former map was used to execute the confusion operation among the pixels of the given image. The latter map introduced the diffusion effects. The security analysis of this work rendered very promising results. This work can be applied in some real world situation to reap its intrinsic benefits, medical imaging, military, commerce, diplomacy, traffic and medicine, for instance. Unluckily, there is an intrinsic limitation of the proposed work, i.e., only the images for which $(m \times n)^{\frac{1}{3}} \in \mathbb {Z}^+$ can be used in the suggested image cipher (m, n), being the size of the given image. This limitation may hinder the applicability of the proposed image cipher for some applications. As a future work, an effort will be made to lift this limitation. Other research direction may be the usage of notion of sphere for image encryption in which mapping from the plane image to the sphere image will be carried out before doing any encryption. It will heighten security for the precious digital images.