Introduction

The rapid expansion of WiFi and 5G has led to the frequent transfer of large digital images across various communication networks. However, the increased frequency of these transfers has made the images more vulnerable to tampering and theft. To ensure the security and privacy of these images before transmission, methods like image encryption and digital watermarking are commonly used. Image encryption is the most straight forward method for protecting digital images1. During the permutation stage, pixel positions are randomly rearranged, while the diffusion stage alters the pixel values of the original image. Techniques used in image encryption include frequency domain transformations, chaos, evolutionary algorithms, neural networks (NNs), and DNA coding. Chaos is particularly popular due to its sensitivity and inherent unpredictability, making it a powerful tool in encryption methods2.

The Internet of Things (IoT) and blockchain technology has offered an advanced solutions for enhancing image encryption techniques. IoT devices can collect and transmit images in real-time making it crucial to secure these data transfers. By embedding encryption protocols directly with IoT devices, images can be protected from unauthorized access as they are captured and transmitted. Blockchain technology can further enhance image encryption by providing a decentralized and immutable ledger for tracking image data. Each transaction involving an image whether it is encrypted or is in its original form, it can be recorded on the blockchain. This ensures that the tampering proof of all the activities related to the stored image are saved on the blockchain, thereby enhancing its security. Combining the use of IoT with blockchain offers a robust framework for securing digital images from capture to transmission3.

IoT devices are interconnected through wireless or wired networks and they provide seamless communication and data exchange. The network connectivity helps the devices to work together and perform multiple tasks. The integration of data analytic, AI, and Machine Learning (ML) algorithms allow the IoT devices to make informed decision and process a large amount of data4. The use of intelligence helps enhance the functionality and efficiency of IoT system. IoT ecosystem contains a number of devices with varying hardware platforms, operating system and protocols. This heterogeneity requires robust frameworks to ensure seamless interaction among different devices. Nowadays IoTs are used in smart homes, health care, industrial IoT, smart cities, agriculture, transportation and logistics5.

Blockchain technology is a revolutionary innovation which has transformed the way data can be recorded verified and shared. It is a decentralized ledger system which ensures transparency security and protection of data on online forums. This decentralized nature of blockchain technology reduces the risk of single point failures, enhancing the systems resilience against attacks. In a blockchain system the transactions are visible to all participants in that network which promotes trust and accountability. Furthermore once a transition is recorded on the blockchain it cannot be altered or deleted which provides us the integrity of data. The key components of blockchain includes blocks, ledger, consensus, cryptographic security and smart contracts. Blockchain contains a series of blocks which are connected with each other and every block contains a list of transaction with time stamp and cryptographic hash of the previous block. This interconnected structure ensures the integrity and order of the data. Blockchain operate on the distributed networks where all the participants also known as nodes maintain a copy of the entire ledger6. The distributed ledger eliminates the need for a central authority and reduces the risk related to the single point of failure. The consensus mechanism of a blockchain technology like proof of work (PoW) or proof of stake (PoS) validates the transactions and eliminates the need for central authority making it more easier to use. Blockchain uses cryptographic algorithms and techniques to secure the transaction and protect the integrity of data. Different pairs of public and private keys are used for encryption and creating. Digital signatures are written into courts which automatically enforce and execute when the defined terms are completed7.

Blockchain technology is now used in cryptocurrencies like Bitcoin. It provides the supply chain management by enhancing the transparency and a temper-proof record of the movement of goods from origin till destination. Blockchain technology is also used in medical in efficiently securing the medical records and improving the patient's care. Other applications of blockchain include financial services, voting system, intellectual property and in real estate8.

The Blockchain-Orchestrated multi-cloud strategy refers to a decentralized system that uses the blockchain technology to coordinate and optimize the management of resources across multiple cloud server providers such as AWS cloud, azure and Google cloud. We have employed this strategy in our proposed image encryption technique as it integrates the inherent advantages of blockchain with the elasticity of a multi-cloud environment. This strategy facilitates secure resource allocation, efficient data distribution and an enhanced redundancy across different cloud platforms. The multi cloud option mitigates the risk of vendor lock in hence improving the system's resilience and in data integrity through continuous verification process which is governed by the blockchain technology9. Besides this, the blockchain orchestrator manages the cryptographic keys and ensures that any transaction or change related to data storage, data retrieval, and data processing are securely logged in and verified. The orchestration layer dynamically optimizes the cloud resource usage and maintains a robust security standard which makes it highly suitable for applications that demand high levels of trust and security in distributed environments.

A research focused on secure and efficient image encryption was proposed which addressed the challenges posed by proliferation of digital images over open networks. The study introduced a 5-stage image encryption algorithm which was designed using Shannons confusion and diffusion principles10.

In the realm of secure steganography, Alexan et al. Introduced “Stegocrypt”, a tri-stage algorithm that enhances data concealment within digital images. This method involved encrypting a secret message using tan logistic map, then converting it to quick response (QR) code which are then decoded back into bit-streams. This scheme used DNA coding in each bit-stream by help of a uniquely-seeded Mersenne Twister key which significantly increased its security11.

Another novel image encryption technique was proposed which integrated the unique image transformation techniques with the principles of chaotic and hyper-chaotic systems. It combined the unpredictable behaviour of Chua system and the hyper-chaotic nature of the Chen system resulting in an expansive key space of 25,20812.

Related works

Alexan W. et al., developed an image encryption scheme that extended the hyperchaotic 4D chen system into fractional-order domain to perform encryption on 3 stages involving discrete Fourier transform (DFT), S-box derived from DFT and lastly a Mersenne Twister encryption key. The use of three stages provided with a promising solution for secure image encryption13.

A novel 3-stage cryptosystem was proposed which utilized a three-stage process which combined chaotic maps and DNA encoding to enhance security. The first stage used a tan variation of logistic map for DNA encoding, the second stage constructed a robust S-box using the Lorenz differential equations and a linear descent algorithm and the third stage applied the original logistic map for further diffusion. This approach offered high security and computational efficiency14.

A study utilized a fractional-order 4D hyperchaotic Chen map combined with sine chaotic map and a hybrid DNA coding algorithm. This approach demonstrated robustness against various attacks15. Additionally, an image encryption algorithm designed for color medical images employed Fibonacci Q-matrices, an S-box in Galois field \({2}^{8}\) and a hyperchaotic system modeling a memristive coupled neural network16.

In recent years the integration of smart cameras and image sensors in industrial processes has been increasingly prevalent, especially for quality assurance. However the widespread in use of these technologies has also raised concerns regarding the security of the data, especially in the context of the industrial internet of things (IIoT). Traditional cryptographic solutions often struggle to provide adequate protection in these environments due to the involvement of third-party excess which is a threat to security. Blockchain technology has emerged as a promising solution to address such trust issues by offering a decentralized and transparent data management system. A study investigated the blockchain-based image encryption scheme where the encrypted image data is purely stored in blockchain increasing both the confidentiality and integrity3.

Not only this the healthcare sector also generates a diverse form of medical data which include scanned images, computerized patient records and confidential information creating challenges for researchers who seek to protect this sensitive information. Traditional methods for storing and transmitting the data, especially through the public cloud environment, expose such data to risks such as eavesdropping and data breaches. Previous works have demonstrated that encrypting medical images before transmission can mitigate these risks with blockchain emerging as a viable solution due to the decentralized structure. A blockchain-based chaotic Arnold’s cat map encryption scheme (BCAES) was proposed which utilized the Arnold cat map for image encryption before sending the encrypted data to the cloud while simultaneously storing a signed document of the plain image on the blockchain. This combination of cloud and blockchain ensures integrity authenticity and confidentiality6.

Another color image encryption scheme utilized the Hennon-zigzag map and chaotic restricted Boltzmann machine (CRBM), which significantly improved security by using a two-phased process of permutation and diffusion. In the proposed scheme the permutation phase employed a henna zigzag map to modulate pseudo-random number sequences for row and column permutations which enhanced the scrambling process. In the diffusion phase, the CRBM generated three separate pseudo-random number sequences which were XORed with the RGB channels of the image separately ensuring the encryption throughout all three channels. This combination of advanced encryption algorithms underscores the growing trend of using decentralized networks for verifying data authenticity17.

A novel blockchain enables secure optimal lightweight cryptography-based encryption BC-LWCIE technique was proposed for the industry 4.0 environment. This proposed scheme integrates the optimal lightweight cryptography LWC, hash functions and optimal key generation by using the chicken swarm optimization (CSO) algorithm that enhances the security by maximizing the Peak Signal-to-Noise Ratio (PSNR). Additionally, the cryptographic pixel values of the deciphered images are securely stored on the blockchain. This technique has outperformed the recent encryption techniques which highlights its effectiveness in securing the image data in IoT environment18.

Contributions of paper

The contributions of this paper are as follows:

  • 1. Introducing a new hybrid image encryption method combining the chaotic maps (logistic and May map) and fractal-based permutation techniques to achieve robust security for breast cancer images.

  • 2. Employing the May map to generate a chaotic sequence and computing an S-box from it introducing a high level of randomness and unpredictability in the encryption process

  • 3. Proposed the integration of a fractal generation method to further shuffle the image pixels after chaotic permutation which adds an extra layer of complexity to the encryption

  • 4. Demonstrates the resilience of the proposed encryption scheme against common cryptographic attacks including differential attacks statistical attacks and brute force attacks

The structure of this paper is as follows: section "Fundamental theory" discuss the fundamental theory of the maps used in the proposed scheme, section "Proposed blockchain-orchestrated multi-cloud" explains the blockchain orchestrated multi-cloud environment and its working, section "Proposed image encryption process" contains the proposed image encryption and decryption technique, section "Simulation results and security analysis" contains the simulations and results and section "Discussion" and "conclusion" concludes the paper.

Fundamental theory

Following fundamental theories are used in our proposed algorithm:

May map

The May Map is a 1D chaotic map which was named after Robert M. May who introduced it as a simple model to study the population dynamics. The May map is characterized by its ability to generate chaotic sequences which depend on the value of its parameters. The standard equation for the May Map is given by:

$${x}_{n+1}={x}_{n}. exp(r.(1-{x}_{n})$$
(1)

Here, \({x}_{n}\) is the current state of the system and \({x}_{0}\) is the initial value. r is the control parameter which determines the chaotic behaviour of the map and \({x}_{n+1}\) is the next state in the sequence. The May Map exhibits chaotic behaviour when the control parameter r is within a certain range, typically around \(r>2.5\). As r increases, the system undergoes bifurcation which leads to a complex dynamics and chaos19.

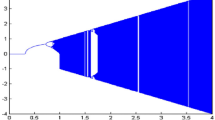
The bifurcation diagram of May map shows the transition from stability to chaos as the parameter r increases. A single stable point splits into two then four and then so on. This is known as period doubling which lead to complex behaviour.

The Lyapunov diagram of May map provides a visual representation of the system’s behaviour as r varies. When \(\lambda <0\) the system shows a stable and non-chaotic behaviour. This region is typically appear as dips or valleys below the zero line as shown in Fig. 1. When \(\lambda >0\) the system shows a chaotic behavior as the positive exponent indicates that trajectories starting from nearby initial conditions diverge exponentially that ultimately leads to unpredictable behaviour.

Fig. 1
figure 1

Bifurcation and Lyapunov exponent diagram of may map.

Full size image

Logistic map

The logistic map is a fundamental mathematical model in the study of chaotic systems. Despite its simplicity, logistic map shows complex and chaotic behavior under specific conditions making it an important part of chaotic theory. The logistic map is defined mathematically as:

$${x}_{n+1}=r.{x}_{n}. (1-{x}_{n})$$
(2)

Here, \({x}_{n}\) is the population at iteration \(n\), chosen normally between \(0\) and \(1\) and \(r\) is the growth rate parameter typically \(r\in [\text{0,4}]\).

The behaviour of logistic map changes drastically with different values of the growth rate \(r\). At \(r>3.57\) the system enters the chaotic regime where the behaviour is highly sensitive to initial conditions and at \(r=4\), the system exhibits full chaos20. One of the most important aspects of logistic map is its bifurcation diagram which represents the transition from order to chaos as the values of parameter \(r\) is changed. The Fig. 2 shows the bifurcation diagram of logistic map representing that how a stable point can split into two, four and eight points and eventually leading to a chaotic state.

Fig. 2
figure 2

Bifurcation diagram of logistic map.

Full size image

Sierpinksi triangle fractal pattern

The Sierpinksi triangle, also known as the Sierpinksi gasket is a well known fractal pattern named after the Polish mathematician Waclaw Sierpinksi. It is self-similar structure and a classic example of geometric shape with a fractional dimension falling between 1D lines and 2D surfaces. The Sierpinksi triangle is constructed by using an iterative process where we start with an equilateral solid triangle and subdivide it into four smaller congruent equilateral triangles and remove the central one. For the remaining triangles, same subdivision and removal is repeated21. Continuing this leads to the fractal pattern called Sierpinksi triangle. The fractal dimension D of the Sierpinksi triangle is given by Eq. 3,

$$D=\frac{log 3}{log 2}\approx 1.585$$
(3)

It shows us that the triangle is complex since the dimension is non-integer.

The Sierpinksi triangle is a fractal pattern that is used in image encryption due to its inherent properties of self-similarity and complexity. It can be used to design robust encryption schemes. The fractal pattern of Sierpinksi triangle such as shown in Fig. 3 is used for generating complex key that are sensitive to initial conditions. The recursive nature of these triangles ensure that a small change in the key gives an entire different encrypted image. The Sierpinksi triangle can also be used for permutation and diffusion process as mapping image according to the Sierpinksi pattern can make the original structure disrupted to such an order that it cannot be reversed by unauthorized party22.

Fig. 3
figure 3

Sierpinksi triangle.

Full size image

Chebyshev map

The Chebyshev Map generates chaotic sequence based on the following equation

$${x}_{n+1}=cos(k.arccos({x}_{n}))$$

Here, \(k\) is the control parameter, usually \(k\ge 2\). \({x}_{n}\) is the value at iteration \(n\) with an initial value \({x}_{o}.\)

Proposed Blockchain-Orchestrated multi-cloud

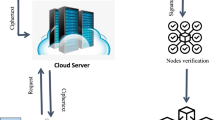
Our proposed algorithm leverages the IoT devices for data capture and employs blockchain orchestrated multi-cloud environment, May Map, Logistic Map and Fractal Based Image encryption scheme to secure the Breast cancer images in hospital settings. The subsequent steps outline the work flow from image capture to decryption and assess by the end user.

Image capture via IoT devices

The initial stage of the process involves the capture of images through IoT enabled devices. These devices may include cameras, sensors or other imaging tools which are deployed within the operational environment to correct a real time image data. The IOT devices continuously monitor and capture the images in a hospital. Before the captured image is transmitted, preliminary processes like compression can be performed on the devices for optimizing the data for secure transmission.

Image encryption process

After receiving the data it is encrypted by using the encryption scheme. Moreover, digital signatures using the hash function are also generated for the images. This dual approach safeguards both the integrity and confidentiality of the data ensuring that the image remains unaltered and accessible only to the authorized recipients. By using these security measures the sender effectively protects the image from tempering and unauthorized access during storage or transmission.

Blockchain-Orchestrated management

After the encryption of images the blockchain orchestrator functions as a decentralized control hub that ensures the secure and efficient handling of data. It is responsible to allocate the storage resources across various cloud providers based on the criteria such as performance, cost efficiency and redundancy requirements. The encrypted images along with their associated Meta data are distributed across the selected cloud providers. The blockchain maintains a transparent record of where each data is stored to ensure traceability and integrity.

Cloud storage and verification

Upon distribution to the cloud providers the encrypted images are securely stored within the respective cloud environment. The encrypted images are replicated across multiple cloud providers which enhances the data availability and provides a fail-safe mechanism in case of data corruption or loss at any single provider. The blockchain continuously verifies the integrity of the stored images by comparing their hashes against the original hash functions recorded in the blockchain. Any changes detected triggers the immediate alert thereby safeguarding data against unauthorized modification or tampering.

Image decryption and access

When an authorized user request access to the stored images the decryption process is initiated. This step involves the retrieval of encrypted images and their associated decryption key followed by the decryption of the images for end-user access. This process can be carried out either within the cloud environment or locally depending on the specific use and security requirements. After the images are decrypted and available to the end user this step completes the cycle ensuring the user disease images which are both secure and unaltered from their original form.

The proposed system, illustrated in Fig. 4, is designed to continuously monitor all the activities related to image encryption storage and access. Regular audits are conducted which ensures that the system remains robust against evolving cyber security challenges. By combining the strengths of IOT blockchain and cloud computing the system ensures confidentiality integrity and availability of sensitive image data thereby addressing the critical security concerns in data management.

Fig. 4
figure 4

Primary components in proposed Blockchain-Orchestrated multi-cloud.

Full size image

Our proposed hybrid image encryption method combines the chaotic maps with fractal-based permutation techniques offering some significant advantages over traditional centralized cloud models. By leveraging decentralized processing, our approach reduces the reliance on centralized servers, thereby decreasing associated infrastructure and maintenance costs. Additionally, this decentralized framework not only improves computational efficiency by distributing processing tasks but also minimizes delays and avoids system failure which is common in centralized setups.

Proposed image encryption process

The details of the proposed image encryption algorithm is given below:

Encryption process

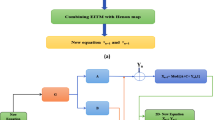
Step 1: Chaotic sequence generation using logistic map

A chaotic sequence is generated using the logistic map which can be shown in Fig. 7. The logistic map is iteratively applied to produce a sequence of chaotic values. The initial value \({x}_{0}\) and the total number of iterations N are chosen based on the number of pixels of image. For example, for an image of size \(256\times 256\), \(N=65536\). Once the chaotic sequence is generated, it is sorted in ascending order and compared with the original sequence. The change in positions is noted as \(SP\). This shifted position sequence serves as the basis for permuting the pixel positions in the image thereby introducing non-linearity and diffusion into the encryption process.

figure a

Algorithm 1. Sorted sequence algorithm.

Step 2: S-box generation using may map

In the first step will initialize the May maps parameter by setting the initial value and the number of iterations to be performed. The chaotic sequence is generated by iterating the May map where each value is calculated by using the formula in Eq. (1). The sequence of the values is sorted in an array S. Subsequently the values in S are normalized to fit within a 8-bit range (0 to 255) that ensures that the resulting S-box entries are suitable for cryptographic operations. The normalized values are then used to generate an initial S-box where each position in the S-box is filled by the values derived from the chaotic sequence. This ensures the high degree of randomness and unpredictability to enhance the uniqueness of S-box. The duplicate values are identified and adjusted. This is done by adding a fixed integer to each duplicate value followed by a modulo operation so that the result remains within the eight bit range. This step is important for maintaining the bijective property of the S-box. Finally the resulting S-box is ready to use in the secure image encryption scheme. The Algorithm 1 gives the pseudo code for S-box generation. Table 1 provides an illustration of proposed S-box and Fig. 5 visualizes the duplicate removal process in S-Box generation.

figure b

Algorithm 2. S-box generation algorithm.

Table 1 S-Box computed by Algorithm 1.
Full size table
Fig. 5
figure 5

Visualization of duplicate removal process in S-box generation.

Full size image

Step 3: Applying S-box to each channel of original image

The original image \(M\) is first split into its three color channels Red, Green and Blue. Each channel represents its intensity values for its respective color across all pixels in the image. The image pixels are substituted by applying S-Box to each channel separately. This substitution process introduces non-linearity and enhances the security of the encryption process by increasing confusion and diffusion of image data. After substitution, the channels recombine to form a distorted image N.

figure c

Algorithm 3. Distorted image algorithm.

Step 4: Diffusion using Chebyshev map

The diffusion step uses the Chebyshev Map, a chaotic system, to generate a sequence of pseudo random numbers from an initial value \({x}_{o}\) and a chaos control parameter \(k\). These numbers are normalized to produce indices corresponding to pixel positions in the image. The distorted image pixel values from step 3 are rearranged (permuted) based on these indices, effectively scrambling the image. This process ensures that a slight alteration in the initial conditions or the key results in a completely different permutation.

figure d

Algorithm 4. Diffusion algorithm.

Step 5: Fractal-based encryption key generation

A Sierpinski Triangle fractal pattern is used as the basis for encryption key generation. The fractal is generated using the logistic map defined in Eq. 2.

Here \(r=3.999\) is the control parameter for chaotic behaviour and \({x}_{0}\) is the initial value. The logistic map is iterated to produce the values of Sierpinski triangle within a \(256\times 256\) matrix. The resulting binary fractal pattern where the non-zero values are set to 255, form the initial encryption key matrix \({K}_{f}.\) This key is further combined with the chaotic sequence generated from the logistic map. A secondary key matrix \({K}_{c}\) is generated by iterating the logistic map with each value scaled to the range \([\text{0,255}]\). The final encryption key \({K}_{e}\) is obtained by performing the XOR operation to ensure that pixel values remain within the 8-bit range:

$${K}_{e}={K}_{f}+{K}_{c} (mod 256)$$
(4)

To elucidate the role of Sierpinski triangle in the key generation process, we have presented a visual representations of fractal pattern used in Fig. 6. The Sierpinski triangle, a well-known fractal, is constructed through recursive subdivision of an equilateral triangles, resulting in a complex, and self-similar structure. In our encryption scheme, these fractal patterns introduce a high degree of complexity and randomness, enhancing the diffusion and confusion properties essential for robust encryption (Fig. 7). The inherent self-similarity and intricate design of the Sierpinski triangle ensures that even minimal alterations in the input leads to significant and unpredictable changes in the encrypted output, thereby substantially strengthening the encryption against potential attacks

figure e

Algorithm 5. Generation of fractal-based key algorithm.

figure f

Algorithm 6. Key generation algorithm.

.

Fig. 6
figure 6

Fractal-key generation.

Full size image
Fig. 7
figure 7

Flowchart of encryption process.

Full size image

Step 6: XORing

The final encrypted image is generated by performing a pixel-wise XOR operation between the diffused image from step 4 and combined fractal encryption key from step 5 producing the final encrypted image \({I}_{e}\).

$${I}_{e}=D\oplus {K}_{e}$$
(5)
figure g

Algorithm 7. Encryption algorithm.

Decryption process

The decryption process can be performed as follows:

  • 1. Generate Fractal based key using the same logistic map parameters and initial conditions

  • 2. Find the reverse S-box using the same parameters of May map

  • 3. Perform a pixel-wise XOR Operation between the encrypted and regeneration encryption key matrix to obtain intermediate image

  • 4. Generate chaotic sequence using Chebyshev Map same initial conditions \({x}_{o}\) and parameter k. Apply reverse permutation using original sequence of indices.

  • 5. Split the image from step 4 into 3 color channels; Red, Blue and Green

  • 6. Apply inverse S-Box mapping for each pixel and restore the original pixel values.

  • 7. Use the sorted indices from the chaotic sequence to reverse permutation and retrieve original image

  • 8. Reshape 1D array back to the image dimension

Simulation results and security analysis

To evaluate the effectiveness and robustness of the proposed image encryption scheme, various experiments and analysis were conducted. The simulation results are crucial in assessing the statistical qualities of encrypted image. A comprehensive set of tests are performed including histogram analysis, correlation coefficient analysis, key sensitivity and differential attacks like NPCR and UACI. Additionally, the metrics such as Means Square Error (MSE), Peak Signal-to-Noise Ratio (PSNR) and Chi-square tests are used to assess the quantitative insights into the encryption quality. The results from these analysis have demonstrated the strength of encryption scheme against potential attacks, highlighting the capability to maintain data integrity and confidentiality.

To test the encryption scheme we have used different medical images from datasets. These medical images includes CT scan image23, Mammography24 and Cancer immunotherapy25 shown in Fig. 8. The encrypted images are shown in Fig. 9. For computational experiments we employed Google Colab as our development environment. Google Colab provides access to virtual machines with varying specifications. Table 2 shows specifications.

Fig. 8
figure 8

Original images.

Full size image
Fig. 9
figure 9

Encrypted images.

Full size image
Table 2 Specifications of development environment Google Colab.
Full size table

Histogram analysis

The histogram analysis assess the pixel intensity distribution of the encrypted images compared to plain image. A uniform histogram in the encrypted image indicates that the pixel values are evenly distributed highlighting that the encryption process effectively masks the original content. This uniformity demonstrate that the images are resistant against statistical attacks since no patterns of the image are revealed. The histograms of the test images as shown in Figs. 10 and 11. The visual distribution and randomness in encrypted image indicates high entropy and randomness as illustrated in Fig. 8.

Fig. 10
figure 10

Histogram of original images.

Full size image
Fig. 11
figure 11

Histogram of encrypted images.

Full size image

Correlation coefficient analysis

The correlation coefficient analysis measures the relationship between adjacent pixels in both the original and encrypted images. In a secure encryption scheme, the correlation between adjacent pixels should be close to zero which indicates that the encryption process has successfully disrupted the inherent spatial relationships in the original image. On the other hand, a low correlation value indicates that the encrypted image does not retain any significant structural similarities with the plain image which makes it difficult for the intruder to reconstruct the image.

The correlation is measured as follows:

$$Corr (x,y)=\frac{Cov (x,y)}{\sqrt{Var (x) \times Var (y)}}$$
(6)

\(Cov (x,y)\) is the co-variance between adjacent pixels x and y, \(Var (x)\) and \(Var (y)\) are the variance values of the pixel x and y respectively. Table 3 indicates the correlation values of original and encrypted images along horizontal and vertical directions. Lower correlation suggests that the encryption algorithm effectively disrupts the relationship between adjacent pixels. Moreover, Figs. 12, 13 and 14 illustrate the relationship between adjacent pixels in the three test images. The scattered distribution of pixel pairs show a lack of correlation between adjacent pixels reflecting the effectiveness of the proposed scheme.

Table 3 Correlation values of original and encrypted images along vertical and horizontal direction.
Full size table
Fig. 12
figure 12

Vertical and horizontal pixel value correlation of encrypted image of mammography.

Full size image
Fig. 13
figure 13

Vertical and horizontal pixel value correlation of encrypted image of CT scan.

Full size image
Fig. 14
figure 14

Vertical and horizontal pixel value correlation of encrypted image of cancer immunotherapy.

Full size image

Differential attack analysis

Two metrics, namely Number of Pixel Rate Change (NPCR) and Unified Average Change Intensity (UACI), used to evaluate the resistance of the encryption scheme against differential attacks.

NPCR means the percentage of different pixels between two encrypted images when the original image is subjected to slight modifications such as changing a single pixel. Whereas, UACI quantified the average intensity of the differences between the two encrypted images. Mathematically,

$$NPCR=\frac{1}{W\times H}\sum_{i=1}^{W}\sum_{j=1}^{H}D\left(i,j\right)\times 100\%$$
(7)
$$UACI=\frac{1}{W\times H}\sum_{i=1}^{W}\sum_{j=1}^{H}\frac{\left|{C}_{1}(i,j)-{C}_{2}(i,j)\right|}{255}\times 100\%$$
(8)

\(W\) and \(H\) are width and height of the image respectively.

\(D(i,j)\) is a binary function defined as:

$$D\left( {i,j} \right) = \left\{ {\begin{array}{*{20}c} 0 & {if\; C_{1} \left( {i,j} \right) = C_{2} \left( {i,j} \right)} \\ 1 & { if \;C_{1} \left( {i,j} \right) \ne C_{2} \left( {i,j} \right)} \\ \end{array} } \right.$$
(9)

\({C}_{1}(i,j), {C}_{2}(i,j)\) are the pixel values at position \((i,j)\) of two encrypted images. A value near 99% for NPCR and 33% for UACI indicates that the encryption process can effectively prevent attackers from predicting the effect of minor changes in the plaintext image on the ciphered image which ensures a high level of security.

Encrypted image quality measure

Mean Square Error (MSE) and Peak Signal to Noise Ratio (PSNR) are the metrics used to assess the visual quality of encrypted image.

MSE calculates the average squared difference between the pixel values of the original and the encrypted images while PSNR measures the ratio of maximum possible pixel value and power of the noise caused by the encryption process. High

$$MSE = \frac{1}{W \times H}\mathop \sum \limits_{i = 1}^{W} \mathop \sum \limits_{j = 1}^{H} \left[ {I\left( {i,j} \right) - I^{\prime } \left( {i,j} \right)} \right]^{2}$$
(10)

\(W\) and \(H\) are width and height of the image respectively and \(I(i,j),{I}{\prime}(i,j)\) are the pixel values of the original and encrypted images at position \((i,j)\).

PSNR is given by,

$$PSNR=10.{\mathit{log}}_{10}\frac{{255}^{2}}{MSE}$$
(11)

Here, 255 is the maximum possible pixel value for 8-bit image. MSE values and low PSNR values indicate that the encryption image significantly differs from the original ensuring that the original image’s content cannot be reconstructed. In medical imaging, maintaining a high PSNR values are essential because even a minor distortion can lead to misinterpretations, potentially affecting the patient diagnosis and treatment. In Computed tomography (CT) scans, preserving image quality is vital for accurate detection of anomalies. Studies have shown that higher PSNR values means better image quality with clearer details especially in CT images26.

Entropy analysis

Entropy measures the amount of randomness or unpredictability in an image. It quantifies the amount of information and uncertainty in image pixels. An entropy value near 8 indicates more randomness and suggests that the image is difficult to predict. The entropy H can be calculated as

$$H=-\sum_{i=0}^{N-1}p({x}_{i}){\mathit{log}}_{2}(p{(x}_{i}))$$

Here, \(p{(x}_{i})\) is the probability of occurrence of pixel value \({x}_{i}\) and N is the number of possible pixel values. In Image encryption, Shannon entropy measures the randomness and unpredictability of pixel intensity distributions. Our proposed algorithm achieves an entropy value of 7.9968 closely approaching the ideal 8 indicating maximum randomness and minimal redundancy.

The values of NPCR, UACI, PSNR and MSE shown in Table 4 indicate the effectiveness of encryption scheme. The high NPCR and UACI values indicate substantial pixel and intensity changes between original and encrypted images, crucial for secure encryption. Meanwhile, the MSE values suggests a high level of dissimilarity between the encrypted and original image and high PSNR values indicate that encrypted images have maintained good quality. Table 5 presents the comparison of entropy values with previous techniques and Table 6 and Fig. 15 compares the NPCR and UACI values.

Table 4 NPCR, UACI, PSNR and MSE values for test images using proposed scheme.
Full size table
Table 5 Comparison of entropy values.
Full size table
Table 6 Comparison of NPCR and UACI.
Full size table
Fig. 15
figure 15

Graph showing the comparison of entropy values, NPCR & UACI.

Full size image

Time complexity

Our proposed scheme can encrypt 32 images of size \(256\times 256\) per second whereas when compared to existing technique like Chaotic deep GAN and HNN-IES our proposed scheme is significantly faster and efficient as depicted in Fig. 1634.

Fig. 16
figure 16

Time complexity of proposed scheme compared with previous techniques.

Full size image

Discussion

In addition to mammography medical images, the proposed scheme can also be applied to other types of medical data such as MRI scans and genetic information. MRI images like CT scans, contain intricate details critical for accurate diagnosis, making the encryption essential to protect patient’s privacy. Similarly genetic data which involves sensitive personal information also required a very strong encryption to prevent third-party unauthorized access. The robust security provided by our encryption method can be adapted to secure these data types, further enhancing the potential of the proposed system in safeguarding a wide range of medical information.

While the proposed encryption scheme demonstrates strong resistance to traditional cryptographic attacks, it is also designed to be resilient against modern threats such as machine learning-based cryptanalysis such as predicting encryption keys and breaking encryption schemes. However, the high randomness introduced by the chaotic maps and the complexity of fractal-based key generation in our approach makes it difficult for machine learning algorithm to successfully predict the key or decrypt image.

Conclusion

In this work we have introduced a novel approach for enhancing image encryption through the integration of chaotic systems, fractal patterns and advanced cryptographic techniques. The proposed method leverages the May map to generate a robust S-box which is then employed to substitute the pixel values in red, green and blue channels of an image. This substitution introduces significant non-linearity and complexity into the encryption process thereby strengthening the security of the image data. This hybrid approach ensures a high level of security by expediting the chaotic nature of the maps and complexity of rectal patterns. The strength of our encryption scheme lies in its ability to combine chaotic and fractal-based approaches which significantly enhances both the randomness and the security of the encryption process.

Future work

The utilization of chaotic maps, and fractal patterns for image encryption is computationally efficient, making it suitable for IoT devices with limited processing capabilities. Studies have demonstrated the feasibility of real-time medical image encryption using improved sequence from chaotic maps, highlighting its applicability in resource-contrainted settings33. However, challenges such as scalability and interoperability must be addressed to ensure robust application. To tackle these issues we plan to develop lightweight encryption modules optimized for low-power devices, ensuring efficient performance without compromising security. The future work will focus on scalable blockchain architectures and comprehensive testing within real-world IoT medical environment to validate the efficiency of proposed scheme. Moreover, future work will explore the application of this technique to different types of data and access their performance in various cryptographic context aiming to further refine and optimize the encryption process.