Global MPPT optimization for partially shaded photovoltaic systems

Abstract

The global demand for electrical energy has witnessed a substantial increase, presenting a challenge for power systems worldwide. In addition to technical considerations, the escalating issue of global warming has become a paramount concern in the planning studies of various sectors. The formulation and resolution of a single-objective non-linear optimization problem are carried out, considering different operational scenarios. Recent heuristic algorithms, including Particle Swarm Optimization (PSO), Cat Swarm Optimization (CSO), Teaching Learning Based Optimization (TLBO), Grey Wolf Optimization (GWO) and Chimp Optimization algorithm (ChOA) are employed to address the complexities associated with maximizing power output under partial shading conditions in solar PV systems. The inherent challenges of achieving MPPT under such conditions make conventional analytic approaches computationally intensive. Hence, this study leverages heuristic algorithms to optimize solar PV system performance, providing efficient solutions to the associated optimization problems. The current research work was performed on a test system using a MATLAB/SIMULINK environment and the results are presented and discussed. From the simulation results, it was found that ChOA have shown higher conversion efficiency of 99.63% with maximum power output of 525.13 W when compared to other optimization algorithms for the given shading pattern condition. Further, ChOA offers easy implementation and faster convergence, outperforming established methods in GMPP search by reducing power oscillations and achieving precise MPP convergence.

Introduction

India is experiencing a surging demand for electricity due to a rapidly growing population, increasing smart city initiatives, and widespread use of electronic devices. This heightened demand raises concerns about elevated carbon emissions and atmospheric pollution. Globally, the energy demand has seen a significant uptick, prompting a shift towards renewable sources over the past two decades, renewable energy generation has witnessed rapid growth, constituting 26.3% of global energy consumption. Notably, hydroelectricity contributes 15.8%, wind energy 5.3%, solar energy 2.7%, and the remaining 2.5% comes from other renewable sources like modern biomass, wave, tidal, and geothermal energy. Solar, Wind, and Biomass are some of the renewable energy sources abundantly available in nature.

Researchers have extensively investigated various techniques for MPPT from solar energy. Femia et al.¹ emphasized the efficiency and cost-effectiveness of the Perturb and Observe (P&O) method towards maximum harness of solar energy under partial shading conditions. Tofoli et al.² conducted a comparative analysis found that P&O significantly increased extracted power and brought the operating point closer to the MPP. Selvamuthu kumaran et al.³ proposed a flexible step size MPP tracking system with efficient performance under uniform atmospheric conditions. Gil-Velasco and Aguilar-Castillo⁴ observed that P&O finds the MPP with less convergence time. Dileep et al.⁵ surveyed perturb and observe methods, categorizing them based on simplicity, implementation, cost, and convergence speed. Ram et al.⁶ found that P&O with fuzzy outperformed Fuzzy and a new delta P&O method under constant insolation levels. Kumar et al.⁷ proposed a superior minimal rule-based fuzzy logic control-based MPPT technique for solar tracking and it converges very fast with high conversion efficiency. Kofinas et al.⁸ examined the MPPT controller by the application of a novel neuron to tune ANN under stable weather conditions to harness maximum solar energy. Nagadurga et al.⁹ used the CSO based MPP tracking method under uniform irradiance conditions, highlighting faster and stable traced MPP. Liu et al.¹⁰ investigated the PSO for MPPT in PV systems across diverse operational scenarios. They have highlighted the advantageous features of the PSO technique, including its straightforward implementation, system independence, and improved efficiency.

Sree et al.¹¹ studied PSO method for stored solar energy in photovoltaic systems and found that PSO achieves the maximum power point (MPP) with a shorter convergence time compared to other reported techniques. Angadi et al.¹² explored performance improvements in solar PV systems by examining the effects of system parameters such as input capacitance and sampling time using the classic P&O MPPT method. Ram et al.¹³ compared P&O with Fuzzy Logic and a new delta P&O method for MPPT tracking by evaluating design considerations, performance, and accuracy under constant insolation levels, and found that P&O with Fuzzy Logic offered better performance. Tajuddin et al.¹⁴ suggested the Differential Evolution technique for obtaining the maximum solar tracking under changing atmospheric conditions. Thangamani et al.¹⁵ also reported the application of differential algorithm for efficient solar tracking under partial shading conditions. Ramli et al.¹⁶ reviewed various methods for tracking the Maximum Power Point (MPP) under uniform and partially shaded conditions, including artificial intelligence, hybrid approaches, and other soft computing techniques and summarized the advantages of various tracking methods to enhance power output in solar PV systems under PSC. Dileep and Singh¹⁷ conducted a comprehensive study on soft computing methods like PSO and Ant Colony Optimization (ACO) for enhanced solar tracking by highlighting their utilization, strengths, and limitations. Li et al.¹⁸ studied a novel GMPP algorithm for higher solar harness with faster convergence rate under changing environmental conditions. Rezk et al.¹⁹ studied PSO and CS optimization techniques for maximizing power output from shaded solar photovoltaic panels, concluded that both PSO and CS techniques are effective in converging to the global optimum, with CS demonstrating a shorter tracking time than PSO in all considered shading patterns.

Nagadurga et al.²⁰ used the TLBO algorithm for MPPT and found reduced current ripple and power oscillations under partial shading conditions. Gangwar et al.²¹ examined the CSO technique for maximum solar harness by using the panels in the form of Phyllotaxy and achieved higher solar energy tracking. Hegazy and Fathy²² conducted various simulation studies under shading patterns by applying PSO, FLC, and TLBO and the authors concluded that TLBO has shown enhanced performance with respect to solar tracking. Javed et al.²³ used novel firefly algorithm under changing conditions and assessed the performance of the algorithm with PSO and stated that the firefly algorithm have shown better results under changing environmental conditions. Eltamay et al.²⁴ studied the GWO technique with FLC to describe the best way to lower oscillations at the GMPP. Mukherjee and Mallick²⁵ used a swarm-based metaheuristic, Levy Flight motivated Adaptive Particle Swarm Optimization (APSOLF) to achieve superior performance. Statistical analysis confirms APSOLF’s advantage over other state-of-the-art methods, with MPPT tracking efficiency exceeding 99.8% and minimal settling time. Mukherjee and Mallick²⁶ studied the control parameter-based self-adaptive particle swarm optimization (SAPSO) technique was introduced to resolve both MPPT and firing angle optimization (FAO) problems. From their simulated and real time validated results indicated that SAPSO coulbe be one of the stops solving approach to maximize the MPPT with greater accuracy. Kumar²⁷ analyzed the load demand and electricity cost from the power grid to get optimum design of MG at specified test locations. Further, they revealed that significant savings of 30.88% and 49.99% of the rolling cost when compared with Fuzzy Logic and mixed-integer linear programming-based energy management system respectively. Alaraj²⁸ examined the hybrid grey wolf optimizer (HGWO) for MPPT. The authors found to be better as it has a maximum efficiency of 94.30% and a minimum convergence factor of 0.20 when compared with other techniques under varying conditions for different topologies. Kumar²⁹ used the adaptive neuro fuzzy inference system (ANFIS)-based new algorithm for maximum power point tracking (MPPT) has been developed and implemented to track MPP in the standalone photovoltaic system (PV). From their study, they reported that percentage error, rise time and voltage fluctuations have enhanced when compared with incremental conductance method.

The comparison of various advanced Maximum Power Point Tracking (MPPT) methods is outlined in Table 1, focusing primarily on soft computing techniques. This comparison highlights key differences based on several criteria. Additionally, it is important to note that the results presented in Table 1 have been validated through different testing environments, including both experimental and simulation-based evaluations.

Table 1 Comparison of performance metrics for different advanced MPPT methods.

Literature surveys highlight their tendency to get stuck in local peaks, especially under shading conditions. The optimization of algorithm parameters and exploration capabilities emerges as critical factors influencing the effectiveness of these optimization approaches. When the complexity of the problem is enhanced, then the existing techniques in the literature are not meeting the research objectives. To address these challenges, the study introduces the Chimp Optimization Algorithm (ChOA) which is specifically designed for GMPP to harness solar energy under fluctuating weather conditions. A primary contribution of this work is the analysis of ChOA’s performance to enhance maximum solar energy under partial shading conditions. While previous research has proposed various techniques to enhance the tracking rate of solar PV systems, some key issues persist and warrant further investigation. This study aims to fill the research gap by developing and applying the Chimp Optimization Algorithm for the MPPT problem. In real-world scenarios, the Chaos Optimization Algorithm (ChOA) competes well with established methods like Grey Wolf Optimizer (GWO) and Particle Swarm Optimization (PSO). Using chaotic maps, ChOA improves exploration and exploitation balance, offering better global search and reducing the likelihood of getting stuck in local optima. It often converges faster than PSO and performs comparably to GWO in complex, dynamic problems. However, ChOA’s success depends on the specific optimization problem and the trade-off between exploration and stability.

The development of the Chimp Optimization Algorithm (ChOA) addresses significant research gaps in the field of optimization, particularly for challenging problems such as partially shaded photovoltaic (PV) systems. Existing algorithms like Particle Swarm Optimization (PSO), Cat Swarm Optimization (CSO), and Teaching-Learning-Based Optimization (TLBO) have shown effectiveness in various scenarios but face inherent limitations when applied to highly complex and nonlinear optimization landscapes. One critical issue is their susceptibility to premature convergence, often resulting in suboptimal solutions due to entrapment in local optima, especially in highly multimodal search spaces typical of partially shaded PV systems. PSO, for instance, relies on a velocity update mechanism that can cause stagnation near local optima. Similarly, CSO often struggles with maintaining adequate exploration in intricate landscapes, leading to reduced solution diversity. While TLBO is recognized for its robustness, it lacks a leader-follower dynamic that is crucial for navigating irregular and dynamic optimization environments. ChOA bridges these gaps by introducing an innovative framework inspired by the intelligent hunting behavior of chimps. Its design incorporates unique mechanisms such as social hierarchy, cooperative behavior, and adaptive strategies, which collectively enhance both exploration and exploitation capabilities. This balance between diversification and intensification enables ChOA to efficiently escape local optima and achieve superior global search performance. Compared to traditional methods, ChOA demonstrates improved convergence speed, accuracy, and stability, making it a highly effective solution for optimizing the nonlinear and complex characteristics of partially shaded PV systems. By addressing the limitations of existing algorithms, ChOA establishes itself as a versatile and adaptive tool, filling a critical void in optimization research.

Maximum power point tracking (MPPT) techniques

There are various MPPT techniques accessible to date and more research is ongoing to develop more robust MPPT techniques. Based on the structure of the algorithms, the MPPT techniques are classified into (i) Conventional (ii) AI Techniques and (iii) Soft computing Techniques. Conventional methods are used mostly because they have a simple and efficient tracking system. Most conventional algorithms can work efficiently when weather conditions are constant and but they fail when working under variable environmental conditions.

Mathematical model of PV cell

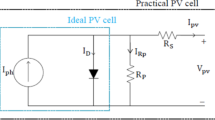
The basic operating principle of a solar cell is the photo-voltaic effect by which solar irradiation is converted into electrical energy. The equivalent circuit of the solar cell with the single-diode model is shown in Fig. 1, which is simple and more accurate.

Fig. 1

Equivalent circuit of solar cell.

The equation for the solar panel output current is as follows

$$I={I_{PV}} - {I_D} - \frac{{{V_{PV}}+I * {R_S}}}{{{R_P}}}$$

(1)

$$I={I_{PV}} - {I_0}\left[ {{e^{\left( {\frac{{q\left( {{V_{PV}}+I * {R_S}} \right)}}{{nKT}}} \right)}} - 1} \right] - \frac{{{V_{PV}}+I * {R_S}}}{{{R_P}}}$$

(2)

$${I_{PV}}=\left( {{I_{P{V_{stc}}}}+{k_i}\Delta T} \right)\left( {\frac{G}{{{G_{stc}}}}} \right)$$

(3)

$${I_0}={I_{0\_stc}}\left[ {{{\left( {\frac{{{T_{stc}}}}{T}} \right)}^3}} \right]\exp \left[ {\frac{{q{E_g}}}{{\eta K}}\left( {\frac{1}{{{T_{stc}}}} - \frac{1}{T}} \right)} \right]$$

(4)

${I}_{0}$ Can be written in a simplified form as

$${I_0}=\frac{{{I_{sc\_stc}}+{K_i}\Delta T}}{{\exp \left[ {\frac{{V{}_{{OC\_stc}}+{K_V}\Delta T}}{{\eta {V_t}}}} \right] - 1}}$$

(5)

where

$${V_t}=\frac{{KT}}{q}$$

(6)

The symbols used for this model are defined as,

• ${I}_{PV}$   Photocurrent in Amp

• ${I}_{D}$     Diode current in Amp

• ${I}_{0}$     Saturation current of the diode in Ma

• ${V}_{T}$    PV array thermal voltage in volts

• q Electron charge in Coulombs

• k Boltzmann constant

• R_sh    Resistance due to recombination of charge carriers in Ω

• R_s     Series resistance in Ω

• η      Diode ideality factor

• E_g    Band gap energy of the semiconductor material

• I_0−STC  Nominal saturation current at STC in Amps

• ${K}_{i}$    Coefficient of short circuit current

• G The irradiance of the solar rays falling on the PV surface in KW/m²

• ${K}_{V}$  Open circuit voltage coefficient

• $\varDelta T$    T-${T}_{STC}$

PSO algorithm

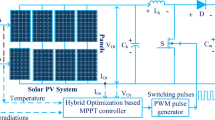
PSO.is a highly effective speculative technique based on the bird’s movement. Among many heuristic approaches, the PSO algorithm is highly adopted due to its simplicity as well as effectiveness. The basic motivation behind this invention is the social behaviour simulation of bird flocking. PSO employs multiple particles to form a swarm that traverses the search space, collaboratively determining the optimal global solution. The PSO is applied to compute the optimization problem, thereby making the candidate solution precise and of better quality. The optimization of a problem with PSO is based on the population size of the candidate size. MPPT of PV strings under shading and the schematic implementation is shown in Fig. 2.

Fig. 2

PV system with partial shading and MPPT controller using PSO.

Case studies

PV string performance was assessed under two partial shading patterns using a PSO-based MPPT controller. The simulation adjusted irradiation for four series-connected PV modules (Fig. 3) at a constant temperature of 25 °C. The Specifications of KC200GT PV module along with DC-DC Boost Converter is given in Table 2.

Fig. 3

Simulation circuit model for PSO algorithm (4 series-KC200GT PV module).

Table 2 Specifications of KC200GT PV module along with DC-DC Boost Converter.

In optimization-based tracking approaches, parameters like C1 and C2 in the PSO algorithm influence performance. These settings are detailed in Table 3.

Table 3 PSO algorithm tuning parameter.

Case 1:

For this case, the irradiation levels follow pattern-1 on each module. The P-V and P-I plots of the PV strings for this partial shading pattern are shown in Fig. 4. Three peaks are present in the plots, indicating local MPP and global MPP points. The GMPP is 544.1 W, with a voltage of 114.008 V and a current of 4.7771 A at the GMPP.

Fig. 4

P-V and P-I curves under first shading patterns stroked on the PV module respectively.

PSO algorithm begins tracking with duty ratios (0, 0.2, 0.6, and 0.8) to explore the P-V plot. The process continues until the halting criterion is met. Figure 5 shows simulation results of power, voltage, and current using PSO for maximum power extraction in the first shading pattern.

Fig. 5

Pattern1 simulation results of voltage, current and power using PSO.

It is observed from the results shown in Fig. 5, the values of power output using the PSO technique is 520.03 W. The statistical results of the PSO optimization algorithm are summarized in Table 4.

Table 4 Statistical results of PSO algorithms for Pattern1.

Case 2:

This case considers shading each module as in pattern-2. The PV and PI graph for the current pattern is shown in Fig. 6. In this shading pattern, GMPP value is 440 W, the voltage value at GMPP is 111.3816 V, and the Current value at GMPP is 4.0515 A.

Fig. 6

Solar power characteristics of PV module under changing conditions.

Figure 3’s Simulink model is employed for pattern 2, the resetting the search space over the P-V characteristics (Fig. 6) to track GMPP under partial shading. Figure 7 displays results of voltage, current, and power using the PSO approach.

Fig. 7

Pattern 2 simulation results of voltage, current and power using PSO.

In particular, the solar PV system power output converges at peak power point with subjective fluctuations from simulation results and the output power obtained from the PSO is 426.41 W. Table 5 represents the statistical results of pattern 2 of PSO algorithm.

Table 5 Statistical results of PSO algorithm for Pattern2.

Use of CSO algorithm based MPPT controller for PV module

In population-based search optimization methods, maintaining a significantly high diversity is crucial during the early stages of the search. This enables the exploration of the entire search space effectively. Conversely, as the optimization algorithm progresses towards convergence and approaches the optimal solution, fine-tuning becomes essential for efficient identification of the global optima. The Cat Swarm Optimization (CSO) algorithm, a naturally inspired meta-heuristic, has established itself as a benchmark in solving optimization problems across various engineering fields. The schematic representation of the CSO algorithm presented in Fig. 8.

Fig. 8

PV system with partial shading and MPPT controller using CSO.

Seeking mode and Tracing mode are the two distinct modes, in which this algorithm interprets the cat behaviour. Virtual cats are then maneuverer in the search space based on these behaviours. The participation of cats in each iteration of seeking and tracing modes is determined by a predefined ratio known as the mixture ratio (MR). In the algorithm, the tracing mode, where cats exhibit performance in pursuing a target, is particularly instrumental. Consequently, it can be inferred that an optimal mixture ratio is a subtle parameter that needs to be set judiciously. Figure 9 indicates the flowchart of CSO algorithm.

Fig. 9

Flow chart interpreting the CSO algorithm.

CSO technique is used to extract the maximum power under partial shading conditions and the results are compared with PSO.

Fig. 10

simulation model circuit for KC200GT PV module.

The simulation model circuit for KC200GT PV module is shown in Fig. 10. CSO algorithm parameters include NP, MR, SRD, and w, with additional SMP, C, CSTD, and NPSTD values. Choosing the population size in CSO balances accuracy and convergence speed: larger populations enhance accuracy but slow convergence, while smaller sizes track faster with higher local optima risk. Table 6 details CSO algorithm tuning parameters.

Table 6 Specifications of CSO algorithm.

Case studies

Case 1:

This section discusses irradiance levels in Pattern1. Under this shading condition, GMPP voltage and current are 114.008 V and 4.7771 A, yielding 544.129 W. CSO algorithm begins tracking using duty ratios (0, 0.2, 0.6, and 0.8) for boost converter to explore and cover the entire P-V plot. A similar procedure is repeated until the halting criterion is met. The simulation results of Output power, voltage, and current employing the CSO method for extracting maximum power under the first shading pattern are shown in Fig. 11.

Fig. 11

Pattern1 simulation results of voltage, current and power output using CSO.

Figure 11 demonstrates that the PV array output power achieved using CSO is 521.41 W. The simulation graph reveals that CSO offers faster tracking compared to PSO, with rapid dissolution of sustained oscillations. CSO technique takes only 0.05 s and PSO approach take 0.085 s to attain 521.41 W and 520.03 W, respectively for the pattern 1. The statistical results comparison of CSO and PSO optimization algorithms are tabulated in Table 7 for pattern 1.

Table 7 Statistical results of CSO algorithm for Pattern1.

Case 2:

For this shading pattern, global peak power (GMPP) is achieved at 440 W, the voltage corresponding to GMPP is 111.3816 V, and the Current value at GMPP is 4.0515 A. The same Simulink model utilized here by implementing CSO based MPPT controller for pattern 2. The results of output voltage, current, and power obtained using the CSO and PSO approaches are presented in Fig. 12.

Fig. 12

Pattern2 simulation results of voltage, current and power output using CSO.

The simulation result obtained from CSO during the second shading pattern shown in Fig. 12 shows less oscillation in power output during searching phase. The output power obtained from CSO is 434.50 W, while PSO yields 426.41 W. Table 8 compares statistical simulation results, highlighting higher power harnessing and conversion ratio with CSO over PSO.

Table 8 Comparative assessment of various algorithms for Pattern2.

Application of TLBO method MPPT controller for solar PV module

This approach explores the novel TLBO method for achieving maximum solar energy under shading conditions. TLBO is applied to maximize the MPP tracking of PV strings, as depicted in the schematic implementation shown in Fig. 13.

Fig. 13

partially shaded PV system with TLBO Based MPPT controller.

TLBO, a metaheuristic by Rao and Savsani³⁰, mimics the teaching-learning process in classrooms. It uses teacher performance and student results as a basis for optimization. Here, students represent the population, subjects are controlled variables, and the algorithm operates in teaching and learning phases to optimize objective functions. Flowchart of TLBO method is shown in Fig. 14.

Fig. 14

Flowchart of TLBO Algorithm.

Case studies

A detailed schematic layout Simulink model by applying the TLBO algorithm is shown in Fig. 15.

Fig. 15

Simulink model circuit (4 series connected KC200GT PV) by applying the TLBO algorithm.

To evaluate the TLBO algorithm for GMPP extraction under the same shading patterns, simulation results are compared with PSO and CSO methods. A quantitative analysis includes tracking speed, efficiency, and power. Tuned TLBO parameters are detailed in Table 9.

Table 9 Tuning parameters of TLBO algorithm.

Case 1:

The GMPP voltage and current under this shading condition are 114.008 V and 4.7771 A, resulting in 544.129 W. The TLBO algorithm initiates tracking by randomly assigning duty cycles to the boost converter, exploring the entire P-V plot. Figure 16 illustrates the power output tracked using TLBO for the solar PV string.

Fig. 16

Pattern1 simulation results of voltage, current and power output of TLBO algorithm.

From the results, the PV array achieves 522.30 W using TLBO, identifying GMPP in just 0.05 s. TLBO demonstrates better performance over other algorithms. Table 10 compares optimization algorithms, showing TLBO achieving 522.30 W in 0.05 s, whereas CSO reaches 520.03 W in 0.085 s for pattern1.

Table 10 Different MPPT algorithms performance assessment for pattern1.

Case 2:

This case is analyzed for pattern 2, a non-homogeneous irradiation pattern that produces two peaks in a P-V curve with a global peak and local peak located at 440.86 W and 389.24 W, respectively which describes that the pattern has two peaks existing with a significant difference between local and global peak values. The values of output voltage, current, and power obtained using the TLBO approach are presented in Fig. 17.

Fig. 17

Pattern 2 simulation results of voltage, current and power output of TLBO algorithm.

The simulation results obtained from TLBO show fewer oscillations during the search of maximum solar tracking under shading conditions. The performance comparison of different optimization techniques under the second shading pattern is tabulated in Table 11.

Table 11 Different MPPT algorithm for performance assessment of pattern 2.

Use of GWO algorithm of MPPT controller for solar PV module

Grey wolves’ natural leadership inspires the GWO optimization technique for maximizing power from solar PV strings under partial shading (Fig. 18). GWO, inspired by grey wolves and chimps, offers advantages like parameter-free implementation, simplicity, and ease of programming compared to other evolutionary algorithms.

Fig. 18

Partially shaded PV system with GWO based MPPT controller.

The GWO is one of the bio-inspired optimization algorithms which is inspired by both the social hierarchy and hunting strategy of grey wolves and chimps. The advantages of the GWO over other well-known evolutionary techniques include no requirement of algorithm-specific parameters for implementation, less complexity and simple programming, and easy implementation. The GWO technique models the leadership hierarchy and hunting behavior of grey wolves presented in Fig. 19. It includes alpha (α), beta (β), delta (δ), and omega (ω) wolves Alpha represents the fittest solution, followed by beta and delta, with omega representing other candidates. The flowchart of GWO technique is shown in Fig. 20.

Fig. 19

Hierarchy of different grey wolf groups.

Fig. 20

Flow chart of GWO technique.

Case studies

Figure 21 depicts the simulation circuit model for MPPT using GWO algorithm. Table 12 lists the tuning parameters for GWO algorithm.

Fig. 21

KC200GT simulation model circuit for MPPT by using GWO algorithm.

A comprehensive comparison of the GWO technique with other swarm intelligence algorithms is conducted on a solar PV system using MATLAB/Simulink 2016a. A sampling time interval of 1 s ensures the system reaches steady-state conditions before reaching GMPP.

Table 12 Tuning parameters of GWO algorithm.

Case-1:

The output voltage, current, and power obtained using the GWO optimization technique for pattern 1 are presented in Fig. 22 by using the specifications given in Table 11.

Fig. 22

Pattern1 simulation results of voltage, current and power using GWO algorithm.

The GWO technique shows minimal oscillations during MPP tracking under shading conditions, demonstrating its ability to pursue global maximum power. Simulation results indicate the PV array achieves 527.44 W using GWO. Table 13 provides a qualitative analysis of maximum power extraction using various techniques.

Table 13 Comparative assessment of MPPT techniques for Pattern1.

Case-2:

In this scenario, pattern-2 is considered for analysis. It has three peaks in the P-V plot and forms a composite situation for getting the GMPP. The Simulink model is utilized for pattern 2 and the results of output voltage, current, and power obtained using the GWO approach are presented in Fig. 23.

Fig. 23

Pattern2 simulation results of voltage, current and power using GWO algorithm.

The simulation results obtained from GWO show fewer oscillations were found when compared to other techniques. The simulation results of pattern 2 with different optimization techniques are presented in Table 14.

Table 14 Comparative performance of various algorithms for pattern 2.

Use of ChOA approach for MPPT controller

Chimp Optimization Algorithm (ChOA) optimizes MPPT in fractional shading for solar PV systems. The network MPP from the solar PV module, delivering it efficiently to utility end. The application of ChOA in a partially shaded PV system is illustrated in Fig. 24.

Fig. 24

PV system with partial shading and MPPT controller using ChOA.

Chimpanzee associations exhibit a fission-fusion dynamic, where individual roles remain constant over time. Each association, represented as an individual, performs specific functions that may evolve. The chimpanzee groups operate independently, with each member utilizing their unique skills for specialized tasks. The function of each chimp are classified as (i) Drivers (ii) Barriers (iii) Chasers (iv) Attackers. Drivers pursue prey without attempting to capture them, Barriers create obstacles in the escape route, Chasers swiftly pursue the prey, and Attackers focus on understanding the prey’s escape strategy.

Chimps may alter their roles during a hunt or maintain the same role throughout. Social incentives, such as support, sex, or grooming, drive chimps to participate in the hunt. Some chimps also seek “Social incentives” like humans, providing them with additional assets compared to other social predators. Sexual impulses may lead chimps to act chaotically in the final stages of the chase.

ChOA mathematical model

Hunting techniques consist of two phases like exploitation and exploration. The following equations are used for chasing and driving prey.

$${{\text{x}}_{{\text{Chimp}}}}({\text{t}}+{\text{1}})={{\text{x}}_{{\text{Prey}}}}\left( {\text{t}} \right) - {\text{a}}.{\text{D}}$$

(7)

Equations from (8) to (10) are designed to provide the values of a, m and C.

$${\text{a}}={\text{2}}.{\text{ f}}.{\text{ }}{{\text{r}}_{\text{1}}} - {\text{f}}$$

(8)

$${\text{C}}=2.{{\text{r}}_2}$$

(9)

$${\text{m}}={\text{Chaotic}}\;{\text{vector}}$$

(10)

The function f reduces nonlinearly from 2.5 to 0 during exploration and exploitation via iteration, using random vectors r_1 and r_2, and regulation vectors and C. D represents distance between elements, and the chaotic vector m aligns with chimp sexual motivation in the search process. Unlike traditional swarm intelligence, chimp optimization involves independent groups with diverse behaviours, mathematically modelled to revise f. Each group uses constant parameters, updating locally and globally. Mathematical model for dynamic coefficients vector (f) in various ChOA groups as shown in Fig. 25.

Fig. 25

Mathematical model for dynamic coefficients vector (f) in various ChOA groups.

• (i) Phase of exploration.

During the attack phase, chimps employ various stages like chasing, blocking, driving to encircle the prey. Attackers typically manage the chase, while drivers, barriers, and chasers are intermittently involved. In the initial iteration, lacking knowledge of the prey’s optimal position, the attacker’s location becomes the assumed prey position. Another crucial ChOA parameter influencing the exploration process is C. This stochastic parameter enhances ChOA’s exploration, reducing the risk of being trapped in local optima. Continuous random values generated by C contribute to the exploration phase across iterations. The approach of attacking can be represented mathematically with the linear decrease off higher value of 2.5 to lower value of 0. The vector’s scope decreases similarly to that of f, defined as a random vector within the range of [−2f, 2f]. Each extension’s random value falls within [−1, 1], allowing a chimp’s placement at any position relative to the available space and prey condition. While the projected chasing and blocking mechanism, somewhat address exploration limits, there remains a risk of ChOA getting trapped in local minima. Impact of ‘a’ on updating chimp location is shown in Fig. 26.

Fig. 26

Impact of ‘a’ on updating chimp locations.

• (ii) Chaotic maps.

Chimps’ chaotic behaviour aids in overcoming local optima issues and slows convergence in solving high-dimensional engineering problems. Various chaotic maps have been employed in this study to enhance ChoA performance, introducing random behaviour, as depicted in the Fig. 27.

Fig. 27

Chaotic random behaviour of chimps.

Fig. 28

ChOA flowchart.

The focussed ChOA flow chart is presented in Fig. 28 with a schematic flowchart guiding the optimization process. Initially, the algorithm randomly selects a population of chimps organized into individual chimp groups. The positions of these chimps are evaluated by the objective function, and the ensuing steps are iteratively performed until the specified stopping criterion is reached. This study specifically employs ChOA to address the non-convex optimization challenge associated with MPPT. The above figure provides a comprehensive overview of the procedural steps involved in utilizing ChOA for MPPT problem-solving.

Case studies

Figure 29 depicts the Simulink setup for comprehensive research on solar PV strings under various shading conditions using ChOA algorithm. Table 15 outlines the tuning parameters for ChOA.

Fig. 29

Simulation circuit for KC200GT PV module series connection under various shading patterns using ChOA algorithm.

Table 15 ChOA technique tuning parameters.

Case-1:

This case focuses on Pattern-1, detailing irradiance levels on modules and presenting P-V, P-I characteristics. For this shading condition, the GMPP voltage and current are 114 V and 4.78 A at 544 W. The output voltage, current, and power obtained using ChOA optimization technique for pattern 1 are presented in Fig. 30.

Fig. 30

Pattern1 simulation results of voltage, current and power using ChOA algorithm.

Chimp Optimization demonstrates smoother MPP search with minimal oscillations in solar PV module power output under shading conditions. ChOA converges rapidly within seconds, contrasting with GWO’s higher average convergence time. Both ChOA and GWO excel in pursuing GWPP under partial shading conditions. The simulation shows GWO yields 527.44 W, whereas ChOA achieves 531.198 W from the PV array. Detailed qualitative analysis is summarized in Table 16.

Table 16 Pattern 1 performance of MPPT controller.

Case- 2:

Examining pattern-2 in this context, Fig. 31 indicates that the use of GWO for MPP tracking introduces significant disturbances and transients in output voltage and power curves during climatic changes. The proposed ChOA method proves to be a more efficient solution because of excellent damping of oscillations over diverse fluctuating conditions. The simulation results of pattern 2 with different optimization techniques are tabulated in Table 17.

Fig. 31

Pattern2 simulation results of voltage, current and power using ChOA algorithm.

Table 17 ChOA algorithm performance comparison with other techniques.

Case-3:

In this case study, pattern-3 is analysed, Pattern 3 ChOA simulation outputs are presented in Fig. 32. Notably, four peaks are observed, with LMPP at 500 W and GMPP at 513.3 W. The voltage is 81.63 V and 6.21 A of current at GMPP, showing a close alignment with the other peaks. Pattern 3 performance of MPPT controller is shown in Table 18.

Fig. 32

Pattern 3 ChOA simulation outputs.

Table 18 Pattern 3 performance of MPPT controller.

Pseudo code for ChOA

The ChOA (Chimp Optimization Algorithm) is a metaheuristic optimization algorithm inspired by the behavior and intelligence of chimpanzees. It involves processes such as chasing, attacking, and social learning to solve optimization problems. The pseudocode representation of the ChOA technique is presented below.

• Initialize the population of chimpanzees (N) randomly in the search space.

• Define the maximum number of iterations (Max_Iter) and other parameters like coefficients and weight factors.

• Evaluate the fitness of each chimpanzee in the population.

• Identify the best solution (Elite) in the population based on fitness.

• Set the iteration counter: Iter = 1.

• While Iter ≤ Max_Iter:

  • a. Update the coefficients controlling exploration and exploitation:

    • i. Update A, C, and other dynamic factors based on the iteration count.

  • b. For each chimpanzee in the population:

    • i. Update the position using the ChOA position update formula:

      • Calculate the positions based on the chasing and attacking mechanism.

      • Incorporate social learning by considering the Elite solution and random interactions.

    • ii. Ensure the new position is within the search space bounds.

      • iii. Evaluate the fitness of the updated positions.

      • iv. Update the Elite solution if a better solution is found.

      • v. Adjust parameters for balancing exploration and exploitation.

• Increment the iteration counter: Iter = Iter + 1.

• End While.

• Return the best solution (Elite) as the final optimized result.

Performance analysis of the metaheuristic techniques

Metaheuristic techniques are inherently stochastic, meaning their performance varies across different runs when searching for the optimal solution. To evaluate the suitability and effectiveness of the proposed algorithm, it has been tested on a set of benchmark functions. The ChOA strategy used fixed-dimension benchmark functions s, which are widely utilized by researchers. The functions listed in Table 19 are multimodal, featuring multiple local optima and one unique global optimum, making them ideal for assessing the exploration capability of the metaheuristic method.

Table 19 Fixed dimension bench mark functions.

The statistical analysis of the proposed strategy was conducted on the selected fixed-dimension multimodal benchmark functions, as shown in Table 19. The proposed method is compared with other recent strategies using similar algorithm parameters: a group size of 30 and a total of 100 iterations. Table 19 presents the mean, standard deviation, worst, and best optimum values obtained over 25 runs.

$$~~~{F_{Mean~}}=~\frac{{\mathop \sum \nolimits_{{i=1}}^{N} {f_i}}}{N}$$

(11)

$${F_{SD}}=\frac{{\mathop \sum \nolimits_{{i=1}}^{N} \left( {{{\left( {{f_i} - ~{F_{mean}}} \right)}^2}} \right)}}{N}$$

(12)

Table 20 Analysis of statistical results on the fixed bench mark functions.

Table 20 shows that variations of the ChOA strategy outperform the base algorithm in most cases, leading to better results across various functions. Figure 33 illustrates the comparison of convergence curves for different heuristic methods on static benchmark functions. The 2D representation of the three-dimensional parameter space shows the search history projected onto the x₁ and x₂ axes, highlighting fitness values and convergence towards different optima, including a global optimum. The proposed strategies demonstrate improved performance by avoiding local optima across multiple runs.

Fig. 33

Convergence plots of the various techniques for fixed dimension test function.

Apart from the ChOA, recently few algorithms are examined for the efficient tracking of solar energy. Gudarzi et al.³¹. Comprehensive Learning Particle Swarm Optimization (CLPSO) has providing insights into their relative performance in terms of cost reduction, computational efficiency, and solution accuracy. Comprehensive Learning Particle Swarm Optimization (CLPSO) outperforms standard PSO, MPSO, and GEPSO in reducing investment costs by 53.34% for standalone and 27.28% for grid-connected microgrid systems. It proves more precise and efficient, making it the best method for optimization problems. Chaieb and Sakly³² used the Simplified Accelerated Particle Swarm Optimisation (SAPSO) combines PSO and Hill Climbing (HC) to achieve a fast, simple, and efficient MPPT process with minimal hardware and software requirements. They concluded that the SAPSO algorithm reduces the search area using HC and simplifies PSO’s complexity. Mukherjee and Mallick²⁶ used the adaptive swarm-based metaheuristic for efficient operation of photovoltaic interfaced inverter and they found that SAPSO technique could be one of the stops solving approach maximization of power point tracking with enhanced accuracy. Similarly, Mukherjee and Mallick³³ also examined the levy flight motivated adaptive swarm optimization in solving the minimization and maximization of problems. They revealed that APSOLF technique have shown significant decrement in percentage of the total harmonic distortion of the inverter output voltage and current as per the IEEE standard. Mukherjee et al.³⁴ inferred that premature convergence adaptive PSO was improved with better exploitation and exploration of levy flight mechanism. Also, they reported that the levy flight mechanism has shown enhanced convergence with higher accuracy, consistency and robustness. Rania et al.³⁵ studied the atom search optimization algorithm and they found better tracking response with power harvesting efficiency of 97.9% with rapid convergence. Celikel et al.³⁶ combined the voltage scanning and Cuckoo search algorithm to obtain maximum power under partial shading conditions. From their results, they inferred that average tracking efficiency and speed were 99.74% and 0.3 s respectively. Belghiti et al.³⁷ introduced a novel MPPT approach using Iref and a PID-controlled Quadratic Boost Converter achieves faster convergence (< 2 ms), minimal oscillations (< 0.25 W), and 99.79% tracking efficiency, outperforming conventional and modern techniques under various conditions.

Comparative statistical analysis

MATLAB/SIMULINK simulations for PSO, CSO, TLBO and Chimp Optimization Algorithm (ChOA) were conducted under different partial shading patterns (G1 to G6). The results, summarized in Table 21, revealed that G1 shading pattern maximized power in the solar photovoltaic system.

Table 21 Simulation results of PV module operated at various partial shading conditions.

The performance of diverse algorithms such as PSO, CSO, TLBO and ChoA were compared. From the simulation results obtained, ChOA outperformed other algorithms by providing significant objective function values with less computational time. In addition, the proposed ChoA approach of maximum power tracking resulted in improving the voltage profile and efficiency, which can be adaptable for coping-up the futuristic, weather changes. Further in PSO, CSO, and TLBO algorithms, there is no leader to control the entire tracking period which can be overcome by Chimp optimization algorithms. ChOA is a highly efficient approach for maximizing solar energy tracking due to its rapid convergence and balanced exploration-exploitation processes. Compared to GWO, ChOA exhibits superior capability in tracing global optima and enhancing solar system power output. In MATLAB/Simulink simulations with various shading patterns, ChOA demonstrates ease of implementation and quicker convergence rates. Comparative analyses with established optimization techniques confirm ChOA’s superior performance in GMPP search, minimizing power oscillations around MPP, and achieving accurate convergence.

Conclusion

This research aims to improve PV system performance in partial shading using optimization techniques such as PSO, CSO, TLBO and ChOA. ChOA’s performance is compared with basic PSO and CSO. From the results obtained, ChOA outperformed other algorithms by providing significant objective function values with less computational time.

• Optimal tracing of LMPP and GMPP towards desired objective function subjected to various operational constraints is a non-linear complex problem. In this research, the improved variants of PSO, CSO, and TLBO were adopted for solving single-objective functions.

• To reach global minima by escaping local minima chances, the exploration and exploitation stages of both algorithms are tuned dynamically w.r.t. iteration in the optimization process. The results obtained at all the stages are shown that the ChOA outperformed GWO, TLBO, CSO, and PSO.

• Comparative analyses with existing optimization techniques confirm ChOA’s superior ability to search for GMPP.

• Simulation results revealed that ChOA have shown higher conversion efficiency of 99.63% with maximum power output of 525.13 W when compared to other optimization algorithms for the given shading pattern condition.