Introduction

As the “weak link” of slope, soft rock always threatens the stability of slope1. In the north and northeast of China, most of the open pit coal mines have soft rock, and there is a large landslide risk. In the actual production process, the soft rock with low strength has the characteristics of water loss, easy shrinkage and cracking, easy expansion in water, wetting and disintegration, and the cracks and pores (including micro-cracks and micro-pores) in the rock are relatively developed2,3, which is related to the particle arrangement of the primary structure of the rock, and the particle rearrangement caused by engineering mechanical disturbance and water change4. This greatly reduces the strength and stability of slope rock mass5, directly affects the safety production of open-pit coal mine6,7, restricts the development of stripping, mining and drainage projects and capacity continuity of open-pit coal mine, and the stability of slope cannot be fully guaranteed. Obviously, the creep characteristics of soft rock, especially the soft rock with water content, have a great influence on the stability of slope, and the safety and stability of slope has an important impact on the sustainable and reliable stripping engineering and the stable development of mine production capacity. The two are closely related, mutually influencing and inseparable, and should be considered jointly. Therefore, it is necessary to study the creep deformation characteristics of water-bearing soft rock to provide theoretical and technical support for safe, efficient and green mining of the open-pit coal mine.

Water is one of the key factors affecting the creep characteristics of rocks, and there are many researches on the creep of rocks under different water-containing states. Such as: Zhu et al.8 based on creep tests of rocks under different water conditions, obtained the understanding that water has a significant effect on the ultimate creep deformation of rocks, and that water content will affect the time for rocks to reach the stable creep stage. Li et al.9 conducted shear creep tests on sandstones with different levels of water content, and found that water was sufficient to increase the creep strain variable and creep strain rate of sandstones, and reduce the creep failure strength value. Shao et al.10 analyzed the influence of dry and saturated states on the creep behavior of quartz sandstone through the uniaxial graded loading creep test, and found that with the increase of water content, the lower the creep failure strength of rock, the obvious creep strain inhibition of rock. Chen11 studied the influence of water pressure on creep rate, creep deformation, creep failure stress level and long-term strength of fractured rock through experimental study on creep characteristics of precast fractured marble under real water pressure. Wang et al.12 found that water would cause the weakening of rock’s creep mechanical behavior and accelerate its creep development time through creep tests under different water-bearing states. Chen et al.13 conducted post-freeze-thaw nuclear magnetic resonance testing and shear creep tests on red sandstone with different water content, revealing the influence mechanism of freeze-thaw cycle and water content change on the microstructure and creep characteristics of red sandstone, and building a reasonable shear creep model accordingly.

Scholars at home and abroad have proposed a variety of creep mechanics models, including integral constitutive model, differential constitutive model and empirical constitutive model14. Fractional calculus is a powerful mathematical tool for solving mechanical modeling problems15. It is used to simulate soils between ideal solids and fluids. Relevant scholars have successfully applied fractional order theory to the study of rock mechanical properties. Liu16 conducted a triaxial creep test on sandstone, analyzed the creep deformation laws of sandstone under different confining pressures, and established a time-dependent creep constitutive model of sandstone based on unsteady fractional order to describe the deformation laws of rock at all stages, especially the acceleration stage. Zhang et al.17 introduced a fractional-order Abel clay pot and established a fractional-order Maxwell model to explore the creep properties of salt rock. Cao et al.18 improved the traditional Nishihara model by using fractional order integral theory and statistical damage theory based on the fractional shear creep test, and carried out a study on the creep characteristics of weak interlayers. Liu et al.19 proposed a new nonlinear fractional-order damage creep model of shale based on the fractional-load creep test of shale, which was used to describe the deformation characteristics of rock creep process. Rock properties and water content have important effects on rock creep properties. It should be improved on the basis of the existing research, so that it can not only accurately reflect the whole process of rock creep, but also ensure the simplification of the form and model parameters, so as to provide theoretical guidance for practical engineering problems.

Therefore, in this paper, Riemann–Liouville’s fractional calculus operator and theory are used to establish a fractional nonlinear creep damage model by connecting fractional order viscous element, nonlinear viscous element and viscoplastic body with switch in series, which is used to simulate the nonlinear gradient process of rock creep phenomenon under different water content conditions. The constitutive equation of the model is constructed. The parameters of creep damage model are identified based on the principle of least squares. The effect of model parameters on deformation is further explored, so that the effectiveness of model parameters can be analyzed and verified, and the applicability of the model in other complex stress environments is increased. In order to provide theoretical basis for stability analysis and disaster prevention of soft rock slope.

Experiment development and results

Sample, device, scheme design

Based on Ye 's20 test data, the argillaceous siltstone used in the experiment is bluish gray, silty, local argillaceous structure, and thick layered structure. The rock blocks were processed into standard cylindrical specimens with a diameter of 38mm and a height of 76mm by indoor sawing (see Fig. 1). The creep test of 4 moisture content samples of 0, 4.56%, 8.47% and 12.38% (saturated state) in Nanning Tertiary silty soft rock was carried out. During the preparation of the sample, the natural samples were first dried at 105 °C to dry, then the dry samples were placed in a saturator and vacuums were pumped in a vacuum barrel for 4 h, and then soaked in distilled water for 6 and 12 h, respectively, to obtain unsaturated samples with water content of 4.56% and 8.47%. The natural samples were directly vacuumed for 4 h and soaked in distilled water for 24 h to obtain saturated samples.

Fig. 1
figure 1

Specimen and test equipment diagram

Full size image

The instrument used in the test is a multifunctional triaxial tester, which consists of three parts: pressure system, measurement system and control system. Among them, the compression system can provide the maximum axial load accuracy of 40 KN (0.01 KN), the maximum confining pressure of 10 MPa, and the deformation measurement accuracy of 0.01 mm in the measurement system. The test specimen and instrument are shown in Fig. 1.

In order to determine the maximum load value in the creep test, conventional triaxial compression tests with silty siltstone with confining pressure of 1 MPa and different water content are carried out to obtain the peak strength σmax, and 90% of the peak strength value is taken as the maximum load applied in the creep test. The creep test was carried out in a stepwise loading mode. Considering the influence of water content on the strength of the sample, the axial loading was divided into 11 stages to avoid the failure of the sample caused by excessive loading stress. The specific loading scheme is shown in Table 1.

Table 1 Test loading scheme design
Full size table

During the creep test, the rock sample is first wrapped with rubber film, and the filter paper and permeable stone are placed at both ends, and then placed in the triaxial pressure chamber to adjust the central position of the sample to avoid eccentric pressure. Then, the chamber of the triaxial instrument is filled with water, and the confining pressure is applied to the predetermined value of 1 MPa at the loading rate of 0.6 kPa s−1, and the displacement of the recorder is cleared to zero. Subsequently, the initial axial load of 1 kN (corresponding to 0.88 MPa of deviating stress) was applied, and the deformation was recorded until stable, that is, when the deformation rate was less than 0.01 mm h−121, the next level of load was applied according to the loading scheme in Table 1 until the sample was damaged and the test was over. Replace the sample and repeat the above steps until complete all creep tests are shown in Table 1. All tests were carried out under constant temperature and humidity at (22.0 ± 0.5)  C and humidity at (40 ± 1) %.

Test result

The relationship between axial strain and time of silty siltstone under different water content is shown in Fig. 2. Based on the principle of Chen’s method22, the creep curve obtained under fractional loading is converted into the creep curve under single-stage loading, as shown in Fig. 3.

Fig. 2
figure 2

Creep curve of rock under graded loading

Full size image
Fig. 3
figure 3

Creep curve of rock under single stage loading

Full size image

Fractional nonlinear creep damage model

In this paper, Riemann–Liouville’s fractional calculus operator and theory are used to establish a fractional nonlinear creep damage model (as shown in Fig. 4) by connecting fractional order viscous element, nonlinear viscous element and viscoplastic body with switch in series, which is used to simulate the nonlinear gradient process of rock creep phenomenon under different water content conditions.

Fig. 4
figure 4

Schematic diagram of fractional nonlinear creep damage model

Full size image

Fractional order viscous element

Because of its perfect theoretical basis, simple model form, clear deformation law and clear basic concept, component model has become an important basis for studying rock creep characteristics23. However, there are some shortcomings in the description of nonlinear properties of rocks, and fractional order operators have significant advantages in the description of rock visco-plastic-plasticity because of the memory of material history, which can make up for the shortcomings of component models24,25. There are many definitions of fractional calculus, including Riemann–Liouville definition, Caputo definition, Grunwald–Letnikov definition, etc. The research usually adopts Riemann–Liouville definition26. Definition of fractional calculus theory is of the most commonly used Riemann–Liouville27,28,29. Let the function f be continuously integrable on (0,+∞), for t > 0, Re(n) ≥ 0, the fractional integral is:

$$\frac{{{\text{d}}^{ - n} [f(t)]}}{{{\text{d}}t^{ - n} }} =_{{t_{0} }} D_{t}^{ - n} f(t) = \frac{1}{\Gamma (n)}\int_{{t_{0} }}^{t} {(t - \xi )^{n - 1} } f(\xi ){\text{d}}\xi$$
(1)

where Г(n) is the Gamma function; n is the fractional order.

Riemann–Liouville fractional differentiation can be defined as: let f∈C, γ > 0, m is the smallest integer greater than γ, let γ = m − n, then have the following form30,31:

$$\frac{{{\text{d}}^{n} [f(t)]}}{{{\text{d}}t^{n} }} =_{{t_{0} }} D_{t}^{n} f(t) = \frac{{{\text{d}}^{m} }}{{{\text{d}}t^{m} }}\left[ {t_{0} D_{t}^{ - \gamma } f(t)} \right]$$
(2)

If f(t) is integrable near t = 0 and satisfies 0 ≤  n ≤ 1, the Laplace transform of fractional calculus is:

$$\left\{ {\begin{array}{*{20}l} {L\left[ {_{0} D_{t}^{ - n} f(t),p} \right] = p^{ - n} \overline{f}(p)} \hfill \\ {L\left[ {_{0} D_{t}^{n} f(t),p} \right] = p^{n} \overline{f}(p)} \hfill \\ \end{array} } \right.$$
(3)

where f(p) is the Laplace transform of f(t).

According to the definition of fractional calculus and Laplace transform, the fractional viscous element can be obtained, as shown in Fig. 5, and its constitutive equation is as follows:

$$\sigma (t) = \eta \frac{{{\text{d}}^{n} \varepsilon_{{1}} (t)}}{{{\text{d}}t^{n} }}$$
(4)
Fig. 5
figure 5

Fractional order viscous element

Full size image

When stress σ(t) = const, according to Riemann–Liouville fractional order theory, fractional order integration of the above formula is as follows:

$$\varepsilon_{{1}} (t) = \frac{\sigma }{\eta }\frac{{t^{\gamma } }}{{{\Gamma }(1 + \gamma )}}$$
(5)

In order to better show the influence law of parameters in the constitutive equation. Taking σ = 4 MPa and η = 0.5 MPa h, Fig. 6a shows the influence law of γ on the creep deformation of components. Taking σ = 4 MPa and γ = 0.5, Fig. 6b shows the effect of η on the creep deformation of the component.

Fig. 6
figure 6

Influence of different parameters on the deformation of Eq. (5)

Full size image

As can be seen from Fig. 6, the influence of parameters γ and η on Eq. (5) shows an exponential function increase with the increase of time, but parameter r shows a stronger influence. And parameter γ has a higher growth rate than parameter η.

Nonlinear viscous element

According to a lot of practical experience, the viscosity coefficient is the attenuation function of stress and the increase function of time. Therefore, the nonlinear formula of a is proposed as follows:

$$\eta (\sigma ,t) = \eta_{1} t^{c} \sigma^{c - 1}$$
(6)

where η1 is the initial viscosity coefficient, and c is the material constant. When 0 < c < 1, η(σ,t) is an increasing function of time and a decreasing function of stress. When c>1, η(σ,t) is an increasing function of both time and stress. When c < 1, η(σ,t) is a decreasing function of both time and stress.

The nonlinear viscous element is constructed from the above formula, as shown in Fig. 7, and its constitutive is as follows:

$$\sigma = \eta (\sigma ,t)\dot{\varepsilon } = \eta_{1} t^{c} \sigma^{c - 1} \dot{\varepsilon }$$
(7)
Fig. 7
figure 7

Nonlinear viscous element

Full size image

where \(\dot{\varepsilon }\) is the creep rate.

The above equation can be obtained by differential solution:

$$\varepsilon_{{2}} (t) = \frac{{\sigma^{(2 - c)} }}{{\eta_{1} (1 - c)}}t^{(1 - c)}$$
(8)

In order to better show the influence law of parameters in the constitutive equation. Taking σ = 4 MPa and η1 = 0.5 MPa h, Fig. 8a shows the influence law of c on the creep deformation of components. Taking σ = 4 MPa and c = 0.5, Fig. 8b shows the effect of η1 on the creep deformation of the component.

Fig. 8
figure 8

Influence of different parameters on the deformation of Eq. (8)

Full size image

As can be seen from Fig. 8, the influence of parameters c and η1 on Eq. (8) shows an approximate linear function increase with the increase of time, but parameter c shows a stronger influence. And parameter c has a higher growth rate than parameter η1.

Viscoplastic body with switch

Based on the non-viscous element proposed by Zhang et al.32,33, a viscoplastic element with switch is constructed by introducing switch G. The component model is shown in Fig. 9. The stress and strain relationship of the viscoplastic element with switch is as follows:

$$\sigma = \eta_{{2}} \frac{{\dot{\varepsilon }(t)}}{{nt^{n - 1} }}$$
(9)
Fig. 9
figure 9

Nonlinear viscous element

Full size image

That is, the constitutive model equation is

$$\varepsilon (t) = \frac{\sigma }{{\eta_{2} }}t^{n}$$
(10)

where \(\dot{\varepsilon }\)(t) is the creep rate, n is rheological coefficient.

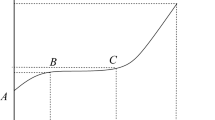
It can be seen from the Fig. 2 that the influence of water content on rock creep deformation is significant. When the rock enters the third stage, internal damage occurs and gradually accumulates, and the rock exhibits obvious nonlinear characteristics34. Therefore, we characterize the creep behavior of rock in the acceleration stage using the viscoelastic-plastic body considering damage.

It is assumed that the damage variable and time of siltstone during creep satisfy a negative exponential function17,35,36, that is,

$$D = 1 - \exp \left( { - \alpha t} \right),$$
(11)

where D is the damage factor, and α is the material constant.

Therefore, the constitutive equation of the accelerated creep element after the damage factor is introduced is as follows:

$$\varepsilon_{3} (t) = \left\{ {\begin{array}{*{20}l} {\frac{\sigma }{{\eta_{2} }}t^{n} \, w = {0}\% } \hfill & {G \, \;{\text{off }}} \hfill \\ {\frac{\sigma }{{\eta_{2} \exp ( - bt)}}t^{n} \, w > {0}\% } \hfill & {G \, \;{\text{on}}} \hfill \\ \end{array} } \right.$$
(12)

In order to better show the influence law of parameters in the constitutive equation. Taking σ = 0.1 MPa, η2 = 0.5 MPa h and n = 0.2, Fig. 10a shows the influence law of b on the creep deformation of components. Taking σ = 0.1 MPa, η2=10 MPa h and b = 0.2, Fig. 10b shows the effect of n on the creep deformation of the component. Taking σ = 0.1 MPa, n = 0.2 and b = 0.2, Fig. 10c shows the effect of η2 on the creep deformation of the component.

Fig. 10
figure 10

Influence of different parameters on the deformation of Eq. (12)

Full size image

As can be seen from Fig. 10, the effects of parameters b, n, and η2 on Eq. (12) all show an increase with the increase of time, in which parameters b and n have the same growth pattern, but parameter b has a greater growth rate. η2 has a stronger influence than b and n at the beginning of time.

Fractional nonlinear creep damage model

To sum up, a fractional-order model is constructed, and its creep equation is as follows:

$$\varepsilon (t) = \varepsilon_{{1}} (t){ + }\varepsilon_{{2}} (t){ + }\varepsilon_{3} (t) = \left\{ {\begin{array}{*{20}l} {\frac{\sigma }{\eta }\frac{{t^{\gamma } }}{\Gamma (1 + \gamma )}{ + }\frac{{\sigma^{(2 - c)} }}{{\eta_{1} (1 - c)}}t^{(1 - c)} { + }\frac{\sigma }{{\eta_{2} }}t^{n} \, w = {0}\% } \hfill & {G\;{\text{ off}}} \hfill \\ {\frac{\sigma }{\eta }\frac{{t^{\gamma } }}{\Gamma (1 + \gamma )}{ + }\frac{{\sigma^{(2 - c)} }}{{\eta_{1} (1 - c)}}t^{(1 - c)} { + }\frac{\sigma }{{\eta_{2} \exp ( - bt)}}t^{n} \, w > {0}\% } \hfill & {G \, \;{\text{on}}} \hfill \\ \end{array} } \right.$$
(13)

Model validation and parameter identification

The fitting analysis of model parameters mainly includes least square method, annealing algorithm, particle swarm optimization algorithm and global optimization algorithm, among which least square method is the most widely used. The least square method finds the data by minimizing the sum of squares of the errors, and thus obtains the function with the best matching degree37. In order to verify the accuracy and effectiveness of the model, the fitting analysis is carried out based on the experimental results. For nonlinear creep problems, at present, the least square method38 of mathematical analysis theory is widely used to nonlinear fit test data, so as to invert the parameters to be obtained17,39. In this study, Matlab R2018a is used to realize the calculation of least squares. The parameters obtained are shown in Table 2. The test curve and fitting function are shown in the Fig. 11.

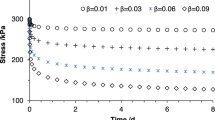
Table 2 describes the parameters of the fractional-order nonlinear creep model
Full size table

As can be seen from the analysis of Fig. 11, the fractional order nonlinear creep model established in this paper can simulate the creep characteristics of soft rocks at different water content in the whole stage, especially the accelerated creep stage, with a fitting degree of at least 0.97 correlation coefficient. According to the curve characteristics, based solely on the creep results of rock with a stress of 0.88 MPa under different water content, it can be seen that with the increase of water content, the greater the elastic deformation and the greater the stable creep deformation value, indicating that water content has a significant effect on the softening of rock, and the presence of water weakens the cementation ability of rock matrix particles and particles40, making it easier for rock to deform under force41. In general, the fractional-order nonlinear creep model can describe the whole creep process of soft rock well, and has the advantages of fewer components, clear physical concept and good fitting effect of creep stage, which is convenient for theoretical guidance for practical engineering problems. In order to further discuss the regularity of parameters in fractional nonlinear creep model. As shown in Fig. 12, rock creep curves under different parameter values are drawn by the control variable method, and the influence of parameter changes on rock creep can be clearly and intuitively seen. Fig. 12(a) shows the influence of parameter r on the decay creep stage and the constant velocity creep stage of the rock. It can be seen that the greater the parameter r, the faster the elastic deformation stage progresses and the greater the transition rate to the decay creep stage. In addition, different parameter r values have an intersection time. Before the intersection time, the larger the parameter value is, the smaller the creep variable is; after the intersection time, the larger the parameter value is, the larger the creep variable is. At the same time, it can be seen that the strain of the fractional-order viscous element increases slowly, which does not increase linearly like the ideal fluid, nor does it remain unchanged like the ideal solid. It can be seen that the element can reflect the nonlinear gradient process of strain25. Figure 12(b,c) shows the influence of parameters n and b on the accelerated creep stage of the rock. The two parameters show the same deformation law, and the creep variables decrease with the increase of the parameters, but the creep curve still maintains the curve characteristics of the original accelerated creep stage.

Fig. 11
figure 11

Comparison of fitting curves of creep model with experimental results under different water content

Full size image
Fig. 12
figure 12

Diagram of creep curve under different parameter values

Full size image

Figure 13 shows the schematic diagram of parameter values under the dual influence of water content and stress. The analysis figure shows that water content has a greater impact on parameters than stress. It can be seen that the moisture content is the key factor affecting the change of creep model.

Fig. 13
figure 13

Schematic diagram of model parameters under the dual influence of rock water content and stress.

Full size image

Conclusions

In this paper, Riemann–Liouville’s fractional calculus operator and theory are used to establish a fractional nonlinear creep damage model by connecting fractional order viscous element, nonlinear viscous element and viscoplastic body in series, which is used to simulate the nonlinear gradient process of rock creep phenomenon under different water content conditions. The constitutive equation of the model is constructed. The parameters of creep damage model are identified based on the principle of least squares. The following research results are obtained:

  1. (1)

    A fractional-order nonlinear creep damage model is established and its constitutive equation is constructed.

  2. (2)

    Combined with the experimental results, the least square method of mathematical analysis theory was used to nonlinear fit the test data and obtain the parameters to be sought. At the same time, it shows that the fractional-order nonlinear creep damage model can describe the rheological constitutive properties of rocks more effectively.

  3. (3)

    The regularity of the parameters in the fractional nonlinear creep model can be obtained. The larger the parameter r is, the faster the elastic deformation stage progresses and the greater the transition rate to the decaying creep stage, which can reflect the nonlinear gradient process of strain. Parameters n and b show the same deformation law for accelerated creep stage of rock, and the creep variable increases with the increase of parameters.

Discussion

Water softens and lubricates the rock, resulting in the reduction of rock strength and endangers slope safety. It is of great significance in theory and engineering practice to study the creep properties of soft rock. But at the same time, jointed rock mass generally exists in rock mass engineering, and its mechanical properties are complicated, which directly affects the safety of rock mass. However, there are few studies on shear creep constitutive model of the joint structural plane, so the author’s team will continue to study this aspect in the next step. The general scheme is as follows: rock sample with jointed structural plane is obtained through geological investigation, shear creep test is carried out to reveal the shear creep characteristics of rock mass with jointed structural plane, creep constitutive equation of rock with jointed structural plane based on fractional order calculus is established, and the regularity of model parameters is further studied.