Introduction

Inductive power transfer (IPT) is a method of wireless power transmission technology (WPT) that is used to wirelessly charge portable electronics devices and electric vehicles (EVs)1,2. IPT is used for short range and medium range distances of 10 s of centimeters3. In this method, the power is transferred through magnetic coupling between two coupled inductors/coils via principle of electromagnetic induction4,5. This method feeds a high-frequency ac source into the transmitting side coil to generate a circulating magnetic field around it6,7. When this field links with the secondary side, or receiving coil, it induces the current and electromotive force (emf), which flows towards the load via the receiver circuit8,9. The receiver circuit can have devices such as rectifiers, filters, and voltage regulators for the purpose of converting and controlling the flow of electrical energy to the load10,11. Due to the air gap between coils, leakage flux might exist12. Analysis of leakage inductance is essential in wireless power transmission systems13. It indicates the energy loss brought on by magnetic flux leakage between linked inductors14,15. The amount of leakage inductance present in the system has an impact on the transfer of power or energy16,17. To achieve higher efficiency, resonant inductive coupling with addition of capacitors either in series or parallel in transmitting and receiving side18,19,20.

Resonance is an important concept in electrical engineering and can be observed in circuits that contain inductors and capacitors21,22. These two components have the ability to store energy and when combined in a circuit, can create a resonant condition23,24,25. At a specific frequency called the resonant frequency, the inductor and capacitor can exchange energy back and forth in a cyclic manner26. This causes the energy to oscillate between the two components, leading to a highly efficient transfer of energy within the circuit27,28. When the frequency of the alternating current in the circuit matches the resonant frequency, a large amount of energy is transferred between the inductor and capacitor, leading to a peak in the current and voltage29,30. To achieve resonance, it is important that the imaginary parts of the inductive and capacitive reactance’s cancel out each other’s effects31. This occurs when the inductive reactance and capacitive reactance become equal32,33,34,35,36. The use of resonance in an inductive power transfer (IPT) system provides a variety of advantages, including the ability to increase power transfer efficiency and transmission range37,38. In a non-resonant IPT system, the efficiency of power transfer is affected by misalignment between the transmitting and receiving coils39,40. On the other side, resonant circuits improve the system’s flexibility and tolerance for misalignment41. A notable advantage of the resonant IPT system is its ability to power many loads simultaneously42,43,44,45,46. Many researches are conducted to obtain constant voltage output using IPT system for WC of EVS such as in47 CV output is realized using SS compensation at 8 cm distance with efficiency of 86.4%48.

In49, proposed SS compensation and did Experimental setup with 8 cm air gap and achieved efficiency above 80%. This paper lacks a thorough investigation of power loss modeling, scalability for applications requiring higher power, and flexibility for EV charging needs. In50, proposed design methodology and optimization of SS compensation and have efficiency of above80%. But this paper does not focus on power capacity, and comprehensive power loss modeling in IPT systems. In51 developed SS compensation for wireless charging applications. The study lacks the efficiency optimization over longer distances and power losses. In52, presented SS compensation for dynamic analysis of IPT system for 7 cm. This paper lacks the focus on efficiency and the modeling of power losses of IPT system. In53, used SS compensation to obtain constant voltage output and transferred 1 kW power transmission at a 2 cm air gap in wireless power transfer systems. This approach, however, is not scalable for longer distances and ignores complex load variations. In54 proposed a novel design approach for SS compensation for constant current and constant voltage outputs and achieved efficiency of 96% 10 cm of air gap. Despite its effectiveness, their approach avoids significant power losses that occur at longer ranges. In55, presented a control method for SS compensation to achieve constant voltage/current charging. The paper lacks a thorough testing for changeable load situations. In56, demonstrated a bidirectional wireless power system with SS compensation and transferred power of 7.7 kW with 91.1% efficiency. Its low scalability for higher power applications is a problem. In57, proposed SS compensation along with single switch step-up resonant inverter for IPT system and achieved 86% efficiency at an 8 cm air gap. However, the usage of a single switch step-up resonant inverter limits its scalability and power losses. In58 used SS compensation for tripolar pads and achieved 87.2% efficiency at a 10 cm air gap. The efficiency of proposed methodology is limited to specific air gap and design constraints of the system. Expect this; it does not evaluate real world variations in load conditions. In59, developed SS compensation to achieve constant voltage output under various load conditions for Evs charging applications. The design methodology achieved an efficiency of 86% for 10 cm air gap. Since gap distance limits the efficiency, and scalability can be a problem for large air gaps. In60 proposed SS compensation and analyzed under various load conditions. This paper does not discuss improving power transfer efficiency. Furthermore, model only focus on specific load conditions and may not be applicable for wide range, dynamic conditions.

The reviewed studies on SS compensation and IPT made significant improvements but lacks in terms of scalability, dynamic load handling capabilities and mathematical modeling of constant voltage output and leakage inductance for reducing power losses. On other hand, our paper made a significant improvement in mathematical modeling of leakage inductance in IPT system which mitigation of power losses. Furthermore, it guarantees a load independent constant voltage output under dynamic load conditions by implementing SS compensation which is also shown via mathematical modeling. To analyze the validity and feasibility of proposed modeling, simulations are conducted in MATLAB/Simulink software. These simulations show that proposed strategy significantly improves charging efficiency, with up to 98% efficiency levels being achieved. These findings demonstrate the usefulness and feasibility of proposed Series-Series compensation, which makes it a viable option for the development of wireless charging technology for electric vehicles in the future.

Novelty of the paper

The novelty of our paper lies in the mathematical modeling of two critical yet often overlooked factors in inductive power transfer (IPT) systems: leakage inductance and power losses. Leakage inductance contributes to power losses and affects real power transmission, as described in Eq. 12. By incorporating these factors, we enable precise evaluation and optimization of IPT systems for wireless charging applications. Additionally, our paper presents a simplified mathematical derivation for SS compensation, ensuring load-independent constant voltage output characteristics, as outlined in Eq. 50. These insights enhance the understanding of IPT system dynamics and contribute to improved real-world performance.

This paper is further structured as follows: sect. “Inductive power transfer system”, provides a brief overview of the inductive power transmission system and emphasizes the value of using mathematical modeling to reduce leakage inductance and power losses. Sect. “Proposed SS-compensated IPT system” focuses on the Series-Series (SS) compensation and its mathematical modeling for constant current and constant voltage output. Sect. “Coil design” presents the simulated results of IPT system without compensation and with compensation and draws comparisons. Limitations have been presented in sect. “Simulations of IPT system without compensation” whereas sect. “Limitations” concludes the paper by offering a comprehensive synopsis of the significant findings and advancements discussed in the preceding sections. Sect. “Conclusion” discussed for conclusion of the research.

Inductive power transfer system

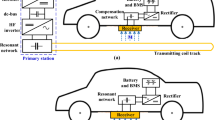
Two basic components of wireless charging system are transmitting coil and receiving coil. The transmitting coil, which is coupled to a power source, creates an alternating magnetic field. This magnetic field serves as the transmission medium for wireless power. The magnetic field is captured by a coil that is fixed firmly to the underside of the electric vehicle (EV) and converted back into required electrical energy by rectifier circuit61,62. A circuit model of an IPT system with two linked inductors with self-inductances of L1 and L2 and a mutual inductance of M is shown in Fig. 1.

Fig. 1
figure 1

Basic Structure of IPT system.

Full size image

Let \({\text{I}}_{1}\) and \({\text{I}}_{{\text{L}}}\) be the corresponding currents flowing through the primary and secondary side coils respectively. The voltage across the primary (\({\text{V}}_{1}\)) and secondary coils (\({\text{V}}_{{\text{L}}}\)) is described by a set of equations that result from the application of Kirchhoff’s voltage law (KVL). These equations enable the power transfer efficiency, resonant frequency, and quality factor of the IPT system to be assessed and optimized. To enhance power transfer efficiency while finding concerning system performance, following equations can be used:

$$V_{1} = j\omega L_{1} I_{1} + R_{1} I_{1} - j\omega M I_{L}$$
(1)
$$0 = j\omega L_{2} I_{L} + R_{2} I_{2} + R_{L} I_{L} - j\omega M I_{1}$$
(2)

Equations 1 and 2 can be written as

$$V_{1} = \left( {j\omega L_{1} + R_{1} } \right)I_{1} - j\omega M I_{L}$$
(3)
$$0 = \left( {j\omega L_{2} + R_{2} + R_{L} } \right)I_{L} - j\omega M I_{1}$$
(4)

In terms of impedances i.e. \(Z_{1} = j\omega L_{1} + R_{1}\) and \(Z_{2} = j\omega L_{2} + R_{2} + R_{L}\) Eq. 3 and 4 are given in Eqs. 5 and 6 respectively:

$$V_{1} = Z_{1} I_{1} - j \omega M I_{L}$$
(5)
$$0 = Z_{2} I_{L} + j \omega M I_{1}$$
(6)

Using Eq. 6, load current is:

$$I_{L} = \frac{{j \omega M I_{1} }}{{Z_{2} }}$$
(7)

Putting Eq. 7 into 5:

$$\left. {\begin{array}{*{20}c} {V_{1} = Z_{1} I_{1} - j \omega M \times \frac{{j \omega M I_{1} }}{{Z_{2} }}} \\ {V_{1} = \left( {Z_{1} + \frac{{\omega^{2} M^{2} }}{{Z_{2} }}} \right) \times I_{1} } \\ \end{array} } \right\}$$
(8)

From Eq. 8, it is observed that primary circuit is impacted by the existence of load on secondary side in regard of voltage drop and power draw47. In this equation, the term (\(Z_{1} + \frac{{\omega^{2} M^{2} }}{{Z_{2} }})\) is the overall impedance as seen from the transmitting side. This impedance’s secondary side-corresponding portion is called reflective impedance as viewed from the primary side (\({\text{Z}}_{{\text{r}}}\)) is given in Eq. 9.

$$Z_{r} = \frac{{\omega^{2} M^{2} }}{{Z_{2} }}$$
(9)

But \(Z_{2} = (R_{2} + R_{L)} + j \omega L_{2}\) then Eq. 9 becomes:

$$Z_{r} = \frac{{\omega^{2} M^{2} }}{{(R_{2} + R_{L)} + j \omega L_{2} }}$$
(10)

By rationalization Eq. 10:

$$\left. {\begin{array}{*{20}c} {Z_{reflected } = \frac{{\omega^{2} M^{2} }}{{(R_{2} + R_{L)} + j \omega L_{2} }} \times \frac{{(R_{2} + R_{L)} - j \omega L_{2} }}{{(R_{2} + R_{L)} - j \omega L_{2} }}} \\ {Z_{reflected } = \frac{{\omega^{2} M^{2} \times [ \left( {R_{2} + R_{L)} - j \omega L_{2} } \right]}}{{(R_{2} + R_{L)}^{2} - J^{2} \omega^{2} L_{2}^{2} }}} \\ {Z_{reflected } = \frac{{\omega^{2} M^{2} (R_{2} + R_{L)} - j \omega^{3} M^{2} L_{2} }}{{(R_{2} + R_{L)}^{2} + \omega^{2} L_{2}^{2} }}} \\ \end{array} } \right\}$$
(11)

Separating real and imaginary parts

$$Z_{reflected } = \frac{{\omega^{2} M^{2} }}{{(R_{2} + R_{L)}^{2} + \omega^{2} L_{2}^{2} }} - j\frac{{ j \omega^{3} M^{2} L_{2} }}{{(R_{2} + R_{L)}^{2} + \omega^{2} L_{2}^{2} }}$$
(12)

Equation 12 shows the reflected impedance in IPT system. This equation contains imaginary part that contributes the leakage inductance. This shows that a large amount of power will be lost in air due to leakage inductances. The active power transferred to secondary side in IPT system can be calculated as:

$$P_{2} = Z_{reflected } \times I_{L}^{2}$$
(13)

According to Eq. 13 the real power given to the load is equal to real power absorbed by the reflected impedance. The actual power transmission is calculated from Eq. 12.

$$P_{2} = \frac{{\omega^{2} M^{2} }}{{(R_{2} + R_{L)}^{2} + \omega^{2} L_{2}^{2} }} \times I_{L}^{2}$$
(14)

In Eq. 14, the impact of the secondary circuit’s total impedance, which includes the load impedance, on the actual power transferred from the supply to the load is clearly seen. This equation demonstrates that using a sufficient capacitor and mutual inductance to compensate for the quantity \({\upomega }^{2} {\text{L}}_{{\text{L}}}^{2}\) is necessary to maximize real power transfer53. For power transfer efficiency to be optimized, this adjustment is essential. Furthermore, it can be concluded through Eq. 8 that lowering \({\text{Z}}_{1}\), which stands for the primary side’s impedance, is crucial for lowering the system’s VA ratings. By including a suitable capacitor in the primary side, which offsets the impact of the primary side inductor, this can be achieved. The system’s overall performance can be improved by carefully considering over and putting the compensations outlined in these equations into practice.

Proposed SS-compensated IPT system

Figure 2 depicts the simplified structure of IPT with SS compensation which includes a two winding transformer to represent transmitting and receiving coil of wireless charging system and a pair of capacitors connected in series with transmitting and receiving coils. SS compensation is a popular and efficient choice among the primary compensations used in IPT systems.

Fig. 2
figure 2

SS compensation in IPT system.

Full size image

SS compensation is developed to give constant current output at its natural frequency as given in Eq. 15.

$$f = \frac{1}{{\sqrt {2\pi LC} }}$$
(15)

Here (L) is the inductance of the coil and (C) is the compensating capacitor. However constant voltage output can also be achieved by frequency tuning, using Eq. 16.

$$\omega_{o} = \frac{\omega }{{\sqrt {1 \pm k^{2} } }}$$
(16)

And angular frequency is given in Eq. 17.

$$\omega = 2\pi f$$
(17)

Here, (ω) is angular frequency for constant voltage mode and (\(\omega_{o}\)) is the angular frequency for Constant current mode and k is the coupling coefficient56.

Compensating capacitors for SS compensation

The equivalent circuit of SS compensated IPT system is depicted in Fig. 2. The primary and secondary side impedance in terms of reflective impedance is given in Eqs. 18 and 1955:

$$Z_{1} = j\omega L_{1} + \frac{1}{{j\omega C_{1} }} + R_{1}$$
(18)
$$Z_{2} = j \omega L_{2} + \frac{1}{{ J \omega C_{2} }} + R_{2} + R_{L}$$
(19)

Total impedance in terms of reflective impedance will be:

$$Z_{T} = j\omega L_{1} + \frac{1}{{j\omega C_{1} }} + R_{1} + Z_{r}$$
(20)

In SS compensation, due to series compensation in secondary side, \({\text{Z}}_{2}\) will be purely resistive then by putting \({\text{Z}}_{2} = {\text{R}}_{{\text{L}}}\) in Eq. 10 we got:

$$Z_{r} = \frac{{\omega^{2} M^{2} }}{{R_{L} }}$$
(21)

As shown in Eq. 21, that SS compensation has only resistive component from secondary side, which means there is no phase shift. Therefore, the compensating capacitors’ values can be calculated under resonant condition by neglecting the internal resistance.

$$Z_{1} = j\omega L_{1} + \frac{1}{{j\omega C_{1} }}$$
(22)
$$Z_{2} = j \omega L_{2} + \frac{1}{{ J \omega C_{2} }}$$
(23)

At resonant conditions \({\text{Z}}_{1}\) and \({\text{Z}}_{2}\) must be equal to zero, and then Eqs. 22 and 23 become:

$$0 = j\omega L_{1} + \frac{1}{{j\omega C_{1} }}$$
(24)
$$0 = j \omega L_{2} + \frac{1}{{ J \omega C_{2} }}$$
(25)

Using Eq. 24 for primary side compensation will be:

$$\left. {\begin{array}{*{20}c} {0 = j\omega L_{1} + \frac{1}{{j\omega C_{1} }}} \\ { - j \omega L_{1} = \frac{1}{{j \omega C_{1} }}} \\ \end{array} } \right\}$$
(26)

Or

$$\omega^{2} = \frac{1}{{C_{1} L_{1} }}$$
(27)

Then primary side compensating capacitors will be:

$$C_{1} = \frac{1}{{\omega^{2} L_{1} }}$$
(28)

Similarly using Eq. 25 for secondary compensation;

$$\left. {\begin{array}{*{20}c} { - j \omega L_{2} = \frac{1}{{ j \omega C_{2} }}} \\ {\omega^{2} = \frac{1}{{C_{2} L_{2} }}} \\ \end{array} } \right\}$$
(29)

Then secondary side compensating capacitors will be:

$$C_{2} = \frac{1}{{\omega^{2} L_{2} }}$$
(30)

At resonant condition on primary and secondary side i.e.\({\text{C}}_{1} = {\text{C}}_{2}\) and \({\text{L}}_{1} = {\text{L}}_{2}\).

$$C = \frac{1}{\omega L}$$
(31)

Hence, from Eqs. 28 and 30 it is evident that in SS compensation compensating capacitors on both the primary and secondary side are independent of magnetic coupling and input frequency. Due to this property, the output current can remain constant regardless of changes in the input frequency or coupling between the coils.

Mathematical modeling of proposed SS compensation

Applying KVL on Fig. 2 we have.

$$V_{1} = Z_{1} I_{1} + j \omega M I_{2}$$
(32)
$$0 = - j \omega M I_{1} + Z_{2} I_{2}$$
(33)

Inductive and capacitive components become equal and cancel each other’s effects at resonance, according to the theory of resonant inductive coupling, which is taken into account for both primary and secondary side i.e.

$$j \omega L_{1} = - \frac{1}{{ j \omega C_{1} }}$$
(34)

And

$$j \omega L_{2} = - \frac{1}{{j \omega C_{2} }}$$
(35)

And here R1 and R2 are very small as compared to RL, so we neglect the effect of R1 and R2 and using resonant condition Z1 = 0 and Z2 = RL.

Then eqs. 32 and 33 becomes:

$$V_{1} = - j \omega M I_{L}$$
(36)
$$j \omega M I_{1} = R_{L} I_{L}$$
(37)

From Eq. 36:

$$I_{L} = - \frac{{V_{1} }}{j \omega M}$$
(38)

Equation 38 shows load independent current output for SS compensation, where M is mutual inductance of loosely coupled coils and (ω) is angular frequency for CC mode. From Eq. 38 primary sides current can be calculated as given in Eq. 39.

$$I_{1} = \frac{{R_{L} I_{L} }}{j \omega M}$$
(39)

Equation 39 shows that input current is dependent on load resistance. Whenever load changes input current also changes and vice versa. The value of angular frequency for constant current output is calculated using \(\omega = 2\pi f\). Equation 37 can be written in terms of \({\text{R}}_{{\text{L}}}\) as:

$$R_{L} = j \omega M\frac{{I_{1} }}{{I_{2} }}$$
(40)

Load voltage in SS compensation

A novel approach that has never been investigated before is the concept of a mathematical equation for load independent constant voltage output in SS compensation. Previous related works have focused on achieving load independent constant voltage by using frequency formulas. However, this section presents a derivation of the mathematical equation that demonstrates that load independent voltage output can be achieved using SS compensation. According to ohm’s law, load voltage can be calculated as:

$$V_{L} = I_{L} R_{L}$$
(41)

Substituting Eq. 40 into 41:

$$\left. {\begin{array}{*{20}c} {V_{L} = I_{L} \times j \omega M\frac{{I_{1} }}{{I_{2} }}} \\ {Or} \\ {V_{L} = j \omega MI_{1} } \\ \end{array} } \right\}$$
(42)

The output voltage of the SS compensation circuit is demonstrated by Eq. 42. However, it is previously stated in Eq. 37, which is used to calculate the primary coil impedance, that the input current and load resistance are indirectly related. To provide a load independent constant voltage output, a method of regulating the input current independent of the load resistance is needed. Input current may be obtained from formula to make load voltage independent of load resistance.

$$V_{1} = Z_{1} I_{1}$$
(43)

Equation 43, it can be written as:

$$I_{1} = \frac{{V_{1} }}{{Z_{1} }}$$
(44)

But impedance of the primary coil is:

$$\left. {\begin{array}{*{20}c} {Z_{1} = j \omega L_{1} + \frac{1}{{ j \omega C_{1} }} + R_{1} } \\ {Or} \\ {\begin{array}{*{20}c} {Z_{1} = j \omega L_{1} + \frac{1}{{j \omega C_{1} }}} \\ {Or} \\ {Z_{1} = \frac{{j^{2} \omega^{2} L_{1} C_{1} + 1}}{{ j \omega C_{1} }}} \\ \end{array} } \\ \end{array} } \right\}$$
(45)

Using property \({\text{j}}^{2} = - 1\) in Eq. 45:

$$Z_{1} = \frac{{1 - \omega^{2} L_{1} C_{1} }}{{ j \omega C_{1} }}$$
(46)

By substituting Eq. 46 in 44

$$\left. {\begin{array}{*{20}c} {I_{1} = \frac{{V_{1} }}{{\frac{{1 - \omega^{2} L_{1} C_{1} }}{{ j \omega C_{1} }}}}} \\ {Or} \\ {I_{1} = \frac{{V_{1} \times j \omega C_{1} }}{{ 1 - \omega^{2} L_{1} C_{1} }}} \\ \end{array} } \right\}$$
(47)

Then by putting Eq. 47 in 43, we get the load voltage given as:

$$\left. {\begin{array}{*{20}c} {V_{L} = j\omega M \times \frac{{V_{1} \times j \omega C_{1} }}{{ 1 - \omega^{2} L_{1} C_{1} }}} \\ {Or} \\ {\begin{array}{*{20}c} {V_{L} = \frac{{j\omega M \times j \omega C_{1} \times V_{1} }}{{ 1 - \omega^{2} L_{1} C_{1} }}} \\ {Or} \\ {V_{L} = \frac{{j^{2} \omega^{2} MC_{1} V_{1} }}{{ 1 - \omega^{2} L_{1} C_{1} }}} \\ \end{array} } \\ \end{array} } \right\}$$
(48)

By using property \({\text{j}}^{2} = - 1\) in Eq. 48:

$$V_{L} = \frac{{ - \omega^{2} MC_{1} V_{1} }}{{1 - \omega^{2} L_{1} C_{1} }}$$
(49)

Again by multiplying and dividing with (-1) to Eq. 49:

$$V_{L} = \frac{{\omega^{2} MC_{1} V_{1} }}{{\omega^{2} L_{1} C_{1} - 1}}$$
(50)

Equation 50 is the proposed mathematical modeling of the SS compensation for load independent constant voltage output behavior. Here M represents mutual inductance of loosely coupled coils and ω is the angular frequency for CV mode, L1 and C1 are inductance and capacitance. The value of angular frequency for CV can be calculated using \({\upomega } = { }\frac{{{\upomega }_{{\text{o}}} }}{{\sqrt {1 \pm {\text{k}}} }}\)63. This mathematical model is an important contribution to this field as it provides a new method for achieving load independent constant voltage output using SS compensation. The proposed mathematical modeling presents a systematic approach to understand and enhance the behavior of SS compensation for wireless charging applications.

Coil design

One of the most important and essential components of the design of IPT systems is coil design. There are several coil shapes that can transfer the desired power levels. The primary coils’ size and shape are often not constrained; however, the secondary coils’ size is frequently constrained64. This is because it is preferred that the secondary coil be as compact as possible because it will be attached to the system that has to be charged. In the literature, coil structures like square, rectangular, hexagonal, and circular are basic and frequently utilized for IPT applications. It is evident that the literature primarily uses circular and rectangular-square forms. The circular helix coil, offering a high level of power transmission efficiency between 80 and 90%, stands out as a particularly noteworthy choice among these geometries46,65. So in this paper circular helix coils are used whose dimension is given below in Table 1. It should be noted that in paper resonant operation is used so primary and secondary coils have same dimensions. To create coils ANSYS software was used which facilitates the modeling and analysis of magnetic coupling between the coils of IPT system. This software helps in calculating the leakage inductance, mutual inductance, coupling coefficient, magnetic field distribution and power losses between coils between the coils. The parameters of coils are randomly designed just to evaluate the significance of mathematical modeling of SS compensation which is the key contribution of this paper. The coil dimensions are given in Table 1. These dimensions are based on mathematically calculated mutual inductance between two coils based on parameters given in Table 2 in which mutual inductance was calculated via mathematical modeling.

Table 1 Coil dimensions.
Full size table
Table 2 Designed parameters.
Full size table

The structure of 3-Dimensional coils is illustrated in Fig. 3. To determine the wireless transmission distance between the coils for the calculated mutual inductance, ANSYS software is utilized for creating and evaluating coils. After performing a number of iterations, the wireless transmission distance for the mathematically calculated mutual inductance is measured as 13.5 cm. The simulation is performed on the basis of designed parameters as given in Table 1. These parameters are selected randomly for simulation purpose by using Eq. 31.

Fig. 3
figure 3

Dimensional coil structure.

Full size image

Simulations of IPT system without compensation

Since the designed IPT system is focused on wireless charging applications especially Evs charging which function under dynamic load scenarios. By focusing on load variations, our research ensures the systems robustness, minimizes leakage inductance, reduces power losses, and demonstrates practical viability under various operating conditions. MATLAB/Simulinksoftware is used to evaluate the performance of IPT based wireless charging system for both compensated and uncompensated condition. The simulations are carried out using a constant DC input voltage of 200 V and under variation load conditions. To examine the systems response, time-domain simulations are run in MATLAB for a predetermined number of microseconds. The resultant current and voltage measured in amperes, volts are plotted to show the effectiveness system under different load scenarios. In all these waveforms the magnitude of voltage in volts and current in ampere are represented along y-axis and time duration of simulation is mentioned along x-axis.

Simulations of IPT system without SS compensation

Figure 4 displays the designed model of IPT system in MATLAB/Simulink software. This shows that there is no any compensation implemented in the model and simulation is run. In this section, IPT model for WC is developed and evaluated without using compensation.

Fig. 4
figure 4

IPT system of WC without compensation.

Full size image

Figure 5a shows the inverter output voltage waveform. Figure 5b shows the primary side current waveform. Figure 5c shows the secondary side current waveform of IPT. Figure 5d represents the load voltage waveform. Upon analyzing Fig. 5b,c, it is evident that the current waveforms are triangular in shape and exhibit noticeable odd harmonics and fluctuations. This could lead to issues with power transmission efficiency, heating, and distortion. In all these waveforms the magnitude of voltage in volts and current in ampere are represented along y-axis and time duration in seconds of simulation is mentioned along x-axis.

Fig. 5
figure 5

(a) Input voltage waveform (b) Input current waveform (c) Output current waveform (d) Output voltage waveform.

Full size image

The overall power quality of an AC system might be reduced by the existence of harmonics and distorted waveforms. Furthermore, the study presented in Fig. 5d reveals fluctuations in the output voltage, which are credited to weak magnetic fields, decreased mutual inductance, magnetic flux loss, and elevated resistance, particularly when there are significant transmission distances between the coils. These non-sinusoidal waveforms can cause distortions and voltage fluctuations, which can negatively influence infrastructure and provide difficulties for wireless EV charging.

Figure 6a displays the values of input and output voltage measured under different load circumferences. Similarly Fig. 6b represents input and output current values under different circumferences. In both figures the magnitude of voltage in volts and current in ampere are represented along y-axis and time duration in seconds of simulation is mentioned along x-axis. From this Figure, it is observed that wireless charging structure faces voltage and current losses. These losses are significant because they lead the transmitted power to decrease substantially. The transferred power decreases as a result of these losses, which ultimately decreases the wireless charging system’s efficiency and effectiveness. The total power delivered from the input to the output of the wireless charging system is decreased when either voltage or current undergoes losses.

Fig. 6
figure 6

(a) Input and output voltage at different loads (b) Input and output current at different loads.

Full size image

Figure 7 displays the transferred power by inductive power transfer system. This graph illustrates that maximum power of 0.16 W power is transferred as illustrated along y-axis in graph against different load illustrated in x-axis power is really transferred by the IPT system. This is due to the transmission distance between the coils; that is, when the coils are further apart, there is insufficient magnetic coupling between them, which leads to the formation of leakage inductance. As the distance between the coils increases, the magnetic field between them decreases, increasing the amount of leakage inductance. Due to the significant power losses caused by voltage and current losses, little power will reach the secondary side. To lessen these losses and increase efficiency, compensatory techniques can be applied, such as the use of compensating capacitors.

Fig. 7
figure 7

Power Transferred by IPT system without compensation.

Full size image

Figure 8 shows the efficiency of inductive power transfer system. It is evident from this graph that IPT system has very low efficiency of 0.16% as illustrated along y-axis in graph against different load illustrated in x-axis. This is explained by the fact that there is a significant impedance mismatch, which is caused by leakage inductance. Because there is little power transfer between the transmitting and receiving coils as a result of the system’s incapacity to overcome the energy loss brought on by the leakage inductance, inefficiency results. The inefficiency of leakage inductance emphasizes the significance of compensation topologies in IPT systems.

Fig. 8
figure 8

Efficiency of IPT system without compensation.

Full size image

Simulations of IPT system with SS compensation

In this paper, series-series SS compensation is proposed for IPT system to construct a wireless charging structure for electric vehicles charging applications. The structure of propose IPT using SS compensation is shown below in Fig. 9. To enable effective and secure wireless charging of electric vehicles, this structure includes all necessary parts and systems with addition of compensation capacitors in series with transmitting and receiving coils.

Fig. 9
figure 9

IPT system with SS compensation.

Full size image

Figure 10a depicts the output voltage waveform of the inverter; this is because inverters are built with inherent features that result in square waveforms. As the current flows through the capacitor is shown in Fig. 10b the primary side current waveform changes to a sinusoidal waveform. Figure 10c shows the secondary side current waveform, assuming a steady-state scenario with constant voltage at roughly 205 V and Fig. 10d the load voltage waveform of the IPT system. These waveforms show improved IPT performance once the compensating capacitors are added. These were measured at fixed 200 V input voltage and 214 kHz switching frequency. The magnitude of voltage and current is mention along y-axis against different loads mentioned in x-axis in the graphs. By adjusting the coils’ impedance matching, power transmission efficiency is increased and reflections are decreased. As a result, distortion- and harmonic-free sinusoidal current waveforms are produced. The compensating capacitors likewise store and release energy as reactive components to keep the voltage level constant.

Fig. 10
figure 10

(a) Input voltage waveform (b) Input current waveform (c) Output current waveform (d) Output voltage waveform.

Full size image

Figure 11a shows how input and output voltages respond during various load conditions. It is mentioned in figures along y-axis that the output voltage is kept at a specific value of 205 V while the input voltage is fixed at 200 V, despite unpredictable different resistances load conditions. This graph shows how the system reacts to various load scenarios while maintaining the output voltage within the desired range. Similarly Fig. 11b shows the input and output currents along y-axis for different load resistances along x-axis. It is crucial to understand the relationship between voltage and current since it has a direct impact on the effectiveness of power transfer and overall system performance of the IPT system. The graphs allow seeing how the system responds to changing load situations by adjusting its current while maintaining a constant output voltage. To keep the primary and secondary sides of the system’s power balance, a dynamic adjustment is required. This information is essential for developing and putting into practice efficient control strategies or compensating approaches that will improve the performance of the wireless charging structure.

Fig. 11
figure 11

(a) Input & output voltage at different loads (b) Input & output current at different loads.

Full size image

Figure 12 displays power curve showing the performance of the suggested system with SS compensation. This graph illustrates power transfer in y-axis at different resistances load conditions as mentioned in x-axis. It indicates that the proposed modeling has a maximum power transfer capability of 2.8 kW as shown along y-axis, which is adequate for quick and effective wireless charging of electric vehicles. The system can produce a significant amount of electricity, as seen by its 2.8 kW power rating, which guarantees quick charging for EVs. This picture illustrates the total power generation capacity of the system, allowing for quick wireless charging of electric vehicles.

Fig. 12
figure 12

Power graph at different loads.

Full size image

In Fig. 13, the efficiency of the proposed compensation for wireless charging is depicted along y-axis with loads ranging at different resistances load conditions as shown along x-axis. The primary objective was to assess the efficiency level for load independent voltage output at these different load values. Efficiency levels exceeding 90% were continuously achieved by this methodology with different load conditions. Notably, an amazing peak efficiency of 98% is obtained throughout this research. This exceptional performance at maximum load demonstrates the effectiveness and dependability of the suggested SS compensation. Achieving high efficiency levels above 90% demonstrates the ability of the suggested compensation to reduce power losses and optimize energy consumption for a range of loads. Across a range of loads, the suggested compensation effectively minimizes power losses and maximizes energy usage. Moreover, the high efficiency levels provide steady and dependable power transfer, improving overall system performance and user pleasure.

Fig. 13
figure 13

Efficiency Vs load resistance.

Full size image

Comparison of IPT system with and without compensation

The results of uncompensated and compensated wireless charging system are presented in the previous section. It is observed that a wireless charging system without compensation suffers from large leakage inductance, power losses and voltage fluctuations. Without compensation, wireless charging process will be prolonged potentially leading to the overheating and damage to the battery. While IPT system with SS compensation has better performance, improved efficiency, sinusoidal waveforms free from distortion and harmonics. When comparing the power transfer capabilities of compensated and uncompensated inductive power transfer-based wireless charging systems, strong evidence exists that supports the use of compensation due to its beneficial effect on system performance as it is capable of maximum power transfer capabilities of 2.8 kW while without compensation only maximum power of 0.15 W is transferred over 13.5 cm. The comparison emphasizes the gains made by compensating, highlighting the importance of the compensation in wireless charging applications. While the maximum efficiency attained by SS compensated IPT system is 98% whereas uncompensated IPT system is only 0.15% which is too low for charging application. Hence from this discussion it is observed that compensation topologies are essential to mitigate the problems brought on by leakage inductance and weak magnetic coupling. The efficiency and effectiveness of wireless charging systems may be limited by these challenges. These restrictions are overcome by adding compensation, which leads to increased charging effectiveness and power transmission capabilities.

Limitations

This paper proposed a design methodology for mathematical modeling of important aspects of wireless charging systems, like power losses in IPT systems and leakage inductance. However, it showed through simulations that the design methodology can achieve load independent constant voltage output characteristics without the need for additional controllers or converters and mitigate these issues using simple SS compensation. The limitations of the study include its only reliance on simulations for validation and its lack of experimental support for performance in real-world scenarios and the adaptability to dynamic load fluctuations and scalability to different distance parameters should be investigated. Furthermore, coil misalignment is still a potential problem that could reduce the power transmission efficiency. Misalignment can affect the system’s performance by altering the mutual inductance hence it must be examined. So, future studies should focus on experimental validation, testing in different contexts, and developing methods to reduce misalignment problems.

Conclusion

This paper explores wireless charging system for electric vehicles using inductive power transfer technology. It highlighted the problems of wireless charging system, such as leakage inductance, weak coupling, and power losses, which can cause voltage fluctuations as well as harm the vehicles battery. To ensure secure, reliable and efficient charging a constant voltage output is necessary. To compensate the leakage inductance and ensure a constant voltage output, many alternative compensation topologies are developed. Among these, SS compensation has been found to be the best choice because it is independent of coupling between the coil and it is easy to understand and easier to apply. So this paper proposed SS compensation to provide load independent constant voltage output for wireless charging applications. The mathematical modeling is proposed for load independent constant voltage output behavior of SS compensation for various load resistances. In order to validate the proposed mathematical modeling, MATLAB/Simulink software is used where the calculated parameters are evaluated. The simulated results clearly show that the proposed SS compensation can transmit power wirelessly over a distance of up to 13.5 cm for different load resistances. This demonstrates the system’s efficiency and adaptability in handling various loads. Additionally, the developed compensation system’s high efficiency of 98% is an impressive achievement for a wide load range from 25 to 90Ω. The findings underscore the pragmatic feasibility and transformative potential of proposed Series-Series compensation topology, positioning it as a robust and auspicious avenue for shaping the future landscape of wireless charging technology for electric vehicles. In essence, our work not only resolves current challenges but also pioneers new frontiers, marking a significant leap forward in the progression of EV charging systems.