Hybrid gabor attention convolution and transformer interaction network with hierarchical monitoring mechanism for liver and tumor segmentation

Abstract

Liver and tumor segmentation is an important technology for the diagnosis of hepatocellular carcinoma. However, most existing methods struggle to accurately delineate the boundaries of the liver and tumor due to significant differences in their shapes, sizes, and distributions, which leads to unclear segmentation of the liver contour and incorrect delineation of the lesion area. To address this gap, we propose a hybrid gabor attention convolution and transformer interaction network with hierarchical monitoring mechanism for liver and tumor segmentation, named HyborNet. Generally, the proposed HyborNet consists of a local and a global feature extraction branch. Specifically, the local feature extraction branch consists of several cascaded gabor attention convolutional blocks, each of which contains a multi-dimensional interactive attention module and a gabor convolutional module. In this way, fine-grained information about the liver and tumor can be extracted, which refines the edge details of the target area and accurately depicts the lesion area. The global feature extraction branch is constructed with a transformer model, which is capable of extracting coarse-grained information about the liver and tumor and accurately distinguishing them from similar tissues. Additionally, we propose a cross-attention-based dual-branch interaction module that adaptively fuses features from different perspectives to emphasize the target region, thereby enhancing the network’s segmentation performance. Finally, a hierarchical monitoring mechanism is employed in the decoding stage, which provides additional feedback from deeper intermediate layers to optimize the segmentation results. Extensive experimental results demonstrate that HyborNet significantly outperforms other state-of-the-art models in liver and tumor segmentation tasks. The proposed model effectively enhances liver image segmentation accuracy, assisting doctors in making more precise diagnoses.

Introduction

The liver is a major metabolic organ in the human body, playing an important role in digestion and excretion. Liver cancer is the most common disease worldwide¹. Many people die from liver cancer every year². Early detection, diagnosis and treatment of hepatocellular carcinoma are essential to improve survival and quality of life for patients. Advances in computer technology have led to the development of many medical imaging techniques. Among them, computed tomography (CT) is a widely used imaging tool³. It is widely used to detect the shape, texture and focal lesions of the liver⁴. Therefore, fast and accurate identification, localization and segmentation of focal areas from CT is an important prerequisite for physicians to make cancer diagnoses and treatment plans for their patients.

In recent years, Convolutional Neural Network (CNN) have gained widespread attention for their superior feature extraction capabilities⁵. By employing multiple filters across various layers, CNN demonstrate robust potential for nonlinear feature representation and are able to handle massive amounts of data efficiently. CNN have achieved impressive results in medical image segmentation tasks. Currently, the majority of effective segmentation architectures are based on the U-Net framework, which employs an encoder-decoder structure with skip connections. This architecture allows the network to simultaneously capture high-level semantic features and low-level spatial details. The encoder progressively reduces the spatial dimensions of the image, extracting hierarchical features, while the decoder reconstructs the image through progressive upsampling of feature maps. The skip connections between corresponding layers in the encoder and decoder preserve fine-grained details, which are essential for accurate pixel-level segmentation. With the development of U-Net, several high-performance medical image segmentation networks have been proposed. For example, Attention U-Net integrates attention mechanisms into the convolutional layers to selectively focus on important features and suppress irrelevant ones, thereby improving segmentation performance for regions with complex boundaries. U-Net++ introduces nested skip pathways to better capture multi-scale features and enhance the flow of information between layers. Additionally, Res-Net integrates residual networks into U-Net, allowing the network to extract deeper features from the target regions in medical images.

Transformer has achieved results in natural language processing (NLP) and computer vision (CV) by exploiting the properties of the self-attention mechanism to acquire global features⁶. One of the most famous is Visual Transformer⁷, which applies Transformer to CV and uses a self-attentive head to efficiently extract global information features in images. Many methods based on transformer are widely used for liver and tumor segmentation. Swin Transformer was introduced in U-Net in to enhance the global nature of the network⁸. To improve the perception of the network and the global understanding of the image journey, Transformer is used instead of down sampling and RDCTrans U-Net is proposed for liver segmentation⁹. To learn the features of different tumors, a dynamic hierarchical Transformer network is proposed using a hierarchical operation with different receptive field sizes¹⁰. In addition, the self-attention mechanism is used as the core of Transformer, and introducing this dot product attention into the model can also capture long-term contextual information and improve the accuracy of liver tumor segmentation¹¹.

Although the above methods achieve good segmentation results, they still fail to take full advantage of the rich local and long-range dependent information contained in medical images. On the one hand, due to the sparse interaction nature of the convolution operation, the sensory field of the CNN-based method can only extract local semantic information of the image, resulting in the background region being recognized as a lesion region. On the other hand, Transformer utilizes the dispense convolution operator and the attention mechanism to map a series of image block sequences into an abstract continuous representation, thus obtaining a global dependence on the whole image and effectively avoiding erroneous segmentation results of the background in medical images. However, the structure of Transformer ignores the local information, and over-segmentation or under-segmentation of different lesion regions can occur. Therefore, there is an urgent need for network models that extract both local features and global information to improve the segmentation accuracy of liver and tumors.

In the process of designing the above model, we encountered three difficulties. The first is that it is more difficult to extract edge details of irregular liver and tumor. The second is how to realize the simultaneous extraction of local and global features. The third is how to achieve effective fusion of local features and global features and exploit their complementarity. We found that the shape, size, and distribution of liver tumors are not fixed. However, the convolution kernel uses the same parameters to extract information at different locations, which cannot emphasize the importance of each feature. In addition, the direction and scale of the convolution kernel are single. Therefore, it is difficult to accurately identify liver tumors and accurately extract the edge texture features of irregular tumors from abdominal CT with rich information. To solve the second problem, we employ a dual-coded branching structure. The local and global encoders extract features independently, thus extracting more comprehensive features from the image and improving the segmentation performance of the model. To address the third issue, we propose Dual-branch interactive module. There are two main challenges in the design of this module. The first challenge is that the features output by the local feature branch and the global branch are different. The second challenge is how to design a reasonable feature fusion scheme that exploits the complementary advantages between the two branches. To solve the above challenges. Firstly, we perform spatial attention and channel attention operations on local features and global features respectively to transform and enhance the output features. Secondly, we encode the corresponding position of the feature maps of different branches, and perform attention cross fusion by receiving the feature maps of their own branch and the feature maps of another branch. The complementarity of global branch and local branch is effectively played to improve the performance of the model.

The main contributions of this paper can be summarized as follows:

• 1. we propose a hybrid gabor attention convolution and transformer interaction network with hierarchical monitoring mechanism for liver and tumor segmentation, named HyborNet, which uses local encoder branch and global encoder branch to extract features independently. Capture more features from the image.

• 2. We propose gabor attention convolution to form the local feature extraction branch to process the downsampled medical images, retrieve the features of the local region, and perform fine-grained extraction of the local detail information of the liver and tumor.

• 3. We propose dual-branch interactive module to achieve feature alignment and efficient fusion, and make full use of the complementary properties of CNN and Transformer to improve the quality of segmentation.

• 4. We propose the hierarchical monitoring mechanism, which is integrated between different layers of the network decoder to restrict the network weights to the target region and optimize the segmentation results.

Related works

Liver and tumor segmentation based on CNN

In recent years, deep learning models such as convolutional neural networks have shown exciting performance in the field of liver tumor segmentation. Long et al. proposed a full convolutional neural network (FCN) for semantic segmentation in the novel, which is based on the principle of CNN and has an encoder-decoder structure¹². Christ et al. combined a cascading FCN model with a dense 3D conditional field to achieve automatic liver segmentation¹³. Liu et al. extracted spatial features from each convolutional block and fused them into the convolutional network to take advantage of multi-scale features¹⁴. To overcome the influence of different tumor sizes and shapes during liver tumor segmentation, the researchers developed the U-Net network. The U-Net architecture was originally developed for medical image segmentation. It consists of two parts, an encoder and a decoder, which are interconnected to form a U-shaped network structure. The encoder can be seen as the feature extraction part, while the decoder can be seen as the feature fusion part. Compared with traditional FCN, U-Net uses feature splicing to realize the fusion of shallow low-resolution information and deep high-resolution information. Appadurai et al. used U-Net as an encoder and a pre-trained efficient network as a decoder for liver lesion segmentation¹⁵. Wu et al. proposed a cascaded U-Net in which two U-Nets are used sequentially to segment the target from coarser to finer. The cascaded U-Net is connected in an end-to-end manner by merging the internal nested connections between the two U-Nets¹⁶. However, the method requires a large number of model parameters, resulting in high computational effort and time overhead. To overcome this limitation, Zhu et al. cascaded U-ADenseNet for fully automatic segmentation using a coarse-to-fine processing strategy¹⁷. Inspired by the success of U-Net, many researchers have improved the network based on U-Net. Zhou et al. proposed U-Net++ based on nested and dense jump connections¹⁸. Dense blocks and convolutional layers were used to improve the accuracy of the segmentation results. Later, Kushnure et al. improved it by using the preactivated multiscale Res2Net as the backbone and adding a channel attention block (PARCA). Applying the channel attention block to long jump connections and applying the attention mechanism to the upsampling process reduces the loss of feature values in both processes to improve the performance of U-Net++¹⁹. Huang et al. used full-scale jump connections and deep supervision, fusing different levels of varying information from the feature maps at full scale while keeping the number of parameters low²⁰. li et al. proposed a network EResU-Net based on the combination of efficient channel attention and ResU-Net ++ to mitigate the effects of uneven sample distribution²¹.

Attention mechanisms can provide neural networks with the ability to focus on inputs, leading to improved model accuracy and efficiency²². To suppress irrelevant features in liver segmentation, Sun et al. proposed a U-Net model based on attention gating²³. Meanwhile, Luan et al. proposed a spatial attention mechanism and a channel attention mechanism to encode semantic features over longer distances using long-hop connections between the encoder and decoder, and to fuse semantic information extracted from contraction and expansion paths²⁴. Fan et al. proposed a multiscale attention U-Net consisting of a positional attention block (PAB) and a multiscale fusion attention block (MFAB). They integrated PAB and MFAB blocks into the bottleneck layer and coding paths to capture features relatively²⁵. Lei et al. designed a Ladder-Aspace Pyramid Pooling (Ladder-ASPP) module using multiscale expansion rates to learn better contextual information²⁶ . Ozcan et al. proposed the Additive Inception-UNet (AIM-UNet) model for computer-aided automatic segmentation of liver and liver tumors, which learns more local features than the standard U-Net model²⁷.

Despite achieving satisfactory segmentation results, the model is limited by the inherent local nature of convolution, which can only capture information from the pixel domain and lacks the ability to explicitly capture global dependencies. In the liver CT segmentation task, global dependencies are crucial for determining the exact location of the liver and tumors. Therefore, CNNs constructed with deeper encoders and active downsampling operations are required to extract more global features. However, successive downsampling operations lead to network redundancy and loss of location information. Therefore, in this paper, we propose dual-coded branching, construct distance dependent branching based on transformer to extract global information, identify the lesion region, and use dual-branching interactive module for high fusion of features to improve segmentation accuracy.

Liver and tumor segmentation based on Gabor

Gabor mimics the human visual system and can detect features in multiple directions and scales. It is suitable for texture representation and recognition²⁸. It is a special kind of convolution, invariant to rotation, scale and shift, so it has been widely used in image processing. Some scholars use Gabor to extract texture features of different tissues and structures in images, which can realize accurate localization and segmentation of organ boundaries. Ashreetha et al. used Gabor to extract features from abdominal CT, and then used a classifier to segment liver²⁹ . Kazemi et al. used Gabor filter banks based on GLCM to extract features³⁰. Bhagya et al. used Gabor filter to minimize noise to improve image quality, and then performed tumor segmentation on liver images³¹.

Gabor filters may not work well when processing images that are low in contrast, blurred, or contain a large number of artefacts. Therefore, the Gabor filter is combined with other feature extraction methods and segmentation algorithms to further improve the accuracy and robustness of the segmentation. Kinnikar et al. used Gabor as a pre-processing tool to generate Gabor features, which were then used as input to the CNN³². To reduce the complexity of CNN training and improve the robustness of the feature representation, Sarwar et al. used Gabor filters in the first or second convolution layer³³ . Luan et al. proposed Gabor convolutional networks to improve the robustness of feature learning to changes in direction and scale³⁴. Recently, Yoo et al. proposed an alternative to traditional pooled wavelets that can accurately reconstruct local information of images³⁵. Based on Gabor, Diao et al. proposed the automatic pseudo-labelling (TAPL) module, which uses the texture information of tumors to enable the neural network to actively learn the texture differences between different tumors to improve the segmentation accuracy³⁶. Mostafiz et al. used Gabor wavelet transform (GWT) and local binary mode (LBP) to combine features with a pre-trained deep CNN model to detect lesions in liver ultrasound and solve problems such as artifacts, speck noise and fuzzy effects in ultrasound³⁷.

Although the above research on Gabor has produced impressive results, there are still two problems. On the one hand, the Gabor filter is sensitive to image quality and noise. If the image quality is poor or there is more noise, the accuracy and stability of the segmentation can be affected. However, Gabor only enhances the ability of the receptive field to extract semantic information such as local edges or textures, but it still cannot achieve accurate segmentation of the target region. Therefore, this paper proposes that the Gabor attentional learnable convolution can effectively solve these problems. Under the guidance of the attention mechanism, the network can pay more attention to global information, and the Gabor-modulated convolution kernel can learn richer feature representations and improve the segmentation accuracy of liver and tumors.

Liver and tumor segmentation based on transformer

Transformers were first proposed in the field of NLP and have achieved state-of-the-art performance in machine translation (ML). Inspired by their great success in NLP tasks, many researchers have investigated the adaptability of transformers in computer vision and medical image analysis tasks. Dosovitskiy et al used Transformer’s recent work in the graphics domain, which is an iconic work³⁸. SETR provides a new perspective where semantic segmentation is reconsidered as a sequence-to-sequence prediction problem for transformers³⁹. Swin Transformer extracts local features within each split window and merges them by self-focusing in continuously moving windows⁴⁰. Ni et al. proposed a region adaptive transformer (DA-Tran) network to segment liver tumors from each CT phase⁴¹. Li et al. proposed a dynamic layered transformer network, called DHT-Net, for liver segmentation. Di et al. fused transformer and directional information into the convolutional network to achieve automatic segmentation of CT images of liver tumors⁴². While Transformer has advantages in extracting global representations, self-attention at the image level rarely captures fine-grained details. Therefore, in this paper, Gabor attention convolution is used to form local feature extraction branches, extract local texture features, and extract local details of liver and tumors in fine grain to improve the segmentation accuracy of liver and tumors.

Method

In this section, we will introduce the HyborNet and the structure of the components in detail. Firstly, the overall structure of our network is presented, followed by describing the details of each component at a theoretical level including: the Gabor attention convolution, the dual-branch interactive module, optimization and the deep-loss monitoring mechanism.

Overview of the proposed network

A qualified model should be able to capture the intrinsic features in medical images. In abdominal CT, due to the imaging principle, the organ is not high contrast, the border is not obvious and it is difficult to distinguish it from other organs. In addition, liver and tumour segmentation is challenging because liver tumours are variable in size and shape. We believe that effective fusion of global and local features can ensure consistency between different features, further improving segmentation performance.

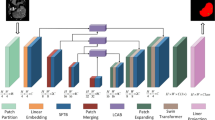
As shown in Fig. 1, HyborNet is based on the classical medical image segmentation network U-Net and adopts an asymmetric dual-flow encoder-decoder architecture. In particular, the network consists of two parallel branches of feature extraction, namely a local feature extraction branch using a CNN structure and a remote dependent feature extraction branch using a transform structure. The CNN branch uses Gabor attention convolution as its basic component, which can represent multi-scale features in fine granularity, enhance the local feature extraction capability of the network, and refine the edge detail texture features. For remote dependent branches, we adopt the PVT¹⁷ framework in the transfer model. Due to its unique pyramid structure and space reduction attention mechanism, PVTv2 has stronger feature extraction capabilities and reduced resource consumption. Therefore, PVTv2 is used.

The overall segmentation process of HyborNet is as follows. For the input image $I \in {R^{w \times h \times c}}$, we first extract pixel-level detail features and object-level global features ${I_i} \in {R^{\frac{W}{{{2^{i + 1}}}} \times \frac{h}{{{2^{i + 1}}}} \times {c_i}}}$ using two trunk branches, respectively, where ${c_i} \in \left\{ {64,128,256,512} \right\}$ , $i \in \left\{ {1,2,3,4} \right\}$. Then, we subtract the global features extracted in the remote dependency branch from the local features extracted in the local feature branch of the corresponding stage to obtain the high-resolution edge profile features, and then perform the maximum pooling downsampling operation. Next, the final extracted local and remote-dependent features from the two branches are fed into the dual-branch interactive module, and the local and remote-dependent features are aggregated for feature aggregation. Secondly, the feature vectors aggregated to contain the local and global features are input to the decoder, while the features of the coding path and the decoder are fused using four jump connections, the first and second jump connections allow the information containing the high resolution texture features in the local feature branch to be obtained at a shallow level and fused into the decoder. The third and fourth bounds pass the deep edge information in the global dependency branch to the decoder. The feature vectors are designed to have high resolution texture and deep edge information to obtain accurate liver and tumour segmentation results. Finally, for each decoding block, a classifier is added to generate multi-scale segmentation maps at different stages for loss function calculation to optimise the segmentation results and improve the segmentation accuracy.

Figure 1

Architecture of the proposed HyborNet for Liver tumor segmentation.

Figure 2

The structure of Gabor attention convolution.

Gabor attention convolution

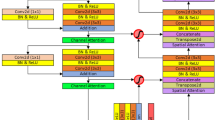
The Gabor Attention Convolution (GAC) is an important part of HyborNet. It is the smallest unit of the encoder and decoder. Although the traditional convolutional neural network uses convolution operations with common parameters, which greatly reduces the computational cost and complexity of the model, the shape, size, colour and distribution of objects at different locations in the image are variable, and the convolution kernel uses the same parameters in each sensor field to extract information without considering the difference information at different locations. Therefore, the performance of standard convolutional operations is limited. GAC proposed in this paper solves this problem well. The structure diagram of Gabor attention convolution is shown in Fig. 2. Specifically, GAC consists of multi-dimensional interactive attention and Gabor learnable convolution. In this paper, the size of the convolution kernel for the Gabor convolution is 5 x 5. The convolution kernel in Fig. 2 has been magnified to more clearly illustrate the directionality of the Gabor convolution kernel. For multi-dimensional interactive attention, rich contextual information can be learned, and multi-scale feature information can be aggregated to remove noise that is not affected by the target region. It not only focuses on the discriminative features of the channel and spatial dimensions, but also establishes the multi-dimensional interaction relationship between the channel and spatial dimensions. In addition, the weighted parameters are adjusted to further blend the characteristics of each view.

Multi-dimensional interactive attention can be divided into four parallel branches: channel dimension attention, channel and width dimension attention, channel and height dimension attention and space dimension attention. The first branch focuses on recalibrating channel level feature representation capabilities. First, we aggregate the spatial features of the input using maximum pooling and average pooling respectively, and define them as $X_{1(\max )}^{c \& c} \in {R^{c \times 1 \times 1}}$, $X_{1(\mathrm{{avg}})}^{c \& c} \in {R^{c \times 1 \times 1}}$. Then, using a multi-layer perceptron (MLP) consisting of two $1 \times 1$ onvolutional layers and an activation function (Rule), the size of the middle layer is set to $R{ \in ^{c/2 \times 1 \times 1}}$ in order to maintain channel resolution and minimize the number of parameters, and the output of the MLP is summed at the element level. The sum output is then passed through the softmax activation function to get the channel-level attention weight ${A_{c \& c}}\left( X \right) \in {R^{c \times 1 \times 1}}$. It can be concluded that the mathematical calculation of the weight mapping of the channel-level attention of the first branch is as follows:

$$\begin{aligned} A_{c \& c}(X)&= \theta \left( \text {MLP}(\text {Maxpool}(X)) + \text {MLP}(\text {Avgpool}(X)) \right) \nonumber \\&= \theta \left( W_2 \xi \left( W_1 \left( X_{1(\max )}^{c \& c} \right) \right) + W_2 \xi \left( W_1 \left( X_{1(\text {avg})}^{c \& c} \right) \right) \right) \end{aligned}$$

(1)

where $\theta$ is the sigmoid function, $\xi$ is the ReLU function, ${W_1} \in {R^{c/2 \times c}}$ and ${W_2} \in {R^{c \times c/2}}$. Finally, the first branch output feature maps $X_1^{c \& c}$ is generated by the following equation:

$$\begin{aligned} X_1^{c \& c} = {A_{c \& c}}\left( X \right) X \end{aligned}$$

(2)

The main role of the second branch is to focus on the interaction of channels and height dimensions. Firstly, X is rotated 90 degrees counterclockwise along the height scale to generate a new semantic feature $X_{2r}^{c \& h} \in {R^{w \times h \times c}}$, Next, feature aggregation of $X_{2r}^{c \& h} \in {R^{w \times h \times c}}$ is performed using maximum pooling and average pooling, $X_{2r(\max )}^{c \& h} \in {R^{1 \times h \times c}}$ and $X_{2r(\mathrm{{avg}})}^{c \& \mathrm{{h}}} \in {R^{1 \times h \times c}}$, respectively.

These outputs are then concatenated with BN using a $K \times K$ convolution operation, and then, using S-type activation function yields the weight mapping of cross attention between channels and height dimensions ${A_{c \& h}}\left( {X_{2r}^{c \& h}} \right) \in {R^{1 \times h \times c}}$. In short, its calculation formula is as follows:

$$\begin{aligned} {A_{c \& h}}(X_{2r}^{c \& h})&= \theta \left( {f^{k \times k}}\left[ \text {Maxpool}\left( X_{2r}^{c \& h} \right) , \text {Avgpool}\left( X_{2r}^{c \& h} \right) \right] \right) \nonumber \\&= \theta \left( {f^{k \times k}}\left[ X_{2r(\max )}^{c \& h}, X_{2r(\mathrm{{avg}})}^{c \& \mathrm{{h}}} \right] \right) \end{aligned}$$

(3)

where $\theta$ is the sigmoid function, ${f^{k \times k}}$ is the $K \times K$ convolution operation with the BN.he second branch output feature maps $X_2^{c \& h}$ s generated by the following equation:

$$\begin{aligned} X_2^{c \& h} = Roated\left( {{A_{c \& h}}\left( {X_{2r}^{c \& h}} \right) } \right) X_{2r}^{c \& h} \end{aligned}$$

(4)

The third branch is mainly concerned with the interaction between the channel dimension and the width dimension. The process of calculating semantic features is similar to the process of calculating channels and high attention. Firstly, the input X is rotated 90 degrees counterclockwise along the width to obtain a new semantic feature $X_{3r}^{c \& w} \in {R^{h \times c \times w}}$. After that, perform the same operation as the previous branch. The calculation process of the attention mechanism of channel dimension and width dimension can be summarized as follows:

$$\begin{aligned} {A_{c \& w}}(X_{3r}^{c \& w})&= \theta \left( {f^{k \times k}}\left[ \text {Maxpool}\left( X_{3r}^{c \& w} \right) , \text {Avgpool}\left( X_{3r}^{c \& w} \right) \right] \right) \nonumber \\&= \theta \left( {f^{k \times k}}\left[ X_{3r(\max )}^{c \& w}, X_{3r(\mathrm{{avg}})}^{c \& w} \right] \right) \end{aligned}$$

(5)

$$\begin{aligned}&X_3^{c \& w} = \text {Roated}\left( {A_{c \& w}\left( X_{3r}^{c \& w} \right) } \right) X_{3r}^{c \& w} \end{aligned}$$

(6)

The main function of the fourth branch is to focus on the characteristics of the target region in the spatial dimension. The calculation process of the spatial attention map and the output of spatial attention can be summarized as follows:

$$\begin{aligned} {A_{h \& w}}(X_4^{h \& w})&= \theta \left( {f^{k \times k}}\left[ \text {Maxpool}\left( X_4^{h \& w} \right) ,\text {Avgpool}\left( X_4^{h \& w} \right) \right] \right) \nonumber \\&= \theta \left( {f^{k \times k}}\left[ X_{4(\max )}^{h \& w}, X_{4(\mathrm{{avg}})}^{h \& w} \right] \right) \end{aligned}$$

(7)

$$\begin{aligned} X_4^{h \& w} = {A_{h \& w}}\left( {X_4^{h \& w}} \right) X_4^{h \& w} \end{aligned}$$

(8)

Finally, in order to further improve the fusion ability of features, we add a learnable weight parameter to the back of the four branches, so the output in the multi-dimensional interactive attention can be summarized as:

$$\begin{aligned} {w_i} = \frac{{\exp \left( {{a_i}} \right) }}{{\sum \limits _{j = 1}^4 {\exp \left( {{a_j}} \right) } }},i = 1,2,...,4 \end{aligned}$$

(9)

$$\begin{aligned} Y \!=\! {w_1}\!\left( {X_1^{c \& c}} \right) \!+\! {w_2}\!\left( {X_2^{c \& h}} \right) \! +\! {w_3}\!\left( {X_3^{c \& w}} \right) \!+\! {w_4}\!\left( {X_4^{h \& w}} \right) \end{aligned}$$

(10)

where ${w_i}$ is the normalized weight coefficient and $\sum {{w_i}} = 1$, ${a_i}$ and ${a_j}$ are the initial weight coefficients.

Due to the limitation of receptive field, standard convolution cannot capture the information difference brought by different locations, which limits the performance of neural networks to some extent. Gabor filter can extract semantic features from medical images in multi-scale and multi-direction, refine texture features, and capture detailed feature information. Gabor’s learnable convolution inherits this ability well. One-dimensional Gabor function was first proposed by Gabor¹⁸. Then, Daugman proposed the two-dimensional Gabor function¹⁹, which can be expressed as a Gaussian kernel function modulated by sine-wave plane waves. The 2D Gabor function typically applied to 2D images is defined as follows

$$\begin{aligned} g_\mathrm{{r}}\left( x, y, \lambda , \theta , \psi , \sigma , \gamma \right) = \exp \left( - \frac{x^{\prime 2} + \gamma ^2 y^{\prime 2}}{2 \sigma ^2} \right) \cos \left( 2\pi \frac{x^{\prime }}{\lambda } + \psi \right) \end{aligned}$$

(11)

$$\begin{aligned} \frac{dx'}{d\theta } = x \cos \theta - y \sin \theta , \quad \end{aligned}$$

(12)

$$\begin{aligned} \frac{dy'}{d\theta } = - x \sin \theta + y \cos \theta \end{aligned}$$

(13)

where, x and y represent the horizontal and vertical coordinates of a pixel in the image, $\lambda$ represents the wavelength, $\frac{1}{\lambda }$ represents the spatial frequency of the cosine function, and $\theta$ is the direction parameter. In addition, $\gamma$ represents the aspect ratio of space, which determines the ellipticity of the receptive field. $\psi$ s the phase offset and $\sigma$ is the standard deviation of the Gaussian factor. the principle of Gabor learnable convolution is to combine a Gabor filter with the Hadamard product of a standard convolution kernel. The specific formula is as follows:

$$\begin{aligned} CG=C\bullet G\left( \lambda , \theta \right) \end{aligned}$$

(14)

where, GC stands for Gabor learnable convolution, C for standard convolution kernel, and $G\left( \lambda , \theta \right)$ for Gabor filter. Accordingly, the scale and direction parameters are denoted by $\lambda$ and $\theta$, respectively. $\bullet$ Indicates the Hadamard product. The dashed line in the Fig. 2 is a schematic of Gabor’s structure.

Dual-branch interactive module

Dual-branch fine fusion is crucial for the success of HyborNet to capture features from two different views of the same image. In order to capture such interactive fusion features, we design a cross-attention based interactive fusion module, the dual-branch interactive module (DIM), as shown in Fig. 3. Specifically, this module aims to fuse feature information between local feature extraction branches and remote dependency extraction branches, and propagate the information interactively in a dynamically learnable manner. Compared to a simple merging of features from different perspectives, the DIM module facilitates an adaptive integration between the two feature representations, thus enabling a more informative feature representation.

The specific process of DIM is as follows: Firstly, for local feature extraction branch ${{\text {C}}_{\text {i}}}$, spatial attention is used as a spatial filter to eliminate feature noise, enhance local details and obtain output ${{{{\hat{\text {C}}}}}_{\text {i}}}$. Channel attention mechanism is applied to remote dependent branch ${\mathrm{{T}}_\mathrm{{i}}}$ respectively to promote the output of global information ${{{{\hat{\text {T}}}}}_{\text {i}}}$ Meanwhile, interactive feature extraction is carried out for ${\mathrm{{C}}_\mathrm{{i}}}$ and ${\mathrm{{T}}_\mathrm{{i}}}$. Secondly, the position coding of the same dimension will be embedded in two branches, two cross-interactive attention modules, by receiving their own branch feature map and another branch feature map to perform attention interaction fusion, producing two outputs ${\mathrm{{c}}_\mathrm{{f}}}$ and ${\mathrm{{t}}_\mathrm{{f}}}$. Finally, the participating feature ${\mathrm{{c}}_\mathrm{{f}}}$, ${\mathrm{{t}}_\mathrm{{f}}}$ and the interactive feature are connected and passed through the residual block to output the resulting feature ${\mathrm{{f}}_\mathrm{{i}}}$. The specific formula is as follows:

Figure 3

The structure of Dual-branch interactive module.

$$\begin{aligned} {\hat{T}}_{i}&= \text {ChannelAttn}(T_{i}) \end{aligned}$$

(15)

$$\begin{aligned} {\hat{C}}_{i}&= \text {SpatialAttn}(C_{i}) \end{aligned}$$

(16)

$$\begin{aligned} b_{i}&= \text {Conv}\left( T_{i} W_1^{i} \odot C_{i} W_2^{i} \right) \end{aligned}$$

(17)

$$\begin{aligned} c_{f}&= \text {CrossAttn}\left( {\hat{C}}_{i} \right) \end{aligned}$$

(18)

$$\begin{aligned} t_{f}&= \text {CrossAttn}\left( {\hat{T}}_{i} \right) \end{aligned}$$

(19)

$$\begin{aligned} f_{i}&= \mathop {\textrm{Re}}\nolimits \text {sideual}\left( c_{f}, t_{f}, b_{i} \right) \end{aligned}$$

(20)

where $\left| \odot \right|$ is Hadamard product and Conv is a 3x3 convolution layer.

In DIM, the attention mechanism is the basic operation for designing the feature fusion interaction module. Taking eigenvector $\mathrm{{Q}},\mathrm{{K}},\mathrm{{V}} \in {\mathrm{{R}}^{\mathrm{{N}} \times \mathrm{{C}}}}$ as an example, the general attention function (Att) mainly functions in the dot product operation after scaling. The formula is as follows:

$$\begin{aligned} \text {Att}(Q,K,V)&= \text {softmax}\left( \frac{QK^T}{\sqrt{C}} \right) V \end{aligned}$$

(21)

However, the implementation of the soft maximum logarithm and attention diagram requires $O\left( {{n^2}} \right)$ space complexity and $O\left( {{n^2}c} \right)$ time complexity. Inspired by the study of self-attention linearization¹¹, we factor the attention map using two functions $\phi \left( \bullet \right)$, $\varphi \left( \bullet \right)$ and roughly estimate the attention map by calculating matrix multiplication of keys and values. The specific formula is as follows:

$$\begin{aligned} \text {Att}(Q, K, V)&= \phi (Q) \left( \varphi \left( K \right) ^T V \right) \end{aligned}$$

(22)

Factorization reduces the space and time complexity to $O\left( {NC} \right)$ and $O\left( {N{C^2}} \right)$,respectively, which are linear functions of sequence length N.In our experiment, we developed an attention-oriented mechanism with $\varphi$ as scale factor $1/\sqrt{C}$ and $\varphi$ as softmax:

$$\begin{aligned} \text {Att}(Q, K, V)&= \frac{Q}{\sqrt{C}} \left( \text {softmax} \left( K \right) ^T V \right) \end{aligned}$$

(23)

Next, although this decomposition of attention is not an unbiased approximation of scaled dot product attention, it can still be considered a generalised attention mechanism that uses Q, K, and V to model feature interactions. Factorising the attention module reduces the computational burden of dot product attention proportionally. Furthermore, since we first compute $S = \mathrm{{softmax}}\left( {{{\left( \mathrm{{K}} \right) }^\mathrm{{T}}}\mathrm{{V}}} \right) \in {\mathrm{{R}}^{\mathrm{{C}} \times \mathrm{{C}}}}$ ,then S can be considered as a data-dependent global linear transformation for each feature vector query Q mapping, which suggests that there may be two equivalent query vectors ${\mathrm{{q}}_1}$ and ${\mathrm{{q}}_2}$ in Q. Therefore, the associated self-attentive output can theoretically be defined as

$$\begin{aligned} \text {Att} \left( \text {Q, K, V} \right) _1&= \frac{q_1}{\sqrt{\text {C}}} \, \text {S} = \frac{q_2}{\sqrt{\text {C}}} \, \text {S} = \text {Att} \left( \text {Q, K, V} \right) _2 \end{aligned}$$

(24)

However, this property can lead to poor results for feature extraction. Specifically, based on this operation, the output will depend only on the structure of the input token, without noticing the differences in the local features. In other words, this property is disadvantageous for image tasks, especially for tasks as intensive as segmentation. To improve the relative relationship between the model tokens, we added a positional coding $\mathrm{{p}} = \left\{ {{\mathrm{{p}}_\mathrm{{i}}},\mathrm{{i}} = - \frac{{\mathrm{{M}} - 1}}{2},...,\frac{{\mathrm{{M}} - 1}}{2}} \right\}$ with window size M to capture the relative attentional mapping $\lambda \mathrm{{Q}} \in {\mathrm{{R}}^{\mathrm{{N}} \times \mathrm{{C}}}}$.

$$\begin{aligned} \mathop {\textrm{Re}}\nolimits \, \text {lAtt}(X)&= \frac{\text {Q}}{\sqrt{\text {C}}} \left( \text {softmax} \left( \text {K} \right) ^T \text {V} \right) + \lambda \text {Q} \end{aligned}$$

(25)

$$\begin{aligned} \lambda \text {Q}&= \text {DepthwiseConv}(\text {V}) \circ \text {Q} \end{aligned}$$

(26)

where $\circ$ is the Hadamard Product. Each element $\lambda \mathrm{{Q}}$ is a relative attention feature plot of the relation $\left( {q,v} \right)$ representing the relation from ${\mathrm{{q}}_\mathrm{{i}}}$ to ${\mathrm{{v}}_\mathrm{{i}}}$ , and aggregating all related value vectors individually into ${\mathrm{{q}}_\mathrm{{i}}}$. he process is shown in Fig. 3, in contrast, $\lambda \mathrm{{Q}}$ is more efficient with $O\left( {NC} \right)$ and $O\left( {NCM2} \right)$ in time.

Optimization

In this section, we will show the process of parameter updating for Gabor convolution. the Gabor Convolutional Filters (GC) are constructed by applying the Hadamard product between the convolutional kernels and the Gabor filters:

$$\begin{aligned} GC(C,\lambda , \theta ) = C \circ G_k(\lambda , \theta ) \end{aligned}$$

(27)

where, $GC$ is the Gabor convolutional, $C$ is the convolutional kernel ,$G_k(\lambda , \theta )$ is the $k$-th Gabor filter with scale parameter $\lambda$ and orientation parameter $\theta$,$\circ$ denotes the Hadamard product (element-wise multiplication).

Using the chain rule, the gradient of the loss function $L$ with respect to the convolutional kernel $C$ is computed as:

$$\begin{aligned} \frac{\partial L}{\partial C} = \frac{\partial L}{\partial GC} \frac{\partial GC}{\partial C} \end{aligned}$$

(28)

Substituting $\frac{\partial GC}{\partial C} = G_k(\lambda , \theta )$ from the previous step, we obtain the final gradient of the loss function with respect to the convolutional kernel:

$$\begin{aligned} \frac{\partial L}{\partial C} = \frac{\partial L}{\partial GC} G_k(\lambda , \theta ) \end{aligned}$$

(29)

Once we have the gradient of the loss function with respect to the convolutional kernel $C_j^l$, we use gradient descent to update the kernel. The update rule for the convolutional kernel is as follows:

$$\begin{aligned} C = C - \eta _C \frac{\partial L}{\partial C} \end{aligned}$$

(30)

where, $C$ is the current convolutional kernel, $\eta _C$ is the learning rate for the convolutional kernel ,$\frac{\partial L}{\partial C}$ is the gradient of the loss function with respect to the convolutional kernel.

Substituting the gradient computed above, the update rule becomes:

$$\begin{aligned} C = C - \eta _C \left( \frac{\partial L}{\partial GC} G_k(\lambda , \theta ) \right) \end{aligned}$$

(31)

The Gabor filter is defined as a product of a Gaussian function and a sinusoidal plane wave. It is written as:

$$\begin{aligned} & g_\mathrm{{r}}\left( x, y, \lambda , \theta , \psi , \sigma , \gamma \right) = \exp \left( - \frac{x^{\prime 2} + \gamma ^2 y^{\prime 2}}{2 \sigma ^2} \right) \cos \left( 2\pi \frac{x^{\prime }}{\lambda } + \psi \right) \end{aligned}$$

(32)

$$\begin{aligned} & x' = x \cos \theta + y \sin \theta \end{aligned}$$

(33)

$$\begin{aligned} & y' = -x \sin \theta + y \cos \theta \end{aligned}$$

(34)

where, $\sigma$ controls the scale of the filter, $\lambda$ is the wavelength, which controls the frequency, $\theta$ is the orientation angle, $\sigma$ is the standard deviation of the Gaussian, $\gamma$is the aspect ratio of the spatial field, $\psi$ is the phase offset, $x, y$ are the image coordinates.

The Gabor filter’s structure allows it to capture both local texture and edge information in an image by modulating sinusoidal components in the frequency domain, which is crucial for image segmentation tasks like liver and tumor delineation.

we calculate the gradients of the loss function with respect to the Gabor filter parameters ($\lambda$ and $\theta$) to update the filters and convolutional kernels during backpropagation.

The gradient of the Gabor filter with respect to the scale parameter $\lambda$ is computed as:

$$\begin{aligned} \frac{\partial g_\mathrm{{r}}}{\partial \lambda } = 2\pi \frac{x'}{\lambda ^2} \exp \left( - \frac{x^{\prime 2} + \gamma ^2 y^{\prime 2}}{2 \sigma ^2} \right) \sin \left( 2\pi \frac{x'}{\lambda } + \psi \right) \end{aligned}$$

(35)

This gradient term ensures that during backpropagation, the Gabor filter adjusts its scale ($\lambda$) to better capture frequency components in the image.

The gradient of the Gabor filter with respect to the orientation parameter $\theta$ is more complex and is given by:

$$\begin{aligned} & \frac{\partial g_\mathrm{{r}}}{\partial \theta } = - \exp \left( - \frac{x^{\prime 2} + \gamma ^2 y^{\prime 2}}{2 \sigma ^2} \right) \left[ \frac{x' \frac{d{x'}}{d\theta } + \gamma ^2 y'^2}{\sigma ^2} \cos \left( 2\pi \frac{x'}{\lambda } + \psi \right) \right. \left. + \frac{2\pi }{\lambda } \frac{d{x'}}{d\theta } \sin \left( 2\pi \frac{x'}{\lambda } + \psi \right) \right] \end{aligned}$$

(36)

$$\begin{aligned} & \frac{dx'}{d\theta } = x \cos \theta - y \sin \theta , \quad \end{aligned}$$

(37)

$$\begin{aligned} & \frac{dy'}{d\theta } = - x \sin \theta + y \cos \theta \end{aligned}$$

(38)

This term ensures that the Gabor filter adapts its orientation ($\theta$) to better align with the edges and textures in the image, improving segmentation performance.

$$\begin{aligned} & \delta _k^\lambda = \frac{1}{J N} \sum _{j=1}^J \sum _{n=1}^N c_{j,n} \frac{\partial L}{\partial GC{j,n}} \frac{\partial GC_{j,n}}{\partial G_k(\lambda , \theta )} \frac{\partial G_k(\lambda , \theta )}{\partial \lambda } \end{aligned}$$

(39)

$$\begin{aligned} & \delta _k^\theta = \frac{1}{J N} \sum _{j=1}^J \sum _{n=1}^N c_{j,n} \frac{\partial L}{\partial GC{j,n}} \frac{\partial GC{j,n}}{\partial G_k(\lambda , \theta )} \frac{\partial G_k(\lambda , \theta )}{\partial \theta } \end{aligned}$$

(40)

During backpropagation, theGabor filters is updated. The scale and orientation parameters are updated as follows.

$$\begin{aligned} \lambda _k= & \lambda _k - \eta _\lambda \delta _k^\lambda \end{aligned}$$

(41)

$$\begin{aligned} \theta _k= & \theta _k - \eta _\theta \delta _k^\theta \end{aligned}$$

(42)

The aforementioned content delineates the update process of learnable parameters in Gabor convolution and Gabor attention convolution.

Hierarchical monitoring mechanism

In the training process, the loss function consists of using the binary cross-entropy loss ${L_{BCE}}$ and the dice loss ${L_{Dice}}$, where ${\mathrm{{R}}_{\mathrm{{gt}}}}$ and ${\mathrm{{R}}_{\mathrm{{seg}}}}$ represent the real label value and the predicted result, respectively. Then ${L_{BCE}}$ and ${L_{Dice}}$ can be defined as

$$\begin{aligned}&{L_{BCE}}\!\left( \! {{\mathrm{{R}}_{\mathrm{{gt}}}}\!,\!{\mathrm{{R}}_{\mathrm{{seg}}}}} \right) \!=\!- \!\left( \! {1\! - \!{\mathrm{{R}}_{\mathrm{{gt}}}}} \right) \log \left( {\mathrm{{1}}\! -\! {\mathrm{{R}}_{\mathrm{{seg}}}}} \right) \! -\! {\mathrm{{R}}_{\mathrm{{gt}}}}\log {\mathrm{{R}}_{\mathrm{{seg}}}} \end{aligned}$$

(43)

$$\begin{aligned}&L_{\text {Dice}}\left( R_{\text {gt}}, R_{\text {seg}} \right) = 1 - \frac{2 R_{\text {gt}} R_{\text {seg}}}{R_{\text {gt}} + R_{\text {seg}} + \varepsilon } \end{aligned}$$

(44)

The $\varepsilon$ in the formula is a small constant set to avoid having a zero denominator. Therefore, the loss function in the experiment can be derived according to ${L_{BCE}}$ and ${L_{Dice}}$.

$$\begin{aligned} L_{\text {Dice}}\left( R_{\text {gt}}, R_{\text {seg}} \right)&= 1 - \frac{2 R_{\text {gt}} R_{\text {seg}}}{R_{\text {gt}} + R_{\text {seg}} + \varepsilon } \end{aligned}$$

(45)

where $\lambda$ was set to 0.5 in this experiment.

In order to improve the stability of the training process, the proposed model applies ${L_{seg}}$ to both decoders in the second stage decoding process to establish a deep supervision loss function. Where ${M_{GT}}$ represents the true segmentation result graph, so the loss $L_s^i$ of the i-th decoder can be defined as

$$\begin{aligned} L_s^i\left( M_{\text {GT}}^i, M_s^i \right)&= L_{\text {seg}}\left( M_{\text {GT}}^i, M_s^i \right) , \quad i = 1, 2, \dots , 4 \end{aligned}$$

(46)

In the above formula, $M_{GT}^i$ is defined as

$$\begin{aligned} M_{\text {GT}}^i&= {\left\{ \begin{array}{ll} M_{\text {GT}} \downarrow _{2^{i-1}} & \text {if } i \ge 2, \\ M_{\text {GT}} & \text {if } i = 1. \end{array}\right. } \end{aligned}$$

(47)

where ${ \downarrow _{{2^{\mathrm{{i - }}1}}}}$ represents the sub-sample of factor ${2^{\mathrm{{i - }}1}}$. In addition, ${L_{seg}}$ is also applied to the output of the shallow decoding process, so the loss of the shallow decoding path can be defined as

$$\begin{aligned} L_c(M_{\text {GT}}, M_c)&= L_{\text {seg}}(M_{\text {GT}}, M_c) \end{aligned}$$

(48)

Finally, the overall loss function during the training of this network can be defined as

$$\begin{aligned} L_{\text {total}}&= L_c + \sum _{i=1}^4 L_s^i \end{aligned}$$

(49)

Experiments

Experimental details and dataset

All models were based on the Pytorch framework and python 3.8, and all experiments were performed on a deep learning workstation equipped with an Intel(R) Core i7-13900K. In addition, it has 32 GB of DDR5 RAM and an NVIDIA GeForce RTX 4090 graphics processing unit (GPU) with 11 GB of RAM. Furthermore, the hyperparameters are set to the same for all models, Initial learning rate is 0.0003, Batch size is 16, Epoch is 200, Optimizer is Adam, Growth rate is 0.001.

The LiTS dataset is a public dataset from the Liver Tumor Segmentation Challenge held by ISBI 2017 and MICCAI 2017 and is currently the most commonly used dataset in liver and tumor segmentation research. The LiTS dataset consists of a training set of 131 CT scans. The number of CT sections contained in each scan ranged from 42 to 1026. the section spacing was 0.45 mm to 6.0 mm. Spacing was 0.45 mm to 6.0 mm. We constructed a training set and a validation set using 90 patients (43,219 axial sections) and 10 patients (1500 axial sections), respectively. The remaining 30 patients (15,419 axial sections) were then included as the trial set.

3DIRCADb is a small dataset containing 22 3D data, in which the image size is 512$\times$512, slice thickness is 1–4 mm, pixel spacing is 0.56–0.86 mm, and slice number is 184–260. It was divided into 17 patients for training and 10 patients for testing.

To enhance the contrast between liver, tumor, and other tissues, the Hounsfield Unit (HU) value of CT images is set to [− 200, 250]. Next, noise equalizes each pixel in CT image according to the gray distribution of adjacent pixels, which further improves the visual quality and diagnostic accuracy of windowed medical images. Additionally, we employed random horizontal flips, random vertical flips, and random scale rotation shifts as data augmentation methods.

Evaluation metrics

To quantitatively analyze the segmentation results, we used five evaluation indicators. including Dice coefficient (DIC), Intersection over Union (IOU),Recall, relative volume difference (RVD), average symmetric surface distance (ASSD), maximum symmetric surface distance (MSD). Let ${\mathrm{{R}}_{\mathrm{{gt}}}}$ and ${\mathrm{{R}}_{\mathrm{{seg}}}}$ be the ground truth and predicted segmentation result. The mathematical formula for these indicators is as follows:

$$\begin{aligned} \text {DIC}&= \frac{2 \left( R_{\text {gt}} \cap R_{\text {seg}} \right) }{R_{\text {gt}} + R_{\text {seg}}} \end{aligned}$$

(50)

$$\begin{aligned} \text {IOU}&= \frac{\left| R_{\text {seg}} \cap R_{\text {gt}} \right| }{\left| R_{\text {seg}} \cup R_{\text {gt}} \right| } \end{aligned}$$

(51)

$$\begin{aligned} \text {Recall}&= \frac{\left| R_{\text {seg}} \cap R_{\text {gt}} \right| }{\left| R_{\text {gt}} \right| }\end{aligned}$$

(52)

$$\begin{aligned} \text {RAVD}&= \frac{R_{\text {seg}}}{R_{\text {gt}}} - 1\end{aligned}$$

(53)

$$\begin{aligned} \text {ASSD}&= \frac{1}{\left| R_{\text {seg}} \right| + \left| R_{\text {gt}} \right| } \left( \sum _{a \in R_{\text {seg}}} \mathop {\min }\limits _{b \in R_{\text {gt}}} d(a, b) + \sum _{b \in R_{\text {gt}}} \mathop {\min }\limits _{a \in R_{\text {seg}}} d(a, b) \right) \end{aligned}$$

(54)

$$\begin{aligned} \text {MSD}&= \left( \mathop {\max }\limits _{i \in R_{\text {seg}}} \left( \mathop {\min }\limits _{j \in R_{\text {gt}}} d(i, j) \right) , \mathop {\max }\limits _{i \in R_{\text {gt}}} \left( \mathop {\min }\limits _{j \in R_{\text {seg}}} d(i, j) \right) \right) \end{aligned}$$

(55)

Experimental results

In order to prove the superiority of HyborNet proposed in this paper, we discuss the segmentation results of HyborNet with state-of-the-art (SOTA) models. These state-of-the-art models can be grouped into two categories, CNN-based methods and CNN-Transformer based methods, where CNN-based methods contain DeepLabv3+⁴³, U-Net⁴⁴, Attention U-Net⁴⁵, ResU-Net⁴⁶, U-Net++⁴⁷, Double UNet⁴⁸. CNN-Transformer based methods containing nnformer⁴⁹, Swim-UNet¹³, TransUNet⁵⁰, Hiformer⁵¹.

In order to analyse the comparison quantitatively, in the first experiment, HyborNet and the state-of-the-art model are run separately on the LiTS dataset for quantitative analysis. The evaluation metrics of the experimental results include DIC, IOU,recall, RAVD, ASSD and MSD, as shown in Table 1. As can be seen from this table, HyborNet outperforms the state-of-the-art methods such as HiFormer, TransUNet, Swin- UNet ,nnformer and Double UNet in almost all metrics. In particular, our method achieves 92.5% and 91.34% for DIC and IOU in segmented liver, which is 0.93% and 0.47 better than HiFormer, which ranks second in most metrics.

In the tumour segmentation task, our method obtains 55.51% in terms of DIC and 42.16% in terms of IOU, which is 0.08% and 1.52% better than HiFormer. In terms of functionality, the CNN-based method has a similar purpose to our GCA, which is to extract local semantic information, and the segmentation is more refined. Meanwhile, the Transformer-based approach shares the same function with our two-branch interaction mechanism, both aiming to expand the sensory field of the extended network and extract rich global features. A visual comparison of the segmentation results is shown in Fig. 4, and it is clear that the qualitative results of our liver and tumour segmentation also achieve the performance of SOTA. Compared to other methods, HyborNet can identify liver and tumour regions well and accurately, segment the edge regions of the liver accurately, and distinguish well tumours with blurred image edges, especially those in small and medium-sized regions of the liver, as well as tumours with similar colours and structures to liver tissues, which are often missed in liver CT readings. Overall, the predicted masks generated by HyborNet have almost the same boundary and shape as the real labels.

In addition, compared to the base model, we can see that two variants of U-Net, including Double UNet and Swim-UNet, achieve an improvement in DIC of 0.02% and 0.03%, respectively, over U-Net, demonstrating the positive impact of a well-designed architecture. In fact, some CNN-based models, such as U-Net++ and Double U-Net, achieve better performance than some transformer-based models, such as Swim-UNet. This phenomenon suggests that both CNNs and transformers can extract intrinsic features in the dataset to some extent. This also supports our idea of improving model performance by combining the two branches. Specifically, HyborNet has a DIC of 95.82%, IOU of 91.34%, recall of 93.14%, RAVD of 0.005, ASSD of 1.82 and MSD of 8.18 for liver segmentation on the LiTS dataset. The DIC of 55.59%, IOU of 42.16%, recall of 49.24%, RAVD of 1.26, ASSD of 9.01 and MSD of 30.89 are the best results for tumour segmentation. The MSD of 30.89 is superior to previous state-of-the-art competitors.

Table 1 Comparison results of the HyborNet method with current popular methods on the LiTS dataset.

Figure 4

Example of liver and tumor segmentation visualization on the LiTS dataset.

To further evaluate the excellent segmentation performance, generalizability and robustness of HyborNet proposed in this paper, we continue our experiments on 3DIRCADb. Table 2 shows the advanced state-of-the-art model and the segmentation results of HyborNet. Again, the measurements are performed by DIC, IOU, recall, RAVD, ASSD and MSD. As can be seen from the table, our HyborNet outperforms the state-of-the-art CNN and Transformer-based methods in almost all evaluation metrics in both liver and tumor segmentation tasks. Specifically, HyborNet has a DIC of 96.86% and an IOU of 91.97 in the segmented liver task, which is an improvement of 0.91% in DIC and 0.15% in IOU compared to the second ranked hi former. In addition, other metrics were also top-ranked. In the tumor segmentation task, HyborNet has a DIC of 59.85% and an IOU of 44.27%, which is an improvement of 0.3% in DIC and 0.24% in IOU over the second most advanced model. These data also show that the combination of local convolutional operations and remote attention dependency is positive for liver and tumor segmentation. HyborNet has excellent segmentation capabilities and can accurately segment liver and tumor regions in abdominal CT.

Table 2 Comparison results of the HyborNet method with current popular methods in the 3DIRCADb dataset.

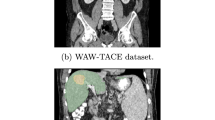
In addition, we also show a visual comparison of the segmentation results for HyborNet and other models in Fig. 5. The first and second columns represent the original abdominal CT sections and the real labels, respectively. The qualitative segmentation results of the proposed HyborNet network and the comparison network are shown below. It can be clearly seen that the predicted masks generated by HyborNet are very similar to the boundaries and shapes of the real labelled values. The segmentation results of HyborNet segment the edges more finely than those of the CNN and Transformer-based methods, and there is no recognition of the background as a target region. This is due to the Gabor Attention Convolution proposed in this paper to extract detailed texture information, as well as the Dual Coding branch to extract rich local and global feature information.

Figure 5

Example of liver and tumor segmentation visualization on the 3DIRCADb dataset.

In order to demonstrate more intuitively that the HyborNet proposed in this paper has superior ability to learn features, we show the segmentation effect with 3D confusion matrices of two datasets. The diagonal histogram shows the corresponding category of each pixel point, the percentage of correct classification, and the others are the percentage of misclassification. From the Fig. 7, it is easy to see that the HyborNet segmentation can well segment the liver and tumour in liver CT. This is benefited from the dual-branch deconstruction proposed in this paper, where the local branch extracts the rich detail information in liver CT well, corresponds to the pixel points of each category, and classifies them correctly as far as possible; and the global-dependent branch extracts the global features, grasps the global categories, and avoids the background misclassification as liver and tumour. Meanwhile, dual-branch interactive module fully integrates local features and context-dependent features to avoid ambiguity of semantic features and improve segmentation accuracy.

Figure 6

Visualisation of proposed ablation results on the LiTS dataset.

Figure 7

Confusion matrix visualization.

Ablation studies

Table 3 Results of the ablation study of the proposed method on the LiTS dataset.

In this section, we have designed a comprehensive ablation study to evaluate the effectiveness of each component in the HyborNet network. The proposed HyborNet network consists of two branch encoders. Therefore, we first designed different combinations of encoders and decoders and conducted experiments on the LiTS dataset. Furthermore, in the ablation study, each comparison model is run in the same data augmentation and computational environment for a fair comparison. We used the U-Net model as the baseline model to incrementally add modules. The experimental results are shown in Table 3, where, for simplicity, U is the benchmark U-Net model, G is the proposed Gabor attention convolution, T is the coding path of the transference, D is the two-branch interactive module proposed in this paper, L denotes the deep loss monitoring mechanism, DG stands for the HyborNet proposed in this paper, and - stands for deletion.

To analyze the effectiveness of GCA, we replace the standard convolution in U-Net with GAC. From the comparison of the experimental data results of U and U+G in Table 3, it can be seen that the performance of U-Net on the LiTS dataset is significantly worse than U+G. In liver segmentation, the DIC and IOU of U+G are increased by 0.05% and 0.04%, respectively, and in tumor segmentation, the IOU is increased by 0.24%. In addition, from Fig. 6, the segmentation of U+G for edges is more refined and the texture is clearer.

In order to analyze the impact of the two-branch Transformer, we improve the single encoder of U-Net into a two-branch encoder, one branch uses GAC, the other branch uses Transformer, and the element-wise addition is performed directly at the end of the encoding stage. In addition, the GAC branch is skip connected with the decoder. From the experimental data results of U+G and U+G+T in Table 3, we can see that U+G+T has significantly higher performance than U+G in both liver segmentation task and tumor segmentation task. In addition, it can be clearly seen from the figure that U+G is easy to mispredict the liver in the normal area as the tumor area, and it is also easy to miss the recognition of the tumor.

In order to analyze the effectiveness of the deep loss monitoring mechanism, the deep loss monitoring mechanism in HyborNet is removed in this paper, and only the real value of the segmentation result is used for the loss function calculation. The experimental results are shown in DG-L and DG in Table 3. DG is superior to DG-L in both liver segmentation and tumor segmentation. Meanwhile, from Fig. 6, it can also be seen that the visualization of the segmentation results of DG is slightly better than that of DG-L. This also verifies that the deep loss monitoring mechanism has a guiding effect on the segmentation results

In addition, the above models built to verify the effectiveness of Dual-branch interactive module and deep loss monitoring mechanism, respectively, happen to be able to demonstrate the impact of skip connection between decoder and encoder of the proposed model. From the results of U+G+T+D and DG-L in Table 3, it can be seen that the results of DG-L are better than U+G+T+D, which also shows that the skip connection of HyborNet makes the feature vectors in the decoding stage have high-resolution texture and depth edge information, and improves the accuracy of segmentation.

Complexity calculation

Model computational complexity is an important aspect in evaluating the performance of a model, Moreover, computational complexity also affects the effectiveness of the model in real clinical diagnosis. We also conducted experiments on LiTS to quantify the computational complexity using the well-known floating-point operations (GFLOPs), inference speed, and number of parameters, and the specific experimental results are shown in Table 5. From the table, it can be seen that the excellent segmentation results achieved by the HyborNet model are realized at the expense of the efficiency of the model. The need for a large number of parameters for the model is one of the main drawbacks of HyborNet, which is mainly due to the existence of two branching coding paths for the network. Specifically, HyborNet outperforms DeepLabv3+ and TransUNet in terms of number of parameters, Flops, and inference time, but not HiFormer, which has the second highest segmentation accuracy.In terms of parameters, the improvement of HyborNet compared to the other models is significant, with a substantial increase in segmentation accuracy, and the model’s parameters are fewer or equivalent, and the inference speed is improved. Overall, our future research will focus on developing lighter, faster segmentation networks while ensuring similar performance. In addition, in the feature fusion stage, the two-branch prioritization and feature alignment during fusion deserves more effort, which has great potential for both performance improvement and model compression.

Table 4 Comparison of computational complexity.

Discussion

With the development of medical imaging devices and deep learning algorithms, more and more neural networks have been proposed for automated analysis of various cancers in various imaging modes. The automatic segmentation of liver and tumor is of great significance in liver disease diagnosis, treatment planning, surgical planning, liver cancer treatment and tumor treatment planning. The liver has complex structural and pathological features, and its shape and structure are highly dependent on the surrounding abdominal organs. In addition, most of the existing liver tumor segmentation methods are unable to comprehensively extract the local and global context features of liver CT, and the segmentation results still appear unclear edge segmentation and wrong segmentation of lesion areas. Automatic liver segmentation has become a challenging task for researchers.

In this work, different from the traditional deep learning methods based solely on CNN and Transformer, we combine the ability of CNN to extract local features with the ability of Transformer to extract global information, and innovatively propose HyborNet on the basis of existing research. In addition, GCA is based on Gabor filter, which can refine the edge information features, make the boundary of target and lesion area clearer, and make the segmentation more accurate. We have conducted extensive validation studies on LiTS17 and 3DIRCADb datasets to evaluate the performance of our method, and the qualitative and quantitative experimental results show that the proposed method not only outperforms the current popular methods in accuracy, but also has strong robustness compared with the current popular methods. The main reasons that the designed HyborNet model is superior to other methods are as follows: (1) CNN branches aggregate multi-scale feature information to remove noise that is not affected by the target region. It not only pays attention to the distinguishing features of channels and spatial dimensions, but also establishes multidimensional interaction between channels and spatial dimensions, while refining texture information and precise boundary segmentation. (2) Establish an interactive fusion mechanism between CNN and Transformer, effectively coupling the feature information between the two, and interactive information transmission in a dynamic and learnable way.

In this paper, target regions are segmented in LiTS17 dataset and 3DIRCADb respectively. Judging from the qualitative and quantitative results of the two visual tasks, the method in this paper is superior to the current popular methods, and the segmentation results are indeed of clinical value. From the above experimental results, it can be seen that in the segmentation experiment on LiTS17, our method not only achieves excellent results in the evaluation of indicator data, but also outperforms the current popular methods in the visualization of segmentation results. At the same time, the experiments conducted on the 3DIRCADb dataset also achieved better results than the current popular methods, which also proved the robustness of the proposed method from the side. Doctors can accurately locate the lesion area according to the size and shape of the partitioned liver and tumor, and judge the benign and malignant tumors.

Although HyborNet performs well in the segmentation task of liver and tumor, the network only performs the segmentation of liver and tumor on two-dimensional abdominal CT sections, and has not utilized the 3-dimensional Z-axis information, and the segmentation task is single. Second, the approach includes a large number of component models, including a full Transformer branch, Gabor attention convolution-based branches, and Dual-branch interactive modules. A parallel dual-branch CNN-Transformer joint mechanism is established to achieve accurate segmentation of lesions from both boundary and regional perspectives. However, it is worth investigating whether these component models can still effectively achieve the design goals and whether they can still achieve the same performance for more complex background environments (such as the target area being submerged in water). In addition, complex component models may lead to excessive number of model parameters and long calculation time. Therefore, the direction of our future work is, first of all, to explore lightweight network architecture, adjust network parameters to balance model complexity and recognition accuracy, and effectively improve network performance. Secondly, the deep learning method of multi-modal medical image segmentation is explored, and different medical images are applied to image segmentation and recognition tasks, so as to classify diseases and segment diseased areas to assist the diagnosis of clinical diseases.

Conclusion

In this paper, we propose HyborNet, which is capable of simultaneously extracting rich local feature information and remote dependency information to perform liver and tumor segmentation in abdominal CT. The proposed network can be trained in an end-to-end manner while achieving better segmentation and classification results. The core idea of the method integrates the CNN and Transformer architectures into a unified architecture with the proposed local feature extraction branch and remote dependency branch. The local feature extraction branch consists of Gabor attention convolution, which is able to extract fine-grained local detail information of liver and tumor. The remote dependency branch is based on Transformer composition, which is capable of modelling remote contextual information between regions. Meanwhile, we propose a dual-branch interactive module to fully integrate local features and context-dependent features to improve the segmentation accuracy of multi-category target regions. In addition, we use a deep loss supervision mechanism to optimize the segmentation results. Finally, we compare HyborNet with other state-of-the-art methods on our public datasets LiTS and 3DIRCADb, and demonstrate that the method proposed in this work achieves good results in liver and tumor segmentation.