Dual-branch image projection network for geographic atrophy segmentation in retinal OCT images

Abstract

Existing geographic atrophy (GA) segmentation tasks can only use 3D data, ignoring the fact that a large number of B-scan images contain lesion information. In this work, we proposed a multistage dual-branch image projection network (DIPN) to learn feature information in B-scan images to assist GA segmentation. Considering that segmenting 3D data slices using a 2D network architecture ignores the neighboring information between volume data slices, we introduced ConvLSTM. In addition, to make the network focus on the attention in the projection direction to capture the contextual relationships, we proposed the projection attention module. Meanwhile, considering that the current projection network uses a unidirectional pooling operation to achieve feature projection, multi-scale features and channel information are ignored in the projection process. Therefore, we proposed an adaptive pooling module that aims to adaptively reduce feature dimensions when grasping multi-scale features and channel information. Finally, to mitigate the effect of image contrast on the network segmentation performance, we proposed a contrastive learning enhancement module (CLE). To validate the effectiveness of our proposed method, we conducted experiments on two different datasets. The segmentation results show that our method is more effective than other methods in the GA segmentation task and the foveal avascular zone (FAZ) segmentation task.

Introduction

Geographic Atrophy (GA) is an advanced progressive lesion of non-exudative age-related macular degeneration, also referred to as complete retinal pigment epithelium and outer retinal atrophy¹. It is estimated that approximately five million people worldwide suffer from GA, with its prevalence increasing exponentially with age². GA is typically bilateral³, and the development and enlargement of the lesions result in irreversible loss of visual function. Therefore, accurate segmentation of the lesion area is of paramount importance for preventing progression and guiding subsequent treatment⁴. Optical coherence tomography (OCT) is a non-invasive and rapid biomedical imaging technology⁵. It can image biological tissues at the micron level and generate high-resolution three-dimensional cross-sectional images, which are widely used in clinical ophthalmology quantitative analysis^6,7. Its high-resolution feature enables clear observation of various retinal diseases⁸, such as macular degeneration and macular holes⁹, pigment epithelial detachment¹⁰, choroidal neovascularization¹¹ and GA¹. OCT plays a vital role in the diagnosis and monitoring of retinal diseases^{12,13,14,15,16}. Figure 1 demonstrates OCT projection and B-scan with GA lesions and the corresponding B-scan GT.

Fig. 1

Example of retinal OCT GA. (a) GA lesion in projection image, (b) GA lesion in B-scan, (c) GT corresponding to the lesion in (b).

Previous work has made great efforts in exploring traditional methods for GA segmentation, including geometric active contours¹⁷, level set methods¹⁸. Niu et al.¹⁹ proposed a Chan-Vese model method based on local similarity factors for reducing computational effort. However, which cannot fully explore the advanced features and semantic information in the image and limits the segmentation performance. Most of the recent GA segmentation methods are deep learning networks^20,21,22. Wu et al.²⁰ proposed a method to creates OCT projection images by applying constrained sub-volume projection to 3D OCT data. Patil et al.²¹ used U-Net to automatically segment geographical atrophic lesions. Spaide et al.²² used two multimodal deep learning networks (U-Net and Y-Net) to automatically segment GA lesions on FAF. However, all of the above methods utilize only the features of the Enface image and ignore the spatial information in the volumetric data. To alleviate this problem, our methods used a 2D network framework while incorporating ConvLSTM to capture the neighboring information between slices of volumetric data. In addition, these methods may suffer from the problem of possible mis-segmentation when segmenting GA edges (low contrast of edge pixels), and it is difficult for the network to classify such hard samples. To alleviate this problem, we proposed a contrastive learning enhancement module (CLE) and select an appropriate sampling strategy to improve the classification ability of the network for difficult samples.

Compared with projection images, OCT volume data can provide detailed information on retinal structure. Li et al.²³ proposed an image projection network (IPN) to achieve three-dimensional to two-dimensional retinal Foveal Avascular Zone(FAZ) segmentation through unidirectional pooling along the volume projection direction. In addition, the IPN V2²⁴ was also proposed to enhance horizontal direction perception capabilities. Morano et al.²⁵ proposed a convolutional neural network (CNN) and self-supervised learning (SSL) method for 3D to 2D segmentation. However, the above methods are only suitable for certain lesion segmentation, ignoring the fact that clinics generally use single line scans and radial scans for B-scan data, which results in little 3D data. In the GA segmentation task, if the network relies only on a small amount of volume data, it may lead poor generalization ability. Meanwhile, they used unidirectional pooling to project the image, ignoring multi-scale features and channel information, and the network is unable to capture spatial relationships at different scales, limiting the ability of the model to understand the overall structure of the image. To address the above issues, we proposed a novel two-stage image projection segmentation method. While using volumetric data, we used a large number of B-scan images for pre-training in the first stage, which alleviates the problems of overfitting and poor generalization ability caused by the over-reliance of the network on a small amount of data. To address the limitation of the 2D network framework in overlooking neighboring information between slices of volumetric data, we introduced ConvLSTM in the second stage. This inclusion ensures that spatial information within the volumetric data is effectively leveraged during the segmentation process. At the meantime, we proposed Adaptive Pooling Module (APM) for capturing multi-scale features and channel information while adaptively reducing the feature dimensions. Furthermore, to enhance the network’s focus on features along the projection direction during the dimensionality reduction process, we proposed a Projection Attention Module (PAM) that calculates the affinity between pixels in the projection direction, thereby establishing long-range dependencies.

Specifically, we proposed a multi-stage Dual-branch Image Projection Network that can obtain pre-training weights using many B-scan images during the pre-training stage. In addition, inspired by Liu et al.²⁶, we propose a Projective Attention Module (PAM) to integrate long-range dependencies by calculating the affinity between two different pixels on each projection column in the B-scan. An Adaptive Pooling Module (APM) is also proposed, which focuses on the channels while extracting and fusing multi-scale features, thus effectively improving the feature utilization. Finally, to ensure that the spatial information in the volumetric data is fully utilized during the segmentation process, we incorporated ConvLSTM to capture the neighborhood information between images in the fine-tuning stage. Utilizing a contrastive learning module to enhance the network’s ability to distinguish boundary features.

Methods

Framework of the proposed method

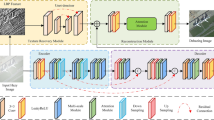
Figure 2 demonstrates the segmentation of retinal GA by our proposed DIPN network through three stages: pre-training, fine-tuning and inference. We have defined the retinal GA segmentation task. In the pre-training phase, training is conducted using the data set ${D}_{train}^{1}={\left\{\left({X}_{n}^{1},{S}_{n}^{1}\right)\right\}}_{n=1}^{N}$, where ${S}_{n}^{1}$ is the corresponding label. The sizes of ${X}_{n}^{1}\in {R}^{C\times H\times W}$ and ${S}_{n}^{1}\in {\left\{\text{0,1}\right\}}^{1\times 1\times W}$ are different, because our method involves dimensionality reduction along the projection direction, finally obtains a line segment. In the fine-tuning phase, the training dataset ${D}_{train}^{2}={\left\{\left({X}_{n}^{2},{S}_{n}^{2}\right)\right\}}_{n=1}^{N}$, where ${X}_{n}^{2}\in {R}^{C\times L\times H\times W}$ denotes the set of 3D images, and ${S}_{n}^{2}\in {\left\{\text{0,1}\right\}}^{1\times L\times 1\times W}$ is the labels corresponding to ${X}_{n}^{2}$. We use the test dataset ${D}_{test}={\{\{{X}_{m},{S}_{m}\}\}}_{m=1}^{N}$(${X}_{m}\in {R}^{C\times L\times H\times W},{S}_{m}\in {\left\{\text{0,1}\right\}}^{1\times L\times 1\times W}$) for testing.

Fig. 2

Flowchart of our proposed method. The data used at different stages are shown in the figure. The first stage uses a single B-scan image for pre-training to enable the network to learn the feature representation. The second stage uses the complete volume data for training to enable the network to fully learn and utilize the proximity information between slices. Finally, testing is performed.

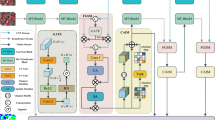
The pre-training stage model is shown in Fig. 3. It consists of an image projection branch (IPB) and a feature complementary branch (FCB), each containing five stages. Each stage is connected to each other and the feature complementary branch passes the extracted feature ${f}_{i}^{APM}(i\in \text{1,2},\text{3,4},5)$ of each stage to the feature projection branch. It is connected to the stage feature ${f}_{i}^{IPB}(i\in \text{1,2},\text{3,4},5)$. The two branch features ${f}^{FB}$ and ${f}^{SB}$ are concatenated and then the contrast loss ${L}^{CLE}$ and the segmentation loss ${L}^{SEG}$ are computed by the projection and segmentation headers.

Fig. 3

Pre-training network architecture. The first branch is the image projection branch (IPB), which incorporates the Projection Attention Module (PAM) that focuses on attention in the projection direction when reducing dimensions. The second branch is our proposed Feature Complement Branch (FCB), which contains the proposed Adaptive Pooling Module (APM) to ensure feature retention and feature fusion during the projection process. When using multiple convolutions for a feature, we use the residual structure.

Projective attention module (PAM)

For retinal OCT B-scan images containing GA lesions, the lesions are usually located near the RPE and exhibit significant translucency (as shown in Fig. 1b), so many previous GA segmentation methods use projection maps or 3D volume data segmentation rather than 2D network segmentation slices. In addition, we observe that the degree of pixel contribution varies from region to region when determining pixel labels in a deep learning-based approach. Therefore, it is crucial to distinguish these feature representations. In order to build rich contextual relationships on local features, we proposed the PAM inspired^26,27,28. The PAM encodes broader contextual information into local features, thus enhancing the representation of local features. Next, we describe in detail how the PAM works.

As shown in Fig. 4 PAM, our proposed PAM is capable of processing features of different scales at different stages. ⨂ denotes the batch matrix multiplication with batch size W. For easy understanding, we take the first PAM in the image projection branch as an example. Given a feature ${\mathbb{R}}^{64\times H\times W}$, we first feed it into a convolutional layer to obtain a new feature $F\in {\mathbb{R}}^{64\times H\times W}$. Then, we feed the feature F into a 1 × 1 convolutional layer to obtain two new feature mappings Q and K, where $\{Q,K\}\in {\mathbb{R}}^{32\times H\times W}$, and arrange them as ${\mathbb{R}}^{W\times H\times 32}$, ${\mathbb{R}}^{W\times 32\times H}$. Then reshape them as ${\mathbb{R}}^{W\times (H\times 32)}$, ${\mathbb{R}}^{W\times (32\times H)}$. We then perform matrix multiplication on Q and K and apply a Sigmoid to compute the space-attentive mapping $Atts\in {\mathbb{R}}^{W\times H\times H}$.

$$\begin{array}{c}{Atts}_{kij}=1-\frac{\text{exp}\left(-{\Sigma }_{c=1}^{32}{Q}_{kic}\cdot {K}_{kcj}\right)}{1 +\text{exp}\left(-{\Sigma }_{c=1}^{32}{Q}_{kic}\cdot {K}_{kcj}\right)}\end{array}$$

(1)

where $\{k,i,j,c|1\le k\le W,1\le i,j\le H,1\le c\le 32\}$, ${Atts}_{kij}$ denotes the influence of position $i$ on position $j$. The closer the feature representations of two positions are, the greater is their correlation. ${Q}_{kic}$ denotes the $i$-th pixel on the $k$-th column in the $c$-th feature map. $\cdot$ represents the element multiplication. At the meantime, we input the feature $F$ into the convolutional layer to generate a new feature mapping $V\in {\mathbb{R}}^{32\times H\times W}$ and reshape it into ${\mathbb{R}}^{W\times (H\times 32)}$. We then perform a matrix multiplication between $V$ and $Atts$ and arrange the result as ${\mathbb{R}}^{W\times H\times 32}$. The result is then fed into the convolutional layer to recover the number of channels, and the result is arranged as ${\mathbb{R}}^{64\times H\times W}$. Finally, we perform an element-wise summation operation between it and the feature $F$ to obtain the final output $E\in {\mathbb{R}}^{64\times H\times W}$ as follows.

$$\begin{array}{c}E=pReLU\left(Conv\left(Perm\left(Atts\otimes V\right)\right)+F\right)\end{array}$$

(2)

where $pReLU$ represents the activation function, $Conv$ and $Perm$ represent 1 × 1 convolution and permutation operations respectively, and $\otimes$ represents matrix multiplication. $F$ represents the input feature. From Eq. (2), it can be inferred that the obtained feature E for each location is a weighted sum of the features of all locations and the original feature. Thus, it has a global context view and selectively aggregates contexts based on spatial attention. Similar semantic features gain from each other, thus improving intra-class compactness and semantic consistency.

Fig. 4

Key components in the framework. Projection Attention Module (PAM) is to make the network focus on the attention in the projection direction to model the dependencies in the projection direction. Adaptive Pooling Module (APM) aims to grasp multi-scale features and channel information while adaptively reducing the feature dimensions. Contrast Learning Enhancement Module (CLE) aims to improve feature differentiation between lesions and their contexts.

Adaptive Pooling Module (APM)

Because GA lesions are translucent, the upper and lower boundaries of the lesion cannot be accurately defined in OCT B-scan images, thus most current GA segmentation methods use Enface image and 3D volume data instead of volume slices. However, segmentation using enface image ignores a large amount of spatial information and also requires a large amount of volume data. Whereas in image projection networks, the feature dimension decreases with increasing depth and a large number of important features may be lost in the dimensionality reduction process. The loss of these important information may cause the model to be unable to effectively capture the subtle features in the image, thus reducing the segmentation performance. Therefor it is very important to effectively reduce feature dimensions and retain important information to the greatest extent. Therefore, we propose the Adaptive Pooling Module (APM) to achieve the above purpose, and the APM structure is shown in Fig. 4. APM performs dimensionality reduction on the features in the feature complementation branch and inputs these features into the image projection branch to complement the features that were lost during the dimensionality reduction process. As shown in Fig. 4, input feature $I\in {\mathbb{R}}^{C\times H\times W}$ to APM and then output feature $O\in {\mathbb{R}}^{C\times P\times W}$. $P$ is the output feature height (the P of the first APM is 256). First, in order to extract multiscale features, we split the input feature $I$ into two parts (in the channel dimension). Splitting the input data into two groups on the channel and processing it through different branching paths. Specifically, each branch is characterized by ${I}_{i}\in {\mathbb{R}}^{\frac{C}{2}\times H\times W}$, $i=1,2$. $C1$ and $C2$ denote 3 × 3 size convolution and 5 × 5 size convolution, respectively. Then, to obtain the multiscale feature map, the multiscale features obtained from the two branches are concatenated in the channel dimension to obtain the whole multiscale feature map M. The process is shown in the following equation.

$$\begin{array}{c}M= Concat\left({C}_{1}\left({I}_{1}\right),{C}_{2}\left({I}_{2}\right)\right)\end{array}$$

(3)

where $M\in {\mathbb{R}}^{C\times H\times W}$, M contains rich deep semantic information. In order to focus on spatial information while also focusing on information between channels. Channel descriptions are obtained using global average pooling in the spatial information of the multiscale feature M. Then, the channel correlation terms are captured by convolution. The correlations between features are captured by these operations. The channel attention $S$ is defined as follows.

$$\begin{array}{c}S= \sigma \left({Conv}_{2}\left(\delta \left({Conv}_{1}\left(AvgPool\left(M\right)\right)\right)\right)\right)\end{array}$$

(4)

where $S\in {\mathbb{R}}^{C\times 1\times 1}$, $\sigma$ represent the sigmoid function, δ represents the ReLU function, and ${Conv}_{1}$ and ${Conv}_{2}$ represent the 1 × 1 convolution. To facilitate the later feature fusion, we reconstruct the multiscale feature $M$ as ${M}{\prime}\in {\mathbb{R}}^{C\times (H/P)\times W}$. In addition, some features may be lost during the extraction of multi-scale features, thus, a reconstruction operation is performed on the input $I$ to obtain ${I}{\prime}\in {\mathbb{R}}^{C\times (H/P)\times W}$. ${I}{\prime}$ is then reweighted and summed along the projection direction of the features to achieve feature fusion. The final output of the APM can be written in the following form.

$$\begin{array}{c}O= Concat(U\left({I}{\prime}\cdot \left(Softmax\left({M}{\prime}\right)\odot Softmax\left(S\right)\right)\right))\end{array}$$

(5)

where $Softmax$ is used to obtain attentional weights in the projection direction and channel dimension. $\odot$ denotes broadcast element-by-element multiplication and $\cdot$ represents element-by-element multiplication. $U$ denotes unidirectional pooling of size $H/P$, and then concatenates P features of size $C\times 1\times W$ along the projection direction. The O obtained through the above steps fuses multi-scale information and channel information, which alleviates the information loss caused by simple unidirectional pooling to some extent. The feature representation thus obtained is richer and more comprehensive and can better reflect the complex structure and semantic information of the input data.

Contrastive learning enhancement (CLE)

We can see in Fig. 1b that the contrast between the GA and the noise and between the borders on both sides of the GA is low. When dealing with regions that are similar to GA features, with insufficiently distinctive features, the network may have difficulty in distinguishing these regions leading to incorrect segmentation. To increase the differentiation of features between GA and its context, we proposed a contrastive learning strategy²⁹.

The CLE module is shown in Fig. 4. We use the projection head for contrast learning after concatenating two branching features. The final output feature of the network is ${f}^{out}\in {\mathbb{R}}^{C\times 12\times W}$($C=32$) . To calculate the contrast loss, the projection head maps each pixel in the feature map to 128 dimensions. The contrast learning head consists of a multi-layer perceptron with two 1 × 1 convolutional layers. In supervised contrast learning, computing contrast loss on a single image would lack category diversity, this is because our OCT images contain only one category. To solve this problem, inspired by^30,31, we propose a pathology samples library, consisting of two parts: one pixel library and one region library. We maintain a queue for every class in the pixel library. We select $V=24$ pixels (random) from each category in each image based on GT labels, these pixels are then arranged into a queue of size $Q=V\times N$ ($N$: Number of images in a batch). This produces a library of samples of size $2\times Q\times D$ (2 is the number of categories, $D$ is a 128-dimensional feature embedding). We also incorporate a region library to trap global semantic information. During training, we calculate the mean and combine it with the pixel embedding of the categories in the image, to obtain a D-dimensional global feature vector. The size of the region library is $2\times N\times D$. Therefore, our sample library size is $2\times (Q+N)\times D$. Note that the pathology sample library only takes effect during the training process.

After establishing the pathology sample library, we need to design a sampling strategy to select more reliable anchors $\mathcal{p}$. In previous work³⁰, it was found that when both positive and negative samples are close to the anchor $\mathcal{p}$ (the reference point that defines the relative relationship between positive and negative samples), it is difficult to distinguish negative samples from them, especially negative samples that are similar to the anchor. Similarly, when both positive and negative samples are far from the anchor $\mathcal{p}$, it is difficult to distinguish the positive samples from them. The specific matching probability formula is as follows.

$$\begin{array}{c}{\rho }_{{\mathcal{p}}^{+/-}}=\frac{\text{exp}\left(\mathcal{p}\cdot {\mathcal{p}}^{+/-}/\uptau \right)}{{\Sigma }_{{\mathcal{p}}{\prime}\in {Z}_{\mathcal{p}}\cup {N}_{\mathcal{p}}}\text{exp}\left(\mathcal{p}\cdot {\mathcal{p}}{\prime}/\uptau \right)}\end{array}$$

(6)

where $\mathcal{p}$ denotes an anchor in the sample library, and ${\mathcal{p}}^{+/-}$ represents the positive samples (for a pixel $\mathcal{p}$ with its GT labeling class, the positive sample belongs to other pixels in the same class) similar to the $\mathcal{p}$ category or dissimilar negative samples in the sample library. $\rho \in (\text{0,1})$ is the matching probability. $\uptau (\uptau >0)$ represents the temperature hyperparameter. ${Z}_{\mathcal{p}}$ represents the set of pixel embeddings for positive samples and ${N}_{\mathcal{p}}$ represents the set of pixel embeddings for negative samples. It can be seen from the Eq. (6), the anchor $\mathcal{p}$ obtained from different sampling strategies will affect the discriminative power in the training samples. A reasonable sampling strategy will improve the distinction between positive and negative samples and help train a more accurate model. We designed a mixed sampling strategy in which we sampled a total of 240 anchor pixels (120 per class) in the maintained sample library. During the collection of positive samples, the first 30% of the hardest samples (negative samples that are close to 1 when the multiplication with the anchor point $\mathcal{p}$ is done, and conversely, positive samples that are close to -1 when the multiplication with the anchor point $\mathcal{p}$ is done) are collected. Then 40% of projection boundary points were randomly sampled, and the remaining 30% are randomly collected from the entire sample library. Negative samples are sampled in the same way as positive samples. After the above is done, we calculate the supervised contrast loss.

$$\begin{array}{c}{L}_{\mathcal{p}}^{CLE}=\frac{1}{\left|{Z}_{\mathcal{p}}\right|}{\Sigma }_{{\mathcal{p}}^{+}\in {Z}_{\mathcal{p}}}\\ -\text{log}\frac{\text{exp}\left(\mathcal{p}\cdot {\mathcal{p}}^{+}/\uptau \right)}{\text{exp}\left(\mathcal{p}\cdot {\mathcal{p}}^{+}/\uptau \right)+{\Sigma }_{{\mathcal{p}}^{-}\in {N}_{\mathcal{p}}}\text{exp}\left(\mathcal{p}\cdot {\mathcal{p}}^{-}/\uptau \right)}\end{array}$$

(7)

$$\begin{array}{c}{L}^{CLE}=\frac{1}{N}{\Sigma }_{i=1}^{N}{L}_{i}^{CLE}\end{array}$$

(8)

where N is the number of anchors in the training dataset. ${L}_{\mathcal{p}}^{CLE}$ is the contrastive loss for individual anchors. ${L}^{CLE}$ is the total contrast loss.

ConvLSTM-based fine-tuning stage

In the pre-training stage, the network (e.g., Fig. 2) learns the GA lesion features using a large number of B-scan images. After obtaining the pre-training weights, in order to exploit the large amount of spatial information contained in the volumetric data. we propose the fine-tuning stage.

As shown in Fig. 5, the network structure before the fine-tuning stage ConvLSTM³² is the same as the pre-training network structure. After using the pre-training weights obtained in the pre-training stage, 3D volume data is input for training. Unlike conventional LSTM methods, convolutional LSTM uses the convolution operator * instead of matrix multiplication to preserve the spatial information of long-term sequences. The entire definition is as follows.

$$\begin{array}{c}{i}_{t}=\sigma \left({X}_{t}*{W}_{xi}+{h}_{t-1}*{W}_{hi}+{c}_{t-1}\circ {W}_{ci}+{b}_{i}\right),\end{array}$$

(9)

$$\begin{array}{c}{f}_{t}=\sigma \left({X}_{t}*{W}_{xf}+{h}_{t-1}*{W}_{hf}+{c}_{t-1}\circ {W}_{cf}+{b}_{f}\right),\end{array}$$

(10)

$$\begin{array}{c}{c}_{t}={c}_{t-1}\circ {f}_{t}+{i}_{t}\circ \text{tanh}\left({X}_{t}*{W}_{xc}+{h}_{t-1}*{W}_{hc}+{b}_{c}\right),\end{array}$$

(11)

$$\begin{array}{c}{o}_{t}=\sigma \left({X}_{t}*{W}_{xo}+{h}_{t-1}*{W}_{ho}+{b}_{o}\right),\end{array}$$

(12)

$$\begin{array}{c}{h}_{t}={o}_{t}\circ \text{tanh}\left({c}_{t}\right).\end{array}$$

(13)

where $\sigma$ is the sigmoid function, $*$ denotes the convolution operation, and $\text{tanh}$ is the hyperbolic tangent function. Input gate ${i}_{t}$, forget gate ${f}_{t}$ and output gate ${o}_{t}$ are the three gates that make up the entire network. ${b}_{i}$, ${b}_{f}$, ${b}_{c}$ and ${b}_{o}$ are the bias terms, while ${X}_{t}$, ${c}_{t}$, and ${h}_{t}$ are the input, active, and hidden states at moment $t$. W represents the weight matrix, e.g., ${W}_{hi}$ is responsible for controlling how the input gate gets its value from the hidden state. $\circ$ denotes Hadamard product.

Fig. 5

Flowchart of the fine-tuning phase. Input volumetric data, segmentation of data slices, and utilization of ConvLSTM to grasp the adjacency between slices.

Loss function

Because GA segmentation is a pixel-level binary segmentation task, we use Dice loss ${L}^{Dice}$ and binary cross-entropy loss ${L}^{BCE}$ to guide model training. Our segmentation loss is calculated as follows.

$$\begin{array}{c}{L}^{Dice}=1-\frac{2\left|P*S\right|}{\left|P\right|+\left|S\right|}\end{array}$$

(14)

$$\begin{array}{c}{L}^{BCE}=-{\Sigma }_{1,w}\left(1-S\right)\text{log}\left(1-P\right)+Slog\left(P\right)\end{array}$$

(15)

$$\begin{array}{c}{L}^{SEG}={{\lambda }_{Dice}L}^{Dice}+{{\lambda }_{BCE}L}^{BCE}\end{array}$$

(16)

where ${\lambda }_{Dice}$ is set to 0.5 and ${\lambda }_{BCE}$ is set to 0.5, $P$ and $S$ represent the predicated segmentation results and the corresponding ground truth, and 1 and $w$ represents the coordinates of the pixel on $P$ and $S$. As shown in Eq. (16), Dice loss is used to evaluate the spatial overlap ratio between the ground truth and the predicted GA area. While binary cross-entropy loss is used to optimize the model at the pixel level.

Finally, the total loss of the proposed DIPN is defined as.

$$\begin{array}{c}{L}^{total}={L}^{SEG}+{{\lambda }_{CLE}L}^{CLE}\end{array}$$

(17)

where ${\lambda }_{CLE}$ is set to 1, ${L}^{CLE}$ is defined as the contrastive learning enhanced loss in the inference stage, excluding the L2 norm.

Experimental and results

Data sets and processing

The proposed method is experimented on two datasets. The first dataset was the retinal geographic atrophy dataset (RGA dataset for short) obtained at Wuhan Aier Eye Hospital. It contains 44 OCT volumes and individual 2823 GA B-scan images. Each OCT volume contains 512 B-scans with a resolution of 1024 × 512. All lesions were manually labeled. In our experiments, we used all the individual 2823 GA B-scan images for the pre-training phase and performed fivefold cross-validation on 34 volume data in the fine-tuning stage (among these 5 parts, one part contains 6 volume data, and the remaining four parts contain 7 volume data each.). We resized the individual B-scan images to 512 $\times$ 512. For the volumes in the dataset, we resized them to 512 $\times$ 512 $\times 512$.

To explore the cross-domain generalizability of our method³³, the second data set is the public data set OCTA500^23,24. It is a multimodal dataset containing two different morphology types (OCT and OCTA), with subsets of two different field of view types, namely OCTA_6M (No.10001-10300) and OCTA_3M (No.10301-10500). The OCTA500 dataset includes 3D FAZ segmentation labels and retinal vessel (RV) segmentation labels. In our experiments, we choose to segment the FAZ region and RV in OCTA-500. For the selection of the two modalities, we do the same as previous work³⁴, select the FAZ data and RV data in OCTA_6M to evaluate our method. This dataset contains 300 subjects and has a volume size of 400 × 400 × 640. For the fairness of the experiment, we based on the previous work³⁴, the data set is divided into training set (No.10001-10180), verification set (No.10181-10200), and test set (No.10200-10300). For more details on the OCTA500 dataset, see²⁴. We resized the dataset to a uniform size of 400 $\times$ 512 $\times$ 512. Due to the lack of separate B-scan images, we skipped the pre-training phase and started training from the fine-tuning phase.

Implementation details

The proposed method is implemented in PyTorch framework, and all experiments are conducted on a single NVIDIA 3090 GPU. Each dataset is independently trained and tested on the model. We train the model using the Adam optimizer with an initial learning rate of 1e-5 and momentum parameters of ${\beta }_{1}=0.9$ and ${\beta }_{2}=0.999$. 250 epochs are trained in the pre-training phase with a batch size of 4. The best weights are migrated to the fine-tuning phase, where 100 epochs are trained in the fine-tuning phase. The test set and the training set are independent during the experiments.

Evaluation metrics

In order to evaluate the segmentation performance in different methods. We quantitatively analyze the experimental results using five metrics as in recent methods²³: the Jaccard index (Jac), the Dice similarity coefficient (DSC), the balanced accuracy (BACC), precision (PRE) and the recall (REC), where Jac and DSC are widely used in evaluating segmentation performance^35,36,37. Using accuracy to evaluate the results may lead to overestimation or loss of significance. To evaluate the accuracy when positive and negative samples are not balanced, we use balanced accuracy instead of general accuracy to evaluate the results. The evaluation metric formula is shown below.

$$\begin{array}{c}Jac=\frac{TP}{TP+FN+FP}\end{array}$$

(18)

$$\begin{array}{c}DSC=\frac{2TP}{2TP+FN+FP}\end{array}$$

(19)

$$\begin{array}{c}BACC=\frac{TPR+TNR}{2}\end{array}$$

(20)

$$\begin{array}{c}PRE=\frac{TP}{TP+FP}\end{array}$$

(21)

$$\begin{array}{c}REC=\frac{TP}{TP+FN}\end{array}$$

(22)

where TP is true positive, TN is true negative, FP is false positive and FN is false negative, TPR is true positive rate, and TNR is true negative rate.

Results and analysis

Performance comparison and analysis

In this section, to evaluate the performance of our proposed method for GA segmentation, we compare it with several other best methods on the RGA dataset. In addition, to verify the significance of our method with the method of others. We performed a two-tailed paired t-test on the results of the above networks, which is significant at P < 0.05 (the smaller the p-value the greater the significance).

In Table 1, compared to UNet++, DoubleUNet helps the network to better focus on both global and local information and utilize multi-scale information to improve the model performance. Therefore, it achieves better results. For the geographic atrophy (GA) segmentation task, limited volume data hinders the performance of 3D segmentation, but this can be alleviated by 2D networks by using a large number of B-scan images. However, 2D networks for volumetric data slice segmentation ignore the spatial information in the volumetric data, leading to jagged edges in the final segmentation results. Unlike the above methods, IPN uses a projection learning module that focus on feature extraction in the projection direction rather than downscaling the features each direction. The feature information is preserved to some extent and better results are achieved. We can see that IPN improves the mean Dice and mean PRE by 2.32% and 2.23%. IPN-V2 uses a planar perceptron on top of IPN, the approach of Lachinov et al. and ResensNet introduced projected skip connections. All three approaches aim to make the network utilize more information. Compared to these methods, PAENet proposes a two-path segmentation framework and incorporates an attention mechanism to enhance the focus of model on lesion regions. PAENet improved segmentation performance of the network, with Dice and JAC reaching 83.74% and 76.63%, respectively. Morano et al. proposed a self-supervised method for modal reconstruction, introducing 3D to 2D projection block connections, resulting in a final Dice score of 84.86% (1.12% improvement over PAENet). In contrast, the proposed DIPN exhibits better performance than all compared methods with an average Dice score of 87.03%. It can be seen that with the multistage two-branch model, our method can utilize a large number of individual B-scans to fully learn the lesion features without neglecting the neighboring information between images in the volumetric data. In addition, our module ensures that the sampling process retains more feature information and utilizes multi-scale features. Finally, we also provide a qualitative comparison in Fig. 6. When segmenting slices of volume data under ConvLSTM, the adjacency information between slices is grasped to fully utilize the spatial information in volume data. In addition, the introduced contrast learning enhancement module strengthens the ability of the network to classify hard samples and improves the segmentation performance of the network. In addition, PAM enables the network to model the long-range dependencies between every two pixels in the projection direction, thus enhancing the representation of important features to reduce the loss of more rich feature information during the projection process. Finally, APM enables the network to focus on spatial information and capture inter-channel correlations to reduce feature loss during projection. Through the synergy of these modules, the network obtains a good segmentation performance.

Table 1 Metrics for each comparison method on the RGA dataset (mean $\pm$ standard deviation). Bold indicates the best performance score. (unit: %). $*$ and $\star$ represent the p-value of the paired t-test between each method and our proposed method DIPN ($*$P < 0.05, $\star$P < 0.01).

Fig. 6

Examples of GA segmentation results for the ten methods on the RGA dataset. The red line represents the ground truth; the green line represents the segmentation result. The content in the white box represents the corresponding Dice score for the image.

Experiments on the OCTA-500 dataset

In this section, we will evaluate the segmentation performance of our method on the OCTA-500 dataset. Quantitative analysis is shown in Table 2, where our methods achieve the best performance in FAZ segmentation. It also achieves good performance in the retinal vessel segmentation task.

Table 2 Metrics scores for each comparison method on the OCTA-500 dataset. (mean $\pm$ standard deviation). Bold indicates the best performance score. (unit: %). $*$ and $\star$ represent the p-value of the paired t-test between each method and our proposed method DIPN ($*$: P < 0.05, $\star$: P < 0.01).

With sufficient 3D data, all these methods can achieve better performance. However, as 3D data decreases and B-scan images increase, our network effectively utilizes B-scan data to learn features and improve segmentation performance. Results from paired t-tests show that the segmentation performance improvement of our method is significant compared to most methods. The segmentation results are shown in Fig. 7.

Fig. 7

Examples of central foveal avascular zone and retinal vessel segmentation results of the six methods on the OCTA-500 dataset. The first to third columns show the segmentation results of different methods on FAZ dataset, with the red line indicating the ground truth and the green line indicating the segmentation results. The figure in the bottom right corner yellow box in each image is an enlarged figure of the segmentation. The fourth to sixth columns are the segmentation results of different methods on the RV dataset, and the red dashed box indicates significant differences in segmentation results of different methods in this area. The content in the white box represents the corresponding Dice score for the image.

Ablation experiments

In this section, we performed a series of ablation experiments on the RGA dataset. The aim is to investigate the role played by different modules of our method (DIPN) during segmentation, and the ablation experiments are set up as follows.

Module ablation experiments

Table 3 shows the segmentation performance of the five modules in our method under different settings. We designed 7 sets of ablation experiments, the first 6 sets of experiments did not use B-scan images for pre-training, and directly input 3D volume data for training in the fine-tuning phase. The experimental design is as follows: (1) The baseline is defined as a segmentation model similar to IPN without our proposed modules. (2) ConvLSTM is added to (1). (3) PAM is added to (2). (4) FCB is added to (3). (5) APM is added to (4). (6) All modules are co-integrated into the baseline architecture. (7) Pre-training based on (6) using B-scan images to obtain pre-training weights, migrating pre-training weights to the fine-tuning stage. Training segmentation of volumetric data is performed in the fine-tuning stage. The results of the ablation experiments are schematically shown in Fig. 8. Pre-train using B-scan images to obtain pre-training weights, migrate the pre-training weights to the fine-tuning stage. Training segmentation of the volume data is performed in the fine-tuning stages. A schematic of the results of the ablation experiment is given in Fig. 8.

Table 3 Quantitative results of the ablation experiment of different modules on the RGA dataset. (mean $\pm$ standard deviation). Bold indicates the best performance score. (unit: %).

Fig. 8

Qualitative results of ablation experiments of the proposed module on GA dataset. (a) GA Enface. (b) Baseline. (c) Baseline + ConvLSTM. (d) Baseline + ConvLSTM + PAM. (e) Baseline + ConvLSTM + PAM + FCB (APM replaced with unidirectional pooling). (f) Baseline + ConvLSTM + PAM + FCB + APM. (g) The fine-tuning stage of our proposed method (Baseline + ConvLSTM + PAM + FCB + APM + CLE) trained without using the pre-training weights of the individual B-scan images. (h) Pre-training weights obtained from the pre-training stage are loaded in the fine-tuning stage. (i) ground truth. The content in the white box represents the corresponding Dice score for the image.

In the second set of experiments (the second row of Table 3), we observed that incorporating ConvLSTM into the network improved the performance by 2.47%(DICE) compared to the baseline. This improvement is attributed to the fact that the baseline segmented volume data slices individually, ignoring the neighboring information between images in the volume data. As a result, the spatial information within the complete 3D volume data was lost, leading to subpar segmentation performance. The ConvLSTM module effectively leverages the information from adjacent slices in the volume data, enabling the network to better utilize the 3D spatial information and enhance the segmentation performance. In the third set of experiments (the third row of Table 3), integrating PAM on top of (2) resulted in a performance increase of 3.69%(DICE). This enhancement is due to the fact that (2) solely relies on convolution operations for feature extraction, lacking explicit attention and utilization of directional information. By calculating the affinities between different pixels along the projection directions, PAM constructs dependencies to emphasize crucial feature information, thereby improving the network’s segmentation performance. In the fourth set of experiments (the fourth row of Table 3), introducing FCB led to a 2.59%(DICE) performance improvement compared to the network without FCB. This indicates that the additional feature information provided by FCB enhances the network’s feature utilization, mitigates feature loss, and enhances segmentation accuracy, demonstrating the necessity of the dual-branch network.

In the fifth set of experiments (the fifth row of Table 3), we observed a 0.23%(DICE) improvement by using APM compared to unidirectional pooling. This validates that APM facilitates multi-scale feature fusion and channel-wise information utilization, thereby increasing feature utilization and enhancing the network’s segmentation performance. Introducing the CLE module in the sixth set of experiments (the sixth row of Table 3) resulted in a 1.04%(DICE) improvement, demonstrating that CLE enhances the network’s ability to differentiate foreground and background, improving boundary distinction and ultimately boosting segmentation performance. In the final set of experiments, we observed a significant improvement in network performance by utilizing a large number of independent B-scan images, with an average Dice increase of 2.32% (from 84.71 to 87.03%). We believe that, compared to networks that only use volume data slices, the network can learn richer and more diverse feature representations from a large number of independent B-scan images. This, in turn, enhances the network’s ability to discriminate GA features, alleviates the issues of poor generalization and overfitting caused by excessive reliance on a small amount of data, and improves segmentation performance.

Figure 8 shows the segmentation results under the influence of each module. As depicted in the Fig. 8b,c, incorporating ConvLSTM in the baseline greatly improves the segmentation performance compared to the baseline network, making the boundaries coherent, which is due to the fact that ConvLSTM utilization of spatial information in the volume data. As can be seen in column (d) of Fig. 8, the problem of segmentation error is alleviated by fusing PAM to increase the attention of the network to the features in the projection direction. We can see from column (e) of Fig. 8 that by using an additional branch to capture features by sending the captured features to various stages of the projection branch. This mitigates the feature loss problem, allowing the network to utilize more semantic information and improve network segmentation. Compared with the segmentation results in column (e), the segmentation results in column (f) are better. This is because FCB can only capture a small number of features as well, while feature dimensionality reduction and multi-scale information fusion can be better performed using APM. As shown in column (g) of Fig. 8, our proposed contrast learning enhancement strategy utilizes the correlation between pixels in an image to cluster pixels of the same category and separate pixels of different categories, which enhances the capability of the model to distinguish between different categories. In column (h) of Fig. 8, the network is pretrained using a large number of individual B-scan images to enable the network to learn more feature representations for subsequent localization and segmentation tasks.

Contrastive learning analysis

In our segmentation task, the low contrast between the GA foreground and background makes it difficult to segment this part of the region correctly. Especially image edges, GA and background and uncertain regions such as noise, noise can greatly affect the segmentation results. To focus the network on indistinguishable foreground and background pixels, we proposed a contrast learning enhancement strategy. Ablation experiments were conducted in order to select suitable contrastive learning strategies. The performance corresponding to different strategies is shown in Table 4.

Table 4 Comparison of different anchor choices in the comparative learning module on the RGA dataset. (mean $\pm$ standard deviation). Bold indicates the best performance score. (unit: %).

To better investigate the effect of different anchor sampling strategies in contrast learning on segmentation performance, we performed experiments on the RGA dataset (Table 4.). Hardest anchor sampling³¹ collects more meaningful pixels and improves the network more significantly than random sampling. By mixing the two sampling methods (random and hardest), the overfitting problem is effectively avoided while improving the robustness of the training set and the training efficiency. Finally, we add a projected boundary anchor sampling strategy because only the projected boundaries are preserved during the dimensionality reduction process, and when the boundaries are misclassified, this can make the edges of the final projected segmentation map not smooth. In order to avoid this problem and accurately categorize the projection boundary anchors, a mixed sampling method of hard anchors, random anchors and projection boundary anchors is proposed.

Interpretability of PAM module

To better understand the PAM module, we visualized the attention map in the second PAM to understand the effect of the PAM module. We choose the attention maps in the second PAM module because the low-level attention maps do not show the region of interest clearly. In addition, the high-level attention map will be smaller because our network gradually reduces the feature dimensions during the projection process. Choosing these two attention maps does not visualize the region of interest.

We can observe from Fig. 9d that when the model predicts GA, it focuses mainly on its own position in the OCT image and less on the whole B-scan, which is consistent to translucency that GA demonstrates in the OCT B-scan image, where the borders on both sides of the lesion are more easily distinguishable. In addition, we can see that the horizontal direction of the GA lesion region also received a small amount of attention laterally. We believe that this is related to the characteristics of the GA lesion, as the GA lesion is in the vicinity of the RPE layer, so the two parts have similar characteristics, which makes the APM give a small amount of attention to this part of the layer region.

Fig. 9

Attention maps in PAM. (a) OCT B-scan with GA lesions. (b) GA regions labeled by the physician. (c) Column labeling of regions obtained by processing (b). (d) Attention maps for GA lesions in (a).

Effects of weighting parameters on loss function

The segmentation network is optimized by a joint loss function consisting of three components (e.g., Eqs. (16, 17)), which influence the learning of the network through different weighting parameters. Theoretically, different loss terms have different value ranges, where ${L}^{Dice}$ and ${L}^{BCE}$ are in [0, 1] and ${L}^{CLE}$ is in [$-\infty$, $+\infty$]. In network training, we observe that the values of these loss terms are in similar ranges. To facilitate our experiments, the range of values of the weights parameter is set to [0.2,0.5,1,2], and the results are listed in Table 5. When ${\lambda }_{Dice}$, ${\lambda }_{BCE}$ and ${\lambda }_{CLE}$ are 0.5, 0.5 and 1, respectively, the segmentation model obtains the highest dice score.

Table 5 Averaged dice of the propose method with different weights for segmentation network loss function. (unit: %).

Conclusion

In this study, we propose a novel OCT retinal geographic atrophy segmentation method using a multistage two-branch network structure. A large number of individual B-scan images are utilized for pre-training in the pre-training stage, followed by 3D volumetric data in the fine-tuning stage to address the current lack of a large amount of volumetric data for GA segmentation. Then, we capture the inter-pixel dependencies through the projection attention module to improve the segmentation precision and accuracy, and extract multi-scale features and channel information through the adaptive pooling module to alleviate the feature loss problem. In addition, we propose a contrast learning enhancement module to mitigate the contrast problem and improve the ability of the model to distinguish features. Finally, we incorporate the ConvLSTM module to utilize the information between neighboring slices, which helps mitigate the problem of volumetric data slice segmentation ignoring the spatial information of volumetric data. Our network effectively combines these components, using a large number of individual B-scans images to pre-train the network, and experimental validation on two datasets demonstrates the soundness and effectiveness of our approach.

However, it is worth noting that our approach is fully supervised, and all labels are obtained by processing pixel-level markers, and obtaining pixel-level markers is labor-intensive. This is one of the reasons why many researchers continue to explore weakly supervised and semi-supervised approaches. In future research, we will continue to explore weakly supervised and semi-supervised GA segmentation. We hope to reduce the labeling time while ensuring the quality of segmentation. At the same time, we will continue to collect larger retinal OCT datasets.