Introduction

The introduction of sustainable development goals aims to promote global peace and prosperity by shaping a future that prioritizes improved recycling and reuse circumstances under environmental changes. One crucial aspect for the existing generation system to achieve better future conditions is the provision of affordable energy, which is essential in reducing carbon emissions. This can be accomplished by considering 17 distinct sustainable goals. As fossil fuels continue to play a crucial part in modern energy networks, their utilization has expanded, leading to a higher demand and rising cost functions. Therefore, it is necessary to find alternative sources of energy that are sustainable in order to make the network more environmentally friendly and to decrease overall emissions in the near future. One crucial factor that facilitates progress in daily survival is the availability of clean energy. Furthermore, non-renewable energy sources should be able to adapt to various climatic circumstances and meet specific criteria, such as minimizing pollution and ensuring equal accessibility for all individuals. If all the aforementioned parameters are met, it is possible to achieve a continuous production in all applications related to industries and other emerging technologies. As a result, the consumption of non-renewable energy sources is minimized because there are natural processing units that handle organic materials. Non-renewable sources, being naturally abundant and inexpensive, can be utilized by a wide range of individuals. Furthermore, their availability will not diminish as their usage continues to expand, thereby enabling the creation of a sustainable environment for future generations. Despite the limited availability of non-renewable sources, the daily generation cases might still expand due to the use of replacement methods to meet growing demands.

Figure 1 depicts the schematic representation of projections for economical and environmentally friendly energy in order to attain sustainable objectives. Figure 1 shows that the demand is determined at the initial step, providing information about the total number of units that need to be produced. The control elements are modified based on the knowledge of creation, resulting in changes to various parameters and the corresponding variation in the supplied energy to different clusters. Only a communication unit that offers wireless representations to networked clusters and information storage units may govern the aforementioned variations. In other sectors, the received energy is compressed and stored, and this process is monitored by the control center. Subsequently, the control center makes suitable judgments, which are then recorded in information units. During the last stage, the entire load is distributed and utilized by all consumers who require affordable energy, thereby establishing a sustainable condition.

Fig. 1
figure 1

Block diagram of proposed sustainable energy units for environmental research.

Full size image

The proposed approach suggests that a smart control unit is attached to monitor the demand required for each time period. Despite the presence of various digital technologies in current methodologies1,2 that employ sensors and associated software for output processing relative to demand, only erroneous measurements are produced as the entire processes rely on forecasts. The predictive technique results in far greater energy wastage, and the saved energy cannot be utilised during any subsequent time periods. In the suggested system, the control units monitor demand and available energy, transmitting the monitored output to all interconnected clusters, where any surplus energy supply will be fully absorbed and stored. Furthermore, within each networked cluster, a coordinated control system is implemented, thereby addressing the primary issue of demand through the pooling of available resources.

Background and related works

In order to identify the most acceptable solutions for affordable energies, it is necessary to examine existing activities that aim to achieve sustainable development goals. The majority of researchers have investigated the feasibility of substituting fossil fuels with alternative energy sources in order to maximize the benefits for a larger user base. Studying previous efforts not only provide information about existing methods, but also allows for better performance, which may be utilized as a guide for constructing current sustainable networks. A real-time load analysis is conducted in1 for electric boat applications, taking into account real-time grid systems. After conducting a meticulous experiment using photovoltaic cells, it was determined that a greater amount of energy is required compared to fossil fuels. Therefore, in order to accommodate load fluctuations, all unfavorable situations are assessed. Remote island power systems cannot achieve coordinated control of voltage and current, even with increased energy input. Network planning is a crucial aspect of transitioning energy sectors. Transformations are necessary to ensure the generation of power that utilizes carbon efficiently2. In order to optimize energy utilization, it is feasible to modify a network and get complete control over energy flows. Subsequently, the economic efficiency of the implemented changes may be observed. In certain scenarios, when a network undergoes modifications, it becomes necessary to adjust the connections required to establish a fully functional network. This adjustment incurs additional costs. Emphasis should always be placed on cost efficiency, as replacement methods should offer affordable clean energy by utilizing existing network connections.

Furthermore, Ref.3 presents pertinent mathematical models that demonstrate the efficacy of substitution methods utilizing renewable energy sources. The majority of mathematical models elucidate the potential methods for constructing a micro grid framework, wherein sources like thermoelectric and solar cells enable the utilization of a greater amount of energy, making it unfeasible to prohibit. To characterize such scenarios, replications can be conducted with real time limitations, ensuring precise replacements in all instances. Furthermore, the aforementioned duplications are unable to prevent the occurrence of time delays, as a specific amount of energy must be regularly updated at control centers to maintain proper functioning. In order to achieve net zero energy, possible analytical representations are presented and verification of such scenarios can also be conducted, leading to appropriate performance improvements4. After upgrading a network, all essential parameters are modified to align with construction options, thereby minimizing the impact of environmental elements. However, the analysis of the impact of changes in network parameters necessitates significant modifications by integrating all network gases as non-renewable sources. An alternative approach to energy utilization involves the use of distributive networks, where refinery measurements are taken in specific locations5. This is because it is not feasible to achieve the objective of sustainable environments under the same energy conditions. When evaluating the listed refineries, several factors are taken into account to determine their economic advantages. The findings indicate that by replacing different types of gases, significant amounts of energy can be conserved for grid-connected electricity in the near future. In addition, real-time situational awareness can be achieved through the use of energy technology, thereby introducing a conditional limitation on focused power.

Similarly, analysis can be conducted using simulations by examining the energy rates associated with the existing historical data. Due to the abundance of data, it is advisable to only rely on software representations to ensure that the generation meets the necessary requirements. In addition to conducting simulation studies, we compare the maximum power utilization of various energy sources, which allows us to explore economic choices for future use. One potential application for cost-effective energy in the future is the utilization of solar cells, which can achieve a maximum productivity of 47%6. By utilizing replacement approaches, it is feasible to attain a greater mass ratio within a range of 10 to 30%, which can then be substituted. Furthermore, it has been noted that the introduction of a cascaded network might alter energy utilisation without any adverse consequences, so effectively mitigating the impacts of radiation. The energy sources supplied in the network must suffer numerous static effects, where renewable sources must have a significant part in using higher coverage ratios7. The majority of the higher proportion that encompasses the current methods utilize fossil fuels, as the choices are based on urgent necessity and cannot be reversed in the future. Consequently, the limitations on energy changes can hinder the overall connection of the network, as it is not possible to establish energy channels based on current requirements. Current generation networks can utilize some wind power networks for both energy generation and storage8. It is necessary to assess the adaptability of architectural changes in order to ensure efficient processing, allowing for the replacement and servicing of any system that requires a suitable energy source. Table 1 presents a comparison between the existing and proposed approaches in terms of objective patterns.

Table 1 Existing vs. proposed.
Full size table

Research gap and motivation

It is realistic from the comparisons22,23,24,25,26,27 that many different methods are used for providing low cost resources for energy representations which are even evaluated using conditional patterns. Due to more availability of fossil fuels even offload emends are made and global energy interconnections in this case id reduced thus offering wholesale electricity according to varying climate conditions. In addition for supplying affordable energy some of the super critical parameters are reduced thus it is not always possible to provide continuous energy supply in accordance with raising demands which in turn reduces the sustainability. Furthermore the renewable energy sources can be created fast but at the same time consumption among different classes of people is much higher thereby creating demands. Hence for providing appropriate resources the following queries must be deciphered.

  • Can the energy sources be created with low energy demands with more amount of energy center connectivity?

  • Whether it is possible to provide energy sources with less consumption and increased amount of generations?

  • Is it possible to create a better way for connecting the non-renewable systems at low cost with reduced radiations?

Novelty

To solve the queries that are present as major gap in existing methods proposed method is introduced with computational intelligence system where energy availability will be checked and supplied based on increasing demands at corresponding time periods. In addition the parametric objectives for computational intelligence optimization for affordable energy resources are as follows.

  • To reduce the demand of non-renewable sources by ensuring proper connectivity with energy centers.

  • To minimize the consumption where at desirable conditions the sources can be utilized thereby more amount of energy sources can be generated.

  • To increase energy collectors are various places at affordable cost with reduced radiations and fuel consumptions.

Proposed system model

The proposed approach dependence on computational intelligence is justified by its proven ability to optimize energy demand-supply dynamics and reduce emissions through predictive analytics and adaptive clustering techniques. Studies on sustainable energy systems have emphasized the importance of integrating advanced algorithms for resource allocation and minimizing environmental impacts. Additionally, proposed method highlight the role of hierarchical clustering and intelligent optimization in addressing challenges such as uneven energy distribution, high emissions, and resource inefficiencies. By leveraging these insights, the proposed model builds upon existing frameworks to offer a scalable, cost-effective, and environmentally conscious solution. This alignment with existing works ensures the model’s relevance and robustness in addressing energy sustainability challenges.

Current energy demands

With the increasing number of manufacturing units and the growing utilization of computational technologies, there is a need to adapt and modify energy demands. The aforementioned energy modification can be facilitated by specific centers that permit energy exchange. Therefore Eq. (1) is defined in relation to the present energy requirements28,29.

$$\:{DD}_{i}=min\sum\:_{i=1}^{n}{\rho\:}_{in}{P}_{i}$$
(1)

Where, \(\:{\rho\:}_{in}\) denotes total energy required, \(\:{P}_{i}\) indicates number of current products.

Equation (1) states that the amount of energy for all changing products may be determined at both the input and output units. Therefore, it is feasible to decrease the growing requirements at each station prior to product utilization.

Proposition 1

The law of demand clearly analyzes the importance on different types of configurations such as low, medium and high level variations. Since for different products demand modes are established an inverse relationship must be established in this case in order to check the changes in cost establishments. Let us consider the demand for products are expressed as \(\:{\mathfrak{k}}_{1}+.+{\mathfrak{k}}_{i}\) with relevant changes to certain applications \(\:{\mathbb{Z}}_{1}+\dots\:+{\mathbb{Z}}_{i}\). Therefore the inversion variations are expressed using Eq. (2) as follows30.

$$\:{\mathcal{L}}_{i}=\sum\:\frac{{\mathfrak{T}}_{i}}{{\mathfrak{V}}_{i}}$$
(2)

Lemma 1

For proving the inversion possibilities it is essential to lower maximum amount of products in considered systems. Hence the consideration is taken to be \(\:{\mathfrak{v}}_{i}\subset\:{\mathfrak{A}}_{i}\). For the above mentioned distributions the functions representations must be made in such a way by considering the price of products therefore \(\:{\varrho\:}_{i}\not\asymp\:{d}_{g}\left(i\right)\). The proof of demand products are represented using Eq. (3) as follows.

$$\:{\mathfrak{F}}_{i}=\sum\:{ı}_{i}{d}_{r}$$
(3)

Energy connectivity

In order to supply clean energy to all products, it is necessary to create a hub at a reasonable cost. Furthermore, the created central location must thoroughly examine each product. If a specific product requires an extra amount of energy, it can be allocated using factory units, as specified in Eq. (4).

$$\:{C}_{i}=max\sum\:_{i=1}^{n}{hb}_{i}\left[\begin{array}{ccc}{\alpha\:}_{1}&\:\cdots\:&\:{\alpha\:}_{i}\\\:⋮&\:\ddots\:&\:⋮\\\:{\alpha\:}_{i}&\:\cdots\:&\:{\alpha\:}_{n}\end{array}\right]$$
(4)

where \(\:{hb}_{i}\) denotes energy centers at various places, \(\:{\alpha\:}_{1}+\dots\:+{\alpha\:}_{i}+\dots\:+{\alpha\:}_{n}\) indicates connectivity at each energy center.

Equation (4) establishes that the creation of a greater number of energy centers will help alleviate the lack of energy transmissions. In order to enhance the sustainability of different products, it is possible to construct non-renewable sources with a predetermined number of units, where flexible movements are not permitted.

Proposition 2

The process of demand and corresponding linear growths must be represented using certain energy size where the exact relationship between different network values and growth factor must be defined in a proper way. Hence the consideration of network values be represented as \(\:{\mathfrak{b}}_{i}\cong\:{n}_{c}\left(i\right)\) that provides unique possibilities for including different configurations according to network size. Hence Eq. (5) is formulated with energy break-up points as follows.

$$\:{\wp\:}_{i}=\prod\:_{i=1}^{n}{\mathfrak{m}}_{i}{\text{{\rm\:O}}}_{i}$$
(5)

Lemma 2

For all the break-up points if network size is increased then relations size between different communicating devices will be maximized. Hence Eq. (6) represented the maximum possibility of increase in network size by using \(\:{n}_{i}\times\:{m}_{i}\) where connectivity can be changed at this point as follows.

$$\:{a}_{p}\left(i\right)=\sum\:{Ϝ}_{z}({n}_{i}\times\:{m}_{i})$$
(6)

Consumption of energy

With a higher number of emissions, it is crucial to regulate the energy use in order to mitigate the growing pollution. Hence, it is imperative to select the appropriate fuel type with precise coefficients that enhance the energy efficiency to 55%. Therefore, Eq. (7) is derived by utilizing average emissions and employing a coefficient matrix as shown below31.

$$\:{em}_{i}=min\sum\:_{i=1}^{n}{RR}_{i}+{\sigma\:}_{a}\left(i\right)$$
(7)

where \(\:{RR}_{i}\) denotes energy rates, \(\:{\sigma\:}_{a}\left(i\right)\) indicates average energy emissions.

Equation (7) states that in order to fully use energy, a sharing mechanism is always necessary, which in turn increases the rate at which the requisite number of population units is obtained. Alternatively, energy consumption can be reduced by taking into account the equilibrium of energy resources available through various actions.

Proposition 3

A minimum share on energy consumption must always be represented in varying terms as created energy cannot be destroyed at any case. Let us consider the created energy \(\:{\mathfrak{r}}_{1}+.+{\mathfrak{r}}_{i}\) where periodic representation is made using \(\:{pt}_{1}+.+{pt}_{i}\) thereby forming equal distribution which is represented using Eq. (8) as follows.

$$\:{\mathfrak{K}}_{1}={\mathfrak{K}}_{i}\not\equiv\:{pt}_{i}$$
(8)

Lemma 3

In order to prove the conditions of equal distribution every maximum energy concentration must be connected to a single network connectivity. Let us consider the energy network concentration be represented using \(\:{\mathcal{u}}_{1}+.+{\mathcal{u}}_{i}\) where self-edge degrees are considered for large energy network connectivity as indicated in Eq. (9).

$$\:{\mathfrak{c}}_{i}\subseteq\:{\kappa\:}_{i}$$
(9)

Energy generation

In order to achieve reductions in energy states for different products, a greater amount of energy needs to be generated in an efficient manner. Therefore, in accordance with the given input, energy production should be optimized at its highest efficiency. This optimization should only take into account the available number of sections, as specified in Eq. (10).

$$\:{GN}_{i}=max\sum\:_{i=1}^{n}{\gamma\:}_{in}(1-{\aleph\:}_{i})$$
(10)

where \(\:{\gamma\:}_{in}\) denotes energy efficiency, \(\:{\aleph\:}_{i}\) indicates effective section utilizations

Equation (10) stipulates that energy must be efficiently utilized across various sections present in all the units under consideration. Therefore, by achieving energy separation, all products may be efficiently utilized without any energy waste, allowing for the generation of precise power that can be delivered to end consumers.

Energy radiations

In order to optimize energy use, it is necessary to reduce radiation emissions to the greatest extent possible. When considering reductions in radiation, it is important to rely on limited available data, as increasing the number of items can negatively impact the sustainability of those products. Hence, it is necessary for the energy spreading ratios to be same, as stated in Eq. (11).

$$\:{ER}_{i}=min\sum\:_{i=1}^{n}{\delta\:}_{r}\left(i\right)\times\:{o}_{d}\left(i\right)$$
(11)

where \(\:{\delta\:}_{r}\left(i\right)\) denotes renewable radiations, \(\:{o}_{d}\left(i\right)\) indicates overcast durations.

Equation (11) signifies that when there are radiations, separations must be conducted uniformly in order to decrease the duration of cloudy conditions. Furthermore, a greater quantity of radiation will only be present if emissions are lowered in specific scenarios.

Preliminary 4

The Planck’s law for energy radiation is applied in the proposed method where in case of appliances it is essential to absorb various forms of energy until some hypothetical conditions are reached. Let us consider absorption of energy as \(\:{\mathcal{A}}_{b}\to\:{\mathfrak{P}}_{i}\) that belongs to various appliances where maximum temperature in this case can be expressed using Eq. (12) as follows.

$$\:{\eta\:}_{i}\subset\:{\aleph\:}_{i}\between\:({\mathfrak{s}}_{1}+\dots\:+{\mathfrak{s}}_{i})$$
(12)

Lemma 4

To prove the necessity for equality the absorbed temperature must reach corresponding equilibrium conditions thereby it is possible to reduce total amount of radiations that are present in the system. For proving low energy radiation conditions the speed of energy \(\:{\vartheta\:}_{i}\to\:{l}_{s}\left(i\right)\) which is nearly equivalent to speed of light is considered and expressed using Eq. (13) as follows.

$$\:{\nu\:}_{i}\parallel\:{l}_{s}\left(i\right)\to\:{\mathfrak{w}}_{i}$$
(13)

Fuel reductions

To attain cost-effective energy while maintaining a consistent pattern of generation, one viable approach is to decrease the utilization of fossil fuels. Therefore, it is essential to monitor the rate of absorption over time in order to establish the appropriate connection constraint, as specified in Eq. (14).

$$\:{FR}_{i}=min\sum\:_{i=1}^{n}{\zeta\:}_{i}({A}_{c}\left(i\right)-{E}_{c}(i\left)\right)$$
(14)

where \(\:{\zeta\:}_{i}\) represents increase in emission rate, \(\:{A}_{c}\left(i\right)\), \(\:{E}_{c}\left(i\right)\) indicates carbon absorption and emissions respectively.

Equation (14) establishes that in order to enhance the growth rate of cheap energies, it is necessary to attain equal proportions. If there are disparities in the representations of absorption and emissions, it can result in artificial fluctuations that contribute to non-sustainable aspects.

Energy production cost

In order to lower the production, cost of using non-renewable sources for replacement, it is necessary to consider aspects such as the type of materials, viscosity, and protection. Based on the factors given above, it is feasible to determine a substitute factor as specified in Eq. (15).

$$\:{PC}_{i}=min\sum\:_{i=1}^{n}{\vartheta\:}_{i}(w,r)+{m}_{d}$$
(15)

where \(\:{\vartheta\:}_{i}(w,r)\) denotes viscosity of surroundings, \(\:{m}_{d}\) indicates type of materials.

Equation (15) exclusively describes cost functions utilizing replacement approaches, hence excluding consideration of other external factors in this scenario. However, the overall cost of non-renewable energy sources can be assessed by considering the installation cost.

Energy collectors

The collector unit has a crucial function in efficiently storing a large amount of energy for effective usage. Therefore, Eq. (16) depicts the potential for overall accumulations in terrestrial settings characterized by emissions that exceed initial projections.

$$\:{CT}_{i}=max\sum\:_{i=1}^{n}{\omega\:}_{in}I{P}_{i}$$
(16)

where \(\:{\omega\:}_{in}\) denotes total amount of storage, \(\:I{P}_{i}\) indicates total input power.

Equation (16) establishes that the collection unit must be optimized and serves as an alternative unit for fossil fuels. Therefore, in the aforementioned scenario, the installation of collectors at each unit will result in an increase in cost.

Objective functions

The objective functions are created using min-max criteria to indicate the conservation of energies at a reasonable cost. This allows for effective comparison of energy conversions with the replacement of fossil fuels. The objective functions for sustainable advances in the suggested method are as follows.

$$\:{obj}_{1}=min\sum\:_{i=1}^{n}{DD}_{i},{em}_{i},{ER}_{i},{FR}_{i},{PC}_{i}$$
(17)
$$\:{obj}_{2}=max\sum\:_{i=1}^{n}{C}_{i},{GN}_{i},{CT}_{i}$$
(18)

In order to ensure sustainability for the given multi-objective functions, it is necessary to incorporate a decision-making strategy. This can be achieved by implementing a computational intelligence technique that utilizes artificial intelligence and machine learning.

Computational optimizations

The main objective of sustainable development units is to find a consistent answer for changing data. To do this, computational intelligence optimizations are selected as an effective decision-making method. By analyzing past data, these optimizations can generate intelligent outputs. In the context of energy transition as a substitute for fossil fuels, intelligent optimization assesses the energy requirements and delivers a higher amount of energy only to the necessary areas. The computational intelligence algorithm effectively minimizes energy waste and enables accurate prediction of future energy trends32. Computational intelligence algorithms, which employ artificial intelligence, have become crucial in minimizing intricate energy forms and facilitating the automatic generation of cost-effective units. One significant benefit of computational intelligence algorithms is their capacity to address all user requirements while conserving available resources, thanks to the provision of consumption patterns with adequate stability. In addition to standard activity analysis, the computational intelligence algorithm also possesses the capability to rectify fluctuating energy patterns, hence ensuring optimal performance with a greater range of sustainable power alternatives. Furthermore, it is possible to generate energy forecasts of all kinds at a lower cost by utilizing enhanced forecasting techniques and achieving lower emission rates. The aforementioned benefits not only enable a user to exploit the potential applications of alternative energy sources, but also facilitate the user in achieving efficient results by enabling the redistribution of energy in non-renewable sources. Moreover, a decentralized method is also adopted for the energy industry in situations where additional resources are needed at different times. Consequently, by effectively controlling the energy flow and optimizing its utilization, it becomes possible to make accurate future predictions and allocate the required resources accordingly.

Hierarchical energy distribution

Given that computational intelligence optimizations involve the distribution of energy based on hierarchical circumstances, it is crucial to partition various areas into clusters. Therefore, if clusters are created, the average number of units can be taken into account, resulting in compact solutions as stated in Eq. (19).

$$\:{DN}_{i}=\sum\:_{i=1}^{n}{DE}_{i}({z}_{i},{r}_{i})$$
(19)

where \(\:{DE}_{i}\) denotes distribution of energy, \(\:{z}_{i},{r}_{i}\) indicates corresponding clusters.

Equation (19) establishes that a hierarchy can be established depending on the available clusters and the related needs of users. Additional data points with identical energy can be provided, even when using dynamic units.

Definition 1

The possibility of energy maximization can be defined by considering the function of total system elements where two constants must be considered. Hence in this type of energy distribution the probability of considering non-renewable sources must be changed with exact time periods. Let us consider the probability of distribution as \(\:{\mathfrak{G}}_{i}\notin\:{\mathfrak{x}}_{i}\) in order to provide continuous energy representations by utilizing \(\:{\mathfrak{t}}_{1}+\dots\:+{\mathfrak{t}}_{i}\). Hence Eq. (20) represents changing functions in various clusters.

$$\:{\mathcal{L}}_{i}=\stackrel{\scriptscriptstyle\text{def}}{=}{\int\:}_{i=1}^{n}\left({\mathfrak{t}}_{1}+.+{\mathfrak{t}}_{i}\right)dt$$
(20)

Proof 1

For the above mentioned case the energy in the form of raising events can be made using a density function that considers all possible arrangements. However for proving the case of energy distribution entire cluster region must be considered with rate \(\:{\text{{\rm\:P}}}_{i}\left(\underset{0\le\:x\le\:1}{\text{max}}{{DN}}_{i}{e}^{-{z}^{2}}\right)\). Also the conditional case is determined using Eq. (21) as follows.

$$\:{{\Psi\:}}_{i}=\left\{\begin{array}{c}{z}_{i}{e}^{-z}\:for\:{1}^{st}\:cluster\\\:{r}_{i}{e}^{-r}\:for\:{2}^{nd}\:cluster\end{array}\right.$$
(21)

Average energy availability

To achieve eternal solutions for energy sustainability, we can evaluate the average number of energy pairs in a single cluster. We can then quantify the pairwise distance using Eq. (22).

$$\:{AY}_{i}=\sum\:_{i=1}^{n}\frac{{P}_{d}\left(i\right)}{{s}_{z}{s}_{r}}$$
(22)

where \(\:{P}_{d}\left(i\right)\) represents pair wise distance, \(\:{s}_{z}\), \(\:{s}_{r}\) denotes size of available energy clusters.

Equation (22) states that if the cluster size is known from a previous data set, it is possible to consistently provide an average energy supply without any increase in demand for any consumers. This form of individual connectivity ensures the long-term viability of all users within a specific group.

Definition 2

In order to increase the sustainability at low energy conditions the probability of equal distribution must be followed in such a way to provide appropriate insights for supporting necessary process. For the above mentioned equal distribution let us consider \(\:{\mathfrak{z}}_{1}+.+{\mathfrak{z}}_{i}\) with balancing criteria \(\:{\nabla\:}_{i}\bullet\:{\mathfrak{z}}_{i}\) where for two user connectivity Eq. (23) is represented.

$$\:{\mathfrak{o}}_{i}\subset\:{\mathfrak{S}}_{h}\left(i\right)$$
(23)

Proof 2

For proving equal distribution of energy cases maximum velocity of fuels that provides more amount of energy be represented with \(\:{\mathfrak{V}}_{1}+\dots\:+{\mathfrak{V}}_{i}\). For the above mentioned case the internal energy before distribution can be indicated as \(\:{\mathfrak{C}}_{i}\) where the conditional distribution in this form can be represented using Eq. (24) as follows.

$$\:{ed}_{i}=\left\{\begin{array}{c}\frac{\mathfrak{K}}{{\mathfrak{K}}_{i}}\:for\:{\mathfrak{o}}_{1}={\mathfrak{o}}_{i}\:\\\:0\:for\:{\mathfrak{o}}_{1}\ne\:{\mathfrak{o}}_{i}\end{array}\right.$$
(24)

Energy clustering cost

A clustering unit is implemented to minimize overall costs by using the sum of squares method to several energy sources. By optimizing the exploitation of existing resources, it is possible to achieve an effective solution for reducing the total cost in the energy network, while the installation cost of each unit cannot be decreased.

$$\:{cost}_{i}=\sum\:_{i=1}^{n}{(z}_{i}-{cr}_{i})+{(r}_{i}-{cr}_{i})$$
(25)

where \(\:{cr}_{i}\) denotes merged clusters.

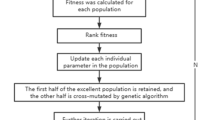
Equation (25) establishes that, in comparison to individual clusters, the combined clusters have the capability to operate according to the energy separation principle. Therefore, it is possible to achieve a partial distribution situation by considering the center point and the radius provided. The block diagrams illustrating the hierarchical clustering process for sustainable energy are depicted in Figs. 2, 3 and 4. The implementation procedure follows the subsequent flow.

Fig. 2
figure 2

Block representations of Intelligence clustering optimization.

Full size image
Fig. 3
figure 3

Flow chart of minimization objective function.

Full size image
Fig. 4
figure 4

Flow chart of maximization objective function.

Full size image

Definition 3

A transparent energy cost database indicates that it can equally coordinated by all individuals as total generated electricity must be available at affordable cost. The property of transparency reduces the risk of physical systems thereby providing appropriate reductions in all creatable forms by using \(\:{\mathfrak{p}}_{1}+.+{\mathfrak{p}}_{i}\). Therefore according to considered definition total cost utilization can be represented using Eq. (26) as follows.

$$\:{\mathfrak{c}}_{i}\propto\:{ut}_{i}\subset\:{\mathcal{p}}_{i}$$
(26)

Proof 3

For proving the total available cost representations a transfer theorem in the form of closed representation can be used with amount of energy considered \(\:{\mathfrak{R}}_{i}\nparallel\:{o}_{i}\). Hence all type of parallel energy resources is not equal as variations in total cost for each type can be observed by following Eq. (27).

$$\:{\mathfrak{i}}_{i}=\prod\:_{i=1}^{n}{\partial\:}_{i}\left({\mathfrak{A}}_{i}\right)$$
(27)

The proposed method for smart grid applications calculates the entire cost by assessing the total energy requirements at specific time intervals. Measurements of this nature are conducted in relation to an existing data collection, thereby establishing a connectivity link for each cluster that directly notifies the control unit about energy consumption levels. Consequently, clusters are combined only at necessary intervals, resulting in a collective energy supply rather than individual allocations for each cluster, with intelligent judgements made based on the specific time period. The use of distinct energy collectors will further minimise generation costs compared to the multiplicative process of fossil fuel generation. Furthermore, Eq. (8) suggests that essential substitutions can be implemented by analysing the surrounding environments, and the types of materials utilised for energy collection can also be diminished, hence reducing the overall costs in smart grid applications.

Algorithm 1
figure a

Hierarchical clustering.

Full size image

Algorithm 1 delineates the necessity for classifications pertaining to diverse energy types interconnected across clusters. To get compact solutions for energy control at various locations, hierarchical distributions are employed for intelligent computations, wherein the total number of users with specific occupational usages is delineated for each cluster. Conversely, the total energy available in each cluster is assessed, and informed judgements are made based on this availability; hence, hierarchical representations enable the storage of greater amounts of energy without necessitating further generation. In addition to availability and classification-based generations, energy from one cluster can be allocated to another cluster based on the available pairwise distance, so effectively reducing the total generation costs. Figure 2 illustrates the significance of each block utilised for classifying energy distributions. In the initial phase, the total number of clusters requiring adequate energy generation and distribution is established, with a focus solely on regional clusters to mitigate energy wastage. Further total size of each cluster is also defined for making significant decisions based on energy sharing and in this case any additional cluster that remains without interconnection can be connected to appropriate clusters (based on computational intelligence). Consequently, the introduction of new pairs inside each cluster alters the total distance, thereby diminishing energy consumption during peak periods as energy distributions are equalised at each stage. The suggested method illustrates the algorithmic flow chart for both minimisation and maximisation objective functions.

Figure 3 delineates the minimisation parameters, specifying the total energy and the associated variations in generated and dispersed energies with clarity. Variations in the energies supplied to each regional cluster result in observable changes in product numbers, prompting an initial assessment of available demand. If demand decreases, the same energy pairings inside each cluster will remain unchanged; however, if demand does not decrease within the corresponding time periods, the total required energy for each scenario will be reassessed from the starting condition. Subsequently, informed decisions are made by assessing the demands for supplementary energy, aiming to minimise total radiation and fuel usage.

Results

This section utilizes non-renewable sources to observe real-time outcomes and measure various parametric analyses. The suggested method aims to simplify energy sources by minimizing waste at the initial stages and efficiently converting energy for future use. Therefore, by implementing this form of usage from the beginning, approximately 30% of energy can be conserved, enabling all users to balance their demands through appropriate distribution methods. Given that the distribution is executed accurately across the respective clusters, every user can effectively utilize the availability of sources that are assessed by a computational intelligence algorithm. In the proposed model, a total of 42 distinct clusters are selected, and the energy requirements for each unit within these clusters are then modified, enabling energy generation at each cluster. The proposed method divides the clusters into low, medium, and large scales depending on the chosen energy requirements, which are determined by the type of product and its related utilizations. A connectivity representation is created based on the total number of utilizations. This representation includes an energy center and provides quick orientations for energy instances using act units. However, for typical needs, just observation phases are offered, resulting in the presence of an average amount of emissions in the clusters being investigated. To achieve the aforesaid connectedness, approximately 67 sections are employed to harness energy from energy centers and distribute it to different locations as needed. Furthermore, the total number of collecting units has been raised from 100 to 112. These units store energy for future usage with a low radiation pattern. Compared to regular operations, the suggested method introduces cost variations at each cluster due to the presence of variations. However, the total cost of clustering is decreased based on the availability of units. Four scenarios are chosen to observe the outcomes, and the importance of these scenarios is given in Table 2.

  • Scenario 1: Demand state and consumption units.

  • Scenario 2: Generation and connectivity points.

  • Scenario 3: Reductions on radiations and emissions.

  • Scenario 4: Minimization of cost.

Table 2 Importance of deliberated scenarios.
Full size table

Discussions

Real-time outcomes can be obtained for all the described scenarios. However, an alternative representation using simulation units allows for a comparison with the existing technique. The computational intelligence algorithm incorporates hierarchical clustering processes to merge analogous representations. This algorithm evaluates two types of knowledge circumstances, namely structured and unstructured, to determine sustainable energy requirements. Additionally, it is feasible to incorporate the functionalities that enable the generation of energy in pairs. Consequently, the simulation tool is designed to accommodate modifications for both the activated and deactivated states. Provided that the necessary parameters are met, it is feasible to store the maximum amount of energy at each collector unit without emitting any radiation. Table 3 presents the environmental parameters necessary for conducting real-time simulations.

Table 3 Simulation parameters.
Full size table

The complete dataset is exclusively processed from interconnected clusters. Therefore, in order to meet energy demands, it is imperative to utilize a smart grid toolbox that provides precise measurements along with availability conditions. Furthermore, in this scenario, the consumptions are evaluated from two sets, ensuring that every potential environmental situation is examined to avoid the influence of external factors. Computational intelligence is applied in this process to analyze the merged data set. The primary rationale for incorporating simulation parameters for energy detection is to account for potential fluctuations in total energy levels over time. In instances where energy levels are rising, it is imperative to employ computational intelligence optimization to implement suitable actions. In addition, each data set is inputted based on pairwise conditions, resulting in a reduction of duplicate data sets.

Scenario 1: demand state and consumption units

In this scenario, the entire demand is measured following the creation of energy units. Additionally, the total number of consumptions for low, medium, and high-quality appliances is observed to ensure that consumption and demand are balanced. Throughout this procedure, the energy consumption of each product is carefully monitored. It is evident that, at present, only a certain quantity of non-renewable energy sources needs to be provided to each product. If a product requires greater resources, it can be classified as a high-demand unit, which allows for the reduction of overall demand and enables comprehensive control. It is crucial to assess the carbon emissions associated with each product in order to determine the level of consumption. Over time, the consumption of non-renewable units should be decreased. Figure 5 displays the aggregate demand and consumption for both the proposed and existing approaches. Table 4 explains the energy consumption for various products.

Table 4 Energy consumption for various products.
Full size table

From Fig. 5 it is realistic that demand and emissions are completed reduced in case of proposed method as compared to existing approach6. The possibility conditions are present with computational intelligence monitoring systems as available energy is checked and distributed within required clusters. Since distribution is carried out in an equal way only consumption will be made by corresponding clusters whereas remaining zones will be neglected. To verify the demand and consumption cases percentage of energy for five clusters is provided in an equal way with 67,73,77,84 and 86% and total amount of products in each cluster is 14,17,21,24 and 29 respectively. For the above mentioned products total consumption is reduced to 31,27,24,20 and 16% in case of existing approach whereas for proposed method total consumption is minimized to 23,18,13,9 and 6%. Hence at low consumption it is possible to reduce the demand of each product in case of proposed computational intelligence optimization.

Fig. 5
figure 5

Total consumption rate for proposed and existing approaches.

Full size image

Scenario 2: generation and connectivity points

While proper utilization reduces consumption through cluster identifications, it is crucial to provide the necessary energy since non-renewable energy sources are inherently challenging to manufacture in nature. Therefore, in this scenario, the generation and connection points of energy are observed by creating energy centers at suitable locations for the purpose of energy sharing. Furthermore, it is imperative to effectively employ all portions inside the cluster. Consequently, energy distribution to end users will be appropriately allocated based on the designated clusters. When generating energy, it is necessary to connect the connectivity points utilizing central coordination points. Later on, the energy can be delivered to the necessary users. After the distribution process is finished, the required energy can be stored and monitored through the utilization of computational intelligence optimization. Figure 6; Table 5 illustrate the energy generation results, which are compared with the current method.

Table 5 Generations for various energy centers.
Full size table
Fig. 6
figure 6

Total number of sections and corresponding energy centers.

Full size image

From Fig. 6 it is obvious that more number of generations is made due to appropriate location of connectivity points in proposed method as compared to existing approach6. The connectivity points for two clusters are examined and only pair wise distance is considered in this case. Since group of users share a common energy in the form of non-renewable sources only fixed connections are provided. However in the fixed connectivity dynamic variations are made to establish full control thereafter increasing the efficiency at maximum extent without any unconventionalities. To prove the outcome of this scenario number of sections are changed with step size of 2, 4, 6, 8 and 10 with number of energy centers as 14,20,26,31 and 37 where for the above mentioned energy centers percentage of generations in case of proposed method is 64, 69, 73, 77 and 82%. With same amount of energy center existing approach generates low energy of 53, 57, 61, 66 and 74% without any additional storage of energy.

Scenario 3: reductions on radiations and emissions

In order to achieve optimal efficiency throughout the entire network, it is imperative to minimize the amount of radiations emitted by all forms of generated energy. The suggested method involves the observation of radiations and emissions in each segment, allowing for the determination of the total radiation pattern. In order to monitor the radiation pattern during periods of generated energy overcast, durations are allocated at each section. This allows for the reduction of individual radiations at regular intervals. If there are additional parts, the radiation pattern will be elevated, making it more challenging to mitigate the impact of emissions. For the purpose of enhancing sustainability, only renewable radiations are taken into account, while reducing the spreading ratio in all relevant sections. This ratio cannot be changed at a later stage. Furthermore, reductions are also implemented in the event of absorptions, as there is a limit to the quantity of energy that may be absorbed. Only when the aforementioned condition is present, it is feasible to employ all applications with a restricted amount of energy. The Table 6 explains the total reductions for emissions with non-renewable sources.

Table 6 Total reductions for emissions with non-renewable sources.
Full size table

Figure 7 provides the comparison outcomes for energy reductions and emissions in case of proposed and existing approach6. From Fig. 7 it is pragmatic that more amount of reductions are present in each section for proposed approach as compared to existing method. These reductions are made due to uniform separations thus providing exact durations by effectively utilizing all sections. To verify this scenario percentage of renewable radiations are considered as 11, 13, 16, 18 and 20 with percentage of emissions as 14, 19, 22, 25 and 28. As the emission spread ratio is reduced reductions are also minimized and it remains at 26, 24, 21, 18 and 12% for proposed method. With same amount of spreading ratio percentage of reductions are observed to be 34, 33, 31, 27 and 25% respectively for existing approach. Therefore as a result it is possible to reduce total amount of emissions if durations and spreading ratios are maintained properly without any demand in energy states.

Fig. 7
figure 7

Reductions in radiations for emission spectrum.

Full size image

Scenario 4: minimization of cost

After generating energy from non-renewable sources, it is necessary to assess the whole cost component and find ways to lower the implementation cost. The suggested method calculates the total cost by considering two distinct limitations. One constraint is determined by the available number of clusters, which identifies a specific component. The other constraint is based on the entire storage capacity. The primary purpose of cost evaluation is to guarantee that non-renewable sources are implemented with proper distribution, in contrast to the prior approach where the entire cost was only considered in relation to storage units. In order to minimize costs in the suggested approach, collectors are strategically positioned to efficiently store the required quantity of energy. Additionally, the storage unit varies depending on the type of material utilized in each situation. Therefore, it is essential to select materials in a careful manner, which will result in additional cost reductions based on the energy sources accessible within the entire clusters. Figure 8; Table 7 present the cost data for both the proposed and existing systems.

Table 7 Comparison of total cost in accordance with merged clusters.
Full size table
Fig. 8
figure 8

Total cost for considered clusters for non-renewable sources.

Full size image

From Fig. 8 it can be observed that total cost is reduced in projected models as compared to existing approach6. Since non-renewable sources are available in a natural way the cost of energy is reduced to 20% as compared to original cost with fossil fuels. But the type of material used in proposed method for utilizing energy sources are not established properly thereby increasing the overall cost. However in the projected method overall cost is reduced in all considered clusters and even after high consumptions the cost is reduced appropriately. To prove total cost measurements number of merged clusters are considered as 7,11,14,18 and 20 where equal amount of energy is required in this case. As a result of merged clusters total cost in proposed method is 759,701,664,623 and 548 dollars whereas for existing approach total cost is increased to 1200,1154,1069,1041 and 1003 dollars.

Conclusions

In order to achieve sustainable development goals, it is crucial to establish cohesive groups that adhere to conditional processes where environmental research can be carried out. Given the complexity of categorizing all the fundamental components associated with the development of the complete environmental system, it is crucial to assess the overall quantity of energy that links both society and individuals. Hence, the suggested method aims to analyze the feasibility of attaining cost-effective energy conditions through diverse sources, and thereafter compare the assessments with existing methodologies for achieving smart solutions by avoiding all environmental threats. In order to transform subversive groups into a structured framework, it is crucial to thoroughly examine all potential methods for implementing reformation approaches. Consequently, the analysis examines the need for energy generation across all products, emphasizing the significant requirement for non-renewable sources in the suggested approach. Furthermore, non-renewable sources are naturally abundant, allowing for the provision of an equivalent conversion factor to meet growing demands while reducing reliance on fossil fuels. Furthermore, the increasing needs and generations are only monitored when computational intelligence optimizations are implemented. Therefore, the projected model takes into account individual clusters. Through the utilization of hierarchical clustering in computational intelligence, users are able to interact with various hubs that are powered by central energy processing units.

The impact of computational intelligence on achieving affordable energy and improving sustainability conditions is evaluated through simulations using four distinct scenarios. These scenarios are analyzed to address both minimization and maximization challenges. In the first scenario, the likelihood of decreased demand for each product is diminished, resulting in a consumption increase of less than 10% when utilizing computational intelligence optimization. In the following situation, the proposed method increases the likelihood of generations to 82% due to reductions in consumption, while the existing strategy decreases it to 74%. On the other hand, the potential for decreasing emissions, which is essential for making energy more affordable, is limited to 12% in the proposed plan, resulting in a total cost decrease to $548.

Limitations and future work

The study illustrates the efficacy of artificial intelligence in optimising non-renewable energy sources, while specific constraints suggest opportunities for future research. The emphasis on non-renewable energy precludes the incorporation of renewable sources, which is essential for a holistic sustainability framework. The scalability of the suggested model for larger and more intricate energy networks has yet to be evaluated, and the absence of long-term experimental validation constrains the practical applicability of the results.

Future research may focus on investigating hybrid energy systems that integrate renewable and non-renewable sources to attain a balanced energy mix. Advanced computational techniques must be explored to improve the model’s adaptability to varying energy requirements and network structures. Moreover, longitudinal studies in real-world settings are essential to confirm the model’s effectiveness among fluctuating environmental and economic circumstances.

Policy implications

Effective policy implications entail requiring the utilisation of computational intelligence for the optimisation of energy demand-supply and the reduction of emissions. Creating industry-specific norms for sustainable energy practices helps enhance accountability. Policies ought to prioritise the promotion of energy-efficient technology and the incorporation of emission controls within production processes. Furthermore, establishing standards for energy storage and clustering techniques can guarantee fair resource allocation and economic efficiency.