Dual-branch dynamic hierarchical U-Net with multi-layer space fusion attention for medical image segmentation

Abstract

Accurate segmentation of organs or lesions from medical images is essential for accurate disease diagnosis and organ morphometrics. Previously, most researchers mainly added feature extraction modules and simply aggregated the semantic features to U-Net network to improve the segmentation accuracy of medical images. However, these improved U-Net networks ignore the semantic differences of different organs in medical images and lack the fusion of high-level semantic features and low-level semantic features, which will lead to blurred or miss boundaries between similar organs and diseased areas. To solve this problem, we propose Dual-branch dynamic hierarchical U-Net with multi-layer space fusion attention (D2HU-Net). Firstly, we propose a multi-layer spatial attention fusion module, which makes the shallow decoding path provide predictive graph supplement to the deep decoding path. Under the guidance of higher semantic features, useful context features are selected from lower semantic features to obtain deeper useful spatial information, which makes up for the semantic differences between organs in different medical images. Secondly, we propose a dynamic multi-scale layered module that enhances the multi-scale representation of the network at a finer granularity level and selectively refines single-scale features. Finally, the network provides guiding optimization for subsequent decoding based on multi-scale loss functions. The experimental results on four medical data sets show D2HU-Net enables the most advanced segmentation capabilities on different medical image datasets, which can help doctors diagnose and treat diseases

Introduction

Medical image segmentation provides important help for doctors to diagnose diseases, analyze pathology, design treatment plans and arrange surgical plans¹. However, manual annotation and segmentation of medical image diagnosis face great challenges in clinical practice. Firstly, the morphological diversity of the lesion region, the similarity between the gray level and the adjacent tissue, and the image noise, under the influence of subjective factors, manual segmentation is prone to over-segmentation and under-segmentation. In addition, medical images have small volume, low contrast, unclear adjacent boundaries, and significant differences in lesion areas between different patients or even between the same patient. Finally, different imaging principles of medical imaging devices lead to different clarity of medical images, which will also lead to low accuracy of segmentation². Therefore, there is an urgent need to exploit advanced computer vision techniques to develop a model that can quickly and accurately identify, localize, and segment target regions in medical images.

U-Net is a revolutionary innovation in the field of medical image segmentation³. It is the encoder-decoder architecture. There are many skip connections from low to high levels between the encoder and the decoder. It can well combine low-resolution and high-resolution information to make up for the information lost in down sampling. It allows U-Net to obtain more accurate pixels, which improves the utilization of information and the accuracy of segmentation. Influenced by U-Net, scholars have developed many variants based on U-Net network and tried their best to improve U-Net network⁴ . The improvement of these algorithms is mainly reflected in three aspects: convolution operation⁵, skip connection⁶, and depth module⁷.

Convolution operation is the basic building block of convolutional neural networks⁸ . Classical convolution operation can make full use of context information to map and extract features from data⁹. scholars introduced the streamlined attention mechanism of variable size and convolution, which fully understood the volume context, and flexibly distorted the sampling grid, so that the model could appropriately adapt to different data patterns.

Skip connection is a breakthrough in U-Net network, which aggregates low-level features in encoder and high-level features in decoder. Previous skip connections simply aggregate low-order and high-order features by concatenation between encoders or decoders¹⁰. TransAttUnet uses additional multi-scale skip connections between decoder blocks to aggregate upsampled features with different semantic scales. In this way, the ability to represent multi-scale context information can be enhanced and discriminative features can be generated¹¹.

The last aspect is the depth block, which is generally the backbone of the network, which also determines the feature inference mode of the network. It has been proved that the performance of the network gradually increases with the increase of depth and width¹². However, as the depth increases, the difficulty of training also increases. To alleviate the shortcomings of these depth modules, several improved networks have been developed using residual blocks¹³, dense blocks¹⁴,and initial residual blocks¹⁵. In order to expand the global feature extraction ability of the network, the attention mechanism is introduced into the depth block. Such as attention gate¹⁶, dual attention¹⁷, spatial and channel attention¹⁸. In addition, Transformer, from the field of natural language processing, has excellent performance by using self-attention mechanism to obtain data features¹⁹.Quite a few researchers have created many medical graph segmentations using Transformer structure or convolutional network structure²⁰,They have shown acceptable results.

Although the above scholars have achieved good results in the field of medical image segmentation, there are still some shortcomings in the segmentation process. Firstly, the common convolutional structure in U-Net network can only extract features from a single aspect, and the semantic features of images are discontinuous. Secondly, the aggregation strategy of skip join treats the context information equally, lacks the combination of high-level and low-level features, and cannot make full use of context dependence. This also leads to unclear segmentation of the boundary of the target region. Finally, most methods are designed for specialized lesions and organs with a single image modality. Since the features of multimodal images are very different from each other, the segmentation results are not ideal for different lesions and organs and different modalities.

During the design of the model, two key challenges were encountered. First, extracting semantic features from the target region at multiple scales proved difficult, particularly when the medical image contrast was low, the target region shape was irregular, distribution imbalanced, and semantic information fragmented. Second, effectively fusing low-level and high-level semantic information while leveraging their complementary nature was necessary. To address the first challenge, we propose a dynamic multi-scale hierarchical module that enhances the network’s multi-scale representation capability at finer granularities. This module selectively refines single-scale features to improve noise resistance. To address the second challenge, we introduce a multilayer spatial attention fusion module, which integrates feature information across both channel and spatial dimensions. It also establishes multidimensional interactions between these dimensions. The module dynamically aggregates various types of semantic features, allowing shallow decoding prediction maps to complement deeper decoding paths. This enables D2HU-Net to select useful contextual features from low-level information and extract high-level semantic and detailed information at different scales under the guidance of high-level features. Moreover, it bridges the semantic differences between organs across different medical images. Simultaneously, the multi-scale features are selectively refined to extract more relevant spatial information. By capturing contextual information of the target, attention features across different scales are effectively fused, addressing boundary blurring and missing regions in target segmentation.

The main contributions of this paper can be summarized as follows:

• 1. A dual-branch dynamic hierarchical U-Net (D2HU-Net) with multi-layer spatial fusion attention is proposed, in which the shallow decoding path provides guidance for the deep decoding path and improves the generalization ability.

• 2. A multi-layer spatial attention fusion module is proposed. It not only focuses on the distinguishing characteristics of channel and spatial dimension, but also establishes the interdimensional interaction between channel and spatial dimension. In addition, the weighted parameters are adapted to further blend the features of each view. Finally, selective nuclear feature aggregation can dynamically aggregate advanced features of different branches/types, effectively improving the accuracy of medical image segmentation

• 3. Dynamic multi-scale layered module is proposed, selectively utilize multi-scale features integrated at different scales, and refine features at each scale. Enhance the ability of multi-scale expression of network features. Improve the precision of segmentation of the target area

• 4. We experiment D2HU-Net on four multi-modal medical image datasets and obtain high segmentation accuracy. The proposed model has good robustness

Related works

CNN-based segmentation networks

In the early medical image segmentation, feature engineering and deep learning²¹ were used to extract image features. With the development of deep learning algorithms, in the absence of any manual features, deep learning-based methods can automatically extract various features from medical images in an end-to-end form for medical image segmentation. Long et al. designed the end-to-end convolutional network architecture FCN for semantic segmentation for the first time²². Influenced by FCN, U-Net architecture is proposed for medical image segmentation. U-Net adopts a strategy of skipping connections, integrating low-level features with high-level features, thereby preserving some detailed features. In the later work, scholars have proposed various improved semantic segmentation models based on U-Net network. Xiao et al. proposed Res-UNet by introducing the weighted attention mechanism and residual connections into U-Net²³. Around the same time, Radiuk et al. proposed that a U-shaped network with nested and dense jump connections was proposed for multi-organ segmentation²⁴. However, these methods only collect features from neighborhood pixels and lack awareness of global image information. In addition, ICNet is proposed as a cascading network architecture to connect multi-resolution feature maps with appropriate label guidance and model compression²⁵. Chen et al. designed GLNet by combining two CNN branches to preserve both the global background and the detailed local information²⁶. These branches interact with each other through a depth feature mapping sharing strategy, resulting in better performance. However, since convolution kernels tend to extract only local regions, this approach often has limitations when modeling remote relationships.

To solve this problem, several methods have been proposed where extended convolution is used instead of step convolution to expand the acceptance field and model non-local information²⁷. In addition, some scholars have proposed to introduce attention mechanism into CNN to improve the network’s focus on features. For example, Wang et al. applied self-attention modules in deep neural networks to explore the validity of non-local dependencies in images, sequences, and videos²⁸. CBAM²⁹ and DANet³⁰ enhance the representation ability of CNN by using the attention mechanism along channel dimension and spatial dimension respectively. These methods have achieved remarkable performance on different tasks. Despite the commendable achievements of the aforementioned scholars, the prevailing convolutional structure is incapable of accommodating multiple perspectives, and the semantic features extracted from the graph exhibit discontinuity. Consequently, this paper proposes a dynamic multi-scale hierarchical module to enhance the multi-scale representation of the network at a finer granularity level, thereby enhancing the segmentation accuracy of the network.

Despite the commendable achievements of the aforementioned scholars, the prevailing convolutional structure is incapable of accommodating multiple perspectives, and the semantic features extracted from the graph exhibit discontinuity. Consequently, this paper proposes a dynamic multi-scale hierarchical module to enhance the multi-scale representation of the network at a finer granularity level, thereby enhancing the segmentation accuracy of the network

Attention mechanisms

Attention mechanisms were originally designed for natural language models. Since attention mechanism can effectively solve the problem that convolution operation cannot highlight the object features and suppress the noise in the network, attention mechanism has become a research hotspot and has been widely applied in the field of computer vision. Wang et al. introduced non-local operations into the spatial attention mechanism to obtain spatial dependencies by calculating the attention force³¹. This is a spatial attention mechanism that focuses on where the effective features are in the feature map. In addition, there are channel attention mechanisms, which are mainly concerned with what are the effective features in the feature graph and suppress the redundant channels of the feature graph. Hu et al. proposed a channel attention mechanism to learn global context features by recalibrating channel dependencies on different channels by squeezing and exciting blocks³². At the same time, Woo et al. proposed the convolutional block attention module (CBAM) to coordinate the joint action of channels and spatial attention mechanisms³³. In recent years, several multi-scale attention mechanisms have emerged. Chen et al. proposed Transattunet to design multi-level guided attention, integrating self-conscious attention modules from self-attention with transform and global Spatial attention into TransAttunet to effectively learn non-local interactions between encoder features³⁴. Huang et al. proposed a cross-concern module in which the network can adaptively capture remote context information from image dependencies³⁵.

However, these methods based on spatial attention mechanisms and channel attention mechanisms are independent dependencies. Therefore, the interaction between the spatial dimension and the channel dimension in the network is limited. multi-layer spatial attention fusion module proposed in this paper can capture the interactive features of each dimension, focus on the important features of the feature graph from four dimensions, and improve the segmentation ability of the network.

Methods

In this section, firstly, D2HU-Net will be briefly introduced. Secondly, the dynamic multi-scale layered module is introduced in detail, which is the basic model of D2HU-Net. Thirdly, the attention mechanism of multi-layer space fusion is introduced theoretically. Finally, the calculation process of the loss function is introduced in detail.

Overview of the proposed network

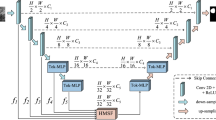
The main purpose of medical image segmentation is to segment the target region from various formats of medical images. In order to realize this process, D2HU-Net based neural network is proposed for medical image segmentation. The specific schematic diagram of D2HU-Net is shown in Fig. 1. Specifically, D2HU-Net contains one encoding path and two decoding paths, thus forming a two-branch image segmentation architecture.

The main function of the coding stage is to encode the input medical images into semantic features. The encoding phase consists of a total of five coding blocks, referred to as $E_1, E_2, E_3, E_4, E_5$ (from top to bottom). The encoder is composed of dynamic multi-scale layered modules, which are described in detail in “Multi-layer spatial attention fusion module”. Behind each encoder block, a downsampling operation using maximum pooling is applied, which serves to double the number of channels for the semantic features.

At the end of the encoder $E_4$ encoding, the shallow decoding path begins to perform semantic segmentation from bottom to top. Among them, the shallow decoding path includes three decoders, which are $D_1^3, D_1^2, D_1^1$ from bottom to top. Both the decoder structure and the encoder structure are composed of dynamic multi-scale layered modules.

Compared to the maximum pooling of the encoder, the decoder is always present, and an upsampling operation by a transposed convolution of $4 \times 4$ increases the space size of the semantic feature by a factor of 2, while doubling the channel size of the feature. The input of the decoder is connected to the output of the encoder at the same scale with the sampled features on the previous decoder. Finally, after the convolution of $1 \times 1$, the segmentation diagram $M_s$ of the shallow path is obtained, which is denoted as. The shallow split path includes 4 encoders and 3 decoders, and the flow is: $E_1 \rightarrow E_2 \rightarrow E_3 \rightarrow E_4 \rightarrow D_1^3 \rightarrow D_1^2 \rightarrow D_1^1.$

The segmentation result of the deep decoding path is the final medical image segmentation result graph, which includes 5 decoders $D_2^i,i=1,2...5$. The decoder of the deep decoding path and the decoder of the shallow decoding path have the same structure. The jump connection of the deep decoding path is not simply directly connected with the output of the decoder at the same scale, but the target feature in the semantic feature is amplified through the multi-layer spatial attention fusion module. The output of the multi-layer spatial attention fusion module is connected with the decoding semantic feature after being upsampled, and then input into the decoder. There is a great difference between shallow semantic features and deep semantic features. Shallow semantic features contain more detailed information, while deep semantic features include more semantic information. The multi-layer spatial attention fusion module fuses useful information from deep semantic features and shallow semantic features, making the network pay more attention to specific information.

Each decoder is classified, and the segmentation graph for each scale is denoted as $M_s^i,i=1,2,3...,6$. This segmentation graph is used to define the multi-layer loss function, which improves the stability of training and the robustness of the model. Finally, the final output diagram of D2HU-Net is obtained through the encoding stage $E_1 \rightarrow E_2 \rightarrow E_3 \rightarrow E_4\rightarrow E_5$, bottleneck and deep decoding path $D_2^5 \rightarrow D_2^4 \rightarrow D_2^3 \rightarrow D_2^2 \rightarrow D_2^1$.

The multi-layer spatial attention mechanism and dynamic multi-scale feature extraction structure of D2HU-Net have been shown to increase the number of parameters and computational complexity of the model while improving the segmentation performance. On larger datasets, the training of the model increases accordingly, especially when computational resources are limited, which may affect the efficiency of practical applications. However, the experimental results demonstrate that appropriately increasing the model’s complexity can effectively enhance the segmentation accuracy, particularly in the context of medical images with multi-scale and complex backgrounds. The model exhibits an improved ability to extract important features.

Fig. 1

Architecture of the proposed D2MU-Net for medical image segmentation.

Fig. 2

Architecture of the dynamic multi-scale layered module.

Dynamic multi-scale layered module

Dynamic multi-scale layered module (DML) is an important basic module of D2HU-Net. DML is composed of two dynamic convolution layers and a layered module. The specific diagram is shown in Fig. 2 , Each dynamic convolution is connected to the batch normalization and Rectified Linear Unit (ReLU) activation functions. The schematic diagram of dynamic convolution is shown in Fig. 2. In form, $\text {Conv}_i$(i=1,2,... K) is the K convolution core of dynamic convolution, so the mathematical formula for dynamic convolution can be defined as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \left[ {\pi _1, \pi _2, \dots , \pi _k} \right] = f_\pi (x) \\ y = \sum \limits _{i = 1}^{k} \pi _i \cdot \text {Conv}_i(x) \end{array} \right. \end{aligned}$$

(1)

where, $x$ and $y$, respectively, dynamically convolve the input and output, $f_\pi$indicating that the semantic features of the input pass through the global average pooling (GAP), the fully connected layer (FC), the ReLU activation function, the fully connected layer (FC), and finally the weight $\pi$ is generated by the Softmax function. In traditional convolution operations, the convolution parameters are static and the same for all inputs, while dynamic convolution adaptively learns the weight value $\pi$ for each input. In summary, each input is represented by a unique set of convolution kernels, so the expressiveness of the network is improved, and the parameters of the model are not increased. For parameter settings of dynamic convolution, the $K$ of dynamic convolution is set to 8, and the convolution kernel size is set to $3 \times 3$. The semantic features that have undergone dynamic convolution will be evenly divided into 4 groups along the channel dimension, denoted as $f_1, f_2, f_3, f_4$. Except that the number of channels becomes a quarter of the original, the other feature scales are the same as the input. expect $f_1$ ,the rest of $f_i$are summed element-wise with the output of the $3 \times 3$ convolution operation with $f_{i-1}$, and then batch normalization (BN) and ReLU activation are applied. This process can be described by the following formula:

$$\begin{aligned} f_i'&= \left\{ \begin{array}{ll} f_i & \text {if } i = 1 \\ \text {Conv}_3\left( f_i \right) & \text {if } i = 2 \\ \text {Conv}_3\left( f_i + f_{i - 1}' \right) & \text {if } i = 3,4 \end{array} \right. \end{aligned}$$

(2)

where $\text {Conv}_3$ represents a convolution layer whose convolution kernel is $3 \times 3$. For these different scales of semantic feature information, we use the method of cross-line fusion information, to exchange and fusion information of $\left( f_1', f_2', f_3', f_4' \right)$, so that each scale of feature information will receive other scales of information. This means that different receiving domains can receive different messages. The specific formula is expressed as follows:

$$\begin{aligned} f_i''&= f_i' + \text {Conv}_1\left( \sum \limits _{i = 1}^4 f_i' \right) , \quad i = 1,2,3,4 \end{aligned}$$

(3)

Since each scale captures multi-scale semantic information in the way of segmentation, in order to solve the problem of weakening information flow caused by segmentation operation, we carry out $1 \times 1$ convolution operation for connected semantic features and fuse mixed semantic features of different scales. The formula is as follows:

$$\begin{aligned} y&= \text {Conv}_1\left( \text {Concat}\left( f_1'', f_2', f_3', f_4' \right) \right) \end{aligned}$$

(4)

where $y$ represents the output after $1 \times 1$convolution. For the output of features, dynamic convolution operations are again performed, along with batch normalization (BN) and ReLU activation. The maximum pooling operation is then performed as an input to the next encoder.

Multi-layer spatial attention fusion module

Multi-layer spatial attention fusion module (MSAF) is an important part of the decoding of D2HU-Net in the deep decoding path. In order to learn rich context information, multi-scale feature information is aggregated to remove the noise affected by non-target regions. Inspired by³⁶ , we propose a space-related module to highlight the features of the target segmentation region step by step. This module is called multi-level spatial attention fusion module.

In contrast to traditional single-attention mechanisms, the proposed multilayer spatial attention fusion module emphasizes spatial features at multiple scales through hierarchical attention mechanisms. This allows the model to capture global context while preserving fine-grained details, improving its accuracy and robustness when processing complex images. Unlike standard channel or spatial attention mechanisms, the multilayer spatial attention fusion module enhances spatial information by performing feature fusion at different levels. This multi-level fusion capability enables the model to analyze images at a finer granularity, effectively balancing both detailed and global information. The specific diagram is shown in Fig. 3.

The input of MSAF is the output result of the encoder at the same scale and the $D_1^1$ output of the shallow decoding path through channel integration. The multi-level spatial attention fusion module can be divided into two parallel multi-level spatial attention stages and the attention fusion stage. The multi-level spatial attention stage can be divided into four parallel branches, including channel dimension attention, channel and width dimension attention, channel and height dimension attention, and space dimension attention.

Firstly, the first branch takes the output of $D_1^1$ in the shallow decoding path as an example, expands the number of channels by using $1 \times 1$ convolution, and performs down sampling operation at the same time to obtain the same feature size as the output of the encoded block, denoted as $M \in {R^{c * h * w}}$ . In the multi-layer spatial attention stage, the first branch focuses on recalibrating channel-level feature representation capabilities. First, we aggregate the spatial features of the input ${M_c}$ by maximum pooling and average pooling, which can be defined as $X_{1(\max )}^{c \& c} \in {R^{c \times 1 \times 1}}$ and $X_{1(\mathrm{{avg}})}^{c \& c} \in {R^{c \times 1 \times 1}}$ . Then, using a multi-layer perceptron (MLP) consisting of two $1 \times 1$ convolutional layers and an activation function (Rule), the size of the middle layer is set to $R{ \in ^{c/2 \times 1 \times 1}}$ in order to maintain channel resolution and minimize the number of parameters, and the output of the MLP is summed at the element level. The sum output is then passed through the softmax activation function to get the channel-level attention weight ${A_{c \& c}}\left( X \right) \in {R^{c \times 1 \times 1}}$ . It can be concluded that the mathematical calculation of the weight mapping of the channel-level attention of the first branch is as follows:

$$\begin{aligned} A_{c \& c}(X)&= \theta \left( \text {MLP}\left( \text {Maxpool}(X) \right) + \text {MLP}\left( \text {Avgpool}(X) \right) \right) \nonumber \\&= \theta \left( W_2 \xi \left( W_1 \left( X_{1\left( \max \right) }^{c \& c} \right) \right) + W_2 \xi \left( W_1 \left( X_{1\left( \text {avg} \right) }^{c \& c} \right) \right) \right) \end{aligned}$$

(5)

where $\theta$ is the sigmoid function, $\xi$ is the ReLU function, ${W_1} \in {R^{c/2 \times c}}$, and ${W_2} \in {R^{c \times c/2}}$ . Finally, the first branch output feature maps $X_1^{c \& c}$ is generated by the following equation:

$$\begin{aligned} X_1^{c \& c}&= A_{c \& c}(X) X \end{aligned}$$

(6)

Fig. 3

Architecture of Multi-layer spatial attention fusion module.

The main role of the second branch is to focus on the interaction of channels and height dimensions. First, $X$ is rotated 90 degrees counterclockwise along the height scale to generate a new semantic feature $X_{2r}^{c \& h} \in {R^{w \times h \times c}}$ , Next, feature aggregation of $X_{2r}^{c \& h} \in {R^{w \times h \times c}}$ is performed using maximum pooling and average pooling, $X_{2r(\max )}^{c \& h} \in {R^{1 \times h \times c}}$ and $X_{2r(\mathrm{{avg}})}^{c \& \mathrm{{h}}} \in {R^{1 \times h \times c}}$ , respectively. These outputs are then concatenated with BN using a $K \times K$ convolution operation, and then, using S-type activation function yields the weight mapping of cross attention between channels and height dimensions ${A_{c \& h}}\left( {X_{2r}^{c \& h}} \right) \in {R^{1 \times h \times c}}$. In short, its calculation formula is as follows:

$$\begin{aligned} A_{c \& h}\left( X_{2r}^{c \& h} \right)&= \theta \left( f^{k \times k}\left[ \text {Maxpool}\left( X_{2r}^{c \& h} \right) ; \text {Avgpool}\left( X_{2r}^{c \& h} \right) \right] \right) \nonumber \\&= \theta \left( f^{k \times k}\left[ X_{2r\left( \max \right) }^{c \& h}; X_{2r\left( \text {avg} \right) }^{c \& h} \right] \right) \end{aligned}$$

(7)

where $\theta$ is the sigmoid function, ${f^{k \times k}}$ is the $K \times K$ convolution layer with the BN. The second branch output feature maps $X_2^{c \& h}$ is generated by the following equation:

$$\begin{aligned} X_2^{c \& h}&= \text {Roated}\left( A_{c \& h}\left( X_{2r}^{c \& h} \right) \right) X_{2r}^{c \& h} \end{aligned}$$

(8)

The third branch is mainly concerned with the interaction between the channel dimension and the width dimension. The process of calculating semantic features is similar to the process of calculating channels and high attention. First, the input X is rotated 90 degrees counterclockwise along the width to obtain a new semantic feature $X_{3r}^{c \& w} \in {R^{h \times c \times w}}$ . After that, perform the same operation as the previous branch. The calculation process of the attention mechanism of channel dimension and width dimension can be summarized as follows:

$$\begin{aligned} A_{c \& w}\left( X_{3r}^{c \& w} \right)&= \theta \left( f^{k \times k}\left[ \text {Maxpool}\left( X_{3r}^{c \& w} \right) ; \text {Avgpool}\left( X_{3r}^{c \& w} \right) \right] \right) \nonumber \\&= \theta \left( f^{k \times k}\left[ X_{3r\left( \max \right) }^{c \& w}; X_{3r\left( \text {avg} \right) }^{c \& w} \right] \right) \nonumber \\ X_3^{c \& w}&= \text {Roated}\left( A_{c \& w}\left( X_{3r}^{c \& w} \right) \right) X_{3r}^{c \& w} \end{aligned}$$

(9)

The main function of the fourth branch is to focus on the characteristics of the target region in the spatial dimension. The calculation process of the spatial attention map and the output of spatial attention can be summarized as follows:

$$\begin{aligned} A_{h \& w}\left( X_4^{h \& w} \right)&= \theta \left( f^{k \times k}\left[ \text {Maxpool}\left( X_4^{h \& w} \right) ; \text {Avgpool}\left( X_4^{h \& w} \right) \right] \right) \nonumber \\&= \theta \left( f^{k \times k}\left[ X_{4\left( \max \right) }^{h \& w}; X_{3\left( \text {4avg} \right) }^{h \& w} \right] \right) \nonumber \\ X_4^{h \& w}&= A_{h \& w}\left( X_4^{h \& w} \right) X_4^{h \& w} \end{aligned}$$

(10)

Finally, in order to further improve the fusion ability of features, we add a learnable weight parameter to the back of the four branches, so the output in the multi-layer space attention stage can be summarized as:

$$\begin{aligned} w_i&= \frac{\exp \left( a_i \right) }{\sum \limits _{j = 1}^4 \exp \left( a_j \right) }, \quad i = 1, 2, \dots , 4 \end{aligned}$$

(11)

$$\begin{aligned} Y&= w_1\left( X_1^{c \& c} \right) + w_2\left( X_2^{c \& h} \right) + w_3\left( X_3^{c \& w} \right) + w_4\left( X_4^{h \& w} \right) \end{aligned}$$

(12)

where, ${w_i}$ is the normalized weight coefficient and $\sum {{w_i}}$ is =1; ${a_i}$ and ${a_j}$ are the initial weight coefficients.

Similarly, it can be concluded that the output of the multi-layer spatial attention stage of the second branch is ${Y_2}$ . After that, we fuse Y and ${Y_2}$ through element-level sum operations to obtain the correlation feature graph of high-dimensional semantic features and low-dimensional semantic features, that is ${E_{yy}} = Y + {Y_2}$. Then, ${E_{yy}}$ is transformed into a global statistical descriptor with scale $c \times 1 \times 1$ by GAP operation. Next, we use $1 \times 1$ convolutional layers with a ReLU activation function for the channel down sampling operation. To preserve as much channel resolution as possible, the down sampled features $z \in {R^{c/2 \times 1 \times 1}}$ . After that, we convert the feature vector z to ${V_Y} \in {R^{c \times 1 \times 1}}$ and ${V_{{Y_2}}} \in {R^{c \times 1 \times 1}}$ using two parallel $1 \times 1$ channel upper sampling layers. Finally, we use two weights to re-calibrate the multi-scale feature maps Y and ${Y_2}$ dynamically, and accordingly, the final output $M = {V_Y}Y + {V_{{Y_2}}}{Y_2}$ .

loss

In the training process, the loss function consists of using the binary cross-entropy loss ${L_{BCE}}$ and the dice loss ${L_{Dice}}$, where ${\mathrm{{R}}_{\mathrm{{gt}}}}$ and ${\mathrm{{R}}_{\mathrm{{seg}}}}$ represent the real label value and the predicted result, respectively. Then ${L_{BCE}}$ and ${L_{Dice}}$ can be defined as

$$\begin{aligned} {L_{BCE}}\!\left( \! {{\mathrm{{R}}_{\mathrm{{gt}}}}\!,\!{\mathrm{{R}}_{\mathrm{{seg}}}}} \right) \!=\!- \!\left( \! {1\! - \!{\mathrm{{R}}_{\mathrm{{gt}}}}} \right) \log \left( {\mathrm{{1}}\! -\! {\mathrm{{R}}_{\mathrm{{seg}}}}} \right) \! -\! {\mathrm{{R}}_{\mathrm{{gt}}}}\log {\mathrm{{R}}_{\mathrm{{seg}}}} \nonumber \\ L_{\text {Dice}}\left( R_{\text {gt}}, R_{\text {seg}} \right)&= 1 - \frac{2 R_{\text {gt}} R_{\text {seg}}}{R_{\text {gt}} + R_{\text {seg}} + \varepsilon } \end{aligned}$$

(13)

The $\varepsilon$ in the formula is a small constant set to avoid having a zero denominator. Therefore, the loss function in the experiment can be derived according to ${L_{BCE}}$ and ${L_{Dice}}$.

$$\begin{aligned} L_{seg}\left( R_{\text {gt}}, R_{\text {seg}} \right)&= \lambda L_{BCE} + L_{Dice} \end{aligned}$$

(14)

where $\lambda$ was set to 0.5 in this experiment.

In order to improve the stability of the training process, the proposed model applies ${L_{seg}}$ to both decoders in the second stage decoding process to establish a deep supervision loss function. Where ${M_{GT}}$ represents the true segmentation result graph, so the loss $L_s^i$ of the i-th decoder can be defined as

$$\begin{aligned} L_s^i\left( M_{\text {GT}}^i, M_s^i \right)&= L_{\text {seg}}\left( M_{\text {GT}}^i, M_s^i \right) , \quad i = 1, 2, \dots , 5 \end{aligned}$$

(15)

In the above formula, $M_{GT}^i$ is defined as

$$\begin{aligned} M_{\text {GT}}^i&= {\left\{ \begin{array}{ll} M_{\text {GT}} \downarrow _{2^{i-1}} & \text {if } i \ge 2, \\ M_{\text {GT}} & \text {if } i = 1. \end{array}\right. } \end{aligned}$$

(16)

where ${ \downarrow _{{2^{\mathrm{{i - }}1}}}}$ represents the sub-sample of factor ${2^{\mathrm{{i - }}1}}$. In addition, ${L_{seg}}$ is also applied to the output of the shallow decoding process, so the loss of the shallow decoding path can be defined as

$$\begin{aligned} L_c(M_{\text {GT}}, M_c)&= L_{\text {seg}}(M_{\text {GT}}, M_c) \end{aligned}$$

(17)

Finally, the overall loss function during the training of this network can be defined as

$$\begin{aligned} L_{\text {total}}&= L_c + \sum _{i=1}^5 L_s^i \end{aligned}$$

(18)

Experiments

Dataset

Synapse multi-organ segmentation dataset: synapse from the Multi-Graph Abdominal Tagging Challenge held by MICCAI 2015. Different from the traditional single organ segmentation, synapse is the segmentation of eight organs in the abdomen, including the aorta, gallbladder, spleen, left kidney, right kidney, liver, pancreas, spleen, and stomach. The dataset included 30 abdominal clinical CT images, with the number of CT sections contained in each scan ranging from 85 to 192, resulting in a total of 3778 two-dimensional images. The size of all 2D slice images is adjusted to $512 \times 512$ , with a voxel spatial resolution of ([0.54   0.54] × [0.98   0.98] × [2.5   5.0]) $mm^3$. In this experiment, 18 samples were divided into training sets, and the remaining 12 were divided into test sets.

Skin Lesion Segmentation: The ISIC 2018 dataset is derived from the ISIC 2018 challenge, which addresses skin lesion segmentation, lesion attribute monitoring, and dermatological classification. The dataset included 2594 images, of which 20.0% were melanoma, 72.0% were moles, and the remaining 8.0% were lipid overflow keratosis. The size of the picture is $512 \times 512$ .

Chest X-Ray dataset: This dataset is a pre-chest lung X-ray, This data comes from the National Library of Medicine, National Institutes of Health, Bethesda, MD. USA and Shenzhen No.3 People’s Hospital, Guangdong Medical College, Shenzhen, China³⁷, The dataset consisted of 710 chest X-ray films and accompanying labels. The size of the image is $512 \times 512$ .

Kvasir-SEG: The Kvasir-SEG dataset contains 1000 polyp images from the Kvasir dataset v2 and their corresponding ground truths, which were manually seemed by physicians and cross-validated by professional gastroenterologists. The image resolutions included in the Kvasir-SEG range from $332 \times 487$ to $1920 \times 1072$ pixels, and we adjusted them to $512 \times 512$ pixels.

In the process of data preprocessing, we carry out random rotation, horizontal inversion and enlargement of the picture. For each data set, we divided the training set, the validation set, and the test set in a 7:1:2 ratio.

Evaluation metrics

In order to quantitatively analyze the segmentation results, we used five evaluation indicators. including Dice coefficient (Dice), Intersection over Union (IOU), relative volume difference (RVD), average symmetric surface distance (ASSD), maximum symmetric surface distance (MSD). Let ${\mathrm{{R}}_{\mathrm{{gt}}}}$ and ${\mathrm{{R}}_{\mathrm{{seg}}}}$ be the ground truth and predicted segmentation result. The mathematical formula for these indicators is as follows:

• 1. Dice coefficient (DIC): It specifically represents the ratio of the area where two objects intersect to the total area. Its value range is [0,1] and the perfect separation value is 1.

  $$\begin{aligned} \text {DIC}&= \frac{2 \left( R_{\text {gt}} \cap R_{\text {seg}} \right) }{R_{\text {gt}} + R_{\text {seg}}} \end{aligned}$$

  (19)

• 2. Intersection over Union (IOU): Overlap rate of segmentation result and real result.

  $$\begin{aligned} \text {IOU}&= \frac{\left| R_{\text {seg}} \cap R_{\text {gt}} \right| }{\left| R_{\text {seg}} \cup R_{\text {gt}} \right| } \end{aligned}$$

  (20)

• 3. Relative Volume Error (RVD): used to indicate the Volume difference between ground truth and predicted segmentation results. The closer the value is to zero, the higher accuracy of the segmentation accuracy.

  $$\begin{aligned} \text {RAVD}&= \frac{R_{\text {seg}}}{R_{\text {gt}}} - 1 \end{aligned}$$

  (21)

• 4. Average symmetric surface distance(ASSD): the average distance between the surfaces of segmentation results ${\mathrm{{R}}_{\mathrm{{seg}}}}$ and the ground ${\mathrm{{R}}_{\mathrm{{gt}}}}$ . Where $\mathrm{{d}}\left( {\mathrm{{a,b}}} \right)$ represents the distance between a and b.

  $$\begin{aligned} \text {ASSD}&= \frac{1}{\left| R_{\text {seg}} \right| + \left| R_{\text {gt}} \right| } \left( \sum _{a \in R_{\text {seg}}} \mathop {\min }\limits _{b \in R_{\text {gt}}} d(a, b) + \sum _{b \in R_{\text {gt}}} \mathop {\min }\limits _{a \in R_{\text {seg}}} d(a, b) \right) \end{aligned}$$

  (22)

• 5. Maximum symmetric surface distance (MSD): The maximum surface distance between the segmentation result ${\mathrm{{R}}_{\mathrm{{seg}}}}$ and the ground reality ${\mathrm{{R}}_{\mathrm{{gt}}}}$, the lower the MSD value, the higher the matching degree between the two sample.

  $$\begin{aligned} \text {MSD}&= \left( \mathop {\max }\limits _{i \in R_{\text {seg}}} \left( \mathop {\min }\limits _{j \in R_{\text {gt}}} d(i, j) \right) , \mathop {\max }\limits _{i \in R_{\text {gt}}} \left( \mathop {\min }\limits _{j \in R_{\text {seg}}} d(i, j) \right) \right) \end{aligned}$$

  (23)

Experimental details

All models were based on the Pytorch framework and python 3.8, and all experiments were performed on a deep learning workstation equipped with an Intel Xeon E5-2680 v4 processor, 35 M of L3 cache, 2.4 GHz clock rate, 14 physical cores/28-way multitask processing. In addition, it has 128 GB of DDR4 RAM and an 8 x NVIDIA GeForce RTX 2080Ti super graphics processing unit (GPU) with 11 GB of RAM. Furthermore, the hyperparameters are set to the same for all models, Initial learning rate is 0.0003, Batch size is 16, Epoch is 200, Optimizer is Adam, Growth rate is 0.0001.

To demonstrate the validity of our proposed D2HU-Net, we compare D2HU-Net with nine SOTA segmentation models, including: FCN³⁸ , U-Net³, ResUNet³⁹, Attention U-Net⁴⁰ , UNet++⁴¹, ResNet++⁴², SWimU-Net⁴³, TransoformU-Net⁴⁴, HiFormer⁴⁵. All comparison methods are set to default parameters. All model weights are retrained on the training set, and the number of training rounds is set to 200. Meanwhile, in order to eliminate the chance of the experiment, we conduct 5 tests on each model on the test set, and select the average value of each evaluation index.

Experimental results and analysis

In order to demonstrate the superiority of the proposed D2HU-Net model in various aspects, we evaluated the D2HU-Net model quantitatively and qualitatively, comparing it with nine advanced methods on four datasets.

• 1. Synapse multi-organ segmentation dataset:The quantitative comparison results between the benchmark model of abdominal organ segmentation task in the Synapse multi-organ segmentation dataset and D2HU-Net are shown in Table 1. D2HU-Net is significantly superior to the other 9 CNN-based SOTA methods. In terms of DICE, TransformU-Net achieves the second-best value, while D2HU-Net achieves 0.87% higher than D2HU-Net. For IOU and RAVD, the increase was 0.79% and 0.09%, respectively. For ASSD and MSSD decreased by 0.5 and 2.02, respectively. Specifically, he steadily outperformed most organ segmentation methods. Figure 4 shows the qualitative segmentation results. The results show that this method can segment fine and complex structures accurately, output more accurate segmentation results, and have stronger robustness to complex backgrounds.

• 2. Skin Lesion Segmentation: The quantitative comparison results between the benchmark model of Skin Lesion Segmentation task and D2HU-Net on the skin lesion segmentation dataset are shown in Table 2. The table of D2HU-Net presented in this paper is ahead of other competitors’ methods in 5 evaluation indicators, except ASSD. Specifically, in terms of DICE, D2HU-Net improved by 1.25% and IOU by 0.12% over the most advanced HiFormer, with significant advantages in both RAVD and MSSD. In addition, the variance of D2HU-Net in each evaluation index is also small, which reflects good stability. For qualitative analysis, Fig. 5 shows the visualization of Segmentation results on the Skin Lesion Segmentation dataset. This shows that our proposed D2HU-Net generates more accurate contours than other comparison models in both small and large area targets, and is closest to the label map. In general, D2HU-Net has the best performance, showing good generalization ability and good robustness.

• 3. Chest X-Ray dataset: The quantitative comparison of the baseline model for Chest X-Ray lung segmentation task in the Chest X-ray dataset with D2HU-Net is shown in Table 3. From the data in the table, we can intuitively see that in addition to RAVD, other indicators of D2HU-Net proposed by us are far ahead of other methods. Due to the simplicity of the data set, the DICE of D2HU-Net is as high as 97.2%, which is 0.3% higher than that of TransformU-Net with the second best value. In terms of IOU, D2HU-Net provided a gain of 0.4%. In addition, there are 0.53 and 3.3 reductions for ASSD and MSSD, respectively. At the same time, the variance is also minimal, indicating that D2HU-Net has good stability. Figure 6 shows some results of qualitative analysis of lung segmentation of X-ray images, indicating that D2HU-Net has achieved

• 4. Kvasir-SEG: The quantitative comparison between the baseline model of the rectal polyp segmentation task on the Kvasir-SEG dataset and D2HU-Net is shown in Table 4. Table 4 lists the specific data of each evaluation index, and we can find that all indexes are better than other models. Specifically, D2HU-Net was 0.7% higher in DICE than the second-best TransformU-Net and 1.7% higher in IOU than HiFormer, with ASSD and MSSD decreasing by 0.63 and 0.02, respectively. Figure 7 shows the segmentation results of some polyp images. The main difficulties in the segmentation of gastrointestinal polyps are that the color of polyps and normal tissue is similar, the boundary is not clear, and the illumination is not uniform. Thanks to the Multi-layer spatial attention fusion module, high-level semantic information and low-level semantic information are fused, which also enables D2HU-Net to segment results closer to labels than other methods and accurately extract polyp structure.

Fig. 4

Visualization of the segmentation results of D2HU-Net and 9 comparison methods on the Synapse multi-organ segmentation dataset.

Fig. 5

Visualization of the segmentation results of D2HU-Net and 9 comparison methods on the skin lesion dataset.

Fig. 6

Visualization of the segmentation results of D2HU-Net and 9 comparison methods on Chest X-Ray dataset.

Fig. 7

Visualization of the segmentation results of D2HU-Net and 9 comparison methods on the Kvasir-SEG dataset.

Table 1 Evaluation indicators ± standard deviation of all competing methods in the Synapse multi-organ segmentation dataset.

Table 2 Evaluation indicators ± standard deviation of all competing methods in the Skin Lesion Segmentation.

Table 3 Evaluation indicators ± standard deviation of all competing methods in the Chest X-Ray dataset.

Table 4 Evaluation indicators ± standard deviation of all competing methods in the Kvasir-SEG.

Ablation studies

In the context above, we demonstrate the effectiveness of the Dynamic multi-scale layered module and multi-layer spatial attention fusion module proposed in this paper from the theoretical level. In this chapter, we will conduct a series of ablation experiments to verify the effectiveness of these modules. It includes Dynamic multi-scale layered module, multi-layer spatial attention fusion module and double branch structure. Relevant experiments were quantitatively analyzed on Synapse multi-organ segmentation dataset, Skin Lesion Segmentation dataset, Chest X-Ray Dataset and Kvasir-SEG.

• 1. Ablation study of dynamic multi-scale layered module: In order to study the effectiveness of dynamic multi-scale layered module, we take the traditional convolutional layer U-Net as the basis. Another contrast model is to use Dynamic multi-scale layered module instead of traditional convolutional blocks. Table 5 shows the specific index data on the four data sets, where U stands for U-Net. It can be seen that U-Net network is superior to U-Net in all indicators after adding DML. IOU improved by 1.82% on the Synapse multi-organ segmentation dataset. On Skin Lesion Segmentation, DICE improved by 1.11%. In the Chest X-Ray dataset, due to the simplicity of the dataset, the values of each indicator were relatively high, but there were small improvements in the indicator data. On Kvasir-SEG, JC is up 2.2 percent. It can be seen from various data that Dynamic multi-scale layered module is helpful to improve the accuracy of segmentation.

• 2. Ablation Study of multi-layer spatial attention fusion module: We first tested the D2HU-Net proposed in this paper on four data sets. Second. We removed MSAF from D2HU-Net, and then conducted training on four data sets before testing. Table 6 shows the specific indicators of D2HU-Net on four data sets, Where D stands for D2HU-Net and M stands for MSAF. In the Synapse multi-organ segmentation dataset, compared with D2HU-Net without MSAF, DICE of D2HU-Net increased by 0.51% and IOU increased by 1.86%. RAVD decreased by 3.75, ASSD and MSSD decreased by 0.42 and 2.03, respectively. In terms of Skin Lesion Segmentation, compared with D2HU-Net without MSAF, DICE of D2HU-Net increased by 1.06% and IOU increased by 0.78%. On the Chest X-Ray dataset, DICE was increased by 0.1%. IOU increased by 0.59%. On Kvasir-SEG, IOU of D2HU-Net increased by 3.07% and IOU increased by 1.95% compared with D2HU-Net without MSAF. It can be seen from the evaluation indexes of the four data sets that the MASF module proposed in this paper is reasonable and helpful to improve the segmentation accuracy of the model.

• 3. Ablation Study of Double branch: In order to verify the rationality of the double branch structure proposed in this paper, we chose U-Net as the base model, and then added double branch structure to the U-Net network model. The model was evaluated on four data sets. Table 7 shows the evaluation index data on the four datasets, where U stands for U-Net and DB stands for double branch. It can be seen from the data in the table that, combined with the two-branch U-Net network, all evaluation indexes are better than the benchmark model U-Net, which can also be seen that the first decoding branch has a guiding effect on the second decoding branch, which improves the accuracy of medical image segmentation.

Table 5 Ablation experimental results of dynamic multi-scale layered module.

Table 6 Ablation experimental results of Multi-layer spatial attention fusion module.

Table 7 Results of ablation experiments for dual decoding paths.

Complexity calculation

In addition to segmentation performance, factors such as inference speed and model size play a pivotal role in determining the practical applicability of clinical diagnostics.The computational complexity of a model can be quantified using the well-known gigafloating-point operations (GFLOPs), inference speed, and the number of parameters.As illustrated in Table 8, D2HU-Net demonstrates notable strengths, ranking third in terms of GFLOPs and second in terms of inference speed. The inference speed is a crucial metric in clinical environments, especially when dealing with a large number of medical images, and D2HU-Net demonstrates superior performance in this regard. However, it should be noted that D2HU-Net requires more parameters due to the presence of two decoding paths, i.e., the dynamic multiscale layering module and the multilayer spatial attention fusion module. Despite its augmented complexity, D2HU-Net exhibits superiority in medical image segmentation accuracy, a trade-off that involves sacrificing spatial complexity for enhanced segmentation precision.

Table 8 Comparison of computational complexity.

Discussion

Our comprehensive experiments on four different modal medical image datasets show that D2HU-Net has certain advantages over other SOTA. In quantitative analysis, all the data show that D2HU-Net can perform multi-modal medical image segmentation very well. From the qualitative analysis, D2HU-Net can also be accurately segmented into target regions, which is also the same as the result of quantitative analysis. In contrast, our D2HU-Net still has some challenges in processing low-contrast, borderless medical images, resulting in inaccurate segmentation. In future work, we will investigate more robust segmentation methods.

Conclusion

In this paper, we propose a medical image segmentation method based on D2HU-Net network, which has three main innovative contributions. Firstly, the proposed D2HU-Net network adopts a double-branch decoding path, the shallow decoding path provides guidance for the deep decoding path, and improves the generalization ability of the network. Secondly, a dynamic multi-scale hierarchical structure is proposed, which can selectively utilize semantic information at different scales, integrate multi-scale features, and refine the features at each scale. The multi-scale expression of network features is enhanced. Thirdly, a multi-layer spatial attention fusion module is proposed. It not only focuses on the distinguishing features of channel and spatial dimension, but also establishes the multi-dimensional interactive relationship between channel and spatial dimension. In addition, due to the different importance of each branch feature map, we propose an adaptive weighting coefficient for each branch to more efficiently fuse feature maps from all four branches. Finally, selective nuclear feature aggregation can dynamically aggregate advanced features of different branches/types, effectively improving the accuracy of medical image segmentation.

Experimental results on four different modal medical image datasets demonstrate the effectiveness and robustness of the proposed D2HU-Net network. At the same time, a series of ablation experiments verify the effectiveness of each module in the proposed D2HU-Net network. Although the proposed D2HU-Net has achieved good classification performance, there is still room for improvement. For example, the proposed dynamic multi-scale hierarchical structure can extract multi-scale features, increase the number of parameters in the network, and improve the complexity of the model. While the experiments confirmed the robustness of D2HU-Net on various datasets, there is still potential to improve the model’s resilience to extremely noisy data or images under extreme conditions. In further work, we will explore how to make the network more lightweight and highly robust to adapt to more segmentation scenarios while improving the accuracy of the network.