Introduction

China has a long history of sunflower cultivation; sunflowers have strong planting applicability, a long industrial chain, significant market demand, and high economic benefits. Sunflowers, according to their type, can be distinguished as edible sunflower seeds and oil sunflower seeds1. The planting area of sunflowers in China is about 1 million hm2, and the output is 2.5 million tons, which is located in fifth place in the world, among which the average annual planting area of edible sunflower seeds is about 650,000 hm2. Edible sunflowers, due to the rich content of fatty acids, amino acids, minerals, vitamins, and other nutrients, but also reduce blood lipids, prevent cardiovascular and cerebral vascular diseases, and other effects3,4,5. Those make the Chinese sunflower seeds food market space more prosperous, as of 2022, China’s edible sunflower seeds market size is about 30 billion yuan6. The current consumer market for sunflower seeds is particularly popular for cooked sunflower seeds under the brands “Cha Cha” and “Yong Jin”. The production process for these brands consists mainly of roasting, drying, baking and boiling steps7,8,9.

Industrial hullers realize hulling mainly by extruding and kneading the material, and the separation of shells and kernels is accomplished by the combination of airflow and screens10. The industrial sunflower seed huller is large, complex, noisy, and unsuitable for household recreation, therefore, it is necessary to design household-type sunflower seed hullers. Shell kernel separation also directly affects the quality and efficiency of the household-type huller. Commonly used separation principles include airflow separation, specific gravity separation, and screening separation. Chi et al., for an eggshell membrane separation device with the problem of a low cleaning rate, designed a gas-suction eggshell membrane multistage cleaning device11; Shi et al. utilized the characteristic difference between the fluid dynamics of jujubes and miscellaneous residues to design a jujube sorting system12. Fan et al. for the combined harvester, there is the problem of high loss rate and impurity rate, designed a strong cleaning ability, the low loss rate of double layer isotropic clearing device13, Gao et al. using the design of the combination of double air outlet and vibrating screen for peanut clearing14. The airflow separation principle is simple, low noise, small, and suitable for small hullers. In contrast, the screening and specific gravity separation principle is structurally complex, large in size, and suitable for handling large quantities of raw materials, but it has excellent separation results. In view of the size and structure of the whole machine of the household-type sunflower seed huller, in order to solve the challenges in terms of noise and size, this device has chosen the airflow separation technology.

The CFD-DEM method can characterize particles’ actual shape, physical parameters, and collision motion, simulate the motion state of particles and the distribution of fluids, and provide more accurate and comprehensive simulation results15,16. Wang et al. evaluated the overall performance of a wheat seed ejection device by selecting different seed ejection angle sizes and directions17. Mahmoud et al. used CFD-DEM modeling to study the influence of cyclone spiral inlet on airflow pattern and biological particle separation process18. The separation effect was evaluated by analyzing velocity and pressure cloud images of cyclone separators with different parameters, and the structural parameters of cyclone separators were optimized to improve their performance by 14%. Therefore, the CFD-DEM coupling method has become an essential means to study the movement characteristics of materials in the airflow, simulate the working characteristics, and optimize the structural parameters.

Separation is a complicated gas-solid two-phase flow coupling process, the physical properties of the whole system are very complicated due to the multiple kinetic energy exchange and fluid changes, the collision between particles, and the interaction between the fluid and particles. Chen et al. used CFD-DEM method to simulate the separation process of rice husk and brown rice, elucidated the process of rice husk separation and explored the mechanism of brown rice loss and rice husk retention by analyzing the collision process of rice husk in the separation pipe19. Wang et al. simulated the movement of threshed corn mixtures in a typical cleaning device, analyzed the factors affecting the tendency of particles to penetrate the sieve holes as well as the various behaviors of particles penetrating the sieve holes, and provided a decision for improving the performance of corn cleaning20. Yuan et al. used the CFD-DEM method to numerically calculate the axial flow and radial stratification phenomenon of rice grain mixture in the separation device and simulated the influence of the diameter and rotation speed of the cylindrical sieve on the particle movement rule and screening characteristics21. Fu designed a variable-slope sieve with a hole structure to improve the cleaning performance of corn cleaning device. The coefficients such as relative mobility and sieve mass ratio were analyzed by CFD-DEM method, and the results showed that this structure was better than the traditional structure in terms of cleaning performance22.Liu through the analysis of screen surface flow velocity and the simulation of the movement of rice grains and impurities under the influence of vortices was carried out23.Amini, Y demonstrated the applicability of CFD simulation in investigating the behavior of fluids in microfluidic devices24.

In this study, the CFD-DEM method was used to simulate the separation process of shell kernel, and the influence of wind speed and air channel angle on the airflow field characteristics and particle movement trajectory was studied, which provided the theoretical basis and technical reference for the design of household-type sunflower seed huller. This paper presents several highlights. First, a kind of shell-kernel separation device applicable to household small sunflower seed hullers was developed. Second, the main factors affecting the shell-kernel separation performance were identified. Third, a coupled simulation of the shell-kernel separation process was constructed. Fourth, the influence law of each factor on the shell-kernel separation was obtained. Finally, the optimal parameter combination was successfully obtained by constructing a multi - factor orthogonal model.The implications of these findings are discussed in order to synthesise them to provide clearer evidence and an evidence-based basis for future research and practice.

Materials and methods

Material properties of sunflower seed kernel and sunflower seed shell

The sunflower seeds used in this study were purchased from “Shihezi Green Pearl Jiuding Market” under the brand name “Chaka Sunflower Seeds”, sunflower kernels and sunflower hulls were obtained by crushing, and the moisture content of the dry basis was 7%±1%. The experiment site was located in Shihezi City, Xinjiang, 85°59′E, 44°19′N, with an atmospheric pressure of 101 KPa, a temperature of 23°, and a relative humidity of 35%. Polylactic acid (PLA) was used to manufacture air channel, shell collection area, and kernel collection area.

The triaxial dimensions of sunflower seed kernels were measured using electronic caliper, the density was measured by drainage method using the electronic balance and a measuring cylinder25. The Shear Modulus and Poisson’s Ratio of sunflower seed kernels and sunflower seed shells were obtained by compression using the Texture Analyzer26,27, the Suspension Speeds were obtained by Suspension Speed Test Stand28, the Coefficient of Static Friction between sunflower seed kernel, sunflower seed shell and PLA were obtained by the slope method, respectively29, the Coefficient of Restitution between sunflower seed kernel, sunflower seed shell and PLA were measured by the Collision Method30. The material properties of sunflower seed kernel, sunflower seed shell and PLA are shown in Tables 1 and 2, and 3.

Table 1 Material properties of the sunflower seed kernel, shell and PLA.
Full size table
Table 2 Weight and specific gravity of each component of sunflower seed.
Full size table
Table 3 Parameters of contact between particles.
Full size table

Structure and working principle

Structure

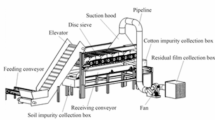
The shell kernel separation device mainly consists of feeding device, angle adjustment plate, particle inlet, shell collection area, air channel, kernel collection area, wind speed sensor, fan, Power adapter, as shown in Fig. 1.

Fig. 1
figure 1

Structural diagram and working principle sketch of shell kernel separation device. (1) Feeding device (2) Material (3) Angle adjustment plate (4) Particle inlet (5) Shell collection area (6) Air channel (7) Kernel collection area (8) Wind speed sensor (9) Fan (10) Power adapter.

Full size image

Working principle

As shown in Fig. 2, under the action of airflow, sunflower seed shells will be blown out of the air channel into the shell collection area, sunflower seed kernels will slide into the kernel collection area along the lower wall surface of the air channel. There is an overlapping interference phenomenon between the particles. The airflow acts on the front-end particles, which are hindered by the front-end particles, to form a longitudinal airflow, which produces a wind resistance effect on the back-end particles31. The force analysis of the movement process of the particles, when the particles from the inlet into the air channel, in the process of falling, by the wind FD, gravity G, resistance Fr, if the particles are blown out of the air channel, you need to meet:

$$\left\{ \begin{gathered} G=\rho V{\text{g}} \hfill \\ {G_x}=G\sin \alpha \hfill \\ {G_y}=G\cos \alpha \hfill \\ {F_{rx}}={F_r}\sin \alpha \hfill \\ {F_{ry}}={F_r}\cos \alpha \hfill \\ {F_D}+{F_{rx}}>{G_x} \hfill \\ \end{gathered} \right.$$
(1)
Fig. 2
figure 2

Analysis of shell kernel separation process.

Full size image

When the particles fall to the lower wall of the air channel, the particles are subject to wind parallel to the air channel FD, gravity G, friction Ff, support FN, will be decomposed along the direction of gravity G. If the particles sliding down the lower wall of the air channel are:

$$\left\{ \begin{gathered} {F_N}={G_y} \hfill \\ {G_y}=G\cos \alpha \hfill \\ {G_x}=G\sin \alpha \hfill \\ {F_f}=\mu {F_N} \hfill \\ {F_f}+{G_x}>{F_D} \hfill \\ \end{gathered} \right.$$
(2)

Where µ-the friction coefficient between the particles and the air channel wall; Gx-the force of gravity parallel to the direction of the air channel, N; Gy-the force of gravity perpendicular to the direction of the air channel, N; α-the angle of the air channel; Fr-the air resistance, N; Fry-the force of air resistance perpendicular to the direction of the air channel, N; Fry-the force of air resistance parallel to the direction of the air channel, N.

According to formula (1) and (2), the trajectory of the particles is related to the air channel angle and wind speed in addition to density and mass.

Selection of fans

The fan choice is crucial for the quality of shell kernel separation, which is the key to the effect of shell kernel separation. The air volume provided by the fan needs to meet the following11.

$$\left\{ \begin{gathered} {Q_0}=\frac{{b\phi }}{{\delta \rho }} \hfill \\ b=\frac{Z}{{60 \times 1000}} \times (0.25\sim 0.3) \hfill \\ \end{gathered} \right.$$
(3)

Where: Q0-airflow rate at the airflow inlet, m3/s; b- Feeding amount of sunflower seed kernel and sunflower seed shell was taken as 1.5/s, and a single sunflower seed was 0.25–0.3 g, i.e. 0.000375kg/s-0.00045kg/s; ϕ-mass fraction of anemone shell accounted for by sunflower seed, taken as 36%; Z-total number of anemone entering the huller in a unit of one minute, taken as 80 grains; δ-mass fraction of sunflower seed shell particles in the air stream of separated sunflower seed shell, taken as 20%11; ρ-air density, taken as 1.2 kg/m3.

From the formula (3), to get 0.00056m3/s < Q0 < 0.00068m3/s. The suspension velocity of the sunflower seed kernel is 4.89m/s, the suspension velocity of the sunflower seed shell is 2.23m/s, and the airflow velocity at the airflow outlet should be greater than the partial velocity of the suspension velocity of the sunflower seed shell parallel to the direction of the air channel, and smaller than the partial velocity of the suspension velocity of the sunflower seed kernel parallel to the direction of the air channel.

$$\left\{ \begin{gathered} v=(2.23\sim 4.89)\sin \alpha \hfill \\ s=\frac{{{Q_0}}}{v} \hfill \\ s={a^2} \hfill \\ \end{gathered} \right.$$
(4)

Where: v-to achieve the separation purpose of the airflow speed in the duct, m/s; s- air channel cross-sectional area, m2; a–air channel width, m.

Q0 = 0.000675m3/s cross-sectional area of the air channel is s = 329mm2, then a = 18.1mm. Considering the wind resistance effect of sunflower seed kernels and shells in the process of falling, in order to reduce the impact on the separation process, it should be ensured that the sunflower seed kernels in the falling process have sufficient time, and then combined with the commercially available fan, so set the length and width dimensions of air channel a1 = 60mm, and at the same time, in order to satisfy the separation speed, then there are:

$$Q=(2.23\sim 4.89)\sin \alpha \times {a_1}^{2}$$
(5)

Calculated Q = 0.0072m3/s, select fan FFR0612DHE, parameters as shown in Table 4.

Table 4 Parameters of axial fan.
Full size table

CFD-DEM calculation method

Gas-phase modeling

In order to analyze the motion characteristics of the two gas-solid phases, a mathematical model based on EDEM and CFD is established to theoretically explain the motion of the airflow and particles in the separation device8.

$$\frac{{\partial \left( {{\varepsilon _g}{\rho _g}} \right)}}{{\partial t}}+\nabla \cdot \left( {{\varepsilon _g}{\rho _g}{\upsilon _g}} \right)=0$$
(6)
$$\frac{{\partial \left( {{\varepsilon _g}{\rho _g}{\nu _g}} \right)}}{{\partial t}}+\nabla {\text{.}}\left( {{\varepsilon _g}{\rho _g}\nu _{g}^{2}} \right)= - {\varepsilon _g}\nabla P+{\varepsilon _g}\nabla \tau +{\varepsilon _g}{\rho _g}g - {R_{g\rho }}$$
(7)
$${R_{gb}}=\frac{{\mathop \sum \nolimits_{{i=1}}^{n} {F_i}}}{{{V_{\text{c}}}}}$$
(8)

Where εg is the gas volume fraction, ρg is the gas density, kg/m3; Vg is the gas flow rate, m/s; t is the time, s; P is the pressure on the gas micromeres, Pa; g is the gravitational acceleration, m/s2; Rgp is the momentum source term, τ is the gas kinetic viscosity; Fi is the drag effect of the particles on the gas, N; Vc is the volume of the grid cell, m3.

Particle contact collision modeling

Data exchange occurs between EDEM and FLUENT in the coupling process, necessitating considering particle-particle collisions and particle-the lower wall of the air channel collisions. To address this, the Hertz-Mindlin non-viscous contact model is employed. According to Newton’s second law, the motion equation of the ith particle are19,32:

$${m_i}\frac{{\partial {V_i}}}{{\partial t}}={m_i}g+{F_D}+{F_P}+(\sum\limits_{{i=1}}^{{{k_c}}} {\mathop F\nolimits_{{c,i}}^{p} )}$$
(9)
$${I_i}\frac{{\partial {\omega _i}}}{{\partial t}}=(\sum\limits_{{i=1}}^{{{k_c}}} {{T_{t,ij}}+{T_{r,ij}})}$$
(10)

Where Vi is the velocity of particle, m/s; ωi is the angular velocity of particle i, rad/s ; Ii is the rotational moment of inertia of particle i, kg·m2; mi is the mass of particle i, kg; FD is the fluid resistance, N; FP is the fluid pressure gradient, N;\(\mathop F\nolimits_{{c,i}}^{p}\) is the collision force with the i on the outer surface of particle p (kc is the number of contact balls per particle surface); Fn, ij is the normal component, N; Ft, ij is the tangential component, N; Tt, ij is the tangential torque, N/m; Tr, ij is the rolling friction torque, N/m.

The contact forces between particles and particles and particles and the inner wall of the air channel are decomposed into normal force Fn, ij, normal damping force Fnd, i j, tangential force Ft, i j, and tangential damping force Ftd,i33, as shown in Fig. 3.

$$\mathop F\nolimits_{{c,i}}^{p} ={F_{n,ij}}+F_{{n,ij}}^{d}+{F_{t,ij}}+F_{{t,ij}}^{d}$$
(11)
$${F_{n,ij}}=\frac{4}{3}{E^ * }\sqrt {{R^ * }} \delta _{{n,ij}}^{{\frac{3}{2}}}$$
(12)
$$F_{{n,ij}}^{d}= - 2\sqrt {\frac{5}{6}} \frac{{lne}}{{\sqrt {{{(lne)}^2}+{\pi ^2}} }}\sqrt {{S_{n,ij}}{m^ * }} {\nu _{n,pq}}$$
(13)
$${S_{n,ij}}=2{E^ * }\sqrt {{R^ * }{\delta _{n,ij}}}$$
(14)
$${F_{t,ij}}=\left\{ \begin{gathered} - {\delta _{t,ij}}{S_{t,ij}}for\,\left| {{F_{t,j}}} \right|<{u_s}\left| {{F_{n,ij}}} \right| \hfill \\ {u_s}\left| {{F_{n,j}}} \right|\frac{{{V_{t,pq}}}}{{\left| {{V_{t,pq}}} \right|}}for\,\left| {{F_{t,j}}} \right| \geqslant {u_s}\left| {{F_{n,ij}}} \right| \hfill \\ \end{gathered} \right.$$
(15)
$$F_{{t,ij}}^{d}= - 2\sqrt {\frac{5}{6}} \frac{{lne}}{{\sqrt {{{(lne)}^2}+{\pi ^2}} }}\sqrt {{S_{t,ij}}{m^ * }} {v_{t,pq}}$$
(16)
$${S_{t,ij}}=8{G^ * }\sqrt {{R^ * }{\delta _{n,ij}}}$$
(17)

where F is is the total force acting on the particle, N; δn, i j and δt, ij are the overlap between particle p and particle q; E* is the equivalent Young’s modulus, Pa; R* is the equivalent radius, m; m* is the equivalent sphere mass, kg; St, ij is the tangential stiffness, N/m; Sn, ij is the normal stiffness, N/m; vn, pq is the normal component of the relative velocity of the contact, m/s; vt, pq is the tangential component of the relative velocity of the contact, m/s; e is the recovery coefficient of the particle p; G* is the equivalent shear modulus, Pa; us is the coefficient of sliding friction; and Vt, p q is the relative tangential velocity of the contact, m/s.

Fig. 3
figure 3

Particle contact model.

Full size image

The mathematical formulas for the tangential moment and rolling friction moment are:

$${T_{t,ij}}={R_i}{F_{n,ij}}$$
(18)
$${T_{r,ij}}= - \mu {R_i}{F_{t,ij}}{\omega _i}$$
(19)

where µ is the coefficient of rolling friction; Ri is the unit direction vector from the center of mass of the particle to the point of contact, ωi is the unit vector of angular velocity at the point of contact of the particle, rad/s.

Simulation modeling

Simulation model

To save computational time on the computer, the separation device was simplified in this study, as shown in Fig. 5. The separation device was modeled using SolidWorks and was imported into ANSYS Workbench and meshed.

Geometric modeling of particles

Sunflower seed shells have an irregular shape and should be obtained using the 3D scanning technique in the modeling process. However, the length-to-thickness ratio of the sunflower seed shell size is too large to generate too many particles when using particle filling in the EDEM. In order to save computational time, the sunflower seed shells were simplified in the simulation experiments to ensure that the simulation volume of the sunflower seed shells was the same as the volume of the sunflower seed shells obtained by 3D scanning the sunflower seed shell to minimize the error in the simulation. As shown in Fig. 4a. SolidWorks modeled the sunflower seed shell and sunflower seed kernel. They were converted to IGES format and imported into the EDEM, and then the API (Application Programming Interface) of the EDEM to generate the particle models.

Fig. 4
figure 4

Geometric modeling and kinetic analysis of particles during their falling.

Full size image

Kinetic analysis of particles during their falling

Due to the different material properties of the sunflower seed shell and sunflower seed kernel, the vertically falling particles will show different trajectories after being subjected to different airflow. As shown in Fig. 4b–d.

$$\left\{ \begin{gathered} {F_{D{\text{xi}}}}={F_D}_{i} \cdot \cos {\alpha _i} \hfill \\ {F_{D{\text{yi}}}}={F_{Di}} \cdot \sin {\alpha _i} \hfill \\ {\beta _i}=\arctan \frac{{{F_{D{\text{xi}}}}}}{{\rho {\text{v}}g - {F_{Dyi}}}} \hfill \\ {F_i}={F_{D{\text{xi}}}} \cdot {\text{sin}}{\beta _i} \hfill \\ \end{gathered} \right.$$
(20)

Where βi is the throw angle°; FDi is the wind force, N; FDxi is the component force of the wind in the x direction, N; FDyi is the wind force in the y direction, N; αi is the air channel angle, °; ρ is the density of the particles, kg/m3; V is the volume of the particles, m3; Fi is the resultant force, N.

The throw angle is larger, and the combined force is larger, the horizontal displacement of particle motion is large3. For different kinds of particles, as shown in Fig. 4b, the wind force and the air channel angle are constant, the smaller the gravity of the particles is, the larger the throw angle of the particles and the combined force are; for the same kind of particles, as shown in Fig. 4b and c, the air channel angle is constant, the larger the wind force is, the larger the throw angle of the particles and the resultant force are.

Setting of simulation parameters

In this study, FLUENT19.2 and EDEM2020 were used to carry out the relevant coupling simulation experiment. The Eulerian multiphase flow model is used in the process of separation. The airflow field was modeled in FLUENT using the standard k-ε viscosity model with a gas density of 1.225 kg/m3, a viscosity of 1.7894 × 10− 5, and a gravitational acceleration of 9.8m/s3. In the coupled simulation module, the Freestream Equation traction model, Saffman Lift, and Magnus Lift models were selected in the coupling simulation module to simulate the force of the airflow field on the particles. The material property parameters and the particle collision coefficients are shown in Tables 1 and 3.

A Particle factory is arranged at the material inlet of the separation device. The quantity ratio of sunflower seed kernel and sunflower seed shell is 2:5. The sunflower seed kernel production rate to 1.5/s, and the sunflower seed shell production rate to 3.75/s. The diameter and size of filled sunflower seed kernels and sunflower seed shells are distributed by normal distribution. The total particle generation time is set to be 52s to ensure the accuracy of the separation rate and loss rate of shells and kernels in the simulation process, and the total simulation time is 54s. To ensure that the time step in Fluent is much larger than that in EDEM and is an integer multiple, the time step in Fluent and EDEM are set to 5 × 10− 4 and 5 × 10− 6, and the number of time steps in Fluent is set to 108,000, respectively.

Bench experiment

Experiment materials

Sunflower seed kernels and sunflower seed shells from 2.1. The experiment apparatus included: shell-kernel separation device, air speed sensor (WD4200), wind speed regulator (ZK-BMG), and electronic balance.

Experiment methods

Sunflower seeds were broken to obtain complete shells and kernels as experimental materials, according to the results of the above simulation experiments, the speed of the fan was adjusted using a wind speed regulator(ZK-BMG) to achieve the optimal operating parameters, and then according to the mixed shell kernel quantity ratio of allocated shell kernels were fed into the shell-kernel separation device, and then after completing the shell kernel separating experiments, the shell and kernels were weighed separately, and the shell kernel separating rate and the rate of loss were calculated.

Validation experiment

According to the above analysis of the results, the bench experiment, according to the better factor level combination A2B3 (wind speed 6 m/s, air channel angle 31 °) for the experiment, repeat the experiment three times to take the average value, the experiment results are shown in Table 5, the shell kernel separation rate of 89.91%, the loss rate of 6.24%, proving the rationality of the device and meet the shell kernel separation device of household sunflower seed huller.

Table 5 Bench validation experiment.
Full size table

Results and analysis

Simulation analysis

Simulation analysis of air channel scheme 1

As shown in Fig. 5a, this is a dimensioned view of the separating device using the air channel scheme 1. Figure 6-a shows the pressure cloud, velocity cloud, and velocity vector images on the symmetric cross-section of the air channel for this scheme. The air channel’s pressure distribution from zone A to zone B is relatively uniform, while the pressure from zone B to zones C and D increases in a gradient. Since zones C and D are farther away from the outlet, the pressure in zones C and D is higher, and the airflow velocity is lower. The shell moves toward the pressure transition in zone C, facilitating the separation process.

Fig. 5
figure 5

Air channels sizing diagrams for different schemes.

Full size image
Fig. 6
figure 6

Air channel pressure cloud image, velocity cloud image and velocity vector image of different schemes.

Full size image

However, according to the data shown in Table 6, when the air channel angle α is 25°, and the wind speed v is 6 m/s, the separation effect of the air channel scheme 1 device is poor. The kernel collection rate is only 64.25%, while the loss rate reaches 5.87%. As shown in Figs. 7 and 8a, the motion of the shell kernel inside the air channel is captured, and the different particles exhibit significant velocity differences as they enter the air channel from the particle inlet, which can be observed by their velocity coding. The sunflower seed kernel’s trajectory is almost vertically downward, while the sunflower seed shells are aggregated with each other, resulting in a decrease of the average velocity in the x-direction, which eventually enters the kernel collection area along the lower wall surface of the air channel. These results indicate that the low shell-kernel separation rate of the separation device under this air channel design is mainly caused by the mutual collision between particles. In addition, according to Fig. 8b, which shows the average value of the combined force on the particles during the separation process, the main source of this force is the mutual collision of the particles during their fall and on the lower wall of the air channel, which then affects the separation effect.

Fig. 7
figure 7

Simulation for air channel angle α = 25° and wind speed v = 6 m/s.

Full size image
Fig. 8
figure 8

Average velocity of the particle at the x-direction and the average of the combined force on the particle.

Full size image
Table 6 Separation effect of air channel angle α = 25°, wind speed v = 6m/s.
Full size table

Simulation analysis of air channel scheme 2

In order to improve the separation effect and reduce the influence of wind resistance on the separation process, a baffle plate was additionally installed in the air channel, as shown in Fig. 4b. Some shells and kernels above the baffle complete the separation under the airflow action. The shells and kernels that have not completed the separation will slide to the area below the baffle and eventually be blown out the air channel. As shown in Fig. 6b, the pressure in the air channel gradually increases from zone C to zones D and E and is more concentrated at DE.

Simulation analysis of air channel scheme 3

A further improved air channel scheme is shown in Fig. 4-c, which mainly consists of components such as an airflow inlet, material inlet, sunflower seed shell outlet, sieve, sunflower seed kernel, and baffle with vent. The inlet is set to 25°, and the kernel with a larger mass enters the inside of the air channel before the shell with a smaller mass; the airflow entering from the inlet is divided into two parts: the airflow below the baffle enters the upper area through the holes. The particles fall onto the baffle, the airflow entering through the vents in the baffle acts on the particles, the particles of smaller mass shake on the baffle, and the airflow acts on the shaken particles to complete the second separation. As shown in Fig. 6-c, the airflow distribution in the air channel is more uniform, and the pressure of the airflow near the air inlet is high; when the airflow enters the B zone, the airflow is blocked by the curved baffle plate and enters the C zone through the vents on the baffle plate. The pressure gradient decreases from the C area to the D area to the E area; when the particles fall to the C area, it is conducive to the particles being blown to the E area.

Model validation

In order to accurately describe the separation effect under different wind speeds and air channel angles, it is stipulated that when the simulation ends, if the kernel is in the shell collection area or stays in the air channel, it belongs to the loss in the separation process. The shell kernel separation rate and loss rate refer to “The technical specification for the quality evaluation of sunflower seed shelling machinery”34. Therefore, two regions are plotted in EDEM post-processing, as shown in Fig. 9: region I, region II, region I is the shell kernel separation rate statistics region, and region II is the loss rate statistics region.

Fig. 9
figure 9

Statistical area of shell kernel separation rate and loss rate.

Full size image
$${E_d}=\frac{{{W_1}}}{M} \times 100{\text{\% }}$$
(21)
$${E_s}=\frac{{{W_2}}}{{{W_1}+{W_2}}} \times 100{\text{\% }}$$
(22)

Where Ed is the Separation rate of shell and kernel; Es is the loss rate; W1 is the kernel mass in region I, g; W2 is the total kernel mass in region II, g; M is the total kernel and shell mass in region I, g.

As shown in Fig. 10-a and b for the shell kernel separation device, in order to verify the reliability of the CFD-DEM coupling method in the simulation study. The separation process simulation was experimentally verified, as shown in Fig. 11-a and b. The shell kernel separation rate and loss rates during the simulation experiments were the same as the changes during the physical verification experiments. A wind speed air volume tester (TES-1340) was used to measure the airflow velocity at the shell outlet, as shown in Fig. 11-c, and the wind velocity at the shell outlet was tested under different air channel angles and wind speed.

Fig. 10
figure 10

Experiment bench for shell-kernel separation device of household-type sunflower seed huller and physical validation experiment diagrams. (1) Air channel (2) Frame (3) Serial port line (4) Transformer (5) Computer (6) Wind speed regulator (7) Kernel collection area (8) Wind speed air volume tester (9) Air speed sensor (10) Shell collection area.

Full size image
Fig. 11
figure 11

Comparison of simulation experiment and validation experiment results.

Full size image
$$C=\left| {\frac{{{U_1} - {U_0}}}{{{U_0}}}} \right|$$
(23)

As shown in Table 7, the T-tests comparing the results of the physical validation experiments with those of the simulation experiments showed that the P-values were all greater than 0.05. The relative errors were all less than 2.00%, indicating no significant difference between the results of the simulation experiments and those of the physical validation experiments. The accuracy and feasibility of the simulation study on the separation of the shell kernel based on the coupled CFD-DEM method were verified.

Where C is the relative error; U1 is the simulation test value; U0 is the physical test value.

Table 7 T-test and relative error of simulation and physical experiment results.
Full size table

Where P > 0.05, there was no significant difference between the simulation experiment and the physical validation experiment; /, Physical verification experiment agree with the results of simulation experiment.

Single factor simulation experiment and result analysis

Influence of wind speed on shell-kernel separation effect

As shown in Figs. 12-a and 13-a, the air channel angle α was set to 25°, and a single factor simulation experiment was carried out in a wind speed of 4m/s-9m/s. Both the shell kernel separation rate and the loss rate showed an increasing trend. When the wind speed was 4m/s, shells could not be blown out of the air channel due to the throwing angle β of the kernel and shell, the small resultant force F, and the interference of multiple particles. When the wind speed exceeds 6m/s, the shell kernel collection rate reaches more than 85%, and the loss rate reaches more than 15%. When the wind speed is 8 m/s-9 m/s, the throw angle β and the resultant force F of the particles are the largest, all shells and most of the kernel are blown into the shell collection area, the shell kernel separation rate reaches the maximum of 100%, and the loss rate is also large. After the above analysis, when the air channel angle is 25°, the optimal wind speed range is 5-7 m/s.

Fig. 12
figure 12

Simulation of shell-kernel separation under different wind speed and air channel angle conditions.

Full size image

Influence of air channel angle on shell-kernel separation effect

With a fixed wind speed of 6 m/s, a single factor experiment was carried out when the air channel angle α was 23–33°.As shown in Figs. 12-b and 13-b, when the air channel angle α = 23°, the shell kernel separation rate and loss rate were the highest, 96.25% and 75.07%, respectively. The reason is that the air channel angle α is the lowest, most of the shells are blown to the shell outlet because of their lightweight. Many of the kernels are trapped in the air channel due to excessive friction with the lower wall of the air channel when the air channel angle α is 25 ~ 31°, the shell kernel separation rate increases. When the air channel angle α is 31°, the shell kernel separation rate is 90.88%, and the loss rate is 7.12%. When the air channel angle α is 31 ~ 33°, the shell kernel separation rate decreases with the increase of the air channel angle α, the horizontal displacement of the sunflower seed shell decreases, and the particles collide with each other and finally slide into the kernel collection area. According to the above analysis, when the wind speed is 6 m/s, the optimal air channel angle is 27–31°.

Fig. 13
figure 13

Influence of wind speed and air channel angle on shell-kernel separation effect.

Full size image

Orthogonal experiments

Taking wind speed A and air channel angle B as experiment factors, and shell kernel separation rate Ed and loss rate Es as evaluation indexes, and carry out two-factor and three-level orthogonal simulation experiments according to the results of the single-factor experiment, the wind speed of 5 ~ 7 m/s and the air channel angle of 27 ~ 31° are the preferred intervals, and the levels of the factors are shown in Table 8.

Table 8 Factor level table.
Full size table

The experiment program and results and range analysis are shown in Table 9. After range analysis, the main order of the influence of each experiment factor on the shell-kernel separation rate Ed was A, B (wind speed, air channel angle), and the better level combination was A3B3, i.e., wind speed of 7m/s, air channel 31°; the main order of the influence of the experiment factor on the loss rate Es was A, B (wind speed, air channel angle), and the better level combination was A1B3, wind speed of 5 m/s, air channel angle 31°.

Table 9 Experiment results and range analysis.
Full size table

The results of the experiment were analyzed by ANOVA by applying IBM SPSS Statistics 27, as shown in Table 10. The effects of wind speed (A) and air channel angle (B) on the shell kernel separation rate Ed and loss rate Es were significant.

Table 10 Analysis of variance (ANOVA) of the results.
Full size table

In Table 10 (**extremely significant) P < 0.001, (*significant) P < 0.005.

In order to get the comprehensive effect of wind speed and air channel angle on shell kernel separation rate and loss rate of the separating device, the experiment results were weighted and analyzed according to the importance of each index by using the comprehensive score method, which prioritizes to ensure its lower loss rate, followed by its higher shell kernel separation rate according to the related separating device studies35,36, but this device serves the family, and the working efficiency is compared to the above mentioned studies, therefore, in order to avoid losses in the separation process, the shell kernel separation rate weighting coefficient was set to 0.3 and the loss rate weighting coefficient was set to 0.7 in this study, and the composite score was used as the evaluation index, and the composite score was calculated as follows:

$$Z=\frac{{D - {D_{\hbox{min} }}}}{{{D_{\hbox{max} }} - {D_{\hbox{min} }}}}$$
(24)
$$U=0.3{Z_1} - 0.7{Z_2}$$
(25)

where Z is the indicator affiliation; D is the indicator value; Dmin is the minimum value of the indicator; Dmax is the maximum value of the indicator; U is the composite score; Z1 is the degree of shell-kernel separation rate affiliation; Z2 is the loss rate affiliation.

Table 11 Comprehensive score and range analysis.
Full size table

As can be seen from Table 11, the influences of various experiment factors on the comprehensive score are as follows: wind speed and air channel. The optimal combination is A2B3, wind speed 6 m/s, and air channel 31°, shell kernel separation Ed rate was 90.88%, and loss rate Es was 7.12%.

Discussion

Although this study shows that wind speed and air channel angle affect the separation effect, there is a limitation that the device’s fan is always kept parallel to the air channel. Even if the air channel angle is changed, the distribution of the airflow field in the air channel cannot be changed, resulting in changes in the shell kernel separation rate without significant fluctuations. In the follow-up study, multiple groups of airflow were considered to act on the particles, the influence of the angle between airflow and the separation effect of wind speed was studied. The air duct angle, the inclination angle of the auxiliary fan, the wind speed of the main fan, and the wind speed of the auxiliary fan can be taken as the research objects to conduct experiments and obtain the optimal parameter combination.

Conclusion

  1. (1)

    The sunflower seed shell and kernel were modeled by studying the physical properties and contact parameters of the sunflower seed shell and the kernel. In the process of shell and kernel separation, the kinetic analysis of sunflower seed shell and sunflower seed kernel led to the conclusion that the factors affecting the effect of shell and kernel separation were the wind speed and the air channel angle.

  2. (2)

    SolidWorks was used to model the air channel structure without baffles. The separation of sunflower seed shell kernels in the air channel was simulated and studied by the CFD-DEM coupling method. The separation effect is poor, and the reasons for the poor separation effect are analyzed from the pressure distribution cloud image of the airflow field, the velocity cloud diagram, and the post-processing results of EDEM software. The final air channel scheme is determined by optimizing the air channel structure and referring to the pressure and velocity diagrams of the optimized air channel airflow field. The shell kernel separation and loss rates under different factors were compared with the simulation results by setting up experiments.

  3. (3)

    The comprehensive scoring results of the orthogonal experiment showed that the main and secondary factors affecting the separation effect were air channel angle and wind speed; the best combination of working parameters was wind speed of 6 m/s and air channel angle of 31°, under which the separation rate of shells and kernels was 90.88%, and the loss rate was 7.12%. The bench experiment shows that under this parameter condition, the separation rate of the shell kernel is 89.91%, and the loss rate is 6.24%.