Introduction

According to the statistics of the International Union of Railways (UIC), railway is still one of the most important transportation modes in the world. In recent years, with the rapid development of high-speed railway construction in many countries, the percentage of high-speed railway operating mileage is increasing year by year worldwide. With the increase of train speed and construction scale, the environmental vibration problems induced by high-speed railway trains has attracted wide attention at home and abroad1,2,3, which may lead to adverse effects on the production and life of the neighboring residents and the safety performance of the building structure4,5,6.

At present, there have been many influential studies on the ground vibration induced by high-speed railway trains, and most of them focused on the propagation characteristics, assessment method and attenuation prediction model. The research methods were mainly about field test, numerical calculation and finite element simulation7,8,9. Among them, the field monitoring test is one of the most direct and effective means to obtain the ground vibration signals around high-speed railways10,11, and it is also an important reference to other research methods12,13,14. However, limited by the layout range of field monitoring stations and existing building structures, the ground vibration induced by high-speed railway trains hundreds of meters or even farther away from the high-speed railway always needs to be predicted by numerical calculation or finite element simulation.

In the study of the ground vibration characteristics, Krylov15 analyzed the field test results and concluded that when the operation speed of high-speed trains exceeds the Rayleigh wave velocity on the ground surface, the ground vibration level increased significantly; Xia16 and Zhai17 conducted field monitoring test and found that the vibration characteristics and propagation laws of monitored vibration signals induced by high-speed railway trains around the railway were closely related to the train operation speed and soil medium properties. And with the train operation speed increasing, the vibration level on ground and adjacent building structures was significantly increased. In the study of vibration assessment method, the International Organization for Standardization(ISO) once developed a series standards of ISO263118,19,24,25. By taking the ISO standards as guiding reference, a lot of countries in the world developed related vibration assessment standards20,21,22,23,24,25,26,27,28,29,30,31,32,33, which suited their own national conditions. Therefore, the assessment index varies with the assessment object. However in general, the PPV is used for evaluating the vibration safety performance of building structures, the PPA used for evaluating human comfort perception in building structures, and the VLZ used for evaluating environmental vibration. And in the study of vibration attenuation prediction, Chen et al.28 discussed the applicability of Bornitz model for high-speed railway environmental vibration prediction. Lei29 and Luo et al.30 studied the of ground vibration assessment method, and put forward a dynamic response prediction model for building structures around high-speed railways. While Yang31, Wu32, Correia33 and Feng34 all studied the ground vibration characteristics as well as the propagation law around high-speed railways by three-dimensional finite element method.

In summary, scholars in this research field have made many valuable achievements, which laid a significant theoretical foundation for the further study. However, there still remains much room for us to explore in-depth. On one hand, most of the previous studies on vibration assessment around high-speed railways were carried out by only one single assessment index, so the assessment results could only reflected a certain aspect of all the vibration control requirements. On the other hand, due to the operation speed of high-speed railway train increasingly faster than that of traditional trains or subway trains, the empirical rail transit vibration attenuation formula might be no longer suitable for predicting the high-speed railway environmental vibration. And also, because the vibration wave field under the high-speed railway bridge was formed by the superposition of multiple piers vibration sources, the environmental vibration prediction model under the high-speed railway bridge was obviously different from that of the high-speed railway embankment, cutting or tunnel structure.

According to the above problems, this paper explored to propose a comprehensive multi-parameters assessment method for ground vibration induced by high-speed railway trains, and a refined ground vibration attenuation prediction model that accorded with the formation mechanism of the vibration wave field under the high-speed railway bridge. In addition, an application example by the refined prediction model was given, and the site selection distance threshold away from the high-speed railways under different types of environmental vibration function areas were divided. The results showed that by the proposed multi-parameters vibration assessment method, the vibration safety performance of building structures, comfort perception of human body and vibration limit of environmental vibration function areas were all taken into consideration comprehensively. Meanwhile, the developed vibration prediction model was verified with better accuracy and wider effective prediction range. The study was expected to provide a theoretical reference for the construction of ground vibration assessment system around high-speed railways, with potential engineering application value in ground vibration attenuation prediction and site selection of building structures under the high-speed railway bridges.

Field monitoring test and analyses

The field monitoring site and the measuring points’ layout in near-field were determined by referring to the field test work of Zhou et al.35. Differently, in order to further analyze the propagation and attenuation characteristics of far-field ground vibration signals induced by high-speed railway trains under the bridge, the field monitoring zone in this paper was extended to 10–200 m away from the high-speed railway, which was only 10–50 m in the monitoring test of35.

Field test situation and equipment

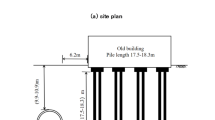
As shown in Fig. 1a, the test site was about 4.1 km away from the high-speed railway station, far away from vibration sources such as highway traffic, residential and industrial areas, which was helpful to arrange monitoring station and collect ground vibration signals induced by high-speed trains. As shown in Fig. 1b, the agricultural shed structure at the site cuts diagonally through the monitoring site zone, with the minimum distance 25 m far away from the high-speed railway to the wall and the maximum distance 30 m.

Fig. 1
figure 1

Field site situation and monitoring equipment.

Full size image

The test site area was widely distributed with wind-blown soil on ground surface, of which the shear wave velocity was between 233.64 m/s to 253.50 m/s, as silty clay in summer while seasonal frozen soil in winter. By sampling the soil at the monitoring site of vibration sensors, conducting indoor geotechnical test and direct shear test referring to the Railway Engineering Geotechnical Test Specification36, the basic physical and mechanical parameters were obtained, as shown in Table 1.

The test monitoring equipment was the Antenna-III high-frequency signal acquisition system developed by the Institute of Geology, China Earthquake Administration, and it’s sampling frequency could be as high as 10 kHz. As shown in Fig. 1c, d, the main components of the system included the host computer, data converter, data hub, high-frequency velocity-type vibration sensors and cables. Among them, the vibration sensors exhibited a maximum sensitivity of 100mV/(mm s− 1) over a frequency response range of 5–800 Hz, which could effectively be used to collect the medium and high frequency ground vibration signals introduced by high-speed railway trains. The layout of some certain measuring point was shown in Fig. 1e.

Table 1 Basic physical and mechanical properties of surface soil.
Full size table

Monitoring points layout and trains’ operating conditions

After selecting the field site, investigating geological environment and choosing monitoring equipment, the monitoring points was arranged with equipment parameters adjusted and pre-test carried out. And the main field monitoring test was carried out only when the background noise vibration was stable and could hardly influence the ground vibration signals induced by high-speed trains.

As shown in Fig. 2a, The monitoring station was located near the high-speed railway bridge piers No.145 ~ No.147 in Fuxin section of Beijing-Harbin high-speed railway. The diameter of the pier bottom was about 4 m and the distance between the adjacent piers was about 25 m. And also, the monitoring station was close to the downward line of high-speed railway from Shenyang to Beijing, while far from the upward line from Beijing to Shenyang. All 25 vibration sensors were buried in the shallow ground surface and deployed along three monitoring lines perpendicular to the track. The monitoring line l1 intersected with the central axis of the No.145 pier on the ground surface. The monitoring line l2 and l3 ran through the wall of agricultural shed structure, while there was no building obstacle in the direction of l1. The distance between l1 and l2 was 40 m, and the distance between monitoring line l2 and l3 was 20 m. The monitoring points along l1, l2 and l3 were arranged at unequal intervals, of which the minimum monitoring distance (the vertical distance between monitoring points and high-speed railway) was 10 m, while the maximum monitoring distance 200 m. The layout of field test monitoring points under high-speed railway bridge could met the characteristics variation of ground vibration signals. The dimension of the girder’s cross section was shown in Fig. 2b.

Fig. 2
figure 2

The monitoring station and girder’s cross section.

Full size image

There was 300 groups of ground vibration signals monitored, induced by 12 high-speed railway trains. The type and operating condition of each high-speed railway train were shown in Table 2.

Table 2 Train type and operating condition.
Full size table

Ground vibration characteristics and influencing factors

In order to avoid the interference of agricultural shed, taking the ground vibration signals collected in the direction of l1 as the study object. And by controlling variables, the influence of high-speed railway train type and operating speed on the ground vibration signals were revealed in both time domain and frequency domain.

When regarding the high-speed railway trains’ type as the only variable, referring to Table 2, we selected the collected ground vibration signals under the operation conditions of CR400AF-G (G928), CR400BF-G (G3604), CRH380BG (G3654)as the study object, of which the high-speed railway trains all ran by at a speed of 210 ± 6 km/h. The time and frequency domain characteristics of the ground vibration signals in l1 induced by the three types of high-speed railway trains were respectively shown in Fig. 3.

Fig. 3
figure 3

Time and frequency characteristics of ground vibration signals introduced by different types of high-speed railway train.

Full size image

When the high-speed railway train running by, the repeated excitation was caused by each carriage, which caused the periodic characteristic in the time-domain waveform. Therefore it could be found that the vibration waveform was all characterized with significant periodic characteristics in the time domain of Fig. 3a–c. Taking the vibration waveform in Fig. 3a as a typical example, the locations of each periodic peaks at N1 and N2 were clearly indicated. Meanwhile, by picking up the time at each vibration response peak, it was found that when under the same high-speed railway train’s operating condition, the time intervals between the adjacent response peaks at each monitoring point in l1 were almost the same. The time intervals in both Fig. 3a, b was about 0.45s, and that in Fig. 3c was about 0.42s.

While in frequency domain, combining with the total length and the number of carriages of each train in Table 2, by picking up the frequencies of main discrete spectral lines, it could be calculated that when the train type was CR400AF-G(G928) or CR400BF-G(G3604), the length of a single carriage was 26.13 m and the frequency interval of the collected signals between each group of discrete spectral lines were all about 2.2 Hz, while when the train type was CRH380BG(G3654), the length of a single carriage was 25.13 m and the frequency intervals were 2.4 Hz. It is obvious that when the running speed of each high-speed railway train was close to each other, the frequency intervals were inversely proportional to the length of each carriage.

While when regarding the operating speed of the high-speed railway trains in Table 2 as the only variable, the collected ground vibration signals under the operation conditions of G3695(100 km/h), G3696(150 km/h), G3654(200 km/h), G924(300 km/h) were considered as the study object, and the types of four trains were all CRH380BG.

The time and frequency domain characteristics of the ground vibration signals in l1 induced by the high-speed railway trains at four different operating speed were respectively shown in Fig. 4.

Fig. 4
figure 4

Time and frequency characteristics of ground vibration signals introduced by the high-speed railway trains at four different operating speed.

Full size image

It can be seen from Fig. 4 that, with the operation speed of CRH380BG-type high-speed railway trains increasing from 100 to 300 km/h, the peak value in time-domain vibration waveform at the monitoring point N1 increased from 0.08434 to 0.2285 mm/s, and the peak value in the frequency-domain increased from 1.414 × 10− 3 to 1.418 × 10− 2. That is, the ground vibration intensity increased by an order of magnitude in both time domain and frequency domain. Besides, the frequency range of main discrete spectral lines extended from 4.4 ~ 14.5 to 9.0 ~ 30.5 Hz, and the frequency intervals increased from 1.5 to 3.3 Hz, of which the frequency intervals were determined by the the train speed and vehicle length jointly. Therefore, it could be concluded that with the high-speed railway trains accelerating, the ground vibration energy increased greatly and the energy of ground vibration signals gradually transferred to the higher frequency part.

In addition, we named the frequency at the discrete spectral lines in each frequency spectrum as characteristic frequency. It could be found in Figs. 3 and 4 that under the operation conditions of each high-speed railway train, as the propagation distance increasing, the response peak value at each discrete spectral line rapidly decayed, while the values of characteristic frequencies remained unchanged. Picking up the characteristic frequencies of the ground vibration signals under the operating conditions of CR400AF-G (G928), CR400BF-G (G3604), and CRH380BG (G3654) in Fig. 3, it could be found that when the operating speed of the high-speed railway train was about 210 ± 6 km/h, the characteristic frequencies under the operating conditions of the three types of high-speed railway train were almost the same, which were respectively about 6.58 Hz ± 0.10 Hz, 8.78 Hz ± 0.10 Hz, 13.09 Hz ± 0.10 Hz, 15.18 Hz ± 0.10 Hz, 18.49 Hz ± 0.05 Hz, 20.70 Hz ± 0.05 Hz, and the characteristic frequency at the maximum peak value under each operating condition was all about 15.18 Hz ± 0.10 Hz. Due to that the model type of the three high-speed railway train G928, G3604 and G3604 was different, it could be inferred that the characteristic frequency 15.18 Hz had no relation to the type model of the high-speed railway train. While in Fig. 4a–c, the characteristic frequency at the maximum peak value in each spectrum under the operating conditions of G3695 (100 km/h), G3696 (150 km/h), G3654 (200 km/h), and G924 (300 km/h) was respectively 14.13 Hz, 16.41 Hz, and 15.18 Hz. And in Fig. 4d, the characteristic frequency also appeared around 13.51 Hz and 16.82 Hz when under the operating condition of G924 (300 km/h). Therefore, it could be inferred that the response peak in 14–16 Hz had no relation to the operating speed of high-speed railway trains either. Therefore, the vibration response characteristics in the frequency range of 14–16 Hz might be related to the structural characteristic of the high-speed railway bridge.

Ground vibration assessment

According to the “Ground vibration characteristics and influencing factors”, there was only slightly influence on the collected vibration signals especially in frequency domain when under different train types, while the operating speed of high-speed railway trains impacted significantly both the frequency response and energy distribution of the collected vibration signals. As result, the monitored ground vibration signals under the operating conditions of high-speed railway trains numbered G3695, G3696, G3654 and G924 were selected as the research objects in all the following study. According to Table 2, the trains’ types of G3695, G3696, G3654 and G924 were all CRH380BG, and their operating speed were respectively about 100 km/h, 150 km/h, 200 km/h and 300 km/h when running by the field monitoring station.

Firstly, taking PPV, PPA and VLZ as the assessment indexes respectively for the field ground vibration assessment, of which PPV was for vibration safety performance assessment of building structures, PPA for human perception comfort assessment and and VLZ for environmental vibration assessment. And then, based on the three separate assessment results as well as considering their advantages and disadvantages and application scope, a multi-parameters assessment method was proposed for field ground vibration induced by high-speed railway trains.

Vibration safety assessment of Building structures by PPV

As ISO recommended, PPV was regarded as control standard for vibration safety of building structures. And it was also stipulated the allowable vibration velocity peaks at the foundations of three types of building structures under traffic vibration in Chinese standard GB/50,868-201337, as shown in Table 3.

Table 3 The allowable peak vibration velocity at the foundation of Building structures under traffic vibration in GB/50868-2013.
Full size table

Picking up the PPV at each monitoring point, and performing the fitting and regression analysis by power function curve in the form of Sadov ‘s formula38. The results were shown in Table 4.

Table 4 Fitting results and regression coefficient of PPV power function curve.
Full size table

As we could see in Table 4 that no matter in the direction of l1, l2 or l3, the Regression coefficients R2 of PPV fitting equations were all more than 0.8, which were even more than 0.9 when under the operating conditions of G3654, G3696 and G3695. As a result, the fitting result was effectively good.

Taking PPV around high-speed railway as the maximum vibration limit of the foundation safety vibration of the adjacent building structures, while the allowable peak vibration velocity in Table 3 as the minimum vibration limit. In this work, we choose the minimum allowable peak vibration velocity 1 mm/s as the ground vibration assessment standard for vibration safety performance of the adjacent building structures. The ground vibration assessment by PPV in the whole field test areas was shown in Fig. 5.

Fig. 5
figure 5

Vibration safety assessment by PPV.

Full size image

Calculating the relative errors between the monitored PPV values and the predicted values at each measuring point in l1, l2, and l3. By comparative analysis, the results showed that within the whole field test zone except for 25–50 m away from the high-speed railway, the maximum predicted error at each monitoring point was always less than 20%. However, within the distance of 25–50 m away from the high-speed railway, the monitored PPV values in l1, l2, and l3 respectively exceed the predicted values by up to 68%, 126%, and 58%. As a result, the relative errors between the monitored values and the predicted values within the 25–50 m away from the high-speed railway were not normal prediction errors, but a local rebound amplification that appeared in the propagation of ground vibration waves induced by high-speed railway trains.

In the field test zone except for 25–50 m away from the high-speed railway, the max prediction error of PPV in l1 only varied from 4% to10%, while the relative error of PPV between the monitored values and prediction values in l2 and l3 varied within 12-18% and 12-41% respectively, which were as about 2 times and 4 times as that in l1. In addition, in the vibration rebound amplification area, the monitored value of PPV in l1 exceeded the predicted one by up to 68%, while in l2 and l3, it exceeded the predicted one by up to 126% and 58% respectively. As a result, it could be concluded that under the field monitoring condition in this article, the building structure had a significant influence on the propagation of ground vibration waves in l2 and l3.

It could be seen that the PPV curves attenuated in the form of power function curve as a whole. However, there appeared local rebound amplification in the range of 25–50 m away from the high-speed railway, as marked in Fig. 5, which was the comprehensive influencing result by various factors including site geological conditions, vibration source characteristic, propagation path of the ground vibration wave, resonance effects, and reflection effect in geological strata. And the faster the high-speed railway trains ran, the more significant the local rebound amplification. On the whole, the PPV of the ground vibration signals induced by each high-speed railway trains was always less than 1 mm/s. Therefore it could be concluded that within the field test area, the PPV of the ground vibration signals met the vibration safety control standard of the adjacent building structures, so the high-speed railway trains posed no threat to the safety performance of the planning building structures.

Human perception comfort assessment by PPA

According to ISO2631-199718, the perception threshold of Wk-weighted vibration acceleration peak for human bodies varied from 0.01 m/s2 to 0.02 m/s2, which was different due to individual physical quality. And among them, 50% people of perceptive and strong could perceive the peak vibration acceleration of 0.015 m/s2. The center frequencies in 1/3 octave band and weighting factors of Wk were shown in Table 5.

Table 5 The center frequencies in 1/3 octave band and weighting factors of Wk.
Full size table

In order to discuss the influence of ground vibration caused by high-speed railway trains on the human perception comfort, it was necessary to equivalently convert the collected field ground vibration signals from the velocity to the acceleration. According to Liu’s study39, for environmental vibration induced by rail transit, the relationship between vibration acceleration level (VAL) and velocity level (VL) at the ith central frequency in 1/3 octave band was

$$VA{L_i}=V{L_i}+20\lg \left( {2\pi f\left( i \right)} \right) - 60$$
(1)
Fig. 6
figure 6

Human body ‘s perception comfort assessment by PPA.

Full size image

where f(i) was the ith central frequency in 1/3 octave band, Hz. The VAL and VL were respectively as follows.

$$VA{L_i}=20\lg \left( {\frac{{a\left( i \right)}}{{{a_0}}}} \right)$$
(2)
$$V{L_i}=20\lg \left( {\frac{{v\left( i \right)}}{{{v_0}}}} \right)$$
(3)

In Eqs. (2) and (3), a(i) was the effective value of the vibration acceleration at the ith central frequency in 1/3 octave band; a0 was the reference value of vibration acceleration and a0 = 10− 6m/s2; v(i) was the effective value of the vibration velocity at the ith central frequency in 1/3 octave band; v0 was the reference value of vibration velocity and v0 = 10− 9m/s2.

According to Eqs. (1), (2) and (3), we conversed the monitored Wk-weighted vibration velocity at central frequencies in one-third octave band to the Wk-weighted vibration acceleration(aWk), that is

$${a_{Wk}}\left( i \right)=2\pi v\left( i \right)f\left( i \right){W_k}\left( i \right)$$
(4)

Picking up the peak values of aWk(i) at each monitoring point, which were exactly the PPA. Take the human body ‘s perception comfort threshold as the assessment standard for PPA, of which the minimum threshold was 0.01m/s2 while the maximum threshold was 0.02m/s2. The human body ‘s perception comfort assessment by PPA in the whole field test areas was shown in Fig. 6.

Due to that the similar operating conditions with the four high-speed railway train might appear repeatedly around the field test site, the human body’s comfort perception should be evaluated by the maximum monitored value of PPA under the four high-speed railway trains’ operation condition at each monitoring point. In Fig. 6a, the maximum monitored value of PPA at N1, N2 and N3 significantly exceeded the maximum threshold as 0.02 m/s2 of human body’s comfort perception, accounting for 29% of the seven monitoring points (N1-N7) in l1, and the maximum monitored value of PPA at N1, N2 and N3 significantly exceeded the minimum threshold as 0.01 m/s2 of human body’s comfort perception, accounting for 43% of the seven measurement points (N1-N7) in l1. In Fig. 6b, the maximum monitored value of PPA at N8-N14 significantly exceeded 0.02 m/s2, accounting for 67% of the nine monitoring points (N8-N16) in l2, and the maximum value of PPA at N8-N14 significantly exceeded 0.01 m/s2, accounting for 78% of the nine measurement points (N8-N16) in l2. In Fig. 6c, the maximum monitored value of PPA at N17-N21 significantly exceeded 0.02 m/s2, accounting for 56% of the nine monitoring points (N17-N25) in l3, and the maximum value of PPA at N17-N22 significantly exceeded 0.01 m/s2, accounting for 67% of the nine measurement points (N18-N25) in l3. Based on the layout positions in Fig. 2a of each measuring point, it could be summarized that under the field test condition in this paper, the largest influencing range of the ground vibration induced by high-speed railway train’s operation on human body’s comfort perception in l1 was 0–50 m away from the high-speed railway, while that in l2 and l3 were both about 0–100 m.

In addition, according to the analysis in Sect. 3.1, the building structure in the field test area influenced the propagation of vibration waves a lot in both l2 and l3. And by the comparative analysis of Fig. 6a–c, it could be found that based on the PPA evaluation index, the building structures expanded the influencing range of the ground vibration on human body’s comfort perception around high-speed railways.

Environmental vibration assessment by VLZ

Referring to ISO2631-1-199718, the Wk weighted VLZ was selected as the assessment indicator of ground vibration signals induced by high-speed railway trains. Taking the vibration limits in diurnal time of the IV-type vibration environmental functional areas (Table 6) in the latest edition of Chinese regulation GB 10070-201X40 as the assessment standard for VLZ, by calculating the effective value of vibration acceleration(ae) and the Wk weighted VLZ of ground vibration signals induced by the four high-speed railway trains, the environmental vibration assessment by VLZ in the whole field test areas was conducted and shown in Fig. 7. Before that, the expressions of ae and VLZ were represented as follows respectively.

Fig. 7
figure 7

Environmental vibration assessment by VLZ.

Full size image
$${a_{\text{e}}}=\sqrt {\sum\limits_{{\text{i}}} {{{\left( {a\left( i \right)} \right)}^2} \cdot {{10}^{\frac{{Wk\left( i \right)}}{{10}}}}} }$$
(5)
$$V{L_Z}=20\lg \left( {\frac{{{a_e}}}{{{a_0}}}} \right)$$
(6)
Table 6 The four types of vibration environmental functional areas and vibration limits in GB 10070-201X40.
Full size table

As we could see in Fig. 7a, in the direction of l1, with the propagation distance away from high-speed railway increasing, the VLZ of ground vibration signals induced by the four high-speed railway trains’ operation gradually attenuated. While in Fig. 7b, c, within the distance range of 25 ~ 45 m away from the high-speed railway in l2 and l3, the VLZ also local rebounded vibration amplification.

Due to that the similar operating conditions with the four high-speed railway train might appear repeatedly around the field test site, the environmental vibration assessment should be conducted by the maximum monitored value of VLZ under the four high-speed railway trains’ operation condition at each monitoring point. The results showed that within 0–200 m away from the high-speed railway in the field test, the maximum values of VLZ at the 7 monitoring points from N1 to N7 in l1, 9 monitoring points from N8 to N16 in l2, and 9 monitoring points from N17 to N25 in l3 all exceeded the daytime vibration limits of each type of vibration environmental functional area in Table 6, accounting for 100%. Therefore, when there was no vibration reduction measurements in the field test zone, within 10–200 m away from the high-speed railway, the ground vibration induced by train’s operation could not meet the construction standards according to Table 6.

A multi-parameters vibration assessment method

According to the Sect. 3.1, 3.2 and 3.3, it was found that the three types of ground vibration assessment results were totally different from each other. Therefore, there came to a conclusion that the ground vibration assessment results varied with different assessment indicators. Among them, in the whole field test zone, by PPV, the ground vibration induced by high-speed railway trains posed no threat to the safety performance of the planning building structures; By PPA, the ground vibration might caused psychological distress and even tension in human bodies, making the field unsuitable for long-term continuous activities; By VLZ, the field test zone was not suitable for planning and constructing environmental vibration function areas when without any isolation and vibration reduction measurements. In summary, the ground vibration assessment results of ground vibration induced by high-speed railway trains should not completely defined only by a single assessment indicator, while should be considered comprehensively from multiple perspectives, such as safety performance of building structures, human perception comfort, and environmental vibration influence. As a result, combined with the assessment results by PPV, PPA, VLZ and their influence range, a comprehensively refined multi-parameters assessment method for ground vibration around high-speed railways was proposed for the blank site around the high-speed railway.

Firstly, based on each assessment indicator and assessment standard value, the sensitive ground vibration range within the whole field test zone under the high-speed railway trains’ operation was separately divided. Among them, by the vibration assessment indicator of PPV, there was no sensitive vibration range that threatened the vibration safety performance of the building structures within 0–200 m away from the high-speed railway. And by PPA, the sensitive vibration range for human perception comfort was 0 ~ 100 m away from the high-speed railway. While by VLZ the significant sensitive vibration range for human living environment was 0 ~ 200 m away from the high-speed railway, covering the whole field test zone. Therefore, it could be concluded that within the field monitoring zone, among the three assessment indicators, the VLZ showed highly sensitive to the ground vibration, the PPA showed moderately sensitive and the PPV showed poor sensitive. On this basis, the ground vibration sensitivity and the sensitive vibration range by the three assessment indicators were arranged from small to large, and application sequence of the three assessment indicators was determined. Finally, according to the specialized vibration assessment object of each assessment indicator, a multi-parameters assessment method for ground vibration around high-speed railways was proposed, as shown in Fig. 8.

Fig. 8
figure 8

A multi-parameters assessment method for ground vibration along high-speed railways.

Full size image

Environmental vibration prediction

The study methods for rail traffic vibration prediction mainly included empirical formula prediction, field test, theoretical analysis and numerical calculation41. Due to the comparative analysis in Sect. 3.4 that the ground vibration induced by high-speed railway trains was the most sensitive under the assessment indicator of VLZ, we chose VLZ as the environmental vibration prediction index. Referring to the ground vibration attenuation formula under the railway traffic load in GB50040-199642, and considering the formation mechanism of the vibration wave field under the high-speed railway bridge, the environmental vibration attenuation prediction model under the superposition of multiple continuous piers vibration sources was explored to be developed and verified.

The empirical prediction formula of rail transit vibration Attenuation

With distance away from the high-speed railways increasing, the empirical prediction formula of ground vibration VLZ induced by rail transit operation was given for comparative analysis as43

$$V{L_Z}_{{\hbox{max} }}=V{L_Z}_{{0\hbox{max} }}+{C_{VB}}$$
(7)

where the VLZmax was the maximum z-vibration level at prediction point as the train passing through, dB; VLZ0max was the maximum z-vibration level at the vibration source, dB; CVB was the vibration correction value, dB.

When the field test environment was fixed and stable, under a certain high-speed railway train’s operating condition, the CVB only depended on the attenuation correction value of distance(CD). And for railway lines on the ground and elevated lines, the CD could be calculated by

$${C_D}=a\lg r+br+c$$
(8)

where, r was the distance away from the prediction point to the a certain bridge pier, m; a was related to the comprehensive attenuation coefficient of body wave and surface wave, which reflected the geometric attenuation characteristics of ground vibration wave; b was related to the specific coefficient of soil absorption and energy attenuation, which reflected the damping attenuation characteristics of the ground vibration wave; c was the amplitude coefficient related to vibration source and soil feature.

Based on Eqs. (7) and (8), the empirical attenuation formula of ground vibration VLZ under the operation of a certain high-speed railway train could be simplified as

$$VL_{Z} = a{\text{lg}} r + br + c^{\prime}$$
(9)

where c’ was a constant value related to the operation condition of the high-speed railway train and propagation medium of ground vibration wave.

According to the calculated value of Wk-weighted VLZ at each monitoring point induced by G3695, G3696, G3654 and G924 in the Sect. 3.3, the coefficients a, b and c in Eq. (9) were fitted, and the fitting results of ground vibration signals by the empirical attenuation formula under the four operating conditions were shown in Table 7.

Table 7 Fitting results of ground vibration signals by empirical Attenuation formula.
Full size table

It was found that under the four operating conditions of high-speed railway trains, the fitting coefficients R2 were all larger than 0.8 in the direction of l1, among which the R2 was larger than 0.9 under the operating conditions of G3695, G3696 and G924, representing good fitting effect. And it indicated that the empirical vibration attenuation formula for urban traditional rail transit was also applicable to the attenuation prediction for ground vibration under the high-speed railway bridge. While due to the propagation obstacles of agricultural shed walls, the fitting coefficients R2 of the empirical attenuation formula in l2 and l3 were significantly smaller than that in l1, resulting that the fitting results in l2 and l3 was poor.

Besides, it was found that in the direction of l1, l2 and l3, the fitting coefficients a and c were different under different operating conditions, which reflected the difference of attenuation characteristics of ground vibration surface wave and body wave. And the fitting values of |a| in l2 were obviously larger than that in l1 and l3. In contrast, due to that the shallow ground soil in field test area was evenly distributed, the coefficient b in the fitting empirical formula were approximately the same in l1, l2 and l3, which reflected the absorption characteristic of ground vibration wave by soil. According to Sect. 1.1 and Table D-4 in HJ435-201843, the shear wave velocity of the soil in the filed test area was 233.64 m/s ~ 253.50 m/s, and the soil type in the test site was medium-soft-soil, based on which the recommended coefficient b for the elevated railway line in HJ435-2018 should be -0.078. However, because the field test was carried out in winter, compared to the medium soft soil, the stiffness of the frozen soil the shallow ground surface was larger while the damping coefficient was smaller, the energy attenuation velocity of the ground vibration signals induced by high-speed railway trains in the field test area was slower than that in summer. Therefore, the fitting values of the coefficient b in Table 7 were all between − 0.06625 and − 0.06623, slightly larger than that recommended in HJ435-201843 (0.078), which was consistent with the practical engineering situation.

The refined prediction model of multi-piers vibration sources

According to the GB50040-199642 in China, the attenuation formula of the ground vibration induced by railway traffic loads was

$${A_r}={A_0}\left[ {\frac{{{r_0}}}{r}{\xi _0}+\sqrt {\frac{{{r_0}}}{r}} \left( {1 - {\xi _0}} \right)} \right]\exp \left[ { - {\alpha _0}f\left( i \right)\left( {r - {r_0}} \right)} \right]$$
(10)

where the r was the distance from the prediction point to the vibration source, m; Ar was the vertical acceleration amplitude at the prediction point, m/s2, of which the distance from the prediction point to the vibration source was r; A0 was the vertical acceleration amplitude at the vibration source, m/s2; f(i) was the disturbance frequency, Hz; ξ0 was the geometric attenuation coefficient related to the vibration area of the source; α0 was the energy absorption coefficient of soil, (s/m); r0 was the radius of the vibration source, m.

In practical engineering, as the high-speed railway train ran through, the ground vibration under the high-speed railway bridge was induced by a continuous excitation of multi-piers vibration sources44. Therefore, when considering the formation mechanism of the vibration wave field, it was necessary to consider the vibration source of the high-speed railway bridge as the superposition of multi-piers vibration sources. Regarding the radius of a pier as the radius of the a single-pier vibration source, the wave field under the vibration source load of a single pier was shown in Fig. 9.

Fig. 9
figure 9

The loading effect under a single-pier vibration source.

Full size image

Defining the piers directly affected by load of the high-speed railway train at a certain moment as the main loaded piers, which was the pier vibration sources causing the ground vibration at that moment. The main loaded piers under the loading of CRH380BG-type high-speed railway train K could be calculated by

$$K=\left\lfloor {\frac{{nL}}{{2{r_0}+l}}} \right\rfloor$$
(11)

where l was the distance between adjacent piers, n was the number of the carriages of the CRH380BG-type high-speed railway train, and L was the length of each carriage.

When the coordinates of the prediction point were (x, y), the distance from the prediction point to the kth main loaded pier rk was

$${r_k}=\sqrt {{{\left[ {x - \left( {{\text{k-1}}} \right)\left( {2{r_0}+l} \right)} \right]}^2}+{y^2}}$$
(12)

The main loaded piers under the action of CRH380BG-type high-speed railway trains were marked from P1 to PK in the order from left to right, as shown in Fig. 10a. And the superposition mechanism of vibration field in shallow ground surface under the action of multi-piers vibration sources was shown in Fig. 10b.

Fig. 10
figure 10

Formation mechanism of the vibration field under the high-speed railway bridge.

Full size image

Assuming that the train load was evenly distributed, the dynamic disturbance force and disturbance frequency f(i) acting on each pier source was the same, and the soil properties on the shallow ground surface under the bridge was consistent. According to the superposition formation mechanism of the vibration field under the high-speed railway bridge, the ground vibration attenuation model under the action of continuous multi-piers vibration sources was improved and established based on Eqs. (10), (11) and (12), as shown in Eq. (13).

$${A_r}=\sum\limits_{{k=1}}^{K} {{A_k}_{0}\left[ {\frac{d}{{2{r_k}}}{\xi _0}+\sqrt {\frac{d}{{2{r_k}}}} \left( {1 - {\xi _0}} \right)} \right]\exp \left[ { - {\alpha _0}f\left( i \right)\left( {{r_k} - \frac{d}{2}} \right)} \right]}$$
(13)

where the Ak0 was the vertical amplitude at the kth pier source, m/s2.

Furthermore, according to Eqs. (5) and (6), the ground vibration attenuation formula by VLZ (Wk-weighted) under the continuous multi-piers vibration sources simplified as

$$V{L_Z}_{r}=20\lg \left\{ {\sum\limits_{{i=1}} {\sqrt {\sum\limits_{{k=1}}^{K} {{A_{k0}}\left( i \right) \cdot {{\left[ \begin{gathered} \left( {\frac{d}{{2{r_k}}}{\xi _0}+\sqrt {\frac{d}{{2{r_k}}}} \left( {1 - {\xi _0}} \right)} \right) \hfill \\ \exp \left( { - {\alpha _0}f\left( i \right)\left( {{r_K} - \frac{d}{2}} \right)} \right) \hfill \\ \end{gathered} \right]}^2} \times {{10}^{\frac{{{w_k}\left( i \right)}}{{10}}}}} } \times {a_0}} } \right\}$$
(14)

According to the VLZ of ground vibration signals monitored under the four high-speed railway trains numbered G3695, G3696, G3654 and G924, the average value of Ak0 in Eq. (14) was fitted. According to Sect. 2.1 and 2.3, the distance between adjacent piers l was 25 m, the number of the carriages of the CRH380BG-type high-speed railway train n was 8, and the length of each carriage L was 25.13 m. So based on the Eq. (11), the number of main loaded piers K under CRH380BG-type high-speed railway train was calculated to be 7. Besides, according to GB50040-199643, for the field test area where the soil type was silty clay, the suggested geometric attenuation coefficient ξ0 was 0.45 and the energy absorption coefficient α0 was 1.45 × 10− 4 (s/m).

Verification of the refined prediction model

According to Sect. 3.1, the building structure in the field test area influenced the propagation of vibration waves a lot in both directions of the monitoring line l2 and l3. Therefore, we took the prediction results in l1 for the verification of the refined prediction mode and the prediction range was 0–500 m away from the high-speed railway. As shown in Fig. 11a, the predicted VLZ curves by both the refined multi-piers vibration sources prediction model and the empirical prediction formula under the operating conditions of G3695, G3696, G3654 and G924 were drawn respectively, and the monitored value of VLZ at each monitoring point in l1 were also specified. Besides, to make the comparison of the monitored values with the predicted ones more clear, the comparison within the whole field test zone(0–200 m away from the high-speed railway) was enlarged, as shown in Fig. 11b.

Fig. 11
figure 11

Comparative analysis of the refined prediction model with the field test and the empirical attenuation formula.

Full size image

It could be found in Fig. 11a that the predicted curves by the refined prediction model attenuated faster than the empirical prediction formula in the near-field of 0–100 m away from the high speed railway, while in the far field more than 100 m away from the high speed railway, the predicted curves by the empirical prediction formula attenuated faster.

From Fig. 11b, it could be seen that the prediction results by the refined multi-piers sources prediction model were obviously closer to the monitored ones. To clearly represent the superiority of the refined prediction model, we picked up the predicted value of VLZ in l1 under four high-speed railway trains by the two prediction models, and separately calculating the relative errors between them and monitored ones at each monitoring point. Naming |r1| as the prediction error by the empirical formula and |r2| as that of the refined model, the prediction accuracy of two prediction models was comparatively represented in Fig. 12.

Fig. 12
figure 12

Prediction accuracy comparison of the two attenuation models.

Full size image

From Fig. 12, it could be seen that |r2| was always less than |r1|, it came to a conclusion that the multi-piers vibration sources prediction model was verified with better prediction accuracy. Besides, under the four high-speed railway train’s operation, the number of measurement points with prediction error |r2| larger than 2% were respectively 0, 1, 3, and 3, accounting for 0%, 14%, 43%, and 43% of the total number of measurement points in l1. While the number of measurement points with prediction error |r1| larger than 2% were respectively 7, 8, 7, and 8, accounting for 71%, 86%, 71%, and 86% of the total number of measurement points in l1. Based on the refined model, the number of measurement points with |r2| larger than 2% was obviously less. Therefore, according to the quantitative analysis, the refined model was characterized with better predictive range.

An application example for ground vibration assessment and prediction

According to Sect. 4.3, the refined multi-piers vibration source prediction model in both prediction accuracy and effective prediction range was verified to be better than the empirical formula. Therefore, based on the refined prediction model and taking vibration limit in daytime in Table 6 as the environmental vibration assessment standard, under the four high-speed railway trains’ operation, the distance thresholds of the four environmental function areas within 0–500 m away from the high-speed railway, were divided in Table 8.

Table 8 The division of distance thresholds.
Full size table

It could be seen from Table 8 that by the refined prediction model, for the I-type environmental function area, the predicted distance thresholds under the operation condition of G3695 and G924 were respectively 174 m and 210 m, while there was no suggested construction place within 0 ~ 500 m away from the high-speed railway condition when under the operation of G3696 and G3654; For the II-type environmental function area, the predicted distance thresholds under the operation condition of G3695, G3696 and G924 were respectively 73 m, 464 m and 98 m, while there was no suggested construction place within 0 ~ 500 m away from the high-speed railway condition when under the operation of G3654; And for the III-type and IV-type environmental function area, there were relevant the predicted distance thresholds under all the four high-speed railway trains’ operation condition.

In summary, according to the ground vibration assessment and prediction results, within 0 ~ 500 m away from the high-speed railway bridge, it was probably unsuitable for the construction of both the I-type and II-type environmental function area, while the maximum distance thresholds for III-type environmental function area was 482 m and he maximum distance thresholds for IV-type environmental function area was 272 m.

However, in engineering practice, in order to avoid mutual interference between human activities and the operation safety of railway transit, the protection range away from the railway was only 0 ~ 10 m or 0 ~ 20 m. For example, the maximum protection range along the high-speed railway is 0 ~ 20 m in China ‘s “Regulations on the Administration of Railway Safety“45, which was significantly less than the predicted distance thresholds that met the daytime vibration limits of the four vibration environmental function areas. Therefore, it was necessary to take reasonable isolation and shock absorption measurements for the building structures along high-speed railways running through the existing urban buildings, as well as for the planning environmental function areas, which was outside the railway protection range while within the available distance thresholds.

Discussion

In order to make the refined prediction model under multi-piers vibration sources in Sect. 4.2 more generalized, the ground vibration under different spacing distances between adjacent piers was predicted by the refined prediction model and comparatively analyzed. Due to that the span of the high-speed railway bridge is generally 20–50 m in practical engineering, the spacing distances in numerical calculations were defined as 5 m, 10 m, 15 m, 20 m, 25 m, 30 m, 35 m, 40 m, 45 m and 50 m respectively. Taking the operation condition of 300 km/h (G924) as an example, the predicted attenuation curves under different spacing distances of the adjacent piers were respectively shown in Fig. 13, in which the x-axis represented the prediction distance and the y-axis represented the predicted value of VLZ.

Fig. 13
figure 13

Predicted attenuation curves under different spacing distances of the adjacent piers.

Full size image

Picking up the predicted values of VLZ at the prediction points that respectively 50 m, 100 m, and 150 m away from high-speed railways in each curve, and the attenuation and decrement percentage of the predicted VLZ at the same prediction point were calculated as the spacing distances between adjacent piers increasing, as shown in Table 9.

Table 9 The predicted VLZ and Attenuation under different spacing distances.
Full size table

By analysis of the predicted VLZ at the same measuring point, it was found that as the spacing distance between adjacent piers increasing, the VLZ value of gradually decreased. And when the spacing distance exceeded 30 m, the decrement percentage at all the prediction points were less than 1%, and the impact of spacing distance on ground vibration response weakened. We hoped that the influencing feature of the spacing distance between adjacent piers on the ground vibration response discussed above could provide a reference in bridge structures’ designing, combing with the structural safety performance and train operation stability.

Conclusion

  1. (1)

    The waveform of ground vibration signals induced by high-speed railway trains were characterized with significant periodic characteristics in time domain and equidistant discrete spectral lines in frequency domain. The train type had a little influence on the waveform in time domain merely, while the running speed of high-speed railway trains impacted a lot in both time and frequency domain. When the type of high-speed railway trains was all CRH380BG, with the high-speed railway trains accelerating from 100 km/h to 300 km/h, the results showed that the ground vibration energy increased by an order of magnitude. Meanwhile, the energy of ground vibration signals gradually transferred to the higher frequency part, among which the main frequency band transferred from 4.4 ~ 14.5 Hz to 9.0 ~ 30.5 Hz, and the frequency intervals of each group of discrete spectral lines turned from 1.5 Hz to 3.3 Hz.

  2. (2)

    Within the field test zone of 25 ~ 50 m away from the high-speed railway, there appeared local rebound amplification of the ground vibration induced by high-speed railway trains. The ground vibration assessment results showed that within 0–200 m away from the high-speed railway, the PPV of the ground vibration signals at each monitoring point were all smaller than 1 mm/s, which met the vibration safety control standard of building structures; In some areas, the PPA exceeded 0.01 m/s2 and even 0.02 m/s2, which might seriously affect the perception comfort of human body and unsuitable for continuous long-term human activities; In the whole field test zone, the VLZ of ground vibration signals at each monitoring point induced by G3654 almost all exceeded the daytime vibration limit of the IV-type environmental function areas, indicating that within 0–200 m away from the high-speed railway, the ground vibration induced by high-speed railway trains impact significantly on the human living environment and unsuitable for the construction of any type of environmental function area when without vibration isolation and reduction measurements.

  3. (3)

    According to influence of ground vibration on the building structures’ safety performance, human perception comfort and human living environment, the ground vibration sensitivity and the sensitive vibration range under the action of high-speed railway trains’ loading effect were respectively assessed and divided by PPV, PPA and VLZ. And by arranging them from small to large, the application sequence of the three assessment indicators was determined. Finally, combining with the assessment object of each indicator, a comprehensive multi-parameters assessment method for ground vibration around high-speed railway was proposed, which was expected to provide a theoretical reference for the construction of ground vibration assessment system around railways.

  4. (4)

    Based on the ground vibration attenuation formula under railway traffic loads in China’s GB50040-1996, combining with the superposition mechanism of multiple piers vibration sources in the wave field under the high-speed railway bridge, a refined ground vibration prediction model under the action of multiple continuous bridge piers vibration sources was proposed. By comparing to the field test results and the prediction results by empirical prediction formula in HJ435-2018, the results showed that by the refined prediction model, the value of the relative error |r2| varied only from 0 to 4.03% within 0 ~ 200 m away from the high-speed railway, which was smaller than |r1| all the time. It was concluded that the refined multi-piers vibration sources prediction model was verified with better prediction accuracy and wider effective prediction range than that of the empirical formula, with potential engineering application value in ground vibration attenuation prediction and site selection of building structures under the high-speed railway bridges.

  5. (5)

    Based on the proposed refined prediction model of multi-piers vibration sources under high-speed railway bridge and multi-parameters assessment method, the application example was given at last. The assessment and prediction results showed that within 0 ~ 500 m away from the high-speed railway bridge, when without isolation and shock absorption measurements taken, it was probably unsuitable for the construction of both the I-type and II-type environmental function area, while the probable distance for III-type environmental function area was 482 m or farther and the probable distance thresholds for IV-type environmental function area was 272 m or farther.