Introduction

In sports, controlling friction and slippage between equipment and the body is important for improving performance1,2,3,4 and preventing injury5,6,7,8. In baseball, pitching is an extremely challenging act that requires sensitive manipulation of the ball’s rotation with the fingertips to control the ball’s trajectory. Previous studies have found that pitch location is influenced by variability in joint kinematics and ball release timing9,10. Friction between the fingers and ball ensures grip of the ball during the pitching motion and at the moment of its release when the tangential force increases drastically with the rolling of the ball, which causes ball spin11. Shibata et al.12 also found that an increase in the tangential force component of the finger force contributed to an increase in the ball spin rate during fastball pitch. Thus, friction plays a key role in pitching performance, including ball spin and pitch control. Nevertheless, no study has assessed the relationship between baseball pitching performance and fingertip–ball friction.

In Major League Baseball (MLB), a strict ban on the use of adhesive substances led to a decline in pitching performance possibly due to changes in friction, such as a decrease in the ball spin rate13 and deterioration of pitch control14. Recent studies have shown that the friction coefficient between the fingertips and the ball’s leather sheet is affected by the application of water and grip-enhancing agents15,16, as well as the type of ball used17. However, it is unclear how these differences in the friction coefficient (i.e., slipperiness) due to finger–ball friction conditions affect the ball’s behavior during the releasing motion and the performance in baseball pitching.

When the friction condition between the fingertips and ball changes, the pitcher may feel the ball “slip” or “grip” during ball release. However, the ball’s behavior during the release process under different finger–ball friction conditions has not been fully understood. Studies have analyzed the forces acting between the fingertips and ball during the ball release process in baseball pitching11,18,19,20. However, it is unclear whether slippage occurs between the fingertips and ball when the friction coefficient is low, such as under wet conditions, and whether slippage does not occur when using grip-enhancing agents. During the acceleration phase following the late cocking phase in the motion of baseball pitching, the ball accelerates forward, leaves the thumb and begins to roll over the fingertips, and is finally released from the fingertips20. As the time between the ball leaving the thumb and its release is extremely short (approximately 10 ms20), high time-resolution motion analysis is required to investigate the relation between the fingertips and ball.

Therefore, this study aimed to estimate the slip distance between the fingertips and ball during the ball releasing motion in 4-seam fastball pitching under different friction conditions, using images from a high-speed camera. Moreover, the effects of the different friction conditions on the slip behavior and slip distance between the fingertips and ball were investigated. Furthermore, the relations of the slip distance with pitching performance indicators were investigated. We hypothesized that the ball–finger slip distance during ball release is significantly affected by the finger–ball friction coefficient, with it being greater under low-friction conditions, such as when wet with water, and shorter under high-friction conditions, such as when rosin powder or pine resin is applied. We also hypothesized that an increase in the slip distance reduces pitching performance, such as the spin rate and pitch control. As the roles of friction and slippage between the fingertips and ball in baseball pitching are still unclear, their clarification is desirable for improving pitching performance.

Results

Effects of finger–ball friction conditions on slip behavior and slip distance between the ball and fingertip

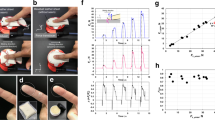
Figure 1A shows the time series change in the group mean ωball and a boxplot of ωball_max for each finger–ball friction condition. The group mean ωball was almost 0 rad/s at t = − 8.0 ms, indicating that little or no ball rotation occurred. Thereafter, ωball gradually increased and continued to increase until 1.0–2.0 ms before ball release, after which the value tended to remain almost constant. ωball tended to be lower in the water application condition than in the no application condition throughout the ball release process. Conversely, ωball tended to be higher in the rosin powder and pine resin application conditions than in the no application condition. Furthermore, differences in ωball between conditions became more pronounced as the release process progressed. These trends were observed in all participants (see Supplementary Fig. S1 online). In the Friedman test, ωball_max was significantly affected by the finger–ball friction condition (χ2(3) = 16.200, p = 0.001, N = 6, W = 0.900). In the post-hoc Dunn test with Bonferroni correction, ωball_max in the water application condition (160.6 ± 27.9 rad/s) significantly decreased by 28.8% and 28.9% compared with the rosin powder application (225.7 ± 10.2 rad/s, p = 0.005, r = − 1.369) and pine resin application conditions (225.7 ± 19.4 rad/s, p = 0.005, r = − 1.369), respectively. We confirmed that there was a strong positive correlation (r = 0.945, p < 0.001) between the ball spin rate calculated from ωball_max and that measured with a Doppler radar tracking system (Trackman, Vedaek, Denmark), with a root mean square error (RMSE) of 136.2 rpm (see Supplementary Fig. S2).

Fig. 1
figure 1

(A) Time series change in the group mean value of the ball angular velocity ωball, and a boxplot of the maximum ball angular velocity ωball_max. (B) Time series change in the group mean angular velocity of the vector from the ball center to the fingertip ωfc, and a boxplot of the maximum angular velocity of the vector from the ball center to the fingertip ωfc_max. (C) Time series change in the group mean difference between the ball angular velocity and angular velocity of the vector from the ball center to the fingertip Δωfb, and a boxplot for the maximum difference in angular velocities Δωfb_max for each finger–ball friction condition. In time series graphs, the solid line indicates the between-participant mean, and the shaded area indicates the between-participant mean ± standard deviation. t = 0 ms indicates the release time of the ball. In boxplots, circles with white spaces are the mean values within participants, and the black circle is the group mean value. * and ** indicate p < 0.05 and p < 0.01, respectively.

Full size image

Figure 1B shows the time series change in the group mean ωfc and a boxplot of ωfc_max for each finger–ball friction condition. The group mean ωfc was approximately 50 rad/s or less at t = − 8.0 ms, which is the time approximately when the thumb has left from the ball. After that, ωfc increased with increasing time, reaching a peak between t = − 1.0 and − 2.0 ms, and then decreased until the ball was released. There was no systematic trend in the time series variation of the group mean ωfc due to differences in the finger–ball friction conditions. These trends were observed in all participants (see Supplementary Fig. S3 online). In the Friedman test, the ball–finger friction condition did not significantly affect ωfc_max (χ2(3) = 0.200, p = 0.978, N = 6, W = 0.011), indicating that the movement of the index fingertip relative to the center of the ball during the ball release process was not affected by the finger–ball friction condition.

Figure 1C shows the time series change in the group mean Δωfb and a boxplot of Δωfb_max for each finger–ball friction condition. The group mean Δωfb tended to decrease with time at around t = − 8.0 to − 6.0 ms, regardless of the finger–ball friction condition. Then, around t = − 5.0 to − 4.0 ms, Δωfb approached 0 rpm, except in the water application condition, indicating that slippage between the fingertip and ball was suppressed. Thereafter, Δωfb increased, with a peak around t = − 2.0 to − 1.0 ms, and then decreased. In the water application condition, Δωfb was positive throughout the analysis, suggesting that slippage occurred throughout the ball release process. The same trends were observed in all participants (see Supplementary Fig. S4 online). In the Friedman test, the group mean Δωfb_max was significantly affected by the finger–ball friction condition (χ2(3) = 13.400, p < 0.004, N = 6, W = 0.744). In the post-hoc Dunn test with Bonferroni correction, Δωfb_max in the water application condition (156.0 ± 36.9 rad/s) was 41.4%and 66.5% larger than in the rosin powder (91.4 ± 24.0 rad/s, p = 0.010, r = 1.278) and pine resin application conditions (93.7 ± 25.7 rad/s, p = 0.022, r = 1.187), respectively.

Figure 2A presents the time series change in Dslip for each participant, and Fig. 2B presents the time series change in the group mean Dslip for each finger–ball friction condition. Although the rate of increase was different, Dslip tended to slightly increase with time at t = − 8.0 to − 6.0 ms in all participants, regardless of the finger–ball friction condition. Dslip tended to level off at t = − 6.0 to − 4.0 ms, except in the water application condition. Then, the normal force acting between the fingertip and ball decreased, which reduced the seam traction, resulting in an increase in Dslip at t = − 4.0 to 0.0 ms. In contrast, in the water application condition, Dslip continued to increase until the moment of ball release (t = 0.0 ms). In other words, in the water application condition, slippage occurred between the fingertip and ball even on the seam, and no seam catching was achieved. Figure 2C shows a boxplot for Dtotal. In the Friedman test, the group mean Dtotal was significantly affected by the finger–ball friction condition (χ2(3) = 15.000, p = 0.002, N = 6, W = 0.833). In the post-hoc Dunn test with Bonferroni correction, Dtotal was 142.3% and 163.8.% larger in the water application condition (21.6 ± 5.3 mm) than in the rosin powder (8.9 ± 3.5 mm, p = 0.022, r = 1.187) and pine resin application conditions (8.2 ± 2.2 mm, p = 0.002, r = 1.461), respectively.

Fig. 2
figure 2

(A) Time series change in slip distance between the fingertip and ball Dslip for each participant. The solid line indicates the within-participant mean, and the shaded area indicates the within-participant mean ± standard deviation. (B) Time series change in the group mean value of Dslip under different finger–ball friction conditions. The solid line indicates the between-participant mean, and the shaded area indicates the between-participant mean ± standard deviation. t = 0 ms indicates the release time of the ball. (C) A boxplot of the total slip distance during the ball release process Dtotal for each finger–ball friction condition. Circles with white spaces are the mean values within participants, and the black circle is the group mean value. * and ** indicate p < 0.05 and p < 0.01, respectively.

Full size image

Effects of finger–ball friction conditions on pitching performance measures

Figure 3 shows boxplots for ball velocity, ball spin rate, horizontal and vertical ball arrival locations, and horizontal and vertical ball release angles. In the Friedman test, the ball velocity (Fig. 3A;χ2(3) = 12.200, p = 0.007, N = 6, W = 0.678), ball spin rate (Fig. 3B; χ2(3) = 16.200, p = 0.001, N = 6, W = 0.900), horizontal ball arrival location (Fig. 3C; χ2(3) = 12.200, p = 0.007, N = 6, W = 0.678), horizontal ball release angle (Fig. 3E; χ2(3) = 10.400, p = 0.015, N = 6, W = 0.578), and vertical ball release angle (Fig. 3F; χ2(3) = 12.600, p < 0.006, N = 6, W = 0.700) were significantly affected by the finger–ball friction condition. The vertical ball arrival location was not significantly affected by the the finger–ball friction condition (Fig. 3D; χ2(3) = 4.600, p = 0.204, N = 6, W = 0.204). As shown in Fig. 3A, the ball velocity was lower in the water application condition than in the rosin powder application condition (p = 0.005, r = − 1.369) and tended to be lower in the water application condition than in the pine resin application conditions (p = 0.083, r = − 1.004). As shown in Fig. 3B, the water application condition significantly reduced the ball spin rate compared with the rosin powder application (p = 0.005, r = − 1.369) and pine resin application conditions (p = 0.005, r = − 1.369). As shown in Fig. 3C, the horizontal ball arrival location was lower and much closer to the target position in the rosin powder application condition than in the water application conditions (p = 0.005, r = 1.369 ), indicating that rosin powder application provides better ball control. As shown in Fig. 3E, the horizontal ball release angle was lower in the rosin powder application condition than in the water application conditions (p = 0.010, r = 1.278). As shown in Fig. 3F, the vertical ball release angle was lower in the rosin powder (p = 0.005, r = 1.369) and pine resin application conditions (p = 0.044, r = 1.095) than in the water application condition.

Fig. 3
figure 3

Boxplots of (A) ball velocity, (B) ball spin rate, (C) horizontal ball arrival location, (D) vertical ball arrival location, (E) horizontal ball release angle, and (F) vertical ball release angle measured with a Doppler radar tracking system. Circles with white spaces are the mean values within participants, and the black circle is the group mean value. * and ** indicate p < 0.05 and p < 0.01, respectively.

Full size image

Correlation between finger–ball slip distance and pitching performance

Table 1 presents the correlation coefficients between Dtotal and pitching performance measures, including the ball release angle. The ball spin rate had a moderate negative correlation with Dtotal overall (rs = − 0.523, p < 0.001), and 4 of the 6 participants showed a strong negative correlation (rs > 0.800, p < 0.001). The ball velocity and vertical ball arrival location had weak negative (rs = − 0.314, p < 0.001) and positive correlations (rs = 0.316, p < 0.001), respectively, with Dtotal overall. The vertical ball release angle had a moderate positive correlation with Dtotal overall (rs = 0.478, p < 0.001). Scatter plots of the relations between the total slip distance Dtotal and pitching performance measures are presented in Fig. 4.

Table 1 Correlation coefficients for the total slip distance Dtotal between the index finger and ball during the ball release process and pitching performance measures assessed with a doppler radar tracking system for all participants and each participant.
Full size table
Fig. 4
figure 4

Relationship between the total slip distance Dtotal and pitching performance measures. (A) ball velocity, (B) ball spin rate, (C) horizontal ball arrival location, (D) vertical ball arrival location, (E) horizontal ball release angle, and (F) vertical ball release angle.

Full size image

Discussion

The objective of this study was to investigate the effect of finger–ball friction conditions on the slip behavior and the slip distance between the fingertips and the ball during baseball pitching and assess the relationship between the slip distance and pitching performance. We hypothesized that the ball–finger slip distance during ball release is significantly affected by the finger–ball friction coefficient, with it being greater under low-friction conditions, such as when wet with water, and shorter under high-friction conditions, such as when rosin powder or pine resin is applied. We also hypothesized that an increase in the slip distance reduces pitching performance, such as the spin rate and pitch control. The present study showed that the ball angular velocity (ωball) during the ball release process in fastball pitching was significantly affected by the finger–ball friction condition (Fig. 1A), whereas the fingertip behavior with respect to the ball center (ωfc) was not significantly affected by the finger–ball friction condition (Fig. 1B). Consequently, the slip distance of the ball with respect to the fingertip (Dslip and Dtotal) was significantly affected depending on the finger–ball friction condition (Fig. 2). Water application significantly increased the slip distance, and rosin powder or pine resin application reduced the slip distance. This order of the slip distance is roughly consistent with the order of the friction coefficients identified in our previous studies15,17. The friction coefficient was lower in the water application condition15 and higher in the rosin powder and pine resin application conditions than in the no application condition17. These results support our first hypothesis.

Figure 1C and 2 present data that provide a deeper insight into the sliding behavior of the ball during the ball release process and the effect of the seam on the traction between the fingertip and ball. When the ball leaves the thumb (t = − 8.0 ms), the braking force by the thumb is lost, which causes a small slip between the ball and index fingertip. Then, the ball begins to rotate against the index fingertip, after which the fingertip catches on the seam of the ball, which inhibits slippage between the ball and fingers (approximately t = − 6.0 to − 4.0 ms). This increases the traction between the fingertips and ball, resulting in an increase in the angular velocity of the ball. As the ball release approaches, the normal force acting between the fingertips and ball decreases, which is thought to weaken the hooking of the seam and consequently increase the slip between the ball and fingertip (t = − 4.0 to − 1.0 ms). Thus, our results indicate that in the ball release process of 4-seam fastball pitching, the ball is released by hooking the fingertip on the seam, which is necessary to create a large ball spin rate, and the ball basically slides against the fingers. However, in the water application condition, slippage occurred throughout the ball release process (t = − 8.0 to 0.0 ms), and the fingertip did not catch on the seam (except for participant f, as shown in Fig. S4), which resulted in a reduction in the ball angular velocity. The results showed that hooking the fingertip on the seam has a significant effect on the ball spin rate and pitch control, in addition to aerodynamic drag21.

As shown in Fig. 3, we found that finger–ball friction conditions had a significant effect on pitching performance in terms of ball velocity (Fig. 3A), ball spin rate (Fig. 3B), and pitch control (Fig. 3C) These results support our second hypothesis. It is known that the ball release angle is related to the ball arrival location22,23, and the finger–ball friction conditions were found to have significant effects on the ball release angle (Fig. 3E, F). In the water application condition, the ball tended to be thrown upward and laterally, leading to a decrease in control. The pitch control in the rosin powder application condition was superior to that in the other conditions, which may be due to the fact that participants were accustomed to rosin powder conditions through practice and games and that rosin powder has a high friction effect. These changes in performance with finger–ball friction conditions can be explained by the relationship with the fingertip–ball slip distance, as shown in Table 1. Overall, there was a weak negative correlation between the ball velocity and slip distance (rs = − 0.314, p < 0.001). Although participants were instructed to throw the ball at a nearly constant velocity (130 km/h), it is possible that the arm velocity was reduced under slippery conditions, such as water application. As reported in the literature24,25, there was a positive correlation (r = 0.523, p < 0.05) between the ball speed and ball spin rate in this study. Our results also showed a strong negative correlation (r = − 0.723, p < 0.05) between the ball spin rate and slip distance among all participants. This indicates that the decrease in the ball spin rate with an increase in slip distance is more significant than the decrease in the ball speed. Additionally, more participants showed a positive correlation between the slip distance and the arrival position of the ball in the vertical direction than in the horizontal direction. This can be attributed to the fact that the vertical release angle of the ball has a positive correlation with the slip distance and may be related to the fact that all the pitchers in this study used the overhand pitching technique because the major axis of the (elliptical) distribution of the ball arrival position is determined by the direction of the throwing arm26. Moreover, it is thought that the ball was released earlier under the water application condition because the fingertip’s catching on the seam was reduced. As a result, the ball was considered to have been released laterally upward.

The results of this study are important in terms of showing how friction between the ball and fingertips affects pitching performance. In not only baseball pitching but also other sports, the friction coefficient between the human body and equipment varies greatly depending on the environment and conditions, such as rain, sweat, friction characteristics of the equipment, and physical characteristics (moisture content and hardness) of the fingertips27,28,29,30. Athletes need to respond flexibly to these changes, and such adaptability is important for athletes. For example, as shown in Fig. 2A, participant f had a smaller slip distance than the other participants in all finger–ball friction conditions, including the water application condition, and thus, his performance was less affected by the friction conditions (Fig. 4, light blue plot). In other words, there was no decrease in performance even in the water application condition. Conversely, participants b and d had large differences in the slip distance between finger–ball friction conditions (Fig. 2A), resulting in a large effect on performance (Fig. 4, orange and purple plots). Further research is needed to understand the differences in adaptation to friction characteristics among individuals, including upper limb motion and finger force characteristics11,20,31. However, when the friction coefficient between the fingertips and ball (µ) is low, it is necessary to increase the normal force of the fingers against the ball (N) to increase the frictional force (F = µN), and such adaptive behavior may lead to elbow and shoulder injuries. The fact that the tightening of restrictions on adhesive substances in MLB led to a decrease in pitching performance13,14 and might have contributed to an increase in elbow and shoulder injuries32 could support this point. We believe that the findings of this study will provide opportunities to expand the discussion on the relationships among friction, performance, and disability in sports and will help in the prevention of injuries and the development of superior equipment.

Some limitations of the present study should be considered. First, the results were obtained only for 4-seam fastball pitching, and it is necessary to examine whether similar results can be obtained for other types of balls, such as the breaking ball. Second, the release timing was determined visually using a high-speed camera. If the determination would have been based on the force acting between the ball and fingers, the release timing might have been a little earlier. Third, only the index finger was analyzed owing to the limitation of the measurement method, and slippage with the middle finger is unclear. Fourth, although almost the same tendency was observed among the participants in this study, experiments with a larger number of participants are needed. There were instances where the effect size r exceeded 1, indicating substantial differences between conditions. However, such a large effect size might result from the small sample size, which also limits the generalizability of our findings. Fifth, we did not take into account the horizontal slip relative to the ball spin axis, which may affect the pitch control and ball release angle. There are two aspects of pitch control, namely, accuracy (bias) and precision (variability). However, due to the small number of pitches, the variability of the ball arrival location was not evaluated in this study and only bias was evaluated, which is the sixth limitation of this study. Although participants were instructed to ensure uniform finger spacing and grip depth regardless of the finger–ball friction condition, it was not possible to quantitatively assess the lack of change in the grasping condition. Therefore, its influence cannot be excluded, which is the seventh limitation of this study.

Conclusions

To our knowledge, this is the first study to investigate the slip distance between the fingertips and ball in baseball pitching. We found that the ball angular velocity during the ball release process was significantly affected by finger–ball friction conditions, whereas the fingertip behavior with respect to the ball center was not significantly affected. As a result, the slip distance of the ball with respect to the fingertip was significantly affected depending on the finger–ball friction condition. We found that in the ball release process, the ball was released by hooking the fingertips on the seam, and the ball slid against the fingers. However, in the water application condition, slippage occurred throughout the ball release process and the fingertips did not catch on the seam. The ball slip distance was found to have a significant effect on pitching performance in terms of ball velocity, ball spin rate, and pitch control. Our findings provide new insights into the understanding of how a ball is released in baseball pitching under different friction conditions and may help improve pitching performance and injury prevention.

Materials and methods

Participants

This study included 6 semiprofessional male baseball pitchers (5 right-handed pitchers and 1 left-handed pitcher) who were from a company baseball league. The mean (± standard deviation) age, height, and body mass of the participants were 29.8 ± 5.8 years, 1.79 ± 0.05 m, and 83.1 ± 6.3 kg, respectively. All participants had an overhand throwing motion. The experimental protocol of this study was approved in advance by the Research Ethics Committee of NTT Communication Science Laboratories (R05-13), and each participant was informed of the experimental methods and precautions and provided written informed consent in advance. All experiments were performed in accordance with the Declaration of Helsinki.

Experimental procedure

Pitching experiments were conducted in an indoor dirt mound. A schematic diagram of the pitching experiment is presented in Fig. 5A. Each participant threw a ball at a square target (0.10 × 0.10 m in size) set up in the low outer corner of the strike zone at a distance of 19.44 m (1 m behind home base), which is equivalent to the distance from the mound to the catcher’s mitt. A right-handed pitcher was required to pitch to the outside low corner of a right-handed batter (orange square was used), and a left-handed pitcher was required to pitch to the outside low corner of a left-handed batter (black square was used) (Fig. 5B), which was in accordance with the way the participants usually practice pitching.

Fig. 5
figure 5

Experimental setup. A participant threw a baseball at a square target (0.10 × 0.10 m in size) set up in the low outer corner of the strike zone at a distance of 19.44 m (1 m behind home base), which is equivalent to the distance from the mound to the catcher’s mitt (A). An orange square was used for a right-handed pitcher (RHP), and a black square was used for a left-handed pitcher (LHP) (B). Markers were used on the ball (C) and the index fingertip (D) for tracking by a high-speed camera. Black circles with a diameter of 4 mm were drawn with a black marker pen on the surface of the ball at 5 equally spaced locations (C) and at the center of the lateral surface of the terminal phalanx of the participant’s index finger (D).

Full size image

Each participant was instructed to throw a 4-seam fastball. The 4-seam fastball was used in this study because it is the most commonly thrown pitch and has been extensively studied in previous research11,12,20,22,33, and the relationship between the ball’s spin axis and the throwing action is simpler in this pitch than in other pitches. During the pitching experiment, a Doppler radar tracking system (Trackman, Vedaek, Denmark) was used to measure release parameters (ball velocity, ball spin rate, and ball arrival location [pitch location] in the vertical and horizontal directions) as measures of pitching performance. As the ball arrival location is known to be affected by the ball release angle22,23, we also measured the ball release angle. For the left-handed pitcher, the left and right sides were inverted with respect to the ball arrival position and ball release angle in the horizontal direction. It is important to note that the arrival position of the ball, as measured by the tracking system, is on the home base and not on the wall where the target is located. The measured ball velocity was fed back to the participants during the practice pitching, and the participants were instructed to pitch at a velocity of approximately 130 km/h based on the measurement results. No feedback on pitch velocity was provided in the experiment. The baseball (1BJBH10000; MIZUNO Corporation, Tokyo, Japan) used in the experiment had a radius of 37 mm and a mass of 145 g. Black circles having a diameter of 4 mm were drawn with a black marker pen on the ball surface at 5 equally spaced locations (Fig. 5C)) and at the center of the lateral surface of the terminal phalanx of the participant’s index finger (Fig. 5D) to serve as markers for tracking by a high-speed camera (2000 frames/s; 1280 × 1024 pixels; MEMRECAM Q2m; NAC Image Technology Inc., Tokyo, Japan). The approximate capture area was set to 750 mm × 600 mm. Images of the pitcher’s fingers and the ball were captured during the release process from the side of the pitcher (Fig. 5A). It is important to note that reflective markers were attached to the fingers and upper limbs, and motion capture was performed simultaneously. However, the data were not used as this was not the main objective of this study.

After warming up, participants first performed the pitching experiment under a no application condition (no application of any agent). Subsequently, they pitched the ball under 3 different conditions (water, rosin powder, and pine resin application) in random order. Considering the effects of fatigue on the pitcher, the number of pitches was limited to five under each finger–ball friction condition. In the water application condition, participants dipped their fingertips into a container of tap water to simulate pitching in the rain. In the rosin powder application condition, participants touched a rosin bag (2ZA-416; MIZUNO Corporation) and allowed the rosin powder to fully adhere to their fingers. In the pine resin application condition, a ball different from the one used in the experiment was sprayed with pine resin (2ZA-434; MIZUNO Corporation), and participants held the ball so that the pine resin adhered sufficiently to their fingertips. After throwing the ball in the rosin powder and pine resin application conditions, participants were instructed to wash their hands to remove any residue and thoroughly dry their fingertips before throwing the ball in the next condition. A new ball was used for each finger–ball friction condition. Previous studies have shown that the friction coefficient is lower in the water application condition15 and higher in the rosin powder and pine resin application conditions than in the no application condition17, and that the friction coefficient is higher in the pine resin application condition than in the rosin powder application condition17. Thus, we used these 4 finger–ball friction conditions to alter the friction coefficient between the fingertips and ball. The interval between sessions under different finger–ball friction conditions was approximately 5 min. As the moisture content of the finger affects finger friction, another experiment was conducted after confirming that the moisture content of the finger returned to normal after 5 min, using a finger moisture sensor17. Participants were instructed to ensure uniform finger spacing and grip depth regardless of the finger–ball friction condition.

Data analysis

An example snapshot taken by the high-speed camera during the ball release process under the no application condition is shown in Fig. 6A. The time when the ball left the fingertips of the index and middle fingers was determined visually and set as the release time (t = 0.0 ms). Although there was slight variation among the participants, the thumb left the ball at approximately t = − 8.0 ms during the ball release process and the ball began to backspin (clockwise direction in Fig. 6A) as it rolled around the fingertips of the index and middle fingers.

Fig. 6
figure 6

(A) An example snapshot taken by a high-speed camera during the ball release process under the no application condition. The time when the ball left the fingertips of the index and middle fingers was determined visually and set as the release time (t = 0.0 ms). (B) A schematic diagram of markers on the ball (P1–P5) and the center of the ball contour (P0). (C) A schematic diagram of markers on the ball and fingertips after coordinate transformation. The ball angular velocity ωball was obtained from the angles of 2 diagonals using the difference method. The position vector of the fingertip marker Pfinger to the ball center marker position P1 was calculated, and the relative angular velocity of the fingertip against the ball center ωfc was calculated.

Full size image

Video analysis software (TEMA Version 4.2-004-64; Photron Ltd., Tokyo, Japan) was used to analyze the high-speed camera images. A total of 36 frames (18 ms) were used for the analysis, including approximately 16 frames (8.0 ms) from the time the ball left the thumb until the ball was released. The software tracked the points drawn on the ball and the outline of the ball to obtain the position coordinates Pi (xi, yi) (i = 1–5) of each marker and the center position P0(x0, y0) of the outline of the ball, respectively, in the high-speed camera images (Fig. 6B). P0 coordinates were determined from the contour data of the ball, using the least squares method. A point drawn on the index fingertip Pfinger (xfinger, yfinger) was also tracked in the same way. Subsequent analyses were performed using MATLAB (MathWorks, Natick, MA, USA).

The spin axis of a fastball is inclined and varies from player to player24,25. Therefore, the camera position and orientation were adjusted for each participant to align the shooting direction with the axis of rotation as closely as possible. To obtain the ball spin rate using the information in the observation plane of the high-speed camera of the ball (x–y plane), the shooting direction of the high-speed camera in the pitching experiment and the rotation axis of the ball must match; however, they did not match. Therefore, the position coordinates of the markers were transformed using Euler angles34 so that the position coordinates of the center marker P1(x1, y1) coincided with the position coordinates of the center of the ball’s outline P0(x0, y0) (Fig. 6B). Details on the coordinate transformation are shown in Appendix A. Participants were instructed to grip the ball so that the marker at the center of the ball (P1) passed through the axis of rotation, and we assumed that the ball rotated around this axis.

We carried out fourth-order, zero-lag, Butterworth low-pass filtering with a 180-Hz cutoff frequency on the coordinates of the markers (x’i, y’i; i = 1–5) and the fingertip marker (x’finger, y’finger) after coordinate transformation. The cutoff frequency was selected so that the ball spin rate, which was calculated using the method explained below, would not increase after the ball release timing (t > 0.0 ms) and could be sufficiently smoothed. Thereafter, the behaviors of the ball and fingertip markers in the x’–y’ plane were analyzed.

Two diagonals were drawn using the markers at the 4 corners on the ball after coordinate transformation (x’i, y’i; i = 2–5). The angular velocities ω1 and ω2 of each diagonal were obtained from the angles of each diagonal using the difference method (Fig. 6C), and the mean value was used as the ball angular velocity ωball. As shown in Fig. 6C, the position vectors of the fingertip marker to the ball center marker (x’finger – x’1, y’finger – y’1) during the ball release process were calculated, and the relative angular velocity of the fingertip against the ball center ωfc was calculated using the following equation:

$${\omega _{fc}}=\frac{d}{{dt}}\left( {{{\tan }^{ - 1}}\frac{{{{y^{\prime}}_{finger}} - {{y^{\prime}}_1}}}{{{{x^{\prime}}_{finger}} - {{x^{\prime}}_1}}}} \right)$$
(1)

If ωball and ωfc are equal, there is no slippage between the index fingertip and ball. Conversely, if there is a difference between ωball and ωfc, there is slippage between the index fingertip and ball. Therefore, we investigated whether slippage occurred and evaluated the effect of finger–ball friction conditions on slippage by obtaining the time series variation of the difference between ωball and ωfc (Δωfb) during the ball release process (t = − 8.0 to 0.0 ms) using the following equation:

$$\Delta {\omega _{{\text{fb}}}}={\omega _{{\text{fc}}}} - {\omega _{{\text{ball}}}}$$
(2)

The slip distance Dslip between the fingertip and ball from the time the ball leaves the thumb to time t in the ball release process (t = − 8.0 to 0.0 ms) was calculated using the following equation:

$${D_{slip}}\left( t \right)={R_{ball}}\mathop \smallint \limits_{{{t_0}}}^{t} \Delta {\omega _{fb}}\left( \tau \right)d\tau$$
(3)

where Rball is the ball radius (37 mm) and t0 = − 8.0 ms. The sum of the slip distance from t = − 8.0 to 0.0 ms was defined as Dtotal.

Statistical analysis

The maximum values of ωball, ωfc, and Δωfb during the ball release process (t = − 8.0 to 0.0 ms; ωball_max, ωfc_max, and Δωfb_max, respectively) were extracted for each finger–ball friction condition. We performed Friedman test to investigate whether ωball_max, ωfc_max, Δωfb_max, Dtotal, ball velocity, ball spin rate, vertical and horizontal ball arrival locations, and vertical and horizontal ball release angles were affected by the finger–ball friction condition. A post-hoc Dunn test with Bonferroni correction was used to identify specific differences in the above variables according to the finger–ball friction condition. We also reported the effect size in terms of Kendall’s W for Friedman’s test and Pearson’s correlation coefficient r for the post hoc Dunn–Bonferroni test. W values and r values of < 0.3 are considered small, between 0.3 and 0.5 are considered moderate, and > 0.5 are considered large35. To investigate the validity of the determination of the ball angular velocity based on the high-speed camera images, the Pearson’s correlation coefficient and the RMSE between the ball spin rate calculated from ωball_max and that measured by the Doppler radar tracking system were calculated.

Additionally, Spearman’s correlation tests were performed to investigate correlations between the total slip distance Dtotal and abovementioned pitching performance measures. Spearman’s correlation coefficient rs values are categorized as follows: 0.00–0.10, very weak correlation; 0.10–0.39, weak correlation; 0.4–0.69, moderate correlation; 0.70–0.89, strong correlation; and 0.90–1.00, very strong correlation36.

All statistical analyses were performed using SPSS Statistics for Windows, Version 19.0 (IBM Corp., Armonk, NY, USA). The significance level was set at p = 0.05.