Introduction

The current promotion of energy transformation has become a global consensus. In recent years, the proportion of renewable energy use has been increasing annually. This has led to the advancement and research of DC-DC converters, which have shown excellent application performance in emerging industries such as photovoltaic power generation technology1 and new energy vehicles2. As a result, there is a growing need for more efficient and high-gain converters.

Converter topologies can be built by adding voltage multiplier structures and cells to the original basic converter type. Traditional DC-DC converters can directly incorporate switched capacitors or switched inductors3,4, but are prone to severe hard switching conditions and duty cycle loss. To address this, propose switched capacitor inductor units5,6 and the switched capacitor inductor network7. Moreover, the active-passive inductor cells proposed in8 can work with multi-switches for cascade expansion with the continuous input current, however, this approach involves challenging control, excessive surge of switch structures, and serious hard-switching conditions, leading to a significant overall loss that reduces the converter efficiency. Given the losses caused by hard switching, auxiliary switches can be added in the traditional converter to form unidirectional or bidirectional cells that can be used to achieve zero-voltage-switching (ZVS), but the gain cannot be improved9. The introduction of coupled inductors is an effective means to increase converter gain. The most common is the double-winding structure10,11, three-winding structures can also be used12,13,14, and the impedance source structure15 is gradually developed. In practical applications, device size and leakage inductance need to be considered. By adding active/passive clamping branches to reduce device voltage stress and utilizing leakage inductance energy, the soft-switching design of the device can be realized to improve efficiency.

The topology can also be reconstructed based on different multi-level connection methods. For the quadric converter with the better gain effect, a single switch design is adopted in16,17, but the hard conduction problem of the switch is serious. The quadratic Boost converter uses a single-switch integrated Cuk structure to improve the gain further, but it still does not solve the problem of hard turn-on of the switch and the input current ripple is large18. The quadric converter is controlled by the same frequency dual switches19, based on the quasi-resonance principle, which reduces the turn-off current of the switches and realizes the ZCS of the diodes. The quadratic converter20 with interleaved three-switch control integrates a gain expansion unit with a floating capacitor to achieve a higher fourth-power gain. Still, it lacks the soft-switching design and has an efficiency of only 92.7%. When interleaved control is adopted, the full-bridge structure can also be applied to the input21, but a more complex soft-switching design is required to reduce the duty cycle loss. The general composition method of the interleaved converter is proposed in22, among which the dual-switch structure is the most widely used23, but boost capability is inferior to that of the quadratic type. Without considering hard switching, a three-switch interleaved topology24 and a four-state switch unit for high-power applications25 are proposed, due to the large number of components, it is difficult to design parameters such as the duty cycle. The quadric and interleaved topology can also integrated with switched capacitors or switched inductors26,27, coupled inductors28,29, etc. To achieve low input current ripple, capacitive clamps are integrated into the interleaved structure, and the converters and their construction method are proposed30. In addition, the dual-switch interleaved structure at the input can be combined with dual coupled inductors to reduce input current ripple while boosting the voltage31,32,33,34. On this basis, by cleverly constructing the coupled inductor voltage multiplier cell to make full use of the leakage inductance energy, can realize the ZCS soft-switching design while increasing the gain32,33,34. In32, the two secondary sides and the D-C branch respectively form a symmetrical voltage multiplier cell. The series secondary side with the D-C branch forms the non-symmetrical multi-winding voltage multiplier cell33,34.

In this paper, the traditional Buck/Boost is used as the basic topology. Using a dual-coupled inductor, the front-stage energy storage structure is interleaved. This allows the input current to be continuous and reduces the current ripple. The passive clamps absorb leakage inductance, and appropriate capacitors are selected for quasi-resonance. The secondary side of the double-coupled inductor connected serial and the D-C branch form a voltage multiplier cell. Proposed a high-gain interleaved quadratic Boost converter with dual coupled inductors and low input ripple, which combines the advantages of quadratic and interleaved topologies, balancing the high gain and high efficiency. While ensuring high gain of the converter, it realizes soft-switching of the quasi-resonant circuit, alleviates the reverse recovery problem of the diode, and ensures that each device has low voltage stress, and the input current with continuous low current ripple, improving the efficiency.

Proposal of converter

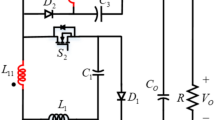
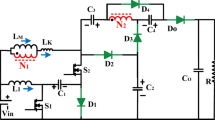
The construction idea of the interleaved quadric Buck/Boost converter with a double-coupled inductor is shown in Fig. 1(a). The double-switch interleaved structure adopted at the input end reduces the current ripple while ensuring the continuous input current. Based on the generalized half-cycle resonance principle, the ZCS can be realized, which can obtain a better soft switching effect and reduce the off-current of the switch. The independent inductance in the previous structure is used as the primary side of the coupled inductance to further improve based on the quadric boost gain. Make flexible use of the D-C branch and select capacitor C2 for quasi-resonance. First, it is clamped on the switch as the passive clamp, absorbing the leakage inductance to relieve the voltage surge of the switches, and reducing the voltage stress. Moreover, it forms a voltage multiplier cell with the serial secondary structure of the double-coupled inductor and realizes the soft-switching. Finally, the equivalent circuit in Fig. 1(b) of the proposed converter is obtained, where the coupled inductor structure is composed of coupled inductor leakage inductance Lk1, Lk2, magnetizing inductance Lm1, Lm2, and an ideal transformer with a turn ratio n = Ns1/Np1=Ns2/Np2.

Fig. 1
figure 1

Proposal of the converter. (a) Construction idea, and (b) Equivalent circuit.

Full size image

Analysis of converter

The converter proposed in Fig. 1. is theoretically analyzed and the following assumptions are made: 1) All diodes are ideal devices, i.e., the on-time is zero, the off-resistance is infinite, and the on-state voltage drop is neglected;2) All capacitors are ideal devices, and capacitors are large enough that their ripple voltage and parasitic effects are negligible.;3) All inductor currents are continuous, i.e., the converter operates in continuous conduction mode (CCM).

Operating principle

There are 8 operating modes within one switching period T, and the driving signals of the switches S1 and S2 are interleaved with a difference of 180°. The basic waveforms of the converter are shown in Fig. 2. The equivalent circuit of each operating mode is shown in Fig. 3.

Mode I[t0-t1]: At the initial, the switch S1 and S2 are turned on, and diodes D1, D2, D3 & D4 are turned off. The input voltage Vi is applied to the primary side Np1 of the coupling inductor through switch S1 and capacitor C1, and capacitor C1 both switch S1 & S2 are used to store energy on the primary side Np2, with the current iLk1 and iLk2 rise linearly. Capacitors C3 and C4 together supply power to the load. At t = t1, the switch S2 is turned off, and this mode ends.

Mode II[t1-t2]: At t = t1, the switch S2 is turned off, while S1 is still turned on, diode D2 is turned on, and diodes D1, D3, and D4 are turned off. The energy of leakage inductance Lk2 is transferred to C2 through capacitor C1 and diode D2, with the current of iD2 decreasing approximately linearly, and the voltage of switch S2 is clamped at VC2. Capacitors C3 and C4 together supply power to the load.

Mode III[t2-t3]: At t = t2, switch S2 remains off, S1 is still on, diodes D2 & D4 are on, and D1 & D3 are off. The energy of leakage inductance Lk2 is completely transferred to capacitor C2, and the input voltage Vi passes through switch S1, and the primary side Np2 is connected in series with the secondary sides Ns1 and Ns2 through the diode D4 to charge the capacitor C4, diode D4 is ZCS on. At t = t3, iD2 drops to zero, i.e., the ZCS off is realized, and the mode ends.

Mode IV[t3-t4]: The switch S2 remains off, S1 is still on, the diode D4 is ZCS on, and the diodes D1, D2 & D3 are off. The input voltage Vi is applied to the primary side Np1 of the coupled inductor through the switch S1, and the primary side Np2 of the coupled inductor is connected to the secondary side Ns1 and Ns2 are connected in series to continue to charge the capacitor C4.

Mode V[t4-t5]: In this interval, switch S2 turns ZCS on at t4, switch S1 keeps on, diode D4 turns ZCS on, and other diodes remain off. The input voltage Vi is applied to the primary side Np1 through switch S1, through the capacitor C1 and the switch S1, S2 is added to the primary side Np2, the current of the switch S2 and the current iLk2 rises linearly; the secondary side Ns1, Ns2, and the capacitor C1, connected in series through the diode D4 charges C4, and the current iD4 decreases linearly. At t = t5, the diode D4 is ZCS turned off, and the mode ends.

Fig. 2
figure 2

Basic waveforms of the proposed converter.

Full size image
Fig. 3
figure 3

The equivalent circuit of converter in (a) mode (I) (b) mode (II) (c) mode (III) (d) mode (IV) (e) mode (V) (f) mode (VI) (g) mode (VII) (h) mode VIII.

Full size image

Mode VI[t5-t6]: At t = t5, the switch S1, and S2 are in the conduction state, diode D3 is ZCS turned on, and the diodes D1, D2 & D4 are all off; the two primary side loops remain unchanged, and the leakage inductance currents iLk1 and iLk2 increase linearly. The quasi-resonant circuit starts working, the secondary sides Ns1 and Ns2 are connected in series through the diode D3 to charge the capacitor C3, and the current iD3 rises from zero. At t = t6, the switch S1 is turned off, and this mode ends.

Mode VII[t6-t7]: At t = t6, switch S1 is turned off, S2 is in a conduction state, diodes D1 and D3 are on, diodes D2 and D4 are off; the quasi-resonant circuit continues to work. The energy of leakage inductance Lk1 is transferred to capacitor C1 through diode D1, and current iD1 decreases linearly; Vi is added to the primary side Np2 through the diode D1 and the switch S2. The voltage of switch S1 is clamped at VC1. At t = t7, iD3 drops to zero, i.e., the ZCS off is realized, end of the quasi-resonant half cycle and the mode.

Mode VIII[t7-t8]: At t = t7, switch S1 is turned off, S2 is in a conduction state, diodes D1 is on, diodes D2, D3 and D4 are off; the energy of leakage inductance Lk1 is transferred to capacitor C1 through diode D1, and current iD1 decreases linearly; Vi is added to the primary side Np2 through the diode D1 and the switch S2. Capacitors C3 and C4 together supply power to the load. At t = t8, the switch S1 is turned on, and this mode ends.

Voltage gain

From Fig. 2, the mathematical expression of the time DxT for the diode D2 current to drop to zero is:

$${D_x}T=\frac{{2\left( {1 - D} \right)}}{{2+n}}T$$
(1)

According to the volt-second balance law of inductors Lm1 and Lm2, there are equations:

$${V_i}DT+\left( {{V_i} - {V_{C1}}} \right)\left( {1 - D} \right)T=0$$
(2)
$$\left( {{V_i}+{V_{C1}}} \right)\left( {2D - 1} \right)T+{V_i}\left( {1 - D} \right)T+\left( {{V_i}+{V_{C1}} - {V_{C2}}} \right){D_x}T+\frac{{\left( {1+n} \right){V_i} - {V_{C4}}}}{{1+n}}\left( {1 - D - {D_x}} \right)T=0$$
(3)

During the rising period DT of diode D3:

$$\frac{{\left( {1+n} \right){V_{C1}}+{V_{C2}} - {V_{C3}}}}{{{n^2}\left( {{L_{k1}}+{L_{k2}}} \right)}}=\frac{{2{I_o}}}{{{D^2}T}}$$
(4)

During the rising period DxT of D4:

$$\frac{{\left( {1+n} \right)\left( {{V_{C2}} - {V_{C1}}} \right) - {V_{C4}}}}{{{n^2}\left( {{L_{k1}}+{L_{k2}}} \right)}}=\frac{{{{\left( {2+n} \right)}^2}{I_o}}}{{2(1+n){{\left( {1 - D} \right)}^2}T}}$$
(5)

According to (1)-(5) and the volt-second balance law of Lm1 and Lm2, the voltage gain expression considering the leakage inductance is obtained as:

$$G=\frac{{{V_o}}}{{{V_i}}}=\frac{{2+n}}{{{{\left( {1 - D} \right)}^2}\left[ {1+AQ} \right]}}$$
(6)

where, \(A{\text{=}}\frac{2}{{{D^2}}}+\frac{{{{\left( {2+n} \right)}^2}}}{{2{{\left( {1+n} \right)}^2}{{\left( {1 - D} \right)}^2}}}\), \(Q=\frac{{{n^2}\left( {{L_{k1}}+{L_{k2}}} \right)}}{{RT}}\) is the influence factor of leakage inductance.

Given the above relationships, the ideal voltage gain (Lk1=Lk2=0) of the converter can be obtained as:

$${G_{ideal}}{\text{=}}\frac{{{V_o}}}{{{V_i}}}=\frac{{2{\text{+}}n}}{{{{(1 - D)}^2}}}$$
(7)

According to (6), the effect of leakage inductance on gain can be plotted, as shown in Fig. 4. In practice, it is necessary to avoid extreme duty cycles while considering leakage inductance and design a suitable turn ratio n to ensure high output voltage.

Fig. 4
figure 4

The curve of voltage gain G in (a) n = 1. (b) n = 1.4.

Full size image

Stress analysis

According to the steady-state analysis, the voltage stress of the switches and each capacitor & diode is obtained:

$${V_{S1}}={V_{C1}}={V_{D1}}=\frac{1}{{1 - D}}{V_i}=\frac{{1 - D}}{{2+n}}{V_o}$$
(8)
$${V_{S2}}={V_{C2}}={V_{D2}}=\frac{1}{{{{(1 - D)}^2}}}{V_i}{\text{=}}\frac{1}{{2+n}}{V_o}$$
(9)
$${V_{C3}}=\frac{{2+n - (1+n)D}}{{{{(1 - D)}^2}}}{V_i}{\text{=}}\frac{{2+n - (1+n)D}}{{2+n}}{V_o}$$
(10)
$${V_{C4}}=\frac{{D(1+n)}}{{{{(1 - D)}^2}}}{V_i}{\text{=}}\frac{{D(1+n)}}{{2+n}}{V_o}$$
(11)
$${V_{D3}}={V_{D4}}=\frac{{1+n}}{{{{\left( {1 - D} \right)}^2}}}{V_i}=\frac{{1+n}}{{2+n}}{V_o}$$
(12)

Considering the current ripple of Lm1 and Lm2, their respective increments are:

$$\left\{ \begin{gathered} \Delta {i_{Lm1}}=\frac{{{V_i}DT}}{{{L_{m1}}}} \hfill \\ \Delta {i_{Lm2}}=\frac{{ - \left( {{V_i}+{V_{C1}} - {V_{C2}}} \right)(1 - D)T}}{{{L_{m2}}}} \hfill \\ \end{gathered} \right.$$
(13)

According to the ampere-second balance law of capacitance, the average current of those diodes D2, D3, and D4 is equal to the output current Io. Combined with the steady-state analysis, the average currents expressions of Lm1 and Lm2, are obtained as:

$$\left\{ \begin{gathered} {I_{Lm1}}=\frac{{D\left( {2+n} \right)}}{{{{\left( {1 - D} \right)}^2}}}{I_o} \hfill \\ {I_{Lm2}}=\frac{{2+n}}{{1 - D}}{I_o} \hfill \\ \end{gathered} \right.$$
(14)

Get the off-current stress of the switches:

$${i_{S1}}=\frac{{2+n}}{{{{\left( {1 - D} \right)}^2}}}{I_o}+\frac{1}{2}\left( {\Delta {i_{Lm1}}+\Delta {i_{Lm2}}} \right)$$
(15)
$${i_{S2}}=\frac{{2+n}}{{1 - D}}{I_o}+\frac{1}{2}\Delta {i_{Lm2}}$$
(16)

Analysis of the peak current of switch S2:

$${i_{S2{\text{peak}}}}={i_{Lm2}}+(1+n){i_{Ns}}=\frac{{2+n}}{{1 - D}}{I_o}+(1+n){i_{Ns}}$$
(17)

where, \({i_{Ns}}=\frac{{{V_i}}}{{1 - D}}\sqrt {\frac{{{C_2}}}{{{L_{m2}}}}} \sin (\frac{1}{{2\sqrt {{L_{m2}}{C_2}} }}{t_r})\), \({t_r}=\pi \sqrt {{n^2}\left( {{L_{k1}}+{L_{k2}}} \right){C_2}}\), the relationship is shown in Fig. 5. Among them, diode D3 completes the half-cycle resonance, achieving better ZCS turn-on and turn-off, and eliminating its reverse recovery problem.

Fig. 5
figure 5

Switch S2 waveform relationship.

Full size image

Input current ripple analysis

The input current of the proposed converter is equal to the sum of the primary currents of both coupled inductors, which can be expressed as:

$${i_{{\text{i}}n}}={i_{Lk1}}+{i_{Lk2}}={i_{Lm1}}+n{i_{Ns}}+{i_{Lm2}} - n{i_{Ns}}={i_{Lm1}}+{i_{Lm2}}$$
(18)

And get:

$$\Delta {i_{in}}=\frac{{\left( {3D - {D^2} - 1} \right)\left( {1 - D} \right)T}}{{{L_{m2}}}} - \frac{{{V_i}\left( {1 - D} \right)T}}{{{L_{m1}}}}$$
(19)

According to (19), since the converter adopts interleaved control, the interleaving of the two primary currents on the input side is conducive to reducing the ripple. Figure 6 shows the changing performance of the input ripple. It can be seen that the changing trend is proportional to the duty cycle.

Fig. 6
figure 6

Input current ripple variation.

Full size image

Soft switching analysis

The presence of leakage inductance affects the rate of change of the current in the diode and switch. According to Figs. 2 and 3, have the following relationships:

$${i_{D4}}\left( t \right)={i_{D4}}\left( {{t_4}} \right)+\frac{{ - \left( {1+n} \right){V_{C1}} - {V_{C4}}}}{{{n^2}\left( {{L_{k1}}+{L_{k2}}} \right)}}\left( {t - {t_4}} \right)$$
(20)

And get:

$${L_{k1}}+{L_{k2}}=\frac{{\left( {1+n} \right){V_o}}}{{{n^2}\left( {2+n} \right)\frac{{d{i_{D4}}}}{{dt}}}}$$
(21)

The leakage inductance can be used to realize the ZCS turn-on of the switch S2 (the current change rate < 30 A/µs) and alleviate the reverse recovery problem of the diode D4.

In addition, diode D3 turns on and off to complete the quasi-resonant half cycle to achieve quasi-resonant soft-switching and eliminate reverse recovery. The periodic conditions need to be met:

$${T_r}=2{t_r}=2\pi \sqrt {{n^2}({L_{k1}}+{L_{k2}}){C_2}}$$
(22)

Performance comparison

The key parameters and performance of the converter proposed in this paper are compared horizontally with other converters. The parameters are in Table 1. Taking the fixed turn ratio of the coupled inductor n = 1 as a reference, the comparison curve of the corresponding performance is shown in Fig. 7.

Among them, the quadric converters17,19,29 have better gain effects, but the hard switching of switches is not solved. The input adopts the interleaved structure 31–34. The remaining converter inputs adopt an interleaved structure31,32,33,34, and all use dual-coupled inductors and double-switch interleaved control to reduce the input current ripple. In31, the hard switching is serious, while the converters32,33,34 realize ZCS soft-switching design.

This paper integrates the advantages of the quadratic converter and the interleaved converter, finds the balance point of improving gain and ensuring efficiency, and proposes a novel interleaved quadratic converter. The voltage gain of the interleaved quadratic converter proposed is higher than that of other topologies, with continuous input current and low ripples. And the voltage stress of the switch is always much lower than the output voltage, the diode voltage stress is also small. Using fewer components and realizing the quasi-resonance circuit’s soft-switching with the reverse recovery problem has been greatly improved.

Table 1 Performance comparison.
Full size table
Fig. 7
figure 7

Comparison with (a) Gain. (b) Number of components. (c) Maximum voltage stress on switch. (d) Maximum voltage stress on Diode.

Full size image

Design guidelines

This section gives the design guideline of the converter, where the input voltage Vi = 24 V; the output voltage Vo = 400 V; the switching frequency fs = 50 kHz; and the rated power Po = 400 W.

CCM condition

When the inductance of the dual coupled inductors Lm1 and Lm2 is small, the converter operates in discontinuous conduction mode (DCM), and its main waveform is shown in Fig. 8. The switching devices have large current stresses. Therefore, in practical applications, the converter needs to operate in CCM mode to ensure system stability.

Fig. 8
figure 8

Basic waveforms of DCM.

Full size image
$$\left\{ \begin{gathered} {L_{m2}} \geqslant \frac{{{{\left( {1 - D} \right)}^2}\left( {1 - {D^2} - 3D} \right)}}{{2{{\left( {n+2} \right)}^2}}} \\ {L_{m1}} \geqslant \frac{{D{{\left( {1 - D} \right)}^4}RT}}{{2{{\left( {n+2} \right)}^2}+{{\left( {1 - D} \right)}^5}\frac{{RT}}{{{L_{m2}}}}}} \\ \end{gathered} \right.$$
(23)

Where Lm2 is more likely to enter the DCM state. Firstly, according to (14), determine the CCM condition of Lm2. The CCM condition of Lm1 can be determined based on the value of the magnetizing inductance Lm2.

Dual coupled inductor

Set the inductor current ripple coefficient ε, and calculate Lm:

$$\left\{ \begin{gathered} {L_{m1}} \geqslant \frac{{{V_i}D{T_s}}}{{\varepsilon {I_{Lm1}}}} \hfill \\ {L_{m2}} \geqslant \frac{{\left( {{V_i}+{V_{C1}} - {V_{C2}}} \right)(1 - D){T_s}}}{{\varepsilon {I_{Lm2}}}} \hfill \\ n=\frac{{{V_o}}}{{{V_{i\hbox{min} }}}}{(1 - {D_{\hbox{max} }})^2} - 2 \hfill \\ \end{gathered} \right.$$
(24)

Take Vimin = 20 V, Dmax = 0.85, consider leakage inductance and rounding, n = 1 is taken. The coefficient ε is taken as 30%, according to (23)-(24), Lm1 = Lm2 = 110 µH is determined.

Capacitor C

Assuming the capacitor voltage ripple coefficient δ, the pulsating voltage Δvc of the capacitor, calculate the lower limit of the value:

$$C \geqslant \frac{{{P_{\text{o}}}}}{{{V_o}\Delta {v_C}{f_s}}}=\frac{{{P_{\text{o}}}}}{{{V_o}\delta {V_c}{f_s}}}$$
(25)

C1 ripple coefficient δ is 0.5%, C3-C4 ripple coefficient δ is 3%, take C1 = 100 µF, C3 = C4 = 20 µF.

The resonant circuit must realize a complete half cycle:

$${C_2}<\frac{{{D^2}{T_s}^{2}}}{{{\pi ^2}{n^2}\left( {{L_{k1}}+{L_{k2}}} \right)}}=\frac{{{D^2}}}{{{\pi ^2}{n^2}\left( {{L_{k1}}+{L_{k2}}} \right){f_s}^{2}}}$$
(26)

It was finally determined that the C2 = 2 × 220 nF.

Control circuit

The Bode plot of the proposed converter is shown in Fig. 9 below. The crossover frequency is around 26.8 kHz, and the corresponding phase margin cannot meet the stability conditions. Using the C block module in the software, the stability and dynamic characteristics of the converter can be further improved by adjusting the compensation parameters.

Fig. 9
figure 9

Open loop Bode diagram of the converter.

Full size image

Figure 10 is a block diagram of the converter control circuit. Where the error value is obtained from the reference voltage Vref and the feedback value Vfd of the sampled output voltage. The error signal passes through the PI controller to generate PWM, and the PWM signals of the switches are given to the two switches respectively. The control of different MOSFETs is completed through the driver circuit. In this way, when the system is disturbed by external interference, the converter can quickly self-adjust under closed-loop PWM control to achieve stable output.

Fig. 10
figure 10

Control block diagram.

Full size image

Experiment and analysis

To ensure that the proposed converter’s principle is accurate and reliable. A 400 W laboratory platform was built. The critical parameters of the prototype are shown in Table 2, and the experimental prototype in Fig. 11.

Table 2 The key parameters of the prototype.
Full size table
Fig. 11
figure 11

Experimental prototype.

Full size image

Experiment verification

The experimental waveform of the input voltage 24 V is shown in Fig. 9. In addition, the experimental waveform under the condition of input voltage 32 V is given as the experimental control group in Fig. 12. The closed-loop responses of the converter are shown in Fig. 13.

Fig. 12
figure 12

Experimental waveforms (Vi=24 V). (a) iNp1, iNp2. (b) iLi, iNs. (c) VS1, iS1 & VS2, iS2. (d) VD1, VD2 & iD1, iD2. (e) VD3, VD4 & iD3, iD4. (f) S2-on & D4-off 3.

Full size image

Figure 12(a), (b) shows the primary and secondary winding currents of the dual-coupled inductor. It can be seen that the winding current waveform is the same as the theoretical analysis. As in Fig. 11(b), the input current is continuous and the ripple is as small as about 15%. Figure 12(c) is the voltage and current waveform of the switches S1 and S2. It can be seen that the voltage stress of switch S1 is about 58 V, the voltage stress of switch S2 is about 133 V, which is about 14.5% and 33.25% of the output voltage, and the converter has very low voltage stress. Moreover, switch S2 realizes ZCS-on and its turn-off current is only 9 A, which is only 46.72% of its maximum value. Quasi-resonance is used to effectively reduce its turn-off current. The voltage and current waveforms of each diode are shown in Fig. 12(d), and (e) respectively. Where the voltage stress of diode D1 is the same as that of switch S1, diode D2 is the same as that of switch S2. Diodes D3 and D4 have the same voltage stress of about 265 V, all below the output voltage. Diode D2 realizes ZCS turn-off and diodes D3 and D4 realize ZCS-on & ZCS-off conductions. Among them, diode D3 eliminates reverse phase recovery through quasi-resonance.It can be clearly seen from the partially enlarged Fig. 12(f) that the ZCS conduction effect achieved by the switch S2 is excellent, and at the same time, the reverse recovery problem of the diode D4 is effectively alleviated with the fluctuation being extremely small.

Figure 13 shows the experimental results of changing the input voltage to 32 V, the waveforms of each device are also consistent with the previous theoretical analysis, which once again verifies the correctness and feasibility of the proposed converter topology.

Figure 14(a), (b) shows the experimental results of the dynamic response to supply and load variation. Among them, the input voltage jumped from 18 V to 26 V, and the load jumped from 400 W at full load to 200 W at half load. The converter can quickly self-adjust under digital proportional-integral (PI) based closed-loop control to achieve stable output.

Fig. 13
figure 13

Experimental waveforms (Vi=32 V). (a) iNp1, iNp2. (b) iLi, iNs. (c) VS1, iS1 & VS2, iS2. (d) VD1, VD2 & iD1, iD2. (e) VD3, VD4 & iD3, iD4. (f) S2-on & D4-off 3.

Full size image
Fig. 14
figure 14

Experimental waveforms (dynamic response) (a) supply variation. (b) load variation.

Full size image

Efficiency and loss analysis

The power losses of the prototype include losses of switches, diodes, coupled inductors, and capacitors. The loss composition of MOSFET is relatively complex and can be divided into three main parts: turn-on, turn-off, and conduction losses, among which S2 realizes ZCS-on.

Based on software simulation, the root mean square current (RMS) of different devices at full load can be obtained, and calculate the corresponding losses of different devices:

$$\left\{ \begin{aligned} P_{S} = & \frac{{f_{s} }}{2}(V_{{DS}} I_{{dS1}} t_{{on}} + V_{{DS1}}^{2} C_{{ossk}} ) + \mathop \sum \limits_{{k = 1,2}} \left[ {I_{{Skrms}}^{2} r_{{Sk}} + \frac{{f_{s} }}{2}(V_{{DS}} I_{{dSk}} t_{{off}} + V_{{DSk}}^{2} C_{{ossk}} )} \right] \\ P_{L} = & \mathop \sum \limits_{{i = 1,2}} I_{{Lkirms}}^{2} r_{{Lki}} + I_{{Nsrms}}^{2} r_{{Ns}} \\ P_{D} = & \mathop \sum \limits_{{k = 1,2,3,4}} (I_{o} V_{{Fk}} + I_{{Dkrms}}^{2} r_{{Dk}} ) \\ P_{C} = & \mathop \sum \limits_{{k = 1,2,3,4}} I_{{Ckrms}}^{2} r_{{Ck}} \\ \end{aligned} \right.$$
(27)

Based on Table 2 device selection, query the parameters according to the device’s product manual to obtain the specific parasitic parameters, etc. Where VDS is the turn-off voltage of switches, toff is the turn-off time of switches, and Coss is the output capacitance of the MOSFETs. VF is the forward voltage drop of diodes, and r is the equivalent series resistance of different devices. In addition, Ids (on or off) are the values of the MOSFETs current at the turn-on or turn-off instants, respectively.

The loss ratio of each component of the prototype is obtained, as shown in Fig. 15. Among them, since the voltage stress of switch S1 is low and S2 realizes ZCS conduction, the overall loss ratio of the switch is not much. Higher current stress in double-coupled inductors affects losses. In addition, due to parasitic parameters, capacitance accounts for a large proportion of losses.

Fig. 15
figure 15

Power loss proportion (Vi=24 V, 400 W).

Full size image

And then get the computational efficiency:

$$\eta =\frac{{{P_o}}}{{{P_o}+{P_{\text{S}}}+{P_L}+{P_D}+{P_C}}}$$
(28)

Figure 16 shows the tested efficiency of the converter (Vi=24 V), the prototype reaches its maximum at around 97.6%. At the full load of 400 W, the prototype efficiency was about 96.3%, close to the calculated 96.6%.

Fig. 16
figure 16

Tested efficiency of the converter (Vi=24 V).

Full size image

Conclusion

Based on the Buck/Boost topology, this paper proposes a high-gain dual-coupled inductor interleaved quadratic converter and realizes a quasi-resonant soft switching design. Its working principle and performance indicators were analyzed in detail, and a 400 W prototype was built for experimental verification. The proposed topology combines the advantages of the interleaved and quadratic types and also introduces other technologies such as coupled inductance and quasi-resonant ZCS soft switching. The converter has good overall performance, achieving a balance between high gain and high efficiency, and is suitable for various applications such as distributed photovoltaic power generation systems. Has the following advantages: (a) The interleaved of the input realizes the quadratic voltage boost effect; (b) A dual coupling structure is introduced to flexibly control the voltage boost by adjusting the turn ratio n. The interleaved input cooperates with double coupling to reduce the current ripple when the input current is continuous; (c) Flexible utilizes multiple groups of D-C branches as clamps for switches to control voltage stress; absorb leakage inductance energy to achieve soft-switching of the device; together with the secondary side connected in reverse series, forming the voltage multiplier cell; (d) Using the quasi-resonant circuit to reduce the turn-off current of the corresponding switch while realizing ZCS, effectively reduces the instantaneous impact and the loss of the device; (e) Based on the cooperation of the quasi-resonant circuit and the D-C branch, the leakage inductance energy is fully utilized to suppress the voltage and current surges in the circuit, further alleviating the reverse recovery problem of the diode; (f) Through the coordination of devices, the performance can be effectively improved, the number of devices can be controlled, and the size of the equipment can be reduced. Sum, high voltage gain, adapting to a wide input voltage range; high efficiency, using advanced topology to improve energy conversion efficiency; suitable for space-constrained scenarios. These characteristics make it a key component in new energy, the Internet of Things, automotive electronics, medical equipment, etc.