Investigation of risk-aware dynamic accident monitoring and early warning technologies for chemical production processes

Abstract

There are numerous hazardous factors in the production processes of chemical enterprises, posing significant risks. This study overcomes the limitations of traditional safety early warning methods that rely on single-dimensional fault parameter monitoring. By innovatively integrating cusp catastrophe theory and risk entropy analysis, it constructs a dual-mode collaborative early warning system of ‘Conventional parameter monitoring-risk situation awareness’ based on multi-source information fusion. This approach objectively evaluates the current operational state and anticipates dynamic changes in risk situations, providing a solid foundation for early accident warnings. The case study demonstrates that precise calculation of risk entropy value changes, $\Delta = 8\mu^{3} + 27v^{2} = 0.03460$ is obtained, indicating that the current chemical production process system is safe and stable, with a low likelihood of system risk escalation. The analysis results align with actual conditions. The research outcomes achieve a three-dimensional dynamic coupling of ‘condition monitoring—mutation warning—trend prediction’ under complex working conditions, offering an engineering application value by providing a technical pathway for transforming chemical process safety from ‘passive response’ to ‘active defense’.

Introduction

The production process of hazardous chemical enterprises involves numerous perilous and detrimental factors, resulting in a high level of risk. Enhancing the dynamic monitoring and early warning systems for accidents during production is a widely employed method for preventing and controlling major industrial incidents worldwide. It also constitutes a crucial endeavor for hazardous chemical enterprises to eliminate safety hazards, prevent accidents, and establish a sustainable mechanism for safe production. In recent years, China has witnessed a series of severe and significant accidents involving hazardous chemicals, such as the 8.12 Tianjin Binhai port warehouse fire and explosion”, the 7.19 Shaoyang Shanghai Kunming high-speed transport truck explosion, and the 11.22 Qingdao economic and technological development zone oil pipeline leakage and explosion. These incidents have resulted in numerous casualties and had a profound societal impact. Given the emphasis on regional economic development strategies at the national level, ensuring supervision within the hazardous chemical industry has become increasingly imperative.

An inherent limitation of the process safety management (PSM) system in conventional chemical enterprises is its lack of integration and isolation from other process operations¹. The timely detection of process accidents heavily relies on monitoring parameters related to process faults. Consequently, it often becomes possible to identify areas for improvement or change only after an accident occurs, resulting in significant delays². The U.S. Chemical Process Safety Center (CCPS) recommends that facilities should proactively monitor the real-time performance of their management systems rather than waiting for accidents to happen, ensuring prompt identification of abnormal information before any accidents occur and taking timely corrective measures³. To promptly reflect the state of process safety, a process safety performance index is employed for monitoring and enhancing overall process safety. Early identification of deteriorating safety performance represents the most crucial yet challenging aspect within the realm of process safety since causes are frequently attributed to a combination factors encompassing operation, maintenance, management practices, organizational aspects as well as prevailing safety culture. Currently, the risk-based design methodology occupies a pivotal position in controlling chemical production processes. This approach comprises three core steps: hazard identification, risk analysis, and decision-making⁴. Among various risk assessment and management methodologies, Hazard and Operability Study (HAZOP) stands out as a qualitative risk analysis tool that relies on guide words. It is extensively utilized in process safety management⁵. HAZOP systematically identifies, analyzes, and evaluates potential risks associated with chemical processes and equipment through structured and methodical reviews⁶. The Bow-tie method⁷, initially developed by the University of Queensland in Australia, serves as an effective risk assessment tool for production processes. It integrates Fault Tree Analysis (FTA) and Event Tree Analysis (ETA) to visually map out the entire process of risk management and control. By linking potential risks to events and their consequences, it provides a comprehensive view of how risks may materialize. Nonetheless, despite its advantages, both the HAZOP and Bow-tie analysis methods have certain limitations. First of all, traditional HAZOP is a structured brainstorming analysis technique that necessitates the involvement of experts and engineers from diverse fields such as process engineering, safety, instrumentation, and management. Consequently, the accuracy and comprehensiveness of risk identification in chemical processes largely hinge on the depth of professional knowledge possessed by the HAZOP team members. In contrast, the Bow-tie analysis method, while effectively illustrating the causal chain reactions of accidents and the protective roles of safety measures in production processes, remains fundamentally rooted in static risk analysis. The reliability of these safety measures is challenging to quantify accurately and often relies more on qualitative descriptions. Bayesian network is a network model used to describe the uncertain causal relationship between variables⁸. In this model, risk factors are regarded as nodes, and the causal dependence between them is analyzed by using conditional probability. BN has become an important tool for quantitative risk assessment of chemical processes^9,10. However, there are still many shortcomings in the traditional BN model research. First, Bayesian Network (BN) modeling requires extensive chemical process knowledge and robust data for accurate parameter estimation. Distorted or incomplete data can result in inference inaccuracies and convergence issues within the BN model. Second, a single BN model is constrained to identifying pairwise relationships between variables, which limits its capability to evaluate the intricate interdependencies and evolving risk causality within chemical processes and equipment. Third, when applying BN models to actual chemical process risk assessment, the initial step involves constructing the BN mathematical framework. However, current approaches frequently depend on subjective modeling techniques that lack precision and reliability. Consequently, developing an efficient and accurate BN model based on comprehensive chemical process knowledge remains a significant challenge in the field of quantitative risk assessment.

Therefore, Risk-aware Dynamic Accident Monitoring and Early Warning Technologies for Chemical Production Processes based on risk entropy is proposed. On one hand, this approach can dynamically reflect the risk status of the chemical production process. On the other hand, it enables early perception of changes in risk conditions, thereby establishing a robust technical foundation for advanced early warning systems. Entropy is a physical concept derived from the field of thermodynamics, representing the degree of disorder and chaos within a system. It serves as a state quantity, where higher entropy corresponds to lower order¹¹. Furthermore, it quantifies the uncertainty associated with system risk¹². The theory of risk entropy explains the emergence and aggregation of accidents in chemical industrial parks through dynamic evolution mechanisms. It enables multidimensional characterization of factors such as accident probability, loss, unpredictability, and uncontrollability. Consequently, it has extensive applications in chemical system risk assessment and emergency prediction^13,14. By analyzing the dynamic changes in system risk, the theory can assess accident risks and predict their future direction within chemical industrial parks. Johnson et al.¹⁵ investigated the relationship between entropy increase and emergencies, highlighting that emergencies arise due to increased entropy and disorder within systems. Spartalis et al.¹⁶ developed a fuzzy entropy-based model for assessing natural disaster risks. In domestic research on entropy theory combined with brittleness theory and dissipative structure analysis by Chen Weike et al.¹⁷, they explained how emergencies occur by examining factors contributing to increased or decreased entropy levels. Wang et al.¹⁸ analyzed the dynamic propagation process of risk entropy within an accident evolution network to provide insights into accident analysis and prevention.

Dynamic accident warning technology is crucial for accident prevention and enhancing safety management. There is an urgent need for research in this area to advance modern safety practices. By integrating dynamic early warning systems, the focus of accident prevention can shift from reactive emergency management to proactive risk monitoring and mitigation. This approach transforms static safety management into a dynamic framework, replacing isolated event handling with a systematic and integrated methodology. Leveraging the cusp catastrophe model and risk entropy theory, we developed a dynamic risk perception and early warning model for chemical enterprises. This model provides decision-makers with a visual representation of evolving risk scenarios, offering a robust foundation for early accident warnings.

Theoretical foundation for dynamic perception and early warning of accidents in chemical industries

Risk situational awareness, as the core of accident early warning technology, enables effective prediction of dynamic safety state changes in chemical production processes by utilizing current extensive monitoring data. Originating from studying human factors in aerospace flight, situation awareness encompasses the acquisition, comprehension, evaluation, and anticipation of future development trends related to elements that can induce alterations in network situations within a large-scale network environment. Risk situational awareness involves comprehending the safety status and potential variations among all entities within a specific area; it entails understanding the present state and changing the trajectory of the entire production process under influences such as equipment operation status, process production procedures, and working environment conditions.

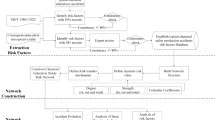
The latest data acquisition, fusion, and analysis technology is utilized to access the existing sensing network data of chemical enterprises, including operation environment monitoring data, production process monitoring data, safety production video monitoring data, security monitoring data, etc., enabling real-time collection and dynamic monitoring of toxic and harmful substances concentration in primary hazard sources as well as safety parameters such as temperature, pressure and liquid level during daily safety monitoring, as shown in Fig. 1. This integration facilitates deep mining and analysis of the collected information for early detection of abnormal mutations in accident occurrence situations through dynamic study and judgment based on advanced early warning technology.

Fig. 1

The system architecture of enterprise accident dynamic perception system.

Mechanism analysis of risk evolution process of chemical production system

There is typically a certain degree of delay in the chemical process safety status supervision process. The awareness of potential accident risks is insufficient, and response measures are often implemented after accidents occur, resulting not only in missed opportunities for accident control but also in significant losses. The dynamic complexity involved in the evolution of the accident state often prevents direct calculation and monitoring to determine the safety state of the chemical process. However, observing changes in the safety state through specific means and detecting sudden shifts by analyzing signs of accident evolution may be possible.

The transition mechanism of system safety state

Chemical enterprises are complex nonlinear systems comprising materials, energy, and information (as illustrated in Fig. 2), thereby inheriting the typical characteristics of nonlinear systems. Non-linearity serves as the intrinsic driver for the system’s self-organizing behavior. Without this internal mechanism, openness would be ineffective, and the transition from disorder to order would not occur. Numerous scholars have proposed the theory of dissipative structures within systems, which are formed and sustained through self-organization. The most fundamental attribute of a dissipative structure is its consumption of externally supplied ordered matter, energy, and information. Without such consumption, the dissipative structure would cease to exist. Consequently, to maintain the dissipative structure of a security system, it is imperative to ensure the system’s openness, allowing for a balanced inflow and outflow of materials, energy, and information. Based on this principle, the concepts of ‘negative entropy flow’ and ‘positive entropy flow’ are introduced to quantitatively evaluate the exchange of material, energy, and information between the security system and its external environment. Since the magnitude of entropy measures the likelihood of spontaneous state realization, changes in entropy can reflect alterations in the degree of disorder within the security system.

Fig. 2

Chemical enterprise material, energy, information schematic diagram.

Chemical enterprises, typically integrated within the petrochemical supply chain, rely on various methods of material transport across the upstream raw material input, midstream production and processing, and downstream product output stages. These processes involve continuous exchanges of materials, energy, and information with the external environment, making them open, complex systems. Within these enterprises, multiple subsystems coexist, including production equipment, hazard sources, and vulnerable targets. According to the theory of dissipative structures, the inherent nonlinear mechanisms of these systems result in constantly shifting safety states, making the prediction of system behavior difficult. This dynamic gives rise to deviations between different state variables, referred to as 'fluctuations,' which represent the driving force that propels the system from an unstable configuration towards a new, stable equilibrium. As depicted in Fig. 3, the parameter $\mu$ represents the degree of deviation of the system from its equilibrium state. The risk state $P$ is a function of $\mu$, where $\mu { = 0}$ corresponds to the equilibrium state, and $\mu_{c}$ denotes the critical state of the system. When $\mu < \mu_{c}$, the system remains stable in its early stage of risk evolution with a relatively smaller increase in risk entropy. However, when $\mu \mu_{c}$, the system surpasses its critical point and enters a nonlinear region. In this phase, under the influence of increased system entropy, random ‘micro-fluctuations’ occur within the park’s risk state. Upon reaching critical points (points c, d, e) in terms of risk states induced by emergencies¹⁹, abrupt changes arise leading to 'macro-fluctuations’. At this juncture, triggering transitions in system’s risk states results in more severe consequences.

Fig. 3

Chemical system risk transition diagram.

Entropy change and the evolution process of risk entropy in chemical systems

In the case of an isolated system (a system devoid of energy and material exchange with its surroundings), over time, the system will invariably progress toward a state of uniform and disordered equilibrium. During this process, the entropy value of the system will continuously increase until it reaches a dynamic equilibrium state, at which point the entropy value remains constant. This phenomenon is referred to as the principle of entropy increase. As an open complex system, chemical production processes involve exchanges of material, energy, and information both within the system itself and with its external working environment (as depicted in Fig. 2). The entropy value corresponds to the safety state of the system; higher values indicate greater disorder while lower values signify higher degrees of order. Within the time interval $dt$, the system entropy $ds$ comprises two components (as depicted in Formula 1). One component is the irreversible increase in risk entropy $d_{i} s$ (positive entropy) generated within the system. This increase acts as the fundamental driver of disorder in the system’s risk state and is characterized by spontaneity and unidirectional irreversibility. The increase in risk entropy for a chemical production system arises from both internal conditions and external environmental factors. Internal conditions primarily encompass storage of hazardous substances, process conditions, and device malfunctions. External environment refers to accidents and natural disasters that disrupt normal operation of the chemical production system. The other component entails external inputs designed to reduce risk by decreasing control entropy $d_{e} s$, also referred to as negative or regulatory entropy. This process ensures the orderly functioning of the chemical production system through the exchange of materials, energy, and information between the system and its environment.$d_{e} s$ can be either positive or negative depending on circumstances. Generating a flow of control entropy to counterbalance risk entropy typically requires exerting coercive forces externally; hence, reduction in risk entropy possesses an inherent mandatory characteristic.

$$ds = d_{e} s + d_{i} s$$

(1)

In summary, during the evolutionary process of system risk state, a dynamic interplay between entropy increase and entropy decrease occurs, and the law governing changes in system risk entropy varies across different stages, as illustrated in Fig. 4.

Fig. 4

The dual dynamic accident monitoring and early warning mechanism model.

• (1) Before the occurrence of emergencies (the accumulation period of entropy).

Due to the accumulation of hazardous materials and the complexities involved in production, storage, and transportation, various factors contributing to the increase in risk entropy within chemical production systems are compounded. This leads to the continuous accumulation of energy driven by dynamic changes, a process characterized by its irreversibility. As destructive energy rapidly accumulates ($d_{i} s \gg 0$), the factors driving risk entropy increase intensify, while the factors controlling entropy, which maintain normal system operations, remain limited within a certain timeframe. During this phase, despite a decrease in control entropy ($d_{e} s0$), it remains smaller than $d_{i} s$. Consequently, the rise in risk entropy prevents its reduction to the minimum threshold. As the system’s overall risk entropy ($ds = d_{e} s + d_{i} s \gg 0$) approaches a critical point, its self-organizing capacity becomes fragile, destabilizing the original equilibrium and gradually shifting the system toward a chaotic and disordered non-equilibrium state.

• (2) When an emergency occurs (the mutation period of entropy).

The second stage indicates that when the abnormal energy reaches its maximum state, surpassing the bearing capacity of the chemical production system, emergencies occur. Due to the entropy value $ds = ds_{\max }$, representing a critical point of system collapse, even a minor disturbance can trigger an increase in entropy. In this process, the system undergoes an abrupt change and enters a chaotic state. It is evident that emergencies fundamentally arise from a brittle collapse process caused by an increase in entropy.

• (3) After an emergency occurs ( decay period of entropy).

The outbreak of emergencies releases a surge of entropy-increasing energy; however, human intervention prevents uncontrolled escalation, as various emergency measures are implemented to curb the worsening of accidents. The significant investment of human and material resources by the emergency response teams in chemical industrial parks effectively enhances the role of risk entropy-reducing factors, mitigating the rapid increase of entropy flow and weakening the accumulation of risk entropy. When the reduction in risk entropy ($d_{e} s \gg d_{i} s$) surpasses its increase, the control entropy flow gains dominance, leading to a gradual decrease in the system’s overall risk entropy. As $ds = d_{i} s + d_{e} s0$, the system progressively enters a new equilibrium state.

Development of a dynamic monitoring and early warning model for accidents in the chemical production process

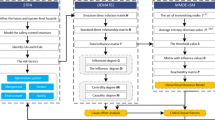
The accident monitoring and early warning of chemical production processes embodies the concept of comprehensive safety management and control. It represents a safety management mode based on all-encompassing and continuous accident monitoring throughout the entire chemical production process. The essence of early warning lies in proactively assessing the system’s safety status, enabling preemptive measures against potential accidents. Achieving preventive measures is the ultimate objective of early warning systems. Early warnings encompass two aspects: prediction and alarm. By analyzing collected accident-related information and evaluating process safety conditions, the early warning system assesses the current operational state of the production system, makes predictive judgments about future trends, and determines whether to issue alarm notifications accordingly.

Based on these fundamental concepts, we propose a dynamic accident monitoring and early warning mechanism model for dual chemical production processes that combines conventional early warnings with dynamic perception-based early warnings (As shown in Fig. 4).

In Fig. 4, it can be seen that:

• (1) Conventional Early Warning: Conventional early warning operates as a single-point alert system. By integrating pre-established risk assessment indicators with real-time risk index data collected during chemical production, dynamic monitoring is performed. An alarm is triggered when clear signs of failure are detected, based on predefined alarm thresholds. A higher system risk entropy indicates a shift toward a disordered state, signaling an increased likelihood of accidents.

• (2) Dynamic Perception Early Warning: Through dynamic perception of fluctuations in safety monitoring parameters during chemical production, evolving risks can be identified in real-time, enabling timely issuance of early warning signals for potential accidents.

The principles and construction of the risk entropy catastrophe model.

The principle of catastrophe model

Catastrophe theory, introduced by the French mathematician René Thom in 1972, provides a framework for predicting and describing abrupt changes in the behavior of complex systems through potential functions. It has broad applications in sociology, economics, water resource management, and energy systems. Common catastrophe models include the cusp, swallowtail, and butterfly catastrophe models. A key feature of these models is their ability to capture the possible states of a system via its potential function, without delving into the internal mechanisms, particularly when analyzing discontinuous shifts near critical points as system parameters change.

The catastrophe function $F(x_{1} )$ in Table 1 represents the potential function of the state variable $x_{1}$ in a system, while the state variable coefficient $u_{1} ,u_{2} ,u_{3} ,u_{4}$ represent the control variable for the state variable.

Table 1 Commonly used mutation models.

Construction of risk entropy mutation model

The dynamic variation of accident risk in chemical production arises from factors contributing to entropy increase and decrease. The development and alteration process of accident risk is jointly determined by the increase and decrease in risk entropy. During this period, the accident state serves as the sole variable, while risk entropy increases and decrease act as two control variables. To analyze this scenario with one state variable and two control variables, we employ the cusp catastrophe model presented in Table 1 and examine it through cusp catastrophe theory. The specific expression can be seen in Formula 2.

$$F(x) = x^{4} + ux^{2} + vx$$

(2)

In the formula, $x$ is the state variable, which is used to reflect the risk state of the production system, and $u = f_{v} (u_{1} ,u_{2} ,u_{3} , \ldots ,u_{m} )$ is the control variable. It is the factor that affects the risk state of the chemical enterprise and promotes the sudden change of the risk state of the chemical production system, which is the entropy increase factor. $v = f_{v} (v_{1} ,v_{2} ,v_{3} , \ldots ,v_{m} )$ is the control variable, which is a variety of factors that reduce the risk degree of the system and reduce the risk entropy to reduce the accident loss by various prevention and control measures taken in the emergency of the chemical production system, that is, the entropy reduction factor.

Monitoring parameter fluctuation distribution probability

The monitoring time set $T = \left\{ {t_{1} ,t_{2} , \ldots ,t_{m} } \right\}$ of the sensing terminal constitutes $t_{1} ,t_{2} , \ldots ,t_{m}$, which is a specific parameter for monitoring in the chemical production process. The discrete monitoring data sequence $E_{i,j}^{k} = \left\{ {e_{1,j}^{k} ,e_{2,j}^{k} , \ldots ,e_{m,j}^{k} } \right\}$ is defined as $e_{i,j}^{k} (i = 1,2, \ldots ,m;j = 1,2, \ldots ,n)$, representing the $j$-th sensing terminal’s monitoring data for parameter $k$ at time $t_{i}$. Corresponding measured values are associated with each sensing terminal, forming a measured matrix to represent the overall risk state of the monitoring parameters in the designated area.

$$F_{T \times E} = \left( {e_{i,j}^{k} } \right)_{m \times n}$$

(3)

The standard monitoring data sequence of this parameter under normal working conditions is set $E_{0}^{k} = \left\{ {e_{1,j}^{k} (0),e_{2,j}^{k} (0), \ldots ,e_{m,j}^{k} (0)} \right\}$, and the fluctuation distribution probability of the monitoring data and its corresponding standard monitoring data is defined:

$$p_{i,j}^{k} = p(e_{i,j}^{k} ,e_{i,j}^{k} (0)) = \left\{ {\begin{array}{*{20}c} {\frac{{\left| {e_{i,j}^{k} - e_{i,j}^{k} (0)} \right|/e_{j}^{k} (\max )}}{{\sum\limits_{j = 1}^{n} {\left[ {\left| {e_{i,j}^{k} - e_{i,j}^{k} (0)} \right|/e_{j}^{k} (\max )} \right]} }}} & {e_{i,j}^{k} \ne e_{i,j}^{k} (0)} \\ 0 & {e_{i,j}^{k} = e_{i,j}^{k} (0)} \\ \end{array} } \right.$$

(4)

Corresponding to the measured matrix of monitoring data, the fluctuation distribution probability matrix $P$:

$$P = \left[ {\begin{array}{*{20}c} {p_{1,1}^{k} } & \cdots & {p_{1,j}^{k} } & \cdots & {p_{1,n}^{k} } \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ {p_{i,1}^{k} } & \cdots & {p_{i,j}^{k} } & \cdots & {p_{i,n}^{k} } \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {p_{m,1}^{k} } & \cdots & {p_{m,j}^{k} } & \cdots & {p_{m,n}^{k} } \\ \end{array} } \right]$$

(5)

In formula (6), the molecular part reflects the fluctuation of the sensing terminal, the denominator part represents the overall fluctuation of the sensing terminal group, $e_{j}^{k} (\max )$ is the monitoring threshold of the risk parameter of the sensing terminal, $p_{i,j}^{k}$ represents the proportion of the fluctuation state of the sensing terminal $j$ data relative to the fluctuation state of the whole sensing terminal group at the monitoring time $t_{i}$, which reflects the data fluctuation distribution of all the sensing terminals of the monitoring parameters, so it is called the data fluctuation distribution probability of the discrete monitoring sequence.

In the actual on-site monitoring process, it is difficult to obtain the complete standard monitoring sequence for some monitoring parameters, or the standard monitoring value is in the numerical range, such as the pressure in the tank, the temperature in the tank, etc. Therefore, for such monitoring parameters, the standard monitoring value is expressed as the average value of the high and low limits of the normal working range. If a certain type of monitoring parameter sensing terminal $e_{j}^{k} (\max )$ is equal or $e_{j}^{k} (\max ) = 0$(indicating the low limit index), the fluctuation distribution probability can be simplified as shown in Formula 6.

$$p_{i,j}^{k} = \frac{{\left| {e_{i,j}^{k} - e_{i,j}^{k} (0)} \right|}}{{\sum\limits_{j = 1}^{n} {\left| {e_{i,j}^{k} - e_{i,j}^{k} (0)} \right|} }}$$

(6)

Data fluctuation trend coefficient

The probability distribution of fluctuations reflects the relative degree of fluctuation in monitoring parameter data at a specific moment. However, the potential impact of individual terminal data fluctuations on risk situations has not been fully considered. Therefore, $\lambda$ is defined as the coefficient value for sensing terminal data fluctuations, representing the extent to which these monitoring parameters may contribute to abnormal situations. The fluctuation coefficient value depends on both the absolute value of monitoring data from the sensing terminal and the hazardous energy level associated with the monitored object. By analyzing comprehensive fluctuation results from sensing terminals, we determine that the magnitude of situation coefficients relies on both probability space $P = \left\{ {p_{1} ,p_{2} , \ldots ,p_{j} } \right\}$ for fluctuation distribution and coefficient space $\lambda = \left\{ {\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{j} } \right\}$, the specific expressions are shown in Formulas (7) and (8).

$$q_{i,j}^{k} = q(\lambda ,p) = \frac{{\lambda_{i,j}^{k} \cdot p_{i,j}^{k} }}{{\sum\limits_{j = 1}^{n} {\lambda_{i,j}^{k} \cdot p_{i,j}^{k} } }}$$

(7)

$$\lambda_{i,j}^{k} = \frac{{\left| {e_{i,j}^{k} - e_{i,j}^{k} (0)} \right|}}{{e_{j}^{k} (\max )}} \cdot d_{i,j}^{k}$$

(8)

The value coefficient of data fluctuation for the j-th sensing terminal, denoted as $\lambda_{i,j}^{k}$, is among them. The corresponding monitoring object’s dangerous energy level coefficient is represented by $d_{i,j}^{k}$. Subsequently, the situation coefficient matrix $Q$ of the measured set and standard set for the respective sensing terminal is obtained.

$$Q = \left[ {\begin{array}{*{20}c} {q_{1,1}^{k} } & \cdots & {q_{1,j}^{k} } & \cdots & {q_{1,n}^{k} } \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ {q_{i,1}^{k} } & \cdots & {q_{i,j}^{k} } & \cdots & {q_{i,n}^{k} } \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {q_{m,1}^{k} } & \cdots & {q_{m,j}^{k} } & \cdots & {q_{m,n}^{k} } \\ \end{array} } \right]$$

(9)

Construction of parameter risk entropy model

The risk evolution of chemical production processes exhibits a high degree of uncertainty and dynamic randomness. Risk entropy serves as an effective measure for quantifying the level of uncertainty in system risks. Shannon introduced the classical information entropy model to assess the amount of information generated by discrete sources.

$$H_{i} = - K\sum\limits_{j = 1}^{n} {f_{ij} \ln f_{ij} }$$

(10)

The entropy value $H_{i}$ in the formula represents the information contained in the $i(i = 1,2, \ldots ,k)$-dimensional date, with a larger $H_{i}$ indicating greater information contented in the $i$-dimensional data of the factor $j$. The proportion $f_{ij}$ denotes the contribution of factor $j$ to the $i$-dimensional data. By incorporating fluctuation distribution characteristics and situation values, we construct a parameter risk entropy representation model suitable for real-time monitoring data in chemical industry parks based on the classical model formula of information entropy. It is evident that when monitoring parameters exhibit no fluctuations, their corresponding risk entropy value becomes zero due to a situation coefficient of zero. Therefore, we define real-time parameter risk entropy $H^{k}$ for fluctuating monitoring parameter k as shown in Eq. (11).

$$H_{i}^{k} = - K\sum\limits_{j = 1}^{{n_{k} }} {q_{i,j} \ln p_{i,j} = - K\sum\limits_{j = 1}^{{n_{k} }} {\frac{{\lambda_{i,j} \cdot p_{i,j} }}{{\sum\limits_{i = 1}^{n} {\lambda_{i,j} \cdot p_{i,j} } }}\ln p_{i,j} } }$$

(11)

Among them, $K$ represents the Boltzmann constant, which is a positive value ($K > 0$). It is taken as $1/\ln n_{k}$. In Eq. (11), where the relationship between the risk state and parameter risk entropy is established. The change in parameter risk entropy depends on variations in the risk state, enabling the measurement of the risk state through monitoring parameters.

System safety state judgment

Due to the nonlinear nature of risk entropy, a polynomial equation consistent with the risk entropy can be constructed by inputting the corresponding entropy data and time parameters. Subsequently, employing diffeomorphism transformation, the system’s risk entropy function in power series form is converted into the standard form of cusp catastrophe. Based on this, the formula (12) presents the constructed risk entropy potential function for chemical production processes.

$$y = \sum\limits_{i = 0}^{4} {a_{i} t^{i} } = z^{4} + uz^{2} + vz + c$$

(12)

Let $r_{i}$($0 < r_{i} < 1$) represent the weight value of the $i$-th risk entropy index in the accident’s evolutionary process ($i = 1,2, \ldots ,n$), where each index’s weight is analyzed using the AHP (Analytic Hierarchy Process)¹³. The determination of these weights is based on the influence factors that each risk entropy index has on the development and evolution of the accident. Consequently, the $1 \times n$-order matrix $R$ is constructed to represent the weight values for risk indices, $R = \left[ {\begin{array}{*{20}c} {r_{1} } & \cdots & {r_{i} } & \cdots & {r_{n} } \\ \end{array} } \right]$.

Among, $y = H \times R = \left\{ {H_{1} ,H_{2} , \ldots ,H_{n} } \right\}$

$$u = \left\{ {\begin{array}{*{20}c} {\frac{{b_{2} }}{{\sqrt {b_{4} } }}} & {b_{4} > 0} \\ {\frac{{ - b_{2} }}{{\sqrt { - b_{4} } }}} & {b_{4} < 0} \\ \end{array} } \right.;v = \left\{ {\begin{array}{*{20}c} {\frac{{b_{1} }}{{\sqrt[4]{{b_{4} }}}}} & {b_{4} > 0} \\ {\frac{{ - b_{1} }}{{\sqrt[4]{{ - b_{4} }}}}} & {b_{4} < 0} \\ \end{array} } \right.$$

$$z = \left\{ {\begin{array}{*{20}c} {(t + q)\sqrt[4]{{b_{4} }}} & {b_{4} > 0} \\ {(t + q)\sqrt[4]{{ - b_{4} }}} & {b_{4} < 0} \\ \end{array} } \right.$$

$$b_{1} = a_{1} - 2a_{2} q + 2a_{3} q^{2} ;b_{2} = a_{2} - \frac{3}{2}a_{3} q$$

$$b_{4} = a_{4} ;q = \frac{{a_{3} }}{{4a_{4} }};{\text{c}} = \frac{{a_{0} }}{{\sqrt[4]{{\left| {a_{4} } \right|}}}}$$

In the formula, $z$ is the state variable of the cusp catastrophe model, that is, the system risk entropy value that characterizes the risk situation of the chemical production process; $u,v$ are the two control variables of risk entropy increase and risk entropy decrease respectively; $a_{i}$ is the conversion coefficient and $c$ is a constant.

By $y^{\prime}(z) = 0$, the equation of the equilibrium surface $M$ of the risk entropy catastrophe model is obtained, as shown in formula (13).

$$4z^{3} + 2uz + v = 0$$

(13)

The critical state of the accident can be obtained by further derivation of $z$ in Eq. (13).

$$y^{\prime\prime}(z) = 12z^{2} + 2u = 0$$

(14)

Combining (13) and (14), the bifurcation set equation $C$ of the system can be obtained, that is, the projection of the crease on the equilibrium surface on the control plane.

$$\Delta = 8u^{3} + 27v^{2} = 0$$

(15)

The $u,v$ values are substituted into the discriminant formula $\Delta = 8u^{3} + 27v^{2}$ to judge the state of the system. If $\Delta > 0$, the risk of the chemical production process system is not excited and remains safe and stable. If $\Delta < 0$, the coordinate ($u,v$) composed of the increase of system risk entropy and the decrease of risk entropy falls within the bifurcation set, the system risk mutates, and the chemical process system may have the risk of accident upgrade; if $\Delta = 0$, the risk of the chemical production process system enters a critical state. At this time, if there are adverse factors, the safety state may transition to the accident mutation state.

Case analysis of accident early warning in chemical enterprises

Overview of a chemical enterprise

A chemical enterprise was established in 2004, primarily engaged in the production and storage of vinyl chloride, situated within the Xiaohudao Chemical Industrial Park in Guangzhou. The plant’s overall layout is approximately rectangular, covering an area of 78,079 m². Under the functional requirements of the production unit, the plant is divided into distinct sections. Moving from west to east, the northern part of the plant comprises a hazardous chemicals storage tank area, waste liquid recovery system, boiler room (standby), and fire pump room. Similarly, moving from west to east in the central part of the plant area are hazardous chemical finished product production plant area and gas storage tank. Lastly, from west to east in the southern section of the factory area lie various facilities such as an office building, canteen, bathroom and dressing room, parking lot, doorman station, etc., maintenance area as well as power distribution room (including generator room, power distribution room, substation room, and transformer site).

Construction of risk entropy index system

Based on the analysis of accident characteristics within the chemical production processes of the enterprise, it is clear that incidents arise from both internal reaction dynamics and external environmental factors. Given the nature of the accidents and the hazardous substances involved in the chemical plant, we have established a risk entropy monitoring index. Table 3 outlines the standard values for the risk entropy index, including lower and upper threshold limits, and the corresponding index symbols for typical internal processes and environmental scenarios.

To focus our discussion, this study narrows its scope to the case of vinyl chloride leakage within the enterprise’s hazardous chemical storage tank area. By utilizing a monitoring platform to gather relevant risk parameter data, we were able to track both environmental conditions and internal risk entropy indices. This enabled an assessment of the evolving risk state under leakage conditions within the enterprise.

Considering the varying significance of different risk entropy indicators in accident evolution, distinct weight coefficients are assigned to them, which consequently exert a certain influence on the final judgment results. Therefore, an enhanced analytic hierarchy process (AHP) is employed to handle expert scoring outcomes and derive the weight values for each risk entropy index (as illustrated in Table 2). By calculating the consistency ratio $CR$, we obtain $CR = 0.05180.1$ and judge that the judgment matrix satisfies the consistency requirements.

Table 2 The table of storage tank devices.

Accident dynamic early warning analysis

According to the constructed risk entropy index system, combined with the monitoring point data collected by the enterprise at different time points, we sampled the monitoring time set $T = \left\{ {t_{1} ,t_{2} , \ldots ,t_{m} } \right\},m = 36$ and the risk monitoring parameter sequence $E_{j}^{k} = \left\{ {e_{1,j}^{k} ,e_{2,j}^{k} , \ldots ,e_{n,j}^{k} } \right\},j = 1,2,3 \ldots ,n$ of the data. The vinyl chloride storage tank area serves as the primary risk source for our enterprise. Due to having a single monitoring object, there is consistency between the monitoring objects corresponding to the monitoring perception terminal. Therefore, referring to Table 3 for the risk entropy index and utilizing the Matlab auxiliary operation tool along with formulas (4)–(11), we calculated the risk entropy value sequence of each parameter as presented in Table 4.

Table 3 Risk entropy indexs.

Table 4 Monitoring parameter risk entropy value sequence.

According to the calculated risk entropy sequence of each parameter, in conjunction with the weight value assigned to each risk entropy index, the resultant system risk entropy sequence can be obtained, as illustrated in Table 5.

Table 5 The system risk entropy value sequence.

The numerical analysis method is employed to conduct polynomial fitting on the risk entropy sequence results obtained in Table 5, and the corresponding fitting outcomes are illustrated in Fig. 5.

Fig. 5

Risk entropy value fitting analysis results.

According to the fitting results, $\Delta = 8u^{3} + 27v^{2} = 0.03460$ can be solved based on Formulas (12)–(15). This indicates the current chemical production process system is deemed safe and stable, with a low possibility of stimulating system risk. The accident risk prediction results have been demonstrated to align well with the actual on-site situation over time. Compared to conventional over-limit early warning methods, dynamic perception and early warning of risk entropy are rooted in monitoring parameter fluctuations within the perception area. Its early warning outcomes possess advantages in terms of comprehensiveness and timeliness.

Conclusion

The latest generation of data acquisition, fusion, and analysis technologies has been utilized to achieve real-time monitoring and dynamic measurement of concentrations of toxic and hazardous substances in major hazard areas, alongside critical safety parameters such as temperature, pressure, and liquid levels during the production process. This integration facilitates comprehensive safety monitoring and information management in chemical enterprises, significantly enhancing capabilities for data mining and analysis. By harnessing dynamic monitoring systems and implementing early warning mechanisms, latent accident risks can be promptly identified, enabling continuous assessment of evolving risk trends within production processes. Moreover, by detecting abnormal shifts in accident trends at an early stage, advanced warning systems can be deployed to mitigate severe consequences arising from major incidents.

• (1) The accident monitoring and early warning of chemical production processes exemplify the concept of comprehensive safety management and control, which entails a safety management approach based on comprehensive and continuous monitoring of accidents throughout the entire chemical production process. This paper proposes to establish a dual dynamic mechanism model for accident monitoring and early warning in chemical production processes, combining conventional early warning methods with dynamic perception-based early warnings, in order to effectively capture the evolving nature of accidents in chemical production and promptly issue appropriate warning signals.

• (2) Building on the theory of risk entropy, we integrate this concept into the analysis of safety conditions within chemical production processes. We introduce the concept of accident risk mutation and investigate its underlying formation mechanism. Theoretical analysis suggests that the dynamics and uncertainty of accident risks in chemical production are driven by factors contributing to both entropy increase and entropy reduction. The evolution of accident risks is thus determined by the interplay between these opposing forces of risk entropy.

• (3) According to the characteristics of accident risk in chemical production processes, and by incorporating the cusp catastrophe model, we have developed a dynamic perception model for assessing the entropy-based accident risks in chemical production processes. The results from our example verification demonstrate that this model enables accurate calculation of changes in risk entropy, thereby providing a foundation for early accident warning systems and safety status assessments within chemical production processes.