Introduction

Cigarette filters (filter sticks1) are a key part of cigarette production, effectively reducing tar, nicotine and other harmful substances in inhaled smoke and reducing the irritation of smoke, thus improving the smoking experience. Some companies add a green core wire that carries flavouring ingredients to enhance the smoking experience of cigarettes during the production of filter sticks. What’s more, the core wire not only improves the flavour of the smoke, but also enhances the filtering effect on the harmful substances in the smoke, thus reducing the harmful effects of smoking on the human body to a certain extent.

During the production of filter rods containing mandrels, the mandrels may deviate from the centre of the rods due to mechanical precision errors, raw material quality and other factors. Mandrel deficiency may also occur in bulk quantities of filter rods when raw materials are changed or mandrels are broken, especially if the mandrel break sensors are interfered with, which may result in a large number of defective products.

In modern logistics and assembly line production, efficient detection of unqualified products or mixed-in clutter is a key production link that can significantly improve product qualification and yield. This process does not only rely on manual operation, but is increasingly achieved with the help of machine vision2 and automation technology3,4,5. Through the vision system and intelligent algorithms, it can quickly and accurately identify and distinguish abnormal products or sundries, thus ensuring smooth operation and efficient production on the production line.

In recent years, with the rapid development of machine vision technology and the advancement of industrial automation, more and more research has been devoted to solving the challenge of real-time monitoring of product quality on high-speed production lines6,7. It has been shown that rapid detection and analysis of defects in object appearance, dimensional changes and other key features can be achieved through traditional and deep learning techniques in machine vision.

In terms of on-line detection of microscopic defects, for example, Zhou et al.8 proposed a machine vision-based chisel edge wear measurement method, which possesses high responsiveness and accurate detection capability, and is more convenient and efficient than the traditional manual measurement using an electron microscope. On the other hand, Seyfollah Soleimani et al.9 have investigated the change detection of fast-turning specimens at the microscopic level, and the results showed that it is possible to detect specimens with diameter changes of more than 1.2 μm using computer vision. In addition, Xue et al.10 proposed a vision-based high-speed laser welding hump detection method, which is able to accurately detect the location where the hump occurs and to avoid misdetection in the absence of a hump. Liu et al.11 proposed a high-speed all-fibre-optic imaging method based on fibre-optic imaging, which is capable of efficiently detecting the subtle changes in micrometre-sized objects.

Most of the above methods can achieve high-precision detection, but it usually requires the support of specialised equipment such as microscopes, and often requires image stitching techniques when dealing with large-volume or large-area objects, and all these factors affect the speed and efficiency of real-time detection. For the detection of macroscopic objects, Tao et al.12 have proposed a method for automatic acquisition, impurity classification and content detection of maize images based on machine vision technology, which can quickly and effectively identify the impurities in maize images. In addition, for detecting appearance information such as size and dimensions, the study by Liu et al.13 demonstrated an online method for detecting the ripeness and diameter of Fuji apples, with an average detection accuracy as high as 98.7% and 93.3%, respectively, and achieved a real-time inference speed of about 56 frames per second.

Research results in high-speed defect detection14,15 and high-precision defect recognition techniques16,17 are increasing. For example, Liu et al.18 proposed a target detection algorithm based on an improved version of RetinaNet specifically for transmission line defect detection. The results show that the method outperforms the traditional method in terms of detection accuracy and efficiency, and meets the accuracy requirements in intelligent inspection.Wang et al.19, on the other hand, proposed a real-time detection network (RDN) integrating speed and accuracy to solve the problem of detecting defects on steel surfaces. The method achieves an advanced recognition speed of 64 frames per second (FPS) with a single GPU on the standard dataset NEU-DET, and achieves an average value of 80.0% in accuracy, which fully meets the dual requirements of inspection speed and accuracy in real production lines.

In terms of technological advancement, Wang et al.20 who employed deep learning algorithms, especially the U-net model, effectively trained a walnut detection model, demonstrating an average intersection ratio of 96.71% and a pixel accuracy of 98.52%. The FFDG-Cascade method proposed by Zhu et al.21, on the other hand, significantly improves the performance and speed of the detector through feature fusion and data generation techniques to effectively deal with the challenges of detecting defects in small targets. Finally, Chun-Chin Hsu et al.22 have introduced an automated optical inspection system for inspecting the surface of precision steel balls using the improved DRAEM technique, which successfully solved the problem of detecting small and inconspicuous defects. The roll out of these technologies has not only improved inspection accuracy, but also significantly enhanced the real-time responsiveness of production lines, bringing significant advances in quality control and efficiency optimization to the manufacturing industry.

Although modern image acquisition systems can easily capture clear images, imaging conditions are limited in complex industrial environments. Machine-generated noise during the production process may interfere with the camera’s sensor, creating unwanted noise in the final image and reducing the quality of the image. Factors such as lighting, acquisition equipment, and production processes can all have an impact on sample acquisition. Limited natural lighting conditions inside the equipment, the narrow space also affects the installation of lighting equipment, and machine operation may cause vibration of the acquisition equipment, which may cause the acquisition of the viewing angle deviation, and in serious cases, the filter bar image will jump out of the camera field of view, affecting the detection results. In high-speed production processing, even if high-resolution acquisition devices are used to improve image quality, real-time performance is sacrificed and the requirements for hardware devices are high23. However, for real-time inspection operations on some higher-speed production lines, especially for the inspection of the centering degree of filter rods and cores studied in this paper, the selection of three-dimensional image acquisition and processing methods cannot meet the high-speed requirements, and there will be spatial errors in two-dimensional image processing. The detection environment is also greatly restricted. Most importantly, the timing of image processing and communication is uncontrollable, which may cause time delay or data loss, further affecting the overall detection efficiency.Currently, there is no effective detection method for core wire offset and missing, therefore, there is an urgent need for an efficient online inspection device that can monitor in real time and discover the quality problems of a single filter rod in time to ensure the stability of the production process and the quality of the product.

In order to solve these problems, a filter rod mandrel detection method is proposed in this paper. By optimizing the image acquisition and processing process and combining with the image analysis algorithm, the method effectively improves the accuracy and real-time detection, and is able to accurately identify the centre degree of the filter rod mandrel and the missing mandrel on the high-speed production line. By reducing spatial errors and improving detection efficiency, the method is able to monitor core offset and missing wires in real time during the production process, ensuring consistency and stability of product quality. This innovative method of filter rod core line inspection not only provides reliable technical support for high-speed production lines, but also provides a new solution in the field of industrial automation inspection, which has important application significance and promotion value.

This paper has the following contributions:

  1. 1.

    image processing optimization: through the use of filtering, noise and other constraints on the image processing of the end face of the filter bar, effectively filtered out some of the interference in addition to the target contour, for the subsequent accurate contour fitting provides a good guarantee, but also for other round bar contour image preprocessing to provide ideas.

  2. 2.

    A vision system and algorithm, in particular an ellipse fitting method, are proposed to accurately obtain the coordinates of the centre points of the filter rods and their internal cores. This is then combined with the Euclidean distance calculation formula to evaluate the offset of the mandrel relative to the filter rod axis, enabling accurate detection and real-time analysis of dimensional deviations.

  3. 3.

    the use of two-dimensional algorithms to correct three-dimensional errors, solve the inspection process due to material deformation and perspective deviation causes three-dimensional errors, improve the accuracy of the inspection.

  4. 4.

    A filter rod quality inspection technology is proposed, which can improve the inspection efficiency and precision, and realise the timely detection and treatment of dimensional deviation in the manufacturing process of filter rod. It effectively reduces human errors and costs, improves the quality control ability on the production line, and provides an innovative quality management solution for the filter rod manufacturing industry.

The rest of the paper is structured as follows: the second section briefly describes the related work, including the reject hub and sampling hub carrying the filter bars and the image acquisition device; the third section describes the proposed detection method in detail, including the camera calibration method, the image pre-processing method, the ellipsoid fitting method, and the error correction method; the fourth section includes the experimental design and the experimental results; and the fifth section concludes the full paper. The overall flow of the system is shown in Fig. 1.

Fig. 1
figure 1

Existing filter rod forming unit. (a) Schematic diagram of the system operation flow. (b) Results of the experimental test of image processing time. (c) Experimental test results of communication time between the upper computer and PLC.

Full size image

Related work

In this section, the experimental setup required for the experiments in the follow-up, the installation requirements of the visual inspection device, the interference of the inspection environment on the inspection device and the corresponding solutions are described.

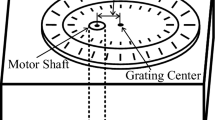
Filter rod forming machines are dedicated to the manufacture of filter rods for a wide range of applications such as tobacco, medical and industrial filtration, as shown in Fig. 1. Their core function is to process raw materials into filter rods that meet the specifications of the filtration needs of different applications.

In the tobacco industry, filter rod forming machines are responsible for the production of the filter portion of cigarettes. Modern filter rod forming machines incorporate automation technology and are capable of fully automated operations from raw material feeding, forming, cutting to packaging. These machines increase productivity, ensure dimensional accuracy and consistency of filter rods, and reduce waste in production through precision control.

Based on the key technologies studied in this paper, the experimental setup for rejecting hubs and sampling hubs in the filter rod forming unit was built. The entire rod core inspection system is integrated into the rod production line and is responsible for detecting non-conforming rods in real time during the production process. The specific process is as follows: after the filter rod passes through the previous station, it first enters the splitting wheel and then the reject wheel. The visual inspection module is set on the upper right side of the reject wheel for inspecting the quality of the filter rods. Filter rods that are faulty during the inspection process are fed into the sampling wheel and subsequently rejected and put into the scrap collection box. Through this system, the qualified filter rods continue to be transferred to the downstream equipment via the output wheel. This is shown in Fig. 2.

Fig. 2
figure 2

Schematic diagram of camera and hub device structure. (1) LED light source (2) air knife (3) air knife fixing bracket (4) camera cover (5) camera stand (6) camera (7) lens (8) reject hub (9) sampling hub.

Full size image

The visual inspection device is to be installed 20 cm from the end face of the reject hub and ensure that it does not interfere with the normal operation of the filter rod production line. Due to the compactness of the machines in the filter rod production line and the safety guards on the outside of the machine, the location and manner of installation of the inspection device is limited. To solve this problem, the camera is fixed inside the protective cover and mounted according to the internal structure of the production line, thus making the overall structure of the inspection unit more compact and saving space.

Filter rods are made from raw material filament bundles through a process of tensioning, relaxing, spraying with plasticisers, gluing and cutting. The filter rods are cut and enter the downstream high-speed rotating hub, causing the raw fibres to scatter in the air and rubbing against the glass generating static electricity, which can interfere with camera image acquisition. As a result, an air knife was installed at the front of the camera’s protective cover to form an air curtain to prevent the raw fibres from touching the glass, thus ensuring the clarity and stability of the image capture.

Methods

In this section, the filter rod detection method proposed in this paper is discussed in depth, including the camera calibration method, the ellipse fitting method, and the errors that occur during the detection process and the error correction method.

Comparison of calibration methods

Camera Calibration is a central step in computer vision and image processing that aims to determine the internal and external parameters of a camera in order to accurately derive information in three-dimensional space from a two-dimensional image. The aim is to build camera models that accurately map the two-dimensional images captured by the camera to the actual three-dimensional world.

Currently, there are a wide variety of common calibration methods, among which the Zhang Zhengyou calibration method is widely used in practical projects due to its high accuracy and powerful adaptability. Meanwhile, the OpenCV library also provides common camera calibration methods. In this paper, we compare the accuracy and robustness of these two calibration methods to select a more suitable calibration scheme.

To ensure the accuracy of the results, this paper uses both methods to calibrate the same set of calibration plate images. The obtained internal reference matrix and distortion coefficients are shown in Table 1.

Table 1 Specific internal reference matrices and distortion coefficients.
Full size table

From the results, it can be seen that Zhang Zhengyou’s method has larger focal values (fx and fy), is more robust to noise or distortion in the image, and is able to estimate the focal length more accurately. The two principal point coordinates (u0 and v0) are close to each other, which indicates that the two methods are more consistent in the principal point estimation. The radial distortion coefficients (k1 and k2) of Zhang Zhengyou’s method are slightly larger, which may indicate that it is more sensitive to the distortions at the edges of the image, and is able to correct the distortions in the edge region better. While the tangential distortion coefficients (p1 and p2) are smaller, indicating that it is more accurate in estimating the tangential distortion. For the higher order distortion coefficients k3, they are close to each other, but the value of Zhang Zhengyou’s method is slightly smaller, indicating that it is more stable in estimating the higher order distortion.

For the high-speed on-line inspection task of filter rods, it is necessary to have certain robustness to the field noise, and for the edge detection existing in this paper, Zhang Zhengyou calibration method is more able to provide help, so this paper chooses Zhang Zhengyou calibration method for camera calibration.

Zhang Zhengyou calibration method

In this paper, the Zhang Zhengyou calibration method is adopted. In the actual calibration process, the calibration plate is firstly photographed with the camera and the pixel coordinates of the intersection points of the black and white frames are obtained by the corner point detection algorithm. Since the corner points are one-to-one correspondence in the world coordinate system and the image coordinate system, the mapping relationship from the world coordinate system to the pixel coordinate system can be calculated from these corner points, so as to obtain the internal and external parameter matrices and distortion coefficients of the camera. The specific algorithm processing flow is shown in Fig. 3.

Fig. 3
figure 3

Zhang Zhengyou calibration process.

Full size image

The core of Zhang Zhengyou’s calibration is to find the camera’s internal reference external and distortion coefficients, which requires solving the internal reference, and the first step is to require solving the single response matrix, which is the product of the internal and external reference matrices:

$$\begin{gathered} H=s\left[ {\begin{array}{*{20}{c}} {{f_x}}&\gamma &{{u_0}} \\ 0&{{f_y}}&{{v_0}} \\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{r_1}}&{{r_2}}&t \end{array}} \right]=sM\left[ {\begin{array}{*{20}{c}} {{r_1}}&{{r_2}}&t \end{array}} \right] \hfill \\ \hfill \\ \end{gathered}$$
(1)

In the above equation, M is the internal reference matrix of the camera; s is the reciprocal of the scaling factor; r1, r2 are the two column vectors of the rotation matrix; t is the translation vector; fx is the focal length of the x-direction sum; fy is the focal length of the y-direction and; u0 is the x-axis start coordinate of the image coordinate system, which is usually 0;

Converting the single response matrix H into 3 column vectors, i.e., H=[h1,h2,h3], we have:

$$H=\left[ {\begin{array}{*{20}{c}} {{h_1}}&{{h_2}}&{{h_3}} \end{array}} \right]=sM\left[ {\begin{array}{*{20}{c}} {{r_1}}&{{r_2}}&t \end{array}} \right]$$
(2)

Since the rotation vectors are of equal length and mutually orthogonal, it is obtained by making λ = s-1 according to these two constraints:

$$\left\{ {\begin{array}{*{20}{c}} {h_{1}^{T}{M^{ - T}}{M^{ - 1}}{h_2}=0} \\ {h_{1}^{T}{M^{ - T}}{M^{ - 1}}{h_1}=h_{2}^{T}{M^{ - T}}{M^{ - 1}}{h_2}} \end{array}} \right.$$
(3)

h1 and h2 are solved by a single response matrix, so only the 5 unknowns in the M matrix need to be solved:

$$B={M^{ - T}}{M^{ - 1}} \equiv \left[ {\begin{array}{*{20}{c}} {{B_{11}}}&{{B_{21}}}&{{B_{31}}} \\ {{B_{12}}}&{{B_{22}}}&{{B_{32}}} \\ {{B_{13}}}&{{B_{23}}}&{{B_{33}}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {\frac{1}{{{\alpha ^2}}}}&{ - \frac{\gamma }{{{\alpha ^2}\beta }}}&{\frac{{{v_0}\gamma - {u_0}\beta }}{{{\alpha ^2}\beta }}} \\ { - \frac{\gamma }{{{\alpha ^2}\beta }}}&{\frac{{{\gamma ^2}}}{{{\alpha ^2}{\beta ^2}}}+\frac{1}{{{\beta ^2}}}}&{ - \frac{{\gamma ({v_0}\gamma - {u_0}\beta )}}{{{\alpha ^2}{\beta ^2}}} - \frac{{v_{0}^{2}}}{{{\beta ^2}}}} \\ {\frac{{{v_0}\gamma - {u_0}\beta }}{{{\alpha ^2}\beta }}}&{ - \frac{{\gamma ({v_0}\gamma - {u_0}\beta )}}{{{\alpha ^2}{\beta ^2}}} - \frac{{v_{0}^{2}}}{{{\beta ^2}}}}&{\frac{{{{({v_0}\gamma - {u_0}\beta )}^2}}}{{{\alpha ^2}{\beta ^2}}}+\frac{{v_{0}^{2}}}{{{\beta ^2}}}+1} \end{array}} \right]$$
(4)

B is a pairwise matrix with six valid elements, i.e.:

$$b={\left[ {\begin{array}{*{20}{c}} {{B_{11}}}&{{B_{12}}}&{{B_{22}}}&{{B_{13}}}&{{B_{23}}}&{{B_{33}}} \end{array}} \right]^T}$$
(5)

Further simplification:

$$h_{i}^{T}B{h_j}=v_{{ij}}^{T}b$$
(6)

This can be obtained by calculation:

$${v_{ij}}={\left[ {\begin{array}{*{20}{c}} {{h_{i1}}{h_{j1}}}&{{h_{i1}}{h_{j2}}+{h_{i2}}{h_{j1}}}&{{h_{i2}}{h_{j2}}}&{{h_{i3}}{h_{j1}}+{h_{i1}}{h_{j3}}}&{{h_{i3}}{h_{j2}}+{h_{i2}}{h_{j3}}}&{{h_{i3}}{h_{j3}}} \end{array}} \right]^T}$$
(7)

This can be obtained using two constraints on the rotation vector:

$$\left[ {\begin{array}{*{20}{c}} {v_{{12}}^{T}} \\ {{{({v_{11}} - {v_{12}})}^T}} \end{array}} \right]b=0$$
(8)

By taking the three images containing at least one checkerboard grid and bringing them into the above equation one can find B. Then by cholesky decomposition one obtains the six degrees of freedom of the camera’s internal reference matrix M, i.e.:

$$\left\{ {\begin{array}{*{20}{c}} {{v_0}=({B_{12}}{B_{13}} - {B_{11}}{B_{23}})/({B_{11}}{B_{22}} - B_{{12}}^{2})} \\ {\lambda ={B_{33}} - [B_{{13}}^{2}+{v_0}({B_{12}}{B_{13}} - {B_{11}}{B_{23}})/{B_{11}}} \\ {\alpha =\sqrt {\lambda /{B_{11}}} } \\ \begin{gathered} \beta =\sqrt {\lambda {B_{11}}/({B_{11}}{B_{22}} - B_{{12}}^{2}} \hfill \\ \gamma = - {B_{12}}{\alpha ^2}\beta /\lambda \hfill \\ {u_0}=\gamma {v_0}/\alpha - {B_{13}}{\alpha ^2}/\lambda \hfill \\ \end{gathered} \end{array}} \right.$$
(9)

The external parameters are then obtained by simplifying according to [h1,h2,h3] = λM[r1,r2,t]. The distortion coefficients are divided into radial distortion and tangential distortion, due to the smaller effect of tangential distortion, usually only radial distortion is considered, while radial distortion can be solved by using the first two terms of the Taylor series expansion around the main point, and then using the least squares method to find the actual distortion coefficients can be.

Filter stick image preprocessing methods

Image preprocessing is a key component in computer vision and image analysis, aiming to improve image quality for more accurate subsequent processing and analysis. This process encompasses a variety of techniques and methods for reducing noise, enhancing features, and adjusting the contrast and brightness of an image to make it more suitable for specific tasks such as feature extraction, target detection, and classification.

The selection and combination of suitable image preprocessing methods should be based on the specific task and the characteristics of the image. A combination of preprocessing techniques is usually required to effectively remove noise, retain key features, and improve the accuracy of subsequent processing. For the task of filter bar and mandrel detection, the usual process consists of removing the noise first with filtering techniques and then optimizing the detection by using edge detection to obtain sharper edges.

Commonly used filtering processes include Gaussian filtering, median filtering, mean filtering and bilateral filtering. Gaussian filtering can effectively remove noise and smooth images while having minimal impact on edges. Depending on the requirements of the image, the effect can be optimized by adjusting the kernel size and standard deviation. Median filtering excels in removing pretzel noise with low computational complexity and better preservation of edge details. Mean value filtering, while simple and suitable for removing random noise, blurs image details and is not suitable for tasks where details need to be preserved. Bilateral filtering, on the other hand, removes noise while maintaining edge detail and usually provides better results despite the complexity of the process. By comparing the effectiveness of these filtering methods in filtered rod and mandrel images, a better selection of suitable preprocessing techniques can be made. The following is an example of Canny edge detection algorithm, comparing the preprocessing effect of several filters on the filter bar and mandrel images and their respective processing time, the processing results are shown in Fig. 4, and the time length of each processing method is shown in Table 2.

Fig. 4
figure 4

Results of single filter processing. (1) original Fig. (2) Grayscale image (3) Gaussian filtering (4) Median filtering (5) Bilateral Filtering (6) Mean Filtering.

Full size image
Table 2 Processing time for different methods.
Full size table

The comparison shows that after using a single filter to process the image, the bilateral filter retains the details of the image edges better, but the processing time is the longest, the processing effect of Gaussian filter and median filter is not much different, but the processing time of Gaussian filter is shorter, and the mean filter has the worst processing effect compared to the other three filters, and it does not retain the details of the image edges.

After the filtered single treatment, two more sets of filter stacking comparison tests were conducted based on the characteristics of each filter. The first set of trials first used bilateral filtering to remove noise and preserve edge detail, and then used Gaussian filtering to further smooth the image. The second set of trials first applied median filtering to remove pretzel noise and then used Gaussian filtering to smooth the image and reduce residual noise. The third group is processed by Gaussian filtering plus median filtering, and the results are shown in Fig. 5, and the processing time of each superimposed filter is shown in Table 3.

Fig. 5
figure 5

Stacked filter processing results. (1) original image (2) greyscale image (3) Gaussian filter, bilateral filter overlay (4) Median Filter, Bilateral Filter Overlay (5) Median filter, Gaussian filter overlay.

Full size image
Table 3 Processing time for each superimposed filtering process.
Full size table

As can be seen from the above figure, the third group of trials is better than the other groups in terms of image edge smoothing, in less time, and the use of two filters superimposed on each other is better than a single filter.

In fact, for the processing of filter bars in this paper contour detection and watershed algorithms can be used in addition to the Canny algorithm. Contour detection (e.g., OpenCV’s findContours) is suitable for extracting object contours, which is easy and efficient, but requires high contour continuity. The watershed algorithm can effectively deal with overlapping or close contours, but it is computationally complex and sensitive to noise, and the watershed algorithm is often used for segmentation of superimposed images, which is not conducive to the subsequent calculation of the distance after segmentation of the filter bar and the core line. Therefore, in this paper, we will compare the Canny algorithm with the findContours method to find out a more suitable processing method for filter bars. In this comparison test, both methods take the processing method of median filter plus Gaussian filter, and the filtering parameters are set the same in order to ensure a single variable, and the test results are shown in Fig. 6.

Fig. 6
figure 6

Processing results of two contour extraction methods. (1) original image (2) greyscale image (3) Canny Edge Detection (4) findCounters Profile Detection.

Full size image

The average detection time of the findContours method is 4.27 ms, which shows that the findContours method is more suitable for the contour detection of filter bars because it can not only deal with complex contour shapes, but also provide high accuracy and efficiency in real-time detection.

Profile centre coordinate extraction

The ultimate goal of filter rod quality testing is to detect unqualified rods, which are judged to be unqualified on the basis of a mandrel offset from the centre of the rod exceeding a threshold value. This process can be achieved through machine learning methods or traditional image processing methods.

From the perspective of real-time and stability, traditional image processing algorithms are based on fixed rules and mathematical operations, with fast computation speeds, which can complete the centring of filter bars and mandrels within milliseconds to meet the real-time needs of high-speed production lines. In contrast, machine learning methods are capable of handling more complex patterns but have slower inference speeds. For example, Tomasz Jurtsch et al.24 proposed a sorting device that uses a convolutional neural network classifier to detect prohibited elements in copper-based metal scrap; the conveyor belt speed of the device is 2.5 m/s, while the filter rod mandrel is loaded at a speed of up to 500 m/min, which is more than triple that of the former. Deqiang He et al.25 used a deep-learning-based target detection network to derive a SSD + Inception V2 combination is suitable for the detection of foreign objects at the bottom of the train, and the average detection time is 53 ms, while the real-time detection speed of filter rods is 14 ms. Therefore, it is difficult for the machine learning method to satisfy the real-time requirements of this paper for the detection of filter rod production line. In addition, the output of the machine learning model may be affected by the quality of the training data and environmental changes, leading to misdetection or omission, which is applicable to the high-speed online inspection of the filter rod core line studied in this paper.

In terms of computational resources, traditional image processing algorithms have low hardware requirements and are able to run efficiently on embedded systems or industrial computers, whereas machine learning methods require high-performance hardware (e.g., GPUs) to support them, which increases cost and system complexity.

In terms of data dependency and implementation difficulty, traditional image processing techniques do not rely on a large amount of labelled data, and are easy to implement and debug based on the physical properties of filter bars and mandrels. In contrast, machine learning methods require a large amount of high-quality labelled data for training, and the data collection and labelling process is time-consuming and complex.

In summary, traditional image processing techniques are more suitable for high-speed online inspection of filter rod quality due to their advantages of high efficiency, stability, low resource requirements and no need for large amounts of labelled data. Although machine learning is excellent in complex pattern recognition, its limitations in real-time, stability and implementation difficulty make it difficult to meet the strict requirements of high-speed production line for filter rod quality detection.

To obtain the relative positional relationship between the filter rod and its core wire, the center points of both the filter rod and the core wire can be determined by combining the Hough Transform or circle fitting. The results of the processing are shown in Fig. 7, and the detailed results of each treatment are shown in Table 4.

Fig. 7
figure 7

Comparison results of centre point extraction methods. (1) Normal contour range (2) Circle fitting method results. (3) Hough’s circle transformation method results.

Full size image
Table 4 Processing time and radius results of center point extraction methods.
Full size table

It is clear that the circle fitting and Hough circle transform methods may be inadequate when the contour of the filter rod is not a standard circle.

From the output data, the size of the image output by image processing is 160 × 160 pixels, which corresponds to the actual physical size of 15 mm, so the scale of the image is 0.0938 mm/pixel (the same as in the subsequent experiments), and the deviation of the least squares circle fitting and the Hough’s circle transform compared to the normal contour radius is 1.2188 mm and 0.5625 mm, respectively, which is more than the detection accuracy.

From the output image, the circle fitting method assumes that the filter bar contour is close to circular, and if the actual contour deviates from the standard circle, the fitting results will be distorted, resulting in inaccurate estimates of the centre and radius of the circle. The Hough Circle Transform method, despite being able to detect circles in irregular shapes, performance significantly degrades when dealing with non-standard circles because of its high circularity requirements and high computational complexity, which may lead to poor adaptability. In addition, both methods are prone to miss detection for circles with small radii. Although the Hough Circle Transform can improve detection sensitivity by turning up the accumulator threshold, this may increase false detection and the processing speed of the Hough Transform is too long compared to circle fitting methods. Therefore, these methods may not provide reliable results when dealing with non-standard rounded filter bar profiles. In order to identify the mandrel in the middle of the filter rod, the following methods can be considered to improve the detection and fitting process: incorporating binarisation prior to the edge detection procedure, converting the filtered image into a black and white image, thereby highlighting the contours in the image, and dividing the image into foreground and background simplifies the subsequent steps of contour detection, allowing the contour detection algorithms to identify and extract the contour information in the image more easily. The Then use the ellipse fitting method to identify the target contour, to get its centre point coordinates and long and short axis radius information and so on. The specific calculation procedure for ellipse fitting is as follows.

General equation of an ellipse:

$$A{x^2}+Bxy+C{y^2}+Dx+Ey+F=0$$
(10)

Assuming that multiple measurements Pi(xi,yi) are now acquired, the fitted objective function is, according to the principle of least squares:

$$E\left( {A,B,C,D,E,F} \right)=\sum\limits_{{i=1}}^{n} {{{\left( {Ax_{i}^{2}+B{x_i}{y_i}+Cy_{i}^{2}+D{x_i}+E{y_i}+F} \right)}^2}}$$
(11)

The partial derivatives of this error function are solved using the Gauss-Newton method to obtain solutions for the parameters A, B, C, D, E, and F. By minimising this error function, the optimal elliptic parameters can be obtained.

Next, the coordinates of the centre of the ellipse (h, k) can be found by using Eq. (12) and Eq. (13):

$$h=\frac{{2AC - BD}}{{{B^2} - 4AC}}$$
(12)
$$k=\frac{{2AE - BD}}{{{B^2} - 4AC}}$$
(13)

The lengths of the long (semi-axis) and short (semi-axis) axes of the ellipse can be found by using Eqs. (14) and (15):

$$a=\sqrt {\frac{{2\left( {A+C} \right)+\sqrt {{{\left( {A+C} \right)}^2}+4{B^2}} }}{{2\left| A \right|}}}$$
(14)
$$b=\sqrt {\frac{{2\left( {A+C} \right) - \sqrt {{{\left( {A+C} \right)}^2}} +4{B^2}}}{{2\left| A \right|}}}$$
(15)

The angle of rotation of the ellipse can be found by using Eq. (16):

$$\theta =\frac{1}{2}\arctan \left( {\frac{B}{{A - C}}} \right)$$
(16)

This angle is the angle between the ellipse and the coordinate axis. Ultimately, the parameters of the fitted ellipse include: the ellipse centre coordinates (h,k); the long (half-axis) and short (half-axis) axes: a and b; and the rotation angle θ. The results obtained by using the improved method to perform the test again are shown in Fig. 8, and the detailed results of each treatment are shown in Table 5.

Fig. 8
figure 8

Ellipse fitting processing results. (1) Normal contour range (2) Circle fitting method results (3) ellipse fitting.

Full size image
Table 5 Processing time and radius results of center point extraction methods.
Full size table

From the output data, since the tilt angle is calculated on the basis of the long axis for subsequent correction results, the experimental record is the radius of the long axis after fitting, and in combination with the image scale, the deviation of the ellipse fitting with respect to the normal contour radius is 0.2949 mm, due to the least-squares circle-fitting and Hough’s Circle Transformation methods.

It can be seen from the images that when the improved method is used for filter bar detection, the detected contours are more closely matched to the actual shape, and the recognition of the core wire contours is more accurate and faster to process. Therefore, the experimental design in subsection 4 of this paper will be based on this method for the detection of filter rods and cores.

After obtaining the coordinates of the centre point of the filter rod and the mandrel, the distance between the two is finally calculated using the Euclidean distance formula, and if the result is less than the threshold value, it is a qualified filter rod, and vice versa, it is an unqualified filter rod.

$$\rho =\sqrt {{{\left( {{x_1} - {x_2}} \right)}^2}+{{\left( {{y_1} - {y_2}} \right)}^2}}$$
(17)

ρ is the distance between the filter rod and the mandrel, and (x1,y1) and (x2,y2) are the coordinates of the centre points of the filter rod and the mandrel, respectively.

Geometric calculations to correct 3D errors

Camera calibration corrects for lens-induced errors when using a monocular camera to capture filter bar and mandrel images. However, as the 2D view is dependent on the angle at which it is taken, changes in the angle can affect how the object is represented in the image, which in turn affects the results of the analysis. When the camera view angle is not perpendicular to the surface of the object, an orientation error occurs, i.e., a deviation between the actual orientation of the object and the orientation displayed in the image26,27. This error makes the shape of the filter bars and mandrels in the image not exactly the same as in reality, as the monocular camera can only show the object through a two-dimensional projection and cannot capture the three-dimensional structure in its entirety, thus introducing viewpoint-related geometric aberrations.

Subsequent calculations with this image will make the calculated result smaller than the actual result, and it is easy to misjudge the failed filter rod as a qualified filter rod. When dealing with three-dimensional data, in order to effectively solve the three-dimensional errors in two-dimensional calculations, multi-view fusion and three-dimensional reconstruction techniques can be used to reconstruct the three-dimensional structure of an object from two-dimensional images acquired from different perspectives and to improve the accuracy by combining the depth information. Meanwhile, perspective correction can correct the geometric distortion in the image, and the geometric model and correction method adjusts the error in the 2D image by matching the actual 3D model. In addition, an error model is built for compensation, which further optimises the measurement and analysis results by quantifying and correcting the errors. These methods can effectively improve the accuracy of 3D data processing. For example, Li et al.28 have proposed a new method for 3D reconstruction of laser powder bed fused parts using an optical field camera, in which a robust mapping relationship between parallax, depth and visually coherent 3D contours is established by utilising binoculars and an optical field light path. The 3D contours of the laser powder bed fused parts are then reconstructed by the mapping established by a single exposure of the light field camera. The method enables 3D contour visualisation of the laser powder bed fused part from multiple viewpoints, which facilitates in situ monitoring of the sputtering distance, 3D spatial points and lines of the printed layer, and the contour of the printed part. Huo et al.29 designed a stereo vision system based on 2D image modelling technology, and proposed an interactive local corner extraction algorithm and an interactive local edge detection algorithm based on commonly used image processing methods, feature point extraction algorithms and edge extraction algorithms, and at the same time, adopted the method of limit constraints to match the feature points extracted from the image, which has high matching accuracy and processing speed. The method has high matching accuracy and fast processing speed, which realises the high-precision 3D reconstruction of the target object.

In this paper, this is achieved by comparing the projection error in a 2D image using a known geometric model. The 3D geometric model of the actual object is compared with the projection extracted from the 2D image to identify geometric distortions or errors. This comparison makes it possible to determine the degree of distortion in the image and its effects, and to correct the image according to the expected shape of the geometric model, thus reducing and correcting errors due to viewing angle and projection. As shown in Fig. 9.

Fig. 9
figure 9

Geometric distortion produced by non-vertical projection of image.

Full size image

From the figure, the actual plane of projection (the plane where the circle O is located)

$${d_r}=\frac{{{d_p}}}{{\cos \theta }}$$
(18)

In order to assess the accuracy of the proposed 3D error correction method for the end face of filter rods, relevant experimental comparisons are made in this paper for the circular filter rod end face model with fixed size. As shown in Fig. 10a, a black background is used for the model in order to get a better fitting effect, but there are slight changes in the lighting effect in the image due to different experimental times, shooting distances and angles. The diameter of the filter rod is 50 mm, the diameter of the mandrel is 5 mm, and the centre of the mandrel is horizontally offset from the centre of the rod by 5 mm. Two different angles (vertical and oblique view) are used to photograph the two models, and the distance that the mandrel is offset from the centre of the rod is calculated and corrected in three dimensions. The experimental results are shown in Fig. 11, and the detailed data before and after correction are shown in Table 6.

Fig. 10
figure 10

Results before and after error correction. (a) Filter rod model dimensions. (b) Vertical target shooting processing results. (c) Non-vertical target shooting processing results.

Full size image
Fig. 11
figure 11

Critical Time Experiment Curve Trend and Interval Distribution Plot. (a) Image processing time monitoring results. (b) Communication time monitoring results.

Full size image

The actual length of the image captured during the experiment was 120 mm, and the pixel length of the output resultant image was 504pixel, so the scale of the image in the above figure is about 0.24 mm/pixel.

Table 6 Experimental data for 3D calibration accuracy assessment.
Full size table

Since it is difficult to place the camera exactly perpendicular to the end face of the filter rod, the results of vertical shooting in the table also have some perspective deviation.

As can be seen from the above figure, if the camera is not vertically acquired images, the results obtained after processing have a large error compared to the actual value, and if directly compared with the threshold value, the unqualified filter bars may be judged as qualified filter bars. However, the error-corrected results are closer to the results of the vertical shots, and after several repetitions of the experiment, the results are similar to the table above, so the geometric correction method based on the standard image proposed in this paper effectively ensures the accuracy of the results, and solves the problem of angular error caused by the lack of camera installation accuracy and vibration caused by the equipment in high-speed operation, which is especially suitable for high-speed on-line inspection of filter rods with mandrels.

Experiment and results analysis

Critical time monitoring

The inspection task in this paper required the completion of 4200 filter rods per minute with an average inspection time of 14 ms per rod. This means that the host computer must complete the image processing in a very short period of time. In order to verify whether the device can meet the detection requirements, we monitored the image processing speed, and the detection time results are shown in Table 7, and the interval distribution is shown in Fig. 12.

Fig. 12
figure 12

Schematic diagram of the structure of the lightening method.

Full size image
Table 7 Image processing time and communication time monitoring results.
Full size table

From the above results, it can be seen that the image processing time and communication time basically meet the requirements of high-speed detection, and the standard deviation of the two is 0.87, with small fluctuations, and the system performance is stable and highly reliable.

Design of lightening method for complex working conditions

Light source selection

Image acquisition is an important part of the filter rod core line inspection system, high-quality images can improve the stability of the system, a reasonable choice of light source type, colour, irradiation method, helps to improve the clarity and stability of the acquisition of the filter rod end face photo, reducing the difficulty of the subsequent image processing algorithms. At present, the visual inspection system generally uses LED lamps as the light source, because it has the advantages of energy efficient, long life, high brightness, easy to adjust and strong customisability, which can meet the needs of a variety of complex inspection scenarios and improve the detection accuracy, so this paper chooses LED lamps as the light source.

Lighting design

LED light source lighting methods are varied, mainly including coaxial lighting, back lighting, ring lighting and parallel lighting, each of which has its own unique advantages and is suitable for specific applications, as shown in Table 8.

Table 8 Characteristics of different lighting methods and applicable occasions.
Full size table

The research object of this paper is the filter rod and its surface core line, real-time detection of the core line relative to the centre of the filter rod offset degree is too large as well as the core line is missing and other defects, so the illumination method is required to eliminate shadows, can highlight the surface details of the filter rod and the core line, and at the same time, control the cost of the design. Due to the small size of the end face of the detected rods, and the camera’s working distance is relatively close, it is proposed to use a ring-shaped lighting method, the light source has a certain angle of inclination, can more effectively irradiate the end face of the rods, combined with the characteristics of the lighting method designed for the lighting system as shown in Fig. 13.

Fig. 13
figure 13

Comparison of images with different exposure times and light powers.

Full size image

In addition, the intensity of light also affects image recognition, especially in high-speed image acquisition when the camera is overexposed prone to drag, and insufficient light can not be detected in the filter bar image. Therefore, in this paper, the exposure time of the camera was adjusted before the formal experiments to ensure that the best image acquisition quality was achieved at the specified rotational speed. The light source used in the experiment is a high-power round COB package LED light source with 220 W power and more than 88,000 lx of illumination, and the debugging results are shown in Fig. 14.

Fig. 14
figure 14

Zhang Zhengyou calibration results.

Full size image

In the experiment, the camera aperture was first set to maximum and the test started with an exposure time of 1500µs. In order to avoid overexposure of the camera, the light source power was set low to ensure that a clear image was obtained at this exposure time and light level. At the initial setting, the contours of the filter bars appeared distorted and the image drag was more severe. Subsequently, by lowering the exposure time and adjusting the light source power appropriately, the drag and distortion of the filter rod image gradually decreased with the shortening of the exposure time. When the exposure time was adjusted to 300µs (or lower), the filter bar image became clearer and the imaging effect was significantly improved, at which time the light source power was 24%.

The actual roll wrapping workshop is a closed indoor closed constant temperature workshop, when the production line is working, the indoor light is always on, and the image acquisition equipment is inside the filter rod moulding machine, compared with the light source in the inspection system, the natural light has very little effect on the image, as can be seen from Fig. 13, when the exposure time is small and there is sufficient illumination, the impact of changing the intensity of the light on the identification of the filter rod and the core wire contour is small. Therefore, in this paper, in the actual field, the camera exposure is adjusted to 500µs and a ring light source with sufficient illumination is installed in front of the camera, which can be well adapted to the production environment of the reel and bale shop.

Camera calibration results

In this paper, the calibration board was calibrated using a 10 × 6 checkerboard grid, and 30 images of the calibration board with different angles were taken to perform the calibration, and the results are shown in Fig. 15.

Fig. 15
figure 15

Human-computer interface during camera acquisition.

Full size image

Also output are the camera’s distortion coefficients, rotation matrix, translation matrix and corrected internal reference matrix. Camera calibration enables the geometric modelling of camera imaging and the effective correction of lens aberrations.

Real-time high-speed inspection of filter rod mandrels

Set the ROI area of the camera before acquisition to ensure that only one filter rod appears in the camera field of view at a time. In addition, this paper designs a human-computer interaction interface based on PyQt, which controls the relevant events through the buttons on the interface and displays the results of image acquisition and processing on the interface. Through this interface, the user can also adjust the frame rate and exposure time of the camera, making the whole inspection system more flexible and convenient, as shown in Fig. 10. Forty filter rods were randomly selected from the filter rod bank and divided into four groups of 10 rods each and ensured that each group contained unqualified rods Each group was subjected to 500 testing experiments, and a total of 2,000 quality tests of the rods were recorded, as shown in Table 9.

Table 9 Experimental results of filter rod sorting.
Full size table

As shown in the experiments, the average detection success rate of the four groups of experiments is 96.8%. There are two main reasons for detection failure: the first one is misclassifying a failed filter rod as a qualified one, which usually occurs when the characteristics of the core wire defects are not obvious, such as slight offset (close to the threshold but not exceeding it) or partial absence (e.g., the core wire is broken but with residual portions), which may cause the algorithm to miss the detection. Since the system has an error correction mechanism, the probability of this happening is very low; in addition, image acquisition and processing delays on high-speed production lines may cause some defective frames to be skipped. The second type is the misclassification of a passing filter bar as failing, usually due to airborne dust being misidentified as a defect. Considering that the main purpose of the system is to detect unqualified filter rods in order to improve product quality, even if one or two qualified rods are occasionally misclassified as unqualified, it will not affect the quality of the final shipped product. The success rate of the detection system studied in this paper has been able to meet the production standards of most cigarette factory workshops.

It can be seen that the method proposed in this paper is capable of real-time detection of filter rods with cores at high speeds. And this device and method can be applied to most of the filter rods in front of the forming machine. Since the workshop environment of each cigarette production line is similar, the system can be put into use directly for production lines with the same detection target. If the detection target changes, such as detecting the roundness of filter rods, it is only necessary to change the distance judgement to the roundness judgement, so the method has high promotion value.

Conclusion

This paper presents an online high-speed quality inspection method designed to detect defective products in a filter rod production line in real time. The method mainly consists of camera calibration, ellipse fitting filter bars and core profile extraction, and error compensation modelling of the results. These methods significantly enhance the detection accuracy. Among them, camera calibration can effectively correct lens aberrations; through appropriate pre-processing methods, the characteristics of filter rods and mandrels are highlighted to simplify the image data and improve the speed of subsequent processing. Combined with the ellipse fitting method, the contours of the filter rods and mandrels can be quickly and accurately identified and deviations calculated with an average processing speed of 2.69 ms. Subsequently, the calculation results are corrected by an error compensation model to further improve the detection accuracy, and the final detection accuracy is up to 0.1, with an accuracy rate of more than 95%.

Through the research of this paper, it is expected to provide an online quality monitoring system for filter rod manufacturers to promote the intelligent upgrade of the production line, so as to improve the product quality, reduce the production cost, and enhance the market competitiveness.

However, false detection may occur during image acquisition in complex environments, e.g., mechanical vibrations of the device may cause changes in the field of view of the camera, causing the target filter bar to jump out of the field of view. Future research will introduce image alignment algorithms to limit the range of image variations and design corresponding rejection devices and methods to achieve a complete intelligent filter bar real-time high-speed quality sorting function.

In addition, despite the advantages of traditional image processing techniques in terms of real-time performance and stability, deep learning methods may exhibit greater robustness under complex backgrounds or noise interference. In the future, the combination of deep learning, AI technology and traditional image processing can be explored, for example, the use of deep learning for the accurate segmentation of the edge region of the filter bar and mandrel, and the AI-based deep learning method can further improve the accuracy of detection. Then combine the ellipse fitting method to obtain the centre coordinates, length of the short and long axes and other data of the filter rods and mandrels, so as to improve the detection accuracy while ensuring real-time performance.

Secondly, the method of filter rod adaptive threshold can be added to the system in the future to enhance the flexibility of the system. In industrial production, the shape and size of the filter rod, the material and the production environment conditions may all change, and a fixed threshold value may lead to false detection or missed detection. By designing an adaptive threshold algorithm, the system can adjust the detection parameters in real time so as to adapt to the changes in the characteristics of the filter rods. The stability and reliability of detection are improved.

Finally, hardware integration and computational efficiency improvement are key directions for future research. In order to achieve more efficient real-time detection, the integration of dedicated hardware (e.g., FPGAs or edge computing devices) can be studied to accelerate the execution of the filter bar image processing algorithm. At the same time, the computational complexity of edge detection and contour fitting algorithms can be optimised, e.g., through multi-scale analysis or parallel computing techniques, to process different features of the filter bars at the same time to further improve the overall efficiency of the system.

By combining AI technology, adaptive threshold algorithms, optimising hardware integration and improving computational efficiency, the filter rod quality inspection system is better able to cope with future challenges, and even in the face of more complex industrial environments and higher inspection requirements, the system is able to achieve high-precision and high-speed intelligent sorting functions, providing stronger support for the intelligent upgrading of filter rod production lines in the cigarette industry.