Introduction

HMTA, an essential chemical compound in the oil and gas industry, is widely used to inject in-situ or preformed particle gel into oil reservoirs1,2,3,4. This material can act as a surface-active agent, significantly affecting sandstone formations’ physical and chemical properties5,6,7,8. Understanding the adsorption behavior of HMTA and other chemicals on petroleum reservoir rocks allows us to optimize industrial processes and increase the efficiency of oil and gas extraction, especially in-situ gel operations9,10,11,12.

One of the critical aspects in the study of adsorption is the effect of crosslinkers on fluid properties and flow behavior in oil reservoirs. Crosslinkers, as compounds capable of turning polymers to gel, can help improve reservoir management and flow in reservoirs13,14. These materials are especially effective in high water cut cases because they improve the possibility of oil extraction by reducing water production from the reservoir15,16,17,18. During the gel in situ injection process, the adsorption of the crosslinker on the rock surface may affect the operation and result in the dilution of the injected gel, which makes it a weak gel19,20. For this reason, many studies have been conducted on crosslinker adsorption in oil reservoirs. Therefore, identifying the adsorption intensity and the mineralogy of the reservoir is mandatory for efficiently simulating the process21,22,23. Prediction and identification of adsorption of polymer and crosslinkers on rock surface is not precisely done, which makes the simulation results poor24,25,26.

It is essential to use different laboratory and analytical methods to investigate the adsorption behavior of chemicals on reservoir rocks27,28,29,30. These methods include adsorption experiments under controlled conditions, mathematical modeling, and thermodynamic analyses31,32. Adsorption experiments usually involve measuring the adsorption capacity using adsorption isotherms, which can provide valuable information about the interactions between the adsorbent and the adsorbent surface33,34,35. Among the standard models for describing adsorption processes, we can mention the Langmuir and Freundlich models36,37,38,39. The Langmuir model assumes that adsorption occurs only on the active points of the adsorbent surface, and each point can only adsorb one molecule. This model is usually suitable for surface adsorption systems and can describe the adsorption behavior well in different conditions40,41,42,43.

Several researches have been conducted on the adsorption of chemicals on oil reservoir rocks and the effects of temperature and pressure on these processes44,45. For example, studies show that increasing the temperature can reduce the adsorption capacity of surfactants on oil rocks42,43,46. This research emphasizes that temperature changes can significantly affect reservoirs’ physical and chemical properties; therefore, understanding these changes is necessary to optimize extraction processes. Other studies have investigated different chemical substances’ effects on carbonate rocks’ adsorption. This research shows that different chemical compounds can have different effects on the adsorption and permeability behavior of rocks, and therefore, choosing the right chemicals for flooding is of great importance.

The primary purpose of this research is to investigate the adsorption capacity of HMTA on quartz and also examine the effect of temperature on the adsorption behavior of this material on sandstone cores. The adsorption behavior and thermodynamic changes will be analyzed using experimental data and adsorption isotherm models. This study can be used as a basis for future research in managing and optimizing the injection of HMTA, especially as a crosslinking agent in the in-situ gel process to oil reservoirs, as well as improving the efficiency of oil and gas extraction.

Finally, this research allows us to provide more effective solutions to optimize industrial processes and reduce costs with a better understanding of HMTA adsorption behavior and temperature effects. Considering the importance of the adsorption of chemicals in the oil and gas industry and its effects on the physical and chemical characteristics of sandstone formations, the results of this research can help to develop new solutions and improve the efficiency of oil and gas extraction. These findings can be a basis for future research in this field.

Materials and methodology

Materials

Adsorbent (quartz)

Quartz (SiO₂) has been chosen as the main adsorbent in this research because it is the main component of sandstone reservoirs47,48. This mineral is found naturally as transparent or semi-transparent crystals and has a high hardness (7 on the Mohs scale), which guarantees stability in harsh conditions49. The density of quartz is about 2.65 g per cubic centimeter, and this feature helps it disperse quickly in sandstone reservoirs. The crystal form of quartz, usually hexagonal, affects its adsorption properties and can affect adsorption processes.

Chemically, quartz has high stability and is resistant to high temperatures and various chemicals. It is generally inert and resistant to acids and alkalis, except fluorine and hot alkali. The silicon structure of quartz allows it to interact with various molecules, which makes it suitable for adsorbing HMTA.

The XRD test results shown in Table 1 indicate that the concentration of quartz in the used sample is more than 96%, indicating this material’s high purity. Also, the SEM images in Fig. 1 show that the size of quartz particles ranges from 10 to 250 µm. This particle size directly affects the contact surface and adsorption capacity of HMTA, and the presence of particles of different sizes can help optimize the adsorption process.

Table 1 XRD analysis results related to sand minerals used in this study.
Full size table
Fig. 1
figure 1

SEM images related to quartz minerals used in this work.

Full size image

Adsorbate (HMTA)

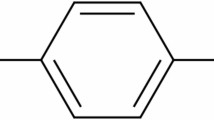
HMTA, investigated as an adsorbent in this research, is an organic compound whose chemical formula is also written as C6H12N4O. This compound consists of six methylene units (–CH2–) and four amine groups (–NH2), and due to its particular structure, it is widely used in various industries, especially in the oil and gas industry50.

HMTA is a crosslinking agent and chemical in gel injection and augmentation processes. This compound is an effective chemical due to its ability to form strong bonds with minerals, especially in sandstone reservoirs. The molecular structure of HMTA is such that it can easily interact with the adsorbent surface (quartz) and facilitate the adsorption process51,52.

Figure 2 shows the chemical structure of HMTA. This structure shows that HMTA has four amine groups that can bond with the quartz surface. These features play a crucial role in increasing the efficiency of the adsorption process and provide the possibility of predicting the behavior of this compound in different conditions.

Fig. 2
figure 2

Chemical structure of HMTA.

Full size image

Experimental procedure

Preparation of aqueous solution

In this research, HMTA solution samples were prepared in distilled water at concentrations ranging from 100 to 100,000 mg/liter. A magnetic stirrer set to 400 rpm was used to dissolve the HMTA in the distilled water, ensuring the desired homogeneity of the solution. The stirring time varied depending on the solution concentration; typically, stirring was maintained for 30 min to ensure complete dissolution. The solutions were prepared in 500 mL beakers, which provided sufficient volume to maintain efficient mixing and homogeneity. This method was critical for achieving consistent concentrations, which were then used to calibrate the laboratory UV device for subsequent measurements. The calibration allowed for precise estimation of unknown HMTA concentrations in future experiments. Accuracy in solution preparation and concentration measurement was crucial, as it directly influenced the experimental outcomes, particularly the analysis of HMTA’s behavior in the presence of quartz and varying experimental conditions.53,54.

Adsorption test as a batch experiment

In this step, to measure the adsorption of HMTA by quartz, the following procedure was followed:

Preparation of HMTA solution: First, HMTA solution was prepared with a specific concentration of 100 to 100,000 mg/liter. These solutions were used as a test medium to investigate the adsorption process.

Addition of quartz: Then, 20 g of granulated quartz was added to 100 mL of HMTA solution. This mixture was stirred for 24 h at the test temperature by a magnetic stirrer at an appropriate speed to help uniformity and increase the contact surface between the quartz and HMTA solution.

Separation phase: After stirring, the quartz particles were separated from the mixture using a centrifuge at 6000 rpm for 30 min. This step helped to separate the quartz from the HMTA solution and ensured that only the remaining solution would be analyzed for concentration measurements.

Measurement of the remaining concentration: The concentration of the remaining solution after quartz separation was measured using a UV device. For this purpose, the MAPADA V-100 D device was used, which provides the ability to measure the concentration of HMTA accurately.

This laboratory procedure comprehensively and accurately enables the assessment of HMTA adsorption by quartz, and the obtained data can contribute to a better understanding of the adsorption processes and the effect of different conditions on this process.

To calculate the adsorption of HMTA on quartz, the following equation is used:

$${q}_{e}=1000\frac{({C}_{i}-{C}_{e}){V}_{s}}{{m}_{q}}$$
(1)

In Eq. (1), qe denotes HMTA adsorption on quartz (mg-HMTA/g-Quartz), Ci refers to the initial concentration of HMTA (mg/L), Ce indicates HMTA residual concentration after adsorption (mg/L), Vs is the volume of solution (L), and mq refers to the weight of quartz (g).

The amount of HMTA adsorption on quartz can be calculated by substituting the values in the equation. This calculation helps to determine the magnitude of HMTA adsorption by quartz and evaluate the effect of different variables on this process. The obtained information can help better understand the behavior of HMTA in different systems and optimize the adsorption conditions for industrial applications.

Measurement of adsorption in porous media

In this step, the adsorption rate of HMTA was checked in Core Flooding mode. This method is effective for simulating the actual conditions of oil reservoirs and evaluating the behavior of chemicals in underground environments55,56,57. In this experiment, first, a sandstone core was accurately prepared. Then, the rock core was placed in the core holder of the Vinci core flooding setup (Model BCF 700). Then, a confining pressure of 500 psi was implemented on the sample.

Preparation of HMTA solution: HMTA solution was prepared with specific concentrations (within the same intervals as previous experiments).

Injection solution: HMTA solution is slowly injected into the core plug until ten pore volumes with the injection rate of 1 mL/m. This step ensured complete contact between the HMTA and the core surface.

Flow measurement: During the test, the flow rate and pressure in the system were recorded. These data were used to analyze the flow behavior and adsorption capacity of HMTA in the stone core.

Measurement of residual concentration: After injection, the residual concentration of HMTA was measured in the liquid phase exiting from the rock core. These measurements can be done using a UV device, similar to the previous steps.

Calculating the amount of adsorption: Based on the changes in HMTA concentration before and after injection, the amount of adsorption of this substance in the sandstone core was calculated. The same equation mentioned in the previous steps is used:

Modeling method and data analysis

Several isotherm models were used to analyze the adsorption data of HMTA on quartz. These models help to describe the adsorption behavior and predict the adsorption capacity in different conditions. The models used included Langmuir Isotherm, Temkin, Freundlich, and the linear model.

Langmuir isotherm model

The Langmuir model assumes that adsorption is a uniform process in which all adsorption sites are similar and independent. This model is especially suitable for chemicals that are adsorbed on the surface of a single layer. Equation (2) represents the general form of the Langmuir model.

$$\frac{{q}_{e}}{{q}_{o}}=\frac{{K}_{L}{C}_{e}}{1+{K}_{L}{C}_{e}} \to \frac{1}{{q}_{e}}=\left(\frac{1}{{K}_{L}{q}_{o}}\right)\frac{1}{{C}_{e}}+\frac{1}{{q}_{o}}$$
(2)

In this equation, qe represents the adsorption rate at equilibrium (mg/g-rock), while qo shows the maximum adsorption capacity. KL is the Equilibrium constant (L/g), which represents the tendency of HMTA to be adsorbed on the quartz surface. This model is usually used in adsorption studies due to its simplicity and good predictability58,59,60.

Temkin model

The Temkin model assumes that the adsorption energy decreases linearly with increasing adsorption charge. This model is based on the non-linear interactions between the adsorbed molecules and the adsorbent surface. Equation (3) represents this model61,62.

$${q}_{e}=\frac{RT}{b}\text{ln}\left({K}_{T}\right)+\frac{RT}{b}\text{ln}({C}_{e})$$
(3)

b represents the Temkin constant, which is related to the adsorption energy, and KT is Temkin’s equilibrium constant. R refers to the gas global constant, which equals 8.314 J/(mol·K), and T is the temperature in K. This model is beneficial when adsorption is done multilayered and helps better understand adsorption behavior at different temperatures63,64,65.

Freundlich model

The Freundlich model is designed for non-linear and multilayer adsorption and is mainly used in systems where the adsorbent surface is heterogeneous. This model is expressed in Eq. (4).

$$\text{ln}\left({q}_{e}\right)=\text{ln}\left({K}_{f}\right)+\frac{1}{n}\text{ln}\left({C}_{e}\right)$$
(4)

In this equation, Kf is the Freundlich constant, which depends on the adsorption capacity; n is an exponent indicating the degree of deviation from the linear isotherm. This model is highly efficient, especially in situations where adsorption occurs in a multilayered and non-linear manner, and it helps explain the variation in adsorption behavior.

Linear model

A linear model is a simple approach to data analysis that can be expressed using Eq. (5).

$$q_{e} = KC_{e} + I$$
(5)

In this equation, qe is the adsorption value, Ce refers to the HMTA concentration values at equilibrium, K shows the slope of the line, and I refers to the intercept of the line. This model is particularly efficient for simulating adsorption behavior under specific conditions and investigating deviations from other isotherms.

Error analysis and model accuracy

Several statistical parameters were used to evaluate the accuracy of isotherm models in describing the experimental data of HMTA adsorption on quartz. These parameters include absolute relative error (ARE), average absolute errors (AAE), average squared error (ASE), and coefficient of determination (R2). The following equations are related to these statistical indicators.

$$ASE=\frac{1}{n}\sum_{i=1}^{n}{({q}_{e,cal-}{q}_{e,lab})}_{i}^{2}$$
(6)
$$AAE=\frac{1}{n}\sum_{i=1}^{n}{\left|{q}_{e,cal-}{q}_{e,lab}\right|}_{i}$$
(7)
$$AAE=\frac{1}{n}\sum_{i=1}^{n}{\left|{q}_{e,cal-}{q}_{e,lab}\right|}_{i}$$
(8)

ASE is one of the most potent error-analyzing methods. However, it highly depends on more significant data; therefore, the error related to the solutions containing a high amount of HMTA will be over-weighted. However, AAE conducts a better error analysis in higher concentrations. ARE tries to minimize functional errors in all ranges.

Thermodynamic modeling of the adsorption process

Thermodynamic modeling was used to investigate the effect of temperature on the adsorption process of HMTA on quartz. This method helps analyze the adsorption behavior and determine the energy changes in the adsorption processes. Thermodynamic parameters such as ΔH0, ΔS0, and ΔG0 can be calculated using experimental adsorption data at different temperatures66,67.

Calculation of Gibbs free energy changes (ΔG)

The Gibbs free energy change for an adsorption process can be calculated using Eq. (9).

$${\Delta G}^{0}=-RTln({K}_{D})$$
(9)

In Eq. (9), KD refers to the thermodynamic equilibrium constant (mole of water/mole of adsorbent). This parameter is determined by calculating the interception of the qe/Ce vs. qe diagram. R denotes the universal gas constant. Here, T refers to the experiment temperature in kelvin (K). Based on the second thermodynamic law, the value of ∆G0 is determined by Eq. (10).

$${\Delta G}^{0}={\Delta H}^{0}-T{\Delta S}^{0}$$
(10)

In the above equation, ∆H0 denotes the system enthalpy change, and ∆S0 refers to the entropy change. The minus value found for ∆G indicates that the process is spontaneous. Otherwise, it is not spontaneous . By combining Eq. (10) and Eqs. (9), (11) will be generated.

$$\text{ln}\left({K}_{D}\right)=-\frac{{\Delta H}^{0}}{RT}+\frac{{\Delta S}^{0}}{R}-1.204$$
(11)

In which 1.204 converts the unit of KD from mole water/mole rock to grwater/grrock. According to Eq. (11), by plotting ln(KD) vs. 1/T, H and ∆S will be determined: slope × R and (intercept + 1.204) × R, respectively.

Results and discussion

Adsorption modeling at 25 ℃ and selection of descriptive model

In this section, the adsorption data of HMTA on quartz were analyzed, and graphs related to the adsorption amount against the final and equilibrium concentrations were drawn. In Fig. 3, the points in this diagram represent the data obtained from the laboratory, which show the actual changes in HMTA adsorption in the test conditions. On the other hand, the connected graphs are the results of fitting different isotherm models to these data, which show the relationship between concentration and adsorption rate well.

Fig. 3
figure 3

Lab data pertains to the adsorption of HMTA on quartz particles and fitting via various models.

Full size image

By analyzing these graphs and deriving equations from fitting different adsorption isotherm models, the obtained results are given in Table 2. This table indicates that the Langmuir model best describes the HMTA adsorption data. This model has been able to simulate the relationship between concentration and adsorption rate accurately, and the statistical values showed a good fit for this model with the experimental data. In particular, the values of R2 and other statistical parameters indicate the high accuracy of this model in predicting the adsorption behavior.

Table 2 Tabulated results obtained from fitting lab data with various adsorption isotherm models.
Full size table

The maximum amount of HMTA adsorption calculated at this stage is 64.23 mg/gr-rock. This value represents the high efficiency of quartz in adsorbing HMTA at a temperature of 25 0C and is especially important in injecting HMTA into the subsurface formations for the in-situ gel process of clay stabilization. These data serve as a basis for optimizing injection processes and investigating the behavior of HMTA in actual oil reservoir conditions.

Based on Table 2, the Langmuir model was chosen as the best model to describe the adsorption process of HMTA, and this choice allows researchers to analyze the future and design injection processes more confidently. This model is a powerful tool for predicting the adsorption behavior in different conditions and can be used in the following stages of research.

Investigating the effect of temperature on adsorption behavior

At this stage, the HMTA adsorption test on quartz was repeated at different temperatures (40, 50, 60, 70, and 80 °C) to investigate the effect of temperature on the adsorption behavior of this substance. Figure 4 and Table 3 present the data obtained from each test. This analysis allows us to understand better the changes in the adsorption capacity of HMTA and the interactions between this material and the quartz surface under the influence of temperature.

Fig. 4
figure 4

Lab data pertain to adsorption of HMTA on quartz particles in different temperatures.

Full size image
Table 3 Tabulated results obtained from adsorption experiments in various temperatures.
Full size table

The results of the experiments showed that the adsorption capacity of HMTA increases significantly with increasing temperature. As seen in Table 3, the adsorption capacity at 25 °C was equal to 64.23 mg/g of rock, while it increased to 93.1 mg/g at 80 °C. This dramatic increase in adsorption capacity indicates significant changes in adsorption behavior, which can be caused by increased thermal and kinetic energy of HMTA molecules. As the temperature increases, the molecules move faster, which helps facilitate the interactions between HMTA and the adsorbent surface.

Modeling the adsorption behavior using the Langmuir model showed that the equilibrium constant K also increases with increasing temperature. This change indicates that the adsorption process is endothermic. In other words, with increasing temperature, the tendency of the system to adsorb HMTA increases, and this result can be well justified by the thermodynamic concept of adsorption at high temperatures. From a thermodynamic point of view, this increase in adsorption capacity and equilibrium constant can be related to the increase in entropy of the system and the decrease in Gibbs free energy (ΔG), which in turn indicates that the adsorption process at high temperatures is carried out naturally and with more energy.

Another important aspect of this study is the effect of temperature on the properties of the quartz surface. Temperature can cause changes in the structure and characteristics of the adsorbent surface, leading to improved or reduced adsorption capacity. For example, at high temperatures, some active sites on the quartz surface may be affected due to physical and chemical changes, which can affect the adsorption behavior of HMTA.

This detailed and scientific analysis of the effect of temperature on the adsorption of HMTA on quartz allows us to understand the adsorption mechanisms under different conditions better. It helps to optimize the injection conditions of HMTA in sandstone formations. These data and results can be the basis of future research and the design of operational processes in managing the injection of chemicals into oil reservoirs.

Thermodynamic modeling

In order to better understand the adsorption process, a thermodynamic analysis was also performed. For thermodynamic analysis, first qe/ce was plotted against qe, and the intercept of the resulting linear regression was the indicator of the Kd value for the studied temperature. Figure 5 is related to the diagram plotted at this stage. As it is clear from the figure, kd values have a direct relationship with temperature.

Fig. 5
figure 5

the plot of qe/ce versus ce of lab data obtained in different temperatures.

Full size image

Table 4 was prepared based on the obtained Kd for different temperatures. Based on Eq. 9 and plotting ln(Kd) in terms of 1/T and finding the slope of the line and the intercept, the enthalpy value of the process was calculated as 16,569 j/mole. This positive enthalpy value shows that the adsorption process of HMTA on quartz is endothermic and is carried out at higher temperatures with incredible speed and intensity. Also, the entropy value of the reaction was calculated to be 94.4 j/mole.k. Based on the obtained data, Gibbs free energy was calculated in Table 4 at different temperatures.

Table 4 Gibbs free energy change calculation for HMTA adsorption process in different temperatures.
Full size table

The values obtained from the calculations showed that ΔG is negative in all months, which means the spontaneous adsorption process of HMTA on quartz particles. This result indicates that the adsorption process is carried out without needing an external energy supply and naturally under test conditions. These thermodynamic changes allow us to understand better the adsorption mechanisms and interactions between HMTA and the surface of sandstone cores.

From a thermodynamic perspective, this behavior indicates that the adsorption process is endothermic. As the temperature increases, the adsorption equilibrium constant also increases, which means that the system has a greater tendency to adsorb HMTA at higher temperatures. These changes can be caused by increasing the kinetic energy of molecules and facilitating surface interactions.

Examining the adsorption behavior in the porous medium

At this research stage, six sandstone cores, whose characteristics are presented in Table 5, were flooded with a solution of 100,000 mg/L of HMTA. Experiments were performed at different temperatures (25, 40, 50, 60, 70, and 80 °C), and the amount of HMTA adsorption in this porous medium was measured through Eq. (1). The findings of this experiment show that the adsorption capacity of HMTA is much lower than the previous experiment on quartz, which depends on the unique nature of the porous media of sandstone cores.

Table 5 Core plug specifications and data obtained from the core adsorption experiment.
Full size table

The reduction of adsorption capacity in this porous medium can be attributed to several factors. One of the main factors is the structure and surface characteristics of sandstone cores. These rocks usually have various holes and voids that can significantly affect the type and amount of adsorption. In particular, the size and distribution of holes in these cores can prevent HMTA molecules from accessing the surface active sites. Also, the presence of other materials in the sandstone structure, such as clay minerals or other impurities, can affect the sorption behavior of HMTA.

However, the corresponding results in Table 5 show that the adsorption behavior and its increase with temperature were also confirmed in this experiment. The adsorption capacity of HMTA at 25 °C was equal to 30 mg/g of rock and increased to 55 mg/g at 80 °C. This change in adsorption capacity with increasing temperature indicates the positive effect of temperature on reactions and adsorption processes. At higher temperatures, the increase in thermal energy causes an increase in molecular movement and a decrease in viscosity. It becomes more soluble at higher temperatures, which can help facilitate the adsorption process. This phenomenon is fundamental in physical processes such as surface adsorption and penetration of molecules into adsorbent surfaces.

Thermodynamically, these changes indicate the endothermic nature of the HMTA adsorption process. As the temperature increases, the adsorption equilibrium constant usually increases, meaning that adsorption occurs naturally and energetically at higher temperatures. This behavior could be due to an increase in entropy and a decrease in Gibbs free energy (ΔG), which in turn favors the adsorption process.

Analyzing the effect of temperature on the adsorption of HMTA in sandstone cores contributes to a deeper understanding of the adsorption mechanisms in porous media and can also help optimize the conditions of HMTA injection into petroleum formations.

When compared to the values summarized in Table 6 from the literature, the adsorption capacity of HMTA on sandstone is within the typical range, neither exceptionally high nor unusually low. This suggests that while the adsorption capacity is moderate, it remains sufficiently significant to be considered in the planning and design phases of in-situ gel treatment processes. Thus, while the observed values may not be outliers, they are still relevant and should be carefully evaluated for their practical implications in reservoir management and optimization strategies.

Table 6 The adsorption capacity of various surfactants on different reservoir rocks.
Full size table

Limitations of the study

This study was conducted using a single type of rock, specifically high-purity quartz, to isolate and analyze the adsorption behavior of HMTA. While this approach provides valuable insights into the interaction between HMTA and quartz, it may not fully represent the complexities of natural reservoir rocks, which typically contain a variety of minerals and impurities. Additionally, to reduce inaccuracies in our experiments, distilled water was used in the batch tests. However, in field applications, fresh water with varying salinity levels is commonly employed, which may affect the adsorption process. These factors should be considered when interpreting the results and extrapolating them to real-world scenarios, where the composition of reservoir rocks and the properties of injected fluids may differ significantly.

Conclusion

This research investigated the adsorption behavior of HMTA on quartz and sandstone cores at different temperatures. The results showed that the adsorption capacity of HMTA increases significantly with increasing temperature so that at 25 and 80 ℃, the adsorption capacity was 64.23 and 93.1 mg-HMTA/g-quartz in batch experiments and 30 and 54 mg-HMTA/g-rock for sandstone cores, respectively. These changes indicate the effect of temperature on the adsorption process and molecular behavior of HMTA under different conditions.

Adsorption modeling using various models showed that the Langmuir isotherm model best fits the experimental data and that the adsorption equilibrium constant increases with increasing temperature. These findings point to the endothermic nature of the adsorption process and indicate that increasing temperature leads to improved interactions between HMTA and the adsorbent surface. This result can help to optimize HMTA injection conditions in oil sand formations.

In addition, the thermodynamic analysis also showed that the Gibbs free energy changes (ΔG) are negative at all temperatures, which means that the adsorption process is spontaneous. This analysis allows us to understand better the adsorption mechanisms and thermodynamic changes in these processes. The increase in entropy and kinetic energy of molecules at high temperatures helps to facilitate the adsorption process and indicates a dynamic and active system.

The results of this research can be used as a basis for future research in managing chemical injection into oil reservoirs and optimizing oil and gas extraction processes. Considering the effects of temperature and characteristics of the porous medium on adsorption behavior, this study can help develop new solutions and improve the efficiency of industrial processes.

Finally, the present research not only contributes to a deeper understanding of HMTA adsorption mechanisms but can also facilitate processes by which chemicals are injected into petroleum formations. These findings can help optimize operating conditions and increase the efficiency of oil and gas extraction.