Experimental study on mechanical properties of fissured loess under true triaxial conditions

Abstract

Fissured loess is one of the important factors that cause geological disasters in the Loess Plateau. This paper analyzes the mechanical characteristics of fissured loess under different confining pressures and different intermediate effective principal stress coefficients b-values by conducting true triaxial tests on fissured loess with different fracture angles. The results show that there are “Concave Points” in the peak stress curves of the fracture loess samples with different angles, and the “Concave Points” are affected by both intermediate effective principal stress coefficients b-values and confining pressure. When the confining pressure is 100 kPa, the major effective principal stress growth rate K-value increases the most under different intermediate effective principal stress coefficients b-values, and the change trend is basically the same, and the major effective principal stress growth rate K-value growth rate decreases with the further increase of confining pressure. The internal friction Angle of the fusible loess sample is not affected by the change of joint and joint dip Angle; With the same intermediate effective principal stress coefficients b-values, the cohesion increases first, then decreases and then increases with the increase of crack Angle. When the fracture Angle is the same, the cohesion approximately increases with the increase of intermediate effective principal stress coefficients b-values. The 0° crack has the greatest influence on cohesion, the 60° crack has the second, and the 30° and 90° crack has the least influence on cohesion.

Introduction

Loess is a kind of special geological material widely distributed in northwest China¹. Various kinds of defects have been formed in loess after long-term development, As shown in Fig. 1, among which there are a large number of fractures of different sizes, causes and angles, which together constitute the fracture network in the soil^2,3,4. Cracks in the soil belong to the structural plane, and the existence of the structural plane changes the original continuity of the soil, thus having an important impact on the mechanical properties of the soil and further leading to the occurrence of geological disasters^5,6,7. Therefore, the research on the influence of mechanical properties of fissured loess is the key to the disaster prevention of fissured loess engineering.

Fig. 1

Fracture state in loess.

At present, scholars at home and abroad have carried out a lot of research on the influence of cracks in rock and soil on soil mechanical properties, and have achieved fruitful results. At present, Xu,Lu and Wen have studied the changes of mechanical properties of soil materials with cracks under uniaxial and trimajor effective principal stress states. Under uniaxial compression, the failure forms of fractured loess are mainly divided into four failure forms: fracture failure, slip failure, slip failure and compressive shear failure⁸. The uniaxial compressive strength presents a "V" shape development with the Angle, and the fracture has a significant control effect on the failure mode and shear strength of loess under uniaxial compression⁹. Under triaxial compression, there are eight types of major effective principal stress–strain curves of fractured loess, and six types of failure deformation modes^10,11. It is found that the failure characteristics of fractured losses are closely related to the spatial morphology and properties of the soil’s original fractures, confining pressure and other factors. Xu and Zhu have studied the change of uniaxial compression failure mode of fractured loess under the disturbance of environmental stress such as dry and wet cycling and vibration load, and found that the main influencing factor of uniaxial compression failure mode is still the initial crack inclination Angle in soil body, indicating that the impact of cracks on soil mechanical properties is more significant than that of other external environments^12,13.

At present, a large number of theoretical and experimental studies have found that the intermediate effective principal stress is an important factor affecting soil materials. Under constant effective mean principal stress p, the magnitude of intermediate effective principal stress b value is significantly correlated with the stress–strain, strength and effective internal friction Angle of eolian sand¹⁴. The tangential shear modulus at the peak deviation stress of the stress–strain curve of structural Marine clay under true trimajor effective principal stress increases with the increase of b value¹⁵. When b value increases from 0 to 0.6, the strength, elastic modulus and internal friction Angle of frozen soil increase with the increase of b value. When b value increases from 0.6 to 1, the cohesion does not change much with b value¹⁶. It can be seen from the above results that the mechanical properties of soil materials in true triaxial state are more complex than those in uniaxial or conventional triaxial state, and b value will seriously affect the deformation development and mechanical properties of soil, so it is necessary to conduct mechanical properties tests in true triaxial state of fractured loess.

The above researches on the mechanical properties of fractured loess mainly focus on uniaxial compression test and triaxial compression test, etc. At present, there are few researches on the changes of mechanical properties of fractured loess under true triaxial state at home and abroad. According to the existing studies, it is found that the failure mode of uniaxial compression of fractured loess under different stress states is more significantly affected by the fracture than other common factors, and becomes the dominant factor affecting the soil failure mode. Therefore, this paper studies loess samples with different fracture angles through true triaxial tests of remolded loess, and loads the soil with different b values under different confining pressures, so as to study the development law of soil shear strength and the influence law of fracture Angle on soil strain development. The research results can provide scientific basis for practical engineering construction and stability evaluation.

Test material and sample preparation

Test facility

The ZSY-3 true triaxial test system was used in this test. The rigid plate loading in the direction of major effective principal stress and intermediate effective principal stress¹⁷ was realized in the test system, and the hydraulic loading in the direction of minor effective principal stress was realized. The three principal stress directions can be loaded independently without interfering with each other, so as to simulate the real stress state of soil. The loading system consists of four parts: axial servo motor dynamic loading system, lateral servo motor loading system, confining pressure loading system and reverse pressure volume control actuator. The specimen is rigidly loaded through the pressure transfer plate axially and laterally, and the confining pressure loading system loads the specimen by applying water pressure to the specimen chamber. The sample is wrapped by latex film, and the upper and lower parts are fastened by screws with the loading base and the axial loading plate, respectively. There are two loading modes: static loading and dynamic loading. The loading path can realize two loading paths: stress loading path and strain loading path, as shown in Fig. 2.

Fig. 2

ZSY-3 true triaxial test system.

Specimen preparation

The test soil was taken from the backfill loess (Q₃) in Yan’an New District, Yan’an City, Shaanxi Province. The original soil retrieved and screened with a 1mm screen. The screened soil sample placed in the oven for drying at 105 °C, and then configured according to the 15% moisture content required by the test. After the soil sample with moisture content was set for 48 h to make the water evenly distributed, the remodeled soil sample was prepared using the special sampler for true triaxial sample. The sample was prepared according to the wet density of 1.5 g cm⁻³ and the size of 70 mm × 70 mm × 150 mm. During the sample preparation process, the soil sample was filled in three times. After each layer of soil sample was filled, the soil sample was compacted, and the surface of the soil sample was chiseled after compacted. Then the loading was continued for the second time, and the steps were repeated until the sample preparation was completed.

In order to reduce the evaporation of water on the surface of the sample during the test, each sample was made before the test was carried out to reduce the dispersion of the test results. Conventional uniaxial and triaxial compression tests were used to study the fracture loess test using cylindrical fracture samples, and the preparation process of this kind of sample is relatively simple, while the preparation process of true triaxial rectangular fracture samples needs to consider the disturbance of each face of the sample during the preparation of fracture, so the production process is more difficult.

Steps for making cracks in this test sample: (1) Firstly, holes of the required crack size are cut in advance on the acrylic plate. The size of the prefabricated crack in this test is 15 × 1 mm. Then, one side of the acrylic plate with crack holes is bonded with another acrylic plate on the adjacent side to form an L-shape. Avoid wear on the four corners of the sample, and make the same panel according to the above operation on the surface with cracks on the opposite side. (2) Fasten the acrylic plate with the soil, and tighten the acrylic plate with the sample using a rubber band to reduce the disturbance caused by the acrylic plate on the soil surface of the sample. (3) Use a straight twist drill with a diameter of 0.5 mm to drill through the cracks cut on the acrylic plate, then use a diamond yarn saw blade to pass through the holes, and use the saw blade to reciprocate the soil mass, cut the soil mass according to the size of the cracks, and finally complete the sample preparation. Then the cracks of the samples at all angles were made according to the above steps, as shown in Fig. 3. Five kinds of samples were set in this test, $\theta =$ 0°, 30°, 60°, 90°and no cracks. This method can effectively reduce the disturbance to the soil in the process of fissure preparation while ensuring a high one-time production rate of the sample. Moreover, the fissure produced has a certain chipping surface, which is close to the state of the loess soil with fissure in the actual geological environment.

Fig. 3

Joint preparation and different fracture Angle samples.

Testing program

This test is an unconsolidated and undrained true triaxial shear test, and the specific test scheme is shown in Table 1. As shown in Fig. 4, the fracture surface is located in the direction of minor effective principal stress, and the direction of intermediate effective principal stress is the complete surface. Stress control was adopted in the test, and the major effective principal stress loading rate was 0.1 kPa/s, the transverse loading rate is 0.1*b kPa/s. Shear failure was considered to occur when the axial strain ${\varepsilon }_{1}$ developed to 10%.

Table 1 Test scheme of fissured loess.

Fig. 4

Sample loading state diagram.

Analysis of test results

Major effective principal stress–strain curve of fractured loess

Under the same b value and confining pressure conditions, the major effective principal stress–strain point diagram of loess with different fracture angles and non-fracture loess under true triaxial shear state is shown in Fig. 4, where W represents non-fracture sample.

As can be seen from Fig. 5, when the confining pressure is 100 kPa, the peak value of major effective principal stress at b = 0, 0.5, 0.75 and 1.0 gradually increases with the increase of fracture Angle. By comparing the major effective principal stress peak value of samples above, it is found that when b = 0.5, 0.75 and 1.0, the impact of fracture Angle on the peak value of major effective principal stress of samples is greater than that when b = 0. On the one hand, this phenomenon is due to the fact that the intermediate effective principal stress promotes the closure of cracks in the sample, during which the soil mass within the vertical influence range of cracks will move towards the fracture surface and further resist the first principal strain. At this time, the axial force is required to resist this phenomenon, resulting in the increase of the major effective principal stress. At the same time, due to the existence of two kinds of inclined cracks at 30° and 60°, under the combined action of confining pressure and major effective principal stress, the sample will slip along the fracture surface to different degrees, and the intermediate effective principal stress will have a certain resistance to the sliding action, which inhibits the development of major effective principal stress and leads to the increase of major effective principal stress. When b = 0.25, the peak value of major effective principal stress decreases first and then increases with the increase of the Angle, but the peak value of major effective principal stress of the samples at 60° and 90° is still less than 0°, indicating that at 30°, the sample is subjected to major effective principal stress and confining pressure, resulting in obvious sliding along the fracture surface, but at this time, the principal stress is small and the resistance to sliding is small. Although the 60° and 90° samples are affected by sliding, the effect is weak, and the Main effective principal stress peak.

Fig. 5

Major effective principal stress–strain curve.

When the confining pressure is 200 kPa, the peak value of major effective principal stress increases gradually with the increase of crack Angle at b = 0 and 1.0. At this time, the soil exhibits the same state as that under the confining pressure of 100 kPa, that is, the sample is significantly affected by crack closure. When b = 0.25, there is little difference between the peak major effective principal stress of 0°, 60° and 90° samples, and only 30° samples are slightly higher than other angles, indicating that under the action of the intermediate effective principal stress, the variation amplitude of the peak major effective principal stress is small under the combined influence of the resistance of soil healing to major effective principal stress and the resistance of intermediate effective principal stress to slip. When b = 0.75, the peak value of major effective principal stress decreases with the increase of fracture Angle, and the sliding effect of sample under this stress state has a significant effect on the change of major effective principal stress of sample. When b = 0.5, the sample at 30° decreases first and then increases, which is the same as when b = 0.25 at 100 kPa confining pressure, indicating that there is a lag in the sliding action at higher confining pressure, and the sliding action still has a significant influence on the stress of the sample.

Under the confining pressure of 300 kPa, the peak value of major effective principal stress of the specimen at b = 0 gradually decreases to that of the specimen at 90°, showing the opposite phenomenon to the previous two confining pressures. Under the action of high confining pressure, the specimen deformation is subject to obvious sliding under the axial load at the initial stage of loading, and the specimen at 0° is difficult to slip due to the horizontal crack. As the fracture Angle develops from 30° to 60°, the peak major effective principal stress of the sample is degraded to a certain extent under the same coaxial strain, indicating that the sliding effect of the 60° sample is significant. The 90° specimen is a vertical fracture, and under the influence of sliding and fracture closure at the initial stage of loading, the variation amplitude of the peak major effective principal stress is large. When b = 0.25, 0.5 and 0.75, the peak value of major effective principal stress decreases first and then increases, indicating that the cracks of the sample are gradually closed during loading. The sample at 30° is more likely to slip along the fracture surface, resulting in a decrease in the peak value of major effective principal stress. The influence of the sliding effect on the sample at 60° and 90° is less than that at 30°, resulting in an increase in the peak value of major effective principal stress. When b = 1.0, the peak value of major effective principal stress increases gradually with the increase of the crack Angle, indicating that the intermediate effective principal stress at this time is resistant to the slip caused by the major effective principal stress, so that the peak value of major effective principal stress of the sample increases gradually with the increase of the crack Angle.

When the confining pressure is different and b = 0, the peak stress point plot is concave at 0°, resulting in a concave point, that is, under the same confining pressure and the same b value, the peak major effective principal stress of the sample without crack to 90° shows a trend of first decreasing and then increasing with the increase of the crack Angle. When the confining pressure is equal to b, the concave point of the peak stress plot of the sample shifts from 0° to 30° and 60° with the increase of the confining pressure. The concave point of the peak major effective principal stress plot of the sample under 100 kPa confining pressure is still the concave point when the fracture Angle is 0°, but the concave point under 200 kPa confining pressure obviously shifts back. At the same confining pressure, the stress peak value of the sample increases gradually with the change of b value, indicating that the change of the intermediate effective principal stress has a significant effect on the strength of the major effective principal stress of the sample. It indicates that although the fracture has an effect on the mechanical properties of the soil, the overall major effective principal stress peak value still increases with the increase of the confining pressure, and the concave point tends to move backward and is not fixed at the 0° fracture sample. It shows that both the b value and the confining pressure have influence on the peak stress of the crack specimen. However, under 300 kPa confining pressure, the concave phenomenon of peak point diagram of major effective principal stress gradually weakens with the increase of b value, and the concave phenomenon weakens.

According to the major effective principal stress–strain point diagram of the samples under each confining pressure, it is found that the inflection point phenomenon occurs in the samples with 90° fracture when b = 0.5, 0.75 and 1.0 under 100 kPa confining pressure, and the phenomenon continues to the state of b = 0 and 0.25 under 200 kPa confining pressure, and then the inflection point phenomenon disappears. This indicates that under this kind of action, the confining pressure on the 90° sample will produce closure perpendicular to the fracture direction, resulting in the need to resist this kind of action at the initial stage of the test, and the major effective principal stress–strain point line shows a high slope. When the axial resistance to this action is completed, the major effective principal stress–strain point line slope decreases, that is, it shows a turning point phenomenon.

Strength characteristics of fissured loess

According to Fig. 4, it can be found that under the same confining pressure for samples with the same crack Angle, the influence of b value on the major effective principal stressof the samples is different. In order to more clearly reflect the influence of different b values and crack angles on major effective principal stresses of samples with the same crack Angle under the same confining pressure, the relative growth rate K was defined, and its expression was as follows:

$$K = \frac{{\sigma_{b}^{\theta } - \sigma_{b = 0}^{\theta } }}{{\sigma_{b = 0}^{\theta } }} \times 100{\raise0.5ex\hbox{$\scriptstyle 0$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 0$}}$$

(1)

where ${\sigma }_{0}^{\theta }$ corresponds to the peak strength of major effective principal stress of the sample at b = 0 under the crack Angle $\theta$, ${\sigma }_{b}^{\theta }$ is the peak strength of major effective principal stressat b = 0.25, 0.5, 0.75, and 1.0 corresponding to the crack Angle $\theta$.

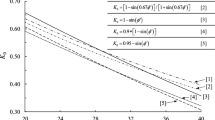
Figure 6 is the point plot of K value obtained under the change of b value for samples with the same fracture Angle and the same confining pressure calculated by Eq. (1). W in the figure represents the sample without fracture.

Fig. 6

Variation curve of K value with b value of samples with different cracks.

From Fig. 6a, when the confining pressure is 100 kPa, the K value of the samples without cracks, 0°, 30° and 60° cracks all presents a trend of first increasing, then decreasing, and then increasing with the increase of b value. When b value is 0.5, the increase amplitude is the smallest, indicating that although the peak value of major principal stress increases with the increase of b value for samples at all angles, the peak value of major principal stress for samples with the increase of b value is small when b value is 0.5. The K value shows a "V" type growth. However, the K value of the 90° crack sample shows an approximate diagonal line with the change of b value. That is, when the crack Angle is 90°, the increase of the peak value of major effective principal stress is steadily increased by the increase of b value, and the increase is much larger than that of other Angle samples.

From Fig. 6b, under the confining pressure of 200 kPa, the K value of samples with crack Angle of 60° and 90° and without crack decreases first and then increases with the increase of b value. Among them, samples with crack Angle of 60° and 90° have a negative semi-axis of K when b value is 0.25 and 0.5, that is, the peak value of major effective principal stress tends to decrease instead of increase when b = 0. When b = 0.75, it returns to the positive semi-axis, and when b = 1.0, a large increase occurs, and the change trend of K value of the two Angle samples is basically the same. The samples with a crack Angle of 30° showed a "V" trend under confining pressure of 100 kPa and 200 kPa. The development trend of the non-fissure samples showed an inverted "N" type development, and the K value increased slightly when b = 0.25, and then decreased to negative semi-axis when b = 0.25, that is, the peak value of the major principal stress increased negatively, and then increased back to the positive semi-axis direction when b = 0.75, but the growth trend decreased when b = 1.0. The K value of the sample with a crack Angle of 0° showed an inverted "V" trend, and the K value gradually increased from b = 0.25, and the K value was much larger than that of other Angle samples, and a slight downward trend occurred after the b value exceeded 0.75. This indicates that under the confining pressure of 200 kPa, although the peak value of major effective principal stress of the sample when b value is 1.0 is larger than that of the sample when b = 0, the increase amplitude and growth trend of the sample are different under different fracture angles.

Figure 6c shows the change point diagram of K value of each crack sample under 300 kPa confining pressure. The development trend of the non-crack sample is the same as that of the crack sample under 200 kPa confining pressure, and both are inverted "N" type; however, the K value is larger, indicating that the relative growth rate of the non-crack sample under 300 kPa confining pressure is much higher than that of the sample under 200 kPa confining pressure. The K value of crack samples at 30° and 90° showed an upward trend, and the K value of crack samples at 30° showed the same development trend as that at 200 kPa, gradually approaching zero on the negative axis before b = 0.75, and then turning to positive growth. The development trend of K value of samples with 60° fracture Angle is "N" type development. The samples with 0° fracture tend to be stable as a whole and hover around zero point, indicating that although the peak value of major effective principal stress changes with the increase of b value, the change is small and tends to be stable compared with other groups of samples.

At 100 kPa, 200 kPa and 300 kPa, the increase amplitude of K value is different, among which the increase amplitude of K value is the largest at 100 kPa, and the trend is basically the same, indicating that the peak value of major effective principal stress at each Angle is basically the same under this confining pressure, and the increase is the most obvious. Under the confining pressure of 200 kPa, the growth rate of K value of the sample slowed down, and only the 0° sample was significantly affected by the change of b value. Under different fracture angles, the growth trend of K value showed a "V" shape, an inverted "V" shape and an inverted "N" shape, and a small negative growth phenomenon occurred with the b value part of the sample at b = 0.25 and 0.5. The development trend of K value of the samples at each crack Angle under the confining pressure of 300 kPa is further slowed down compared with that under the confining pressure of 200 kPa, indicating that the peak value of major effective principal stress of the samples under this confining pressure is further reduced under the influence of b value, and the development trend of K value as a whole presents an "N" type or inverted "N" type development.

Development law of second principal strain and first principal strain

Figures 7, 8 and 9 show the diagrams of first principal strain-second principal strain points obtained for the loess samples with the same b value, the same confining pressure and different fracture angles under the true triaxial state. Figures 7, 8 and 9 show the plots of first principal strain-second principal strain points under confining pressure of 100 kPa, 200 kPa and 300 kPa respectively. Through the three sets of point plots, it is found that the second principal strain development with first principal strain can be divided into three stages of shear development, stabilization stage and dilatancy development of the second principal strain in the sample.

Fig. 7

Relation curve of ${\varepsilon }_{2}-{\varepsilon }_{1}$ under confining pressure of 100 kPa.

Fig. 8

Relation curve of ${\varepsilon }_{2}-{\varepsilon }_{1}$ under confining pressure of 200 kPa.

Fig. 9

Relation curve of ${\varepsilon }_{2}-{\varepsilon }_{1}$ under confining pressure of 300 kPa.

From Fig. 7, when b = 0, the variation trend of second principal strain with first principal strain is mainly manifested in two stages: shear deformation and stable development. With the increase of b value, the stable development stage is reduced, and obvious dilatancy deformation occurs. Meanwhile, when b value is 0.25 and 0.5, the lateral shear deformation of the sample decreases, and it enters the lateral strain stability stage earlier. At the same time, the development stage of dilatancy is advanced and more obvious. However, when the b value reaches 0.75 and 1.0, the lateral shear deformation of the sample returns to the state when b = 0, but the steady development stage is still reduced and the dilatancy deformation is obvious. It shows that the b value has obvious influence on the development trend of lateral deformation of the sample under 100 kPa confining pressure. By comparing the development trend of the second principal strain curves of the samples at different angles with the same corresponding b value in Figs. 7 and 8, it is found that, except when b = 0, the shear shrinkage development stage of the samples at other b values has a longer change process with first principal strain, the stable development stage has no significant change, and the dilatancy stage shorters with first principal strain development process. When the confining pressure b = 0 of 200 kPa is absent of intermediate effective principal stress, the lateral pressure at the early loading stage makes it easier for the fractured specimen to produce dilatancy deformation in the direction of major effective principal stress, resulting in the need for greater major effective principal stress to resist dilatancy deformation. After the resistance is completed, the specimen and lateral deformation occur, so that the dilatancy deformation of the specimen under this state develops in a longer and more obvious stage with first principal strain. Figure 8 shows the variation curve of second principal strain in samples with first principal strain under different b values when the confining pressure is 300 kPa. Under this confining pressure, the shear shrinkage and stability stages are longer, while the dilatancy stages are obviously shortened. This is because under this confining pressure, the lateral deformation of the sample is more difficult, and most shear deformation occurs in all directions.

From Fig. 7, when 100 kPa confining pressure b = 0, the intermediate effective principal stress is consistent with the major effective principal stress and does not change. At the initial loading stage, the confining pressure is much larger than the major effective principal stress, resulting in different degrees of shear deformation on the lateral side of the sample in the early loading stage. Among them, the specimen with a fracture Angle of 90° is the most obvious, and the fracture is vertical fracture at this Angle. In the test process, confining pressure is applied first, so the shear shrinkage deformation of the specimen is the most obvious under confining pressure, and the second principal strain develops rapidly in this stage. However, with the increase of first principal strain, the curve appears a break point, and this phenomenon is gradually resisted with the increase of major effective principal stress, and then tends to be stable with first principal strain. In the sample with crack Angle of 0°, the second principal strain increases slowly with the development of first principal strain. In the sample with crack Angle of 30° and 60°, after a short period of slow growth, the middle principal strain tends to be stable with the gradual increase of first principal strain. When b = 0.25, under the combined action of confining pressure and intermediate effective principal stress, the second principal strain of the samples at 60° and 90° crack Angle changes little with the first principal strain in the initial loading stage. However, due to the presence of cracks, the second principal strain curve increases to the negative semi-axis with the change of the first principal strain, and the samples appear lateral dilatation deformation. The second principal strain of 0° and non-fissure samples develops rapidly in the early loading stage, but the break point appears earlier than when b = 0, and then the curve shows a stable trend. In the second half of the test, there is a certain degree of dilatancy deformation compared with the first and middle of the test, which is because the specimen appears dilatancy deformation in the direction of the second principal strain with the development of the major effective principal stress. The curve of the sample with 30° fracture develops gently in the whole process of the test, and only a small dilatancy deformation occurs in the late stage, indicating that the lateral deformation of the sample is small at the 30° fracture Angle. When b = 0.5, the samples without crack, 0° and 30° crack showed a similar development as those when b = 0.25, the samples with 60° crack changed from dilatancy deformation to shear shrinkage deformation, and the samples with 90° crack still showed a progressive dilatancy deformation trend. When b = 0.75, the 90° crack specimen develops from dilatation deformation to shear shrinkage deformation, which is due to the gradual increase of the intermediate effective principal stress, which becomes the dominant factor affecting the development of the second principal strain. The 0°, 30° and 60° fracture samples showed the same trend at b = 0.75 and 1.0, all of which showed small shear deformation in the early stage of the test and tended to be stable, and the dilatation deformation of the samples under the action of major effective principal stressin the late stage of the test resulted in small lateral dilatation deformation.

From Fig. 8, the Angle diagram of each fracture obtained by 200 kPa confining pressure b = 0 shows that under this confining pressure, the sample presents dilatation deformation with the development of second principal strain, which is different from that under 100 kPa confining pressure, and the sample without fracture still presents shear shrinkage deformation compared with that under 100 kPa confining pressure. However, the change of second principal strain is obviously less than that under 100 kPa confining pressure, indicating that the change of soil second principal strain under 200 kPa is slow, and high confining pressure has a consolidation effect on the sample in the initial stage of the test, which affects the development of sample deformation. With the gradual increase of major effective principal stress, the fissure specimens enter dilatancy deformation faster. With the gradual increase of b value, the second principal strain gradually resists the lateral dilatation deformation, but it can be seen from other b value curves that the 60° fracture specimens have strong resistance to the lateral dilatation deformation. When b = 1.0, this phenomenon disappears, and the diagram of the second principal strain point shows that it increases first and then tends to be stable, and finally there is a certain degree of dilatancy. The fracture samples of 0°, 30° and 90° showed the same regularity at b = 0.25, 0.5, 0.75 and 1.0, that is, the second principal strain increased rapidly in the early stage of the test, but tended to be stable in the middle stage of the test, and decreased slightly in the late stage of the test.

From Fig. 9, when b = 0 at 300 kPa confining pressure, the 90° fracture specimen exhibits the same second principal strain change as the first two confining pressures, but under the action of high confining pressure, the shear shrinkage deformation generated by confining pressure on the specimen is less than the second principal strain at 100 kPa and 200 kPa. The specimens with 0°, 30° and 60° fractures all showed dilatancy deformation under this confining pressure, and the dilatancy deformation became obvious with the increase of first principal strain. The 30° fissure sample showed a small shear deformation at the initial stage of the test, and then the second principal strain of the sample changed from shear to dilatancy deformation under the action of major effective principal stress, and the lateral dilatancy deformation gradually became obvious with the increase of first principal strain. With the gradual increase of b value, the shear shrinkage deformation of the 0° crack specimen under 300 kPa confining pressure becomes gradually obvious, and reaches the maximum value when b = 1.0, indicating that the 0° crack has the most obvious influence on the second principal strain of the sample under 300 kPa, and the shear shrinkage deformation is manifested. Compared with other confining pressures, it is found that except for b = 0, the 0° crack at 300 kPa has the greatest influence on the second principal strain in the sample, and the second principal strain increases gradually with the increase of b value. The variation trend of the second principal strain of the samples with 30°, 60° and 90° fracture angles at 300 kPa confining pressure is basically the same as that at 200 kPa confining pressure, but the shear deformation in the direction of the intermediate effective principal stress is smaller due to the higher confining pressure.

Variation law of generalized shear stress-second principal strain curve

Figure 10 shows the point diagram of the variation of generalized shear stress with intermediate effective principal stress under the same confining pressure at the same Angle and different b values.

Fig. 10

$q-{\varepsilon }_{2}$ relationship curve under different confining pressures and same Angle.

It can be seen from Fig. 10 that the slope of the point plot of the samples at different fracture angles increases gradually under different confining pressures, and the samples show strain hardening with the development of the second principal strain. It can be seen from Fig. 10a–c that with the increase of confining pressure, when b = 0 and b = 0.25, with the increase of generalized shear stress, the development of second principal strain develops from full dilatancy deformation to first dilatancy deformation, then shear contraction deformation and finally dilatancy deformation, and finally returns to full dilatancy deformation under 300 kPa confining pressure. When b = 0.5, 0.75 and 1.0, the generalized shear stress gradually increases with b value under different confining pressures, but the shear deformation at 100 kPa confining pressure of b = 0.5 is much larger than that at 100 ka confining pressure of b = 0.75 and 1.0, and the shear deformation of the sample gradually increases with the increase of b value under 200 kPa and 300 kPa confining pressure. At the same time, with the increase of confining pressure at each b value, the second principal strain of the sample shows a trend of increasing shear shrinkage deformation.

Figure 10d–f shows the point diagram of the development of generalized shear stress with the second principal strain under different confining pressures. It can be seen that the sample shows obvious shear shrinkage deformation when b = 0.25 under confining pressure of 100 kPa, followed by dilatant deformation, indicating that under such confining pressure and loading mode, The second principal strain development of 30° fracture specimens is different from that of other fracture Angle specimens. Under the confining pressure of 300 kPa and b = 1.0, with the development of generalized shear stress, the second principal strain appears transverse runout. This phenomenon is due to the mutual resistance between the lateral dilatancy effect of major effective principal stresson the sample and the shear shrinkage deformation of the intermediate effective principal stress on the sample at this time, so that the development of the point plot shows a transverse jump phenomenon. Under other confining pressure and b value, the development law of 30° crack specimen is basically consistent with that of 0° crack specimen.

Figure 10g–i shows the point diagram of the variation of generalized shear strain with second principal strain for samples with 60° fracture Angle under different confining pressures. The point plots of the samples under the three confining pressures all show the same behavior as those of the samples with 30° fracture, and all show lateral jump phenomenon. This is because when the fracture Angle of the samples is 60°, the samples are more prone to slip failure along the fracture plane with the increase of major effective principal stress, thus making the lateral dilatancy deformation of the samples more serious. Make the dot plot appear as a horizontal jump phenomenon. Compared with the curves of 0° and 30° fracture samples, it is found that when b = 0.5, the sample develops from shear deformation to dilatation in the second half of the test at all three angles, but unlike the 0° and 30° fracture samples, there is only a dilatation development trend, and the 60° fracture sample completely develops into dilatation deformation beyond the zero point, indicating that b = 0.5 has a great influence on the development of principal strain in the sample. And different from other angles. When b = 0.5 under 300 kPa confining pressure, the generalized shear stress of the sample is greater than b = 0.75. The point plot shows that, as the sample gradually develops from shear shrinkage deformation to dilatation deformation, the intermediate effective principal stress will resist the lateral deformation caused by the major effective principal stress, so that the sample can withstand greater generalized shear stress.

Figure 10j–l shows the point diagram of the development of generalized shear stress with intermediate effective principal stress for samples with 90° crack Angle under various confining pressures. At 100 kPa confining pressure, the development trend of the sample at b = 0.5 is the same as that at the b value at 60°, indicating that b = 0.5 has a great influence on the development trend of the second principal strain in the sample. At the same time, under 200 kPa confining pressure, the principal strain development of other samples is smaller than that of the other two confining pressures except when b = 0.75, indicating that 200 kPa confining pressure has a significant effect on the second principal strain development of 90° fracture samples. Under the confining pressure of 300 kPa, there is no lateral dilatancy deformation in the early loading stage, because the 90° crack is a vertical crack in the sample, and the sample is more likely to collapse along the direction of the intermediate effective principal stress under the action of high confining pressure, thus offsetting the dilatancy deformation in the early loading stage. With the development of generalized shear stress, each b value sample has obvious transverse jump phenomenon under the action of high generalized shear stress, which may be due to the effect of major effective principal stress under high confining pressure, which makes the sample more prone to lateral deformation, while the lateral side is constantly resistant under the action of intermediate effective principal stress and confining pressure, resulting in skip phenomenon.

Change of strength characteristics of samples with cracks

Figure 11 shows the critical state line on the p–q plane with the change of confining pressure obtained for each fracture sample under the same b value respectively.

Fig. 11

Critical state line of fracture specimen in p-q plane.

From Fig. 11, with the increase of confining pressure, the critical state line under each b value presents a roughly parallel relationship, and its relationship is expressed as follows:

$$q = kp + a$$

(2)

where k is the slope of the critical state line, and a is the intercept of the critical state line.

The internal friction Angle $\varphi$ and cohesion force c of soil mass can be expressed as^18,19:

$$\sin \varphi = \frac{{\sqrt 3 k\cos \theta_{L} }}{{3 - \sin \theta_{L} k}}$$

(3)

$$c = \frac{{a(\sqrt 3 \cos \theta_{L} + \sin \theta_{L} \sin \varphi )}}{3\cos \varphi }$$

(4)

$$\tan \theta_{L} = \frac{2b - 1}{{\sqrt 3 }}$$

(5)

where ${\theta }_{L}$ is the stress Lord Angle.

The strength parameter c of the sample at each crack Angle can be obtained by calculating Eqs. (3), (4) and (5), as shown in Table 2. It can be seen from the table that, compared with the non-crack specimens, the internal friction Angle of the crack specimens is little affected by whether there is joint or not and the change of joint inclination Angle. The internal friction Angle of the crack specimens is roughly the same under all b values, which is consistent with the conclusion calculated by Zhu¹³ through conventional triaxial tests. Under the same b value, the cohesion of samples with different crack angles increases first, then decreases and then increases with the increase of Angle, while the cohesion of samples with the same Angle increases with the increase of b value. Compared with the non-crack sample, the 0° crack sample has the greatest influence on the cohesion of soil mass, followed by the 60° crack sample, and the 30° and 90° crack sample has little influence on the cohesion of soil mass. This is because the existence of crack makes the failure surface of the sample more likely to develop along the fracture surface, which reduces the mutual friction strength of soil mass in the fracture interface after failure, and thus leads to the reduction of the strength index of the crack sample. At the same time, it shows that cracks have obvious deterioration effect on soil strength index.

Table 2 Strength parameters of samples with different crack angles.

Conclusion

In this paper, true triaxial shear tests with different confining pressures and different b-values are carried out on fenced loess with different angles. The main conclusions are as follows:

• (1) The major effective principal stress peak value of loess samples with different fracture angles shows three different development modes: gradually increasing, decreasing first and then increasing, and gradually decreasing. With the increase of the fracture Angle, “concave point” appears in the point plot of the major effective principal stress peak of the fractured loess samples at different angles, and the “concave point” is affected by both b value and confining pressure.

• (2) By defining the relative growth rate of major effective principal stress, it is found that when the confining pressure is 100 kPa, the K value increases the most under different b values, and the changing trend is basically the same. When the confining pressure is 200 kPa, the growth of K value slows down, and only the sample with crack Angle 0° is significantly affected by b value. When the confining pressure is 300 kPa, the development trend of K value further slows down compared with that of 200 kPa.

• (3) At 100 kPa confining pressure, the stable development stage decreases with the increase of b value, and the dilatancy deformation is obvious. When the confining pressure is 200 kPa, the shear development stage increases, the stable development stage has no obvious change, and the dilatancy stage is shortened, except when b = 0. When the confining pressure is 300 kPa, the shear shrinkage development stage and the stability stage of the sample are longer, while the dilatancy development stage is obviously shortened.

• (4) At 0° fracture Angle, with the increase of confining pressure, the second principal strain changes from complete dilatancy deformation to first dilatancy deformation, then shear contraction deformation and finally dilatancy deformation. At 30° fracture Angle, when the confining pressure is 100 kPa and b = 0.25, the second principal strain shows obvious shear shrinkage deformation; when the confining pressure is 300 kPa, the second principal strain appears transverse jumping with the increase of generalized shear stress. When the fracture Angle is 60° and 90°, the variation trend of generalized shear stress-second principal strain under different confining pressures is basically the same as that when the fracture Angle is 30°.

• (5) The strength parameters c, φ. of samples with different fracture angles are obtained by calculation. The internal friction Angle of the c fracture sample is not affected by the change of joint and joint dip Angle, and the internal friction Angle of the sample is basically the same under different b values. With the same b value, the cohesion increases first, then decreases and then increases with the increase of crack Angle. When the fracture Angle is the same, the cohesion approximately increases with the increase of b value.