Abstract
In this paper, the problem of L2-gain analysis and anti-windup fault-tolerant control is investigated by using the multiple Lyapunov functionals method for a class of saturated switched delayed systems with actuator faults. A sufficient condition for the state to be bounded is given for the closed-loop system and under this condition the disturbance tolerance problem is transformed into a convex optimization problem with linear matrix inequality constraints. Then, the L2-gain analysis of the closed-loop system is carried out. Next, by designing the anti-windup (AW) fault-tolerant controller, the maximum allowable disturbance capability as well as the minimum restricted L2-gain upper bound is obtained. Finally, the numerical examples are given to verified the effectiveness of the proposed method by comparing the state response under the action of the AW fault-tolerant controllers and the standard controllers.
Similar content being viewed by others
Introduction
As an important class of hybrid systems, switched systems consist of a finite number of continuous-time or discrete-time subsystems and a switching law that orchestrates the running of a specified subsystem at each instant of time. Due to practical significance, switched systems have been applied in many fields, such as chemical process control, switching of power system networks, certain robot control systems and the other fields. Thus various performance indexes of switched systems become particularly significant, and then the research methods have attracted a lot of attention in recent years1,2,3,4,5. For instance, both6 and7 proposed the common Lyapunov function method to investigate the stabilization problem of the switched systems. Because the common Lyapunov function is difficult to obtain, the research results of this method are relatively scarce. However, the single Lyapunov function method8, the average dwell time method9, and the multiple Lyapunov functions method10,11 are widely applied in switched systems. What is more, there will always be a variety of external interference in the practical systems12. Because the L2-gain is often used to measure the interference suppression capability of systems, the analysis and design of the L2-gain of the switched systems have received a great deal of attention13. In14, finite-time boundedness and finite-time L2-gain analysis for a class of discrete-time switched systems were investigated by using the average dwell time method. In15, the problem of exponential stability and L2-gain analysis was investigated for switched singular systems, by using the multiple discontinuous Lyapunov functions approach.
It is well known that actuator saturation or input saturation is unavoidable for practical control systems, because the device as the actuator is subjected to a certain physical limit or the output amplitude of the actuator reaches the limit, which can lead to performance degradation or even instability if not properly handled16,17,18,19,20,21,22,23. Specifically, when the control input reaches its saturation limit, the system effectively operates in an open-loop manner, as the actuator can no longer provide the required control effort. This can lead to performance degradation, loss of controllability, or even instability, especially in systems with high gain or aggressive control strategies. Thus, the analysis and control synthesis of switched systems subject to actuator saturation have attracted a considerable attention24. In general, there are two main approaches to address the saturation nonlinearity: the saturation nonlinearity is represented as polytopic sets25 and the saturation nonlinearity is described as a local sector nonlinearity based on anti-windup (AW) strategy26,27. Qi et al.25 studied the event-triggered control problem for networked switched systems with actuator saturation by making use of the average dwell time. Zuo et al.26 focused on the event-triggered stabilization problem for a class of switched systems with actuator saturation is investigated based on multiple Lyapunov function method and the average dwell time approach.27 was concerned with the L2-gain analysis and anti-windup control problems for switched delay systems subject to actuator saturation by using the average dwell-time method. Because anti-windup compensator will only work when actuator saturation occurs to ensure the stability and performance of the system, this method is a common and effective technique to deal with the problem of actuator saturation from the perspective of practical application.
In addition, in automated production, actuator faults may result in unsatisfactory performance, instability, or even disastrous consequences.Thus, the fault-tolerant control strategy is proposed28,29,30,31. Due to large and complex equipment for switched systems with multiple subsystems, actuator faults are inevitable. And then, for switched systems fault-tolerant control has received extensive attention in recent years32,33,34,35. Based on the observer method,32 introduced a new robust fault tolerant control design for continuous-time switched systems based on the mode-dependent average dwell time method.33 investigated a robust integrated fault estimation (FE) and fault-tolerant control (FTC) strategy for a class of continuous-time switched systems in the presence of sensor faults. In34, an active fault-tolerant tracking control (FTTC) scheme was proposed for switched linear systems with actuator faults by using the adaptive observer technique. In35, a fault tolerant control strategy was proposed for uncertain switched systems by using the multiple Lyapunov functions method.
On the other hand, the time-delayed phenomenon is also frequently encountered in a large number of dynamical systems. Moreover since time-delay widely exists in various practical fields and it may cause oscillation, divergence, or even instability, many researchers have devoted themselves to studying time-delay systems36,37,38. Two widely used methods for analyzing systems with delays are the Razumikhin method and the Lyapunov–Krasovskii functional (LKF) method. The Razumikhin method is based on constructing a Lyapunov function (rather than a Lyapunov functional) and ensuring that it satisfies specific conditions to guarantee stability for time-delay systems. The key idea is to use a Lyapunov function of the current state and impose conditions that relate the current state to the delayed state. It is particularly useful for systems with constant or slowly varying delays. However, for systems with fast-varying or large delays, the Razumikhin method can lead to conservative stability conditions, as it does not fully capture the delay’s time-varying nature. Unlike the Razumikhin method which uses a Lyapunov function of the current state, the LKF method method constructs a functional that depends on the entire state history over a time interval. This approach is particularly effective for systems with time-varying delays, as it provides a more accurate representation of the delay’s impact on system dynamics. The LKF method is known for yielding less conservative stability conditions compared to the Razumikhin method, making it suitable for systems with larger or more complex delay profiles. Therefore, during the past few decades, the problems of control for time-delay systems have gained special considerations39,40,41,42. Rahimi et al.39 introduced a fault compensation control approach for a class of affine nonlinear time-delay systems using adaptive dynamic programming (ADP) and by establishing an observer, the ADP-derived approach facilitates the estimation of potential actuator faults within the system. In40 new sufficient conditions guaranteeing the asymptotic stability of the studied system were proposed by constructing a novel Lyapunov–Krasovskii functional, by using some linear matrix inequalities (LMIs) and by designing an appropriate switching signal. Chen et al.41 was concerned with the anti-windup design problem for linear time-delay systems with actuator saturation by utilizing the information of the time delay sufficiently and proposed the generalized delay-dependent sector conditions. Rahimi42 introduced an online fault-tolerant control method for nonlinear time-delay systems with actuator faults using a policy iteration algorithm and proposed a new performance index function to account for time-delay states, from which control laws are derived.
To sum up, switched systems have attracted significant attention due to their wide applications. However, the presence of actuator saturation, actuator failure, and time delays in uncertain environments poses significant challenges to system stability and performance. Actuator failures are particularly critical in practical applications, as they can lead to severe performance degradation or even catastrophic system breakdowns. Moreover, the inherent uncertainty in system parameters, combined with time delays and actuator saturation, further complicates the control design, making it essential to develop robust strategies that can handle these issues simultaneously. Existing methods primarily focus on addressing the switched time delays systems with actuator saturation, while the simultaneous consideration of actuator failure, time delays, uncertainty and actuator saturation, remains largely unexplored. Addressing this gap is crucial for improving the reliability, safety, and efficiency of practical systems, especially in safety–critical applications. In this paper, we propose a novel framework that integrates multiple Lyapunov functionals and anti-windup control techniques to ensure robust performance under actuator saturation and failure, even in the presence of time delays and system uncertainties.
Specifically with the aim to fill the gap, we will study the L2-gain analysis and anti-windup fault-tolerant control of a class of switched systems with actuator saturation and time-varying time delay by using the multiple Lyapunov functionals approach. Firstly, for each subsystem, the AW fault-tolerant controller consisting of a dynamic state feedback (DSF) controller and an AW compensator is constructed. Then a sufficient condition for the system state to be bounded is derived and the maximum allowable level of disturbances is obtained by solving the constrained optimization problem. Then, the similar method is applied to derive a sufficient condition for the existence of the constrained L2-gain, and the minimum upper bound of the constrained L2-gain is obtained by solving the constrained optimization problem. Next, by solving the new optimization problem based on the above two optimization problems, the dynamic feedback controller gain and AW compensator gain of the controller are obtained. Finally, a numerical example is given to show the effectiveness and feasibility of the method.
The paper is organized as follows. In Section "Problem formulation and preliminaries", the problem formulation and preliminaries are given. In Section "Disturbance tolerance", a sufficient condition for the closed-loop system to have a bounded state trajectory under the action of an external disturbance is given and the maximum tolerable disturbance level is obtained. In Section "L2-gain analysis", a sufficient condition for the existence of a constrained L2-gain within the set of tolerable disturbances is given and a minimum upper bound on the constrained L2-gain is obtained. In Section "Anti-windup fault-tolerant controller design and optimization", the optimization based on AW fault-tolerant controller is carried out. In Section "Numerical simulation", a simulation example is given and finally the conclusion is drawn.
Problem formulation and preliminaries
Consider a class of linear uncertain saturated switched systems with time-delay and external disturbances as follows
where \(\tau (t)\) is the time-varying delay term satisfying \(0 \le \tau (t) \le \tau ,\) \(\dot{\tau }(t) \le h < 1\) and \(\tau\) and \(h\) are known constants, the initial conditions \(x(t_{0} + \theta ) = \varphi (\theta )\), \(\forall \theta \in \left[ { - \tau ,\;0} \right]\), \(t_{0} \in R_{ + }\) \(\varphi (\theta ) \in \left\{ {\varphi \in (C\left[ { - \tau ,0} \right],R^{n} );\;\left\| \varphi \right\|_{c} \le v,v > 0} \right\}\), \(\left\| \varphi \right\|_{c} = \sup_{ - \tau \le t \le 0} \left\| {\varphi (t)} \right\|\), \(x \in {\text{R}}^{n}\) is the system state vector,\(u \in {\text{R}}^{q}\) is the control input vector, \(\omega \in R^{h}\) is the external disturbance input vector and \(z \in {\text{R}}^{p}\) denotes the controlled output vector, \(\sigma :[0,\:\infty ) \to I_{N} = \{ 1,\: \cdots ,\:N\}\) denotes switching signal and it is a piecewise right continuous constant and \(\sigma = i\) means that the \(i\) subsystem is activated. Switching signals are represented by the following switching sequence
\(A_{i} \in {\text{R}}^{n \times n}\),\(A_{di} \in {\text{R}}^{n \times n}\),\(B_{i} \in {\text{R}}^{n \times q}\),\(E_{i} \in {\text{R}}^{n \times h}\) and \(C_{i} \in {\text{R}}^{n \times n}\) are constant matrices, and \(\Delta A_{i}\), \(\Delta A_{di}\) and \(\Delta B_{i}\) are time-varying uncertainty matrices with the following structure
where \(O_{i}\), \(F_{1i}\), \(F_{2i}\), and \(F_{3i}\) are known constant matrices of appropriate dimensions describing the uncertainty, \(\Gamma (t)\) is an unknown, time-varying real matrix satisfying Lebesgue measurability condition, and satisfies
\(sat:{\text{R}}^{q} \to {\text{R}}^{q}\) is the standard vector-valued saturation function. The definitions are as follows:
Obviously, without loss of generality, we assume unit saturation limits, since non-standard saturation functions can always be obtained by altering the matrix by employing appropriate transformations, and for simplicity, and in accordance with the notation prevalent in the literature, we adopt the notation \(sat( \bullet )\) to denote both scalar and vector saturation functions.
It is well known that the \(L_{2}\)-gain can be used to analyze the disturbance attenuation ability of systems. However, for systems with actuator saturation, the large external perturbations will result in unbounded states and thus we make the following assumption:
where \(\pi\) is a positive number.
The key question to address is: What is the maximum value of \(\pi\) such that the state remains bounded for all \(\omega (t) \in W_{\pi }^{2}\)? This analysis is conducted under the condition of zero initial state. This problem is commonly referred to as disturbance tolerance. Once the maximum \(\pi\) has been determined (denoted as \(\pi^{*}\)), the focus can shift to studying the disturbance rejection capability for \(W_{\pi }^{2}\) with \(\pi < \pi^{*}\). The disturbance rejection capability can be quantified by the restricted L2-gain over a given \(W_{\pi }^{2}\) or by the magnitude of the bound on the state trajectories.
Remark 1
In this work, the term ‘bounded state’ refers to a system state whose values remain within a specified range under all operating conditions. Similarly, ‘external perturbations’ are defined as disturbances or influences originating from outside the system that affect its behavior.
Remark 2
The external disturbances considered in this work include integrally bounded disturbances, which are characterized by their bounded energy over time interval. Specifically, the disturbances are assumed to satisfy the condition that their integral over time is bounded by a constant. This type of disturbance model is commonly encountered in practical systems, where disturbances may not be bounded instantaneously but have finite energy over time. The integrally bounded disturbance model is particularly relevant for capturing the cumulative effects of disturbances, such as environmental noise, measurement errors, or external forces, which can significantly impact system performance . By considering this type of disturbance, the analysis ensures robustness against a wide range of real-world disturbance profiles.
Considering actuator failures, we introduce a fault matrix \(M{}_{i}\), in which
where \(m_{ijl}\) and \(m_{iju}\) are given constants, \(m_{ij} = 0\) means that the j-th actuator is completely disabled, and \(m_{ij} = 1\) indicates that the j-th actuator is normal and namely normal actuator means that the actuator is operating without any faults. Further, \(0 < m_{iju} < m_{ij} < m_{ijl} < 1\), represents the j-th actuator partial failure.
Let
Then,
and
Thus, the resulting matrix \(M_{i}\) can be rewritten as
where \(\left| {L_{i} } \right| = diag\left\{ {\left. {\left| {l_{i1} } \right|,\left| {l_{i2} } \right|,...\left| {l_{iq} } \right|} \right\}} \right.\).
From the above equation, it can be seen that for the subsystem \(i\), the matrix \(M_{0i}\) is a constant matrix and the fault matrix \(M_{i}\) is only related to the charge of uncertainty matrix \(L_{i}\), then the closed-loop system containing actuator faults is
From43, we design the following AW controller containing DSF controller and AW compensator
where \(u(t)\) is the controller state, \(E_{ci} \in R^{q \times q}\) is the AW compensator gain, matrices \(F_{i} \in R^{q \times n}\) and \(G_{i} \in R^{q \times q}\) are the DSF controller gain.
From (9) and (10) the above closed-loop system can be rewritten as the following form
Then, we define some new variables and matrices as follows
The resulting closed-loop system can be rewritten as
with initial conditions \(\varphi_{\eta } (\theta ) = \eta (\theta )\),\(\theta \in \left[ { - \tau ,0} \right]\), \(\psi (v) = (sat(v) - v)\), \(v = \hat{N}_{i} \eta = u(t)\), and \(\dot{\eta }(t) = \chi (\eta (t))\).
To facilitate derivation in the rest of this article, we introduce the following lemmas and definitions.
Definition 1 44: System (12) is said to have a restricted L2-gain less than \(\gamma\) over \(\sigma\), from the disturbance input \(\omega\) to the controlled output \(z\), if the following inequality holds along the solution of (12),
where \(\omega (t) \in W_{\pi }^{2}\) and \(\eta (0) = 0\) is the initial state .
Definition 2 44: Let \(P \in {\text{R}}^{(q + n) \times (q + n)}\) denote the positive definite matrix, and define the ellipsoid
For the matrix \(\hat{N}_{i}\),\(H_{i} \in {\text{R}}^{q \times (q + n)}\), we define the following symmetric polyhedron
where \(\hat{N}_{i}^{j}\), \(H_{i}^{j}\), denote the \(j - th\) row of the matrices \(\hat{N}_{i}\) and \(H_{i}\) , respectively.
Lemma 1
Wang and Zhang45: For the symmetric matrix.
the following three conditions are equivalent:
Lemma 2
Wang and Zhang45: Suppose that \(\Pi_{1} \in {\text{R}}^{g \times k}\),\(\Pi_{2} \in {\text{R}}^{r \times k}\) and \(\Delta \in {\text{R}}^{k \times r}\), are some given matrices. If \(\left\| \Delta \right\| \le 1\), then there exists a scalar \(\varepsilon > 0\) such that the following matrix inequality holds:
\(\Pi_{1} \Delta \Pi_{2} + \Pi_{2}^{T} \Delta^{T} \Pi_{1}^{T} \le \varepsilon_{1} \Pi_{1} \Pi_{1}^{T} + \varepsilon_{1}^{ - 1} \Pi_{2}^{T} \Pi_{2}\).
Lemma 3
Wang and Zhang45: Suppose that \(\Pi_{1} \in {\text{R}}^{g \times k}\), \(\Pi_{2} \in {\text{R}}^{r \times k}\),\(\Delta_{1} \in {\text{R}}^{k \times r}\),\(\Delta_{2} \in {\text{R}}^{s \times r}\) and \(\Pi_{3} \in {\text{R}}^{r \times s}\) are some given matrices. If \(\left\| {\Delta_{1} } \right\| < 1\) and \(\left\| {\Delta_{2} } \right\| < 1\), then there exists \(\rho > 0\) which makes the following matrix inequality holds:
\(\Pi_{1} \Delta_{1} \Pi_{3} \Delta_{2} \Pi_{2} + \Pi_{2}^{T} \Delta_{2}^{T} \Pi_{3}^{T} \Delta_{1}^{T} \Pi_{1}^{T} \le \rho \Pi_{1} \Pi_{1}^{T} + \rho^{ - 1} \left\| {\Pi_{3} } \right\|^{2} \Pi_{2}^{T} \Pi_{2}\).
Lemma 4
Cao et al.47: For any \(z,y \in {\text{R}}^{n}\),and positive definite matrix \(X \in {\text{R}}^{n \times n}\), there is.
Lemma 5
Sun et al.46: For any constant matrix \(Z^{T} Z > 0\) and a scalar \(\tau > 0\) the following integral inequalities hold.
Lemma 6
Zhang44: Consider the function \(\psi (v)\) defined above, if \(\eta \in L(\hat{N}_{i} ,H_{i} )\), then the relation.
holds for any matrix \(J_{i} \in {\text{R}}^{q \times q}\) diagonal and positive definite.
In this paper, our objective is to design a switching law and the anti-windup fault-tolerant controller such that the maximum allowable disturbance capability and the minimum restricted L2-gain upper bound are obtained for the resulting closed-loop system.
Disturbance tolerance
In this section, by combining Jason inequality and by using the multiple Lyapunov–Krasovskii functionals approach, a sufficient condition for the state trajectory of the closed-loop system (12) to be bounded is given under the assumption that the AW compensator gain \(E_{ci}\) and the DSF controller gain \(K_{i}\) are known. In other words, this section is dedicated to the analysis of the problem, while the design aspects are not discussed here.
Theorem 1
For given scalars \(\tau\),\(h\), if there exist positive definite matrices \(P_{i}\),\(Q_{1}\),\(Q_{2}\),\(Z\), any matrices \(R_{i}\),\(W_{i}\),\(H_{i}\), positive definite diagonal matrices \(J_{i}\), and positive real numbers \(\beta_{ir}\), \(\varepsilon_{1i}\), \(\varepsilon_{2i}\), \(\varepsilon_{3i}\), \(\varepsilon_{4i}\), \(\varepsilon_{5i}\), \(\varepsilon_{6i}\), \(\varepsilon_{7i}\), \(\varepsilon_{8i}\), \(\varepsilon_{9i}\), \(\varepsilon_{10i}\), \(\varepsilon_{11i}\), \(\varepsilon_{12i}\), \(\rho_{1i}\), \(\rho_{2i}\), \(\rho_{3i}\), \(\rho_{4i}\), \(\rho_{5i}\), \(\rho_{6i}\), such that the following matrix inequalities hold.
where
and
where \(\overline{\lambda } (P_{i} )\), \(\overline{\lambda } (Q_{1} )\), \(\overline{\lambda } (Q_{2} )\), \(\overline{\lambda } (Z)\), denote the maximal eigenvalues \(P_{i}\), \(Q_{1}\), \(Q_{2}\), \(Z\), respectively, then for the closed-loop system (12), the state trajectory starting from the region \(\mathop \cup \limits_{r = 1}^{N} (\Omega (P_{i} ,\kappa ) \cap \Phi_{i} )\) will remain inside the region \(\mathop \cup \limits_{i = 1}^{N} (\Omega (P_{i} ,\kappa + \pi ) \cap \Phi_{i} )\), and the corresponding switching law is designed as
Proof:
See the appendix.
Here, the disturbance tolerance problem is formulated to ensure that the state of the system is bounded in the presence of external disturbances and actuator saturation. As previously mentioned, actuator saturation, which limits the control input’s magnitude, inherently requires determining the maximum allowable disturbance—the largest disturbance tolerance level the system can tolerate without losing stability or violating performance requirements. The problem is framed as an optimization task, aiming to maximize the allowable disturbance bound while respecting actuator limits and stability constraints. In terms of the inequality (47) (See the appendix), we can know the scalar \(\kappa + \pi\) can reflect the allowable disturbance capacity of closed-loop system. Thus, according to Theorem 1 it is known that the maximum allowable interference level of the closed-loop system (12) can be derived by solving the following optimization problem
For the convenience of solving the problem, we transform the above optimization problem into a convex optimization problem with linear matrix inequality constraints.
Multiply \(diag\left\{ {T_{1}^{ - 1} ;T_{1}^{ - 1} ;T_{1}^{ - 1} ;T_{1}^{ - 1} ;J_{i}^{ - 1} ;I;T_{1}^{ - 1} } \right\}\) on the left side and \(diag\left\{ {T_{1}^{ - T} ;T_{1}^{ - T} ;T_{1}^{ - T} ;T_{1}^{ - T} ;J_{i}^{ - T} ;I;T_{1}^{ - T} } \right\}\) on the right side of inequality (15), in order to obtain the LMI solvable conditions, and let \(T_{2} = \delta_{1} T_{1}\), \(T_{3} = \delta_{2} T_{1}\) and \(\delta_{1} ,\delta_{2} \ne 0\), where \(T_{1}\) is an invertible matrix. Therefore, it is justifiable to take a series of linear transformations to derive the following new variables:
Next, after making the above treatment of conditions (15), applying the lemma1, we can derive the following inequality,
where
Next, we will explain that, constraint \(\Omega (P_{i} ,\kappa + \pi ) \cap \Phi_{i} \subset L(\hat{N}_{i} ,H_{i} ),\forall i \in I_{N}\) can be transformed into the following matrix inequality
where \((\kappa + \pi )^{ - 1} = \varsigma\), \(\hat{N}_{i}^{j}\), \(H_{i}^{j}\) denotes the j-th row of \(\hat{N}_{i}\) and \(H_{i}\) respectively and \(\delta_{ir} > 0\),
Let \(G_{i} = P_{i} - \sum\limits_{r = 1,r \ne i}^{N} {\delta_{ir} (P_{r} - P_{i} )}\), and then from switching law (17), it is clear that
and
Thus, we get
Finally, we haveand
Thus, (21) implies that the constraints \(\Omega (P_{i} ,\kappa + \pi ) \cap \Phi_{i} \subset L(\hat{N}_{i} ,H_{i} ),\forall i \in I_{N}\), can be transformed into (20).
Then, multiplying \(diag\left\{ {T_{1}^{ - 1} ;I} \right\}\) on the left side and \(diag\left\{ {T_{1}^{ - T} ;I} \right\}\) on the right side of inequality (20), we obtain
Thus the optimization problem (18) can be formulated as the following optimization problem
Remark 3.
The use of LMIs in this work is motivated by their ability to provide a systematic and computationally efficient framework for analysis and design. LMIs are particularly suitable for handling complex constraints, such as robustness to uncertainties, performance requirements, and time-varying delays, which are common in the system under study. By transforming the problem into an LMI framework, the analysis becomes more tractable, and solutions can be obtained efficiently using well-established algorithms.
If we do not consider the fault of the actuator and adopt the conventional anti-windup controller, we can get the corollary 1.
Corollary 1:
For given scalars \(\tau\),\(h\), if there exist positive definite matrices \(P_{i}\),\(Q_{1}\),\(Q_{2}\),\(Z\), any matrices \(R_{i}\),\(W_{i}\),\(H_{i}\), positive definite diagonal matrices \(J_{i}\), and positive real numbers \(\beta_{ir}\), \(\varepsilon_{1i}\), \(\varepsilon_{2i}\), \(\varepsilon_{3i}\), \(\varepsilon_{4i}\), \(\varepsilon_{5i}\), \(\varepsilon_{6i}\), \(\varepsilon_{7i}\), \(\varepsilon_{8i}\), \(\varepsilon_{9i}\), \(\varepsilon_{10i}\), \(\varepsilon_{11i}\), \(\varepsilon_{12i}\), \(\rho_{1i}\), \(\rho_{2i}\), \(\rho_{3i}\), \(\rho_{4i}\), \(\rho_{5i}\), \(\rho_{6i}\), such that the following matrix inequalities hold.
where
then for the closed-loop system (12), the state trajectory starting from the region \(\mathop \cup \limits_{i = 1}^{N} (\Omega (P_{i} ,\kappa ) \cap \Phi_{i} )\) will remain inside the region \(\mathop \cup \limits_{i = 1}^{N} (\Omega (P_{i} ,\kappa + \pi ) \cap \Phi_{i} )\).
If we do not consider the anti-windup compensation cases, we can get the corollary 2.
Corollary 2:
For given scalars \(\tau\),\(h\), if there exist positive definite matrices \(P_{i}\),\(Q_{1}\),\(Q_{2}\),\(Z\), any matrices \(R_{i}\),\(W_{i}\),\(H_{i}\), positive definite diagonal matrices \(J_{i}\), and positive real numbers \(\beta_{ir}\), \(\varepsilon_{1i}\), \(\varepsilon_{2i}\), \(\varepsilon_{3i}\), \(\varepsilon_{4i}\), \(\varepsilon_{5i}\), \(\varepsilon_{6i}\), \(\varepsilon_{7i}\), \(\varepsilon_{8i}\), \(\varepsilon_{9i}\), \(\varepsilon_{10i}\), \(\varepsilon_{11i}\), \(\varepsilon_{12i}\), \(\rho_{1i}\), \(\rho_{2i}\), \(\rho_{3i}\), \(\rho_{4i}\), \(\rho_{5i}\), \(\rho_{6i}\), such that the following matrix inequalities hold.
where
then for the closed-loop system (12), the state trajectory starting from the region \(\mathop \cup \limits_{i = 1}^{N} (\Omega (P_{i} ,\kappa ) \cap \Phi_{i} )\) will remain inside the region \(\mathop \cup \limits_{i = 1}^{N} (\Omega (P_{i} ,\kappa + \pi ) \cap \Phi_{i} )\).
\({\mathbf{L}}_{2}\)-gain analysis
In this section, by using the multiple Lyapunov functionals approach, sufficient conditions for the existence of the restricted \(L_{2}\)-gain of the closed-loop system (12) are given. Likewise, we assume that the gain matrix \(K_{i}\) of the anti-windup controller is given beforehand and the corresponding maximum value of the tolerable disturbance \((\kappa + \pi )^{*}\) has been obtained. Similar to the preceding section, this section focuses solely on the L2-gain analysis problem, while the design of anti-windup fault-tolerant controllers is not discussed at this stage.
Theorem 2:
Consider the closed-loop systems (12), for given scalars \((\kappa + \pi ) \in \left( {0,(\kappa + \pi )^{*} } \right]\) and \(\gamma > 0\), if there exist positive definite matrices \(P_{i}\),\(Q_{1}\),\(Q_{2}\),\(Z\), any matrices \(R_{i}\),\(W_{i}\),\(H_{i}\), positive definite diagonal matrices \(J_{i}\), and positive real numbers \(\beta_{ir}\), \(\varepsilon_{1i}\), \(\varepsilon_{2i}\), \(\varepsilon_{3i}\), \(\varepsilon_{4i}\), \(\varepsilon_{5i}\), \(\varepsilon_{6i}\), \(\varepsilon_{7i}\), \(\varepsilon_{8i}\), \(\varepsilon_{9i}\), \(\varepsilon_{10i}\), \(\varepsilon_{11i}\), \(\varepsilon_{12i}\), \(\rho_{1i}\), \(\rho_{2i}\), \(\rho_{3i}\), \(\rho_{4i}\), \(\rho_{5i}\), \(\rho_{6i}\), such that the following matrix inequalities hold.
and
where
then under the action of the switching law (26) for all \(\forall \omega \in W_{\pi }^{2}\), the restricted \(L_{2}\)-gain from \(\omega\) to \(z\) for the closed-loop system (12) is less than \(\gamma\).
Proof:
See the appendix.
It follows from Theorem 2 that for each given \((\kappa + \pi ) \in \left( {0,(\kappa + \pi )^{*} } \right]\), the minimum upper bound on the restricted \(L_{2}\)-gain of the closed-loop system (12) can be obtained by solving the following optimization problem
For the convenience of solving the problem, we transform the above optimization problem into a convex optimization problem with linear matrix inequality constraints.
Multiply \(diag\left\{ {T_{1}^{ - 1} ;T_{1}^{ - 1} ;T_{1}^{ - 1} ;T_{1}^{ - 1} ;J_{i}^{ - 1} ;I;T_{1}^{ - 1} } \right\}\) on the left side and \(diag\left\{ {T_{1}^{ - T} ;T_{1}^{ - T} ;T_{1}^{ - T} ;T_{1}^{ - T} ;J_{i}^{ - T} ;I;T_{1}^{ - T} } \right\}\) on the right side of inequality (24).
Next, after making the above treatment of conditions (24), applying the lemma1, we can derive the following inequality,
where \(\zeta = \gamma^{2}\).
Then applying a similar approach to Eq. (25) yields
Thus the optimization problem (27) can be transformed into the following optimization problem.
Anti-windup fault-tolerant controller design and optimization
In this section we design the anti-windup controller as a variable to be designed, which allows the performance of the closed-loop system (12) to be further improved by solving the optimization problem with linear matrix inequality constraints.
Let \(Y_{i} = K_{i} X\). Then, the matrix inequalities (19) and (28) are equivalent to the following two inequalities, respectively
where
\(\begin{gathered} \Theta_{171i} = \hat{A}_{i} X^{T} + I_{R} Y_{i} + X\hat{A}_{i}^{T} + Y_{i}^{T} I_{R}^{T} + \varepsilon_{1i} \hat{B}_{i} M_{0i} M_{0i}^{T} \hat{B}_{i}^{T} + \varepsilon_{2i} \hat{T}_{i} \hat{T}_{i}^{T} \hfill \\ \quad \; + \varepsilon_{3i} \hat{T}_{i} \hat{T}_{i}^{T} + \rho_{1i} \hat{T}_{i} \hat{T}_{i}^{T} + 4\rho_{2i} \hat{T}_{i} \hat{T}_{i}^{T} + \overline{{R_{1} }} + \overline{R}_{1}^{T} + \sum\limits_{r = 1,r \ne i}^{N} {\beta_{ir} (\overline{P}_{r} - \overline{P}_{i} )} , \hfill \\ \end{gathered}\)\(\Theta_{172i} = \hat{C}_{i} X^{T} + \delta_{2} X\hat{A}_{i}^{T} + \delta_{2} Y_{i}^{T} I_{R}^{T} + \overline{R}_{2}^{T} - \overline{R}_{1} + \overline{W}_{1}\),
\(\Theta_{174i} = \delta_{1} X^{T} \hat{A}_{i}^{T} + \delta_{1} Y_{i}^{T} I_{R}^{T} - {\text{X}}^{T} + R_{4}^{T}\),
and
Therefore, the problem of estimating the disturbance tolerance of the closed-loop system (12) can be described as an optimization problem as follows
and the minimum upper bound on the restricted-gain of the closed-loop system (12) can then be obtained by solving an optimization problem as follows.
Then, we can obtain the anti-windup compensator gain matrix \(E_{ci}\) by solving the optimization problems (33) and (34), and the corresponding dynamic state feedback controller gain matrix can be solved as \(K_{i} = Y_{i} X^{ - 1}\).
Remark 4.
Transforming the above optimization problem into a convex optimization problem offers several key benefits. First, convex optimization ensures global optimality, meaning that the solution obtained is the best possible within the feasible region. Second, convex problems can be solved efficiently using well-established algorithms, making them computationally tractable even for large-scale systems. Third, complex constraints or nonlinearities can often be expressed as linear matrix inequalities (LMIs) or other convex forms, simplifying the analysis and design process. Additionally, convex optimization provides a robust framework for incorporating uncertainties and disturbances, ensuring that the solution remains valid under a wide range of conditions. The scalability of convex optimization also allows for the extension of the problem to more complex systems or additional design requirements without significantly increasing computational complexity. Finally, the solutions derived from convex optimization are often directly applicable to real-world systems, ensuring that theoretical results translate effectively into practice.
Numerical simulation
All simulations in this study are conducted using MATLAB (version R2022a) as the primary software tool. This environment was selected for its versatility in implementing and analyzing the proposed control strategies. To illustrate the effectiveness of the proposed method, we consider the following linear uncertain saturated switched systems with time-delay and external disturbances as follows.
where \(i \in I_{2} = \left\{ {\left. {1,2} \right\}} \right.\),
Assuming that the range of actuator faults is \(0.1 \le m_{ij} \le 0.9\), and according to the continuous fault model we can get
Now, the simulation parameters and initial conditions are as follows (In other words, in order to carry out the simulation, they are specified in advance.):
Then, by solving the optimization problem (33) we can obtain the following feasible solution
\(T_{1} = \left[ {\begin{array}{*{20}c} {0.0137} & {0.0000} & {0.0007} & {0.0000} \\ {0.0000} & {0.0128} & { - 0.0001} & {0.0003} \\ {0.0007} & { - 0.0001} & {0.0080} & {0.0001} \\ {0.0000} & {0.0003} & {0.0001} & {0.0055} \\ \end{array} } \right]\).
\(X = \left[ {\begin{array}{*{20}c} {73.1691} & { - 0.1116} & { - 6.4170} & {0.0199} \\ { - 0.1116} & {77.9296} & {1.0207} & { - 3.7385} \\ { - 6.4170} & {1.0207} & {125.5027} & { - 2.0679} \\ {0.0199} & { - 3.7385} & { - 2.0679} & {180.7436} \\ \end{array} } \right]\).
\(P_{1} = \left[ {\begin{array}{*{20}c} {0.0019} & {0.0000} & {0.0002} & {0.0000} \\ {0.0000} & {0.0017} & { - 0.0000} & {0.0000} \\ {0.0002} & { - 0.0000} & {0.0006} & {0.0000} \\ {0.0000} & {0.0000} & {0.0000} & {0.0003} \\ \end{array} } \right]\).
\(P_{2} = \left[ {\begin{array}{*{20}c} {0.0021} & {0.0000} & {0.0002} & {0.0000} \\ {0.0000} & {0.0018} & { - 0.0000} & {0.0001} \\ {0.0002} & { - 0.0000} & {0.0007} & {0.0000} \\ {0.0000} & {0.0001} & {0.0000} & {0.0003} \\ \end{array} } \right]\).
\(Y_{1} = \left[ {\begin{array}{*{20}c} { - 318.3617} & {4.8696} & {89.4905} & { - 9.2179} \\ {4.2237} & { - 358.2789} & { - 10.5659} & {375.4733} \\ \end{array} } \right]\).
\(Y_{2} = \left[ {\begin{array}{*{20}c} { - 396.0882} & {1.3173} & { - 20.5940} & {2.1260} \\ {2.2872} & { - 433.6065} & { - 7.6846} & { - 135.3035} \\ \end{array} } \right]\).
\(S_{1} = \left[ {\begin{array}{*{20}c} {0.5860} & {0.0031} & { - 0.0001} & { - 0.0007} \\ {0.0031} & {0.5868} & { - 0.0002} & { - 0.0008} \\ { - 0.0001} & { - 0.0002} & {0.5832} & {0.0000} \\ { - 0.0007} & { - 0.0008} & {0.0000} & {0.5834} \\ \end{array} } \right]\).
\(S_{2} = \left[ {\begin{array}{*{20}c} {0.5878} & {0.0053} & { - 0.0003} & { - 0.0005} \\ {0.0053} & {0.5892} & { - 0.0003} & { - 0.0005} \\ { - 0.0003} & { - 0.0003} & {0.5831} & {0.0000} \\ { - 0.0005} & { - 0.0005} & {0.0000} & {0.5831} \\ \end{array} } \right]\).
The AW compensator gains for the closed-loop system are
The dynamic state feedback controller gains of the closed-loop system are
Furthermore, Table 1 shows the corresponding relation of the maximum allowable disturbance \((\kappa + \pi )^{*}\) and different values of \(\tau\) by solving the optimization problem (33). The results of Table 1 indicate that the allowable disturbance ability of the closed-loop system (35) became lower with the increase of \(\tau\).
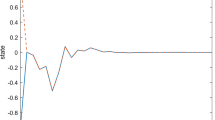
Then, we select \(\omega (t) = \sqrt {2(\kappa + \pi )^{*} } e^{ - t}\) as external interference input for simulation. Figure 1 shows the state response curve of the switched system (35). Figure 2 shows the controller state of the system. The control input signal for the switched system (35) is shown in Figs. 3, and 4 shows the switching signal of the switched system. In Fig. 4, the switching signal based on the multiple Lyapunov functionals approach is depicted. The signal alternates between subsystem 1 and subsystem 2. Specially, according to the switching law we designed, subsystem 1 is activated during \(\eta^{T} (P_{2} - P_{1} )\eta \ge 0\) and subsystem 2 is activated during \(\eta^{T} (P_{1} - P_{2} )\eta > 0\).
State response of the switched system (35).
Controller state response of the switched system (35).
Input signals for switched system (35).
Switching signals for switched systems (35).
In addition, if we set \(E_{c1} = E_{c2} = 0\), then the optimal solution obtained base on Corollary 2 is \((\kappa + \pi )^{*} = 2.4913\). Obviously, this shows that the interference tolerance of the closed-loop system is enhanced under the action of the anti-windup compensator.
Based on the points discussed above, we have obtained the maximum allowable disturbance by using the multiple Lyapunov functional approach and anti-windup control techniques. Next, we perform L2-gain analysis to ensure that the minimum L2- gain is obtained under the different allowable disturbance levels based on the maximum allowable disturbance, meaning that under the anti-windup compensator, the system effectively minimizes the impact of disturbances on the output. Thus, for each given \((\kappa + \pi ) \in \left( {0,(\kappa + \pi )^{*} } \right]\), we estimate an upper bound on the restricted \(L_{2} -\) gain of the closed-loop system (35). Then, solving the optimization problem (34), we can consider the following scenarios:
1.if \(\kappa + \pi = 0.5\) we obtain \(\gamma = 2.5840\)
2.if \(\kappa + \pi = 1.5\) we obtain \(\gamma = 2.7739\)
3.if \(\kappa + \pi = 2.5\) we obtain \(\gamma = 3.4096\)
4.if \(\kappa + \pi = 3\) we obtain \(\gamma = 4.8482\)
Figure 5 shows the curve of different \((\kappa + \pi ) \in (0,(\kappa + \pi )^{*} ]\) and restricted \(L_{2}\)-gain \(\gamma\), which indicates that the disturbance attenuation ability of the closed-loop system became lower with the increase of external disturbance.
The restricted \(L_{2}\)-gain of the switched system (35).
When the actuator fails, the state response curve obtained base on Corollary 1 is shown in Figs. 6 and 7 for switched system (35) with the conventional anti-windup controller . Here, the meaning of conventional anti-windup controller is that it is designed without considering the failure of the actuator. Obviously, Figs. 6 and 7 show that the state trajectories of the system with the actuator failure are unbounded under the conventional anti-windup controller. However, the state trajectory under the anti-windup fault-tolerant controller can always stay within this bounded set (see Figs. 1 and 2). Thus, the anti-windup fault-tolerant controller designed according to our proposed method has better fault tolerance capacity.
State response of system (35) under conventional anti-windup controller.
Remark 5.
It should be noted that (31), (22), (32) and (29) are not LMI and cannot be easily solved. If some scalar parameters are given a priori, then the problem of estimating the disturbance tolerance and the problem of obtaining the minimum upper bound on the restricted L2-gain are formulated as a set of LMI optimization problems with regard to other unknown variables and solved by the feasp solver of MATLAB. Although this becomes a little more conservative. The conservatism of the LMI approach primarily arises from the pre-specification of certain scalar parameters to enable numerical solvability. While this introduces some conservatism, it ensures practical applicability. Regarding scalability, our method is theoretically applicable to higher-order systems with more than two switching states, as the LMI framework can accommodate larger matrices and additional constraints. However, computational complexity may increase with system order and the number of switching states.
Conclusion
In this paper, the problem of anti-windup fault-tolerant control for a class of uncertain time-delay switched systems with actuator saturation and actuator faults is investigated by using the multiple Lyapunov Krasovskii functionals approach. Firstly, the sufficient conditions for the tolerance disturbances are derived, and under this condition the disturbance tolerance problem is transformed into a convex optimization problem with linear matrix inequality constraints. Then, based on this condition the L2-gain analysis of the closed-loop system is carried out. Next, by designing the AW controller, the maximum allowable disturbance capability of the closed-loop system as well as the minimum restricted L2-gain upper bound is obtained. Finally, a numerical simulation example is given to verify the effectiveness of the proposed method in this paper.
In comparison to the existing research on saturated switched systems with time-varying delays, this paper presents three notable distinctions: Firstly, we propose the anti-windup (AW) controller that integrates a dynamic state feedback (DSF) controller and an AW compensator to handle saturation nonlinearity, in contrast to the prevalent approach in existing studies where saturation nonlinearity is modeled using polytopic sets48 and from the perspective of practical application, the anti-windup method we propose is a common and effective technique to deal with the problem of actuator saturation. Secondly, our work addresses the issue of fault-tolerant controller design, a consideration largely absent in prior research, which predominantly focuses on designing standard controllers without accounting for potential actuator faults20,21. Lastly, this paper employs the multiple Lyapunov–Krasovskii functionals method to analyze saturated switched systems under actuator failure, eliminating the necessity for the solvability of the fault-tolerant control problem at the subsystem level. This stands in contrast to the majority of existing literature, which relies on the arbitrary switching strategy48,49 or the average dwell-time technique, both of which necessitate solvability conditions for each individual subsystem.
In this paper, we assume that some scalar parameters are given in advance for the convenience of solving the linear matrix inequality. But actually, these parameters affect the maximum allowable disturbance level and the minimum restricted L2-gain upper bound, so how to choose these parameters to obtain the maximum allowable disturbance level and the minimum restricted L2-gain upper bound is a very interesting and challenging research direction. Some intelligent optimization algorithms, such as the particle swarm algorithm and the gray wolf optimization algorithm, may be beneficial in finding optimal solutions for these parameters and deserve further investigation. In addition, Zeno phenomenon generated by min-switching laws will bring a lot of trouble, which will lead to fatal damage for practical engineering systems. Therefore, in our future work, we will use the dwell time method to investigate the fault-tolerant control problem of switched systems with actuator saturation and actuator failure and the designed switching laws based on the dwell time method can effectively avoid Zeno phenomenon. On the other hand, this study provides a foundation for several promising extensions. One potential direction is to apply the proposed methods, including the multiple Lyapunov functionals and anti-windup techniques, to nonlinear systems with actuator saturation and failure. Nonlinear systems often exhibit more complex dynamics, and extending our approach to such systems could further enhance its applicability. And, exploring adaptive or event-triggered control strategies50 within this framework could offer new insights into handling uncertainties and improving system performance. These extensions mentioned above represent valuable avenues for future research.
The proposed methods for switched time-delay systems with actuator saturation and failure, based on multiple Lyapunov functionals and anti-windup techniques, have significant potential for real-world applications. For instance, they can be applied to enhance the stability and performance of industrial control systems (e.g., chemical processes51,52 and manufacturing), unmanned aerial vehicles (UAVs), power systems (e.g., smart grids), and autonomous vehicles. These systems often encounter challenges such as actuator limitations, switching dynamics, and time delays, which can be effectively addressed by our approach. By improving robustness and reliability in such applications, our results contribute to solving critical engineering problems in practice.
Data availability
All data generated or analysed during this study are included in this published article.
References
Qi, W. Zong, G. Hou, Y. & Chadli, M. SMC for discrete-time nonlinear semi-Markovian switching systems with partly unknown semi-Markov kernel. IEEE Transactions on Automatic Control, 68(3), 1855-1861(2022).
Shi, H. et al. Robust predictive fault-tolerant switching control for discrete linear systems with actuator random failures. Comput. Chem. Eng. 181, 108554 (2024).
Qi W H, Li R K, Park J H, et al. Observer-based stabilization for discrete nonlinear semi-Markov jump singularly perturbed models with mode-switching delay. Sci China Inf Sci 68(4), 149201(2025).
Wang, Q., Yu, H., Wu, Z. G. & Chen, G. Stability analysis for input saturated discrete-time switched systems with average dwell-time. IEEE Trans. Syst. Man Cybern.: Syst. 51(1), 412–419 (2018).
Wang, J. & Zhang, X. Non-fragile stabilization of nonlinear switched systems with actuator saturation. Journal of Control and Decision 10(2), 260–269 (2023).
Aleksandrov, A. On the existence of a common Lyapunov function for a family of nonlinear positive systems. Syst. Control Lett. 147, 104832 (2021).
Gao, F., Wu, Y., Zhang, Z. & Liu, Y. Global fixed-time stabilization for a class of switched nonlinear systems with general powers and its application. Nonlinear Anal. Hybrid Syst 31, 56–68 (2019).
Song, Z. & Zhai, J. Practical output tracking control for switched nonlinear systems: A dynamic gain based approach. Nonlinear Anal. Hybrid Syst. 30, 147–162 (2018).
Zhang, T., Li, J., Xu, W. & Li, X. Stability and L2-gain analysis for impulsive switched systems. Commun. Nonlinear Sci. Numer. Simul. 78, 104854 (2019).
Niu, B. et al. Multiple Lyapunov functions for adaptive neural tracking control of switched nonlinear nonlower-triangular systems. IEEE Trans. Cybern. 50(5), 1877–1886 (2019).
Wang, R., Hou, L., Zong, G., Fei, S. & Yang, D. Stability and stabilization of continuous-time switched systems: a multiple discontinuous convex Lyapunov function approach. Int. J. Robust Nonlinear Control 29(5), 1499–1514 (2019).
Shen, M., Wang, X., Park, J. H., Yi, Y. & Che, W. W. Extended disturbance-observer-based data-driven control of networked nonlinear systems with event-triggered output. IEEE Trans. Syst. Man, Cybern.: Syst. 53(5), 3129–3140 (2022).
Lu, L., Lin, Z. & Fang, H. L2 gain analysis for a class of switched systems. Automatica 45(4), 965–972 (2009).
Lin, X., Du, H., Li, S. & Zou, Y. Finite-time boundedness and finite-time l2 gain analysis of discrete-time switched linear systems with average dwell time. J. Franklin Inst. 350(4), 911–928 (2013).
Wei, J., Zhi, H. & Liu, K. Stability and L 2–Gain analysis of linear switched singular systems by using multiple discontinuous Lyapunov function approach. Trans. Inst. Meas. Control. 41(15), 4197–4206 (2019).
Jia, S. & Shan, J. Finite-time trajectory tracking control of space manipulator under actuator saturation. IEEE Trans. Industr. Electron. 67(3), 2086–2096 (2019).
Wang, Q., Ma, L., Wang, D. & Ma, X. Stabilization bound of singularly perturbed switched nonlinear systems subject to actuator saturation using the Takagi-Sugeno fuzzy model. Asian J. Control 24(1), 415–426 (2022).
Shen, M., Wang, X., Zhu, S., Wu, Z. & Huang, T. Data-driven event-triggered adaptive dynamic programming control for nonlinear systems with input saturation. IEEE Trans. Cybern. 54(2), 1178–1188 (2023).
Zhao, G. & Wang, J. Finite time stability and -gain analysis for switched linear systems with state-dependent switching. J. Franklin Inst. 350(5), 1075–1092 (2013).
Zhang, X., Li, X., Shi, J., & Tong, S. (2020, July). L2-gain analysis for switched saturated systems based on anti-windup technique. In 2020 39th Chinese Control Conference (CCC) (pp. 1255–1260). IEEE.
Zhang, X., Li, X., Wang, Y., & Mu, K. (2020). Stability analysis and design of switched saturated systems based on anti-windup technique. In 2020 39th Chinese control conference (CCC) (pp. 1261–1264). IEEE.
Nguyen, A. T., Sentouh, C. & Popieul, J. C. Fuzzy steering control for autonomous vehicles under actuator saturation: Design and experiments. J. Franklin Inst. 355(18), 9374–9395 (2018).
Peng, H., Li, F., Zhang, S. & Chen, B. A novel fast model predictive control with actuator saturation for large-scale structures. Comput. Struct. 187, 35–49 (2017).
Zeng, H. B., Teo, K. L., He, Y., Xu, H. & Wang, W. Sampled-data synchronization control for chaotic neural networks subject to actuator saturation. Neurocomputing 260, 25–31 (2017).
Qi, Y., Xu, X., Lu, S. & Yu, Y. A waiting time based discrete event-triggered control for networked switched systems with actuator saturation. Nonlinear Anal. Hybrid Syst 37, 100904 (2020).
Zuo, Z., Li, Y., Wang, Y. & Li, H. Event-triggered control for switched systems in the presence of actuator saturation. Int. J. Syst. Sci. 49(7), 1478–1490 (2018).
Chen, Y., Fu, Z., Fei, S. & Song, S. Delayed anti-windup strategy for input-delay systems with actuator saturations. J. Franklin Inst. 357(8), 4680–4696 (2020).
Wang, Y., Xu, N., Liu, Y. & Zhao, X. Adaptive fault-tolerant control for switched nonlinear systems based on command filter technique. Appl. Math. Comput. 392, 125725 (2021).
Aouaouda, S. & Chadli, M. Robust fault tolerant controller design for Takagi-Sugeno systems under input saturation. Int. J. Syst. Sci. 50(6), 1163–1178 (2019).
Huang, S. & Xiang, Z. Robust reliable control for uncertain switched nonlinear systems with time delay under asynchronous switching. Appl. Math. Comput. 222, 658–670 (2013).
Salwa, Y., Saida, B. & Abderrahim, K. Diagnosis and fault tolerant control against actuator fault for a class of hybrid dynamic systems. Meas. Control 56(7–8), 1240–1250 (2023).
Ladel, A. A., Benzaouia, A., Outbib, R. & Ouladsine, M. Robust fault tolerant control of continuous-time switched systems: An LMI approach. Nonlinear Anal. Hybrid Syst 39, 100950 (2021).
Elouni, M., Hamdi, H., Rabaoui, B., Rodrigues, M., & Braiek, N. B. (2025). An Integrated Sensor Fault Estimation and Fault-Tolerant Control Design Approach for Continuous-Time Switched Systems. J. Dyn. Syst. Meas. Control, 147(4).
Elouni, M., Rodrigues, M., Hamdi, H., Rabaoui, B., & BenHadj Braiek, N. (2024). Adaptive proportional integral derivative fault tolerant control for continuous-time switched systems: A highly maneuverable aircraft technology (HiMAT) vehicle application. Trans. Inst. Meas. Control, 01423312241289631.
Benzaouia, A., & Telbissi, K. (2017, May). Fault tolerant control for uncertain switching discrete-time systems with actuator failures. In 2017 6th International conference on systems and control (ICSC) (pp. 383–390). IEEE.
Mao, J., Zou, W., Guo, J. & Xiang, Z. Observer-based finite-time sampled-data control for a class of nonlinear time-delay systems. IEEE Trans. Syst. Man, Cybern.: Syst. 54(3), 1645–1657 (2024).
Mao, J., Zou, W., He, W. & Xiang, Z. Practical finite-time sampled-data output feedback stabilization for a class of upper-triangular nonlinear systems with input delay. IEEE Trans. Syst. Man Cybern.: Syst. 53(6), 3428–3439 (2023).
Park, M., Kwon, O., Park, J. H., Lee, S. & Cha, E. Stability of time-delay systems via Wirtinger-based double integral inequality. Automatica 55, 204–208 (2015).
Rahimi, F. Adaptive dynamic programming-based fault tolerant control for nonlinear time-delay systems. Chaos, Solitons Fractals 188, 115544 (2024).
Mohammed, C., Noureddine, C., & El Houssaine, T. (2019). Robust stability of uncertain discrete-time switched systems with time-varying delay by Wirtinger Inequality via a switching signal design. In 2019 8th International conference on systems and control (ICSC) (pp. 525–532). IEEE.
Chen, Y., Li, Y. & Fei, S. Anti-windup design for time-delay systems via generalized delay-dependent sector conditions. IET Control Theory Appl. 11(10), 1634–1641 (2017).
Rahimi, F. (2024). An online fault-tolerant control approach based on policy iteration algorithm for nonlinear time-delay systems. Int. J. Syst. Sci. 1–16.[42]
Zhou, L., Wang, C., Wang, Q. & Yang, C. Anti-windup control for nonlinear singularly perturbed switched systems with actuator saturation. Int. J. Syst. Sci. 49(10), 2187–2201 (2018).
Zhang, X. (2017).\(L_{2}\)‐gain analysis and anti‐windup design of switched linear systems subject to input saturation. Asian Journal of Control, 19(2), 672-680
Wang, J. & Zhang, X. Non-fragile robust stabilization of nonlinear uncertain switched systems with actuator saturation. J. Control, Autom. Electr. Syst. 34(1), 18–28 (2023).
Sun, J., Liu, G. P. & Chen, J. Delay-dependent stability and stabilization of neutral time-delay systems. Int. J. Robust Nonlinear Control: IFAC-Affiliated J. 19(12), 1364–1375 (2009).
Cao, Y. Y., Sun, Y. X. & Cheng, C. Delay-dependent robust stabilization of uncertain systems with multiple state delays. IEEE Trans. Autom. Control 43(11), 1608–1612 (1998).
Qian, Y., Xiang, Z. & Karimi, H. R. Disturbance tolerance and rejection of discrete switched systems with time-varying delay and saturating actuator. Nonlinear Anal. Hybrid Syst. 16, 81–92 (2015).
Wei, Y., Sun, L., Jia, S., Liu, K. & Meng, F. Disturbance attenuation and rejection for a class of switched nonlinear systems subject to input and sensor saturations. Math. Probl. Eng. 2019(1), 5653619 (2019).
Zouari, F., Ibeas, A., Boulkroune, A. & Cao, J. Finite-time adaptive event-triggered output feedback intelligent control for noninteger order nonstrict feedback systems with asymmetric time-varying pseudo-state constraints and nonsmooth input nonlinearities. Commun. Nonlinear Sci. Numer. Simul. 136, 108036 (2024).
Shi, H., Gao, W., Jiang, X., Su, C. & Li, P. Two-dimensional model-free Q-learning-based output feedback fault-tolerant control for batch processes. Comput. Chem. Eng. 182, 108583 (2024).
Shi, H. et al. Model-free output feedback optimal tracking control for two-dimensional batch processes. Eng. Appl. Artif. Intell. 143, 109989 (2025).
Acknowledgements
This work was supported by the Natural Science Foundation of Liaoning Province of China (No.2020-MS-283). This work was supported by the Basic Scientific Research Fund of Education Department of Liaoning Province of China (LJKMZ20220731).
Author information
Authors and Affiliations
Contributions
Chaosheng Hao and Xinquan Zhang wrote the main manuscript text and Chaosheng Hao prepared figures . All authors reviewed the manuscript. Xinquan Zhang: Funding acquisition; investigation; supervision; visualization; writing—review and editing.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Proof of Theorem 1:
From (16), if \(\forall \eta \in \Omega (P_{i} ,\kappa + \pi ) \cap \Phi_{i}\), then \(\eta \in L(\hat{N}_{i} ,H_{i} )\). According to Lemma 6 for \(\forall \eta \in \Omega (P_{i} ,\kappa + \pi ) \cap \Phi_{i}\), \(\psi (v) = (sat(v) - v)\) satisfies the sector condition (14). By the switching law (17), then the following Lyapunov–Krasovskii functionals are selected as.
\(V(\eta ) = V_{i} (\eta ) = \eta^{T} (t)P_{i} \eta (t) + \int_{t - \tau (t)}^{t} {\eta^{T} (s)Q_{1} \eta (s)ds + \int_{t - \tau }^{t} {\eta^{T} (s)Q_{2} \eta (s)} } ds + \int_{ - \tau }^{0} {\int_{t + \theta }^{t} {\dot{\eta }^{T} (s)Z\dot{\eta }(s)ds} } d\theta .\) Then, according to Lemma 4, 5, we can know that there exist any matrices \(W_{i}\), \(R_{i}\), such that the following inequality holds
where
Then, for \(\forall \eta \in \Omega (P_{i} ,\kappa + \pi ) \cap \Phi_{i} \subset L(\hat{N}_{i} ,H_{i} )\), the derivative of \(V_{i} (\eta )\) along the trajectory of the closed-loop system (12) with respect to time is
By using the free weighting matrix approach, for appropriate dimension matrices \(T_{1}\), \(T_{2}\) and \(T_{3}\),we can have the following equality:
Combining inequality (38) and equality (39), we can have
Then, several items in Eq. (39) can be processed into the following form by Lemma 2 and 3
Thus we can obtain
where
\(\begin{gathered} \Theta_{11i}{\prime} = T_{1} (\hat{A}_{i} + I_{R} K_{i} ) + (\hat{A}_{i} + I_{R} K_{i} )^{T} T_{1}^{T} + \varepsilon_{1i} T_{1} \hat{B}_{i} M_{0i} M_{0i}^{T} \hat{B}_{i}^{T} T_{1}^{T} + \varepsilon_{1i}^{ - 1} I_{R} I_{R}^{T} + \varepsilon_{2i} T_{1} \hat{T}_{i} \hat{T}_{i}^{T} T_{1} \hfill \\ \quad \;\;\; + \varepsilon_{3i} T_{1} \hat{T}_{i} \hat{T}_{i}^{T} T_{1} + \varepsilon_{3i}^{ - 1} \hat{F}_{i}^{T} \hat{F}_{i} + \rho_{1i} T_{1} \hat{T}_{i} \hat{T}_{i}^{T} T_{1} + \rho_{1i}^{ - 1} \left\| {F_{3i} M_{0i} } \right\|^{2} I_{R} I_{R}^{T} + 4\rho_{2i} T_{1} \hat{T}_{i} \hat{T}_{i}^{T} T_{1} \hfill \\ \quad \;\;\; + 4\varepsilon_{4i} T_{1} (\hat{B}_{i} + I_{R} E_{ci} )M_{0i} M_{0i}^{T} (\hat{B}_{i} + I_{R} E_{ci} )^{T} T_{1}^{T} + \varepsilon_{5i}^{ - 1} I_{R} I_{R}^{T} + \rho_{3i}^{ - 1} \left\| {F_{3i} M_{0i} } \right\|^{2} I_{R} I_{R}^{T} + \varepsilon_{7i}^{ - 1} \hat{F}_{i}^{T} \hat{F}_{i} \hfill \\ \quad \;\;\; + \varepsilon_{9i}^{ - 1} I_{R} I_{R}^{T} + \varepsilon_{11i}^{ - 1} \hat{F}_{i}^{T} \hat{F}_{i} + \rho_{5i}^{ - 1} \left\| {F_{3i} M_{0i} } \right\|^{2} I_{R} I_{R}^{T} + Q_{1} + Q_{2} + R_{1} + R_{1}^{T} . \hfill \\ \end{gathered}\) And then multiplying inequality (15) from the left by \(\xi^{T} (t)\) and from the right by \(\xi (t)\) can result in
Combining inequality (41), (42), and (43) we can have
By the switching law (17) it is easy to see that the following inequality is true.
Combining inequality (41), (42), (43) and (44), we can easy obtain the following inequality
Integrating both sides of inequality (45) from \(t_{0}\) to \(t\) yields
and according to the switching law (17), it can be seen that at the switching moment \(t_{k} (k \in Z^{ + } )\),\(V_{i} (\eta (t_{k} )) = V_{r} (\eta (t_{k} ))\), \(i,r \in I_{N}\), \(i \ne r\), combining inequality (46) we can arrive at
and
Since \(V(\eta (0)) \le \kappa\), \(\int_{0}^{\infty } {\omega^{T} \omega dt \le \pi }\), it follows that
Inequality (47) indicates that the state trajectory for the closed-loop system (12) from set \(\mathop \cup \limits_{i = 1}^{N} (\Omega (P_{i} ,\kappa ) \cap \Phi_{i} )\) will remain within the set \(\mathop \cup \limits_{i = 1}^{N} (\Omega (P_{i} ,\kappa + \tau ) \cap \Phi_{i} )\) and the proof is complete.
Proof of Theorem 2:
Applying a method similar to the proof of Theorem 1, we selected the following Lyapunov–Krasovskii functionals.
\(V(\eta ) = V_{i} (\eta ) = \eta^{T} (t)P_{i} \eta (t) + \int_{t - \tau (t)}^{t} {\eta^{T} (s)Q_{1} \eta (s)ds + \int_{t - \tau }^{t} {\eta^{T} (s)Q_{2} \eta (s)} } ds + \int_{ - \tau }^{0} {\int_{t + \theta }^{t} {\dot{\eta }^{T} (s)Z\dot{\eta }(s)ds} } d\theta .\) According to Lemma 4, 5, we can know that there exist any matrices \(W_{i}\),\(R_{i}\), such that the following inequality holds
where
Then, for \(\forall \eta \in \Omega (P_{i} ,\kappa + \pi ) \cap \Phi_{i} \subset L(\hat{N}_{i} ,H_{i} )\), the derivative of \(V_{i} (\eta )\) along the trajectory of the closed-loop system (12) with respect to time is
By using the free weighting matrix approach, for appropriate dimension matrices \(T_{1}\), \(T_{2}\) and \(T_{3}\),we can have the following equality:
Combining inequality (50) and equality (51), we can obtain
The treatment of equality (51) is the same as the treatment of equality (39) in Theorem 1.
Thus it is possible to obtain
And then multiplying inequality (24) from the left by \(\xi^{T} (t)\) and from the right by \(\xi (t)\) can result in
Combining inequality (53), (54) and (55), we can have
By the switching law (26), it is easy to see that the following inequality is true.
Combining inequality (53), (54), (55) and (56), we can easy obtain the following inequality
Integrating both sides of inequality (57) from \(t_{0}\) to \(t\) yields
Thus, we have
And according to the switching law (26), it can be seen that at the switching moment \(t_{k} (k \in Z^{ + } )\),\(V_{i} (\eta (t_{k} )) = V_{r} (\eta (t_{k} ))\), \(i, \, r \in I_{N}\), \(i \ne r\), and combining inequality (56) we can arrive at
With zero initial condition we can obtain
which means that the switched system (12) has the restricted \(L_{2}\)-gain from \(\omega\) to \(z\) over \(W_{\pi }^{2}\) less than or equal to \(\gamma\).This proof is completed.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Hao, C., Zhang, X. Anti-windup control of saturated switched delayed systems with actuator faults. Sci Rep 15, 12259 (2025). https://doi.org/10.1038/s41598-025-95658-8
Received:
Accepted:
Published:
Version of record:
DOI: https://doi.org/10.1038/s41598-025-95658-8