Deep spatio-temporal dependent convolutional LSTM network for traffic flow prediction

Abstract

With the rapid development of economy, the concept of intelligent transportation system (ITS) and smart city has been mentioned. The most important part of building them is whether they can accurately predict traffic flow. An accurate traffic flow forecast can help manage traffic, plan travel paths in advance, and rationally allocate public resources such as shared bicycles. The biggest difficulty in this task is how to solve the problem of spatial imbalance and the problem of temporal imbalance. In this paper, we propose a deep learning algorithm STDConvLSTM. Firstly, for spatial features, most scholars use convolutional neural networks (with fixed kernel size) to capture. However, this does not solve the problem of spatial imbalance, i.e. each region has a different size of correlated regions (e.g., the busy area has a wider range of correlated regions). In this paper, we design a space-dependent attention mechanism, which assigns a convolutional neural network with a different kernel size to each region through attention weights. Secondly, for time features, most scholars use time series prediction models, such as recurrent neural networks and their variants. However, in the actual forecasting process, the importance of historical data in different time steps is not the same. In this paper, we design a time-dependent attention mechanism that assigns different weights to historical data to solve the time imbalance. In the end, we ran experiments on two real-world data sets and achieve good performance.

Introduction

In recent years, with the rapid development of the economy, people’s demand for the construction of smart cities and intelligent transportation systems has become more and more intense. The most important point is to solve the problem of traffic flow prediction. By mining and analyzing traffic flow data, we can find out some potential traffic patterns and predict the future traffic flow. In simple terms, traffic flow forecasting predicts the future traffic flow based on the historical data of the city. It can provide reference value for mass travel and avoid congested areas. Moreover, it can provide a basis for traffic management and prevention by letting traffic managers know the traffic situation in advance.

However, since the problem of traffic flow prediction has become a hot topic, the biggest difficulties include two aspects, spatial dependence and time dependence. (i) Spatial dependence. We know that the crowd flow prediction of a certain area in a city will be affected by the surrounding area. Therefore, most scholars use convolutional neural network (CNN) to obtain spatial features. However, they ignore the problem that the extent to which each area is affected by the surrounding area is not fixed. For example, some shopping malls can be influenced by a larger area around them. (ii) Time dependence. Traffic flow data has the characteristics of closeness, period and trend. Closeness means that the closer the data is to the predicted data, the greater the impact. Period refers to the hidden patterns of traffic data for each day. Trend refer to the hidden patterns of traffic data for each week. These characteristics indicate that there are some data in the historical data that have a greater impact on the predicted results.

Early methods can be roughly divided into three categories. In the first category, prediction models were established based on spatial correlation. For example, Zhang et al.¹ and Thaduri et al.² used CNN for traffic flow prediction. In the second category, a prediction model is established based on time correlation. For example, Yang et al.³ and Tian et al.⁴ used LSTM for flow prediction. The third type is to build prediction models by combining temporal correlation and spatial correlation. For example, Narmadha et al.⁵ and Zhao et al.⁶ use convolutional neural network and long short-term memory network to model spatial and temporal features respectively. However, the first and second types of methods only consider spatial or temporal dependencies. Although the third kind of method considers the time dependence and space dependence, it does not consider the problem of temporal imbalance and spatial imbalance.

In this paper, we propose a spatio-temporal dependent attention convolutional LSTM network for traffic flow prediction, which uses the time-dependent attention mechanism and the space-dependent attention mechanism to solve the problem of temporal imbalance and spatial imbalance respectively. The main contributions of this paper are as follows:

• We design a selective kernel attention method called the space-dependent attention mechanism to address the spatial imbalance problem. Firstly, we feed the data into convolutional neural network of different kernel sizes. Secondly, we fuse all the output results. Finally, a multi-layer fully connected network is used to obtain multiple sets of attention vectors. Then, the output of the space-dependent attention mechanism is obtained by weighted summation of the attention vector and the output of the convolutional neural network.

• We designed a time-dependent attention mechanism to solve the problem of temporal imbalance. Specifically, firstly, the data is fed into the spatio-temporal feature extraction module. Then, each historical data is given a different weight by using a time-dependent attention mechanism on the previous time step of the predicted data and the historical data.

• The STDConvLSTM model was evaluated on two real-world data sets, and the experimental results show that the algorithm has competitive performance compared with the baseline algorithm.

The overall structure of the subsequent paper is as follows. Section “Related works” is related work. Section “STDConvLSTM framework” is the STDConvLSTM model. The experimental process is described in section “Experiments”. Finally, the conclusion is presented in section “Conclusion”.

Related works

The research of traffic flow prediction problem goes through the following processes. In the first stage, most scholars use time series prediction models to model traffic data, such as HA algorithm⁷, ARMA algorithm⁸, ARIMA algorithm and its variants^9,10,11,12, VAR algorithm¹³, etc. These algorithms cannot obtain nonlinear characteristics in traffic data. Kumar et al.¹⁴ designed a seasonal ARIMA algorithm for traffic prediction. Shahriari et al.¹⁰ proposed a joint model (E-ARIMA) for traffic prediction, and the results show that the prediction results are improved.

In the second stage, with the popularity of machine learning algorithms, SVM algorithm^15,16, Bayesian algorithm¹⁷, KNN algorithm¹⁸, SVR algorithm¹⁹, XGBoost algorithm²⁰ and other algorithms have been applied to the field of traffic prediction by many scholars. Compared with the first stage, the prediction accuracy is improved, but due to the limit of model capacity, only shallow features of traffic data can be captured. Luo et al.²¹ proposed a traffic prediction method combining KNN and LSTM network. Feng et al.²² proposed a multi-kernel SVM model based on spatio-temporal dependence for traffic prediction. In addition, some scholars have tried to model by combining time series prediction methods and machine learning methods. Chi et al.²³ proposed a joint model combining ARIMA and SVM. The ARIMA algorithm is used to predict the linear part of the time series, and the SVM is used to predict the nonlinear part.

In the third stage, with the development of hardware and the progress of data collection equipment, deep learning was gradually developed and applied to various fields. Deep learning has a deeper network, which has certain advantages in extracting deep features of traffic data. The early deep learning networks include FNN²⁴, DBN²⁵, etc. Traffic data is a kind of spatio-temporal sequence data, which has temporal correlation and spatial correlation. Firstly, for temporal dependencies, many researchers use recurrent neural networks²⁶ and their variants (LSTM²⁷, GRU²⁸) to capture. For example, Fu et al.²⁹ used GRU and LSTM to predict the future traffic flow, and the experimental results show that it is better than ARIMA model. Chen et al.³⁰ combined autoencoder and GRU algorithm for short-term traffic flow prediction. However, this way ignores the spatial correlation of traffic data. Secondly, many scholars use CNN³¹ to extract the spatial dependence of traffic flow data. For example, Zhuang et al.³² designed a framework combining CNN algorithm and BiLSTM algorithm for short-term traffic prediction. In addition, some scholars have applied convolutional recurrent neural network and its variants (ConvLSTM³³, ConvGRU) to simultaneously capture the temporal correlation and spatial correlation of traffic flow data. For example. He et al.³⁴ proposed a framework based on ConvLSTM algorithm and residual network for traffic prediction. The third stage method can extract the spatial dependence and time dependence of traffic flow data at the same time. However, it can not solve the problem of temporal imbalance and spatial imbalance.

Considering the spatio-temporal correlation of traffic data, Zhang et al.³¹ designed a deep learning framework. Firstly, the features are extracted from the data. After that, the spatial correlation analysis and temporal correlation analysis are carried out, and the STFSA algorithm is used to optimize the data selection. Finally, CNN is used to establish the prediction model. Ren et al.³⁵ proposed a deep learning model, GL-TCN. The core architecture of the model includes local spatial component, local time component, global trend component and external component. GL-TCN effectively captures the spatio-temporal dynamics of traffic flow through these four key components as well as the final fusion component. Fang et al.³⁶ proposed GSTNet model, which is based on multi-resolution spatio-temporal block and global correlation spatial module. The multi-resolution time module of GSTNet is introduced to capture short-term proximity and long-term periodicity in traffic flow. Zheng et al.³⁷ proposed a novel hybrid deep learning architecture for traffic flow prediction. The proposed model consists of one Conv-LSTM module and two Bi-LSTM modules. The Conv-LSTM module is composed of convolutional neural network and LSTM network. The convolutional neural network is used to extract the spatial features of traffic flow, and then connected to the LSTM network to obtain the temporal features of traffic flow. The Bi-LSTM module is used to extract the periodic features of traffic flow. Then, the spatio-temporal features and periodic features are fused into feature vectors through the feature fusion layer. Finally, the feature vectors are fed into two fully connected layers for performing the prediction. Sattarzadeh et al.³⁸ proposed a model that integrates ARIMA, Conv-LSTM, and bidirectional LSTM. The model uses the ARIMA model to extract linear regression features of traffic data, and the Conv-LSTM component combines CNN and LSTM to capture both spatial and temporal features.

In the fourth stage, as the attention mechanism was developed, it swept all fields in an instant and achieved good results. Hu et al.³⁹ proposed an innovative STADN model with Dynamic Spatio-temporal Network (DSTN), novel transform-gated LSTM (NTG-LSTM), and Spatial Attention mechanism (SAM) as core components. The DSTN aims to comprehensively deal with dynamic spatial and temporal dependencies in traffic prediction. The spatial dependence between regions is captured by Convolutional Neural Network (CNN), the flow gating mechanism is introduced to learn the dynamic spatial dependence, and the periodic offset attention mechanism is used to solve the problem of periodic time variation. On the other hand, NTG-LSTM focuses on reducing the interference of short-term mutation information on traffic prediction, retains long-term dependence information by changing the gating mechanism, and adjusts the gating output range to learn short-term dependence. Finally, SAM is used as a spatial attention mechanism to calculate the similarity between regions through the dynamic time warping distance, which realizes the sensitive capture of the mutual influence relationship between different regions. Huang et al.⁴⁰ proposed a deep learning method, which consists of convolutional neural network, PredRNN network, and attention mechanism. Among them, convolutional neural network is used to capture the spatial correlation of traffic data. The PredRNN network is used to simultaneously capture temporal and spatial dependencies. Finally, the attention mechanism is used to correlate the closeness, periodicity and trend of traffic data. Huang et al.⁴¹ used ConvLSTM network, CNN and attention mechanism to capture the spatio-temporal correlation of traffic data. Experimental results show that the best performance is achieved compared to the baseline algorithms.

Definition

Grid map

Fig. 1

Grid map (Source: Google Maps).

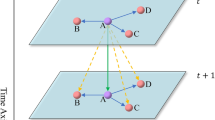
As shown in Fig. 1, we divide the city into $M\times N$ regions.

Statistics of crowd inflow and outflow in area $r_{2}$

Fig. 2

Crowd inflow and outflow (Source: Google Maps).

As shown in Fig. 2, we count the number of crowd inflows and the number of crowd outflows in each time interval region $r_{2}$. For example, given a time interval of half an hour, the number of crowd inflows in region $r_{2}$ is the sum of the number of crowds entering region $r_{2}$ from other regions except region $r_{2}$. The number of crowd outflows is the sum of the number of people entering other regions from region $r_{2}$.

Inflow matrix and outflow matrixs

Fig. 3

Inflow matrix and outflow matrix in New York City.

We can follow Definition 2 to obtain the number of crowd inflows and the number of crowd outflows in all regions in each time interval. In this way a tensor $X\in R^{2\times M\times N}$ can be obtained for each time interval. Figure 3 shows the data of one time interval.

Traffic flow prediction problem

We use historical observations ($\{\ldots ,{X_{t-i}},\ldots ,{X_{t-1}},{X_t}\}$) and predict the future crowd flow ($\hat{X}_{t + 1}$). ($X_{i}\in R^{2\times M\times N}$)

$$\begin{aligned} \hat{X}_{t + 1} = STDConvLSTM(\ldots ,{X_{t-i}},\ldots ,{X_{t-1}},{X_t}) \end{aligned}$$

(1)

STDConvLSTM framework

Fig. 4

STDConvLSTM framework.

Model input

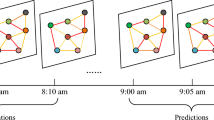
We select the data related to the prediction time respectively according to the inherent characteristics of traffic flow data (closeness, periodicity, trend). We predict the data for $t+1$ time intervals on day T. The closeness data selects previous ten time intervals of the predicted data $\left\{ X_{t-9}^{day=T},X_{t-8}^{day=T},\ldots ,X_{t}^{day=T} \right\}$. The three days before the predicted data are selected as period data, and the data from the previous time interval to the next time interval of the predicted data are selected for each day (for example, the data of day $T-1$ is $\left\{ X_{t}^{day=T-1},X_{t+1}^{day=T-1},X_{t+2}^{day=T-1} \right\}$). We select the data from day $T-7$ as the trend data, specifically, the data from the previous time interval to the next time interval of the predicted data $\left\{ X_{t}^{day=T-7},X_{t+1}^{day=T-7},X_{t+2}^{day=T-7} \right\}$. From the timeline presented in Fig. 4, the specific input data can be clearly discerned.

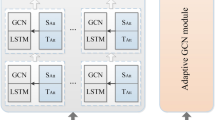
Spatio-temporal feature extraction module

Figure 4 shows the overall framework of the STDConvLSTM model. Firstly, each input data ($X_{i}$) is fed into a multi-layer convolutional neural network to extract the spatial dependence of the data, as shown in Fig. 5.

Fig. 5

Multi-layer convolutional operation (Convs).

The formulation of the multi-layer convolution operation is as follows:

$$\begin{aligned} I_{i}^{\left( k \right) }=ReLU\left( W_{i}^{\left( k \right) }*I_{i}^{\left( k-1 \right) } +b_{i}^{\left( k \right) }\right) , \end{aligned}$$

(2)

where k denotes the number of convolution layers, $I_{i}^{(k)}$ denotes the output of the ith data in the kth convolutional layer, $I_{i}^{(k-1)}$ denotes the output of the ith data in the $(k-1)$th convolutional layer, ReLU() represents the Rectified Linear Unit, w and b are the learning parameters, and $I_{i}^{0}=X_{i}$.

Fig. 6

Selective kernel network and residual network.

Secondly, we feed $\left\{ I_{1},I_{2},\ldots I_{i},\ldots \right\}$ into the SK (Selective Kernel) network and the residual network, Fig. 6 shows the detailed process. For each data $I_{i}$, first, convolutional neural network with kernel size of $1\times 1$, $3\times 3$, $5\times 5$, $7\times 7$ is used to perform convolution operation on the data respectively, and the padding parameter is set to keep the output dimension consistent. Second, the results $\left\{ U_{1},U_{2},U_{3},U_{4}\right\}$ are fused by using the element-wise summation operation to obtain U (the data dimension is $C\times H \times W$). After that, we perform the global average pooling operation on the H dimension and the W dimension to obtain S, whose dimension is the number of channels. After that, we use the fully connected network (FC) to reduce the dimension to get Z. After that, the fully connected network and Softmax operation are used again to obtain the attention vectors $\alpha _{1}$, $\alpha _{2}$, $\alpha _{3}$, $\alpha _{4}$, and do element-wise multiplication with $\left\{ U_{1},U_{2},U_{3},U_{4}\right\}$ respectively. After that, the element-wise addition operation is used on the four results to obtain the output V of the SK network. To preserve the characteristics of the original data, we use a residual network. In the SK network, space-dependent attention mechanism is used to assign different weights to convolutional neural networks with different kernel sizes. In this process, we solve the problem of data imbalance in space. The formula for this process is as follows:

$$\begin{aligned} & U = U_{1}\oplus U_{2}\oplus U_{3}\oplus U_{4}, \end{aligned}$$

(3)

$$\begin{aligned} & S=Pooling(U), \end{aligned}$$

(4)

$$\begin{aligned} & Z=FC(S), \end{aligned}$$

(5)

$$\begin{aligned} & \alpha _{1},\alpha _{2},\alpha _{3},\alpha _{4} =Softmax(FC(Z)), \end{aligned}$$

(6)

$$\begin{aligned} & Z=\alpha _{1}\otimes U_{1} \oplus \alpha _{2}\otimes U_{2} \oplus \alpha _{3}\otimes U_{3} \oplus \alpha _{4}\otimes U_{4}, \end{aligned}$$

(7)

$$\begin{aligned} & T=I+V, \end{aligned}$$

(8)

where $\oplus$ is element-wise addition operation, Pooling is global average pooling operation, FC is fully connected network, $\otimes$ is element-wise multiplication operation.

Fig. 7

ConvSLTM unit.

Fig. 8

Multi-layer ConvLSTMs.

The output data $\left\{ T_{1},T_{2},\ldots T_{i},\ldots \right\}$ can be obtained after the input data $\left\{ I_{1},I_{2},\ldots I_{i},\ldots \right\}$ passes through the SK network and the residual network. We put the closeness data, period data and trend data into the ConvLSTM network to capture the spatio-temporal characteristics of traffic data. The ConvLSTM network is a model proposed by Shi et al.⁴² for precipitation prediction, which integrates the characteristics of spatial feature extraction of convolutional neural network and the characteristics of temporal feature extraction of LSTM network, as shown in Fig. 7. It mainly controls the transformation degree of data through input gate ($i_{t}$), forget gate ($f_{t}$) and output gate ($o_{t}$). The input gate controls how much new information is entered, the forget gate controls how much old information is discarded, and the output gate controls the output of the new state. Compared with the LSTM network, it replaces the multiplication operation in the data transmission process with the convolution operation, and the specific formula is as follows:

$$\begin{aligned} & i_{t}=\sigma \left( W_{xi}*T_{t}+ W_{hi}*H_{t-1}+b_{i}\right) , \end{aligned}$$

(9)

$$\begin{aligned} & f_{t}=\sigma \left( W_{xf}*T_{t}+ W_{hf}*H_{t-1}+b_{f}\right) , \end{aligned}$$

(10)

$$\begin{aligned} & o_{t}=\sigma \left( W_{xo}*T_{t}+ W_{ho}*H_{t-1}+b_{o}\right) , \end{aligned}$$

(11)

$$\begin{aligned} & C_{t}=f_{t}\odot C_{t-1}+i_{t}\odot tanh\left( W_{xc}*T_{t}+ W_{hc}*H_{t-1}+b_{c}\right) , \end{aligned}$$

(12)

$$\begin{aligned} & H_{t}=o_{t}\odot tanh\left( C_{t} \right) , \end{aligned}$$

(13)

in which $*$ denotes the convolutional operation, $\odot$ denotes the Hadamard product, $T_{t}$ represents the input data of tth time step, $H_{t}$ represents the output data of tth time step, $C_{t}$ represents the cell state of tth time step, $\sigma$ is Sigmoid function, tanh is tanh function, $W_{i}$ and biases $b_{i}$ are the learning parameter.

For the multi-layer ConvLSTM network, the output of the previous layer serves as the input of the subsequent layer, as shown in the Fig. 8.

Temporal-dependent attention module

Fig. 9

Closeness attention module.

In this subsection, we solve the problem of temporal imbalance through the temporal-dependent attention mechanism. We respectively use the data of the previous time interval of the prediction data and the closeness data, the period data, and the trend data for the temporal attention operation.

As shown in the Fig. 9, for the closeness attention module, we use the data of the previous time interval of the prediction data ($H_{t}^{day=T}$) and the output data ($\left\{ H_{t-9}^{day=T},H_{t-8}^{day=T},\ldots ,H_{t-1}^{day=T} \right\}$) of the closeness data after passing through the spatio-temporal feature extraction module for attention operation. First, we stretch the data to $\left\{ \bar{H} _{t-9},\bar{ H} _{t-8},\ldots ,\bar{H} _{t}\right\}$ using the Flatten operation, and use matrix multiplication on them to get weight vectors $\left\langle \alpha _{t-9},\alpha _{t-8},\ldots ,\alpha _{t-1} \right\rangle$. After that, the Softmax operation is used to normalize them, and the result and $\left\{ H_{t-9}^{day=T},H_{t-8}^{day=T},\ldots ,H_{t-1}^{day=T} \right\}$ are weighted and summed to obtain the final closeness attention vector ($A_{c}$). The formula for the specific implementation is given below:

$$\begin{aligned} & \alpha _{k}=\bar{H_{t}}\times \left( \bar{H}_{k} \right) ^{T}, \;\;\;\;\;\;\;\;\;\; \forall k\in [ t-9,t-1 ] \end{aligned}$$

(14)

$$\begin{aligned} & \bar{\alpha } _{k}=\frac{exp\left( \alpha _{k} \right) }{\sum _{k=1}^{t-1}exp\left( \alpha _{k} \right) }, \;\;\;\;\;\;\; \forall k\in [ t-9,t-1 ] \end{aligned}$$

(15)

$$\begin{aligned} & A_{c}=\sum _{k=t-9}^{t-1}\bar{\alpha _{k}}H_{k}, \end{aligned}$$

(16)

where $\times$ represents the matrix product, $\left( \cdot \right) ^{T}$ means transpose operation, $A_{c}$ represents closeness attention tensor.

For the period attention module, we use the same way for the data $H_{t}^{day=T}$ and $\left\{ X_{t}^{day=T-3},\ldots ,X_{t}^{day=T-2},\ldots ,X_{t+2}^{day=T-1} \right\}$ to obtain the period attention vector ($A_{p}$). For the trend attention module, we can use the same method for data $H_{t}^{day=T}$ and $\left\{ X_{t}^{day=T-7},X_{t+1}^{day=T-7},X_{t+2}^{day=T-7}\right\}$ to obtain the trend attention vector ($A_{t}$).

Finally, we aggregate $A_{c}$, $A_{p}$, $A_{t}$ and $H_{t}^{day=T}$, and then feed them into a multi-layer deconvolution neural network to obtain the output of the model.

Experiments

Dataset preprocessing

The TaxiNYC dataset divides the city of New York into a 10$\times$20 grid map. The BikeNYC dataset divides the city of New York into a 21$\times$12 grid map. The original data are travel records. We follow the calculation method in section “Definition” to calculate the crowd inflow matrix and the crowd outflow matrix for each time interval. In this paper, we use the BikeNYC and TaxiNYC datasets for subsequent experiments. The TaxiNYC dataset contains 60 days of data (from 1/1/2015 to 3/1/2015). We use 40 days of data, 10 days of data, 10 days of data as training set, validation set, and test set, respectively. The BikeNYC dataset contains six months of data (from 4/1/2014 to 9/30/2014). We use 4 months of data, 1 month of data, 1 month of data as training set, validation set and test set, respectively. Before putting the data into the model, we scale the data to [0, 1] using Min-Max normalization.

The maximum value, minimum value, mean value and standard deviation of TaxiNYC dataset are 1289, 0, 38.8, and 103.9. The maximum value, minimum value, mean value and standard deviation of BikeNYC dataset are 737, 0, 10.7, and 30.3.

Compared models

In this paper, we use the following comparison models.

• (1) HA⁷: HA uses the historical average for the prediction of future values.

• (2) ARMA⁸: ARMA represents a fundamental methodology in time series analysis, which is based on AR model and MA model.

• (3) CopyYesterday: CopyYesterday uses yesterday’s crowd flow as the predicted value.

• (4) CNN: CNN mainly perform the prediction of future values by capturing spatial features.

• (5) ConvLSTM⁴²: ConvLSTM integrates the advantages of LSMT model and CNN for spatio-temporal feature extraction. The experiment used four ConvLSTM layers, each layer of convolution operation using 32 filters with a kernel size of 3.

• (6) ST-ResNet¹: ST-ResNet uses CNN and residual connection to predict future values. The experiment used two layers of residual units, each convolution operation using 32 filters with a kernel size of 3.

• (7) PCRN⁴³: PCRN uses ConvLSTM to build a pyramid structure to predict future values. The experiment used three ConvLSTM layers, each convolution operation using 32 filters with kernel size of 3. In addition, the convolution kernel size when data is aggregated is set to 1.

• (8) DeepSTN+⁴⁰: DeepSTN+ is an improved version of ST-ResNet. In the experiment, the ResPlus unit is set to 2, the number of channels for ConvPlus is set to 2. The separated channels are set to 8. The number of filters for the convolution kernel is set to 32 with a kernel size of 1. The dropout rate is set to 0.1.

• (9) MAPredRNN⁴⁰: MAPredRNN algorithm uses the attention module to extract the features of traffic flow, and adopts PredRNN to capture the space-time characteristics of traffic flow. In the experiment, the convolution module, ConvLSTM module and deconvolution module were all set to two layers, and the convolution kernel size was all 3.

• (10) SE-MAConvLSTM⁴⁵: SE-MAConvLSTM algorithm is composed of ConvLSTM module and Squeeze-and-Excitation network. The ConvLSTM module has two layers and the convolution kernel size is 3.

In this paper, RMSE is used for model evaluation. The formula is as follows:

$$\begin{aligned} RMSE=\sqrt{\frac{1}{N}\sum _{i}\sum _{j}\left( x_{ij}-\hat{x_{ij}} \right) ^{2}}, \end{aligned}$$

(17)

where $x_{ij}$ and $\hat{x_{ij}}$ denote the true and predicted values, respectively, N denotes the number of all predicted regions.

The Settings of the experimental parameters are shown in Table 1.

Table 1 Parameter of STDConvLSTM model.

Fig. 10

The training and validation process of STDConvLSTM on two dataset.

The convergence of STDConvLSTM

Figure 10a, b show the training process and validation process of the BikeNYC dataset and TaxiNYC dataset, respectively. We can see from the figure that the RMSE of the training set keeps decreasing as the number of epochs increases. The RMSE on the validation set goes down, flattens out, and then goes up a little bit. This indicates that the STDConvLSTM model achieves convergence on both datasets.

Performance comparison

Table 2 Comparison of different algorithms.

Table 2 shows our experimental results on the two datasets. From the table, we can see that the MAPredRNN model has the best experimental results on the TaxiNYC dataset, and the RMSE of the STDConvLSTM model is 0.014 higher than it. On the BikeNYC dataset, the best result is achieved on the STDConvLSTM model with an RMSE of 6.206.

Traditional traffic prediction methods, such as HA, ARMA, Copyyesterday, have relatively poor performance compared with deep learning methods (TaxiNYC data sets of RMSE were 21.833, 17.232, 18.453. BikeNYC data sets of RMSE were 15.989, 16.518, 14.64.). The fundamental reason lies in the limited ability of the model to capture nonlinear features.

Due to the increased ability to capture nonlinear features, the overall results of deep learning methods show an improved state. CNN adds the ability to capture spatial features and achieves RMSE of 16.881 and 13.651 on TaxiNYC dataset and BikeNYC dataset, respectively. Since the ConvLSTM model can capture both temporal and spatial features, the performance improvement is more obvious (RMSE of 12.533 and 6.821 on the two datasets, respectively). The residual connection is added to the ST-ResNet network, which can retain the data features of each layer. Compared with the ConvLSTM model, the performance of the ST-ResNet network is improved by 3.9% and 4.1% on the two data sets, respectively.

DeepSTN+ is an improved version of the ST-ResNet model, and the overall performance is similar. MAPredRNN adds an attention mechanism, which improves the performance compared to the previously described models. Our proposed model STDConvLSTM model adds a spatial attention module and a temporal attention model, and the performance is also improved. Compared to the MAPredRNN model, the STDConvLSTM model has a performance degradation of 0.1% on the TaxiNYC dataset and a performance improvement of 2.6% on the BikeNYC dataset.

Model variant experiments

In this subsection, we do two sets of variant experiments to test the effectiveness of the module. First, we tested whether the residual connection is valid for the experimental results.

• STDConvLSTM-NoResNet: We remove the residual connections in the SK network.

• STDConvLSTM.

Table 3 Results on the validity of the residual connection.

From Table 3, we can see that the performance on both datasets improves after adding residual connections. This result shows that the residual connection module is effective for improving the performance of the model.

Second, we tested whether adding more data would improve model performance. Due to the closeness, period and trend of traffic data, we increase the data set one by one.

• STDConvLSTM-C: We only use closeness data for our experiments..

• STDConvLSTM-CP: We use both closeness data and period data for our experiments..

• STDConvLSTM: We conduct experiments using closeness data, period data and trend data.

Table 4 Experimental results for progressively increasing datasets.

From Table 4, we can see that the performance of the model is improved step by step by adding period data and trend data. This result shows that the addition of period data and trend data is effective for improving model performance.

A case study

Fig. 11

A case study of STDConvLSTM on the TaxiNYC data set.

Fig. 12

A case study of STDConvLSTM on the BikeNYC data set.

When the STDConvLSTM model achieves the best performance, Figs. 11 and 12 show a case on the TaxiNYC dataset and BikeNYC dataset, respectively. The four images correspond to the true values (inflow matrix/outflow matrix) and the predicted (inflow matrix/outflow matrix) values. As you can see from the picture, the predicted and true values are relatively similar.

Error analysis

Table 5 Error analysis of the TaxiNYC dataset.

Table 6 Error analysis of the BikeNYC dataset.

We give the maximum values of all grid errors and the standard deviations of all grid errors for our proposed algorithm and the comparison algorithm in Tables 5 and 6. As can be seen from the table, STDConvLSTM algorithm has lower maximum error and standard deviation.

Conclusion

In this paper, we focus on the temporal imbalance and spatial imbalance of traffic flow data, and we propose a spatio-temporal dependent convolutional LSTM network. For the problem of time imbalance, we propose a time-dependent attention mechanism, which is realized by giving different weights to historical data. For the problem of spatial imbalance, convolutional neural networks with different kernel sizes are mainly used and different weights are assigned to different convolutional neural networks through the spatial attention mechanism. Experiments on two real-world data sets show that the model achieves good performance.

In the future work, we try to propose better strategies to solve the temporal imbalance problem and the spatial imbalance problem.