Metaparameter optimized hybrid deep learning model for next generation cybersecurity in software defined networking environment

Abstract

The Software Defined Networking (SDN) method has evolved to project future systems and collect novel application needs for several years. SDN delivers sources for enhancing management and system control by splitting data and control plane, and the control logic is federal in a controller. Conversely, the central logical control is a perfect objective for malicious assaults, chiefly Distributed Denial of Service (DDoS) threats. Deep Learning (DL) is one of the influential models useful in cyber-security, and numerous Network Intrusion Detection (NIDS) were developed in current studies. Some researchers have specified that deep neural networks (DNN) subtly perceive adversarial assaults. These attacks are examples of definite worries that cause DNNs to misclassify. Therefore, this manuscript develops a novel Cybersecurity in Software-Defined Networking utilizing Hybrid Deep Learning Models and a Binary Narwhal Optimizer (CSSDN-HDLBNO) approach. The presented CSSDN-HDLBNO approach provides a scalable and effective solution to safeguard against evolving cyber threats in DDoS attacks within the SDN environment. Initially, the CSSDN-HDLBNO approach utilizes min-max normalization to scale the features within a uniform range using data normalization. Furthermore, the binary narwhal optimizer (BNO)-based feature selection is accomplished to classify the most related features. For the DDoS attack classification process, the attention mechanism with convolutional neural network and bidirectional gated recurrent units (CNN-BiGRU-AM) is employed. To ensure optimal performance of the CNN-BiGRU-AM model, hyperparameter tuning is performed by utilizing the seagull optimization algorithm (SOA) model to enhance the efficiency and robustness of the detection system. A wide range of simulation analyses is implemented to certify the improved performance of the CSSDN-HDLBNO technique under the DDoS SDN dataset. The performance validation of the CSSDN-HDLBNO technique portrayed a superior accuracy value of 99.40% over existing models in diverse evaluation measures.

Introduction

Conventional system structures could not tackle necessities like accessibility, high-speed connection, higher bandwidth, virtualization, cloud computing, and dynamic management¹. Consequently, SDNs with a programmable, dynamic structure and flexibility replaced classical networks. The main intention of SDN is to decouple the plane of control from advancing planes². In addition, this structure enables more adaptable network management for the network operator. In SDN, the control plane might contain one or more controllers depending upon the utilization and size of the network. OpenFlow is a prominent protocol that creates a secured connection between the network controller and devices to verify the finest path for the several applications extending on top of the controller³. Despite several advantages SDN offers, security is still the main problem between the research community and enterprises. While specific security attacks were widespread in computer networks, SDN has transported its security attacks. There are diverse attack vectors recognized with SDN. The primary attack vector for SDN is DDoS threats⁴. The main intention of the threat is to generate computing sources inaccessible to legal users. This threat generally exceeds one bot, intruded by software from harmful code. The primary process is easier; the DDoS threat can rapidly spread and cause massive damage to the network, but the security process is complicated. While the network administrator can recognize probable threats, it might not be sensible to account for simultaneous attacks in the real world⁵. Hereafter, it is vital to execute specific security guidelines on the controller. Thus, well-organized mitigation rules and detection methods is intended for future network structures like SDN. Subsequently, the controller is the vital, intelligent portion of the SDN; multiple methods like Neural Networks (NN) and Machine Learning (ML) might be employed to utilize network security⁶.

Dual diverse methods have been followed by the Intrusion Detection System (IDS) to recognize DDoS attacks, such as anomaly- and signature-based recognition approaches. DL and ML methods are powerful devices that offer the cognitive ability to identify security violations. It has undergone substantial development owing to its processing and storage abilities and the accessibility of massive datasets. DL and ML methods can assist by employing the network behaviour absorbed from historical data and offer forecasts for future packets depending on the training dataset⁷. ML-based approaches have shown the classification of attack and legal traffic. ML-based methods can offer more effectual, smarter, and dynamic solutions for SDN. To guarantee security, recognizing DDoS threats is essential for promptly captivating the required measure. Processing SDN data movement with the ML-based DDoS attack recognition method incorporated into the SDN framework can result in a self-determining system that could act and learn⁸. Furthermore, SDN having an incorporated ML application might be a reference method to form a secured framework in research offering the incorporation of 5G networks. As network infrastructures grow increasingly complex, conventional systems face difficulty to meet the demands of scalability, high throughput, and flexible management⁹. With the swift adoption of cloud computing and virtualization, new approaches are required for maintaining performance and security in dynamic environments. SDN provides a promising solution by giving centralized control and improved programmability, allowing for effectual management and monitoring. However, the growing threat of cyber-attacks, specifically DDoS attacks, highlights the requirement for advanced detection systems to protect these modern networks. The integration of DL methods with optimized algorithms gives an effective way to address these security challenges in SDN environments¹⁰.

This manuscript develops a novel Cybersecurity in Software-Defined Networking utilizing Hybrid Deep Learning Models and a Binary Narwhal Optimizer (CSSDN-HDLBNO) approach. The presented CSSDN-HDLBNO approach provides a scalable and effective solution to safeguard against evolving cyber threats in DDoS attacks within the SDN environment. Initially, the CSSDN-HDLBNO approach utilizes min-max normalization to scale the features within a uniform range using data normalization. Furthermore, the binary narwhal optimizer (BNO)-based feature selection is accomplished to classify the most related features. For the DDoS attack classification process, the attention mechanism with convolutional neural network and bidirectional gated recurrent units (CNN-BiGRU-AM) is employed. To ensure optimal performance of the CNN-BiGRU-AM model, hyperparameter tuning is performed by utilizing the seagull optimization algorithm (SOA) model to enhance the efficiency and robustness of the detection system. A wide range of simulation analyses is implemented to certify the improved performance of the CSSDN-HDLBNO technique under the DDoS SDN dataset. The major contribution of the CSSDN-HDLBNO technique is listed below.

• The CSSDN-HDLBNO model scales the input data within a specific range, which enhances the model’s stability and convergence during training. This pre-processing step ensures that features with diverse scales do not disproportionately influence the model. Standardizing the data assists the model in learning more effectively, resulting in improved overall performance.

• The CSSDN-HDLBNO technique utilizes the BNO model to choose the most relevant features from high-dimensional datasets, enhancing the model’s performance. Mitigating overfitting ensures the model generalizes better, resulting in improved accuracy. This approach effectively narrows the features, making the training process more efficient and robust.

• The CSSDN-HDLBNO methodology implements the CNN-BiGRU-AM model to capture spatial and temporal patterns in network traffic. The AM model improves this by concentrating on critical features, enhancing the method’s capability to detect DDoS attacks precisely. This integration ensures effective and precise attack classification based on complex sequential data.

• The CSSDN-HDLBNO method utilizes SOA to fine-tune the hyperparameters of the CNN-BiGRU-AM model, improving its overall performance. By effectually exploring the hyperparameter space, SOA assists in detecting optimal settings, mitigating training time and enhancing accuracy. This optimization process ensures the model delivers robust results for DDoS attack classification.

• The integration of CNN-BiGRU-AM for DDoS classification, BNO-based feature selection, and SOA-based hyperparameter tuning presents a novel hybrid approach that crucially enhances classification accuracy and efficiency. This method utilizes the merits of DL, optimized feature selection, and fine-tuned hyperparameters to deliver real-time, precise detection of DDoS attacks in network traffic. The novelty is in incorporating these advanced techniques to create a more effectual and adaptable solution for dynamic cybersecurity challenges.

Related works

Hammadeh et al.¹¹ projected an advanced hybrid method incorporated within the ONOS controller. This method associates the ML model with an entropy-based investigation to improve the identification of lower and higher volumes of DDoS threat over dual classification tasks. By utilizing the ability to ONOS controller, this work progresses intrusion detection, strengthening resilience and deeper knowledge of network patterns against developing cyber-attacks. In¹², an ML-based method was introduced. This work also incorporates an ML-based recognition segment into the controller and setup surroundings. Traffic is taken by a logging method inserted into the SDN-WISE controller, which writes network logging into a pre-processed log file and changes into a dataset. The ML DDoS recognition segment is incorporated into the SDN-WISE controller to categorize SDN-IoT network packets. In¹³, an innovative hybrid method that associates statistical approaches with ML capability to address the mitigation and DDoS detection threat in SDN surroundings was developed. The statistical stage of the method employs an entropy-based recognition method. In contrast, the ML stage applies a clustering method to examine the effect of active consumers on the entropy of a system. Wang et al.¹⁴ employ an ML approach to categorize SDN traffic as both normal and attack traffic. Afterwards, the feature selection approach, like the wrapper-based and filter-based Fisher score approaches, used the analysis of variables (ANOVA) f-test for finely-granulated recognition. Next, a rule-based recognition approach utilizing the Renyi joint entropy model is applied to identify DDoS threats in the SDN controller. In¹⁵, multiple unsupervised or semi-supervised ML methods are introduced to oppose prolific abnormal data on a computer network. Mainly, five unsupervised ML methods, comprising Deep Belief Network (DBN), Isolation Forest (I-Forest), Generative Adversarial Network (GAN), One-Class Support Vector Machine (OCSVM), and Restricted Boltzmann Machine (RBM) are applied. This work utilizes these methods individually and associates to analyze their anomaly detection performance. Liu et al.¹⁶ projected an ML and feature-engineering-based method to identify DDoS threats in SDNs. Initially, the CSE-CIC-IDS2018 database was normalized and cleaned, and the optimum feature sub-set was created by utilizing an enhanced binary grey wolf optimizer model. Subsequently, the optimum feature sub-set was tested and trained on SVM, RF, XGBoost, DT, and k-NN ML models, from where the finest classifier was chosen for DDoS threat recognition. In¹⁷, supervised ML methods, including DT, Logistic Regression (LR), SVM, AdaBoost, and RF, and unsupervised methods like K-means clustering were utilized to categorize Telnet, Domain Name System (DNS), Voice traffic flow, and Ping simulated employing the Distributed Internet Traffic Generator (D-ITG) device. It efficiently classifies and manages kinds of traffic depending on their application. Mozo et al.¹⁸ developed a complete investigation to incorporate these ML modules in a distributed setup to offer secured end-to-end protection against cyber-attacks. Additionally, to tackle the crucial energy consumption problem in telecom manufacturing, the research harnesses entirely possible advanced Green AI models to enhance the complexity and size of ML methods, minimize their energy utilization, and maintain their capability to detect possible cyber-attacks precisely.

Sumathi and Rajesh¹⁹ propose a hybrid GBS-based IDS, integrating Back Propagation Network (BPN), Self Organizing Map (SOM), and Grey Wolf Optimizer (GWO) models for cloud computing to improve intrusion detection. Feature selection uses a correlation-based approach, with hyperparameters fine-tuned through GWO. Perumal and Arockiasamy²⁰ introduce an SDN-based DDoS attack detection and mitigation system for IoT using data cleaning, feature selection, a two-layer deep architecture with classifiers, and the MUAE optimization method for improved QNN performance. Sokkalingam and Ramakrishnan²¹ present a hybrid ML-based IDS model. Feature selection is performed by utilizing 10-fold cross-validation, and SVM parameters are optimized with hybrid Harris Hawks optimization (HHO) and particle swarm optimization (PSO) methods. Manivannan and Senthilkumar²² propose an adaptive recurrent neural network-based fox optimizer (ARNN-FOX) method for effectual network intrusion detection, using gray level co-occurrence matrix (GLCM) for feature selection and the FOX algorithm to adjust ARNN hyperparameters for improved security. Sumathi, Rajesh, and Lim²³ utilize a long short-term memory (LSTM) network with an autoencoder-decoder strategy, optimizing parameters using hybrid HHO and PSO models. Yzzogh and Benaboud²⁴ propose a DDoS attack detection approach by utilizing multiple k-means models for clustering and the naive Bayes (NB) method for binary classification. Sumathi, Rajesh, and Karthikeyan²⁵ improve DDoS attack detection by utilizing ML-based IDS models, integrating C4.5, SVM, and k-nearest neighbour (KNN) with feature selection and 10-fold cross-validation to achieve enhanced accuracy and performance. Ali et al.²⁶ propose a Genetic Algorithm Wrapper Feature Selection (GAWFS) technique for feature selection, incorporating Chi-squared, GA, and correlation methods. Detection accuracy is improved using a stacking ensemble of MLP, SVM, and RF. Sumathi and Rajesh²⁷ detect and mitigate DDoS attacks by utilizing Artificial Neural Network (ANN) methods, namely BPN and Multilayer perceptron (MLP), with feature selection and tuning through a hybrid HHO-PSO methodology. Alotaibi et al.²⁸ propose an Enhancing Software-Defined Networking Security with Deep Learning and Hybrid Feature Selection (ESDNS-DLHFS) technique for protecting data privacy in SDN-assisted IoT platforms by utilizing hybrid crow search arithmetic optimization algorithm (HCSAOA) for feature selection, deep bidirectional-LSTM (Deep BiLSTM) for intrusion detection, and enhanced artificial orca’s algorithm (EAOA) for hyperparameter tuning. Sumathi and Rajesh²⁹ develop and improve methods for quickly and accurately detecting DDoS attacks in network transactions employing ML techniques. Chauhan and Atulkar³⁰ utilize the Jaya Optimization approach for feature selection in SD-IoT’s IDS and show that training an LGBM classifier with selected features improves performance compared to using all features. Muthamil Sudar and Deepalakshmi³¹ aim to improve Software-Defined Network (SDN) security by detecting and mitigating DDoS attacks through a two-level mechanism: an entropy-based technique for early detection and a C4.5 ML technique for attack confirmation and packet dropping. Jambulingam et al.³² propose a hybrid approach by integrating MobileNetV2, ShuffleNet V2, and Lion Optimization (LO) models for feature selection. Muthamil Sudar and Deepalakshmi³³ aim to secure SDN by utilizing an intrusion detection mechanism in both the control and data planes, employing flow-based and signature-based systems with ML and rule-based classifiers to detect malicious activities. Presekal et al.³⁴ introduce a hybrid DL methodology by integrating graph convolutional LSTM for anomaly detection in power system OT networks, giving robust detection of cyber-attacks and real-time attack localization. Sudar et al.³⁵ propose an ML-based TCP Flooding Attack Detection (ML-TFAD) technique by using proxy-based mechanisms and the C4.5 decision tree (DT) model to detect SYN and ACK flood attacks before reaching the server. Nissar, Naja, and Jamali³⁶ incorporate cost-sensitive learning and Optuna-driven hyperparameter optimization to improve DoS attack detection on the CAN network, minimizing misclassification costs and improving model efficiency. Arun Prasad, Mohan, and Vinoth Kumar³⁷ propose the Hybrid Metaheuristics with Deep Learning Enabled Cyberattack Prevention (HMDL-CAP) model for SDN, integrating spiral dynamics optimization for feature selection, a hybrid convolutional neural network with recurrent neural network (HCRNN) for intrusion detection, and pelican optimization algorithm (POA) for hyperparameter tuning, improving cyberattack prevention. To enhance threat mitigation, Pasupathi, Kumar, and Pavithra³⁸ introduce three packet marking methods: Linear, Remainder, and Probabilistic. The model incorporates ML methods such as LR, Random Forest (RF), SVM, and others, with rigorous data pre-processing to enhance network security and model performance.

Despite the improvements in DDoS detection and mitigation utilizing ML and hybrid methods in SDN and IoT environments, various limitations still exist. Many existing techniques are computationally intensive, affecting real-time detection capabilities. Furthermore, some models suffer from low generalizability across several attack types and network conditions. Feature selection remains challenging, with some methods failing to optimize feature sets, resulting in lesser detection accuracy. The dependency on massive datasets for training and model evaluation also raises concerns about scalability and robustness. Moreover, existing methods mainly concentrate on specific attack types, neglecting the detection of emerging or novel attack vectors. There is also a requirement for more effectual, scalable, and generalized models capable of adapting to growing cyber threats.

Materials and methods

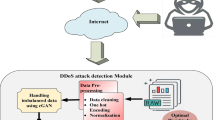
This manuscript develops a novel CSSDN-HDLBNO method. The main intention of this method is to provide scalable and effective solutions to safeguard against evolving cyber threats in DDoS threats within the SDN environment. The developed CSSDN-HDLBNO method contains various stages: min-max normalization, BNO-based feature selection, CNN-BiGRU-AM-based classification process, and SOA-based hyperparameter tuning. Figure 1 represents the whole working process of the CSSDN-HDLBNO model.

Fig. 1

Working process of CSSDN-HDLBNO method.

Stage 1: min-max normalization

At the primary phase, the CSSDN-HDLBNO approach utilizes min-max normalization to scale the features within a uniform range using data normalization³⁹. This is a prevalent technique for feature scaling, specifically when the data has varying ranges. It converts the data into a fixed range, usually [0, 1], making it appropriate for models sensitive to the scale of input features, such as neural networks and distance-based algorithms. The merit of choosing this model over other techniques, such as Z-score normalization, is its simplicity and efficiency. It ensures that all features contribute equally to the learning process of the model, avoiding the dominance of features with larger scales. Furthermore, it is computationally inexpensive, making it ideal for real-time applications with significant speed. However, It is particularly efficient when the data distribution is not Gaussian, unlike standardization methods, which assume normality.

Min-max normalization is a pre-processing system generally employed in DDoS attack recognition within SDN to naturally measure input features into a fixed range [0, 1]. This certifies that every feature donates similarly to the ML method, averting any solitary feature from controlling owing to its more excellent mathematical range. By altering raw data, min-max normalization improves the recognition model performance, making it more accurate and stable. In the background of DDoS attack recognition, the model can effectively distinguish between malicious and normal traffic patterns. This pre-processing phase is vital in decreasing outliers’ effects and enhancing recognition techniques’ training speed. Generally, min-max normalization is crucial in improving the efficiency and robustness of DDoS recognition in SDN environments.

Stage 2: feature selection using the BNO method

Next, the BNO-based feature selection was applied to classify the most related features⁴⁰. This nature-inspired optimization algorithm outperforms feature selection by effectively exploring the search space for optimal solutions. It is specifically efficient in selecting a subset of relevant features, mitigating the dimensionality of the dataset, and enhancing model performance by eliminating redundant or irrelevant features. The merit of choosing BNO over other techniques, namely Genetic Algorithms or PSO, is its fast convergence and capability for handling binary problems, which is ideal for selecting discrete features. Moreover, its balance between exploration and exploitation enables it to avert local optima, making it more robust and accurate in finding the optimum feature subsets. This results in faster model training times and enhanced generalization capability. Figure 2 illustrates the BNO framework.

Fig. 2

Structure of the BNO model.

This section defines the Narwhal Optimizer (NO), a simulation and mathematical method. The Narwhal is an extraordinary marine animal, recognized for its distinctive longer, spiral tusk. Their speckled brown or gray marked skin gives an efficient mask in the frozen Arctic. Narwhals live in the Arctic waters.

Social structure

Narwhals form social clusters known as $\:pods$, which might contain twelve to a hundred people. Several pods are $\:nurseries$ fabricated entirely of females and their young, whereas others contain males and juveniles. Varied groups can also occur at any time, comprising females, males, and young.

Migration

In the summertime, narwhals make pods ranging between 10 and 100 individuals and travel near the seashore. During the winter, they travel to deeper water under densely packed ice.

Diet

Before capturing and eating fish, narwhals use their longer tusks to startle them. Their diet mainly consists of polar, Greenland halibut, and Arctic cod.

Communication and coordination

Narwhals utilize sound for either navigation or hunting. Their languages comprise whistles, clicks, and knocks, essential in communication. Clicks are mainly valuable for perceiving prey and recognizing difficulties at short distances. Communication between narwhals is critical for coordinating set actions with pursuing prey. They utilize different vocalizations, like whistles and clicks, for echolocation to navigate and find prey. In detail, shorter sparkles of clicks aid them in recognizing objects under the water, like possible prey.

These languages help narwhals manage their actions and preserve the unity of the groups while capturing and hunting for prey. After the prey is identified, communication inside the pod frequently improves, using languages utilized to signal the existence of prey, coordinate the attack, or communicate data about possible attacks. The behaviour of narwhals in hunting and communication stimulates this.

During this NO, all solutions characterize the location of the narwhals inside the search area, which might be similar to possible solutions for the optimizer problem. Once narwhals recognize possible targets, they interconnect by transfer signals, and the communication inside the pod frequently gets more robust. Finding prey depends upon echolocation, a method by which narwhals produce snaps into the water and pay attention to the frequent echoes to decide the location of the prey.

Initialize

Firstly, the optimizer model starts through a collection of randomly generated solutions, all demonstrating the location of a narwhal ($\:X$). During every iteration of the model, these positions are upgraded constantly and are described by the succeeding matrix:

$$\:X=\left[\begin{array}{llll}{X}_{\text{1,1}}&\:{X}_{\text{1,2}}&\:\dots\:&\:{X}_{1,d}\\\:{X}_{\text{2,1}}&\:{X}_{\text{2,2}}&\:\dots\:&\:{X}_{2,d}\\\:\dots\:&\:\dots\:&\:\dots\:&\:\dots\:\\\:{X}_{n,1}&\:{X}_{n,2}&\:\dots\:&\:{X}_{n,d}\end{array}\right]$$

(1)

Here, $\:n$ characterizes the narwhal’s population size, and $\:d$ refers to the size of decision variables.

Single emission

After directing, narwhals interchange locations and utilize signals to discover their prey. It is assumed that the moderately lower intensity signals are initially associated with the narwhals’ exploration stage of the searching region. The signal of the narwhal is established by its location and how it recognizes its environment. The next is an explanation of how emission works:

$$\:{S}_{E}\left({X}_{i}\right)=\frac{0.1}{1+\alpha\:\cdot\:\Vert{X}_{i}-{X}_{prey}\Vert}$$

(2)

Now, $\:{X}_{i}$ denotes the location of $\:i\:th$ narwhal, and $\:{X}_{prey}$ represents the location of the prey that might additionally identify the signal and have variations in its area (Narwhal prey, like fish, may locate the sounds of narwhals).

$\:\left|\left|{X}_{i}-{X}_{prey}\right|\right|$ $\:Kk$ denotes the Euclidean distance between the location of $\:i\:th$ narwhal and the possible prey. $\:\alpha\:$ represents a factor of control, which manages the intensity of the signal.

Signal propagation

The mainly distributed signal would pass over the water and is characterized as the function, which relies on how frequently the narwhals interact. The meaning of the function of the propagation is as shown:

$$\:{S}_{P}\left({X}_{i}\right)={S}_{E}\left({X}_{i}\right)\times\:{P}_{R}\left({X}_{i},\:{X}_{prey}\right)$$

(3)

Here, $\:{P}_{R}\left({X}_{i},\:{X}_{prey}\right)$ denotes a function of propagation that is applied to propagate the signal. These functions are described as shown:

$$\:{P}_{R}\left({X}_{i},\:{X}_{prey}\right)=\text{e}\text{x}\text{p}\left(-\frac{\Vert\:{X}_{i}-{X}_{prey}{\Vert\:}^{2}}{2\times\:({\sigma\:}^{t}{)}^{2}}\right)$$

(4)

Now $\:{\sigma\:}^{t}$ refers to the standard deviation at $\:t$ $\:th$ iteration that manages an influence decay by distance.

Determine that communication should be local when σt contains smaller values, whereas a larger value of $\:{\sigma\:}^{t}$ should be global and adjusted to larger distances. The $\:{\sigma\:}^{t}$ value reduces linearly above the iterations. It begins with $\:{\sigma\:}_{0}.$

$$\:{\sigma\:}^{t}={\sigma\:}_{0}-\left(\frac{t}{T}\right)\times\:{\sigma\:}_{0}$$

(5)

Position update

By all iterations, the position of narwhals is upgraded constantly. It is upgraded regarding the propagation and emission of the signal. By applying the succeeding encryption to updated locations at all steps, this is mimicked iteratively in time:

$$\:{X}_{i}^{t+1}={X}_{i}^{t}+{△}^{t}$$

(6)

$\:{△}^{t}$△}^{t}\) characteristics step at $\:t\:th$ iteration, and the succeeding equations can specify it.

$$\:{△}^{t}=\beta\:\times\:\left|{S}_{P}\left(i\right)*{X}_{prey}-{X}_{i}\right|$$

(7)

$$\:\beta\:={r}_{1}-\frac{1}{{\sigma\:}^{t}+1}$$

(8)

$\:\beta\:$ denotes a parameter associated with the $\:{\sigma\:}^{t}$ that controls the propagation decay.

As stated before, the prey can identify the sign produced by the narwhals. In other words, the prey is influenced by the emitted signal, as presented. $\:{S}_{P}\left(i\right)*{X}_{prey}.$ To design the NO model for the particular situation, a binary form of the method which combines the function of sigmoid is proposed in the following way:

$$\:S\left(Z\right)=\frac{1}{1+{e}^{-{z}_{i}}}$$

(9)

$$\:X=\left\{\begin{array}{l}1,\:if\:S\left(Z\right)\ge\:\sigma\:\\\:0,\:if\:S\left(Z\right)<\sigma\:\end{array}\right.$$

(10)

Now, $\:\sigma\:$ refers to randomly formed variables inside intervals $\:0\:$and$\:\:1$. The location of the narwhal characterizes the absence or the presence of features.

In the BNO model, the objectives are united into a solitary objective formulation such that a current weight identifies each significance of an objective. Here, the fitness function (FF) is considered, which unites both objectives of feature selection (FS) as exposed in Eq. (11).

$$\:Fitness\left(X\right)=\alpha\:\cdot\:E\left(X\right)+\beta\:*\left(1-\frac{\left|R\right|}{\left|N\right|}\right)$$

(11)

where $\:Fitness\left(X\right)$ signifies the fitness value of subset $\:X,$ $\:E\left(X\right)$ represents the classifier rate of error by utilizing the chosen features in the $\:X$ subset, $\:\left|N\right|$ and $\:\left|R\right|$ denotes the amount of original and chosen features correspondingly, $\:\alpha\:$ and $\:\beta\:$ refer to weights of classification error and the ratio of reduction, $\:\alpha\:\in\:\left[\text{0,1}\right]$ and $\:\beta\:=(1-\alpha\:)$.

Stage 3: classification process using CNN-BiGRU-AM model

For the DDoS attack classification process, the CNN-BiGRU-AM is employed⁴¹. This model integrates the merits of CNN, BiGRU, and AM to create a powerful classification model. CNN effectually extracts local features from input data, while BiGRU captures both past and future dependencies in sequences, giving a more comprehensive understanding of temporal information. The attention mechanism assists the model concentrate on the most relevant parts of the input, enhancing accuracy by prioritizing important features and mitigating noise. This incorporation gives superior performance over conventional models such as simple CNNs or RNNs, particularly in tasks with complex patterns and long-term dependencies. The AM model improves interpretability, making the model more transparent in decision-making, which is often lacking in other methods. Figure 3 represents the architecture of the CNN-BiGRU-AM method.

Fig. 3

Architecture of CNN-BiGRU-AM method.

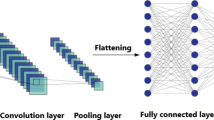
CNNs have robust grid data processing abilities and are extensively employed for tasks such as image analysis. CNNs are one of the kinds of feed-forward NNs with intricate structures, which are effective at handling higher‐dimensional information and mechanically removing features. The main CNN structure comprises many layers: pooling, a convolutional, an input, a fully connected (FC), and an output. The convolutional layer holds a group of convolutional filters, which extract spatial features from input data. In the convolutional layer, input data is convolved with filters of fluctuating weights to excerpt essential features, aiding the evaluation of how well dissimilar data positions equal the features. The CNN procedures input data over feature changes and extractions from the pooling and convolutional layers to originate higher‐level features. The processes for feature extraction are given below:

$$\:{x}_{j}^{m}=f\left({w}_{j}^{m}*{X}^{m-1}+{b}_{j}^{m}\right)$$

(12)

Here, $\:{w}_{j}^{m}$ denotes the weight matrix of 1st convolution kernel of the layer; $\:{X}^{m-1}$ refers to an output of $\:the\:m$-1 layer; $\:{x}_{j}^{m}$ indicates the $\:jth$ feature of the $\:mth$ layer; “*" represents the convolutional operator; $\:{b}_{j}^{m}$ specifies the bias term. In this study, the $\:ReLU$ activation function is employed for CNN, which adapts the linear units of the convolutional layer as per the below-mentioned formulation:

$$\:f\left(z\right)=\text{m}\text{a}\text{x}(0,x)$$

(13)

Manifold feature matrices are produced by extracting data from the convolutional layer. When computational complexity decreases, the pooling layer extracts the most significant features. The pooling layer procedures the feature matrices attained from the layer of convolutional utilizing a pooling kernel, as definite by the below-given equation:

$$\:{x}_{j}^{m}=f\left({w}_{j}^{m}*{X}^{m-1}+{b}_{j}^{m}\right)$$

(14)

While $\:{X}_{j}^{m}\left(v\right)$ denotes the element of the $\:jth$ feature matrix of $\:an\:mth$ layer in the pooling kernel area, $\:{y}_{j}^{m+1}\left(w\right)$ refers to an element of $\:jth$ feature matrix of the $\:m+1$ layer afterwards pooling; $\:{D}_{w}$ represents the area enclosed by the $\:jth$ pooling kernel.

Lastly, the FC layer incorporates these features by mapping the pooled data to an output layer. The single convolutional structure of CNN can decrease computational complexity and improve processing speed. In LiB’s RUL forecast framework, CNN efficiently captures mature features linked with battery ability degradation. This reduces the requirement for physical feature engineering by constantly removing higher-quality features from raw data utilizing the layers of convolutional. In the highest fusion layer, feature spectrograms of convolved data are merged, and local data is filtered to remove the greatest values while decreasing the dimensions of a feature. The FC layer then handles the extracted higher‐level features to make the CNN output.

The GRU is a basic type of LSTM and includes dual gates such as a reset and an update. The reset gate selectively fails to recall irrelevant data from the preceding time step, decreasing interference with essential features. The update gate defines how much prior state data is kept, thus improving the correlation among time-based features. For similar accuracy, the structural optimizer of GRU outcomes has fewer training parameters and faster convergence than LSTM. The computational procedure for every GRU unit is expressed as follows.

$$\:\left\{\begin{array}{l}{r}_{t}=\sigma\:({W}_{r}{x}_{t}+{U}_{r}{h}_{t-1})\\\:{z}_{t}=\sigma\:({W}_{Z}{x}_{t}+{U}_{Z}{h}_{t-1})\\\:\stackrel{\sim}{{h}_{t}}=\text{t}\text{a}\text{n}\text{h}({r}_{t}\circ\:U{h}_{t-1}+W{x}_{t})\\\:{h}_{t}=(1-{z}_{t})\circ\:\stackrel{\sim}{{h}_{t}}+{z}_{t}\circ\:{h}_{t-1}\end{array}\right.$$

(15)

While $\:{r}_{t}$ denotes the reset gate, its value is set as $\:0$; the more data from the preceding moment wants to be forgotten. $\:{z}_{t}$ refers to an update gate, which is fixed as 1, and more data from the prior moment is remembered. $\:\stackrel{\sim}{{h}_{t}}$ indicates the candidate hidden layer (HL) state, imitating the input data at $\:the\:tth$ moment and the selective holding of output at the moment $\:t‐1$. $\:{h}_{t-1}$ refers to an output of the HL at $\:tth$ moment$\:.$ $\:{h}_{t}$ indicates an output of HL at $\:tth$ moment$\:.$ $\:\sigma\:$ specifies the activation function of Sigmoid; $\:tanh$ denotes an activation function; $\:{W}_{t},\:Ur,\:Wz,\:Uz,\:W,\:U$ indicates the training parameter matrices.

BiGRU captures dependencies between the start and end of a sequence by assigning data both backwards and forward. When equated to conventional unidirectional GRUs, BiGRU seizures more contextual data and improves the model’s performance by considering both backwards and forward data. BiGRU is a bi-directional recurrent network that unites dual GRUs with reverse propagation directions. It includes data movement from previous to future and vice versa, improving the model’s capability for capturing dependencies in both directions.

The output of every BiGRU unit moment is defined by the bias at $\:tth$ moment, the forward-propagate GRU output $\:\overrightarrow{{h}_{t}},\:$and the backwards-propagate GRU output $\:\overrightarrow{{h}_{t}}$. The 3 modules are jointly affected. Its mathematical equation is expressed below:

$$\:\left\{\begin{array}{c}\overrightarrow{{h}_{t}}=GRU\left({x}_{t},\overrightarrow{{h}_{t-1}}\right)\\\:\overleftarrow{{h}_{t}}=GRU\left({x}_{t},\overleftarrow{{h}_{t-1}}\right)\\\:{h}_{t}-\alpha\:\overrightarrow{{h}_{t}}+\beta\:\overleftarrow{{h}_{t}}+{c}_{t}\end{array}\right.$$

(16)

While $\:GRU(\cdot\:)$ denotes the computational process for $\:GRU$, the $\:\overrightarrow{{h}_{t}}$ and $\:\overleftarrow{{h}_{t}}$ represent the forward and backward $\:GRU$ HL outputs; correspondingly, $\:{\alpha\:}_{t},{\beta\:}_{t}$ indicates the corresponding HL output weights; $\:{c}_{t}$ refers to HL offset equivalent to $\:{h}_{t}.$

The AM has established its efficiency in numerous DL applications, such as image processing, machine translation, and time series prediction. The AM permits the system to selectively focus on dissimilar portions of an input series and evaluate the interdependencies among these elements. In this study, attention weights are computed depending on the similarity among sets of input vectors and are independent of exterior factors. The primary formulation is expressed in the mathematical expression below:

$$\:{h}_{t,{t}^{{\prime\:}}}=\text{t}\text{a}\text{n}\text{h}\left({W}_{g}{h}_{t}+{W}_{g}^{{\prime\:}}{h}_{{t}^{{\prime\:}}}+{b}_{h}\right)$$

(17)

$$\:{e}_{t,{t}^{{\prime\:}}}=\delta\:\left({W}_{e}{h}_{t,{t}^{{\prime\:}}}+{b}_{e}\right)$$

(18)

$$\:{a}_{t,{t}^{{\prime\:}}}=soft\text{m}\text{a}\text{x}\left({e}_{t,{t}^{{\prime\:}}}\right)$$

(19)

$$\:{l}_{t}={\sum\:}_{{t}^{{\prime\:}}}{a}_{t,{t}^{{\prime\:}}}{h}_{{t}^{{\prime\:}}}$$

(20)

Between them, $\:{h}_{t,{t}^{{\prime\:}}}$ refers to the HL output of the BiGRU layer; $\:{W}_{g}$ and $\:{W}_{g}^{{\prime\:}}$ resemble the weight matrices of HLs $\:{h}_{t}$ and $\:{h}_{{t}^{{\prime\:}}}$ correspondingly; $\:{e}_{{t,t}^{{\prime\:}}}$ denotes the output of sigmoid activation; $\:\delta\:$ indicates an element-wise sigmoid function; $\:{W}_{e}$ represent the weight matrix; $\:{a}_{t,{t}^{{\prime\:}}}$ specifies the soft$\:\text{m}\text{a}\text{x}\:$activation of $\:{e}_{t,{t}^{{\prime\:}}}.$ $\:{l}_{t}$ calculates attention or significance assumed by a token in the HL of the AM to dissimilar neighbouring tokens at an exact time step. $\:{l}_{t}$ takes relevant data from the HL in the present token input sequence at $\:the\:tth$ time step; it aids the technique in utilizing both- succeeding and preceding data to improve its representation and understanding of input data. To calculate the attention‐focused HL representation $\:{l}_{t}$, the model naturally unites data from every time-step $\:{t}^{{\prime\:}}$ in an input sequence; they depend upon their significance to the present token at $\:t$he time-step$\:.$ The AM united with BiGRU efficiently captures BiGRU’s sequence data output. By conveying diverse weights to an output state, the method can dynamically alter the concentration on dissimilar features to highlight those critical to the objective task.

Stage 4: hyperparameter tuning using SOA model

To ensure optimal performance of the CNN-BiGRU-AM model, hyperparameter tuning is achieved using the SOA to enhance the efficiency and robustness of the detection system⁴². This method is chosen because it can effectively explore complex search spaces and optimize parameters. Inspired by the natural behaviour of seagulls, the algorithm outperforms in global exploration and local exploitation, which assists in finding optimal solutions to high-dimensional problems. Compared to conventional optimization techniques, namely grid or random search, SOA has improved convergence rates and averts getting trapped in local minima. Its flexibility and efficiency make it ideal for tuning hyperparameters in ML methods, giving more accurate results with less computational cost. The adaptability of the SOA technique to diverse types of models and datasets additionally improves its merit over conventional techniques. Figure 4 demonstrates the steps involved in the SOA method.

Fig. 4

Steps involved in the SOA methodology.

An SOA generally has dual stages, i.e., migration and attack. Seagulls exist in the distribution of non-interfering to avoid location collisions before migrating. After the exit, seagulls used to travel in the way of seagulls, which has the finest fitness. Throughout the migration method, the seagull’s locations were upgraded slowly depending upon the rightest seagull. In migration, seagulls often affect another bird and retain a spiral‐shaped drive. The above behaviours stimulate researchers to progress a novel bio‐inspired metaheuristic technique called SOA. A short-term explanation of SOA is presented below.

Migrating.

Here, the behaviours of seagull clusters were pretended. The variable $\:A$ has been presented to evade the location collisions:

$$\:A={f}_{i}-\left(x\cdot\:\left(\frac{{f}_{i}}{{\text{M}\text{a}\text{x}}_{iter}}\right)\right)$$

(21)

Where $\:{f}_{i}$ is applied for controlling the frequency of variable $\:A$, and it is straightly reduced from $\:{f}_{i}$ to $\:0.x$ signifies the present iteration count, and $\:{\text{M}\text{a}\text{x}}_{iter}$ denotes the maximum count of iteration. Once the variable $\:A$, the location of the novel search individual is upgraded by the mentioned mathematical equation:

$$\:{\overrightarrow{C}}_{s}=A\cdot\:{\overrightarrow{PoS}}_{s}\left(s\right)$$

(22)

Meanwhile, $\:{\overrightarrow{C}}_{s}$ denotes the location of an individual exploration that is not hit with a new individual search. $\:{\overrightarrow{PoS}}_{s}$ is the present location of an examined individual. Once the initial locations of seagulls are defined, search units will travel with the finest fitness. This kind of behaviour is mathematically expressed below:

$$\:{\overrightarrow{Mov}}_{s}=B\cdot\:\left({\overrightarrow{Pos}}_{fs}\left(x\right)-{\overrightarrow{Pos}}_{s}\left(x\right)\right)$$

(23)

Here, $\:{\overrightarrow{Pos}}_{fs}\left(x\right)$ denotes the search unit. $\:B$ refers to a randomly generated value that controls local and global exploration. By deducting the location of the finest and present individuals and multiplying a variable $\:B$, every hunt unit would slowly attempt the finest exploration individual. Lastly, upgrading the search unit position is defined below:

$$\:{\overrightarrow{Di\text{s}}}_{s}=\left|{\overrightarrow{C}}_{s}+{\overrightarrow{Mov}}_{s}\right|$$

(24)

Attacking.

In this procedure, seagulls can alter their flying speed and positions to express a curved drive in the air. This action is portrayed in a 3D space by numerical formula, and the upgraded location of the search unit is computed below:

$$\:X=R\cdot\:\text{c}\text{o}\text{s}\left(N\right)$$

(25)

$$\:Y=R\cdot\:\text{s}\text{i}\text{n}\left(N\right)$$

(26)

$$\:Z=R\cdot\:N$$

(27)

$$\:R=U\cdot\:{e}^{NV}$$

(28)

$$\:{\overrightarrow{Pos}}_{s}\left(x\right)=\left({\overrightarrow{Dis}}_{s}\cdot\:X\cdot\:Y\cdot\:Z\right)+Po{s}_{fs}\left(x\right)$$

(29)

In the above equations, $\:R$ signifies the radius, and $\:N$ means a randomly produced number within an interval of $\:\left[\text{0,2}\pi\:\right]$. $\:V$ and $\:U$ are employed to represent the form of a spiral. $\:e$ indicates the foundation of the algorithm.

The FS is the significant factor prompting the outcome of SOA. The parameter range procedure contains the solution-encoded technique for appraising the efficiency of the candidate solution. Here, the SOA reflects accuracy as the main norm for designing the FF. Its mathematical formula is expressed below:

$$\:Fitness\:=\:\text{m}\text{a}\text{x}\:\left(P\right)$$

(30)

$$\:P=\frac{TP}{TP+FP}$$

(31)

Here, $\:FP$ and $\:TP$ signify the positive values of false and true, respectively.

Performance validation

In this segment, the experimental validation of the CSSDN-HDLBNO method is studied below the DDoS SDN dataset⁴³. The dataset consists of 50,000 samples below dual classes, as demonstrated in Table 1. The total number of features is 22; however, only 17 are selected. The suggested technique is simulated by employing Python 3.6.5 tool on PC i5-8600k, 250GB SSD, GeForce 1050Ti 4GB, 16GB RAM, and 1 TB HDD. The parameter settings are provided in the following: learning rate: 0.01, activation: ReLU, epoch count: 50, dropout: 0.5, and batch size: 5.

Table 1 Details of the dataset.

Figure 5 validates the confusion matrix the CSSDN-HDLBNO method produces below different epochs. The performances indicate that the CSSDN-HDLBNO model has effectual detection and identification of all dual classes specifically.

Fig. 5

Confusion matrix of CSSDN-HDLBNO model (a-f) Epochs 500–3000.

The DDoS attack detection of the CSSDN-HDLBNO approach is found below different epochs in Table 2; Fig. 6. The values of the table imply that the CSSDN-HDLBNO approach is properly renowned for all the samples. With 500 epochs, the CSSDN-HDLBNO methodology offers an average $\:acc{u}_{y}$ of 99.03%, $\:pre{c}_{n}$ of 99.03%, $\:\:rec{a}_{l}$ of 99.03%, $\:{F}_{measure}$of 99.03%, and $\:AU{C}_{score}\:$of 99.03%. Besides, with 1000 epochs, the CSSDN-HDLBNO methodology offers an average $\:acc{u}_{y}$ of 99.16%, $\:pre{c}_{n}$ of 99.16%, $\:\:rec{a}_{l}$ of 99.16%, $\:{F}_{measure}$ of 99.16%, and $\:AU{C}_{score}\:$of 99.16%. Moreover, with 1500 epochs, the CSSDN-HDLBNO methodology offers an average $\:acc{u}_{y}$ of 99.16%, $\:pre{c}_{n}$ of 99.16%, $\:\:rec{a}_{l}$ of 99.16%, $\:{F}_{measure}$ of 99.16%, and $\:AU{C}_{score}\:$of 99.16%. Also, with 2500 epochs, the CSSDN-HDLBNO methodology offers an average $\:acc{u}_{y}$ of 99.28%, $\:pre{c}_{n}$ of 99.28%, $\:\:rec{a}_{l}$ of 99.28%, $\:{F}_{measure}$ of 99.28%, and $\:AU{C}_{score}\:$of 99.28%. At last, with 3000 epochs, the CSSDN-HDLBNO methodology offers an average $\:acc{u}_{y}$ of 99.40%, $\:pre{c}_{n}$ of 99.40%, $\:\:rec{a}_{l}$ of 99.40%, $\:{F}_{measure}$ of 99.40%, and $\:AU{C}_{score}\:$of 99.40%.

Table 2 DDoS attack detection outcome of CSSDN-HDLBNO technique under distinct epochs.

Fig. 6

Average outcome of CSSDN-HDLBNO technique (a-f) Epochs 500–3000.

Figure 7 illustrates the training (TRA) $\:acc{u}_{y}$ and validation (VAL) $\:acc{u}_{y}$ performances of the CSSDN-HDLBNO technique below epoch 3000. The $\:acc{u}_{y}\:$values are calculated through an interval of 0-3000 epochs. The figure emphasized that the values of TRA and VAL $\:acc{u}_{y}$ show an increasing trend, indicating the capacity of the CSSDN-HDLBNO approach with maximum performance through multiple repetitions. In addition, the TRA and VAL $\:acc{u}_{y}$ values remain close across the epochs, notifying lesser overfitting and displaying the higher performance of the CSSDN-HDLBNO approach, which assurances reliable prediction on unseen samples.

Fig. 7

$\:Acc{u}_{y}$ curve of CSSDN-HDLBNO technique under Epoch 3000

Figure 8 shows the TRA loss (TRALOS) and VAL loss (VALLOS) graph of the CSSDN-HDLBNO technique below epoch 3000. The loss values are computed across an interval of 0-3000 epochs. The TRALOS and VALLOS values exemplify a diminishing trend, which indicates the proficiency of the CSSDN-HDLBNO approach in equalizing a tradeoff between data fitting and generalization. The constant decrease in loss and securities values improves the performance of the CSSDN-HDLBNO approach and tunes the prediction results after a while.

Fig. 8

Loss curve of CSSDN-HDLBNO technique under Epoch 3000.

In Fig. 9, the precision-recall (PR) curve examination of the CSSDN-HDLBNO approach under epoch 3000 analyses its outcomes by scheming Precision beside Recall for all the class labels. The figure depicts that the CSSDN-HDLBNO technique constantly achieves higher PR values over distinct class labels, which notified its capability to keep a substantial portion of true positive predictions between each positive prediction (precision) while similarly getting a significant proportion of actual positives (recall). The stable increase in PR analysis between all class labels reveals the efficacy of the CSSDN-HDLBNO method in the classification process.

Figure 10 examines the ROC curve of the CSSDN-HDLBNO model below epoch 3000. The performances indicate that the CSSDN-HDLBNO technique attains superior ROC results across each class, illustrating substantial proficiency in discriminating the distinct class labels. This consistent tendency of higher ROC values through several class labels exemplifies the capable outcomes of the CSSDN-HDLBNO technique on predicting classes, which implies the robust nature of the classification process.

Fig. 9

PR curve of CSSDN-HDLBNO technique under Epoch 3000.

Fig. 10

ROC curve of CSSDN-HDLBNO technique under Epoch 3000.

The comparative study of the CSSDN-HDLBNO approach with existing techniques is depicted in Table 3; Fig. 11^44,45. The simulation result highlighted that the CSSDN-HDLBNO approach outperformed greater performances. According to $\:acc{u}_{y}$, the CSSDN-HDLBNO model has a maximum $\:acc{u}_{y}$ of 99.40%. In contrast, the RF, DT, CNN, GRU, SGD, NGBooST, Adaboost, and CNN-GRU-Attention methodologies have minimal $\:acc{u}_{y}$ of 99.06%, 98.06%, 96.06%, 98.01%, 98.07%, 93.08%, 83.08%, and 99.30%, correspondingly.

In addition, according to $\:Pre{c}_{n}$, the CSSDN-HDLBNO model has a maximum $\:Pre{c}_{n}$ of 99.40%. In contrast, the RF, DT, CNN, GRU, SGD, NGBooST, Adaboost, and CNN-GRU-Attention methodologies have minimal $\:Pre{c}_{n}$ of 99.07%, 91.08%, 75.07%, 97.19%, 93.06%, 92.06%, 77.55%, and 99.83%, correspondingly. Furthermore, according to $\:{F}_{measure}$, the CSSDN-HDLBNO model has a maximum $\:{F}_{measure}$ of 99.40%. In contrast, the RF, DT, CNN, GRU, SGD, NGBooST, Adaboost, and CNN-GRU-Attention methodologies have minimal $\:{F}_{measure}$ of 99.07%, 94.06%, 76.08%, 99.39%, 93.06%, 93.06%, 98.85%, and 99.65%, correspondingly.

Table 3 Comparative analysis of CSSDN-HDLBNO approach with existing methodologies^44,45.

Fig. 11

Comparative analysis of CSSDN-HDLBNO approach with existing methodologies.

Table 4; Fig. 12 show the comparative study of the CSSDN-HDLBNO technique regarding training time (TT) is identified. According to TT, the CSSDN-HDLBNO approach offers a diminishing TT of 05.01 s, while the RF, DT, CNN, GRU, SGD, NGBooST, Adaboost, and CNN-GRU-Attention models obtain better TT values of 10.58 s, 23.74 s, 11.44 s, 16.18 s, 10.80 s, 22.65 s, 19.70 s, and 10.46 s, respectively.

Table 4 TT outcome of CSSDN-HDLBNO technique with recent models.

Fig. 12

TT outcome of CSSDN-HDLBNO technique with recent models.

Conclusion

This manuscript develops a novel CSSDN-HDLBNO approach. The CSSDN-HDLBNO approach presents a scalable and effective solution to safeguard against evolving cyber threats in DDoS attacks within the SDN environment. Initially, the CSSDN-HDLBNO approach utilizes min-max normalization to scale the features within a uniform range using data normalization. Next, the BNO-based feature selection is employed to classify the most related features. For the DDoS attack classification process, the CNN-BiGRU-AM is utilized. To ensure optimal performance of the CNN-BiGRU-AM model, hyperparameter tuning is performed using the SOA to enhance the efficiency and robustness of the detection technique. A wide range of simulation analyses is implemented to certify the improved performance of the CSSDN-HDLBNO technique under the DDoS SDN dataset. The performance validation of the CSSDN-HDLBNO technique portrayed a superior accuracy value of 99.40% over existing models in diverse evaluation measures. The limitations of the CSSDN-HDLBNO technique comprise the reliance on a limited set of data for training and testing, which may affect the generalization capabilities of the model to unseen attack patterns or real-world traffic. Furthermore, the computational cost of training DL methods and the complexity of optimizing multiple parameters can restrict the scalability of the proposed approach in large-scale networks. Another limitation is the lack of real-time performance evaluation under diverse network conditions, which may affect the efficiency of the system in dynamic environments. Future work can concentrate on expanding the dataset to comprise various attack scenarios, enhancing the efficiency of the model through lightweight architectures, and exploring adaptive detection techniques to improve real-time performance and scalability across diverse SDN deployments. Further integration with threat intelligence systems could also be explored to give a more comprehensive security framework.