A robust pressure drop prediction model in vertical multiphase flow: a machine learning approach

Abstract

Predicting pressure drop in multiphase flow is crucial for optimizing tubing size, wellhead pressure (WHP), completion design, cost management, and other production-phase objectives. While various correlations and models exist to calculate pressure drops, their accuracy diminishes significantly when applied to outlier datasets beyond their intended parameter ranges. Not only that, as reported by many studies, most of the empirical correlations and mechanistic models have an error, which is quite high and intolerable. This study introduces a novel Adaptive Neuro-Fuzzy Inference System (ANFIS) model for accurately predicting pressure drops in vertical wells carrying multiphase fluids. A comprehensive dataset of 335 experimental records was compiled from diverse sources to encompass a wide range of parameters, ensuring the robustness of the proposed model. Key input parameters include WHP, oil rate, water rate, gas rate, inner diameter, surface temperature, and flow length. The ANFIS model was rigorously evaluated using different methods, such as cross plot, error distribution, Kruskal-Wallis (KW) test, error boxplot and violin graphs, Confidence Interval (CI), and statistical error metrics. The latter includes Average Absolute Percentage Error (AAPE), Root Mean Square Error (RMSE), and the coefficient of determination (R²) to prove the ANFIS model’s performance. The proposed ANFIS model was compared with the most commonly used published models. Results demonstrate that the ANFIS model outperforms existing methods, achieving an AAPE of 2.92%, an RMSE of 1.9638%, and an R² of 0.9645. KW test, error boxplot, violin graphs, and CI results indicated that the best model for predicting pressure drops is the proposed ANFIS model. These findings establish the ANFIS model as a reliable and superior tool for predicting pressure drops in vertical wells with multiphase flow, offering significant advancements in design accuracy and operational efficiency.

Introduction

Background

Predicting pressure drop in vertical wells carrying multiphase fluids is essential for selecting tubing size, wellhead pressure (WHP), completion schemes, cost management for production phases, and other design objectives. A pressure drop can happen when the resistance to fluid flow causes frictional forces. The friction changes some fluid’s hydraulic energy into thermal energy, which cannot be changed back to hydraulic energy; the pressure of the fluid drops, as mandated by the conservation of energy¹. A petroleum engineer’s responsibility is to raise production lifetime by preventing unnecessary production, monitoring production through chokes, and growing production or reservoir lifetime by choosing a suitable choke on production wells². An accurate pressure drop plays a key role in designing and selecting the appropriate chokes.

Many independent variables can potentially affect the pressure drop³. Some studies found relationships between pressure drops, pipe diameter, and length. The pressure drops can be related inversely to the pipe diameter and directly proportional to the pipe length⁴. The presence of water increases the level of complexity as liquid holdup plays a critical role in pressure drop determination. The liquid holdup is the accumulation of liquid in the pipeline due to the difference in velocity, “slip,” between the phases, and the influence of gravity⁵.

Precisely forecasting pressure drops in flowing or gas-lift wells remains a significant challenge, leading to the development of many specialized models tailored to specific conditions. However, a universally accepted solution applicable to various scenarios has yet to emerge. This complexity arises primarily from the intricate nature of the two-phase flow, which is difficult to analyze even under controlled conditions⁶.

In some instances, gas travels at a significantly higher velocity than the liquid, resulting in a downhole flowing density of the gas-liquid mixture that exceeds the expected density derived from the produced gas-liquid ratio, even when corrected for temperature and pressure. Additionally, the velocity of the liquid along the pipe wall can fluctuate over short distances, leading to variations in frictional losses. Conversely, the liquid phase may become almost entirely entrained within the gas under different conditions, contributing minimally to frictional resistance along the pipe walls⁶.

The interaction between the two phases, particularly the differences in velocity and flow geometry, is crucial in determining pressure drop. These factors serve as the foundation for classifying different two-phase flow regimes, influencing the selection of appropriate predictive models. Developing a comprehensive and accurate approach to pressure drop prediction requires accounting for the dynamic behavior of both phases, including phase distribution and the impact of operational and reservoir conditions⁶.

Literature review

Measuring the pressure drop in vertical sections of the well is not practical as it involves a high cost. Therefore, early efforts to estimate the pressure drop in vertical single-phase flow can be dated back to 1952 based on the predictive schemes of Poettman and Carpenter⁷, Baxendell and Thomas⁸, Gould et al.⁹, Fancher and Brown¹⁰. However, the main limitation of the abovementioned methods is that no single correlation can predict the pressure drop under the wide range of operating conditions faced in various well situations, as shown in a study by Hasan and Kabir¹¹.

Furthermore, Hagedorn & Brown¹² and Beggs and Brill¹³ developed models to predict the pressure drop. However, new models were needed as the flow’s complexity increased due to the reduced flow rate and pressure in the producing wells.

Then, as the complexity and uncertainty increased, several mechanistic models were developed, such as Ansari et al.¹⁴, Hasan and Kabir¹⁵, and Kabir and Hasan¹⁶. Detailed descriptions and equations related to the abovementioned methods can be found in the reference section. Many studies have been conducted to verify the accuracy of these methods, and as a result, different techniques have been developed for various conditions (Mukherjee and Brill¹⁷, Espanol¹⁸, Camacho¹⁹, Messulam²⁰, Lawson and Brill²¹, Chierici al²², Aggour et al.²³, Pucknell et al.²⁴, Kaya et al.²⁵, Tengesdal et al.²⁶, Vohra et al.²⁷). Although mechanistic models were developed to improve the prediction of the empirical correlations, many studies have shown that with the elimination of datasets, these techniques give no advantage²⁸. These methods decrease accuracy when predicting in-situ conditions because most of them were developed under laboratory conditions²⁸. In addition, experience showed that empirical correlations and mechanistic models failed to provide a satisfactory and reliable tool for estimating pressure drop in multiphase flowing wells.

Machine learning methods, on the other hand, have revolutionized the petroleum engineering industry. Models developed using machine learning such as Artificial Neural Networks (ANN), Adaptive Neuro-Fuzzy Inference Systems (ANFIS), and Support Vector Machines (SVM) outperform traditional empirical or mechanistic approaches in terms of accuracy and adaptability.

ANNs have been used in several studies to obtain the Bottom Hole Pressure (BHP) with stunning accuracy. For instance, Jahanandish et al.²⁹ used an ANN method to predict the BHP based on 413 data points and achieved a correlation coefficient (R) of 0.922 with a Root Mean Square Error (RMSE) of 5.855²⁹. Similarly, Osman et al.³ demonstrated even higher accuracy (R = 0.973 and RMSE = 2.801) using a smaller dataset of 206 records. These studies highlight the strength of ANNs in integrating diverse input variables, such as oil, gas, and water flow rates, as well as reservoir and operational properties, to model complex interdependencies effectively³. Ebrahimi and Khamehchi³⁰ used 1740 data points to predict the BHP using the ANNs, achieving R values between 0.7 and 0.93 across different configurations³⁰. Adebayo et al.³¹ used the ANN and SVM and achieved R values of 0.93 and 0.95, respectively, for BHP prediction³¹.

Some learning algorithms of fuzzy neural networks can be found in literature, such as (Jang et al.³², Juang and Lin³³, and Kokal and Stanislav³⁴. Although Jang introduced the ANFIS method in the early 1990s (Jang and Sun³⁵), it has recently shown high performance in many oil and gas applications. A review of previous works reveals that ANFIS has been used successfully in water flooding for injection profile objectives³⁶, oil production prediction³⁷, reservoir oil bubble point prediction³⁸, prediction of petrophysical properties such as porosity and permeability³⁹, prediction of reservoir oil solution gas-oil ratio⁴⁰, correlation properties of crude oil system prediction⁴¹, prediction of compressional wave velocity⁴², and modeling reservoir fluid Pressure–Volume–Temperature (PVT) properties⁴³. In addition, the results of their research encourage the authors to use ANFIS to predict pressure drop in complex multiphase flow in vertical flowlines.

ANFIS models have also shown significant promise by combining the adaptability of neural networks with the interpretability of Fuzzy Logic (FL). Al-Shammari⁴⁴ applied ANFIS to a dataset of 596 records, achieving R = 0.93 for BHP prediction⁴⁴. Similarly, Nwanwe and Duru⁴⁵ used ANFIS with 1001 data points, incorporating variables such as Well Bottom Hole Temperature (WBHT), tubing Internal Diameter (ID), and oil American Petroleum Institute (API) gravity to achieve excellent predictions of the BHP⁴⁵.

Table 1 compares the previous methods used to predict pressure drop and BHP in petroleum engineering. Traditional empirical and mechanistic models, such as those by Beggs and Brill¹³, Mukherjee and Brill¹⁷, and Orkiszewski⁶, rely on established physical principles like energy balance equations or dimensional analysis. While these models have been widely used, their accuracy is typically constrained by assumptions and simplified relationships.

However, these conventional methods may struggle with the complexity and nonlinearity of multiphase flow in pipelines, limiting their predictive accuracy. The integration of symbolic differential forms (Hagedorn and Brown¹⁰) and mechanical energy balance equations (Mukherjee and Brill¹⁷) have improved model reliability. Yet, they still face challenges in adapting to varying conditions.

To address these limitations, data-driven approaches such as the ANN and the ANFIS have been developed. ANN-based models (Osman et al.¹, Jahanandish²⁹, Adebayo et al.³¹) show superior predictive capabilities, achieving high R and lower RMSE values compared to traditional methods. Machine learning models developed with machine learning tools such as ANN, ANFIS, and SVM reveal better performance due to their ability to model nonlinear relationships in complex datasets. For instance, ANNs achieved high accuracy with R values up to 0.973³, while ANFIS achieved comparable results with R = 0.93⁴⁴. Hybrid approaches, such as the ANN-SVM combination by Adebayo et al.³¹, further enhancing predictive accuracy, achieving R = 0.95 with RMSE values significantly lower than traditional methods.

The ANFIS models (Al-Shammari³², Nwanwe, and Duru³³) further enhance prediction accuracy by combining FL with neural networks, effectively handling uncertainties in reservoir conditions. Al-Shammari³²’s model was used to predict the BHP, and after that, some of them found the pressure drop based on the BHP. Nwanwe and Duru’s³³ model did not consider the temperature as input to predict the pressure drop, which resulted in high errors due to the lack of ratio to the amount of free gas³⁰. Jian et al.⁴⁶ stated that they developed the model to predict the pressure drop in vertical gas. However, they created a model for forecasting liquid holdup in wellbores. Their model is based on the liquid holdups and gas velocities at the annular—churn, churn—slug, and slug—bubble boundaries. Their model has an average percentage error of 220.1% in the churn flow. Ghalem et al.⁴⁷ used deep learning methods, Long Short-Term Memory (LSTM), and Gated Recurrent Unit (GRU) to predict the BHP. Al Wahaibi et al.⁴⁸ applied the ANFIS method to predict pressure drop in horizontal and near horizontal pipes. Their model was created based on 450 data sets collected from the Asian continent. Their ANFIS model had an average absolute percentage error (AAPE) of 13.256, the best performance model compared to the models studied in their research⁴⁸. Nwanwe et al.⁴⁹ used the ANN to predict the liquid holdup based on superficial gas velocity, superficial liquid velocity, liquid viscosity, ID of pipe, liquid density, angle of inclination, and surface tension.

Table 1 The previous models’ comparison.

In our previous studies, the ANFIS method showed highly accurate prediction models for the drilling Rate of Penetration (ROP)^53,54, the oil formation volume factor⁵⁵, bubble point pressure⁵⁶, the GOR below the bubble point pressure⁵⁷, the oil flotation behavior in a stable oil-water emulsion⁵⁸. Our experiences in machine learning and artificial intelligence applications in petroleum engineering revealed that the ANFIS method has successfully predicted many parameters. Furthermore, machine learning methods with FL components show some of the most effective and successful applications in petroleum engineering to manage, control, and understand complex non-linear problems⁵⁹.

Therefore, this study aims to present a new ANFIS model for estimating the pressure drop in vertical wells carrying multiphase fluids (oil, water, and gas) with a better accuracy that can work for a wide range of data and to compare its performance with other methods. In addition, this study used the ANFIS method to predict the pressure drop directly in vertical wells.

Research significance

The novelty of this study relies on using the ANFIS, a hybrid scheme composed of FL and ANN. It is an efficient and robust tool because it can manage the uncertainty of vagueness and imprecision³². Furthermore, ANFIS offers advantages over standard mathematical formulations; the inference process is close to human thinking. This human thinking feature helps ANFIS to deal with complex non-linear problems. In addition to the abovementioned advantages, the FL model can be combined with ANN to form ANFIS⁶⁰, Jang and Sun³⁵, Hagan et al.⁶¹, Kasabov⁶², Jang et al.³², Tsoukalas⁶³, Babuska⁶⁴. A considerable number of studies have designed and examined different types of hybrid fuzzy-neural networks and their potential applications in computer science, pattern recognition, bioinformatics, and petroleum engineering (Babuska⁶⁴, Jang⁶⁰, Jang and Sun³⁵, Hagan et al.⁶¹, Kasabov⁶², Jang et al.³², Tsoukalas⁶³, Babuska⁶⁴, Cuddy⁶⁵, , Fang and Chen⁶⁶, Hambalek and Reinaldo⁶⁷. In addition, the proposed ANFIS model in this study can be used to directly predict the pressure drop accurately. Furthermore, the proposed ANFIS model in this study considers the temperature as one of the used inputs which is an important parameter to be considered in predicting the pressure drop as highlighted earlier.

Methodology

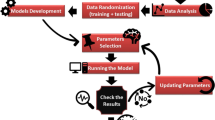
Figure 1 shows the flowchart of applying the ANFIS method to predict the pressure drop. First, the data for the pressure drop was collected using WHP, oil rate, water rate, gas rate, inner diameter, surface temperature, and length as inputs, followed by a pre-processing step to prepare the data. The 70% of pre-processed data is then used to train the ANFIS model for pressure drop prediction. Next, the proposed ANFIS model is evaluated using graphical and statistical methods, such as cross-plotting, error distribution, and the coefficient of determination ($\:{\text{R}}^{2}$), to assess its accuracy using 30% of the data. Finally, the proposed ANFIS model’s performance is compared with previously published models applying some approaches, such as statistical error analysis, cross-plotting, and the Kruskal-Wallis (KW) test, to validate its effectiveness.

Fig. 1

The present study flowchart.

Data collection and pre-processing

335 collected datasets from the Middle East fields are used to build the ANFIS model. The selection of input variables is based on the most common and available variables used in the empirical and mechanistic correlations⁶⁸. The predictor variables used in this study are WHP, oil rate, water rate, gas rate, inner diameter, surface temperature, and length. The target or output value is pressure drop. The overview of the datasets used in this study is summarized in Table 2. Table 2 shows the minimum, maximum, and average of the target, which is the pressure drop, and the independent parameters, which are WHP, oil rate, water rate, gas rate, inner diameter, surface temperature, and length. As shown in Table 2, pressure drop, WHP, oil rate, water, rate, gas rate, inner diameter, surface temperature, and length at the ranges (1077–2927) psi, (160–545) psi, (2200–25000) bbl/d, (0-8424) bbl/d, (1078-19658.2) MSCF/d, (6.064–10.02) inch, (63–186) ^oF, and (500-26700) ft, respectively.

Table 2 Data ranges for ANFIS model development.

MATLAB code is developed to construct the ANFIS model. The datasets are divided into the training dataset (70%) and the testing dataset (30%). 70% of the data was used to create the model, and 30% was used to test or validate the model using the data not used in the training dataset. The same testing dataset was used to validate the proposed ANFIS and previous models to make a fair comparison between all models.

The histograms of the target, which is the pressure drop for the collected data, are depicted in Fig. 2. Figure 2 shows a histogram demonstrating the distribution of pressure drop values in psi across different intervals. The histogram displays a bell-shaped distribution, with the highest frequency observed in the interval [2175, 2415] psi, representing that most pressure drop values fall within this range. The distribution appears slightly skewed, with fewer occurrences at the lower and upper extremes. This visualization shows valuable insight into the variability of pressure drop values.

Fig. 2

Pressure drop histogram.

The histograms of the predictors: WHP, oil rate, water rate, gas rate, inner diameter, surface temperature, and length for the collected data are shown in Figures S1-S7 in the Supporting Information.

Figure 3 illustrates the R between the predictor parameters and the target, highlighting the significance of these relationships for both the collected data. As illustrated in Fig. 3, the pressure drop has a high R with a length where R equals 0.628. A moderate negative correlation was reported with surface temperature where R is -0.456. however, weak negative correlations with water rate, inner diameter, and WHP have been noticed where R’s are − 0.183, -0.086, and − 0.036, respectively. Additionally, weak positive correlations with gas and oil rates have been reported where R’s are 0.155 and 0.299, respectively. In summary, the analysis reveals that for the collected data, the length is the most influential parameter on pressure drop, followed by surface temperature. The other parameters have low R. Although inner diameter and WHP have weak correlations, they were used as inputs because these parameters were applied in the previous models to consider them in this study. In addition, when the correlation is weak between the parameters and the parameters considered, it will not affect the model’s accuracy; however, when the correlation is strong between the parameters and the parameters not considered, it will affect the model’s accuracy. Therefore, in this study, we considered most of the parameters used to predict the pressure drop to prove a high accuracy.

Fig. 3

The relative importance of inputs with the pressure drop for the overall data.

The Box and Whisker (BAW) method was applied to select and eliminate outliers from the dependent and independent variables to get clean data. The BAW Plot was introduced by Tukey⁶⁹. The BAW plot contains Lower Quartile (Q1), median, Upper Quartile (Q3), Interquartile (IQR), lower extreme (Q1-1.5 x IQR), and upper extreme (Q3 + 1.5 x IQR). Any values less than the lower extreme and more than the upper extreme are considered outliers. After the data were cleaned by removing the outliers, the cleaned data were used to create the ANFIS model to predict the pressure drop.

Adaptive neuro-fuzzy inference system (ANFIS) modeling

Many studies have shown successful models in petroleum engineering using FL, such as predicting reservoir engineering parameters, porosity, permeability, rock properties, and other applications⁵⁷. In addition, in subsection 2.4, Literature models’ comparison, we mentioned that some of our previous studies proved the high accuracies of ANFIS models in petroleum engineering applications. Therefore, the ANFIS model was selected in this study to predict the pressure drop in the vertical wells carrying multiphase fluids.

ANFIS is a fuzzy inference system employed under an adaptive framework. It combines machine learning algorithms and fuzzy inference systems, which work on a neural network platform⁷⁰. It has found applications in various domains. FL can work with the vagueness of human duties and convert it from qualitative knowledge into more rigorous quantitative analysis. It can also be adaptable to uncertainty, which is present in most systems. Therefore, combining the ANN and FL decreases the errors associated with the defined fuzzy membership function⁷¹.

In ANFIS, FL membership functions are tuned with the help of a hybrid learning algorithm, i.e., a combination of the least-square method and the back-propagation gradient descent method for adapting to the environments. FL brings human-like reasoning features into the ANFIS. Such a hybrid combination provides a dual advantage of human-like reasoning and an adaptive network for refining fuzzy rules. Such a hybrid learning scheme makes it an efficient method for learning non-linear functions and, consequently, an efficient and robust predictor.

In a traditional fuzzy system, an expert is responsible for crafting the if-else-based relationship between the input and output. On the other hand, ANFIS is adaptive and can automatically tune the fuzzy membership rules according to the environment. Jang⁶⁰ has described in detail the main structure and learning process of ANFIS.

The fuzzy interference system includes four main sections. The first is knowledge-based analysis, which can be used to define the membership functions used in the dataset with FL rules. The second section is the interference engine, which can be applied to modify and refine the fuzzy rules. The third section is fuzzification, which can transform the crisp input data into fuzzy numbers through fuzzy sets known using linguistic terms. The fourth section is defuzzification, which can transform fuzzy interference into crisp numerical data^72,73.

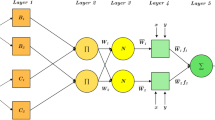
As shown in Fig. 4, ANFIS is composed of five layers. To describe the working principle or the procedures of an ANFIS, we have utilized two input parameters, denoted as x1 and x2, and one response variable. The ANFIS uses “if-then” fuzzy rules to describe the relationship between input and output parameters. In addition, the model includes two fuzzy rules, which are based on Takagi and Sugeno types of fuzzy rules, and they can be expressed as follows:

Fig. 4

The basic structure of ANFIS.

Rule 1:

If x₁ is A₁ and x₂ is B₁, then

$${f_{\text{1}}}={p_{\text{1}}}{x_{\text{1}}}+{q_{\text{1}}}{x_{\text{2}}}+{r_{\text{1}}},$$

(1)

Rule 2:

If x₁ is A₂ and x₂ is B₂, then

$${f_{\text{2}}}={p_{\text{2}}}{x_{\text{1}}}+{q_{\text{2}}}{x_{\text{2}}}+{r_{\text{2}}}$$

(2)

where p₁, q₁, r₁, p_{2 ,} q₂ and r₂ are the trainable parameters weights and bias. A₁, B₁, A_{2 ,} and B₂ represent linguistic signal. The detail of every single layer shown in Fig. 4 is described in the below following:

Layer 1: Fuzzification layer.

Each node i in this layer is considered an adaptive node, which is represented by a node function:

$${O_{{\text{1}},{\text{i}}}}={\mu _{Ai}}(x)$$

(3)

Where O_1,i refers to the response i^th node and µ_Ai symbolizes a membership function (MF), and the following three-parameter functions represent them⁷⁴:

$$\:{u}_{Ai}\left(x\right)=exp[-(\left(\frac{x-{c}_{i}}{{a}_{i}}{)}^{2}{)}^{bi}\right]\:\text{f}\text{o}\text{r}\:i\hspace{0.17em}=\hspace{0.17em}\text{1,2}\:$$

(4)

where parameters a_i, b_i and c_i are premise variables that can modify the shape referred to as the premise of the membership function.

Layer 2: Rule layer.

every node in this layer is a fixed node labelled as $\:{\Pi\:}$, and the output of nodes in this layer is the product of all the incoming signals, for instance^74,75:

$${O_{{\text{2}},i}}={w_i}={\mu _{Ai}}(x) \times {\mu _{Bi}}(x)\,\,{\text{for}}\,\,\,i\,=\,{\text{1}},{\text{2}}$$

(5)

where, O_2.i is the output of layer 2, W_i is the firing strength of the i^th rule, and µ is the membership function (MF) value in FL.

Layer 3: Normalization layer.

The i^th node in this layer normalized the firing strengths, W_i. The ratio of the firing strength of the ith rule to the sum of all rules’ firing strength is calculated according to the following equation⁷⁴:

$$\:{O}_{3,\:i}\:={\stackrel{-}{w}}_{i}=\:\frac{{w}_{i}}{{w}_{1}+{w}_{2}}\text{f}\text{o}\text{r}\:\text{i}=\:1,\:2\:$$

(6)

Where, O_3.i is the output of layer 3, and W_i is the normalized firing strength.

Layer 4: Defuzzification layer.

Every node in this layer is an adaptive node with a node function, indicating the contribution of the i^th rule towards the overall output. The output of this layer is calculated as⁷⁶:

$$\:{O}_{4,\:i}\:={\stackrel{-}{w}}_{i}{f}_{i}=\:{\stackrel{-}{w}}_{i}{(p}_{i}x+{q}_{i}y+{r}_{i})\:\:\:\text{f}\text{o}\text{r}\:\text{i}\:=\:1,\:2\:$$

(7)

Layer 5: Output layer.

In this layer, the calculation is performed using the following equation:

$$\:{O}_{5,\:i}\:=\:\sum\:_{i}{\stackrel{-}{w}}_{i}{f}_{i}=\:\frac{\sum\:_{i}{w}_{i}{f}_{i}}{\sum\:_{i}{w}_{i}}\:\:\text{f}\text{o}\text{r}\:\text{i}=\:1,\:2\:$$

(8)

The ANFIS is trained using various learning methods; the main objective of training an ANFIS is to identify the membership function⁶⁰. The algorithm applies the least squares technique to determine the forward transport section.

The consequent variables [p_i, q_i, r_i ] on the layer 4. The errors are propagated backwards in the backward transport section, and using gradient descent improves premise variables [ai, bi, ci].

The ANFIS method offers some advantages compared to other methods. It has demonstrated superior learning capabilities and can conduct highly non-linear mappings with fewer parameters than other approaches. It excels in handling noisy data and can effectively resolve classification and regression problems, even with accurate or missing input data.

The structure of ANFIS is designed to facilitate parallel computation, providing a well-structured knowledge representation that integrates seamlessly with other design systems. This capability allows ANFIS to decide the mapped relationships between parameters quickly. Another advantage of the ANFIS is its reduced training time due to its smaller dimensions and the initialization of parameters based on the specific problem. These features make the ANFIS a powerful tool for complex application modeling tasks⁷⁷.

The ANFIS is highly flexible and can be employed for various problems, incorporating control systems, pattern recognition, and signal processing. It can be customized to fit specific problem requirements. The ANFIS is more robust to variations and uncertainties in the input data, which makes it particularly useful in real-world applications where data may not be clean or complete. The FL component of ANFIS permits it to operate uncertainty and imprecision in data, which is a common issue in many real-world scenarios. It is designed to update its parameters incrementally as new data becomes available, permitting it to advance incessantly without retraining from scratch. The ANFIS is scaled to control large datasets and complex problems by altering the number of fuzzy rules and the structure of the neural network. The parameters of ANFIS can be finely tuned to enhance application performance, providing a high degree of customization. Therefore, the ANFIS method was used in this study to obtain a highly accurate model to predict the pressure drop^78,79,80.

The proposed ANFIS model peculiarity

The proposed ANFIS model stands out due to its ability to integrate the learning capabilities of neural networks with the interpretability of FL systems, ensuring accuracy and transparency in predicting the pressure drop in vertical wells. Unlike traditional empirical correlations, the ANFIS model accommodates a wide range of parameters, including WHP, oil rate, water rate, gas rate, inner diameter, surface temperature, and tubing length, effectively capturing multiphase flow’s nonlinear and dynamic interactions. This characteristic allows the model to deliver robust predictions. The adaptability of the ANFIS framework enables the continuous refinement of its predictive accuracy, ensuring reliable performance even with heterogeneous datasets.

Another key peculiarity of the model is its exceptional statistical performance compared to existing methods. The proposed ANFIS model achieved an AAPE of 2.92%, an RMSE of 1.9638%, and an R² of 0.9645, demonstrating its predictive superiority. These metrics reflect the model’s robustness in accurately estimating pressure drops across various operational conditions. Additionally, the ability of the ANFIS model to generalize well across diverse datasets makes it a practical tool for real-world applications in the petroleum industry. This unique adaptability, accuracy, and generalization make the proposed ANFIS model a significant advancement for pressure drop prediction in vertical multiphase flows. In addition, this study can be used to predict the pressure drop directly. Another benefit of this study is that the proposed ANFIS model was created based on the temperature, an essential parameter for accurately predicting the pressure drop in vertical wells.

Criteria of models’ performance evaluations

First, the proposed ANFIS model was trained using 70% of the total dataset. The training dataset was evaluated using statistical error analysis, namely, the R², AAPE, and RSME, to check the accuracy of the proposed ANFIS model. After the proposed ANFIS model can accurately predict the pressure drop, 30% of the total dataset not used in the training dataset was used to validate the proposed ANFIS model using different statical error analyses, like R² and AAPE. In addition, the cross-plotting, KW test, error boxplot and violin graphs, and confidence for the proposed ANFIS and previously published correlations are presented in this study to evaluate and compare the model and correlations.

Statistical error analysis

The statistical error analyses used in this study were calculated using Eq. 9 to 15.

Deviation error ($\:{E}_{i}$)

The deviation error ($\:{E}_{i}$) can be determined as follows:

$$\:{E}_{i}=\frac{Predicted\:pressure\:drop-measured\:\text{p}\text{r}\text{e}\text{s}\text{s}\text{u}\text{r}\text{e}\:\text{d}\text{r}\text{o}\text{p}}{measured\:\text{p}\text{r}\text{e}\text{s}\text{s}\text{u}\text{r}\text{e}\:\text{d}\text{r}\text{o}\text{p}}$$

(9)

i = 1, 2, 3, …, n.

Average percentage error (APE).

APE is obtained from Eq. (10):

$$\:\text{A}\text{P}\text{E}\:=\left(\frac{1}{n}\right){\sum\:}_{i=1}^{n}{E}_{i}\text{*}100$$

(10)

Average absolute percentage error (AAPE).

AAPE is given in the following:

$$\:\text{A}\text{A}\text{P}\text{E}\:\:=\:\left(\frac{1}{n}\right){\sum\:}_{i=1}^{n}\left|{E}_{i}\right|\text{*}100$$

(11)

Average absolute error (AAE).

AAE is given in the following:

$$\:\text{A}\text{A}\text{E}\:=\:\left(\frac{1}{n}\right){\sum\:}_{i=1}^{n}\left|{E}_{i}\right|$$

(12)

The coefficient of determination ($\:{R}^{2}$)

$\:{R}^{2}$ is estimated from:

$$\:{R}^{2}=1-\frac{{\sum\:}_{i=1}^{n}[measured\:\text{p}\text{r}\text{e}\text{s}\text{s}\text{u}\text{r}\text{e}\:\text{d}\text{r}\text{o}\text{p}-predicted\:\:\text{p}\text{r}\text{e}\text{s}\text{s}\text{u}\text{r}\text{e}\:\text{d}\text{r}\text{o}\text{p}{]}^{2}}{{\sum\:}_{i=1}^{n}[measured\:\:\text{p}\text{r}\text{e}\text{s}\text{s}\text{u}\text{r}\text{e}\:\text{d}\text{r}\text{o}\text{p}-\underset{\_}{\varDelta\:}\:\text{p}\text{r}\text{e}\text{s}\text{s}\text{u}\text{r}\text{e}\:\text{d}\text{r}\text{o}\text{p}\:{]}^{2}}$$

(13)

where $\:\underset{\_}{\varDelta\:}{E}_{s}\:\:=\:\frac{1}{n}{\sum\:}_{i=1}^{N}[measured\:\:\text{p}\text{r}\text{e}\text{s}\text{s}\text{u}\text{r}\text{e}\:\text{d}\text{r}\text{o}\text{p}\:{]}_{i}$

Standard Deviation (STD).

The STD is represented in the following equation:

$$\:STD=\sqrt{\frac{{\sum\:}_{i=1}^{n}[{x}_{i\:errors}{-{\stackrel{-}{x}}_{errors}]}^{2}}{n-1}}$$

(14)

Root mean square error (RMSE).

The RMSE is calculated from Eq. (15):

$$\:RMSE=\sqrt{\left[\frac{1}{n}{\sum\:}_{i=1}^{n}{E}_{i}^{2}\right]}$$

(15)

Kruskal–Wallis (KW) test

The KW test evaluates whether there are statistically significant differences among groups. This study used the KW test for the predicted and measured values to indicate the pressure drop in two groups. The KW test is a nonparametric rank test that tests the Null Hypothesis (*H_O) that the data from all groups come from a single population. The KW test is a one-way Analysis of Variance (ANOVA), which assumes a normal data distribution. This test can be used here to show any differences between the measured and predicted pressure drop values obtained from the proposed ANFIS and previously published models. In this test, the differences between the measured and predicted pressure drop values can be checked and proved by this test for the proposed ANFIS and previously published models.

The probability (p)-value obtained from the statistical analysis represents the probability of observing the data if the *H_O​ is true, where *H_O​ states no significant difference between the measured and predicted values. A p-value more significant than 0.05 means failing to reject *H_O​ or accept the *H_O, indicating that the predicted values are not significantly different between the measured and predicted values and, therefore, prove good agreement between the measured and predicted values. Conversely, p-values less than or equal to 0.05 indicate rejecting *H_O​, proving a significant difference between the predicted and measured values. The p-value serves as a critical metric for assessing the predictive performance of the models⁸¹.

Violin graphs

A violin plot is a powerful visualization that combines features of a box plot and a density plot to display the distribution of a dataset. It offers insights into the data’s spread, central tendency, and probability density. The central portion of the violin plot contains a box that shows the IQR, like a box plot, with a line indicating the median. The “violin” shape, created by mirroring a kernel density estimation on both sides, reveals the data’s distribution, making it easy to identify skewness, multimodal distributions, and variations in density. Violin plots show more information about the shape of the data, making them useful for comparing distributions across multiple categories or assessing the uncertainty and variability in modeling errors. The violin plot is a valuable tool for visualizing the error distribution of different models’ performances. The width of each violin shape indicates the frequency of errors at various levels, helping to identify error concentration, skewness, and outliers. The symmetrical structure of the violins provides insight into the distribution, showing whether errors are normally distributed or exhibit multimodal characteristics⁸². This visualization is particularly useful for comparing the models, as it displays differences in error dispersion and central tendencies. By using violin plots, we can better evaluate the stability and overall predictive accuracy of the proposed ANFIS and previously published models.

Error boxplot

In this part, the $\:{E}_{i}$ was determined using Eq. 9 for the proposed ANFIS and previously published correlations. Then, the boxplot was used to show and compare this error ($\:{E}_{i}$) for the proposed ANFIS and previously published correlations. A BAW plot, identified as a box plot, is a statistical visualization utilized to show the distribution of a dataset. It contains a rectangular box that signifies the IQR, spanning from Q1 to Q3, with a horizontal line inside the box indicating the median. The “whiskers” extend from the box to show the range within 1.5 times the IQR, apprehending most data points. Any data points beyond this range are considered outliers. Moreover, the mean may be represented with a small square. This visualization effectively summarizes data distribution, highlighting central tendency, variability, and potential outliers. This plot assessed model performance or errors by showing a clear statistical summary of the error distribution.

Confidence interval (CI)

A Confidence Interval (CI) can be obtained from the mean of the estimate plus and minus the STD in that estimate by using the Eq. 16:

$$\:\text{C}\text{I}=\stackrel{-}{x}\pm\:\text{z}\text{*}\frac{STD}{\sqrt{n}}$$

(16)

Where CI Confidence Interval; $\:\stackrel{-}{x}$: mean (average), and in this study, AAPE was used for the previously published and proposed ANFIS models; z: confidence level value and here z = 2 to obtain a 95% confidence; STD: Standard Deviation⁸³.

A CI shows a range of values within which the actual value of a parameter, such as a prediction error, is expected to fall with a certain probability (typically 95%). It accounts for variability in data and provides insight into the reliability and precision of a model’s predictions. In this study, CIs are used to compare the performance of the proposed ANFIS model against several previously published correlations. By including upper and lower bounds as well as the mean, the CI provides a comprehensive evaluation of the accuracy and consistency of each model. The narrower the interval, the more precise the model, while a lower mean error reflects greater accuracy⁸³.

Results and discussions

The developed ANFIS model results

Figure 5 shows a schematic of the proposed ANFIS model. Figure 5 demonstrates the ANFIS used to predict pressure drop based on inputs, which are WHP, oil rate, water rate, gas rate, inner diameter, surface temperature, and pipe length. The inputs are processed through Input Membership Functions (Inputmf) that convert the crisp input values into fuzzy sets. Logical operations, represented by nodes, form the basis for rule evaluation, determining how the inputs interact to influence the output. In the rule layer, blue nodes represent logic, which are then aggregated to produce fuzzy Output Membership Functions (Outputmf). These are subsequently defuzzied into a single crisp output, predicting the pressure drop. Figure 5 exemplifies how FL enables accurate modelling and analysis of the pressure drop.

Fig. 5

Schematic of the proposed model.

To facilitate understanding and implementation of the developed ANFIS model, the hyperparameters of the developed ANFIS model, including weight functions used in the model, are discussed. The ANFIS model employs Gaussian membership functions for each input parameter (e.g., WHP, oil rate, water rate, gas rate, inner diameter, surface temperature, and length), with weights determined by training the model on the dataset using hybrid optimization methods (a combination of least squares and gradient descent), Table 3. The weights represent the contribution of each fuzzy rule to the final output. For instance, the pressure drop prediction is calculated as a weighted sum of the fuzzy rules’ outputs, where the weights are derived from the model’s training process. The Sugeno type was used in this developed ANFIS to show the best model. The type of membership function is Gaussian curve membership. The training type for the developed ANFIS model is genfis2. The cluster center’s influence range is the most critical parameter in the ANFIS model and is 1.426, Table 3. Table 3 presents the key parameters and their corresponding description and/or values, while Fig. 5 illustrates the overall architecture of the developed ANFIS model, including the layer-by-layer computation process. This detailed framework ensures transparency in the model’s construction and functionality, enabling users to replicate or customize it for specific datasets.

Table 3 The developed ANFIS model’s hyperparameters.

To demonstrate its practical application for future prediction, we provide an example. Consider a hypothetical scenario where field parameters include a WHP, an oil rate, a water rate, a gas rate, an inner diameter, a surface temperature, and a vertical length. When the inputs are fed into the ANFIS model, the system processes them through the defined membership functions and fuzzy rules, yielding an accurate pressure drop prediction. This process is visualized in Fig. 5, which outlines the step-by-step data flow through the ANFIS architecture. By integrating the weight functions and rules with this practical workflow, the developed model becomes a valuable tool for industry practitioners, allowing them to input real-time field data and obtain reliable pressure drop predictions for optimizing well performance and design.

The importance of the developed ANFIS model is to accurately predict the pressure drop, which is a critical parameter in petroleum engineering as it directly impacts the design, optimization, and economic feasibility of oil and gas production systems. Accurate prediction of pressure drop in multiphase flow systems is essential for selecting appropriate tubing sizes, determining optimal WHP, designing surface facilities, and ensuring fluid-safe and efficient transportation. The accuracy of pressure drop calculations is crucial for guaranteeing reliable system performance and decision-making. Furthermore, pressure drop influences key processes like artificial lift optimization, flow assurance, and predicting phenomena such as slugging or hydrate formation, which can disrupt production operations³. Understanding pressure behavior helps design injection patterns and optimize fluid mobility ratios for improved oil recovery⁸⁴. Excessive pressure drop near the wellbore can lead to mechanical failure of the formation, resulting in sand production and associated operational challenges⁸⁵. Reservoir engineers analyze pressure drops to design effective completion strategies, including gravel packing or screen installations⁸⁶.

Previously published correlations and empirical models often exhibit limited accuracy when applied to conditions beyond their calibration range. Inaccurate pressure drop predictions can result in over- or under-designing production equipment, leading to financial losses or operational risks. Misestimating pressure drops can lead to operational inefficiencies, such as insufficient lifting power, equipment failures, or suboptimal production rates, ultimately increasing operational costs and reducing overall field recovery. Overestimating pressure drop may necessitate unnecessarily high compression or pumping power while underestimating it could result in fluid flow interruptions or equipment damage⁸⁷. Therefore, achieving high accuracy in pressure drop predictions enhances operational efficiency and supports better planning and resource allocation in petroleum engineering projects.

The proposed ANFIS performance evaluation results

The proposed ANFIS model accurately predicted the pressure drop, and it was evaluated using cross-plotting, error distribution, and different statistical error analyses.

Figures 6 and 7 show the cross-plotting of the predicted pressure drop against the actual pressure drop in a multiphase flow line for training and testing data sets, respectively. A closer look into the plots shows that the lines for the training and testing data sets are well-fitted on the scatter plots. The data points are closely aligned with the diagonal line, representing an ideal match between predictions and actual measurements for the training dataset in Fig. 6 and the testing dataset in Fig. 7. The high R² of 0.9832 for the training dataset and (R² = 0.9645) for the testing dataset indicates high predictive accuracy in predicting the pressure drop effectively.

Furthermore, this fact is proved by the AAPE, which is reported as 1.8123 for the training dataset in Fig. 6.929 for the testing dataset in Fig. 7. A strong correlation between the two (predicted and measured) pressure drops and low AAPE is thus presented. Moreover, the uncertainty of the measured pressure drop is assumed to be less than 0.5%, which introduces bias and discrepancy between the two data sets during both processes of training and testing, respectively. Such a low AAPE value highlights minimal deviation between predicted and actual values, reflecting the robustness of the ANFIS approach used. This plot is a visual validation of the model’s ability to predict pressure drops accurately. Therefore, the pressure drop prediction potential of the ANFIS is affirmed.

Fig. 6

Cross plot of pressure drop (training set).

Fig. 7

Cross plot of pressure drop (testing set).

Table 4 shows the statistical error analysis of the proposed model to predict the pressure drop. As shown in Table 4, the proposed ANFIS model has RMSE of 2.2148 and 1.963 psi for the training and test datasets, respectively. The prediction of pressure drops by applying the ANFIS model yields good AAPE of 1.8123% and 2.929% for training and testing datasets. The proposed ANFIS model has R² of 0.9832 and 0.9645 for training and testing datasets, respectively, and has STD of 1.3630 and 1.9101 for the training and testing datasets, respectively. The six statistical error analyses applied to judge the effectiveness of the ANFIS model show that the proposed ANFIS model has high accuracy in predicting the pressure drop. The results confirm the model’s strong predictive capability for pressure drop across training and testing datasets.

Table 4 Statistical error analysis of the ANFIS model.

Figures 8 and 9 present the error distribution for the training and testing datasets, respectively. In Fig. 8, the errors for the training dataset range from − 5 to 5, with the majority clustered around zero, indicating minimal deviation from actual values. Similarly, Fig. 9 shows that the errors for the testing dataset range from − 7 to 7, with most errors also concentrated around zero. This consistent clustering of errors near zero in both datasets suggests that the proposed ANFIS model is highly accurate in predicting pressure drop. The slight difference in error ranges between the training and testing datasets indicates good generalization to unseen data without significant overfitting. Overall, Figs. 8 and 9 show the robustness and accuracy of the ANFIS model in predicting pressure drop effectively. Most of the errors are concentrated around zero, indicating that the model’s predictions are accurate and close to the actual values for training and testing datasets.

Fig. 8

Error distribution for the training dataset.

Fig. 9

Error distribution for the testing dataset.

Comparisons of the proposed ANFIS and previous models

Statistic error analysis comparison

A comparative analysis is performed to assess the efficiency of the proposed ANFIS model developed with frequently used models to predict the pressure drop. The eight frequently used correlations and models in this scope are Duns and Ros⁵⁰, Hagedorn and Brown¹², Orkiszewski⁶, Aziz and Govier⁵², Beggs and Brill¹³, Gray⁵¹, Mukherjee and Brill¹⁷, and Ansari et al.¹⁴. The models were compared based on the computed statistic error analysis values of AAPE, R², Maximum Absolute Error (MaxAE), Minimum Absolute Error (MinAE), RMSE, and STD, as shown in Fig. 10 (a-c). The models were ordered based on the low values of AAPE and the high values of R².

Figure 10 (a) shows the RMSE and AAPE for the previous and proposed ANFIS models. The data illustrated in Fig. 10 (a) shows that the proposed ANFIS model achieves the lowest values for both AAPE and RMSE. The Beggs & Brill¹³ model emerges as the second-best method for predicting the pressure drop. In more detail, the previous models demonstrate AAPE values exceeding six and RMSE values greater than 8. In contrast, the proposed ANFIS model significantly improves with AAPE values under three and RMSE values below 2. This substantial reduction in error metrics highlights the superior accuracy of the proposed ANFIS model in predicting pressure drop. Therefore, based on the comparative analysis shown in Fig. 10 (a), the proposed ANFIS model is confirmed to be highly accurate for predicting pressure, outperforming current models in the literature by an outstanding margin.

Fig. 10

(a) RMSE and AAPE comparison of the previous and proposed ANFIS models. (b) R² and MinAE comparison of the previous and proposed ANFIS models. (c) STD and MaxAE comparison of the previous and proposed ANFIS models.

Figure 10 (b) shows the R² and MinAE of the previous and proposed ANFIS models. Figure 10 (b) shows that the proposed ANFIS model achieves the highest R² value of 0.96, indicating superior performance in predicting pressure drop. In contrast, the second-best model, Beggs & Brill¹³, has an R² value of less than 0.86. The significance increases in R² by the proposed ANFIS model, exceeding 10% improvement over the existing models, underscores its enhanced accuracy in pressure drop prediction. This improvement highlights the effectiveness of the ANFIS method in capturing the complex relationships within the data, leading to more reliable and precise predictions.

Figure 10 (c) shows the STD and MaxAE of the previous and proposed ANFIS models. Figure 10 (c) demonstrates that the proposed ANFIS model performs the lowest values in both STD and MaxAe when compared to the existing models. Specifically, the proposed ANFIS model exhibits an STD of 1.9 and a MaxAE of 8.34. The Beggs & Brill¹³ model shows significantly higher values, with an STD of 7.9 and a MaxAE of 24.9. The other preceding models, which follow the Beggs & Brill¹³ model in performance, have STDs ranging from 8.1 to 14.6 and MaxAEs ranging from 24.2 to 50.6. The decrease in MaxAE, from values as high as 24.9 to just 8.34, underscores the exceptional accuracy of the proposed ANFIS model in predicting pressure drop. By minimizing these error metrics, the proposed ANFIS model shows a substantial performance improvement and provides evidence of its superior reliability and accuracy in pressure drop predictions.

The statistical error analysis in Figs. 10 (a-c) reveals that the proposed ANFIS model significantly outperforms existing models in predicting pressure drop. The proposed ANFIS model achieves the lowest values for RMSE, AAPE, STD, and MaxAE and the highest R²-value, demonstrating superior accuracy and reliability. Specifically, the proposed ANFIS model consistently shows error metrics far lower than those of the Beggs & Brill¹³ and other preceding models, highlighting its exceptional capability to capture complex relationships within the data and make precise predictions. The significant reductions in prediction errors and improvements in accuracy indicators affirm the proposed ANFIS model as a highly effective and reliable tool for pressure drop prediction, surpassing current models.

Figure 11 is a pictorial view of this study: the AAPE vs. R² plot shows the best-performing models in the upper left corner with the lowest magnitudes of AAPE and the highest R². Therefore, the proposed ANFIS model shows the lowest value for AAPE of 2.929% and the highest value for R² of 0.9645. These results highlight the implications and robustness of the proposed ANFIS model compared to previous models. Moreover, as shown in Fig. 11, the second-best model is the Beggs & Brill¹³ model, with an AAPE of 6.4278% and R² of 0.8667. The last-rank model is Aziz and Govier’s⁵² model, which has 12.0968% AAPE and 0.5158 R². In summary, prediction results obtained by the proposed ANFIS model surpass all models in terms of prediction accuracy.

Fig. 11

AAPE and R² of the proposed ANFIS and previous models.

Cross-plotting comparison

After comparing the proposed ANFIS model and the other models using statistical error analysis, the performance of all previous models is described using the cross-plotting in Fig. 12. The cross-plotting of the proposed ANFIS model for the training and testing datasets was discussed earlier in the ANFIS model section. The ANFIS model demonstrates the best performance among all other models, an expected result given its superior error metrics and accuracy indicators. Figure 12 compares the predicted pressure drops from various correlations with the measured pressure drop. The 45^o degree line shows the ideal correlation where the expected pressure drop equals the measured values, serving as a benchmark for model accuracy. Each data point illustrates the performance of a specific model, and their proximity to the diagonal indicates the prediction accuracy. While some correlations, such as Mukherjee and Brill¹⁷ and Beggs and Brill’s¹³ correlations, cluster closer to the 45^o degree line, others demonstrate noticeable deviations, showing underprediction or overprediction for some points. Figure 12 underscores the importance of selecting appropriate models to ensure accurate pressure drop predictions in multiphase flow scenarios. This comparison can aid engineers in identifying suitable models for pressure drop prediction to help design and optimize production systems.

Fig. 12

Cross-plotting for the previous models to predict the pressure drop.

In addition, the cross-plotting for each previous correlation of all previous correlations is shown in Figures (S8-S15). The density of the dots surrounding the line indicates the good accuracy of these models. In addition, the highest accuracy for some models is attained if the prediction is made for pressure values below and/or above 1500 psi. These results demonstrate the ineffectiveness of counterpart models and correlations in pressure drop prediction for a wide range. On the contrary, the proposed models (ANFIS and ANN) could predict the pressure drop for a wide range of values with great accuracy, as discussed earlier in the ANFIS model section.

Kruskal-Wallis (KW) test comparison

The models that accepted *H_O​ include the proposed ANFIS model (p = 0.9308), Beggs & Brill¹³ (p = 0.2467), and Dun & Ros⁵⁰ (p = 0.0577), Table 5. The high p-values indicate strong agreement between the predicted and measured values, showcasing their robustness and accuracy. Notably, the proposed ANFIS model significantly outperforms other models, demonstrating its superior ability to predict pressure drops with minimal deviation. Beggs & Brill also performs relatively well, although its predictive accuracy is slightly lower than that of the proposed ANFIS model.

In contrast, the models that reject *H_O​, such as Gray⁵¹ (p = 0.000026), Hagedorn & Brown¹² (p = 0.000010), and Orkiszewski⁶ (p = 0.000090), Table 5, shows significant differences between the measured and predicted values. The *H_O is rejected, so there is a substantial difference between the measured and predicted values. The low p-values show the limitations of these models in accurately predicting pressure drops, potentially due to using empirical correlations and limited data ranges. Other models, such as Aziz & Govier⁵² and Ansari et al.¹⁴, also fall into this category with varying degrees of deviation.

Table 5 P values of KW test at 95% significance level.

Error boxplot and violin graphs comparison

Figures 13, 14 and 15 show the error boxplot and violin graphs to compare the predictive accuracy of the proposed ANFIS model with several previously published correlations, including Beggs & Brill¹³, Duns & Ros⁵⁰, Ansari et al.¹⁴, Mukherjee & Brill¹⁷, Orkzwiski⁶, Gray⁵¹, Hagedorn & Brown¹¹, and Aziz & Govier⁵².

The violin plot (Fig. 13) combines the spread and density of errors, showing where most predictions fall within the error range. It highlights how the ANFIS model has a much narrower and symmetrical distribution (mean = median = mode) centered near zero error, unlike traditional models’ broader and skewed distributions. The mean = median = mode means that most of the points of the proposed ANFIS model have almost zero error. However, the previously published correlations have some points of error far from the centered near zero error, Fig. 13.

The other models are Beggs & Brill¹³, Duns & Ros⁵⁰, Ansari et al.¹⁴, Mukherjee & Brill¹⁷, Orkzwiski⁴⁵, Gray⁵⁰, Hagedorn & Brown¹², and Aziz & Govier⁵¹ display broader distributions, signifying more considerable variations in error values, with some showing significant deviations both above and below the zero-error line, Fig. 13. Models such as Aziz & Govier⁵¹ and Hagedorn & Brown¹¹ have the broadest distributions, suggesting more significant uncertainty and less predictive reliability Fig. 13. In contrast, the proposed ANFIS model maintains a relatively small error range, reinforcing its robustness in making accurate predictions. This comparison highlights the effectiveness of the ANFIS approach in minimizing prediction errors, making it a promising alternative to conventional empirical and theoretical models.

The box plot (Fig. 14) complements this by emphasizing each model’s quartile ranges, median, mean, and outliers. It reveals that the ANFIS model has a lower mean error and significantly no outliers, meaning its predictions are more consistent and reliable compared to the others. On the other hand, the previously published correlations have some outliers, which are the points that are far from the zero error.

The proposed ANFIS model demonstrates remarkable accuracy and robustness in its predictions. Its tightly clustered error distribution and minimal outliers suggest that it effectively captures the underlying relationships in the data, handling complexities that may arise from nonlinear behaviors in flow systems. The near-zero median error indicates high reliability, while the reduced IQR signifies minimal prediction variability. This performance reflects the strength of ANFIS in combining neural networks’ learning capabilities with FL’s reasoning and interpretability. The proposed ANFIS model is a highly reliable choice for accurate pressure drop predictions.

On the other hand, the previously published correlations show more significant error spreads and greater variability in Figs. 13 and 14. The presence of more substantial outliers and wider IQRs for the previously published correlations indicates their limited ability to capture the complexities of real-world systems compared to the proposed ANFIS model. These findings highlight the need for advanced, data-driven approaches like ANFIS to overcome the limitations of previous models, ensuring better accuracy and broader applicability.

Among the empirical models, Aziz & Govier⁵² and Hagedorn & Brown¹² exhibit the most extensive errors, with many outliers suggesting less reliability in their predictions. Other models, such as Orkzwiski⁴⁵ and Gray⁵⁰, show moderate performance but still have relatively large error distributions. The Beggs & Brill¹³ and Duns & Ros⁵⁰ models have lower error variability than the others, but their median and mean errors remain higher than those of the proposed ANFIS model. The consistent performance of the ANFIS model, with minimal outliers and a narrower range of errors, highlights its potential as a robust alternative for improving prediction accuracy in pressure drop prediction.

Figure 15 shows an error boxplot with violin graphs for the previously published and proposed ANFIS models to display the models’ errors with a combination of these graphs; however, the previous figure (Fig. 14) clearly showed the outliers for the models. The proposed ANFIS model shows a significantly lower error distribution than conventional models, as shown in the violin plot. The proposed ANFIS model has a narrow spread of error percentages, with most values concentrated around zero, indicating high accuracy and precision. The black box (25–75% interquartile range) is compact, and the median error is close to zero, reinforcing the model’s robustness. The reduced variance and minimal outliers suggest that ANFIS effectively captures complex nonlinear relationships in the dataset, making it a reliable predictive tool with superior performance.

On the other hand, the previously published models, including Beggs & Brill¹³, Duns & Ros⁵⁰, Ansari et al.¹⁴, Mukherjee & Brill¹⁷, Orkzwiski⁶, Gray⁵¹, Hagedorn & Brown¹², and Aziz & Govier⁵², show broader distributions of error percentages. These previously published models show wider IQR ranges and extended tails, indicating higher variability and a greater likelihood of extreme errors. The median errors deviate from zero compared to ANFIS, suggesting potential biases or limitations in their predictive capabilities to predict the pressure drop in the vertical wells. The more extensive spread of errors and occasional extreme deviations highlight the difficulty of accurately modeling complex fluid dynamics with previously published models, reinforcing the advantages of using AI-driven methodologies like the proposed ANFIS to find the pressure drop.

Figures 13, 14 and 15 show that the proposed ANFIS model is highly accurate in predicting the pressure drop compared to the previously published models.

Fig. 13

Error boxplot with violin graphs for the previously published and proposed ANFIS models.

Fig. 14

Error boxplot graphs for the previously published and proposed ANFIS models.

Fig. 15

Error boxplot with violin graphs for the previously published and proposed ANFIS models.

Confidence interval (CI) comparison

Figure 16 shows the CI for the previously published and proposed ANFIS models. As shown in Fig. 16, the proposed ANFIS model demonstrates the best performance among all models presented in the figure. Its narrowest CI exhibits the lowest mean error, indicating high accuracy. The small range between the upper and lower bounds reflects the model’s consistency across different datasets or conditions. This superior performance highlights the robustness of the ANFIS model.

As shown in Fig. 16, the previously published correlations show varying levels of accuracy and precision, as indicated by their CIs and mean errors. Correlations like those of Beggs & Brill¹³, Duns & Ros⁵⁰, and Ansari et al.¹⁴ exhibit moderate performance, with overlapping intervals suggesting similar predictive capabilities. On the other hand, correlations such as Aziz & Govier⁵² and Hagedorn & Brown¹² have higher mean errors and wider CIs, reflecting lower reliability and more significant variability in their predictions. While correlations like Gray⁵¹ and Orkiszewski⁶ perform slightly better, they still fall short compared to the proposed ANFIS model. These results show that the proposed ANFIS model is the optimum model to predict the pressure drop.

Fig. 16

Confidence interval for the previously published and proposed ANFIS models.

Conclusions

The developed ANFIS model is important for accurately predicting the pressure drop, which is a critical parameter in petroleum engineering as it directly impacts the design, optimization, and economic feasibility of oil and gas production systems. The accuracy of pressure drop calculations is crucial for ensuring reliable system performance and decision-making. Reservoir engineers analyze pressure drops to design effective completion strategies, including gravel packing or screen installations⁸⁶.

While traditional empirical and mechanistic models have been widely used, their accuracy is typically constrained by assumptions and simplified relationships. In comparison, machine learning models’ performance is due to their ability to model nonlinear relationships in complex datasets. Al-Shammari³², Nwanwe, and Duru³³ models improve forecast accuracy, effectively handling reservoir uncertainty. However, Al-Shammari³²’s model was applied to predict the BHP, and after that, some of them found the pressure drop based on the BHP. Nwanwe and Duru’s³³ models did not consider the temperature as input to predict the pressure drop, which resulted in high errors due to the lack of a ratio to the amount of free gas³⁰.

The novelty of this study is that it uses ANFIS, a hybrid scheme composed of FL and ANN. It is an efficient and robust tool because it can handle the uncertainty of vagueness and imprecision³². Furthermore, ANFIS offers advantages over standard mathematical formulations; the inference process is relatively close to human thinking. Furthermore, the proposed ANFIS model in this study considers temperature as one input of the used inputs, an important parameter to consider when predicting pressure drop. Also, the proposed ANFIS model was used to predict the pressure drop directly compared to other models, which were used first to find the BHP; then, they found the pressure drop based on the BHP.

In this study, 335 datasets collected from different sources were used to develop the ANFIS model. The performance of the proposed ANFIS model was evaluated through cross plot, error distribution, KW test, error boxplot and violin graphs, CI, and different statistical error analyses, such as AAPE and RSME. The efficiency of the ANFIS model was tested against nine well-known models.

The proposed model demonstrated excellent accuracy, with the lowest error (AAPE of 2.92%), the lowest RMSE (1.9638%), and the highest R² (0.9645). Thus, the ANFIS outperforms the models currently used in the industry.

The outcomes gained in this paper lead to the following conclusions:

• 335 datasets collected from different sources were used to develop the ANFIS model to predict the pressure drops accurately.

• The proposed ANFIS model predicts the pressure drop based on WHP, oil rate, water rate, gas rate, inner diameter, surface temperature, and length.

• The proposed ANFIS model was evaluated using cross-plot, statistical error analyses, error distribution, KW test, error boxplot and violin graphs, and CI to show the ANFIS model’s performance.

• The proposed ANFIS model was compared with the previously published model: Beggs & Brill¹³, Duns & Ros⁵⁰, Ansari et al.¹⁴, Mukherjee & Brill¹⁷, Orkzwiski⁶, Gray⁵¹, Hagedorn & Brown¹², and Aziz & Govier⁵².

• The proposed ANFIS model is the optimum model for predicting pressure drops, with the lowest AAPE of 2.92%, the lowest RMSE of 1.9638%, and the highest R² of 0.9645.

• The KW test, error boxplot and violin graphs, and CI results indicated that the proposed ANFIS model is the best model for predicting pressure drops.

• The error boxplot and violin graphs show that the proposed ANFIS model has a high accuracy in predicting the pressure drop compared to the previously published models.

• The CI figure demonstrates that the proposed ANFIS model is the best performance model to predict the pressure drop compared to all previously published models. The proposed ANFIS model’s CI is the narrowest and displays the lowest mean error, indicating high accuracy. The small range between the upper and lower bounds reflects the model’s consistency across different datasets or conditions. This superior performance shows the high accuracy of the ANFIS model in finding the pressure drop in the vertical wells.

• The second rank model to predict the pressure drops in this study is Beggs & Brill¹³ with AAPE of 2.929%, RMSE of 1.9638, and R² of 0.9645.

• The last rank model to predict the pressure drops in this study is Aziz & Govier⁵² with AAPE of 12.0968%, RMSE of 15.824, and R² of 0.5158.

Benefits and limitations of the proposed ANFIS model

The developed ANFIS model can accurately predict the pressure drop within the following ranges: pressure drops (1077–2927) psi, WHP (160–545) psi, oil rate (2200–25000) bbl/d, water rate (0-8424) bbl/d, gas rate (1078-19658.2) Mscf/d, inner diameter (6.065–10.02) inch, surface temperature (63–186) °F, and length (500-26700) ft. However, the benefits of the developed ANFIS model in predicting pressure drops exceed its limitations. The developed ANFIS model to find the pressure drops was assessed using different methods: cross plot, statistical error analyses, error distribution, KW test, error boxplot and violin graphs, and CI. The results indicate that the developed ANFIS model best predicted the pressure drops.