Introduction

Climate change is a pressing global challenge with profound implications for ecosystems, economies, and human livelihoods. General Circulation Models (GCMs) are indispensable tools for understanding climate variability and projecting future scenarios. The Coupled Model Intercomparison Project (CMIP), established under the World Climate Research Programme (WCRP), provides a standardized framework for assessing GCMs. Its sixth phase (CMIP6) incorporates significant advancements, including improved resolution, scenario designs, and representation of physical processes, making it a crucial resource for climate research1,2. However, regional applications of GCMs often face significant uncertainties due to differences in spatial resolution, parameterization schemes, and calibration methods3,4. These uncertainties are particularly critical for regions like Bangladesh, where the impacts of climate variability are deeply intertwined with socio-economic and environmental conditions.

Bangladesh is one of the most climate-vulnerable countries globally, facing a range of challenges, including cyclones, floods, droughts, and rising sea levels5,6. Its geographical characteristics, with low-lying floodplains and a monsoon-dominated climate, make it particularly susceptible to climate-induced disasters. The average annual precipitation is around 2200 mm, while temperatures vary between 15 °C in winter and 34 °C in summer, significantly influencing agriculture, water resources, and disaster management7,8,9,10,11,12,13,14,15,16,17,18. Climate projections for key variables such as precipitation, maximum temperature (Tmax), and minimum temperature (Tmin) are essential for addressing these challenges. However, the coarse spatial resolution of many GCMs limits their ability to capture localized climatic features, necessitating robust evaluation and optimization methods for their selection and application.

Although studies have explored GCM performance in regions such as India, Iran, and North Korea using multi-criteria decision-making (MCDM) techniques like the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS)19,20,21, similar evaluations for Bangladesh remain scarce. Kamruzzaman et al.22 used Shannon’s Entropy to evaluate CMIP6 models for precipitation climatology, while Kamruzzaman et al.23 compared the performance of CMIP5 and CMIP6 models for Bangladesh using global performance indicators. These studies highlighted the superior performance of CMIP6 over CMIP5 but did not employ comprehensive ranking methodologies across multiple climatic variables and time scales. Additionally, research in other regions, such as East Asia24, Vietnam25, and Pakistan26, has demonstrated the efficacy of TOPSIS in ranking GCMs for localized applications. This study builds on these efforts, pioneering a novel approach by evaluating 19 CMIP6 GCMs for their ability to replicate precipitation, Tmax, and Tmin in Bangladesh using a robust multi-metric framework.

The evaluation spans from 1986 to 2014, with ERA5 reanalysis data serving as the observational benchmark. Seven statistical metrics, including Kling-Gupta Efficiency (KGE), Nash–Sutcliffe Efficiency (NSE), and Mean Absolute Error (MAE), are employed to assess GCM performance across seasonal and annual time scales27. The application of TOPSIS facilitates the derivation of seasonal and annual rankings, culminating in a comprehensive ranking metric (RM) to identify the most reliable models. Such integrative approaches are increasingly recognized as essential for addressing the uncertainties inherent in GCM outputs20,28,29.

Another novel aspect of this study is its comparison of ensemble mean techniques, specifically Arithmetic Mean (AM) and Bayesian Model Averaging (BMA). Ensemble methods are widely used to reduce uncertainties in climate projections by combining outputs from multiple models. While AM provides a straightforward averaging approach, BMA assigns weights to individual models based on their historical performance, offering a more probabilistic representation of uncertainties30,31. Previous research has demonstrated the superiority of BMA in reducing biases and improving the accuracy of ensemble projections, as shown in studies conducted in hydrology, ecology, and climate science32,33. By applying these ensemble techniques to climatic variables for Bangladesh, this study offers valuable insights into optimizing projection methodologies for regions with complex climatic conditions.

This research stands out for its multi-faceted approach to addressing the gaps in climate modeling for Bangladesh. It combines advanced statistical metrics, MCDM techniques, and ensemble optimization to identify the most reliable GCMs and ensemble methods for projecting precipitation, Tmax, and Tmin. Unlike previous studies that focused on individual variables or limited time scales, this study integrates seasonal and annual evaluations, offering a comprehensive assessment of GCM performance. The findings are expected to provide actionable insights for policymakers, researchers, and practitioners, enabling more accurate climate projections essential for disaster management, agricultural planning, and sustainable development. Furthermore, the methodological framework developed here can be adapted to other regions facing similar climatic challenges, highlighting its broader applicability and significance in advancing climate science.

Study area & data collection

Study area

Bangladesh, located between latitude 20.34º N and 26.38º N and longitude 88.01º E and 92.41º E, is a country defined by its unique geographical features (Fig. 1). Bounded by India on three sides and the Bay of Bengal to the south, it is a low-lying riverine nation where most of the land barely rises above 10 m above sea level, except for hilly regions in the southeast and parts of the north34. Bangladesh is one of the most densely inhabited countries in the world, with approximately 1329 people residing per km2. Its geographical location gives rise to distinct seasons, as classified by the Bangladesh Meteorological Department (BMD): pre-monsoon, Monsoon, post-monsoon, and Winter35. Pre-monsoon months, particularly April and May, are characterized by scorching temperatures exceeding 45 °C and minimal precipitation, occasionally punctuated by thunderstorms. The Monsoon season, spanning June to September, brings the heaviest precipitation, with around 80% of the annual precipitation occurring during this time. Post-monsoon, in October and November, witnessed a decline in temperatures. The winter months, December to February, are cold and dry, with January being the coldest. Bangladesh is also known as the GBM delta due to the presence of three major rivers: the Ganges, Brahmaputra, and Meghna, making it prone to various types of floods, including monsoon floods, flash floods, and cyclone floods, which pose significant challenges to the country34.

Fig. 1
figure 1

Elevation map of the study area. The elevation values are expressed in meters above mean sea level (MSL). Source: Digital elevation model (DEM) from https://earthexplorer.usgs.gov/.

Full size image

Data collection

This work used historical climate data from 19 GCMs obtained from the CMIP6 portal (https://esgf-node.llnl.gov/projects/cmip6/ from 1986 to 2014. They focused on GCMs from the CMIP6 dataset with consistent data availability from 1986 to 2014, covering essential climate variables like precipitation, maximum temperature (Tmax), and minimum temperature (Tmin). ECMWF Reanalysis v5 (ERA5) (https://www.ecmwf.int/en/forecasts/dataset/ecmwf-reanalysis-v5/) is considered as the observed data. This research focuses on three essential climate variables: Precipitation, Tmax, and Tmin. ERA5 is a product of blending model simulations with observed data. To evaluate its effectiveness as a substitute for observational data, it was validated against in-situ measurements from 29 meteorological stations in Bangladesh. The study sought to ascertain the precision of ERA5 in reproducing the seasonal and temporal distribution of precipitation, maximum temperature (Tmax), and minimum temperature (Tmin). The results are illustrated in Figure S1. The monthly mean precipitation, Tmax, and Tmin of ERA5 strongly correlate with in-situ data, suggesting its ability to replicate the annual cycle. The scatter plots of ERA5 versus in-situ data from 1985 to 2014 show strong relationships, with high R-squared values of 0.90 for precipitation, 0.99 for Tmax, and 0.97 for Tmin. The results confirm ERA5 as a suitable substitute for in-situ data and support its use in climatological research in Bangladesh.

The data is carefully examined seasonally and annually to ensure a thorough and geographically specific study. The seasonal study centres on the four typical seasons of Bangladesh: Pre-monsoon, Monsoon, Post-monsoon, and Winter. The seasons are crucial in determining the country’s climate and significantly affect agriculture, water resources, and energy consumption.

The study successfully resolved the resolution discrepancies among the model datasets, which presented a substantial obstacle. The model datasets have been standardized and adjusted to a constant resolution of 0.250 × 0.250, ensuring that the model datasets are aligned with the ERA5 grid.

The research includes a thorough and diversified collection of models from the CMIP6 dataset, as outlined in Table 1. The aim is to include a diverse range of models with different strengths and capacities to comprehensively evaluate their ability to reproduce the specific climate patterns and variations in Bangladesh accurately. Nineteen GCMs were selected based on the availability of both historical simulations and future projections of two key climate variables, precipitation and temperature, for four SSPs (SSP1-2.6, SSP2-4.5, SSP3-7.0, SSP5-8.5). These climate variables are essential for assessing climate change’s impacts, and including four SSPs ensures a comprehensive representation of potential climate outcomes. Therefore, selecting GCMs based on these criteria enables a robust analysis of possible future climate scenarios.

Table 1 List of CMIP6 models used in this study, including their institution, country of origin, and horizontal resolution.
Full size table

Methodology

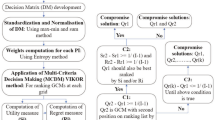
This study is based on a grid-wise analysis of error metrics between GCMs and observed datasets, where the GCMs are interpolated with the same grid point as the observed data. The seasonal and annual rankings of GCMs are based on an MCDM approach. In contrast, the overall ranking of GCMs is based on the ability to replicate seasonal and annual precipitation and temperature patterns36,37. TOPSIS has been used as an MCDM approach38. To mitigate uncertainties, ensemble means are calculated based on their cumulative performance for replicating precipitation, maximum temperature, and minimum temperature. They are used for calculating ensembles via two methods, namely, arithmetic mean (AM) and Bayesian model averaging (BMA). The flowchart of the methodology is given in Fig. 2.

Fig. 2
figure 2

The flowchart summarizes the methodology used in this study.

Full size image

Bilinear interpolation

It is important to note that all 19 GCMs utilized in this research operate at different resolutions. The coarse resolutions of these GCMs do not align with the observed datasets, and they may not yield robust results for a relatively small study area like Bangladesh.

The current study applies bilinear interpolation to re-grid GCMs to a common resolution of 0.250 × 0.250 to address this discrepancy and align the GCMs with the observed datasets. Bilinear interpolation is a statistical method employed to re-grid datasets while preserving the underlying climate signal, as previously discussed by Ahmed et al.39. Bilinear interpolation functions by calculating a weighted average based on the values of the four nearest ERA5 grid locations to estimate the value at the interpolation point. The weight assigned to each ERA5 grid location is the inverse of the distance between the interpolation location and the observed data points. This process ensures a more consistent and coherent dataset for further analysis and comparison with observed data.

Error metrics

Evaluating climate models and their agreement with observed data is crucial in climate change projections. In this study, the assessment is based on seven key error metrics, namely Mean Absolute Error (MAE), Mean Square Error (MSE), Normalized Root Mean Square Error (NRMSE), Nash–Sutcliffe Efficiency (NSE), Index of Agreement (d), Pearson Correlation Coefficient (r), and Kling Gupta Efficiency (KGE). These metrics comprehensively assess GCMs’ performance in replicating observed climate patterns. The utilization of the ‘hydroGOF’ package in RStudio ensures a rigorous and standardized approach to calculating these metrics, enabling researchers to make informed decisions and improve the accuracy of climate projections. This multifaceted evaluation process is instrumental in advancing our understanding of climate dynamics and enhancing the reliability of climate modelling.

Mean absolute error (MAE)

MAE is the arithmetic mean of pairwise absolute error between observed and model datasets. The expected value of MAE is 0. A value closer to 0 indicates better agreement between observed and model variables40

$$\:\text{M}\text{A}\text{E}=\frac{1}{N}\sum\:_{i=1}^{N}\left|\left({s}_{i}-{O}_{i}\right)\right|$$
(1)

Where,

Si = Modeled data, Oi = Observed data, N = Number of Observations.

Mean square error (MSE)

MSE measures the average squared Euclidian distance between observed data and modeled data. The value of MSE is always positive, and the expected value is 0. Value closer to zero indicates a better degree of agreement among modeled and observed variables40

$$\:\text{M}\text{S}\text{E}=\frac{1}{N}\sum\:_{i=1}^{N}{\left({s}_{i}-{O}_{i}\right)}^{2}$$
(2)

Where,

Si = Modeled data, Oi = Observed data, N = Number of Observations.

Normalized root mean square error (NRMSE)

The root mean square error illustrates the Euclidean distance between observed and modeled values, and the NRMSE expresses the percentage disagreement between them. The expected value of this goodness of fit test is 0. Closer to 0 means less distance between the observed and the modeled variables. It avoids scale dependency40.

$$\:\text{NRMSE\:}=100\frac{\sqrt{\frac{1}{N}\sum\:_{i=1}^{N}\:{\left({S}_{i}-{O}_{i}\right)}^{2}}}{{O}_{max}-{O}_{min}}$$
(3)

Where,

Si = Modeled data, Oi = Observed data, N = Number of Observations, Omax is the maximum value of observed data, Omin is the minimum value of observed data.

Nash–Sutcliffe efficiency (NSE)

NSE is a normalized statistical method that compares the magnitude of residual variance among observed and modeled datasets41. The value of this goodness of fit test ranges from – infinity to 1. The most desired value is 1, which indicates a perfect match between modeled and observed data.

$$\:\text{N}\text{S}\text{E}=1-\frac{\sum\:_{i=1}^{N}\:{\left({S}_{i}-{O}_{i}\right)}^{2}}{\sum\:_{i=1}^{N}\:{\left({O}_{i}-\stackrel{-}{O}\right)}^{2}}$$
(4)

Where,

Si = Model data, Oi = Observation data, N = Number of Observations.

Index of agreement (d)

The d identifies proportional and additive differences between the observed and modeled means and variances. The value ranges from 0 to 1. 1 is the most desired value. It indicates a perfect match, whereas 0 indicates no agreement between observed and modeled variables. It was developed by Willmott in 198142

$$\:d=1-\frac{\sum\:_{i=1}^{N}\:{\left({O}_{i}-{S}_{i}\right)}^{2}}{\sum\:_{i=1}^{N}\:{\left(\left|{S}_{i}-\stackrel{-}{O}\right|+\left|{O}_{i}-\stackrel{-}{O}\right|\right)}^{2}}$$
(5)

Where,

Si = Model data, Oi = Observation data, N = Number of Observations.

Pearson correlation coefficient (r)

The r measures the strength and relationship between two variables. A value closer to 1 represents a strong positive relationship and is the most desired value. The value of r ranges from − 1 to 1.

$$\:r=\frac{\sum\:\left({O}_{i}-\stackrel{-}{O}\right)\left({S}_{i}-\stackrel{-}{S}\right)}{\sqrt{\sum\:{\left({O}_{i}-\stackrel{-}{O}\right)}^{2}\sum\:{\left({S}_{i}-\stackrel{-}{S}\right)}^{2}}}$$
(6)

Where,

Si = Model data, Oi = Observation data.

Kling Gupta efficiency (KGE)

KGE evenly combines the three sections of the Nash-Sutcliffe efficiency (NSE) of model errors: correlation, bias, and a ratio of variances, or coefficients of variation. It has become a popular method for calibrating and assessing hydrological models43. KGE value closer to 1 represents a more accurate model. It was founded and modified by Kling and Gupta44,45.

$$\:\begin{array}{c}KGE=1-\sqrt{(r-1{)}^{2}+(\beta\:-1{)}^{2}+(\gamma\:-1{)}^{2}}\\\:\beta\:=\frac{{\mu\:}_{s}}{{\mu\:}_{o}}\\\:\gamma\:=\frac{{\sigma\:}_{s}/{\mu\:}_{s}}{{\sigma\:}_{o}/{\mu\:}_{o}}\end{array}$$
(7)

Where r is the Pearson correlation coefficient between models (s) and observations (o), β is the bias ratio, γ is the variability ratio, µo is the mean of observation data, µs the mean of modeled data, and σo is the standard deviation of the observation data. σs is the standard deviation modeled data.

Technique for order of preference by similarity to ideal solution (TOPSIS)

The process of ranking GCMs is intricate, and relying on a single metric can lead to misleading outcomes. MCDM techniques offer a robust approach to assessing GCM performance. TOPSIS stands out as a widely recognized and dependable method among these techniques. It excels in consistently handling parameter variability and is preferred by researchers for its simplicity and effectiveness.

The foundation of TOPSIS lies in the concept that the chosen alternative should be closest to the ideal solution and farthest from the anti-ideal solution. This study adopts a hybrid approach to achieve more accurate results. Initially, error metrics are weighted using the entropy method. These weights are subsequently employed as inputs in the TOPSIS methodology, as suggested by previous research38,45.

  1. 1.

    The calculation of TOPSIS involves a series of well-defined steps, as commonly followed by researchers in the field38,45,46. This systematic approach ensures a rigorous and reliable evaluation of GCMs, ultimately aiding in more informed decision-making in climate modeling. The first step is the calculation of the Separation Measure \(\:({D}_{a\:}^{+}\)) of each alternative from the ideal solution, that is, the Euclidean distance of each criterion from its ideal value, and summing these for all criteria (j is equal to 1, 2, 3,. J) for each alternative a.

$$\:{D}_{a}^{+}=\sqrt{\sum\:_{j=1}^{j}\:{\left({w}_{j}{f}_{j}\left(a\right)-{w}_{j}{f}_{j}*\right)}^{2}}$$
(8)

where, j = 1, 2, …J;

fj(a) = for criterion j, alternative a’s normalized value;

\(\:{f}_{j}*\) = criterion’s normalized ideal value j;

\(\:{w}_{j}\) = assigned weight to the criterion j.

  1. 2.

    The second step is calculating the separation distance Euclidean distance from the anti-ideal value of each criterion (j is equal to 1, 2, 3, 4, 5…. J), these for the specific alternative a, i.e. \(\:{D}_{a}^{-}\), is calculated for each alternative from the anti-ideal solution.

$$\:{D}_{a}^{-}=\sqrt{\sum\:_{j=1}^{j}\:{\left({w}_{j}{f}_{j}\left(a\right)-{w}_{j}{f}_{j}**\right)}^{2}}$$
(9)

where fj** = Normalized anti-ideal value of criterion j.

  1. 3.

    The third step is the calculation of relative closeness by using Eq. (10) for any alternative a, which yields Ca. Alternatives are sorted based on the Ca values. The superiority of the alternative increases with the value of Ca.

$$\:{C}_{a}=\frac{{D}_{a}^{-}}{\left({D}_{a}^{-}+{D}_{a}^{+}\right)}$$
(10)

Comprehensive rating metrics (RM)

RM is pivotal in addressing the challenge of determining the best-performing GCM when rankings are performed separately for seasonal and annual data. Since GCM rankings can vary significantly across seasons, it can be difficult to identify a single model as the top performer. A model that ranks first in one season may perform differently and rank lower in another. The RM offers a comprehensive assessment of model performance by considering their rankings across different time scales, including seasonal and annual data36.

The calculation of the RM value incorporates the performance of models in four distinct seasons and the annual scale, allowing for a more holistic evaluation. The formula for calculating the RM value is as follows:

$$\:RM=1-\frac{1}{nm}\sum\:_{i=1}^{n}\:{rank}_{i}$$
(11)

Where RM represents the Rating Metric value, a pivotal indicator in evaluating the performance of GCMs in climate simulations, n signifies the number of time scales under consideration in the study. In this specific research, the value of n is set at 5, encompassing the four seasons and the annual period. m represents the number of GCMs that are subjected to evaluation.

An RM value that approaches 1 serves as an indicator of the best-performing model. It suggests that the model consistently exhibits high performance across all seasons and the annual time frame, making it a reliable choice for climate simulations. This metric offers a more robust and consistent method for identifying GCMs that excel across various time scales, ensuring more dependable climate projections and research outcomes.

Identification of ensemble members and development of the multi-model ensemble mean

Confronting the uncertainties inherent in climate projections is a complex endeavor, as these uncertainties stem from many factors. These factors include the intricacies of GCM structures, underlying assumptions, initial conditions, and parameterizations. However, one effective approach to this challenge is identifying a subset of GCMs that consistently exhibit superior performance. The multi-model ensemble (MME) reduces uncertainty in climate projections stemming from disparities in the structures of GCMs and the uncertainty introduced by variations in initial conditions and model parameterizations47. This approach enhances the accuracy of climate projections and is widely adopted in climate science. Lutz et al.48 have emphasized the practicality of relying on a single GCM or a small ensemble of GCMs for assessing the impacts of climate change. Multiple studies, including those by Weigel et al.49 and Miao et al.50, have stressed that relying solely on a single GCM falls short of addressing the uncertainties associated with future climate projections. Therefore, making an ensemble of GCMs to bolster the robustness of climate change impact assessments is imperative. This approach offers a pathway to mitigate uncertainties, harness the strengths of specific GCMs, and mitigate their limitations, ultimately leading to more reliable and comprehensive climate projections.

The primary objective of this study was to choose four highly-rated GCMs to create a Multi-Model Ensemble (MME) for the variables Precipitation, Tmax, and Tmin. It is important to note that there is currently no universally accepted standard for establishing the ideal number of GCMs for a Multi-Model Ensemble (MME). Studies frequently evaluate a variety of GCMs, usually ranging from 3 to 10, based on their performance ranking in descending order. For example, Xuan et al.51 utilized a collection of 10 highly ranked GCMs to simulate precipitation in Zhejiang, China. In their study on China, they constructed Multivariate Model Ensembles (MMEs) to analyze daily temperature extremes. Khan et al.52 conducted a study in Pakistan. They chose six commonly used GCMs from the top 10 rated GCMs for daily temperature and precipitation. In another study, Ahmadalipour et al.53 utilized the four highest-rated GCMs to replicate the daily patterns of precipitation and temperature in the Columbia River Basin, located in the Pacific Northwest region of the United States. Hussain et al.54 employed the three most highly ranked GCMs to create a Multi-Model Ensemble (MME) for predicting precipitation in the tropical rainforests of Borneo, specifically in Malaysia.

The present study uses top-ranked GCMs based on the cumulative performance in replicating precipitation and temperature for ensemble mean calculation. There are various methods for calculating ensemble mean. This study compares Arithmetic Mean (AM) and Bayesian Model Averaging (BMA) methods.

Arithmetic mean (AM)

This method calculates the simple mean of outputs. This ensemble mean is calculated by dividing the sum of models by the number of models. This method may not work if any ensemble member has a high deviation from observed data.

$$\:\stackrel{-}{S}=\frac{{S}_{1}+{S}_{2}+\cdots\:{S}_{n}}{n}$$
(12)

Where,

S = Ensemble Members.

n = Number of Models.

Bayesian model averaging (BMA)

BMA is a weighted average method of ensemble mean calculation. By weighing each posterior distribution according to its probabilistic likelihood measures, BMA can infer the posterior distribution of the forecasting variables, with the forecasts with the best performance receiving higher weights than those with the worst performance. By assigning a weight to each candidate model based on its statistical evidence, which is correlated with the model’s independence and competency, the BMA technique provides an alternative to choosing one model from a group of candidate models. Several model combinations are made possible by the BMA technique, which implicitly solves the model dependence problem by estimating a distribution of model weightsThe mean value of the distribution can be used as the output of MME forecasting because BMA offers a probabilistic manner of synthesizing findings among numerous models. Similarly, the variance and confidence interval display potential ranges for the predicted variables; the uncertainty is thus defined. BMA has consequently evolved into a representative metric for MME forecasting55,56. This study applies BMA to each grid point on an annual average dataset to calculate the ensemble mean of top-ranked models. The basic equation of BMA is following

$$\:P(y\mid\:D)=\sum\:_{m=1}^{M}\:P\left(y\mid\:{M}_{m},D\right)P\left({M}_{m}\mid\:D\right)$$
(13)

where:

\(\:P(y\mid\:D)\) is the posterior predictive probability of the outcome \(\:y\) given the data \(\:D\).

\(\:{M}_{m}\) represents the \(\:m\)-th model in the set of \(\:M\) models.

\(\:P\left(y\mid\:{M}_{m},D\right)\) is the posterior predictive probability of \(\:y\) given the data \(\:D\) under model \(\:{M}_{m}\).

\(\:P\left({M}_{m}\mid\:D\right)\) is the posterior probability of model \(\:{M}_{m}\) given the data \(\:D\).

The posterior probability of each model \(\:P\left({M}_{m}\mid\:D\right)\) can be computed using Bayes’ theorem:

$$\:P\left({M}_{m}\mid\:D\right)=\frac{P\left(D\mid\:{M}_{m}\right)P\left({M}_{m}\right)}{\sum\:_{k=1}^{M}\:\:P\left(D\mid\:{M}_{k}\right)P\left({M}_{k}\right)}$$
(14)

where:

\(\:P\left(D\mid\:{M}_{m}\right)\) is the marginal likelihood of the data given model \(\:{M}_{m}\).

\(\:P\left({M}_{m}\right)\) is the prior probability of model \(\:{M}_{m}\).

The denominator \(\:{\sum\:}_{k=1}^{M}\:P\left(D\mid\:{M}_{k}\right)P\left({M}_{k}\right)\) is a normalizing constant ensuring that the posterior probabilities sum to 1 .

By simplifying the concept, it can be said that BMA involves five steps. The first is to define a set of candidate models \(\:\left\{{M}_{1},{M}_{2},\dots\:,{M}_{M}\right\}\). Secondly, Assign prior probabilities \(\:P\left({M}_{m}\right)\) to each model. Thirdly, compute the marginal likelihood \(\:P\left(D\mid\:{M}_{m}\right)\) for each model. Fourthly, calculate the posterior model probabilities \(\:P\left({M}_{m}\mid\:D\right)\). Finally, the weighted average of the predictions or parameter estimates across all models is computed.

In our study, the ensemble approach, including BMA, is applied at the grid level and uses monthly data for the analysis. This method captures fine-scale spatial and temporal variability in the climate projections, ensuring a more detailed and accurate assessment of climate variables such as precipitation, Tmax, and Tmin.

Result

Before evaluating the GCMs, it was necessary to validate the data sets used in the analysis. The ERA5 reanalysis data were compared against observed meteorological data from 29 stations across Bangladesh, covering the period from 1985 to 2014. This initial validation ensured that the ERA5 data accurately represented the climatic conditions in the study area, providing a reliable basis for the GCM assessment. GCMs were evaluated based on their Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) scores, calculated for both seasonal and annual scales. A higher TOPSIS score indicates better model performance. It is important to recognize that different models may excel in different seasons. To provide a comprehensive ranking of GCMs, an overall assessment was conducted using a Rating Metrics (RM) metric, where a higher RM value signifies a superior model. Additionally, a comparison was made between two commonly used ensemble means to determine their relative effectiveness.

Validation of ERA5 data

Figure S1 presents a comprehensive validation of ERA5 reanalysis data against observed meteorological data from 29 stations across Bangladesh for the period 1985–2014. The annual cycles of monthly mean precipitation, maximum temperature (Tmax), and minimum temperature (Tmin) are depicted in panels (a), (b), and (c), respectively. In these panels, the blue lines represent the spatially aggregated observed data, while the yellow lines depict the ERA5 reanalysis data. The close alignment of the ERA5 data with the observed data throughout the year indicates that ERA5 effectively captures the seasonal variations in precipitation and temperature over Bangladesh.

Further validation is provided through scatter plots (d), (e), and (f), which compare the monthly mean values of precipitation, Tmax, and Tmin from observations versus ERA5 reanalysis data. Each scatter plot includes an R² value, indicating the strength of the correlation between the two datasets. The high R² values (0.90 for precipitation, 0.99 for Tmax, and 0.96 for Tmin) demonstrate a strong agreement, suggesting that ERA5 reanalysis data are reliable for replicating the observed climatic conditions in Bangladesh.

The validation process involved spatially aggregating the monthly mean values from all 29 stations to create a single representative value for each month and each parameter. This approach ensured a comprehensive comparison, accounting for regional variations within Bangladesh and providing robust insights into the performance of ERA5 data. The strong correlation and close alignment observed in Figure S1 validate using ERA5 reanalysis data for climatic studies and applications in Bangladesh.

Rankings of GCMs in in replicating seasonal and annual precipitation, Tmax, and tmin

Table 2 ranks GCMs based on their effectiveness in replicating seasonal and annual precipitation, maximum temperature (Tmax), and minimum temperature (Tmin). This assessment involved the use of TOPSIS scores based on seven goodness-of-fit tests. Figures 3, 4, 5, 6 and 7 complement this analysis by visually depicting the spatial patterns of these climate variables, comparing observed data with outputs from the highest and lowest-ranked GCMs. These figures underscore the spatial accuracy and discrepancies of the models, providing valuable insights into their strengths and limitations for climate research and application.

Table 2 Ranking of GCMs in replicating seasonal and annual precipitation, maximum temperature and minimum temperature.
Full size table
Fig. 3
figure 3

The spatial patterns of pre-monsoon precipitation, maximum and minimum temperature. The top row displays observed data, the middle row represents the results of first-ranked GCMs, and the bottom row depicts findings from the last-ranked GCMs.

Full size image
Fig. 4
figure 4

The spatial patterns of monsoon precipitation, maximum and minimum temperature. The top row displays observed data, the middle row represents the results of first-ranked GCMs, and the bottom row depicts findings from the last-ranked GCMs.

Full size image
Fig. 5
figure 5

The spatial patterns of post-monsoon precipitation, maximum and minimum temperature. The top row displays observed data, the middle row represents the results of first-ranked GCMs, and the bottom row depicts findings from the last-ranked GCMs.

Full size image
Fig. 6
figure 6

The spatial patterns of winter precipitation, maximum and minimum temperature. The top row displays observed data, the middle row represents the results of first-ranked GCMs, and the bottom row depicts findings from the last-ranked GCMs.

Full size image
Fig. 7
figure 7

The spatial patterns of annual precipitation, maximum and minimum temperature. The top row displays observed data, the middle row represents the results of first-ranked GCMs, and the bottom row depicts findings from the last-ranked GCMs.

Full size image

Across all seasons and the annual climate, the GCM rankings reveal significant variability in model performance:

Pre-monsoon

ACCESS.CM2 performs best in replicating precipitation, capturing the general spatial distribution observed in real data. However, it underestimates total precipitation volume by 42%, particularly in the northeastern and southwestern regions, where local convective rainfall is most intense. For Tmax, INM.CM4.8 closely mirrors observed patterns, with minor underestimation in the central regions, particularly around the Sylhet basin. MPI.ESM1.2.HR excels in Tmin, accurately reflecting cooler temperatures in the northern highlands but underestimates Tmin by 15%, especially in the southeastern Chittagong Hill Tracts. In contrast, FGOALS.g3, KACE.1.0.G, and CanESM5 rank lowest for precipitation, Tmax, and Tmin, respectively, showing significant underestimations and spatial inaccuracies, such as a failure to represent the sharp precipitation gradient from the coast to the interior.

Monsoon

UKESM1.0.LL leads in simulating precipitation, capturing the spatial distribution of heavy monsoon rains with high accuracy, particularly along the Meghna estuary and the central floodplain regions, though it underestimates by 4%. INM.CM5.0 ranks highest for Tmax, with a minor 1% underestimation, but it struggles slightly in representing the cooler temperatures in the eastern highlands. MRI.ESM2.0 tops Tmin rankings, reflecting the cooler temperatures in the northern regions almost perfectly. However, FGOALS.g3, KACE.1.0.G, and MIROC6 rank lowest, showing substantial errors, such as overestimating precipitation in the arid western regions and misrepresenting the coastal temperature gradients.

Post-monsoon

ACCESS.CM2 again ranks highest for precipitation, accurately depicting the retreat of monsoon rains and the resulting spatial patterns, particularly in the northwest. However, it underestimates the total volume by 23%, especially in regions like the Barind Tract. INM.CM5.0 leads for Tmax, slightly overestimating temperatures along the western border by 0.7%. Interestingly, KACE.1.0.G, which performed poorly for Tmax in other seasons, ranks highest for Tmin during the post-monsoon, accurately capturing cooler nights in the northwestern plains. Conversely, FGOALS.g3, KACE.1.0.G, and CanESM5 show the poorest performance for precipitation, Tmax, and Tmin, respectively, with significant deviations from observed patterns, such as underestimating the dry season intensification in the west and failing to capture the Tmin gradient from the north to the south.

Winter

CNRM.ESM2.1 tops the rankings for winter precipitation but slightly overestimates total volume by 10%, particularly in the northern region where winter rains are scarce. Its strength lies in capturing the spatial distribution of precipitation across the country, including the fog-induced winter drizzle in the northeast. INM.CM4.8 is the best for Tmax, with a 12% overestimation, particularly in the western border regions, while UKESM1.0.LL excels in Tmin, closely reflecting the cold conditions in the north and northeast. ACCESS.CM2, KACE.1.0.G, and CanESM5 rank lowest for precipitation, Tmax, and Tmin, respectively, showing significant overestimations and spatial inaccuracies, such as misrepresenting the colder temperatures in the northwest and overestimating precipitation across the southern districts.

Annual climate

ACCESS.CM2 is the top model for annual precipitation, effectively capturing the spatial variability across the country, including the high precipitation zones along the eastern hills and the Meghna basin. However, it underestimates the total precipitation by 15%, especially in the northern plains. INM.CM4.8 ranks highest for Tmax, achieving a perfect score, accurately depicting the temperature gradient from the cooler northern regions to the hotter southern plains. MRI.ESM2.0 also scores perfectly for Tmin, reflecting the observed Tmin patterns with high accuracy, though with a minor underestimation of 12% in the cooler northern areas. On the other end, FGOALS.g3, KACE.1.0.G, and CanESM5 perform the worst for precipitation, Tmax, and Tmin, with significant underestimations and spatial misrepresentations, such as failing to capture the annual precipitation maxima in the eastern hills and underestimating the Tmin in the northern districts.

These consolidated findings highlight the variability in GCM performance across different climatic variables and seasons, emphasizing the importance of careful model selection tailored to specific research objectives. While top-ranked models generally offer reliable simulations, the limitations of lower-ranked models underscore the need for ensemble-based approaches to improve the accuracy and reliability of climate projections.

Overall GCM rankings for precipitation, maximum and minimum temperatures

Different error matrices are used to calculate TOPSIS, which results in different ranks for the same GCM in different seasons53,57. Table 3 ranks Global Climate Models (GCMs) based on their performance in simulating annual precipitation, maximum temperature (Tmax), and minimum temperature (Tmin), providing overall rankings and RM values that indicate each model’s reliability and accuracy. The RM value is calculated based on the models’ performance to replicate the spatial pattern of precipitation, Tmax, and Tmin in seasonal and annual timescales. A high RM value indicates a better capacity to replicate the seasonal and annual patterns of climate variables. The RM values are based on the seasonal and annual ranking scores of GCMs. ACCESS.ESM1.5 emerges as the top model with an RM value of 0.68, excelling particularly in Tmax (6th) and Tmin (8th). Following closely is ACCESS.CM2 and UKESM1.0.LL, both with RM values of 0.67. ACCESS.CM2 is notably strong in precipitation (ranked 1st) and Tmin (ranked 4th), while UKESM1.0.LL leads in Tmin (ranked 1st) and also performs well in precipitation (ranked 3rd).

Table 3 Overall ranking of GCMs based on RM score.
Full size table

In the mid-range, MRI.ESM2.0 and EC.Earth3 shows balanced capabilities across all variables, with RM values of 0.59 and 0.58, respectively. These models rank highly in Tmin and precipitation, indicating their versatility and reliability in climate simulations. Conversely, models like FGOALS.g3 and CanESM5 rank lowest with RM values of 0.25 and 0.15, respectively, reflecting significant challenges in accurately simulating climate variables, particularly Tmin.

The rankings in Table 3 highlight the variability in GCM performance, emphasizing the importance of choosing robust models for accurate climate projections. The results also underscore the advantage of ensemble approaches that combine multiple models to enhance the accuracy and reliability of climate simulations.

Fig. 8
figure 8

The spatial patterns of precipitation maximum and minimum temperature overall ranked GCM data. The top row exhibits observed data, the middle row displays results from the first-ranked GCM, and the bottom row showcases findings from the last-ranked GCM.

Full size image

Figure 8 comprehensively compares simulated spatial patterns for mean annual precipitation. Tmax and Tmin derived from GCMs ranked 1 and 19 against ERA5 data as a benchmark. This analysis aims to evaluate the effectiveness of the GCMs in accurately reproducing observed climate variables. Including maps from only the best and least performing GCMs effectively illustrates the variability in model performance across the region. Presenting all maps potentially overwhelms the focus of the analysis. By selectively presenting these key examples, the discussion remains concise while still conveying the necessary insights into GCM performance. GCMs securing the top rank (rank 1, specifically ACCESS.CM2 for precipitation, INM.CM4.8 for Tmax, and UKESM1.0.LL for Tmin) demonstrate superior performance, closely mirroring the spatial patterns observed in ERA5 for precipitation, Tmax, and Tmin. This alignment suggests a high degree of agreement between the simulated climate variables of the best-performing GCMs and the ERA5 reference data.

Conversely, GCMs positioned at rank 19 (indicating poorer performance, namely FGOALS.g3 for precipitation and KACE.1.0.G for Tmax and CanESM5 for Tmin) exhibit substantial disparities when compared to ERA5 precipitation, Tmax, and Tmin. Notably, GCMs at rank 19 underestimate precipitation and temperature in the study area. The differences highlighted in Fig. 8 underscore the limitations of the worst-performing GCMs in accurately capturing observed climate conditions over a significant region within the study area. The observed similarities or discrepancies in spatial patterns with ERA5 data underscore the variable accuracy levels among GCMs, emphasizing the crucial role of model evaluation in gauging their reliability for climate simulations in the study region.

Fig. 9
figure 9

Scatter plot of spatially averaged annual precipitation from GCMs against ERA5 data from 1986 to 2014.

Full size image

A robust evaluation of 19 Global Climate Models (GCMs) is presented in Figs. 9 and 10, and 11, comparing their simulations against the esteemed ERA5 dataset for precipitation, maximum temperature (Tmax), and minimum temperature (Tmin). Ranked by their performance, each figure offers a grid-to-grid analysis of annual average data spanning 1986–2014.

Fig. 10
figure 10

Scatter plot of spatially averaged annual maximum temperature from GCMs against ERA5 data from 1986 to 2014.

Full size image
Fig. 11
figure 11

Scatter plot of spatially averaged annual minimum temperature from GCMs against ERA5 data from 1986 to 2014.

Full size image

A crucial metric for model accuracy is each figure’s alignment of scatter points. A tight clustering around the diagonal signifies strong agreement between a GCM and observed data. Notably top-ranked GCMs such as ACCESS.CM2 (precipitation), INM.CM4.8 (Tmax), and UKESM1.0.LL (Tmin) demonstrate this desirable pattern, highlighting their proficiency in replicating observed spatial trends.

Conversely, the scatter plots for lower-ranked GCMs reveal discrepancies. FGOALS.g3 consistently underestimates precipitation, while KACE.1.0.G and CanESM5 struggle with both Tmax and Tmin across the study area. These deviations from observed data expose limitations in accurately capturing regional climate dynamics.

This comprehensive comparison underscores the critical importance of meticulous model evaluation. Choosing the most suitable GCMs for future climate projections in this region hinges on a rigorous assessment of their strengths and weaknesses, particularly their fidelity in replicating observed conditions.

Identification ensemble member and calculation of ensemble mean

Ensemble members are chosen based on the cumulative performance of a model to replicate both precipitation and temperature. After completing the overall ranking of GCMs for precipitation, Tmax, and Tmin, the RM value for each GCM is again calculated based on the rank of precipitation and temperature. Overall ranks for the three variables are used as input in calculating the RM value. Table S1 shows the cumulative performance of GCM in replicating precipitation and temperature. GCMs with higher RM values can better capture the spatial pattern of precipitation and temperature. The top five models based on the RM value are selected as ensemble members. These models are ACCESS.ESM1.5, ACCESS.CM2, UKESM1.0.LL, MRI.ESM2.0, EC.Earth3. For precipitation, Tmax and Tmin, ACCESS.ESM1.5 ranked 4,6 and 8, ACCESS.CM2 ranked 1, 14,4 UKESM1.0.LL ranked 3,15,1 MRI.ESM2.0 ranked 11,9,3 EC.Earth3 ranked 2,12,10 respectively.

BMA and AM are employed to calculate the ensemble mean. Figure 12 visually represents the performance of these two ensemble methods in capturing the spatial patterns of precipitation, Tmax, and TMin. BMA is more effective for precipitation in replicating the spatial pattern. In contrast, AM falls short of capturing the pattern in the southeastern hilly area. Both methods tend to underestimate precipitation’s upper and lower limits, but BMA provides values closer to the observed data.

Fig. 12
figure 12

Spatial patterns of (a) ERA5 precipitation, (b) ERA5 maximum temperature, (c) ERA5 minimum temperature, (d–f) MME-based on the Arithmetic mean (AM), and (g–i) MME-based on the Bayesian Model Averaging (BMA) algorithm for mean annual precipitation and maximum and minimum temperature for the period 1986 to 2014.

Full size image

For Tmax, BMA excels at capturing the temperature pattern, while AM struggles to replicate the pattern in the northern region. Additionally, the upper and lower limits of Tmax closely align with observed data in the BMA model, while AM tends to overestimate the upper limit. In the case of Tmin, BMA performs better in capturing the temperature pattern, with lower and upper limits closely matching the observed data. Conversely, AM underestimates both the lower and upper limits.

Figure 13 displays a scatter plot comparing the performance of the BMA and AM of GCMs at each grid point. It is evident from the figure that points in BMA consistently outperform AM in replicating spatial patterns, offering advantages in precipitation, Tmax, and Tmin distributions. At a broad level, BMA emerges as a more practical approach for accurately representing the spatial intricacies of these climate variables.

Fig. 13
figure 13

Scatter plots of averaged precipitation, maximum temperature (Tmax), and minimum temperature (Tmin) for two scenarios: (a-c) Multiple Model Ensemble (MME) based on the Arithmetic Mean (AM) algorithm and (d-f) MME based on Bayesian Model Averaging (BMA). These scatter plots are compared against ERA5 data, covering the period from 1986 to 2014.

Full size image

Table 4 compares Arithmetic Mean (AM) and Bayesian Model Averaging (BMA) for calculating multi-model ensemble means. Overall, BMA consistently outperforms AM across all examined variables: precipitation, maximum temperature (Tmax), and minimum temperature (Tmin).

Table 4 Comparison of arithmetic mean (AM) and bayesian model averaging (BMA) in calculating multi-model ensemble mean.
Full size table

For precipitation, BMA slightly outperforms AM in terms of R2, with values of 0.0.78 for BMA and 0.66 for AM. BMA reduces the MAE from 348.54 (AM) to 189.06, indicating improved accuracy in precipitation estimation. The RMSE is also notably lower in BMA (277.80) than AM (601.68 ), reflecting a reduction in prediction errors. BMA substantially improved the KGE from 0.59 (AM) to 0.82, indicating superior overall performance. The most notable change is the NSE from − 0.59in AM to 0.71 in BMA, demonstrating that BMA is better at representing precipitation variability. It is further supported by the fact that BMA has a greater d of 0.93 than AM, which is 0.75. For Tmax, the disparity between BMA and AM is even more pronounced. BMA exhibits superior performance with an impressive R2 of 0.62, compared to 0.35 in AM. BMA significantly reduces the MAE from 4.60 (AM) to a mere 0.26, showcasing a substantial improvement in accuracy. The RMSE is significantly lower in BMA (0.38) compared to AM (4.73), highlighting the capacity of BMA to provide more precise temperature estimates. BMA substantially improves the KGE from 0.28 (AM) to an impressive 0.65, indicating superior overall performance. Furthermore, the shift from a markedly negative NSE value of -10.34 in AM to a positive 0.37 in BMA demonstrates the ability of BMA to represent temperature patterns accurately, supported by a notably higher d of 0.87 in BMA compared to 0.34 in AM.

For Tmin, BMA and AM exhibit close R2 values of 0.78 and 0.66, respectively. However, BMA offers improved accuracy with a reduced MAE of 0.24 compared to 4.21 in AM. The RMSE is also lower in BMA (0.31) than in AM (3.47), suggesting better accuracy in representing minimum temperatures. The KGE value is higher for BMA (0.82) than AM (0.45). Notably, the transition from a negative NSE value of -6.50 in AM to a positive NSE of 0.71 in BMA underscores the ability of BMA to represent Tmin effectively, further supported by a notably higher d of 0.93 in BMA compared to 0.39 in AM.

Discussion

This study evaluated the performance of GCMs in Bangladesh by interpolating them to the resolution of ERA5 data (0.25°). In previous studies, GCM performance has been evaluated using various grid resolutions. In many cases, GCMs are re-gridded to a resolution that closely matches the average grid size of all models36,52,58,59,60. In some cases, GCMs have also been aggregated to the coarsest resolution among the investigated models for comparison57,61. Aggregating GCM data to larger grid cells can obscure finer-scale climate features and processes, such as the influence of topography, land cover, and other geographic characteristics62,63. This loss of detail can result in inaccurate representations of climate conditions in the study region, leading to potentially misleading conclusions.

However, most commonly, GCMs are re-gridded to match the resolution of reference data for comparison. For instance, Mishra et al.64 adjusted GCM data to the 1.0° resolution used by the Indian Meteorological Department, while Pour et al.65 and Hassan et al.66 re-gridded to the GPCC resolution of 0.5°. Li et al.67 also used a 0.5° resolution based on observed data, and Jain et al.68 employed the 0.25° APHRODITE resolution. CMIP6 GCMs were re-gridded to a finer 1° × 1° resolution to assess performance in South America69 and Iran70. Additionally, Gusain et al.71 re-gridded both CMIP5 and CMIP6 outputs to the 0.25° APHRODITE resolution to evaluate their accuracy in simulating the Indian monsoon. This study also followed this most widely used approach of GCM performance evaluation by interpolating them to the resolution of the reference data use.

GCMs, due to their coarse resolution, fail to resolve small-scale convective precipitation, which is a key driver of rainfall in tropical and subtropical regions. Consequently, they often underestimate total precipitation in these regions67.

The findings of this study highlight the significant variability in the performance of different GCMs when simulating climatic variables such as precipitation, maximum temperature (Tmax), and minimum temperature (Tmin) over Bangladesh. The results underscore the importance of model selection and ensemble methodologies in improving the accuracy of climate simulations in regions with complex climatic patterns.

Our study aligns with and extends previous research in several key areas. The superior performance of ACCESS.CM2 in simulating precipitation is consistent with earlier findings by Kamruzzaman et al.30, who noted its effectiveness in capturing regional precipitation patterns in Bangladesh. Similarly, the strong performance of INM.CM4.8 for Tmax aligns with results reported by Shiru and Chung72, further validating the robustness of these models in different climatic contexts. Gebisa et al.73 also found similar results for the Baro River Basin, the western highlands of Ethiopia.

The application of Bayesian Model Averaging (BMA) in calculating ensemble means has consistently shown to be more effective than the Arithmetic Mean (AM) method. This finding corroborates the conclusions drawn by Raftery et al.74, who highlighted the superiority of BMA in reducing bias and enhancing predictive accuracy in ensemble forecasts. The key advantage of BMA lies in its unique approach to weighting individual model predictions based on their probabilistic likelihood measures. This means that models that historically perform better are given higher weights, thus refining the overall ensemble prediction.

Clyde75 and Hoeting et al.76 further emphasized that it enhances predictive accuracy and provides a more comprehensive description of predictive uncertainty. This dual benefit is critical in climate modeling, where understanding the range and probability of potential outcomes is as important as predicting the most likely outcome. The weighted average of predictions helps mitigate the risk of any single model’s biases overly influencing the ensemble result, thus offering a balanced and realistic forecast.

Fernandez et al.77 and Ellison78 discussed BMA’s utility, showcasing its application across various scientific disciplines beyond meteorology and climate science. Their studies demonstrated that BMA can effectively manage uncertainties and improve the reliability of predictions in different contexts, including economic forecasting and ecological studies. This broad applicability underlines the versatility and robustness of the BMA approach.

Recent applications in hydrologic modeling, as discussed by Neuman and Wierenga and further explored in studies like Darbandsari and Coulibaly73 and Duan et al.79, illustrate the growing adoption of BMA in fields requiring precise and reliable predictive models. In hydrology, for instance, BMA has been used to enhance groundwater modeling by integrating multiple model outputs to provide a consensus prediction that is more accurate and reliable.

Given these findings, BMA emerges as a preferred method in climate modeling, particularly for regions like Bangladesh that experience significant climatic variability. The nuanced and robust nature of BMA makes it particularly suitable for capturing the complexities of such regions, providing accurate predictions and a clear understanding of the associated uncertainties. This capability is crucial for developing effective adaptation and mitigation strategies in response to climate change, highlighting the practical importance of adopting BMA in regional climate studies like Bangladesh.

Despite the advancements, the study has several limitations that need to be addressed in future research. One significant limitation is using bilinear interpolation to downscale GCM outputs to a finer resolution (0.25°) to match ERA5 data. While this approach was chosen to leverage the finer-resolution data for more detailed analysis, it may introduce “new” information unsupported by the original coarse-resolution GCM data, potentially leading to inaccuracies or random artifacts. An alternative approach would be to re-grid all data, including ERA5, to the coarsest resolution available among the GCMs (e.g., CanESM5 and MIROC.ES2L), thus avoiding the introduction of potentially spurious details. However, applying this approach to Bangladesh, a relatively small country with complex topographical and climatic features, could result in the loss of critical spatial information. The trade-off between resolution and data integrity is particularly challenging in regions like Bangladesh, where fine-scale climatic variations are significant.

Additionally, the focus on a limited set of climatic variables—precipitation, Tmax, and Tmin—does not fully encompass other critical aspects of climate change, such as humidity, wind patterns, or extreme weather events. Including a broader range of variables could provide a more comprehensive understanding of the potential impacts of climate change.

Despite its validation, the reliance on ERA5 reanalysis data poses a limitation due to potential biases inherent in the reanalysis process. High-resolution, in-situ observational data quality and availability are crucial for validating and refining climate models, underscoring the region’s need for enhanced data collection efforts.

This study provides valuable insights into the selection and optimization of GCMs for climate simulation in Bangladesh, highlighting both the strengths and limitations of current modeling approaches. The findings emphasize the need for ongoing refinement of model selection criteria and ensemble methodologies to improve the accuracy and reliability of climate projections. Addressing the identified limitations through more detailed models, a broader range of climatic variables, and improved data quality will be crucial for advancing climate science and supporting effective climate adaptation strategies in Bangladesh and similar regions.

Conclusion

The study optimizes an MME mean of GCMs for simulating precipitation, Tmax, and Tmin in Bangladesh, a country with unique geographical and climatic characteristics. The research employs a rigorous methodology involving the evaluation of 19 GCMs based on multiple error metrics, seasonal and annual rankings, and an MCDM approach (TOPSIS).

The key findings of the study are as follows:

  1. 1.

    Different GCMs perform differently in different seasons, reflecting the complex nature of climate modeling. Therefore, an overall ranking is necessary to determine the most reliable models.

  2. 2.

    The RM, which considers seasonal and annual rankings, helps identify the best-performing GCMs. ACCESS.CM2, INM.CM4.8, and UKESM1.0.LL is the best GCM for simulating precipitation, Tmax, and Tmin, respectively, while FGOALS.g3, KACE.1.0. G and CanESM5 rank the lowest.

  3. 3.

    The ensemble means of the GCMs that ranked top in cumulative ranking for precipitation and temperature is calculated to reduce uncertainty in climate projections. The MME mean of the top five GCMs (ACCESS.ESM1.5, ACCESS.CM2, UKESM1.0.LL, MRI.ESM2.0, EC.Earth3 ) computed using BMA and AM show that BMA outperforms AM in capturing the spatial patterns of precipitation and temperature, making it a preferred choice for ensemble mean calculations.

This study has significant implications for Bangladesh’s climate modelling and projection efforts, where accurate predictions are crucial for disaster management and policy planning. By providing a systematic approach for GCM selection and ensemble mean calculation, the research enhances our ability to make more reliable climate projections in a region prone to rapid and extreme climate shifts. Additionally, the study underscores the importance of considering multiple metrics and techniques to optimize ensemble modelling for improved accuracy and decision-making in climate science.