Ultrabroadband microwave metamaterial absorber with dielectric lossy layer

Abstract

Metamaterial absorbers exhibit high absorption and flexible tuning ability has been widely applied in energy harvesting, radiative cooling, and radar cross-section reduction. In this paper, an ultra-broadband microwave metamaterial absorber containing a lossy meta-dielectric layer was proposed. The lossy layer was a PLA meta-layer with resistive ink coating on the sidewall of the periodic structure. Through tuning the thickness and height of the resistive ink coating on the side wall, the effective impedance of the absorber was modified to match the air impedance. It could enhance the absorption in an ultrabroad microwave frequency band. Simulation results showed that over 90% absorptivity was obtained in an ultra-broad frequency range from 4.4 to 60 GHz, with a relative absorption bandwidth of 173%. Moreover, within the entire absorption band, the absorptivity was uniform, and the peak fluctuation was only 0.053. In addition, the absorber was insensitive to the wave incident angle. Even under a big oblique incident angle of 45°, the average absorptivity was still 95% and the absorption band shifted only 0.5 GHz. Detailed investigations revealed that the resistive ink coating on the PLA middle meta-layer significantly enhanced absorption within the frequency range from 20 to 60 GHz and maintained high absorption at wide incidence angles. It proved that the middle meta-layer effectively broadened the absorption band and made the absorptivity insensitive to the wave incidence angles. The experimental results of the fabricated prototype absorber effectively verified our design. We believe it has good potential in inflight vehicle stealth.

Introduction

Absorbers with ultrahigh absorption, broad working band, and incident angle insensitivity are highly required by energy harvesting, radiative cooling, and radar cross-section reduction^1,2,3. The first metamaterial absorber was introduced by Landy et al. in 2008⁴. It operated in the microwave range and exhibited ultrahigh absorptivity. Afterward, metamaterial absorbers in various frequency bands, such as terahertz^5,6,7, infrared^8,9,10, and visible regions^{11,12,13,14,15} were investigated. They usually consist of a metallic bottom layer, a dielectric spacer layer, and a frequency-selective surface (FSS) ^16,17,18. Gobinda Sen proposed a microwave absorber exhibiting over 90% absorption in the frequency range of 10.2–15.2 GHz¹⁹. In the same year, they extended the high absorption band from 8.86 to 15.5 GHz²⁰. To extend the absorption band, M. Olszewska-Placha suggested using low conductivity FSS²¹. Indium tin oxide (ITO) ^3,22,23 and resistive ink were considered to be the best choices. Using ITO as the FSS and the bottom layer, Zhang et al. achieved over 90% absorption in broadband from 8.3 to 17.4 GHz²³. In 2021, Qi Fan inserted an air layer and a water substrate into the ITO meta-absorber²⁴. The absorption bandwidth was dramatically enlarged. Over 90% absorptivity in the frequency range of 14.4–39.4 GHz was realized. The relative absorption bandwidth was 93%. Compared to ITO, the square resistivity of the resistive ink could be easily controlled by varying their thickness^21,25. Saptarshi Ghosh screen printed the resistive ink FSS as a meta-absorber, and over 90% absorption from 5.52 to 16.96 GHz was obtained²⁶.

However, the absorption performance deteriorates greatly with oblique incidence. For example, in 2022, Chang Yang proposed a meta-absorber with a broad working band from 4.1 to 18.2 GHz²⁷. However, the absorption decreased dramatically to 80% when the incident wave angle was 45°. In 2023, Helin Yang proposed a metamaterial absorber using a double-layer ITO and a water-filled substrate²⁸. Although the absorption in low frequency was enhanced, over 90% absorptivity was achieved in the frequency range of 6.1–35.2 GHz, the high absorption still could not be maintained when the incident angle was larger than 30°. Achieving broadband absorption with a large incident angle is currently a challenge.

In this paper, we introduced a PLA meta-layer with the resistive ink coating on the side wall into the commercial metal/dielectric/FSS absorbers. Ultra-high absorption is achieved with a millimeter-high resistive ink coating. The effective impedance of the absorber was flexibly modified by the PLA meta-layer coated with resistive ink. Hence, through the careful design of the unit cell, impedance matching between absorber and air was obtained in an ultrabroad band. As a result, an ultrahigh and uniform absorption was achieved in an ultra-broadband from 4.4 to 60.0 GHz, resulting in a remarkable relative bandwidth of 173%. The absorption fluctuation was only 0.053 in the entire frequency band. More importantly, when the microwave incident angle was increased to 45°, the absorption remained as high as 95%, and the absorption band showed only a slight blue shift of 0.5 GHz for both TE and TM waves.

Absorber design, methods, and simulation

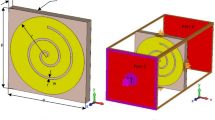
The unit cell of the proposed microwave metamaterial absorber is shown in Fig. 1a, which contains four layers: the top PLA anti-reflection meta-layer, the resistive ink FSS painting on a thin PLA plate, the middle PLA meta-layer with resistive ink coating, and the copper bottom layer. The cross-section of the middle meta-layer is shown in Fig. 1b.

Fig. 1

The unit cell structure of the proposed broadband microwave metamaterial absorber. (a) the structure of the four layers, and (b) the cross-section of the middle meta-layer.

The absorber could be modeled by the equivalent circuit²⁹, was depicted in Fig. 2a. A side view of the equivalent multi-layer structure is shown in Fig. 2b.

Fig. 2

(a) The equivalent circuit model of the unit cell of the absorber. (b) Side view of the equivalent multi-layer structure.

For the proposed absorber, the input impedance of the bottom copper layer $\:{Z}_{in}^{4}$ = 0, the input effective impedance of the middle meta-layer $\:{Z}_{in\:}^{3}\:$is

$$\:{Z}_{in\:}^{3}=j{Z}_{equ}^{TE,TM}\text{tan}\left({\gamma\:}_{3}{t}_{3}\right)$$

(1)

where $\:{Z}_{equ}$ is the effective characteristic impedance of the middle meta-layer.

$\:{Z}_{in\:}^{2}$ represents the input impedance of the ultra-thin substrate of FSS, can be calculated by the transmission line theory³⁰.

$$\:{Z}_{in\:}^{2}={Z}_{2}^{TE,TM}\frac{\:{Z}_{in\:}^{3}+j{Z}_{2}^{TE,TM}\text{t}\text{a}\text{n}\left({\gamma\:}_{2}{t}_{2}\right)}{{Z}_{2}^{TE,TM}+j\:{Z}_{in\:}^{3}\text{t}\text{a}\text{n}\left({\gamma\:}_{2}{t}_{2}\right)}$$

(2)

$\:{Z}_{in}^{1}\:$is equal to the parallel connection between the FSS impedance ($\:{Z}_{fss}$) and $\:{Z}_{in\:}^{2}$, can be calculated as

$$\:{Z}_{fss}=R+j(\omega\:L-\frac{1}{\omega\:C})$$

(3)

$$\:{Z}_{in}^{1}=\frac{{Z}_{in\:}^{2}{Z}_{fss}}{{Z}_{in\:}^{2}+{Z}_{fss}}$$

(4)

We assumed that the unit cell pattern of FSS was a square loop. R, L, and C are related to the geometric parameters of FSS³¹.

$\:{Z}_{in}$ represents the input impedance of the top dielectric layer. It’s also the impedance of the absorber, can be calculated as

$$\:{Z}_{in}={Z}_{1}^{TE,TM}\frac{\:{Z}_{in\:}^{1}+j{Z}_{1}^{TE,TM}\text{t}\text{a}\text{n}\left({\gamma\:}_{1}{t}_{1}\right)}{{Z}_{1}^{TE,TM}+j\:{Z}_{in\:}^{1}\text{t}\text{a}\text{n}\left({\gamma\:}_{1}{t}_{1}\right)}$$

(5)

$\:{Z}_{in}^{i}$ (where i = 1, 2, 3) represents the input impedance between the respective layers, $\:{Z}_{i}^{TE}=\left(\omega\:{\mu\:}_{0}{\mu\:}_{i}\right)/{\gamma\:}_{i}$, $\:{Z}_{i}^{TM}={\gamma\:}_{i}/\left(\omega\:{\epsilon\:}_{0}{\epsilon\:}_{i}\right)$. $\:{Z}_{1}$, $\:{Z}_{fss}$, $\:{Z}_{2}$ and $\:{Z}_{equ}$ is the characteristic impedance of the top dielectric layer, FSS, ultra-thin substrate of FSS, and middle meta-layer, respectively. $\:{\gamma\:}_{i}=\omega\:\text{c}\text{o}\text{s}\theta\:\sqrt{{{\epsilon\:}_{i}\:\mu\:}_{i}}/{c}_{0}$, is the propagation constant, respectively. $\:\omega\:$ is the angular frequency of the incident microwave, $\:{t}_{i}$ is the thickness of the dielectric layers, $\:{\epsilon\:}_{i}$, $\:{\mu\:}_{i}$ are the complex permittivity and permeability of the dielectric layers, $\:{c}_{0}$ is the speed of light. $\:\theta\:$ is the incident angle. R, L, and C are the resistance, inductance and capacitance of the FSS. Based on the impedance matching theory³², the reflection coefficient of the absorber is defined as

$$\:\varGamma\:=\frac{{Z}_{in}-{Z}_{0}}{{Z}_{in}+{Z}_{0}}$$

(6)

The reflectivity is $\:{\left|\varGamma\:\right|}^{2}$. $\:{Z}_{in}$ is the impendence of the absorber. According to Eq. (6), the reflectivity is zero when the impedance of the absorber $\:{Z}_{in}$ matches the impedance of the air $\:{Z}_{0}$, $\:{Z}_{in}={Z}_{0}$.

The $\:{Z}_{equ}$ was studied by simulation using CST Microwave Studio³³. It could be calculated by the S-parameter inversion method³⁴. We used CST to model the structure of the middle meta-layer with resistive ink coating and obtained the reflection coefficient (S₁₁) and transmission coefficient (S₂₁) of the structure. The effective electromagnetic parameters of the materials were obtained by using the S-parameter inversion method³⁴.

$$\:{n}_{equ}=\frac{1}{{k}_{0}t}{cos}^{-1}\left[\frac{1}{2{S}_{21}}\right(1-{S}_{11}^{2}+{S}_{21}^{2}\left)\right]$$

(7)

$$\:{Z}_{equ}=\sqrt{\frac{{(1+{S}_{11})}^{2}-{S}_{21}^{2}}{{(1-{S}_{11})}^{2}-{S}_{21}^{2}}}$$

(8)

$\:{\epsilon\:}_{3}$ and $\:{\mu\:}_{3}$ are the effective complex permittivity and permeability of the middle meta-layers with resistive ink coating, and can be expressed as

$$\:{\epsilon\:}_{3}={n}_{equ}/{Z}_{equ},\:{\mu\:}_{3}={n}_{equ}\bullet\:{Z}_{equ}.$$

(9)

$$\:{Z}_{in\:}^{3}=j\sqrt{\frac{{(1+{S}_{11})}^{2}-{S}_{21}^{2}}{{(1-{S}_{11})}^{2}-{S}_{21}^{2}}}\:\text{tan}\left({\gamma\:}_{3}{t}_{3}\right)$$

(10)

$\:{Z}_{equ}$ was modified by adjusting the square holes’ side length ($\:{b}_{2}$), the thickness and height (h) of resistive ink coating. By substituting equations (10) and Eq. (2) to Eq. (5) into Eq. (6), we obtained the reflection coefficient of the absorber. Therefore, based on the above equations, the initial geometric parameters of the absorber could be derived by utilizing the impedance inversion method.

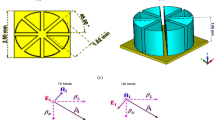
In our design, the PLA plate with the complex permittivity of $\:2.10-j0.147\:$was used as the substrates²⁶. Its complex impedance was modified by adjusting the geometric parameters of the periodic unit cell. When the PLA plate thickness ($\:{t}_{1}$) was 2.1 mm and the unit cell was constructed by the 5 × 5 periodic square holes with the side length ($\:{b}_{1}$) of 2.3 mm, its effective characteristic impedance was 305.2$\:-$j6.5. For the FSS layer, the low Q resonance was formed by Y-Shield resistive ink (resistivity is 2800 S/m) ²⁶. The FSS was screen printed on a thin PLA plate with a thickness ($\:{t}_{2}$) of 0.1 mm. The unit cell pattern of FSS was a square loop. Based on the equivalent circuit model, R, L, and C can be calculated and related to the geometric parameters of FSS. The parameter of the square loop was p = 17 mm, a = 11.5 mm, w = 3.5 mm. The $\:{R}_{s}$= 89 Ω/□ was realized by setting the resistive ink thickness to 4 $\:\mu\:\text{m}$. The effective characteristic impedance $\:{Z}_{equ}$ is related to the geometric parameters of the square hole and resistive ink coating. Initially, the thickness was set to 7 mm and 3 × 3 square holes were used as a unit cell. By changing the square holes’ side length ($\:{b}_{2}$), the thickness and height (h) of resistive ink coating, the real and imaginary parts of the impedance of the middle meta-layer could be controlled. The flexible impedance control of the middle meta-layer provided a way to achieve absorber impedance matching to the air.

After the optimization of the side length ($\:{b}_{2}$) and the thickness and height (h), the parameters of the absorber unit cell were obtained. They are summarized in Table 1. The total thickness of the absorber was 9.7 mm.

Table 1 The geometric parameters of the unit cell (unit is mm).

When the bottom copper layer was 0.5 mm thick, the transmittance was zero. Therefore, the absorptivity of the absorber can be calculated as $\:A=1-\:{\left|\varGamma\:\right|}^{2}$.

The absorption performance of the proposed microwave metamaterial absorber was simulated at normal incidence using CST Microwave Studio. Periodic boundary conditions were adopted in the x and y directions, an open boundary condition was adopted in the z direction. The incident microwave frequency was scanned from 2 to 60 GHz. The absorption spectrum with incident TE wave is shown in Fig. 3. The absorber presents an over 90% absorption from 4.4 to 60 GHz. Compared to the calculation result using the equivalent circuit model, they are in good agreement.

Fig. 3

The absorption spectra of the proposed absorber calculated by an equivalent circuit model and CST simulation.

We studied the complex impedance of the middle meta-layer with different resistive ink coating thicknesses ($\:{t}_{4}$) and heights (h), as shown in Fig. 4. The effective impedance of the middle meta-layer was calculated by the S-parameter inversion method³⁴. From Fig. 4a, as the thickness of the resistive ink coating increased, the impedance oscillation became stronger. From Fig. 4b, as the height of the resistive ink coating increased, the impedance oscillation peaks exhibited a blue shift. This indicated that by changing the thickness and height of the resistive ink coating, the real and imaginary parts of the impedance of the middle meta-layer can be controlled.

Fig. 4

The complex impedance of the middle PLA meta-layer with different resistive ink coating thicknesses and heights at normal incidence. (a) resistive ink coating thicknesses ($\:{t}_{4}$=2, 6, and 10 $\:\mu\:\text{m}$). (b) resistive ink coating heights (h = 2, 3, and 4 mm).

The middle meta-layer was crucial to the performance of the absorber. Both the side length of the square holes and the thickness and height of the resistive ink coating should be carefully designed. To optimize the absorber performance, we studied the complex impedance of the absorber with different resistive ink coating thicknesses ($\:{t}_{4}$) and heights (h), as depicted in Fig. 5. Compared to the absorber without resistive ink coating ($\:{t}_{4}=0$), the effective impedance of our absorber varied much weaker along the incident wave frequency in a broadband. It benefits to obtain uniform absorption. The results demonstrated that the flexibly modified middle meta-layer contributed to the ultra-broadband absorption. Within an ultra-broadband from 5 GHz to 60 GHz, the effective complex impedance of the absorber matches well with the air, which indicates a broadband high absorption.

Fig. 5

The effective complex impedance of the absorber with different resistive ink coating thicknesses ($\:{t}_{4}$= 0, 2, 6, 10, 14, and 18 $\:\mu\:\text{m})$ and heights (h = 2, 3, 4, 5, and 6 mm). (a, c) real part and (b, d) imaginary part of the complex impedance.

With the known effective complex impedance, the absorptivity of the absorber could be calculated. The results in Fig. 6 illustrate that high absorption within an ultra-broad frequency band can be obtained with the optimized resistive ink coating thickness and height. Compared to the absorber without resistive ink coating, the absorptivity with the coating is much higher and flatter. It should be noted that when the ink coating thickness exceeded 10$\:\:\mu\:\text{m}$ or the coating height was less than 2 mm, the absorptivity was reduced. Moreover, as the height of the resistive ink coating increased, the absorption spectra exhibited a redshift and absorptivity fluctuation became stronger. It means there are the optimized ink coating thickness and height.

Fig. 6

The simulated absorption spectra of the absorber with different resistive ink coating thicknesses and heights. (a) resistive ink coating thicknesses ($\:{t}_{4}$= 0, 2, 6, 10, 14, and 18 $\:\mu\:\text{m}$). (b) resistive ink coating heights (h = 2, 3, 4, 5, and 6 mm).

Results and discussions

The optimized absorption performance was achieved when the side length ($\:{b}_{2}$) of the square holes was 4.2 mm, the resistive ink coating thickness ($\:{t}_{4}$) was 4$\:\:\mu\:\text{m},$ and height (h) was 4 mm.

Absorption performances and effective impedance of the proposed absorber

The absorption spectrum of the proposed absorber was simulated, as shown in Fig. 7a. Simulation results showed that over 90% absorptivity was obtained in an ultra-broad frequency range from 4.4 to 60 GHz, with a relative absorption bandwidth of 173%. Moreover, within the entire absorption band, the absorptivity was uniform. The effective impedances of the proposed absorber with resistive ink-coated middle meta-layer are presented in Fig. 7b. The results show that the normalized real part of the impedance is close to 1 and the imaginary part of the impedance is close to 0 over the whole frequency band of 4.4–60.0 GHz. This indicates good impedance matching with air over ensures high absorptivity.

Fig. 7

(a) The simulated absorption spectrum of the optimized absorber. (b) The effective impedances of the optimized absorber.

Power loss induced by different layers

Fig. 8 shows the power loss induced by the four layers, individually. It revealed that the power loss was mainly contributed by the FSS layer and the middle meta-layer. Notably, although the FSS layer could absorb about 50% of incident electromagnetic waves in the frequency range of 4.4–22.0 GHz, the absorption decreased dramatically to only 30% in high frequency range. While the middle meta-layer kept high power absorption in the whole frequency range of 4.4–60.0 GHz, which ensured the ultra-broad absorption band. Moreover, the top PLA anti-reflection meta-layer helped to improve the absorption in high frequency range.

Fig. 8

Power loss induced by different absorber layers.

Physical mechanism of the absorption of our proposed absorber

The simulation results demonstrated that the real and imaginary parts of the impedance of the middle meta-layer can be controlled by changing the thickness and height of resistive ink coating. Meanwhile, the effective impedance of the absorber can be flexibly modified by the middle meta-layer with resistive ink coating, contributing to ultra-broadband absorption. The flexible impedance control of the middle meta-layer provided a way to achieve absorber impedance matching to the air. Moreover, the power loss was mainly contributed by the FSS layer and the middle meta-layer. The FSS contributed significantly to high absorption in the low-frequency range of 4.4–20.0 GHz. While in the frequency range of 4.4–60.0 GHz, the middle meta-layer kept high power absorption, which ensured the ultra-broad absorption band. To expand the absorption bandwidth, we add a top PLA dielectric layer. The top PLA anti-reflection layer improved the absorption at high frequency. By combining a copper bottom layer, a middle meta-layer with a resistive ink coating, a resistive ink FSS, and a top dielectric layer, our proposed absorber achieved a good impedance matching with the air in an ultra-broadband. This mechanism greatly reduced the reflection and enhanced the absorption in the ultra-broadband.

Absorption characteristics of the proposed absorber at different polarization angles (ϕ)

In addition, the absorption characteristics at different polarization angles ($\:\phi\:$) under normal incidence were simulated. As shown in Fig. 9, the absorption was insensitive to the polarization state of the incident waves due to the geometric symmetry of the unit cell structure.

Fig. 9

The simulated absorption spectra of the proposed absorber for incident waves with different polarization angles ($\:\phi\:$ = 0°, 15°, 30°, 45°, 60°, 75°, and 90°).

Absorption characteristics of the proposed absorber at different incident angles (θ)

Moreover, the absorption characteristics of the proposed absorber at different incident angles ($\:\theta\:$) were investigated. As shown in Fig. 10, the absorptivity was maintained over 90% in the frequency range of 4.9–60.0 GHz for both TE and TM waves, even under the oblique incident angle of 45°. As the microwave incident angles increased, the absorption band shifted only slightly to a higher frequency. The blue shift of 0.5 GHz was observed when the incident angle changed from 0° to 45°. When the incident angle increased to 45°, the average absorptivity was 94.3% and 95.5% for the TE and TM waves in the frequency range of 4.9–60.0 GHz, respectively.

Fig. 10

The simulated absorption spectra of the absorber under oblique incidence. (a) TE and (b) TM waves under the incident angle of θ = 0°, 15°, 30°, and 45°, respectively.

More detailed, the absorption fluctuations ($\:\varDelta\:A$) relative to the average absorptivity in the frequency range of 5–60 GHz with different incident angles were calculated, as shown in Fig. 11. Although the peak-to-peak fluctuation increased slightly with the increase of the incident angle, the strongest absorption fluctuation for both TE and TM waves was only 0.053. The results indicated that the proposed absorber had uniform absorption in the ultra-broad frequency band and was insensitive to the incident angle of the microwaves.

Fig. 11

The absorption fluctuations ($\:\varDelta\:A$) relative to the average absorptivity in the frequency range of 5–60.0 GHz under different microwave incident angles. (a) TE and (b) TM waves with the incident angles of θ = 0°, 15°, 30°, and 45°.

The advantages of the proposed absorber

By introducing the middle lossy meta-dielectric layer with resistive ink coating, the real and imaginary parts of the effective impedance of the absorber are flexibly controlled. Hence, impedance matching with air was obtained in an ultra-broadband. The resistive ink coating on the PLA middle meta-layer significantly enhanced absorption within the frequency range from 20 to 60 GHz. More than 90% absorptivity in an ultra-broad frequency range covering 4.4 to 60 GHz was realized, with a relative absorption bandwidth of 173%. The relative absorption bandwidth was superior compared with the recently published research results. In addition, the resistive ink coating weakened the resonance of the absorption spectrum and made the absorption insensitive to the wave incident angle. The absorptivity was maintained over 90% in the frequency range of 4.9–60.0 GHz for both TE and TM waves, even under the oblique incident angle of 45°.

In Table 2 we compared the performances of our absorber to those of the recently published absorbers. The proposed absorber exhibited a much broader absorption bandwidth and wider incident angle range.

Experimental verification

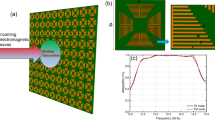
A prototype was fabricated to experimentally validate the proposed broadband absorber. 3D printing technology was exploited to fabricate the top and middle PLA meta-dielectric layer with periodic holes. Screen printing technology was used to uniformly print the resistive ink coating on the PLA substrate. The different layers were cut according to the design and pasted with each other. The prototype consisted of 10 × 10 units with an overall side length 180 mm, as shown in Fig. 12a. Measurement set up, as shown in Fig. 12b. In the experiment, we used the arch reflectance test system to measure the reflectivity of the fabricated absorber. The AV3672D vector network analyzer was used as the signal source, and two pairs of Horn broadband antennas (2–18 GHz and 18–40 GHz) were used to emit and receive the electromagnetic waves. Pre-calibration was performed using standard metal plates of the same size in the test environment. Then the prototype was placed under the frame arch system for measurement.

Table 2 Performance comparison to recently published relevant works.

Fig. 12

(a) Photograph of the fabricated prototype, and (b) Measurement set up.

Firstly, the reflectivity under normal incidence was measured. Since the transmittance was zero, we could calculate the absorption. The measurement result is shown in Fig. 13a, along with the simulated absorption spectrum. The measured result is in good agreement with the simulated result in the whole measurable frequency range of 3–40 GHz. The stronger absorptivity fluctuation might come from the fabrication error or measurement noise.

Moreover, to verify the absorption performances at different wave incidence angles, the reflectance spectra of the absorber prototype were measured by adjusting the angle of the horn antenna. The measured absorption spectra of the absorber prototype for TE wave under oblique incidence are shown in Fig. 13b. In the frequency range of 4.8–40 GHz, the high absorption could be maintained within the incidence angle range of 45°. When the incident angle increased from 0° to 45°, the average absorptivity was 94.1%, 95.4%, 95.5%, and 95.6%. With the incident angle increased, no significant absorption band shift was observed. It proved that our design was insensitive to the wave incident angle, which was an outstanding property of the proposed absorber.

Fig. 13

(a) The simulated and measured absorption spectra of the absorber under normal incidence. (b) The measured absorption spectra of the absorber for TE wave under the incident angle of θ = 0°, 15°, 30°, and 45°, respectively.

Conclusions

In this paper, we proposed an ultra-broadband metamaterial microwave absorber with resistive ink coating on a meta-dielectric layer. The unit cell of the absorber consisted of a top PLA meta-dielectric layer, a resistive ink FSS, a middle PLA meta-dielectric lossy layer with resistive ink coating, and a bottom copper layer. The middle meta-dielectric lossy layer was employed to modify the effective complex impedance of the absorber, thereby optimizing the absorption performance. Simulation results demonstrated that the absorptivity was significantly enhanced by the resistive ink coating. When the thickness of the resistive ink coating was 4 μm, the proposed absorber exhibited uniform and high absorption in an ultra-broad frequency range of 4.4–60.0 GHz, with a relative absorption bandwidth of 173%. The average absorptivity was 95%, with an absorption fluctuation (∆A) relative to the average absorptivity of only 0.053.

Moreover, the excellent absorption performance was insensitive to the incident angle. Throughout the variation in incident angles (ranging from 0° to 45°), both the absorption frequency range and the average absorptivity remained stable. The maximum frequency shift was only 0.5 GHz. When the incident angle increased from 0° to 45°, the average absorptivity in the frequency range of 4.9–60.0 GHz changed from 94.6 to 94.3%. The average absorptivity kept nearly constant in the whole incident angle range.

In the experiment, we fabricated the absorber prototype and measured its absorption. The ultrahigh average absorptivity of 94.1% was obtained within the whole measurable frequency range of 4.2–40 GHz. The measured result was in good agreement with the simulated result, which proved our design well. In addition, with the incident angle increased, the measured absorption kept still high. With the 45° TE wave incidence angle, the average absorptivity was 95.6%, and no significant absorption band shift was observed.

These results demonstrated that our work provided a more flexible approach to optimizing absorption performance. This methodology opens up new possibilities for the design of ultra-broadband, wide-angle absorbers and can be extended to applications in various frequency regions, including terahertz, infrared, and visible.