Introduction

Now-a-days, renewable energy power is supplied into utility grid (UG) and pays more attention because of high fossil fuel prices, energy demand boom, and ecological pollution. Within numerous renewable energy resources (RESs), like tidal, wind, solar, biomass, geothermal and so on, the solar PV system is highly attractive and considered as a promising green resource due to more availability, cost-free, eco-friendly, safe-resource1,2,3,4,5,6,7. The solar PV modules transmit light into electrical energy but the energy attained from the photovoltaic module performs less voltage source of direct current and provides less conversion effectiveness. The electronic converter of power transforms DC into AC to increase the effectiveness and transmit less voltage direct current source into usable alternating current source. Traditional inverter topologies, like CSI & VSI are used to transmit the power of solar produced electrical power into UG4. At the time, these topologies need extra converter stage of DC/DC resulted in the power conversion of 2 stages, also it needs interfacing transformer to insert power to grid. This topology does not increase the difficulty of the circuit but increases the requirements of space and cost. The single-stage power conversion of solar satisfies every control objective, such as synchronization with grid voltage, maximum power point tracking (MPPT) and lesser harmonic content in output current. Presently, various solutions for a grid-tied photovoltaic system with traditional 2-level and MLI are stated in the literatures8,9.

In 2-level inverter, it inserts maximal photovoltaic power into grid with the unity of power factor (PF). Even though, due to high frequency of switching, the system gets failed because of high loss of power, high voltage stress and higher order harmonics10,11,12. The MLI is developed and because of its significant properties it is used more. They provide power rating, less dv/dt device switch voltage stress, lesser THD, less voltage of switch and so on. Also, the MLI is appropriate for the applications of higher power medium voltage and specifically it overcome by cascaded MLI and neutral point clamped MLI13,14,15. In these applications of moderate voltage, the neutral point clamped (NPC) MLI and cascaded MLI needs transformer to attain isolation of electrical among active direct current sources of H-bridge or its converter cells. This condition presents losses, improves the footprint converter, creating expensive, complex and large16,17,18,19,20,21,22. During unbalanced network conditions, the important limitations of cascaded multilevel converter (MLC) integrated with the transformer to make circulation of current among the phases and occur asymmetrical phase voltages23,24,25,26,27,28,29. In medium voltage applications, the modular multilevel inverter (MMI) has the capability to exchange cascaded MLC30,31,32. Recently, for the applications of medium power, intensive research is carried in modular multilevel converters (MMC) and it is highly probable. The modular multi-level converters have various benefits over traditional multi-level topologies. Even though, modular multilevel converters are examined with various applications but not stated in literatures with single-stage photovoltaic power conversion of solar system33,34.

This manuscript presents a grid-tied photovoltaic system featuring a modular multilevel inverter (MMI) topology that utilizes a hybrid approach. The proposed control topology combines the MAO algorithm with a RERNN, collectively known as the MAO-RERNN technique. This control method effectively mitigates variations in system parameters and external disturbances, ensuring that load demands are met optimally. The proposed MAO-RERNN control topology is employed in MATLAB/Simulink.

State of art

Previous research in the literature has focused on integrating power electronics with renewable energy sources through various methods and features. The most relevant studies related to this research are reviewed below;

To function the asynchronous motor drive for maritime applications, D. S. Vanaja et al.35 have performed the growth of solar PV-fed MMI with less switch count. The performed marine water-pumping system contains modular inverter, asynchronous motor drive, and photovoltaic panel. The performed topology gives the output of 11-levels using the sources of asymmetric direct current. The performed modular multilevel inverter was categorised as 5 direct current sources, and it was activated by the photovoltaic panel. For interconnecting a floating PV system into power grid, R. Bekhouche et al.36 have evaluated a novel integrated control method depends on predictive control model and the rejection control of active disturbance to regulate a modular multilevel converter used. The evaluated control system combines an active disturbance rejection controller for regulating DC-link voltage with an optimized predictive control model to effectively manage power flow and minimize circulating currents in the modular multi-level converter (MMC). Then, the excessive count of sub-modules in modular multilevel converters improves the complexity of Model Predictive Control |(MPC) control and for selecting the voltage vector, the calculation time to be synthesized based on the needed cost function. The optimized method was presented to lessen the calculation time and vector voltage reference application depends on local optimization for every elementary hexagon.

A. Hassan et al.27 proposed a nine-level MLI topology utilizing a single DC source, which minimizes the component count. These capacitors are self-charging and possess an inherent capability for balancing. The suggested topology was improved as nineteen -Level configuration. The alteration was suggested by including a supply of single and a couple of switches. The main aim of suggested method was a set of relative studies were conducted with other structures depending on few performance of assessing parameters37. Thus, for the capacitance of capacitors, a simple method was suggested to improve its boundary. Y. Jin et al.38 developed a simple and rapid software-based fault detection and localization (FDL) method for grid-connected modular multi-level converters. First, discrepancies between the measured and estimated state variables were calculated 

D. S. Vanaja and A. A. Stonier39 have performed a new efficient MMI with increasing performance parameters. These were grid synchronization, switching and harmonic reduction. The reductive model of modular multilevel inverter contains the switches of 3 bi-directional and 8 uni-lateral to create a symmetrical output of 9-level from which equal design was utilised to construct the output of 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31-level with asymmetric sources of direct current. For the levels of positive generation and negative generation, the performed structure needs a H-bride. Decrease in switch count to reduce the modular multilevel inverter loss and improves the effectiveness of modular multilevel inverter. The particular harmonic elimination method provides pulses to performed model and the Harris hawk’s optimization (HHO) was utilised for calculating the switching angles. A closed-loop control system was executed for the photovoltaic fed modular multilevel inverter from which the proportional integral (PI) gain controllers were altered by using Harris hawk’s optimization and the firefly controller.

For obtaining higher count of levels in output voltage with enhanced power quality (PQ), D. S. Vanaja et al.40 have presented a new control topology for MLI with less count of power switches. The diode clamped MLI structure was altered and the gating signals were produced by using the optimization method of harmonic in the basic frequency by Satin Bower Bird optimization (SBO) method. Also, it improves the quality of output waveform with less THD, improved effectiveness and less power losses of switching. In grid-connected applications, the inverter was presented for its competent operation capacity. For several load conditions, the brief simulation was done and the outcomes are presented. For connecting renewable energy sources in stand-alone and/or grid-tied modes of operation, Ahmed A. Hafez et al.41 have presented the MMC application. Under various climatological operating conditions, a simple and new power control of active and reactive was presented to provide the presented multilevel converters likewise the photovoltaic arrays function in Maximum Power Point (MPP). Through constraint optimization, the presented active-reactive control was executed by the controller of Proportional Integral and its factors were defined. To construct the proportional integral of the main controller, the Genetic Algorithm (GA) was used. The main function was modelled to improve the stability margin of system while mitigating the overshoot. Thus, the presented modular multilevel converter provides an additional degree of freedom for generating/absorbing the reactive power.

Implementation of MMI

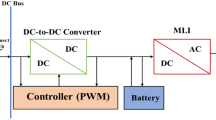
The multilevel inverter contains three bidirectional switches, eight switches of unidirectional and 4 sources of direct current. The components are organized to attain the levels of chosen voltage. The operation of bi-directional switch prevents the voltages of positive or negative and permits the flow of current in both directions42. A mutual emitter configuration 23 is chosen for the proposed topology as it has low conduction losses and requires only 1 driver circuit of gate. The components arrangement of MMI is shown in Fig. 1. The modular MLI is functioned in the modes of symmetrical and asymmetrical based on DC supply input. The modular MLI is appropriate for solar photovoltaic applications as 4 isolated DC sources are utilized. By using multiple PV panels with its own boost converters implementation complexity and improves cost.

Fig. 1
figure 1

Modular Multilevel Inverter.

Full size image

The single photovoltaic panel with SIMO boost converter are utilized in proposed system to mitigate the count of direct current sources. Due to the cascaded link of proposed topology rises the level of voltage. Modes of operation of symmetric system are shown in Fig. 2.

Fig. 2
figure 2figure 2

Modes of operation of symmetric system.

Full size image

Implementing solar PV system

For concerning the merchantable photovoltaic panel, the solar photovoltaic panel is provided as an input supply for multilevel inverter is intended. The problems among the array of solar photovoltaic generation system are the amount of electrical power produced through the array of solar photovoltaic is varying with weather, i.e., the magnitude of radiation. For the specific region, the intended photovoltaic panel consider the difference in irradiance and temperature by analysing the information of those parameters. The modelling of every PV cell and the modules of solar are used to understand the needed panel rating. For the proposed structure, one of the poly-crystalline silicon based solar panel is analysed. The SIMO boost-converter is shown in Fig. 3.

$$i = i_{Solar} - \mu_{1} - \mu \,_{2} - \,\frac{{v_{S} + 1 * r_{S} }}{{r_{P} }}$$
(1)
$$\mu_{1} = i_{DS} \, * \left( {e^{{\frac{{v_{S} + 1 * r_{S} }}{{e_{1} * v_{th} }}}} - 1} \right)$$
(2)
$$\mu_{2} = i_{DS\,\,2} \, * \left( {e^{{\frac{{v_{S} + 1 * r_{S} }}{{e_{2} * v_{th} }}}} - 1} \right)$$
(3)

where, \(i\,_{Solar}\) specifies the produced current through solar cell. \(i_{DS}\) and \(i_{DS\,2}\) is denoted as diode saturation currents. \(V_{th}\) specifies thermal voltage of intended solar-cell. The Coefficients of emission equivalent to diode as \(e_{\,1}\),\(e\,_{2}\)

$$i_{Solar} = i_{\sigma } \, * \left( {{\raise0.7ex\hbox{${i_{S\,o} }$} \!\mathord{\left/ {\vphantom {{i_{S\,o} } {i_{\sigma \,o} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${i_{\sigma \,o} }$}}} \right)$$
(4)
Fig. 3
figure 3

SIMO boost-converter.

Full size image

Here, \(i_{SO} \,\) and \(i_{\sigma 0} \,\) is denoted as irradiance current and solar current.

In Fig. 3, the single solar panel has twenty-four solar cells. In solar module, the open and short circuit of every cell is 0.5 V and 7 A. These twenty-four cells are joined in series to attain 7 A and 12 V in standard test condition. The desired DC links are developed by adding capacitors and diodes, and these are the important benefits of SIMO boost converter. The converter of direct current to direct current is a self-balancing converter that contains high conversion ratio, then the current output is continuous and there is no need for transformer.

PV power system model

In smart homes, photovoltaic (PV) systems are typically installed on rooftops as part of the overall PV power system design. While the photovoltaic source alone may not fully meet the home’s electricity demands, it becomes beneficial when utility electricity prices are high. The configuration of the PV power system is shown in Fig. 4.

Fig. 4
figure 4

PV power system configuration.

Full size image

The generation of power by PV is elaborated in below equation,

$$E_{PV} (t)\,\,\,\,\,\,\,\,\,\,\,\forall t\, \in \,\left\{ {1,\,2,\, \cdots 24} \right\}$$
(5)

For every time slot \(t_{\alpha } \, - t_{\beta }\), energy is produced by the photovoltaic sources, the net energy is produced through the photovoltaic sources for all day is shown below,

$$E_{PV} \, = \,\sum\limits_{{t = t_{\varepsilon } }}^{{t_{\beta } }} {E_{PV} (t)}$$
(6)

The capacity of meeting PV is minimum and they only integrated to compute in the below equation,

$$E_{PV} \, \ge \,E_{PV}^{\min }$$
(7)

The projection of photovoltaic (PV) power generation is integrated into a smart home forecasting device using a planner-based application. However, the power produced by the PV source can be significantly affected by adverse weather conditions, including solar irradiance, the area of the photovoltaic system, outdoor temperature, and the efficiency of the inverter. Thus, the overall power of output produced by photovoltaic is elaborated in below eqn,

$$E_{PV} = \eta_{PV} \, \times \,A_{PV} \, \times \,I_{r} \,\left( {1 - 0.005\,(T_{a} (t) - 25)} \right)$$
(8)

Grid-integration of proposed MMI

Figure 5 depicts closed-loop control system of grid-tied modular multilevel inverter. The main constraint of grid-tied inverter is current and it is inserted at a certain range from the source of photovoltaic. With the help of DC/DC converter the photovoltaic array voltage is increased to the necessary level based on voltage intensity of grid. Also, the controller of DC-to-DC converter is manufactured with the MPPT to enhance the cost, continuity and the efficiency of photovoltaic network. The method of perturbation and observation (P&Q) is accepted from maximum power point tracking controller due to less specified parameters. Under fast increasing solar radiation, this method is used to operate in photovoltaic grid tied network. By controlling the power factor, the modular multilevel inverter inserts the power of sinusoidal into utility. For grid injection, the inverter transmits the power of direct current from PV panels to the power of alternating current. The important part of grid is operation of photovoltaic network.

Fig. 5
figure 5

Closed-loop control system of grid-tied modular multilevel inverter.

Full size image

The proposed closed-loop control system has 6 control loops, and these 6 control loops are inserted into grid. The 6 control loops, like control loop of current is used to control the current of inverter and general control loop of voltage is utilized to compensate the general DC link voltage. The proportional integral gain controller is presented in net controller block of voltage and current in the control system is altered by Harris hawk’s optimization. The voltage controller of the proportional integral in the general voltage control loop receives the error by comparing the reference value with the determined value using a comparator. By altering the proportional-integral (PI) gain of the voltage-type controller, the general voltage controller can produce an inverter current with the highest amplitude. The reference grid current is then determined by multiplying this inverter current by a sine-wave signal produced by a phase-locked loop (PLL). In order to enable synchronization with the grid, the PLL makes sure that the inverter current stays in phase with the grid voltage and converts the grid voltage into a sine-wave signal. The controller is made depending on the power balance principle within the inverter of input and output. A sinusoidal current that is free of ripples is introduced into the grid by aligning the instantaneous grid current with the reference grid current. For the proportional integral current type of controller, the resultant error is provided as an input to increase the grid current from instant to reference, the gain of proportional integral controller (Kp, Ki) is regulated.

Proposed methodology

The MAO algorithm is inspired by the axolotl’s birth, breeding, tissue regeneration, and its aquatic habitat43,44. The RERNN possesses a unique memory capability. Additionally, an enhanced conjugate method, combined with the generalized Armijo search technique, improves the convergence rate for training the Recalling-Enhanced Recurrent Neural Network (RERNN) model45,46.

Mexican axolotl optimization algorithm (MAO)

The MAO method is a metaheuristic algorithm that draws inspiration from the life cycle and characteristics of the axolotl. It draws motivation from various aspects of the axolotl’s life, including its regenerative abilities, breeding behaviors, and aquatic lifestyle. The axolotl is the sexed creature and its populations are categorised as male and female. The ability of axolotls is modifying its colour, and considers that they modify its color to hide its body and avoids hunters. The fundamental steps in the transition of axolotls from larvae to adults are represented by the acronym TIRA, which stands for Transition, Injury and Restoration, Reproduction, and Assortment. The Mexican Axolotl Optimization method34 is defined and operates in four iterative phases. To increase the power extraction and its effectiveness, the proposed method is used to less the loss. The stepwise procedure is explained in the following steps,

Step 1: Initialization

Here, the output of MAO Eq. (21) is given as an input for RERNN.

Step 2: Check the iteration

The data processing stops when the number of iterations is less than the maximum iteration threshold.

Step 3: Random Generation

The populations are generated randomly.

Step 4: Fitness Calculation

Depending on the objective function, the system loss is reduced.

$$F_{c} = Min\left( {P_{L}^{*} } \right)$$
(9)

Step 5: Classification of Male female population

Due to axolotls, individual axolotls are classified into male population and female population to help the growth of axolotls based on its sex, and 2 sub-populations are attained.

Step 6: Process of Conversion from larvae state to adult state

From larvae to adult, start the conversion. In this larva to adult state, the male individual axolotls may change in water and by adjusting its color in the direction of male is suited best with environments. Based on the objective function from male and female axolotls, select the finest axolotls.

For male and female, find the inverse probability transition,

$$p(M,F)_{j} = \frac{{Obj(M_{j,} F_{j} )}}{{\sum {Obj(M_{j} ,F_{j} } )}}$$
(10)

Updating the population of male and female

If probability is higher than process of random, update the population of male and female. Thus, male population is updated as,

$$M_{ji} = M_{ji} + M_{best,i} - M_{ji} * \alpha$$
(11)

Else, the color of male axolotl is changed and it is expressed as,

$$M_{ji} = Min_{i} + Max_{i} - Max_{j} * R_{i}$$
(12)

where, \(\alpha\)—transition parameter, \(M_{j}\)- male axolotl, \(R_{i}\) specifies random number.

Also, if values of female probability is lower than random value population values are updated as,

$$F_{ji} = F_{ji} + F_{best,i} - F_{ji} * \alpha$$
(13)

Else, the value of female coloured axolotl as,

$$F_{ji} = Min_{i} + (Max_{i} - Max_{i} ) * R_{i}$$
(14)

From the computations, the best parameter value is updated. The flow chart of MAO is illustrated in Fig. 6.

Fig. 6
figure 6

Flow chart of MAO.

Full size image

Step 7: Injury and restoration process

Transferring the axolotls in water may cause injuries and accidents. This stage is injury stage. Lose state is when probability is injured, then start the regeneration procedure. Thus, it is expressed below,

$$\overline{P}_{ji} = Min_{i} + (Max_{i} - Max_{i} ) * R_{i}$$
(15)

Step 8: Reproduction and Assortment process

Male axolotl lays sperm, female axolotl gathers that sperm named Gloca to put in the sperm of female axolotl. Assuming that an axolotl lays 2 eggs and after it hatching its egg, the process of assortment begins. Also, if young larva is finest and it is interchanged as position of finest.

Step 9: Stopping criteria

If stopping criterion is satisfied then find the solution of optimum, else repeat the process.

Recalling-enhanced RNN

The structure of the recalling-enhanced RNN consists of seven layers, including the various layers39. The configuration of the recalling-enhanced RNN, which supports multiple inputs and multiple outputs, is illustrated in Fig. 7. The steps implicated in RERNN is explained below,

Fig. 7
figure 7

Structure of Recalling-enhanced RNN with multiple-inputs multiple-outputs.

Full size image

Step 1: Initialization

In this step, the EV parameters, Vectors weight- count of hidden-nodes and count of repetition are initialized.

Step 2: Random value Generation

After initialization, the input vectors are produced at random. At the same time, input parameters for electric vehicle (EV) systems, such as battery state of charge (SOC), engine speed and torque, battery power, and electric motor (EM) speed and torque, are also generated randomly.

Step 3: Check the iteration

When compared with maximal repetition, the recapitulation of the process is less, and then the data process will stop.

Step 4: Finding the learning rate

The learning rate is established using the comprehensive Armijo search method, and the equation is extracted as follows:

$$e\left( {W^{K} + l_{r} P^{K} } \right) \le e\left( {W^{K} } \right) + \alpha_{1} l_{r} e_{W}^{K} (P^{K} )^{T},\, \alpha_{1} \ge 0$$
(16)

Step 5: Calculate new weight

The gradient descent method is retained to establish the new weights, calculated using the following equation:

$$w^{k + 1} = w^{k} + L_{R} P^{k}$$
(17)

Step 6: Maximal iteration

Once the maximum restatement is reached, the process stops. Otherwise, the repetition value increases, and the process continues to step 2.

Step 7: Calculate the direction

The conjugate gradient descent algorithm includes as,

$$P^{k} = - E_{w}^{k} + \beta P^{k - 1}$$
(18)
$$\beta = \frac{{\alpha E_{w}^{k} (P^{k - 1} )^{t} }}{{P^{k - 1} (P^{k - 1} - E_{W}^{k} )}},\alpha \in (0,1)$$
(19)

he process then proceeds to step 4, where it repeats again. Figure 8 illustrates the flowchart of RERNN.

Fig. 8
figure 8

Flowchart of RERNN.

Full size image

Result and discussion

Simulation results and discussion

This section analyses a hybrid controller for a modular multi-level inverter (MLI) in a grid-connected photovoltaic generation system. The anticipated controller is implemented in MATLAB/Simulink, and its implementation is compared with classical methods. Figure 9 illustrates the output of the 31-level asymmetric MLI. The obtained peak value (Vpeak) is 300 V. Simulation of using PSO Approach (a) grid voltage, (b) grid current is shown in Fig. 10. The obtained peak value (Vpeak) is 300 V and current (Ipeak) is 5.7 V. The ssimulation results of using EPO Approach (a) grid voltage, (b) grid current is shown in Fig. 11. The simulation results of grid voltage using EPO Approach is shown in Fig. 11a. The obtained peak value (Vpeak) is 320 V. The ssimulation results of grid current using EPO Approach is shown in Fig. 11b. The obtained peak value (Ipeak) is 5.8 V. Figure 12 depicts waveforms of output (a) grid voltage and (b) grid current, (c) active power, (d) reactive power by utilising proposed method. Figure 13 shows that MAO-RERNN controller inserts the current of sinusoidal to grid and improves the current of grid in phase with grid voltage.

Fig. 9
figure 9

Output voltage of 31-level asymmetric MLI.

Full size image
Fig. 10
figure 10

Simulation of using PSO method (a) grid voltage, (b) grid current.

Full size image
Fig. 11
figure 11

Simulation of using EPO Approach (a) grid voltage and (b) grid current.

Full size image
Fig. 12
figure 12

Waveforms of Output for (a) grid voltage, (b) grid current, (c) active power, (d) reactive power using proposed method.

Full size image
Fig. 13
figure 13

Waveforms of Output for (a) Grid Voltage and (b) Grid Current using MAO-RERNN Proposed.

Full size image

Waveforms of Output for (a) Grid Voltage, (b) Grid Current using proposed MAO-RERNN is shown in Fig. 13. Figure 13 specifies even the power factor is changed from 45° lagging to leading; the current in the grid is fixed. At 0.1 s, the grid current remains sinusoidal because of the fast acting of MAO-RERNN controller under transient condition. Figure 14 displays performance of MAO-RERNN under voltage Sag. At 0.1 s along with a reference current 5 A, the voltage sag is generated. Figure 14 specifies that the grid current is not disturbed then it is placed in phase with the voltage of grid under voltage sag condition. Also, the voltage of sag is detected as 210 V. Figure 15 displays Performance of MAO-RERNN under voltage swell. From 230-375 V, the voltage distribution increases when load is removed suddenly at 0.1 s in proposed method. Figure 15 specifies that over a period of time, the grid current is fixed and it is placed in phase with grid voltage. By using grid control system, the voltage swell is balanced all over the process. In the sinusoidal wave shape, the control system of grid preserves the current of grid. If voltage swell continues to be un-checked, the over-heating arises; also it terminates the modules of inverter.

Fig. 14
figure 14

Performance of MAO-RERNN under voltage sag.

Full size image
Fig. 15
figure 15

Performance of MAO-RERNN under voltage swell.

Full size image

Calculation of power loss

The loss calculation of modular multilevel inverter is task of dynamic. The multilevel inverter consists of semiconductor switches, like insulated-gate bipolar transistor (IGBT), metal–oxide–semiconductor field-effect transistor (MOSFET), and diodes, which contains a particular power loss. The losses are separated into 3 various kinds, they are blocking, conduction losses and triggering. During the specific voltage, the losses are generated by an electronic switch and it is known as blocking loss. For loss calculation, this loss is very less when compared with another 2 loss and it is not considered. The disadvantage in computation loss is because of current ratings use in modular multilevel inverter in the switches of semiconductor. If output is met at value, the switch from that arm modifies current under switching process. Further, the difficulty of calculating the loss of power is because of the frequency of switching. The switching count is increased to get higher quantity of levels and also the switching frequency differs through every switch. Thus, the loss of computation is increased.

Conduction loss

The power transfer during the turn-on operation of the insulated-gate bipolar transistor (IGBT) is determined in its ON state. While the IGBT is active, the power dissipated is influenced by the device, and this dissipation is calculated based on the power consumed during the ON state. Further, by handling the duty-cycle with loss of conduction, the average dissipated power is attained. The proposed modular multilevel inverter has 2-way switches from that the peak voltage is attained by combining the switch of 1-way with 2 diodes. The loss of conduction for the switch of 2-way is (\(\rho_{CDN(T)\,IGBT\,}\)). Thus, it is expressed below,

$$\rho_{CDN(T)\,IGBT\,(b)} = \,\left( {v_{OV} + 2v_{dI} } \right)\,\,i_{K} \,\sin \,\omega T + 2\,r_{dI} i_{K}^{2} {\text{Sin}}^{2} \,\omega T + r_{0\,\,v} \,i_{K}^{\delta + 1} \,{\text{Sin}}^{\delta + 1} \,\omega$$
(20)

where \(v_{OV}\) and \(v_{dI}\) specifies voltages of IGBT and diode during conduction. \(r_{OV}\) and \(r_{Di}\) specifies resistances of IGBT and diode under conduction, \(i_{K} \,\) specifies passing of current via switch, δ specifies is datasheet of insulated-gate bipolar transistor. Similarly, the loss of ON state for a uni-directional switch is given below,

$$\rho_{CDN(T)\,IGBT\,(u)} = \left( {v_{OV} + v_{dI} } \right)\,\,i_{K} \,\sin \,\omega T + \,r_{dI} i_{K}^{2} {\text{Sin}}^{2} \,\omega T + r_{0\,\,v} \,i_{K}^{\delta + 1} \,{\text{Sin}}^{\delta + 1} \,\omega$$
(21)

The total ON state loss of modular multilevel inverter is given below,

$$\rho_{CDN(T)\,} = \Delta \cdot \,\rho_{CDN(T)\,IGBT\,(u)} + \nabla .\,\rho_{CDN(T)\,IGBT\,(b)}$$
(22)

Here, during conduction, Δ specifies net count of two-way switches and \(\nabla\) specifies net count of one-way switches. uni-directional and bi-directional switches is represented as \(IGBT\,(u)\) and \(IGBT\,(b)\).

Switching losses

While considering an insulated-gate bipolar transistor, the loss is related with switch and anti-parallel diode. The frequency of switching is directly proportional to the loss of triggering. Mainly, the loss of triggering is used to measure the total inverter loss. Nearly, 5 significant features has the effect of switch behavior, like current flowing via switch, blocking voltage of switch, stray inductance, gate resistance, temperature occur in semi-conductor junction. From semiconductor switches, the loss generated for various applications are generally considered as a main limitation for multi-level inverters. Also, these losses increases the cost of operating and less the performance of inverter. In the proposed topology, there are, 8 1-way and 3 2-way switches are presented. Mainly, the triggering losses are connected to the triggering frequency of the switches of one-way (\(F_{U}\)) and two-way (\(F_{b}\)). The switching loss of presented inverter is expressed below,

$$\rho_{SW} = \rho_{SW\,(u)} + \rho_{SW\,(b)} = \partial \sum\limits_{I = 1}^{2} {\left[ {\frac{1}{6}v_{u} i_{l} tF_{U} } \right]} + \sum\limits_{I = 1}^{4} {\left[ {\frac{1}{6}v_{u} i_{l} tF_{F} } \right]} + \sum\limits_{I = 1}^{2} {\left[ {\frac{1}{6}v_{b} i_{l} tF_{b} } \right]}$$
(23)

Here,\(v_{u}\), \(v_{b}\) specifies standing voltage of 1- and 2-way switches, \(i_{l}\) specifies root mean square(RMS) of load current,\(t = T_{on} + T_{off}\). By putting, \(\frac{{t * i_{l} }}{6} = \partial\), the equation becomes,

$$\rho_{SW} = \partial \sum\limits_{I = 1}^{4} {\left[ {v_{u} F_{F} } \right]} + \partial \sum\limits_{I = 1}^{4} {\left[ {v_{u} F_{F} } \right]} + \sum\limits_{I = 1}^{3} {\left[ {v_{b} \,F_{b} } \right]}$$
(24)

Under the fundamental frequency, the switching losses are eliminated for operating switches. Also, the common emitter structured with the switch of 2-way generates very less loss of switching. So, when compared with other asymmetric structures, the switching loss in MMI is considerably very small.

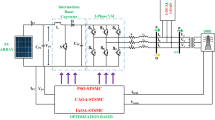
Experimental results and discussion

A 3 kW thirty-one MMI is implemented as Hardware-In-Loop (HIL) as depicted in the Fig. 16. In which 24 V DC is obtained from solar PV and stepped up into 300 V with the help of SIMO DC-DC converter with PSO based MPPT controller. The regulated DC voltage is fed to 31 level MMI which is triggered through dSPACE-DS1202. The triggering pulses are simulated in MATLAB/RT1 in the back end and real time pulses are generated through dSPACE in the front-end. The output voltage and current are sensed through sensors and given to Microlab-connector panel for processing. The MMI switches are implemented with IRF840-MOSFET with 8A current handling rating with maximum operating frequency of 3 MHz. Figure 17. Shows the three phase voltage waveform and individual waveforms generated in experimental set up using MAO-RENN waveform. Figure 18. Is the evident that the capacitor voltage balancing achieved and it attains steady value. Figure 19 Shows the THD analysis of voltage and current waveforms of MMI controlled by MAO-RENN control algorithm. The THD performance shows that the voltage waveform contains only 3.2% THD and current waveforms contain 2.2% THD as satisfying the IEEE standards.

Fig. 16
figure 16

Experimental arrangement.

Full size image
Fig. 17
figure 17

Experimental waveform of Three-phase voltage waveform and phase voltage waveforms using MAO-RENN controller.

Full size image
Fig. 18
figure 18

Capacitor voltage waveform using MAO-RENN controller.

Full size image
Fig. 19
figure 19

THD analysis of voltage and current waveform of MMI.

Full size image

Conclusion

This research presents a hybrid control topology for a MMI in a grid-connected photovoltaic generation system. The performance of the proposed method is estimated using the MATLAB/Simulink tool, and its results are compared graphically with existing methods. The 31-level MMI is integrated into the grid for practical applications. Experiments were conducted on the grid-connected photovoltaic system using optimization methods such as PSO and EPO. The simulation results indicate that when the proposed method is implemented with the Harris Hawk Optimization approach, the system maintains stability while improving the grid voltage in phase with the grid current and effectively balancing voltage swell and sag. Overall, the findings conclude that the MAO-RERNN-based proportional-integral controller significantly reduces harmonics, introducing minimal harmonic current into the grid. Additionally, comparative analysis of the suggested inverter in asymmetric mode demonstrates that it demands fewer switches to achieve the desired voltage levels.