Introduction

The task of text classification, a cornerstone of natural language processing (NLP), has recently attracted increased interest. Its applications span a wide range of fields, including sentiment analysis1,2,3, document categorization4, medical codes prediction5, legal studies6, patent classification7, and financial analysis8. Among these, Multi-label Text Classification (MTC) stands out as a particularly complex challenge. In MTC, the goal is to assign multiple labels to a given text, where the set of labels often exhibits a hierarchical structure. This structure implies a relationship between labels, such that information pertaining to one label can influence the inference of another, thereby adding complexity to the classification task.

The current approaches to the MTC task can be broadly classified into two categories: (1) methods that predict labels using textual information alone, and (2) approaches that combine both label and textual information for prediction. The first category of methods relies on local and global features extracted by text encoders to forecast labels. Notable examples include CNN-based models9,10 that address data imbalance issues caused by a lack of samples for child labels. Other works in this category focus on incorporating semantic information from text11. While these methods are effective at capturing textual subtleties, they generally fail to account for relationships between labels.

The second category of methods aims to integrate textual and label information. Strategies include weight initialization12, learning label hierarchies13,14,15, and the use of capsule networks16,17. These approaches improve the efficiency of MTC by leveraging label information but often achieve only a superficial understanding of the label hierarchy. The graph convolutional network (GCN)-based model18 shows promise in learning a deep label hierarchy but does not fully exploit label information, focusing exclusively on correlative aspects and overlooking label distinctiveness.

Despite substantial progress, a critical gap in research persists: the majority of current methods do not effectively utilize both the distinctive and correlative aspects of label information to optimize hierarchical multi-label classification. This shortcoming restricts the effectiveness of these models, especially in complex, hierarchical label structures where both types of information are essential for accurate classification.

Fig. 1
figure 1

Sample of label tree structure from RCV1-v2 dataset where grey, yellow, green, blue denotes root, first-level, second-level, third-level labels respectively. The variable \(s_{ij}\) indicates the similarity between label i and label j.

Full size image

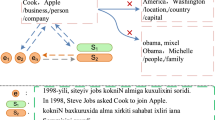
The concurrent consideration of correlative and distinctive information is fundamental to achieving a deep understanding of the label hierarchy, thus improving the effectiveness of MTC. As depicted in Fig. 1, the similarity \(s_{23}\) between nodes 2 and 3 represents distinctive information, which is presumed to be maximized due to the lack of connecting edges, whereas the similarity \(s_{26}\) signifies correlative information, presumed to be minimized.

This paper presents Hierarchical Contrastive Learning for Multi-label Text Classification (HCL-MTC). HCL-MTC explicitly models the hierarchical label structure as a directed graph, defining graph edges as contrastive knowledge between labels. This modeling approach facilitates the nuanced integration of both distinctive and correlative label information, enhancing the model’s capacity to capture the full complexity of the label hierarchy. To further improve the performance of label contrastive learning, we introduce a sampling hierarchical contrastive loss function. This loss function is designed to maximize the distinction between unrelated labels and minimize the similarity between closely related labels, thereby refining the model’s classification abilities.

In practical application, given training texts, the model first generates text features based on local and global information extracted from the text encoder. A linear converter then transforms these text features into label-wise features. Subsequently, the contrastive learner aggregates information from each label, incorporating insights from correlated labels based on their contrastive knowledge.

The primary contributions of this work can be succinctly summarized as follows:

  • Introduction of a novel methodology, HCL-MTC, which conceptualizes the label tree structure as a directed graph. This framework incorporates contrastive knowledge between labels to enhance the learning process effectively.

  • Development of a sampling hierarchical contrastive loss function to effectively utilize label contrastive knowledge. This innovative loss function is designed to improve the discriminative capabilities of the model in multi-label text classification scenarios by focusing on maximizing the distinction between unrelated labels while minimizing similarities between closely related labels.

  • Extensive empirical validation on two widely recognized public datasets demonstrates that HCL-MTC achieves significant improvements over existing state-of-the-art multi-label text classification methods.

Related work

MTC endeavors to assign hierarchical labels to given text inputs. Existing solutions for MTC can be broadly classified into different approaches based on their source of information and modeling strategies.

Text-based approaches

These approaches rely solely on the rich textual information inherent in the text at both word and sentence levels. They primarily leverage this information for predicting hierarchical labels without directly using label structure in the learning process.

Convolutional neural network (CNN) based methods: CNN-based methodologies are prevalent in MTC tasks due to their adeptness at capturing local contextual information. For instance, Kim19 demonstrated the effectiveness of CNNs in text classification. Following this, more advanced models like the Seq2Seq model11 utilized dilated convolution and a hybrid attention mechanism to discern semantic units in texts. This approach helps in capturing broader contexts which are essential in multi-label settings.

Enhanced CNN models: Further developments include models by Shimura et al.9 and Yang et al.10, which introduced fine-tuning techniques in CNN to propagate upper-level information to lower levels. Additionally, the integration of two single CNNs using a siamese approach for tail categories was explored to enhance model sensitivity towards less frequent labels. These methods, however, primarily focus on textual information and often overlook the crucial inter-label relationships that are pivotal in hierarchical multi-label classification.

Hybrid approaches

These methods incorporate both text and label information, attempting to utilize the hierarchical structure of the labels alongside the textual features to improve classification.

Initial hidden layer utilization: Baker and Korhonen12 initialized the final hidden layer of a CNN model to leverage label co-occurrence relations. This approach demonstrated that integrating label information at an early stage in the model can prime the network to better utilize label correlations.

Capsule networks and label embeddings: Chen et al.17 introduced a capsule network that incorporates label probabilities to enhance the representation of hierarchical relationships. Similarly, methods like those presented by Huang et al.15 and Yang et al.20 embed label vectors into the model and learn the label structure from upper to lower levels. These strategies aim to capture label hierarchies more effectively but often only achieve a shallow understanding of these relationships.

Graph convolutional network (GCN) based models: Recent advancements have seen the use of GCN-based models18,21 which formulate edge features based on word co-occurrence or label dependencies. These models leverage the structure of labels, which can be organized as trees or directed acyclic graphs (DAGs), to enhance classification performance. These approaches demonstrate promise but frequently rely heavily on prior probabilities and predefined label structures.

Hierarchical models

These models are specifically designed to leverage the hierarchical structure of labels, using various strategies to enhance the understanding and utilization of this structure in classification tasks.

Edge feature formulation in GCN-based models: Traditional GCN-based models like those by Marcheggiani and Titov22 and Lu et al.23 often initialize the adjacency matrix randomly or use basic schemes. However, some works21,24,25 define edge weights based on word information, such as word co-occurrence, word similarity, and point-wise mutual information. These methods attempt to enhance the model’s capacity to utilize textual and structural information concurrently.

Contrastive knowledge based edge formulation: In contrast, our approach formulates edge features based on the contrastive knowledge between labels, offering a significant departure from the reliance on word-related information. This novel strategy uses contrastive learning to directly encode the relationships between labels into the graph structure, thereby enhancing the model’s ability to understand and utilize the full spectrum of label information, both correlative and distinctive.

Proposed method

In this research, we propose a novel framework called Hierarchical Contrastive Learning for Multi-label Text Classification (HCL-MTC), which delineates contrastive learning methods through two primary components: (1) the transition matrix parameter of the Graph Convolutional Network (GCN), and (2) the introduction of a sampling hierarchical contrastive loss. The subsequent discussion begins with a thorough formulation of the problem, followed by a detailed explanation of our proposed HCL-MTC framework.

Problem formulation

In the domain of MTC, we consider a set of m predefined labels, denoted as \(L=\{l_1,l_2,...,l_m\}\). Given a training set of N instances, represented as \(\{(T_1,Y_1), (T_2, Y_2),...,(T_N,Y_N)\}\), where \(T_i=\{x_1, x_2,...,x_n\}\) signifies the \(i^{th}\) text instance, with n being the length of the text and \(x_i\) denoting the \(i^{th}\) word, and \(Y_i\) indicating the subset of L assigned to \(T_i\), the objective of the MTC task is to predict \(\hat{y}_i\) for each test text. It is noteworthy that: i) Each text instance is associated with one or more labels from the set L; ii) The labels often organize themselves into a tree structure, indicating the existence of both correlative and distinctive information among the labels; iii) The sample size of a child node in the label hierarchy is typically smaller than that of its parent node, reflecting a hierarchical distribution of data among the labels.

Hierarchical contrastive learning for MTC

Fig. 2
figure 2

The overall structure of the HCL-MTC model (Hierarchical Contrastive Learning for Multi-label Text Classification), which elucidates the principal components and the process flow from input data to multi-label classification output. The model architecture is composed of a text encoder for capturing local and global textual features, a linear converter that transforms these features into label-specific representations, and a hierarchical contrastive learner which exploits the relationships between labels to enhance classification performance. The hierarchical contrastive learner is structured as a directed graph, where each node aggregates information from its parent, child, and self-nodes, guided by a learned weighted adjacency matrix that encodes label contrastive knowledge.

Full size image

As depicted in Fig. 2, our proposed model is composed of four main components: a text encoder, a feature extractor, a linear converter, and a hierarchical contrastive learner. When presented with a sentence, the text encoder and feature extractor work together to capture both local and global context, producing a text feature representation. This text feature is then passed to the linear converter, which adjusts its dimensionality to align with that of the label-wise feature space. The final component, the hierarchical contrastive learner, takes into account the contrastive relationships between labels, interpreting these relationships as transition probabilities, thereby completing the model architecture.

Input: Before being processed by the text encoder, the input text undergoes a transformation through a pre-trained embedding matrix. Given a text sequence \(T=\{x_1, x_2,...,x_n\}\), where each \(x_i\) represents a word in the text, each word is converted into a corresponding vector \(\omega _i\), This embedding process results in the construction of the input matrix \(I=\{\omega _1,\omega _2,...,\omega _n\}\), which serves as the input to the text encoder.

Text encoder: A variety of text encoders, including Recurrent Neural Networks (RNN)26 and their derivatives such as Long Short-Term Memory (LSTM)27 and Gated Recurrent Unit (GRU)28, have been utilized to capture global context within texts. In recent years, pre-trained models with fine-tuning capabilities, like BERT29 and XLNet30, have shown remarkable performance across a range of Natural Language Processing (NLP) tasks and can be effectively used as text encoders. For the sake of experimental consistency, we opt for the same text encoder, Bi-GRU, as employed in18. The Bi-GRU encoder layer processes the input matrix \(I=\{\omega _1,\omega _2,...,\omega _n\}\) , where the hidden vector of a Bi-GRU is computed as follows:

$$\begin{aligned} \begin{aligned}&\overrightarrow{h}_t=GRU(\overrightarrow{h}_{t-1},\omega _t),\\&\overleftarrow{h}_t=GRU(\overleftarrow{h}_{t+1},\omega _t),\\&h_t=[\overrightarrow{h}_t,\overleftarrow{h}_t], \end{aligned} \end{aligned}$$
(1)

where \(\overrightarrow{h}_t\) and \(\overleftarrow{h}_t\) are the forward hidden vector and backward hidden vector at time step t. The output \(h_t\in \mathbbm {R}^{2\mathbbm {u}}\) of the Bi-GRU is the concatenation of \(\overrightarrow{h}_t\) and \(\overleftarrow{h}_t\) where \(\mathbbm {u}\) indicates the number of hidden units of each unidirectional GRU. The resulting global feature maps are \(H=\{h_1,h_2,...,h_n\}\).

Feature extractor: We employ a CNN model to extract n-gram features from the global feature maps H obtained from the text encoder. The choice of CNN is driven by three key considerations: (1) The local connectivity property naturally models n-gram compositions through sliding window operations; (2) Parameter sharing mechanism enhances robustness to lexical variations; (3) Hierarchical filters enable automatic discovery of salient phrase-level patterns. Let \(F\in \mathbbm {R}^{g \times 2\mathbbm {u}}\) represent a convolutional kernel, and let \(H_{i:i+g-1}\) denote a region of the global feature map spanning g words. The local feature can be formulated as follows:

$$\begin{aligned} \begin{aligned} c_i=F\odot H_{i:i+g-1} + b, \end{aligned} \end{aligned}$$
(2)

where \(\odot\) denotes the component-wise multiplication, and \(b\in \mathbbm {R}\) denotes a bias term. The feature maps of f filters at \(i^{th}\) channel can be denoted as \(C_i=\{c_i^{1},c_i^{2},...,c_i^{f}\}\). Next, we apply the k-max pooling method to filter the top k most informative word combinations which can be formulated as follows:

$$\begin{aligned} \begin{aligned} P=&flatten(max(k,[C_1,C_2,...,C_{n-g+1}]))\\ \end{aligned} \end{aligned}$$
(3)

Given that K convolutional kernels are used, the final text feature is obtained by concatenating the outputs from each kernel. Let \(P^k\) denote the output of the \(k^{th}\) kernel, where \(k \in {1, 2, \ldots , K}\). The concatenation of these outputs forms the final text feature, represented as: \(O=[P^1,P^2,...,P^K]\). Unlike recurrent architectures that process tokens sequentially, our CNN design allows parallel feature extraction across all text positions, significantly improving computational efficiency for long texts.

Linear converter: The role of the linear converter is to bridge the gap between text semantics and label characteristics through dimension-aware transformation. Motivated by the need to preserve computational efficiency while maintaining interpretable label projections, we formulate this process as a trainable linear mapping. Specifically, given the text feature \(O\in \mathbbm {R}^{K}\) extracted from diverse n-gram patterns, the converter first applies weight matrix \(M\in \mathbbm {R}^{d_w\times K}\) to project features into latent label space. This linear design intentionally avoids introducing nonlinear distortions, allowing direct interpretation of label-feature correlations. The subsequent reshape operation then reorganizes the \(d_w\) dimensional output into \(V\in \mathbbm {R}^{m\times d_n}\), where m corresponds to the predefined number of labels and \(d_n\) configures the feature depth per label. The dimension adjustment from \(d_w\) to \(m \times d_n\) is mathematically guaranteed when \(d_w = m \times d_n\), ensuring structural compatibility for downstream label-wise operations.

Hierarchical contrastive learner: The Graph Convolutional Network (GCN)31 is utilized to represent structural relationships between nodes, including classification labels. In graph-based representations, edges encode the relationships between nodes. Traditional GCNs22,23 often initialize the transition matrix randomly and rely on error backpropagation to learn node relationships, frequently disregarding information about node correlations. Zhou et al.18 mitigated this limitation by defining edge features based on the prior probability of label dependencies. Nonetheless, this approach mainly concentrates on learning correlative information between labels, neglecting the distinctiveness of labels.

In contrast, our proposed hierarchical contrastive learner constructs connections between graph nodes using label contrastive knowledge. Building upon the framework of Hierarchy-GCN18, we represent the label tree as a directed graph, where each node aggregates information from its parent nodes, child nodes, and itself. This aggregation process is dynamically guided by a learned adjacency matrix, which encodes directional relationships between nodes based on contrastive similarities.

Let \(\mathcal {G} = (\mathcal {V}, \mathcal {E})\) represent the directed graph, where \(\mathcal {V} \in \mathbbm {R}^{m \times d_n}\) denotes the set of m nodes, each corresponding to a label with a feature vector \(v_k \in \mathbbm {R}^{d_n}\), and \(\mathcal {E}\) represents the set of directed edges. The neighborhood N(k) of node k includes its parent node, child nodes, and itself. The connections between nodes are captured by the adjacency matrix \(\textbf{A}\), where each element \(A_{j,k}\) is computed based on the contrastive similarity between the feature vectors of node j and node k.

Specifically, the contrastive similarity \(a_{j,k}\) is defined as the absolute value of the cosine similarity between the feature vectors \(v_j\) and \(v_k\):

$$\begin{aligned} a_{j,k} = \left| \frac{v_j \cdot v_k}{||v_j|| \cdot ||v_k||}\right| \end{aligned}$$

Each \(a_{j,k}\) represents the strength of the connection between node j and node k, and is used to populate the corresponding entry \(A_{j,k}\) in the adjacency matrix \(\textbf{A}\). Higher values of \(a_{j,k}\) indicate stronger similarity and thus a more direct flow of information from node j to node k, while lower values encourage information transfer across less similar nodes, promoting diversity in the learning process.

The feature information from node j is transferred to node k through an intermediate representation \(\mu _{j,k}\), which is influenced by the contrastive similarity and a transfer bias \(b_l^k\):

$$\begin{aligned} \mu _{j,k} = a_{j,k} v_j + b_l^k \end{aligned}$$

To regulate this transfer, a gating mechanism is applied. The gate, parameterized by a direction-specific weight matrix \(W_g^{d(j,k)}\) and a gate bias \(b_g^k\), ensures that the flow of information is controlled based on the relative importance of the neighboring node:

$$\begin{aligned} g_{j,k} = \sigma (W_g^{d(j,k)} v_j + b_g^k) \end{aligned}$$

This gating function, \(g_{j,k}\), modulates the contribution of node j to node k, allowing the model to selectively filter the information passed between nodes. After gating, the hidden state of node k is updated by aggregating the gated information from all its neighbors, followed by a ReLU activation function to introduce non-linearity:

$$\begin{aligned} h_k = \text {ReLU}\left( \sum _{j \in N(k)} g_{j,k} \cdot \mu _{j,k}\right) \end{aligned}$$

The adjacency matrix \(\textbf{A}\), which governs the structure of the graph, is dynamically learned from the contrastive similarities between node features. It captures both top-down and bottom-up flows, with a symmetric relationship between the two directions: \(A_{j,k}\) for top-down flow is equal to \(A_{k,j}\) for bottom-up flow. Additionally, each node retains self-loops with \(A_{k,k} = 1\), ensuring that a node always retains its own information during the aggregation process. This dynamic construction of the adjacency matrix allows the model to adapt to the hierarchical label structure and to capture the intricate dependencies between nodes, facilitating effective learning from both similar and dissimilar nodes within the hierarchy.

Sampling hierarchical contrastive loss

The hierarchical contrastive loss aims to capture both distinctive and correlative information between labels in a hierarchical structure. To clarify its formulation, we provide an intuitive explanation before introducing the technical implementation.

Intuitive explanation: in a label tree, parent-child pairs can transfer information bidirectionally, while information between different parent nodes remains distinct. Thus, the hierarchical contrastive loss focuses on two main objectives:

  • Maximizing distinctive information: reducing the similarity between different parent nodes to enhance label distinctiveness.

  • Minimizing correlative information: increasing the similarity between a parent node and its child nodes to reflect hierarchical correlation.

Loss function formulation: Let \(v_{p_i}\) and \(v_{c_k}\) denote the embeddings of parent node \(i\) and child node \(k\), respectively. The similarity between two nodes is measured using the cosine similarity, given by:

$$\begin{aligned} s(v_a, v_b) = \frac{v_a \cdot v_b}{\Vert v_a\Vert \cdot \Vert v_b\Vert }, \end{aligned}$$

where \(\cdot\) denotes the dot product, and \(\Vert \cdot \Vert\) represents the vector norm. Using this similarity metric, we define two key components of the hierarchical contrastive loss:

1. Distinctiveness Term: This term minimizes the similarity between pairs of parent nodes \(v_{p_i}\) and \(v_{p_j}\) (where \(i \ne j\)), ensuring that different parent nodes are well-separated in the representation space:

$$\begin{aligned} L_{\text {distinctive}} = \sum _{p_i \in \mathcal {V}} \sum _{p_j \in \mathcal {V}, j \ne i} \exp (s(v_{p_i}, v_{p_j})). \end{aligned}$$

2. Correlation Term: This term maximizes the similarity between parent nodes \(v_{p_i}\) and their respective child nodes \(v_{c_k}\), capturing the semantic correlation in the hierarchy:

$$\begin{aligned} L_{\text {correlative}} = \sum _{p_i \in \mathcal {V}} \sum _{c_k \in \text {child}(i)} \exp (-s(v_{p_i}, v_{c_k})). \end{aligned}$$

Combining these two terms, the overall hierarchical contrastive loss is defined as:

$$\begin{aligned} L_{d} = L_{\text {distinctive}} + L_{\text {correlative}}, \end{aligned}$$

This formulation enforces a tradeoff between maximizing distinctiveness and minimizing correlation, ensuring that the learned embeddings adhere to the hierarchical structure.

Computational optimization via sampling: enumerating all node pairs is computationally intensive. To address this, we employ a sampling mechanism. For each hierarchical level, only two randomly selected parent nodes and one randomly selected child node are included in the computation of the hierarchical contrastive loss.

Sampling strategy:

  • For each parent node \(p_i\), randomly select two other parent nodes \(p_j\) and \(p_k\) for comparison.

  • In the direct child node set of \(p_i\), randomly select one child node \(c_k\).

  • Compute the loss using the selected node pairs.

To better illustrate this process, Fig. 3 shows the hierarchical structure and the sampling strategy.

Fig. 3
figure 3

Illustration of the Hierarchical structure and sampling strategy. Specifically, two parent nodes (e.g., \(p_1\) and \(p_2\)) and one child node (e.g., \(c_{11}\)) are randomly selected to compute the hierarchical contrastive loss. The objective is to maximize the distinctive information between \(p_1\) and \(p_2\) while minimizing the correlative information between \(p_1\) and \(c_{11}\). Here, \(c_{ij}\) represents the j-th child node of the i-th parent node.

Full size image

Classification

The final node features are fed into a fully connected layer, and the probability of node k being activated can be formulated as:

$$\begin{aligned} \begin{aligned} p_k = \sigma (W_kh_k+b^k), \end{aligned} \end{aligned}$$
(4)

where \(W_k \in \mathbb {R}^n\) is the weight vector for node k, \(h_k \in \mathbb {R}^n\) represents the feature vector of node k, \(b^k \in \mathbb {R}^n\) is the bias term for node k, and \(\sigma\) denotes the activation function, typically a sigmoid function in the context of multi-label classification to ensure the output is in the range ([0, 1]), interpretable as a probability.

The model then assigns labels to a given test text based on the probabilities \(p_k\) of the corresponding nodes. Labels with probabilities greater than a predetermined threshold \(\theta\) are considered as predicted labels for the test text. This threshold \(\theta\) is a hyperparameter that can be tuned to balance the precision and recall of the model’s predictions.

Loss function

The HCL-MTC model integrates three different types of losses: binary cross-entropy loss, recursive regularization loss32, and sampling hierarchical distance loss. The overall loss function is formulated as follows:

$$\begin{aligned} \begin{aligned} L_c =&-\sum _{i=1}^my_ilog(y_i^\prime)+(1-y_i)log(1-y_i^\prime),\\ L_r =&\sum _{i\in \mathcal {V}}\sum _{j\in child(i)}\frac{1}{2}||\omega _i-\omega _j||^2,\\ L =&L_c+\lambda _1L_r+\lambda _2L_d, \\ \end{aligned} \end{aligned}$$
(5)

Here, \(L_r\) represents the recursive regularization loss, which involves the parameters of the final fully connected layer, \(y_i\) indicates the ground truth label, and \(y_i^\prime\) represents the predicted probability of the \(i^{th}\) label.

Experiments

Dataset description

We assess the efficacy of our proposed model using two publicly available datasets: RCV1-v2 and Web-of-Science (WoS).

Reuters corpus volume I (RCV1-v2): This dataset represents a refined version of the original RCV1-v1 data, made available for research purposes33. It encompasses a total of 804,414 manually categorized newswire stories spanning 103 topics. Each newswire story has the potential for assignment to multiple topics.

Web of Science (WoS): The WoS dataset comprises metadata from 46,985 published papers34. This dataset includes abstracts, domains, and keywords. The abstract serves as the input for text classification, while the domain represents the label hierarchy. Additionally, the keywords offer descriptions of the subsequent label level. The dataset is characterized by a total of 141 domains.

Evaluation metrics

We use the standard evaluation metrics of Micro-F1 and Macro-F132 to measure our experimental results.

  • Micro-F1 considers the overall performance of the model which is calculated by overall precision and recall of all the labels.

  • Macro-F1 considers the local performance of the model which gives equal weight to all labels.

Specifically, the computation of the Micro-F1 score and Macro-F1 score is elucidated below:

$$\begin{aligned} \begin{aligned}&micro F1 = \frac{2\sum _{l\in L}TP_l}{\sum _{l\in L}2TP_l+FP_l+FN_l},\\&macro F1 = \frac{1}{|L|}\sum _{l\in L}\frac{2TP_l}{2TP_l+FP_l+FN_l}, \end{aligned} \end{aligned}$$
(6)

Here, \(TP_t\), \(FP_t\), and \(FN_t\) denote the true-positives, false-positives, and false-negatives, respectively, for the label \(l \in L\).

Experimental setup

To provide a comprehensive evaluation, we compared our model against several baselines and state-of-the-art models. The baselines include CNN, RNN, RCNN, and hierarchical models like HiLAP, HMCN, and HiAGM. The specific implementation and training details are as follows:

Table 1 Implementation details: dropout shows the dropout rate in the embedding layer and MLP layer, GRU dropout shows the dropout rate in the Bi-GRU layer and Node dropout shows the dropout rate in the node transformation layer.
Full size table

All experiments are conducted in PyTorch35. To ensure comparability with18, we adopt similar implementation parameters. The 300-dimensional word embedding vector is initialized using GloVe pretrained embeddings36. A vocabulary size of 60,000, comprising the most frequent words, is employed, with removal of words occurring less than twice. We use the Adam optimizer37 to minimize the total loss. The penalty coefficient for recursive regularization is set to \(1 \times 10^{-6}\), and for sampling hierarchical distance loss, it is set to \(1 \times 10^{-5}\). The maximum number of epochs is set at 400, and the model stops training if no improvement is observed within 50 epochs. Additional implementation details are provided in Table. 1.

Experimental results

Table 2 Experimental results of MLP baselines, state-of-art models and our proposed model.
Full size table

We systematically evaluate our proposed model on two public datasets, conducting a comprehensive comparison with 12 MLP baselines and state-of-the-art models based on micro-F1 and macro-F1 metrics. The assessment of our model is performed on the test subset, employing the best model determined on the validation subset. The outcomes of our proposed model are presented in Table 2.

Discussion: the experimental findings yield several key conclusions:

  • Performance on RCV1-v2: our proposed model surpasses all existing models on the RCV1-v2 dataset, exhibiting a noteworthy enhancement of 0.58% in the Micro-F1 score and 0.94% in the Macro-F1 score compared to the HiAGM-TP\(_{GCN}\) model. These improvements are statistically significant (\(p < 0.05\)).

  • Performance on WoS: on the WoS dataset, HCL-MTC demonstrates considerable improvements of 0.65% and 0.74% in terms of Micro-F1 and Macro-F1, respectively. These improvements are also statistically significant (\(p < 0.05\)).

  • Macro-F1 improvement: HCL-MTC primarily boosts the Macro-F1 score across both datasets, indicating its proficiency in handling classes with fewer samples and effectively addressing the challenge of data sparsity.

  • Hierarchical learning impact: Our proposed model represents an enhancement of the HiAGM-TP\(_{GCN}\) framework by integrating a contrastive learning method into its core architecture. Specifically:

    • We leverage the similarity between label pairs as transition parameters in the GCN network, in contrast to utilizing the prior probability of label dependencies.

    • The sampling hierarchical contrastive loss introduced to the total loss helps the model learn the label hierarchy more effectively.

  • Distinctiveness and correlation management: The hierarchical contrastive loss aids in minimizing correlative information between parent nodes and their children while maximizing distinctiveness between different parent nodes. This contributes to the overall performance improvement.

Ablation test

We perform an ablation test to systematically analyze the influence of the similarity transition matrix and the sampling hierarchical contrastive loss on the proposed model. The results of this ablation study are presented in Table 3.

The outcomes of the ablation study provide valuable insights. Notably, the performance of HCL-MTC without the inclusion of the similarity transition matrix and the sampling hierarchical contrastive loss exhibits a significant decrease across all datasets, as evident in both Micro-F1 and Macro-F1 metrics. This substantial performance decline underscores the crucial contributions of both the similarity transition matrix and the sampling hierarchical contrastive loss to the overall efficacy of HCL-MTC. Additionally, an interesting observation is the larger decrease in macro-F1 performance compared to micro-F1. This discrepancy can be attributed to the fact that macro-F1 treats each class equally, disregarding imbalances in the distribution of samples across classes. Consequently, our proposed method demonstrates a capacity to mitigate the challenges associated with class imbalance.

Table 3 Ablation study of the HCL-MTC with varying different components on RCV1-v2 and WoS datasets. w/o similarity denotes the HCL-MTC without similarity transition matrix and w/o contrastive loss denotes the HCL-MTC without sampling hierarchical contrastive loss.
Full size table

The rationale behind these findings can be elucidated as follows:

  • Facilitating deep label hierarchy learning: The objective is to encourage the child node to aggregate more information from its parent, or vice versa, enabling the model to learn deep label hierarchies along the correct path. The similarity transition matrix plays a pivotal role in this process, assigning higher transition probabilities to label pairs that exhibit greater similarity.

  • Role of sampling hierarchical contrastive loss: This loss function aids the model in minimizing similarity information from parent nodes to their child nodes, while simultaneously maximizing the distinctiveness between parent nodes. Consequently, the sampling hierarchical contrastive loss contributes to guiding the model towards optimal solutions during the training process.

Limitations and future work

While the proposed model demonstrates significant improvements over existing methods, it has notable limitations that warrant further investigation:

  • Scalability issues: The hierarchical contrastive loss and similarity transition matrix can become computationally expensive as the number of labels increases, potentially limiting scalability for extremely large label sets. Future work could explore techniques such as hierarchical sampling methods, low-rank approximations of similarity matrices, or distributed training strategies to improve computational efficiency.

  • Data sparsity: In cases of extreme data sparsity, particularly for low-frequency labels, the model may struggle to learn meaningful relationships. Future research could address this by incorporating data augmentation strategies, synthetic data generation, or transfer learning from related tasks with richer datasets to enhance the model’s robustness in sparse settings.

  • Highly imbalanced label distribution: Despite improvements in Macro-F1 scores, extreme class imbalance remains challenging, especially for labels with limited instances. Potential solutions include dynamic label reweighting, advanced oversampling techniques, or self-supervised pretraining tailored to underrepresented labels.

  • Complex hierarchical structures: For datasets with exceptionally deep or irregular hierarchical structures, the model may face difficulties in capturing accurate relationships, particularly when hierarchical depths exceed those seen during training. Developing adaptive mechanisms, such as recursive representations or depth-aware loss functions, could allow the model to better handle varying hierarchical complexities.

  • Domain-specific vocabulary: When the label vocabulary is highly domain-specific, the pretrained GloVe embeddings may insufficiently capture semantic nuances, potentially affecting performance. Fine-tuning embeddings on domain-specific corpora, integrating domain knowledge through external knowledge graphs, or leveraging domain-adapted language models could mitigate this issue.

  • Generalizability across domains: While the model has demonstrated improvements on specific datasets, its adaptability across diverse domains remains limited. Future work should involve extensive testing across datasets from varied domains and tasks to evaluate robustness. Additionally, exploring domain adaptation techniques could enhance its generalizability.

In conclusion, while the proposed HCL-MTC model achieves promising results, addressing these limitations could further enhance its scalability, robustness, and applicability. Future research directions include optimizing computational efficiency for large-scale label sets, improving methods to handle data sparsity and class imbalance, developing adaptive approaches for complex hierarchical structures, and ensuring robust generalization across diverse domains and specialized vocabularies.

Conclusions

This paper introduces the Hierarchical Contrastive Learning for Multi-label Text Classification (HCL-MTC) framework, which leverages Graph Convolutional Networks (GCN) with a similarity transition matrix and sampling hierarchical contrastive loss. These innovations enhance the model’s ability to learn deep label hierarchies and capture both correlative and distinctive knowledge between labels.

Experiments on the RCV1-v2 and Web of Science (WoS) datasets demonstrate the superior performance of HCL-MTC, achieving Micro-F1 scores of 84.54% and 86.47% and Macro-F1 scores of 64.29% and 81.02%, respectively. These results highlight the model’s robustness in handling data sparsity and class imbalance, establishing HCL-MTC as a highly effective solution for multi-label text classification.