Research on blindsight technology for object recognition and attitude determination based on tactile pressure analysis

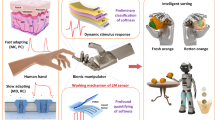
Abstract

Aiming at the existing robotic hand’s reliance on visual guidance for object recognition during the grasping process, which is limited by environmental lighting and object occlusion, this paper is committed to proposing a method for object recognition and posture determination based on contact force feedback. The paper first constructs a contact surface deformation model for classic button operations and grasping operations in power systems, based on Hertz contact and elastoplastic unloading theories, laying the theoretical foundation for the vector mechanics decomposition of the contact surface. It then proposes a dimensionality reduction analysis method for vector force arrays, identifying the boundary force characteristics of the contact surface to decompose the 3D contact surface into separate force planes and reducing the angle dimension in the vector array to a two-dimensional scalar array that only includes the magnitude of the force, thus laying the data foundation for introducing convolutional neural networks (CNNs). Through training and learning the mechanical features of the contact surface, the paper achieves perception and posture determination of objects during pressing and grasping processes. Practical experiments demonstrate that the proposed method for rapid analysis and extended posture determination of the grasping surface based on CNNs can achieve millimeter-level precision in grasping position determination and a two-dimensional posture angle of less than 1 degree for the grasped object, generally meeting the requirements of power system business scenarios. The blind-sense technology explored in this paper can be widely applied to non-visual perception at the end of humanoid robots and has significant engineering guidance value.

Introduction

Soft grasping is the foundation of a robotic hand’s precision grasping. Unlike rigid contact grasping, soft grasping produces varying degrees of deformation on the contact surface. Existing mechanical detection methods are unable to accurately identify the posture of the grasped object and the stability of the contact surface. Macroscopic visual acquisition outside the robotic hand’s sensors can, to some extent, obtain the posture of the grasped object, but it is limited by on-site lighting conditions and occlusions. During fine operations, macroscopic visual detection is not suitable. Therefore, scholars have conducted extensive research on the stability of grasping and posture determination, including the generation of datasets, grasping algorithms, multimodal perception, functional and adaptive grasping, and real-time interaction.

Reference¹ provides an efficient framework for synthesizing diverse and stable grasping posture data, generating the large-scale simulation dataset DexGraspNet, which significantly enhances the performance of dexterous robotic hand grasping synthesis algorithms. Reference² divides the grasping process into static grasping gesture generation and reinforcement learning-based execution of grasping based on target gestures, allowing the algorithm to generalize across various objects and adapt to downstream tasks. Reference³ proposes strategies for handling objects of various shapes and features, adapting to changes in geometric shapes, textures, or lighting conditions, and demonstrating extensive adaptability to a wide range of objects. Additionally, Reference⁴ achieves functional dexterous grasping for robotic arms through a human-to-robot grasping redirection module, transferring human grasping postures to different robotic hands. Reference⁵ combines vision-language-action models with diffusion models to enhance the dexterous control capabilities of robotic arms, significantly improving the success rate of pick-and-place tasks. Reference⁶ proposes a multi-object detection system based on the Yolov5 algorithm, combined with a monocular structured light module, to enable robotic hands to acquire depth information of objects and improve positioning accuracy. Reference⁷ decomposes human grasping diversity into “how to grasp” and “when to grasp,” achieving real-time interaction with humans through the combination of diffusion models and reinforcement learning. Reference⁸ improves the grasping accuracy of robotic hands for complex objects by using dual-viewpoint point cloud stitching, which is applicable to a variety of industrial and scientific research scenarios.

However, in existing research, there is little mention of identifying the stability of contact and the rationality of the grasped object’s posture through a tactile pressure vector matrix during the grasping process. A vector matrix is a matrix constructed from pressure values with direction. Unlike rigid contact grasping, where the pressure is approximately perpendicular to the contact surface, the pressure matrix of the contact surface can be approximated as a scalar matrix when analyzing it. The deformation of the contact surface during soft grasping means that the direction of the force is not unique, but it also provides a way to analyze the forces during grasping to determine the stability of contact and the rationality of the grasped object’s posture⁹. In reference¹⁰, the visual grasping method is utilized for small and delicate objects. However, it encounters a precision bottleneck in the feature extraction of tiny objects. It is highly vulnerable to interference from minute textures and complex backgrounds, leading to identification errors. Moreover, for rapidly moving minute targets, the tracking and grasping response speeds are insufficient, making it difficult to meet the requirements of high-speed grasping. In reference¹¹, reinforcement learning is applied to grasping in cluttered and dynamic scenes. Nevertheless, during the training process, the efficiency of environmental exploration is low, and the convergence is slow, with a substantial amount of time being wasted on ineffective attempts. In the face of complex and changeable environments, the strategy update is not timely, and the adaptability to newly emerging object layouts and dynamic changes is poor, resulting in a high grasping failure rate. In reference¹², a multi-fingered robotic gripper is designed for grasping complex objects. However, the coordinated control among the fingers is intricate, and it is challenging to rapidly optimize the coordination strategy for objects of different shapes and textures. The perception and control precision of each finger are inconsistent. When grasping objects with complex shapes, uneven force distribution is likely to occur, leading to the slippage or damage of the objects. In reference¹³, a compliant end-effector and visual feedback are employed to grasp deformable objects. However, there is a delay in the real-time monitoring of object deformation by the visual feedback. For objects with a high degree of complex deformation, the model struggles to accurately predict the deformation trend. The compliant mechanism fails to achieve an optimal balance between force control and shape adaptation, thereby affecting the grasping stability. In reference¹⁴, a soft robotic gripper driven by a flexible shaft is expounded upon for use in unstructured and uncertain environments. However, the modeling of various uncertain factors in the environment is incomplete. When the environment changes rapidly or there are unknown interferences, the reliability of the grasping decision decreases. The computational complexity is high, and in scenarios with stringent real-time requirements, it is impossible to plan grasping actions in a timely manner. In reference¹⁵, deep learning-based visual servoing is applied to grasping. However, the training of the model relies heavily on a large quantity of high-quality labeled data, which incurs high costs for data acquisition and annotation. In practical applications, changes such as scene illumination and occlusion easily lead to a decline in the performance of the model. Its generalization ability to new scenes is limited, making it difficult to ensure stable grasping. In reference¹⁶, a high-precision grasping system for industrial applications is elaborated. However, under the interference of complex electromagnetic and vibration factors in the industrial field, the stability of the system is affected, resulting in fluctuations in the grasping precision. The system has poor adaptability to different industrial environments, requiring frequent parameter adjustments, and it is challenging to rapidly deploy it to new industrial scenarios. In reference¹⁷, a soft robotic gripper is used for delicate operations. However, the existing design suffers from a lack of durability. After long-term use, the material properties deteriorate, affecting the grasping performance. In terms of precise force control and the execution of complex actions, the control algorithm is complex, and the effect is not entirely satisfactory, making it difficult to complete high-difficulty delicate tasks. In reference¹⁸, grasping that combines tactile sensing and force control is considered. However, the precision and resolution of the tactile sensor are limited, resulting in an incomplete perception of the subtle features on the surface of the object. During the dynamic grasping process, the force control algorithm has a slow response to the real-time adjustment of the force, making it difficult to adapt to the force changes at the moment of grasping the object.

Combining the existing research mentioned above, this article will first analyze the force analysis brought about by the deformation of the contact surface during soft grasping. Secondly, it will construct a two-dimensional vector array and explore the edge recognition method. Finally, through the analysis of the edge morphology, it will evaluate the firmness of the contact and determine the rationality of the posture of the grasped object.

Analysis of the force state of the deformed contact surface

This chapter will combine the inspection scenarios of power systems to elaborate on scenarios such as button pressing, tool picking up, and knob operating, illustrate the inadaptability of the current rigid contact grasping as well as the deformation and force characteristics of the contact surface during soft grasping, and focus on analyzing the relationship between the directional characteristics of force and the state of the grasped object. In the theory of contact pressure analysis, there are the Hertz Contact Theory¹⁹ and the Elastoplastic Contact Theory²⁰. Among them, the Hertz Contact Theory is applicable to the button pressing scenario, where the contact area undergoes small deformation and the contact surface is elliptical. The objects in contact can be regarded as elastic half-spaces, and only distributed vertical pressure acts on the contact surface. The contact radius, which is the edge of the two-dimensional vector force array to be studied in this paper later, follows Eq. 1:

$$a = \sqrt[3]{{\frac{3FR}{{4E^{*} }}}}$$

(1)

where $E^{*}$ is the equivalent elastic modulus²¹, which follows Eq. 2

$$E^{*} = \frac{{E_{1} E_{2} }}{{E_{1} \left( {1 - \nu_{2}^{2} } \right) + E_{2} \left( {1 - \nu_{1}^{2} } \right)}}$$

(2)

where F is the contact load, R is the curvature radius of the contact object, E₁ and E₂ are the elastic modulus of the contact object, and $\nu_{1}$ and $\nu_{2}$ are the Poisson’s ratio of the contact object.

During tool picking up and knob operating, the elastic contact theory model is applicable. The characteristics are that elastic deformation occurs in the contact area, and the pressure distribution on the contact surface is highly localized, rapidly decaying with increasing distance from the contact surface. The initial yield contact radius $a_{ec}$, which lies between elastic and plastic deformation, satisfies Eq. 3:

$$a_{ec} = \sqrt {\frac{{3\sigma_{y} R}}{{4E^{*} }}}$$

(3)

Among them, $\sigma_{y}$ is the yield strength of the material, and $E^{*}$ is also the equivalent elastic modulus. Comparing with Eq. 1, we can very easily see the similarity between the equations, that is, the yield strength of the material is equivalent to the contact load before plastic deformation. Therefore, when interpreting the mechanical mechanism of soft grasping, the Hertz Contact Theory and the Elastoplastic Contact Theory can be used uniformly.

Business scenario and contact surface morphology analysis

The button touch scenario is one of the typical scenes of flexible contact. The size of a general touch button is a rectangle of 4 mm × 6 mm or a circle with a radius of 4 mm. There are also irregular shapes with an area of 300 mm², as shown in Fig. 1.

Fig. 1

In the button touch scenario, different buttons have different tactile sensations, which yield varying results in mechanical analysis.

These buttons are closely arranged and there is a possibility of combined triggering. The buttons are made of micro-switches, as shown in Fig. 2 below.

Fig. 2

Micro-switches. The activation of the switch requires proper pressing; too light a press may cause failure to trigger, while too forceful a press may cause hardware damage.

The action spring undergoes deformation when subjected to a force. When the deformation reaches a critical point, it rapidly moves the movable contact into or out of contact with the stationary contact, thereby completing or breaking the circuit. The effective travel distance is generally 1.5–2 mm. The combined process is shown in Fig. 3.

Fig. 3

The button triggering mechanism achieved through conduction.

As shown in Fig. 3, in order to prevent the accidental triggering of the button caused by vibration, there is a gap between the surface of the button depicted in Fig. 1 and the microswitch in Fig. 2. Only when this gap is overcome and the button stroke shown in the figure is achieved can an effective trigger be formed. Meanwhile, it can also be observed that although the areas of the buttons are different, the transmission mechanisms are the same. Therefore, based on Eq. 4, it can be deduced that the actual pressures required for different buttons will vary.

$$F = P*A$$

(4)

The following section will further analyze the deformation of the contact surface during the button pressing process. As shown in Fig. 4.

Fig. 4

The deformation highly related to the button shape during the soft contact process of a classic button.

As shown in Fig. 4, the deformed area is highly similar to the shape of the button, with a flat contact surface that conforms to the Hertz Contact Theory. Additionally, since the button size is smaller than the touching mechanical finger, the deformation also exhibits a wrapping characteristic. From this, it can be inferred that during the soft contact process, there must exist non-vertical vector forces that can help us identify the edge state of the contact surface. In tool contact, the deformation of the contact surface is more pronounced, as shown in Fig. 5.

Fig. 5

In the contact process involving tools with edges, the deformation of the contact surface tends to become more complex.

As shown in Fig. 5, the contact surface deformation is more pronounced. The deformed area is highly similar to the shape of the object, with a flat contact surface that conforms to the Hertz Contact Theory. However, since the object’s size is smaller than the touching mechanical finger, the deformation also exhibits a wrapping characteristic. This wrapping characteristic no longer satisfies the conditions of Hertzian contact but still belongs to elastic contact. Therefore, through the extension of the wrapped contact surface, the approximate posture of the grasped object can be identified.

Vector force state analysis

For forces in space, they can be decomposed and calculated according to the three-dimensional coordinates of x, y, and z²², and they satisfy Eq. 4:

$$\left\{ \begin{gathered} F_{x} = F\cos \theta_{x} \hfill \\ F_{y} = F\cos \theta_{y} \hfill \\ F_{z} = F\cos \theta_{z} \hfill \\ \end{gathered} \right.$$

(5)

Among them, $\theta_{x}$, $\theta_{y}$, $\theta_{z}$ are the angles between the force and the x-axis, y-axis, and z-axis, respectively. Equation 4 represents the most straightforward method for decomposing vector forces in three-dimensional space. However, during contact analysis, the decomposition of forces into three-dimensional Cartesian coordinates has limitations, especially when the deformation of the contact surface is random. In such cases, the spatial three-dimensional decomposition may lead to a weakened correlation between the direction of the force and the contact surface. Therefore, this paper will adopt a polar coordinate system to express spatial forces²³, and the expression for spatial forces satisfies Eq. 6:

$$\vec{F} = F_{r} \hat{r} + F_{\theta } \hat{\theta }$$

(6)

Among them, $\hat{r}$ and $\hat{\theta }$ are the unit vectors in the radial and angular directions, respectively. After accumulating a certain amount of deformation and vector force theory, one can re-examine the pressing operation from a mechanical perspective, as shown in Fig. 6:

Fig. 6

(a) Shows the contact of an object from a mechanical perspective. In (b), the position marked is the edge of the button. (c) Represents the direction of the contact surface deformation with arrows. It can be seen that in (a), at the edge, the force is no longer perpendicular to the contact surface.

We can very easily observe the differences in the direction of the force and the changes in its magnitude. In the figure, the length of the arrow indicates the magnitude of the force, while the direction of the arrow is related to the deformation of the contact surface. When the direction of the force is perpendicular to the contact surface, it indicates that this part of the area has undergone elastic deformation with the object and is closely attached. As the contact surface transitions to the edge of the object, the direction of the force forms an acute angle with the vertical direction. This suggests that the wrapping characteristic of the pressing operation analyzed in Section “Business scenario and contact surface morphology analysis” manifests as an inward squeezing force mechanically, which aids in our analysis of stability and identification of the object’s edge. In tool contact, the direction of the force exhibits a high degree of interlacing characteristics²⁴, as shown in Fig. 7.

Fig. 7

The directional characteristics of force during the contact process with an irregular object.

In the figure, the boundary lines of the force direction are strongly correlated with the surface boundary lines of the object. At the intersection of surfaces, which is the region where the “edge” is located, the force is perpendicular. On the planes on both sides of the edge, the force exhibits symmetrical angles. The size of these angles is related to the angle formed by the intersection of the normal to the object’s surface and the perpendicular line to the edge. According to Eq. 6, by choosing the radial direction to coincide with the normal, the force-bearing surface can be decomposed, and thus vector array edge recognition can be carried out.

Vector array edge recognition method

In image edge recognition, the classic method^{25,26,27,28,29} involves converting RGB images to grayscale and then detecting edges through gradient search. Similarly, edge recognition is necessary for identifying the contact surface during grasping. However, the method of image graying has become ineffective in this context. Due to the nature of soft grasping, determining boundaries based on the magnitude of contact surface pressure has also become inaccurate. On the other hand, edge recognition is a necessary process for judging the stability of grasping or pressing and is a key technology for breaking through the limitations of visual-based grasping posture. This thesis will mainly discuss the dimensionality reduction of vector force arrays to achieve contact surface edge recognition and ultimately form a depiction of the force-bearing surface.

Dimensionality reduction of vector force arrays

Let $X$ be a data matrix of size $n \times p$, where $n$ represents the number of samples and $p$ represents the number of features. Let $y$ be an $n$-dimensional label vector, indicating the category of each sample. If there exists a matrix $W$ of size $p \times k$ such that $XW$ is a matrix of size $n \times k$, and $k < p$ holds true within it, then dimensionality reduction is achieved^30,31,32,33. Below, we will further elucidate this by combining the two classic operations of pressing and grasping, using vector force data. As shown in Fig. 8.

Fig. 8

Two forces of the same magnitude. If the force perpendicular to the contact surface is considered a one-dimensional force, then the force with an angle is a two-dimensional force.

The directionality of force means that even two forces of the same magnitude can have different effects on a surface. Each vector force data with a different direction represents a dimension³⁴. Therefore, we need to decompose the force into two components: one perpendicular to the contact surface and the other parallel to it. By re-forming the matrix with the force perpendicular to the contact surface, the directional dimension of the force can be eliminated. Taking the force matrix of size $3 \times 3$ as an example, the effects before and after dimensionality reduction are shown in Fig. 9.

Fig. 9

The force distribution within the region is divided into a 3 × 3 grid, with each grid cell representing the average force in that area. Using 90 degrees as the reference angle, this process yields 9 sets of data.

As shown in Fig. 9, under elastic contact, the ideal scalar dimensionality reduction data shows that the central pressure value is the highest, gradually decreasing towards the periphery. However, in tool grasping, the dimensionality reduction of vector mechanics, which solely relies on vector force decomposition, finds it difficult to reduce the dimensions of multiple force-bearing surfaces as shown in Fig. 10. Therefore, it is necessary to explore the mechanical feature analysis of complex contact surfaces, decomposing a single vector array formed by n force-bearing surfaces into multiple vector arrays composed of individual force-bearing surfaces, and then applying vector decomposition to each vector array.

Fig. 10

There are four distinct contact surfaces identified by the direction of the forces.

The principle and process of decomposing the force-bearing surfaces in the figure are shown in Fig. 11 below.

Fig. 11

A complex force-bearing surface decomposed into four independent surfaces through pressure vector decomposition.

At this point, the paper has completed the discussion of the dimension order reduction of the posterior vector force array from the theoretical level and practical operation level. We successfully obtain a scalar array of forces that can be found on the edge, and further, we can conduct subsequent force surface profiling analysis.

Force-bearing surface feature recognition based on contact mechanical characteristics

Convolutional Neural Networks (CNNs) are frequently applied in image feature extraction^{35,36,37,38,39}. However, in this paper, there are no pixel points. Instead, dimensionality-reduced pressure sensor data is used, which also meets the pooling and classification requirements of Convolutional Neural Networks. Therefore, this section will explore the recognition of force-bearing surfaces using Convolutional Neural Networks with pressure sensor data. As shown in Fig. 12.

Fig. 12

Convolutional processing of dimensionality-reduced pressure sensor data.

It mainly consists of multiple convolutional and pooling operations to achieve the extraction of image feature maps. In this process, the convolutional layers capture the spatial features of the image. Ultimately, the task is completed by combining a fully connected network and a classifier. The capture and abstraction of information by the pooling layers, as shown in Fig. 13, serve to reduce the dimensionality of the image feature data collected by the convolutional layers through different receptive fields, thereby enhancing the network’s computational efficiency and generalization ability. The role of the classification layer is to connect the task objectives with the feature quantities through a fully connected network to accomplish the specified task.

Fig. 13

Schematic of feature processing. A similar method was used in Fig. 9 to form partitioned area data.

Due to the randomness in the size of the force-bearing surface caused by grasping and pressing operations, to ensure that the network has consistent sensitivity to boundary boxes of different scales, the square root of its width and height is used as the prediction result. That is, the final position information obtained becomes $(x,y,\sqrt w ,\sqrt h )$, and its loss function is as shown in Eq. (7).

$${\text{ loss }} = \sum\limits_{i = 0}^{{s^{2} }} {\text{ coordError }} + {\text{ iouError }} + {\text{ classError }}$$

(7)

Among them, ${\text{coordError}}$ represents the coordinate error between the predicted box and the ground-truth box; ${\text{iouError}}$ denotes the Intersection over Union (IoU) error; and ${\text{classError}}$ stands for the classification error. Their respective calculation methods are shown in Eqs. (8) to (10):

$$\begin{gathered} \sum\limits_{i = 0}^{{s^{2} }} {\text{ coordError }} = \lambda_{{\text{coord }}} \sum\limits_{i = 0}^{{S^{2} }} {\sum\limits_{j = 0}^{B} {\prod\limits_{ij}^{obj} {\left[ {\left( {x_{i} - \widehat{{x_{i} }}} \right)^{2} + \left( {y_{i} - \hat{y}_{i} } \right)^{2} } \right]} } } \hfill \\ + \lambda_{{\text{coord }}} \sum\limits_{i = 0}^{{S^{2} }} {\sum\limits_{j = 0}^{B} {\prod\limits_{ij}^{obj} {\left[ {\left( {\sqrt {w_{i} } - \sqrt {\hat{w}_{i} } } \right)^{2} + \left( {\sqrt {h_{i} } - \sqrt {\hat{h}_{i} } } \right)^{2} } \right]} } } \hfill \\ \end{gathered}$$

(8)

$${\text{iouError }} = \sum\limits_{i = 0}^{{S^{2} }} {\sum\limits_{j = 0}^{B} {\prod\limits_{ij}^{obj} {\left( {c_{i} - \hat{c}_{i} } \right)^{2} } } } + \lambda_{{\text{noobj }}} \sum\limits_{i = 0}^{{S^{2} }} {\sum\limits_{j = 0}^{B} {\prod\limits_{ij}^{obj} {\left( {c_{i} - \hat{c}_{i} } \right)^{2} } } }$$

(9)

$${\text{classError }} = \sum\limits_{i = 0}^{{s^{2} }} {\prod\limits_{i}^{obj} {\sum\limits_{c \in classes} {\left( {p_{i} (c) - \hat{p}_{i} (c)} \right)^{2} } } }$$

(10)

In the equations, $x$ and $y$ are the center coordinates of the predicted bounding box by the network; $w$ and $h$ are the width and height of the predicted bounding box; $c$ is the predicted class value; $p$ is the probability of the predicted class; $\hat{x}$, $\hat{y}$, $\hat{w}$, $\hat{c}$, $\hat{p}$ are the corresponding ground-truth value; $\prod\nolimits_{i}^{obj} {}$ indicates that the target falls into cell i ; $\prod\nolimits_{ij}^{obj} {}$ indicates that the target falls into the j-th bounding box of cell i, and $\prod\nolimits_{ij}^{noobj} {}$ indicates that the target does not fall into the j-th bounding box of cell i.

In practical robotic grasping and pressing operations, the objects being grasped are not flat surfaces, which can lead to the emergence of multiple contact areas. Alternatively, if the object being pressed is too large, the entire contact area may be filled to the maximum size allowed by tactile image analysis. If the NMS (Non-Maximum Suppression) algorithm is directly used to eliminate detection boxes with a high IoU, it can result in the failure to effectively detect contact areas. Therefore, this paper also needs to improve the default NMS algorithm, modifying it to soft-NMS as shown in Eq. (11).

$$s_{i} = \left\{ \begin{gathered} s_{i} ,I_{ou} (M,b_{i} ) < N_{t} \hfill \\ s_{i} (1 - I_{ou} (M,b_{i} )),I_{ou} (M,b_{i} ) \ge N_{t} \hfill \\ \end{gathered} \right.$$

(11)

Among them: $s_{i}$ represents the confidence value of the bounding box; $M$ represents the bounding box with the highest confidence value in the specified bounding box set; $b_{i}$ represents any bounding box in the bounding box set; $N_{t}$ represents the set threshold, which is empirically valued between 0.3 and 0.7.

Soft-NMS can avoid the problem of bounding box misdeletion that occurs in NMS by introducing an additional factor. To expedite the bounding box screening process, the relevant tuples are first sorted in ascending order based on their score values. Subsequently, the overlap ratio between each pair of bounding boxes is calculated according to Eq. (12). This overlap ratio is the quotient of the intersection and union of the two bounding box regions.

$$\mathop {U_{(p,q)} }\limits_{\substack{ p = [1,n - \alpha ) \\ q = [p + 1,n] } } = \frac{{{\text{ inter }}_{(p,q)} }}{{{\text{area}}_{(p)} + {\text{area}}_{(q)} - {\text{ inter }}_{(p,q)} }}$$

(12)

In the equation, $U_{(p,q)}$ and ${\text{inter }}_{(p,q)}$ represent the overlap ratio and overlap area of bounding boxes p and q , with units of % and mm² ; ${\text{area}}_{(p)}$ and ${\text{area}}_{(q)}$ represent the areas of bounding boxes p and q , with units of mm² ; n is the total number of bounding boxes; α is the threshold for acceptance or rejection; for bounding box $p$, count the number $Smu_{i}$ of $\mathop {U_{(p,q)} }\nolimits_{q = [p + 1,n]} \ge \beta$ , if $Smu_{i} > \alpha$ , then discard bounding box $p$ , otherwise, keep it, where ${\text{ inter }}_{(p,q)}$ and ${\text{area}}_{(p)}$ can be calculated using Eqs. (13) to (14):

$$\begin{aligned} {\text{inter }}_{{(p,q)}} & = {\text{Max}}\left( {0,\left( {{\text{Min}}\left( {x_{2}^{p} ,x_{2}^{q} } \right) - {\text{Max}}\left( {x_{1}^{p} ,x_{1}^{q} } \right) + 1} \right)} \right) \\ & \quad \times {\text{Max}}\left( {0,\left( {{\text{Min}}\left( {y_{2}^{p} ,y_{2}^{q} } \right) - {\text{Max}}\left( {y_{1}^{p} ,y_{1}^{q} } \right) + 1} \right)} \right) \\ \end{aligned}$$

(13)

$${\text{area}}_{(p)} = \left( {x_{2}^{p} - x_{1}^{p} + 1} \right) \times \left( {y_{2}^{p} - y_{1}^{p} + 1} \right)$$

(14)

Stability and pose determination of grasped objects

After the analysis in Chapters 2 and 3, which clarified the deformation of the contact surface and the characteristics of the force during pressing and grasping, as well as how to identify the shape features of the grasping contact surface through pressure, this chapter will continue to explore the stability of pressing and grasping and the determination of posture through the bounded extension of the contact surface, based on the size of the contact surface and the direction of the force.

Contact stability assessment

Stability is used to determine whether a grasping posture can firmly hold an object without it slipping or falling. “Stability” refers to the ability of the grasping action to counteract any external forces acting on the object, including gravity, impact forces caused by the object’s motion inertia, and forces applied from the outside. The more difficult it is to find an external force that can disrupt the current state of the object being grasped, the more stable the grasp is considered to be. To select a stable grasp, strategies are ranked based on their robustness against external disturbances, with the most robust grasp being selected. Different grasp metrics can be used to evaluate the stability of a grasp. In this paper, grasp quality, which is related to the grasp wrench space⁴⁰ and force closure⁴¹, is primarily used as the metric⁴². The points where the hand and the object come into contact are called contact points, and the contact forces are applied to the object through the normal vectors at these contact points, as discussed in Section “Force-bearing surface feature recognition based on contact mechanical characteristics”. For two-dimensional objects, analyzing forces alone is insufficient because an external torque could also be applied to the object along the Z-axis. A grasp must be able to counteract not only external forces but also any arbitrary external torques. To calculate the torque of each contact force, see Eq. 15:

$$M_{i} = \vec{r}_{i} \times n_{i}$$

(15)

To analyze the stability of a grasp, a more compact way to represent forces and torques is used by combining them into a single vector known as the wrench matrix. For a two-dimensional object, the wrench matrix for a single contact point is defined as a 3 × 1 vector, composed of the x and y components of the unit normal contact force and the torque generated by this force, denoted as $\left[ {\begin{array}{*{20}l} {n_{x} } \hfill & {n_{y} } \hfill & M \hfill \\ \end{array} } \right]^{T}$. Extending the concept of the wrench matrix to three-dimensional objects, it becomes a 6 × 1 vector $\left[ {\begin{array}{*{20}l} {n_{x} } \hfill & {n_{y} } \hfill & {n_{z} } \hfill & {M_{x} } \hfill & {M_{y} } \hfill & {M_{z} } \hfill \\ \end{array} } \right]^{T}$. If these wrenches can counteract any arbitrary external wrenches, the grasp is considered stable. The projections of the forces from the four contact points in Fig. 14 into the wrench space are as follows:

Fig. 14

Projections of the forces from the contact points in the wrench space.

As mentioned above, each wrench can be scaled by an arbitrary positive coefficient. Therefore, the combined wrench of the four contact points can be represented as the sum of the scaled wrenches.

Figure 15 illustrates the total wrench space, which covers the region that can be reached by arbitrarily scaling and combining the four wrenches shown in Fig. 14. It is evident from this figure that the set of contact points cannot cover the entire wrench space, thus the grasp depicted in Fig. 15 is unstable. Specifically, this grasp cannot generate a force $- \omega_{{{\text{ext}}}}$ outside the yellow enclosed region to counteract external forces.

Fig. 15

The closed region formed by the forces, with a question mark indicating the direction where there is a lack of force to counteract $- \omega_{{{\text{ext}}}}$.

Pose determination of grasped objects

The ultimate goal of grasping is to pick up an object in the correct posture, which involves the technical points discussed in the previous sections. First, a three-dimensional understanding of the object to be grasped is required. Each surface of the object that can be grasped has its unique contact surface morphology. For example, as shown in Fig. 7, there are significant differences in the contact surface morphology on the edges and faces. These differences can be used to initially identify the grasping surface. However, as analyzed in Sections “Vector force state analysis” and “Force-bearing surface feature recognition based on contact mechanical characteristics”, the grasping process involves not only pressure perpendicular to the contact surface but also rotational forces. Therefore, by combining rotational forces, the distance of the grasping point from the object’s center of gravity can be further determined, as shown in Fig. 16 below.

Fig. 16

Schematic diagram of posture determination. Due to the presence of the unequal rotational forces F3 and F4, it can be inferred that L1 must be less than L2.

Figure 16 shows the preliminary form after the extension of the force-bearing surface. After vector force analysis, different contact parts have different magnitudes of rotational forces, hence Fig. 17.

Fig. 17

Different grasping positions correspond to different pressing forces and rotational forces.

As can be seen from Fig. 17, the magnitude and direction of the forces can accurately reflect the posture of the grasped object. For a given object, different grasping positions result in different contact surface morphologies. It is evident that grasping at the center of gravity is the most stable, with minimal rotational force and a well-organized contact surface. Conversely, the further away from the center of gravity the grasp is, the more difficult it becomes to maintain the desired posture of the object. Moreover, the contact surface may become complex and twisted due to the excessive rotational force.

Experimental verification

In order to verify the above viewpoints, in this chapter, evaluation indicators based on factors such as precision and inspection speed will be established. An effectiveness analysis will be conducted for the recognition of the grasped objects and the recognition of their postures. Meanwhile, a comparative analysis will be carried out to examine the performance differences of other visual schemes. To obtain the training data, this paper constructs a model of the objects involved in the routine operations of the power system. During the pressing or gripping operations, each contact surface will move along the surface of the object with a step size of 2 mm to construct the dataset. The schematic diagram of the data collection is shown in Fig. 18.

Fig. 18

Schematic diagram of data collection.

This paper is committed to using graph-based video recognition methods to achieve a contact perception similar to that of humans during the contact process. The contact perception discussed in the paper mainly involves dimensionality-reduced pressure data. When evaluating the recognition capability of the tool, this paper uses the mean Average Precision (mAP) as the metric⁴³. Therefore, concepts such as Intersection over Union (IoU), predicted bounding box area, ground-truth bounding box area, precision, recall, and PR curve are involved⁴⁴. Among them, IoU follows Eq. 12 in Section “Force-bearing surface feature recognition based on contact mechanical characteristics”. By setting an IoU threshold, then traversing and calculating the IoU between different confidence-level predicted bounding boxes and ground-truth bounding boxes, and comparing it with the threshold, TP and FP can be determined. The detection boxes with IoU greater than the set threshold are considered TP, while the redundant detection boxes are considered FP. For those with IoU less than the threshold, they are classified as FP. The equation for calculating precision is shown in Eq. 16:

$$precision = TP/(TP + FP)$$

(16)

In the equation, TP represents the true positives, i.e., the samples correctly classified as positive, while FP represents the false positives, i.e., the negative samples incorrectly classified as positive. Recall, which indicates the proportion of true positives among all actual positive samples, is calculated according to Eq. 17:

$$recall = TP/(TP + FN)$$

(17)

In the equation, FN represents the false negatives, i.e., the negative samples correctly classified as negative. In object detection, since the threshold is set manually, the value of the threshold will affect both recall and precision. Therefore, by setting multiple confidence thresholds to obtain multiple pairs of precision and recall values, and plotting recall on the y-axis and precision on the x-axis, a PR (Precision-Recall) curve can be obtained. The Average Precision (AP) indicates the area under the PR curve. The mean Average Precision (mAP) is the average of the AP values for all classes, representing the overall detection performance of the algorithm for all targets. mAP is commonly used as a standard to evaluate the detection performance of object detection models. Additionally, if one solely pursues improvements in detection precision, it can easily lead to increased computational complexity and poor scalability of the model. Therefore, another important performance metric for object detection algorithms is detection speed (Frames Per Second, FPS), which refers to the number of images the detector can process per second under the same hardware conditions, or the time required by the detector to process a single image (excluding image preprocessing). In this paper, FPS indicates the number of images that can be processed per second, with a higher FPS indicating a faster detection speed of the model.

Verification of blind sensing

This paper models the objects involved in the routine operations of power systems, such as pressing or clamping operations. For each contact surface, data set construction is carried out along the object surface with a step length of 2 mm. The model used is the YOLOv5n model with improved soft-NMS, and the training results are shown in Fig. 19 below.

Fig. 19

Training results of contact recognition.

As shown in the figure, the results are as follows: F1 = 0.97, Recall = 97.58%, Precision = 96.64%, score_threshold = 0.5, mAP = 96.34%, FPS = 62 frames per second. Some recognition effects are shown in Fig. 20.

Fig. 20

Partial recognition effect diagram (a) Large screwdriver handle (b) Small Xin hex key (c) Eccentric circular button.

Pose recognition verification

After verifying the object recognition capability through the contact process in Section “Verification of blind sensing”, the pressure data perpendicular to the contact surface has been analyzed. By entering the weight, center of gravity position, and length parameters of specific objects and combining them with the dataset, the posture of the grasped object can be determined. Further analysis can be conducted in conjunction with the diagram of rotational force magnitudes shown in Fig. 17. The results are presented in Fig. 21.

Fig. 21

Pose recognition effect diagram.

In the figure, the first number represents the angle between the object and the horizontal plane, with clockwise direction being positive, and the unit is degrees. The second number indicates the distance from the center, with the unit being millimeters (mm). Since the dataset is constructed with a step size of 2 mm, the minimum distance is less than 2 mm. From this, it can be concluded that during a single contact process, the spatial posture of the object can be accurately recognized. As a comparison, this article will make a comparison with the method of pure image recognition. The comparison will mainly be carried out in terms of the accuracy of object recognition, the recognition of the object’s posture, and other aspects. Firstly, in terms of object recognition, occlusion and changes in lighting are the two main factors that interfere with image recognition. In the recognition of tools, detail recognition is also of crucial importance. We will first compare the ability of vision to recognize objects in different scenarios, mainly reproducing the research results of Reference 10. As shown in Fig. 22.

Fig. 22

Recognition rates of the same object in different scenarios.

As can be seen from the figure, when there is sufficient light, the recognition rate of the tools is extremely high. However, once the key features of the tools are occluded, the correct recognition rate experiences a significant decline. In a low-light environment, if the probability threshold for recognition is set at 0.3, the visual recognition scheme is even unable to identify the objects. In terms of detail analysis, this time we will mainly compare two objects with similar appearances but obvious differences in details. As shown in Fig. 23.

Fig. 23

Recognition of an Allen wrench and a star-shaped wrench.

It can be seen that there are indeed bottlenecks in visual analysis for visual recognition. High-magnification visual sensors can capture details, but they are not suitable for scenarios with dynamic conditions and poor focusing environments. In contrast, tactile recognition can complement the corresponding shortcomings and enable object recognition.

Conclusion

Soft grasping, or more precisely, soft manipulation, is the key to the operational perception of bionic robotic hands. This paper begins with an analysis of the business scenarios and the morphology of contact surfaces, examining the changes in contact surfaces and the characteristics of contact surface force vectors. Subsequently, the paper conducts dimensionality reduction research on the analysis of vector forces, and innovatively performs image-like decomposition on the processed two-dimensional matrices. This approach allows for direct perception of the grasping state of the contact surface without relying on video. Finally, the paper explores the key elements of grasping, namely the stability of the grasp and the posture of the grasped object. The proposed technology based on Convolutional Neural Networks (CNN) for rapid analysis of the grasping surface and extended posture determination can achieve millimeter-level precision in grasping position determination, with a two-dimensional posture angle of the grasped object less than 1 degree. Overall, this meets the requirements of the power system business scenarios. It has the following advantages in terms of scalability and versatility:

From the perspective of scalability, this technology demonstrates strong adaptability to objects of different shapes. For objects with regular shapes, such as cubes and cylinders, the pressure sensor array can accurately identify the posture of the objects by measuring the pressure values at various points and the degree of deformation of the contact surface according to the preset algorithm. For objects with irregular shapes, the scalability advantage of the technology is even more prominent. Benefiting from the distributed characteristics of the pressure sensors, even if the object has a complex shape, each sensor can independently sense the local pressure and deformation. The system integrates these scattered pieces of information and, through the operation of the force-bearing surface analysis algorithm, can still construct the overall posture model of the object and achieve precise identification. This endows the technology with broad application potential when dealing with real-world objects with diverse shapes.

In terms of versatility, this technology performs well when faced with objects made of different materials. For rigid materials, such as metals, the deformation of the contact surface under pressure is relatively small. The pressure sensors can rely on their high-precision measurement of pressure changes to determine the posture of the objects. For flexible materials, such as rubber and fabrics, they are prone to significant deformation under pressure. The sensors can keenly capture these deformation characteristics and, combined with the pressure data, accurately identify the posture of the objects. This means that this technology can play a role both in the grasping of metal parts in industrial production and in the manipulation of flexible tissues in the medical field, highlighting its remarkable versatility.

Under complex environmental conditions, changes in temperature can have an impact on both the pressure sensors and the materials of the objects themselves. Temperature changes may cause the materials to expand or contract due to heat, affecting the pressure conduction and the deformation mode of the contact surface. However, by introducing a temperature compensation algorithm, which can monitor the environmental temperature in real-time and correct the sensor data, the performance of the technology can be maintained to a certain extent. Changes in lighting conditions mainly affect visual recognition and have basically no direct interference with the tactile sensing technology based on pressure and the deformation of the contact surface. This enables it to stably achieve the identification of the object’s posture even in complex lighting conditions or even in the absence of light, demonstrating good versatility and stability. It has important application value in scenarios with complex lighting conditions, such as in warehousing and logistics and disaster rescue.