Explicit solitary wave structure for the stochastic resonance nonlinear Schrödinger equation under Brownian motion with dynamical analysis

Abstract

This study, analyzed the explicit solitary wave soliton for the stochastic resonance nonlinear Schrödinger equation under the Brownian motion. The Schrödinger equations are mostly used to describe how light moves via planar wave guides and nonlinear optical fibres. Analytical technique is applied to gained the various solitary waves and soliton solutions for the resonance nonlinear Schrödinger equation namely, generalized exponential rational function method. This approach is used to find several new trigonometric, exponential, and hyperbolic solutions under the noise. This method is provided us the soliton solutions for nonlinear models that is a computed using an efficient, accurate, capable, and trustworthy method. Furthermore, by varying the parameters, a few graphs of the developed solutions are shown to illustrate the physical setup of stochastic solutions. We anticipate that the obtained results will have significant potential applications in quantum mechanics, magneto-electrodynamics, optical fibres, and heavy ion collisions. Moreover, using the Galilean transformation, the dynamical system of the governing equation is obtained, and the theory of the planar dynamical system is used to carry out its sensitivity, chaotic and bifurcation. By providing certain two- and three-dimensional phase pictures, the existence of chaotic behaviors of the resonance nonlinear Schrödinger equation is examined by taking into account a perturbed term in the resulting dynamical system.

Introduction

The nonlinear Schrödinger (NLS) equation^1,2,3 has been recognised since the starting of the of nonlinear phenomena translated into integrable models and these model describing evolution of solitons in nonlinear media⁴. As such, it is essential in a wide range of contexts, from atomic Bose–Einstein condensates⁵ to nonlinear optics, plasmas, and water waves and nonlinear optics⁶. Additionally, it was discovered in the 1970s that vector (multi-component) NLS models are created when waves of various frequency interact⁷. Since then, multi-component NLS models and multi-soliton complexes that arise in various applications, and researchers have a significant amount of research, which is not surprising. These include spatial solitons that are incoherent⁸ and partially coherent⁹, soliton wavelength-division multiplexing¹⁰. The dynamics and collisions of multi-component solitary waves¹¹ and their stability in 1-D, and 2-D environments were also examined in this context^11,12.

Sakaguchi and Malomed considered the nonlinear-Schrödinger solitons, resonant nonlinearity management. They examined how higher-order and fundamental solitons in the 1-D NLS models are affected by a periodic modulation of the nonlinearity coefficient. They discovered through simulations that if the modulation frequency $\omega$ is near the solitons’s intrinsic frequency, then the fundamental soliton’s reaction to the weak perturbation is resonant, as explained by a simple analysis¹³. Ghanbari, Inc finding the precise specific solutions for the resonance NLS equation using a novel generalised exponential rational function approach¹⁴. Ali et al. analyzed the modulation instability in soliton solutions of the nonlinear Schrödinger equation with the dual power law nonlinearity and resonant NLS equation¹⁵. Grébert and Thomann proposed the quintic NLS equation and resonant dynamics¹⁶. Witthaut and Mossmann studied the NLS equation bound and resonance states in simple model systems. They examine the Gross–Pitaevskii equation, also known as the stationary NLS equation, for a single delta potential and a delta-shell potential¹⁷. Zayed and Al-Nowehy considered the resonant NLS equation with parabolic law nonlinearity and its applications using the new $\phi ^{6}$-model expansion method¹⁸. Düll and Schneider explored the justification of a resonant Boussinesq model using the NLS equation¹⁹. Williams et al. studied the dynamical features and stability of solitary waves in the resonant NLS equation. They first analyzed the modulational stability of plane waves, determining how the related conditions differ from the NLS case²⁰. Moiseyev and Cederbaum examined the tesonance solutions of the NLS equation for the fragmentation of trapped condensates and tunnelling lifetime²¹.

In this paper, we examine the exact solitons solutions under the effects of noise using the generalized exponential rational function method²². The RNLS equation is considered as

$$\begin{aligned} i H_t+\tau H_{xx}+\rho F (|H|^2) H+ \lambda \left( \frac{|H|_{xx}}{|H|}\right) H=0. \end{aligned}$$

(1)

If x stands for non-dimensional distance, $\tau$ is the dispersion coefficient, $\lambda$ and $\rho$ represent the nonlinearity coefficient, and F is a real-valued function, and H(x, t) would be a state variable. Kerr-law nonlinearity $F(H)=H$ occurs in nonlinear fibre optics when the light’s refractive index is proportional to its intensity. In recent years, physics, biology, chemistry, climatic dynamics, geophysics, and other fields have generally acknowledged the need of taking random effects into account when modeling, forecasting, evaluating, and simulating complex processes. Stochastic differential equations are those that take time-dependent random fluctuations into account. A fundamental model in aligning wave phenomena under noise together with periodic forcing operates under the name of stochastic resonance nonlinear Schrödinger equation (SR-NLSE). The extended nonlinear Schrödinger equation (NLSE) formulates as the SR-NLSE which integrates noise elements and resonant input from external forces making it highly applicable for systems with coexisting noise and forces such as optical fibers and Bose–Einstein condensates as well as biological networks. SR-NLSE demonstrates the integrated relationship of nonlinearity with dispersion alongside noise effects and periodic modulation which produces unusual noise-enhanced signal transmission together with stochastic resonance phenomena that augment weak signal detection. SR-NLSE describes the physical interaction which lets noise-generated fluctuations match periodic driving forces to develop coherent structures like solitons or breathers in systems where no periodic driving would normally occur. The model leads to significant findings about noise effects on non-linear systems which has various applications extending from photonics to neuroscience. This study investigates how solutions of the SR-NLSE operate while inspecting the underlying stochastic resonance mechanisms in nonlinear wave systems. We consider the stochastic RNLS equation forced in the Itô sense by multiplicative noise is considered as follows

$$\begin{aligned} i H_t+\tau H_{xx}+\rho (|H|^2) H+ \lambda \left( \frac{|H|_{xx}}{|H|}\right) H-i \varpi \beta _t H=0, \end{aligned}$$

(2)

where $\beta (t)$ is the standard Wiener process and $\beta _t=\frac{d\beta }{d t}$ is the multiplicative time noise with $\varpi$ control parameter. In this study, we merely take into account the noise in the space as a constant. First, lets define $\beta (t)$, the Brownian motion. The random procedure that fulfills: $\beta (t), t\ge 0$ are continuous functions of t. $\beta (t)- \beta (s)$ has a normal distribution with mean 0 and variance $t - s$, is known as a Brownian motion, and for $s < t$, $\beta (t)- \beta (s)$ is independent of the past, this is also known as independence of increments.

Ahmad and Younas worked on the (3 + 1)-dimensional nonlinear extended quantum Zakharov–Kuznetsov equation using the unified method²³. Ali et al. explored the solitary wave solutions for the fractional Wazwaz–Benjamin–Bona–Mahony system using the Khater technique²⁴. Hussain et al. used the extended and modified tanh-function method for the fractional Benjamin-Ono model²⁵. Bilal and Ahmad worked on the dynamical soliton model by three versatile analytical mathematical methods²⁶. Many academics have studied NLPDEs in the past few decades in an effort to find exact solitary wave solutions. Solitons are a unique class of solutions distinguished by their stability, shape-preserving behavior, and importance in nonlinear physics. They are defined as any solution that exactly satisfies a given equation. A subset of exact solutions with extra special characteristics are called soliton. Then, over the past three decades, a variety of analytical and numerical techniques have been developed in response to the search for soliton solutions, such as the unified tanh approach²⁷, new Kudryashov and extended hyperbolic function schemes²⁸, new auxiliary equation approach²⁹, improved F-expansion techniques^30,31, modified Khater (MK) method³², advanced auxiliary equation^33,34, generalized auxiliary equation³⁵, modified extended auxiliary equation mapping approach^36,37. But in this study we used the generalized exponential rational function method to explored the different types of solitary wave solutions. This approach is provided us the different forms of solitons such as dark, singular, complex dark-singular, mixed solitons along with the exponential and explicit solitary wave solutions. Moreover, this approach is easy to compute mathematically as well.

This manuscript’s main goal is to thoroughly investigate the dynamics captured by the provided equation. As a first step, the Galilean transformation is used, which results in the development of a matching dynamical system linked to Eq. (2). Particularly in the setting of classical mechanics, the Galilean transformation is a useful technique for transforming PDEs into systems of ordinary differential equations (ODEs). When dealing with issues requiring relative motion between various inertial reference frames, this transformation is crucial. The Galilean transformation enables a smooth transition from a frame of reference moving at a constant velocity to a stationary frame during the PDE to ODE conversion process. The phrases including spatial derivatives in the original PDEs can be reformed into terms involving only temporal derivatives by suitably accounting for this relative motion. The resulting system of ODEs is easier to solve thanks to this transformation, which also streamlines the mathematical analysis. As a result, the Galilean transformation offers a strong mathematical foundation for examining physical phenomena in classical mechanics, enabling researchers to better understand system dynamics from the easier-to-manage perspective of ODEs. Moreover, a detailed bifurcation analysis is carried out using the well-established theory of planar dynamical systems, which clarifies the complex behaviors displayed by the system. This study explores the domain of chaotic occurrences within the controlled model, going beyond bifurcations. In order to achieve this, an external term is added to a dynamical system. In order to fully comprehend the complex dynamics at work in the domain of chaotic phenomena within the controlled model, a number of 2D and 3D phase portraits are constructed and examined as part of the investigation of chaotic behaviors.

Moreover, we use the GERF method to get the exact solutions for stochastic RNLS equation. We may obtain the stochastic solutions for the stochastic RNLS (2) by applying the stochastic complex wave transformation. While all previous research assumed that the solution for the Schrödinger equation was deterministic, in this study we postulate for the first time that is under stochastic. Due to the significance of RNLS equation (2) in numerous branches of chemistry, physics, and engineering, these obtained solutions are essential for comprehending a number of challenging physical processes. We use Mathematica11.1 tools to offer some figures that illustrate the impact of the stochastic term. Finally, we discuss how noise affects the solutions that are obtained.

Methodology

In this section, we discussed the general methodology of GERFM in the following manner^38,39,40:

Step 1: Let, we consider the nonlinear partial differential equation (NLPDE) as follows

$$\begin{aligned} W(H, H^2, H_x, H_t, H_{xx},\ldots )=0. \end{aligned}$$

(3)

Step 2: Consider the complex wave transformation to convert PDE in to ODE such as

$$\begin{aligned} H(x,t)= \hbar (\eta ), \quad \text{ where } \quad \eta =x+c t. \end{aligned}$$

(4)

We derive a ODE as follows in Eq. (3).

$$\begin{aligned} W(\hbar , \hbar ', \hbar '', \hbar ^2, \hbar '\hbar ...)=0, \end{aligned}$$

(5)

where $'=\frac{d}{d\eta }$.

Step 3 Let’s suppose the general solutions in the form of summation of the Eq. (5) using the GERFM as

$$\begin{aligned} \hbar (\eta )=c_0+\sum _{k=1}^{m}c_k\varphi (\eta )^{k}+\sum _{k=1}^{m}d_k\varphi (\eta )^{-k}, \end{aligned}$$

(6)

where $c_0, c_k$ and $d_k$ are the constants that are found to me later, and $\varphi (\eta )$ has the following general solution such as

$$\begin{aligned} \varphi (\eta )=\frac{f_1 e^{r_1\eta }+f_2 e^{r_2\eta }}{f_3 e^{r_3\eta }+f_4 e^{r_4\eta }}, \end{aligned}$$

(7)

where $r_j,f_j(1=j=4)$ are constants to be ascertained. We can determine m by applying the idea of balance.

Step 4 A polynomial equation is gained by replacing Eq. (6) into Eq. (5). When we set all of the polynomial’s coefficients to zero, we obtain an algebraic equation system.

Step 5 A polynomial equation is gained by replacing Eq. (6) into Eq. (5). When we set all of the polynomial’s coefficients to zero, we obtain an algebraic equation system.

Mathematical analysis

The resonance nonlinear Schrödinger equations of mathematical analysis is covered in this section, along with the application of the new MGERF techniques to the suggested system (shown in (2)) are displayed. Consider the wave transformation^41,42

$$\begin{aligned} H(x,t)=\hbar (\eta ) e^{\iota \gamma +\varpi \beta (t)-\varpi ^{2} t}, \qquad \text{ where } \qquad \eta =x+ct,~~~ \text{ and } \quad \gamma =\theta -{\alpha } x+\sigma t, \end{aligned}$$

(8)

where ${\alpha }$ is the travelling wave width, $\sigma$ indicates the wave number of the soliton, h is its velocity, $\xi$ representing the coefficient of velocity dispersion, and $\theta$ is the soliton’s phase component. $\beta (t)$ is the Brownian motion while $\varpi$ is the control parameter. using the above transformation Eq. (7a) to an ODE, which yields real and imaginary components such as

$$\begin{aligned} \iota c \hbar '(\eta )-\sigma \hbar (\eta )+\xi \hbar ''(\eta )-2\xi \iota {\alpha } \hbar '(\eta )+\xi {\alpha ^2} \hbar (\eta )+\rho \hbar ^{3}(\eta )+\lambda \hbar ''(\eta )=0. \end{aligned}$$

(9)

The real part is taken as

$$\begin{aligned} (\xi +\lambda )\hbar ''+(-\sigma +\xi {\alpha ^2})\hbar +\rho \hbar ^3=0, \end{aligned}$$

(10)

moreover, from the imaginary part, we get $c=2\xi {\alpha }.$

Application to GERF technique

In this portion, we explore the exact soliton solutions for the underlying model using the GERF technique. So, we we apply the homogeneous balancing on Eq. (10) and get $m=1$. Substitute this value into the Eq. (6) and get the following form

$$\begin{aligned} \hbar (\eta )=c_0+c_1\varphi (\eta )+d_1\varphi (\eta )^{-1}. \end{aligned}$$

(11)

Following a few steps, the following families of non-trivial solutions of Eq. (2) can be produced by using Eq. (11) into Eq. (10):

Family of solution 1: If we choose $[f_1, f_2, f_3, f_4]=[-1,-1,1,-1]$ and $[r_1, r_2, r_3, r_4]=[1,-1,1,-1]$, then Eq. (7) changes into,

$$\begin{aligned} \varphi (\eta )=-\frac{\cosh (\eta )}{\sinh (\eta )}. \end{aligned}$$

(12)

The set of equations is derived by substituting Eq. (11) into Eq. (10) using Eq. (12). These set of equations can be solved with Mathematica to provide the following unknown constants,

Set 1: Choosing the set $c_0=0,~~c_1=0,~~d_1=\frac{\sqrt{2} \sqrt{\delta \lambda +\delta \tau }}{\sqrt{2 \lambda \rho +3 \rho \tau }},~~{\alpha }=\frac{\sqrt{\delta }}{\sqrt{-2 \lambda -3 \tau }},$ dark soliton is obtained under noise as follow,

$$\begin{aligned} H_{1}(x,t)=\left( -\frac{\sqrt{2} \sqrt{\delta \lambda +\delta \tau }}{\sqrt{2 \lambda \rho +3 \rho \tau }} \tanh \left( \frac{\sqrt{\delta } \left( \frac{2 \sqrt{\delta } t \tau }{\sqrt{-2 \lambda -3 \tau }}+x\right) }{\sqrt{-2 \lambda -3 \tau }}\right) \right) e^{i \left( \theta +\delta t-\frac{\sqrt{\delta } x}{\sqrt{-2 \lambda -3 \tau }}\right) +\varpi \beta (t)-\varpi ^{2} t}. \end{aligned}$$

(13)

Set 2: Choosing the set $c_0=0,~~c_1=\frac{\sqrt{2} \sqrt{-\delta \lambda -\delta \tau }}{\sqrt{4 \lambda \rho +3 \rho \tau }},~~d_1=-\frac{\sqrt{2} \sqrt{-\delta (\lambda +\tau )}}{\sqrt{\rho (4 \lambda +3 \tau )}},~~{\alpha }=\frac{\sqrt{\delta }}{\sqrt{4 \lambda +3 \tau }},$ the dark-singular soliton solution is obtained under noise as follow,

$$\begin{aligned} H_{2}(x,t)= & \left( \frac{\sqrt{2} \sqrt{-\delta (\lambda +\tau )}}{\sqrt{\rho (4 \lambda +3 \tau )}} \tanh \left( \frac{\sqrt{\delta } \left( \frac{2 \sqrt{\delta } t \tau }{\sqrt{4 \lambda +3 \tau }}+x\right) }{\sqrt{4 \lambda +3 \tau }}\right) \nonumber \right. \\ & \left. -\frac{\sqrt{2} \sqrt{-\delta \lambda -\delta \tau }}{\sqrt{4 \lambda \rho +3 \rho \tau }} \coth \left( \frac{\sqrt{\delta } \left( \frac{2 \sqrt{\delta } t \tau }{\sqrt{4 \lambda +3 \tau }}+x\right) }{\sqrt{4 \lambda +3 \tau }}\right) \right) e^{i \left( \theta +\delta t-\frac{\sqrt{\delta } x}{\sqrt{4 \lambda +3 \tau }}\right) +\varpi \beta (t)-\varpi ^{2} t}. \end{aligned}$$

(14)

Family of solution 2: If $[f_1, f_2, f_3, f_4]= [-i, i, 1, 1]$, $[r_1, r_2, r_3, r_4]= [i, -i, i, -i]$, then Eq. (7) changes into,

$$\begin{aligned} \varphi (\eta )=-\frac{\sin (\eta )}{\cos (\eta )}. \end{aligned}$$

(15)

The set of equations is derived by substituting Eq. (11) into Eq. (10) using Eq. (15). This set of equations can be solved with Mathematica to provide the following unknown constants,

Set 1: Choosing the set $c_0=0, c_1=\frac{\sqrt{2} \sqrt{-\delta \lambda -\delta \tau }}{\sqrt{2 \lambda \rho +\rho \tau }}, d_1=0, {\alpha }=-\frac{\sqrt{\delta }}{\sqrt{2 \lambda +\tau }},$ the solitary wave solution is obtained under noise as follow,

$$\begin{aligned} H_{3}(x,t)=\left( \frac{\sqrt{2} \sqrt{-\delta \lambda -\delta \tau }}{\sqrt{2 \lambda \rho +\rho \tau }} \tan \left( \frac{\sqrt{\delta } \left( x-\frac{2 \sqrt{\delta } t \tau }{\sqrt{2 \lambda +\tau }}\right) }{\sqrt{2 \lambda +\tau }}\right) \right) e^{i \left( \theta +\delta t+\frac{\sqrt{\delta } x}{\sqrt{2 \lambda +\tau }}\right) +\varpi \beta (t)-\varpi ^{2} t}. \end{aligned}$$

(16)

Set 2: Choosing the set $c_0=0, c_1=\frac{\sqrt{2} \sqrt{-\delta \lambda -\delta \tau }}{\sqrt{8 \lambda \rho +7 \rho \tau }}, d_1=-\frac{\sqrt{2} \sqrt{-\delta (\lambda +\tau )}}{\sqrt{\rho (8 \lambda +7 \tau )}}, {\alpha }=-\frac{\sqrt{\delta }}{\sqrt{8 \lambda +7 \tau }},$ the solitary wave solution is obtained under noise as follow,

$$\begin{aligned} H_{4}(x,t)= & \left( \frac{\sqrt{2} \sqrt{-\delta \lambda -\delta \tau }}{\sqrt{8 \lambda \rho +7 \rho \tau }} \tan \left( \frac{\sqrt{\delta } \left( x-\frac{2 \sqrt{\delta } t \tau }{\sqrt{8 \lambda +7 \tau }}\right) }{\sqrt{8 \lambda +7 \tau }}\right) \nonumber \right. \\ & \left. -\frac{\sqrt{2} \sqrt{-\delta (\lambda +\tau )}}{\sqrt{\rho (8 \lambda +7 \tau )}} \cot \left( \frac{\sqrt{\delta } \left( x-\frac{2 \sqrt{\delta } t \tau }{\sqrt{8 \lambda +7 \tau }}\right) }{\sqrt{8 \lambda +7 \tau }}\right) \right) e^{i \left( \theta +\delta t+\frac{\sqrt{\delta } x}{\sqrt{8 \lambda +7 \tau }}\right) +\varpi \beta (t)-\varpi ^{2} t}. \end{aligned}$$

(17)

Family of solution 3: If $[f_1, f_2, f_3, f_4]=[1, 0, 1, 1]$, $[r_1, r_2, r_3, r_4]=[ 1, 0, 1, 0]$ then Eq. (7) changes into,

$$\begin{aligned} \varphi (\eta )=\frac{e^{\eta } }{e^{\eta }+1}. \end{aligned}$$

(18)

The set of equations is derived by substituting Eq. (11) into Eq. (10) using Eq. (18). This set of equations can be solved with Mathematica to provide the following unknown constants,

Set 1: Choosing the set $c_0=-\frac{\sqrt{\delta } \sqrt{\lambda +\tau }}{\sqrt{\lambda \rho +3 \rho \tau }}, c_1=\frac{2 \sqrt{\delta } \sqrt{\lambda +\tau }}{\sqrt{\rho (\lambda +3 \tau )}}, d_1=0, {\alpha }=-\frac{\sqrt{2} \sqrt{\delta }}{\sqrt{-\lambda -3 \tau }}$ the exponential function solution is obtained under noise as follow,

$$\begin{aligned} H_{5}(x,t)= \left( \frac{2 \sqrt{\delta } \sqrt{\lambda +\tau }}{\sqrt{\rho (\lambda +3 \tau )} \left( \exp \left( \frac{\sqrt{2} \sqrt{\delta } \left( x-\frac{2 \sqrt{2} \sqrt{\delta } t \tau }{\sqrt{-\lambda -3 \tau }}\right) }{\sqrt{-\lambda -3 \tau }}\right) +1\right) }-\frac{\sqrt{\delta } \sqrt{\lambda +\tau }}{\sqrt{\lambda \rho +3 \rho \tau }}\right) e^{i \left( \theta +\delta t+\frac{\sqrt{2} \sqrt{\delta } x}{\sqrt{-\lambda -3 \tau }}\right) +\varpi \beta (t)-\varpi ^{2} t}. \end{aligned}$$

(19)

Family of solution 4: If $[f_1, f_2, f_3, f_4]=[ 1-i, 1+i, 1, 1]$, $[r_1, r_2, r_3, r_4]= [i, -i, i, -i]$ then Eq. (7) changes into,

$$\begin{aligned} \varphi (\eta )=\frac{\sin (\eta )+\cos (\eta )}{\cos (\eta )}. \end{aligned}$$

(20)

The set of equations is derived by substituting Eq. (11) into Eq. (10) using Eq. (20). This set of equations can be solved with Mathematica to provide the following unknown constants,

Set 1: Choosing the set $c_0=-\frac{\sqrt{2} \sqrt{-\delta (\lambda +\tau )}}{\sqrt{\rho (2 \lambda +\tau )}},c_1=\frac{\sqrt{2} \sqrt{-\delta \lambda -\delta \tau }}{\sqrt{2 \lambda \rho +\rho \tau }}, d_1=0, {\alpha }=\frac{\sqrt{\delta }}{\sqrt{2 \lambda +\tau }},$ the solitary wave solution is obtained under noise as follow,

$$\begin{aligned} H_{6}(x,t)= \left( \frac{\sqrt{2} \sqrt{-\delta \lambda -\delta \tau }}{\sqrt{2 \lambda \rho +\rho \tau }} \left( \tan \left( \frac{\sqrt{\delta } \left( \frac{2 \sqrt{\delta } t \tau }{\sqrt{2 \lambda +\tau }}+x\right) }{\sqrt{2 \lambda +\tau }}\right) +1\right) -\frac{\sqrt{2} \sqrt{-\delta (\lambda +\tau )}}{\sqrt{\rho (2 \lambda +\tau )}}\right) \nonumber \\e^{i \left( \theta +\delta t-\frac{\sqrt{\delta } x}{\sqrt{2 \lambda +\tau }}\right) +\varpi \beta (t)-\varpi ^{2} t}. \end{aligned}$$

(21)

Set 2: Choosing the set $c_0=-\frac{\sqrt{2} \sqrt{-\delta (\lambda +\tau )}}{\sqrt{\rho (2 \lambda +\tau )}},c_1=0,d_1=\frac{2 \sqrt{2} \sqrt{-\delta \lambda -\delta \tau }}{\sqrt{2 \lambda \rho +\rho \tau }},{\alpha }=\frac{\sqrt{\delta }}{\sqrt{2 \lambda +\tau }},$ the solitary wave solution is obtained under noise as follow,

$$\begin{aligned} H_{7}(x,t)=\left( \frac{2 \sqrt{2} \sqrt{-\delta \lambda -\delta \tau }}{\sqrt{2 \lambda \rho +\rho \tau } \left( \tan \left( \frac{\sqrt{\delta } \left( \frac{2 \sqrt{\delta } t \tau }{\sqrt{2 \lambda +\tau }}+x\right) }{\sqrt{2 \lambda +\tau }}\right) +1\right) }-\frac{\sqrt{2} \sqrt{-\delta (\lambda +\tau )}}{\sqrt{\rho (2 \lambda +\tau )}}\right) e^{i \left( \theta +\delta t-\frac{\sqrt{\delta } x}{\sqrt{2 \lambda +\tau }}\right) +\varpi \beta (t)-\varpi ^{2} t}. \end{aligned}$$

(22)

Family of solution 5: If $[f_1, f_2, f_3, f_4]=[ -3, -1, 1, 1]$, $[r_1, r_2, r_3, r_4]= [1, -1, 1, -1]$ then Eq. (7) changes into,

$$\begin{aligned} \varphi (\eta )=\frac{-\sinh (\eta )-2 \cosh (\eta )}{\cosh (\eta )}. \end{aligned}$$

(23)

The set of equations is derived by substituting Eq. (11) into Eq. (10) using Eq. (23). This set of equations can be solved with Mathematica to provide the following unknown constants,

Set 1: Choosing the set $c_0=-\frac{2 \sqrt{2} \sqrt{\delta (\lambda +\tau )}}{\sqrt{\rho (2 \lambda +3 \tau )}},c_1=-\frac{\sqrt{2} \sqrt{\delta \lambda +\delta \tau }}{\sqrt{2 \lambda \rho +3 \rho \tau }}, d_1=0, {\alpha }=-\frac{\sqrt{\delta }}{\sqrt{-2 \lambda -3 \tau }},$ the dark soliton solution is obtained under noise as follow,

$$\begin{aligned} H_{8}(x,t)= \left( -\frac{2 \sqrt{2} \sqrt{\delta (\lambda +\tau )}}{\sqrt{\rho (2 \lambda +3 \tau )}}-\frac{\sqrt{2} \sqrt{\delta \lambda +\delta \tau }}{\sqrt{2 \lambda \rho +3 \rho \tau }} \left( \tanh \left( \frac{\sqrt{\delta } \left( x-\frac{2 \sqrt{\delta } t \tau }{\sqrt{-2 \lambda -3 \tau }}\right) }{\sqrt{-2 \lambda -3 \tau }}\right) -2\right) \right) \nonumber \\e^{i \left( \theta +\delta t-\frac{\sqrt{\delta } x}{\sqrt{2 \lambda +\tau }}\right) +\varpi \beta (t)-\varpi ^{2} t}. \end{aligned}$$

(24)

Set 2: Choosing the set $c_0=-\frac{2 \sqrt{2} \sqrt{\delta (\lambda +\tau )}}{\sqrt{\rho (2 \lambda +3 \tau )}},c_1=0,d_1=-\frac{3 \sqrt{2} \sqrt{\delta \lambda +\delta \tau }}{\sqrt{2 \lambda \rho +3 \rho \tau }}, {\alpha }=\frac{\sqrt{\delta }}{\sqrt{-2 \lambda -3 \tau }}$ the dark soliton solution is obtained under noise as follow,

$$\begin{aligned} H_{9}(x,t)=\left( -\frac{2 \sqrt{2} \sqrt{\delta (\lambda +\tau )}}{\sqrt{\rho (2 \lambda +3 \tau )}}-\frac{3 \sqrt{2} \sqrt{\delta \lambda +\delta \tau }}{\sqrt{2 \lambda \rho +3 \rho \tau } \left( -\tanh \left( \frac{\sqrt{\delta } \left( \frac{2 \sqrt{\delta } t \tau }{\sqrt{-2 \lambda -3 \tau }}+x\right) }{\sqrt{-2 \lambda -3 \tau }}\right) -2\right) }\right) \nonumber \\e^{i \left( \theta +\delta t-\frac{\sqrt{\delta } x}{\sqrt{2 \lambda +\tau }}\right) +\varpi \beta (t)-\varpi ^{2} t}. \end{aligned}$$

(25)

Family of solution 6: If $[f_1, f_2, f_3, f_4]=[-1, 0, 1, 1]$, $[r_1, r_2, r_3, r_4]= [0, 1, 0, 1]$ then Eq. (7) changes into,

$$\begin{aligned} \varphi (\eta )=-\frac{1}{e^{\eta }+1}. \end{aligned}$$

(26)

The set of equations is derived by substituting Eq. (11) into Eq. (10) using Eq. (26). This set of equations can be solved with Mathematica to provide the following unknown constants,

Set 1: Choosing the set $c_0=\frac{\sqrt{\delta } \sqrt{\lambda +\tau }}{\sqrt{\lambda \rho +3 \rho \tau }},c_1=\frac{2 \left( \frac{\delta ^{3/2} \lambda \sqrt{\lambda +\tau }}{\sqrt{\rho (\lambda +3 \tau )}}+\frac{\delta ^{3/2} \tau \sqrt{\lambda +\tau }}{\sqrt{\rho (\lambda +3 \tau )}}\right) }{\delta \lambda +\delta \tau },d_1=0, {\alpha }=-\frac{\sqrt{2} \sqrt{\delta }}{\sqrt{-\lambda -3 \tau }},$ the exponential function solution is obtained under noise as follow,

$$\begin{aligned} H_{10}(x,t)= \left( \frac{\sqrt{\delta } \sqrt{\lambda +\tau }}{\sqrt{\lambda \rho +3 \rho \tau }}-\frac{2 \left( \frac{\delta ^{3/2} \lambda \sqrt{\lambda +\tau }}{\sqrt{\rho (\lambda +3 \tau )}}+\frac{\delta ^{3/2} \tau \sqrt{\lambda +\tau }}{\sqrt{\rho (\lambda +3 \tau )}}\right) }{(\delta \lambda +\delta \tau ) \left( \exp \left( -\frac{\sqrt{2} \sqrt{\delta } \left( x-\frac{2 \sqrt{2} \sqrt{\delta } t \tau }{\sqrt{-\lambda -3 \tau }}\right) }{\sqrt{-\lambda -3 \tau }}\right) +1\right) }\right) e^{i \left( \theta +\delta t+\frac{\sqrt{2} \sqrt{\delta } x}{\sqrt{-\lambda -3 \tau }}\right) +\varpi \beta (t)-\varpi ^{2} t}. \end{aligned}$$

(27)

Family of solution 7: If $[f_1, f_2, f_3, f_4]=[ 1, 0, 1, 1]$, $[r_1, r_2, r_3, r_4]= [1, 0, 1, 0]$ then Eq. (7) changes into,

$$\begin{aligned} \varphi (\eta )=-\frac{\sinh (\eta )}{\cosh (\eta )}. \end{aligned}$$

(28)

The set of equations is derived by substituting Eq. (11) into Eq. (10) using Eq. (28). This set of equations can be solved with Mathematica to provide the following unknown constants,

Set 1: Choosing the set $c_0=0,c_1=-\frac{\sqrt{2} \sqrt{\delta \lambda +\delta \tau }}{\sqrt{2 \lambda \rho +3 \rho \tau }},d_1=0, {\alpha }=\frac{\sqrt{\delta }}{\sqrt{-2 \lambda -3 \tau }}$ the dark soliton solution is obtained under noise as follow,

$$\begin{aligned} H_{11}(x,t)=\left( \frac{\sqrt{2} \sqrt{\delta \lambda +\delta \tau } }{\sqrt{2 \lambda \rho +3 \rho \tau }} \tanh \left( \frac{\sqrt{\delta } \left( \frac{2 \sqrt{\delta } t \tau }{\sqrt{-2 \lambda -3 \tau }}+x\right) }{\sqrt{-2 \lambda -3 \tau }}\right) \right) e^{i \left( \theta +\delta t-\frac{\sqrt{\delta } x}{\sqrt{-2 \lambda -3 \tau }}\right) +\varpi \beta (t)-\varpi ^{2} t}. \end{aligned}$$

(29)

Set 2: Choosing the set $c_0=0, c_1=-\frac{\sqrt{2} \sqrt{-\delta \lambda -\delta \tau }}{\sqrt{4 \lambda \rho +3 \rho \tau }}, d_1=\frac{\sqrt{2} \sqrt{-\delta (\lambda +\tau )}}{\sqrt{\rho (4 \lambda +3 \tau )}}, {\alpha }=\frac{\sqrt{\delta }}{\sqrt{4 \lambda +3 \tau }}$ the dark-singular soliton solution is obtained under noise as follow,

$$\begin{aligned} H_{12}(x,t)= & \left( \frac{\sqrt{2} \sqrt{-\delta \lambda -\delta \tau }}{\sqrt{4 \lambda \rho +3 \rho \tau }} \tanh \left( \frac{\sqrt{\delta } \left( \frac{2 \sqrt{\delta } t \tau }{\sqrt{4 \lambda +3 \tau }}+x\right) }{\sqrt{4 \lambda +3 \tau }}\right) \nonumber \right. \\ & \left. -\frac{\sqrt{2} \sqrt{-\delta (\lambda +\tau )}}{\sqrt{\rho (4 \lambda +3 \tau )}} \coth \left( \frac{\sqrt{\delta } \left( \frac{2 \sqrt{\delta } t \tau }{\sqrt{4 \lambda +3 \tau }}+x\right) }{\sqrt{4 \lambda +3 \tau }}\right) \right) e^{i \left( \theta +\delta t-\frac{\sqrt{\delta } x}{\sqrt{4 \lambda +3 \tau }}\right) +\varpi \beta (t)-\varpi ^{2} t}. \end{aligned}$$

(30)

Family of solution 8: If $[f_1, f_2, f_3, f_4]=[2-i, 2+i, 1, 1]$, $[r_1, r_2, r_3, r_4]= [ i, -i, i, -i]$ then Eq. (7) changes into,

$$\begin{aligned} \varphi (\eta )=\frac{\sin (\eta )+2 \cos (\eta )}{\cos (\eta )}. \end{aligned}$$

(31)

The set of equations is derived by substituting Eq. (11) into Eq. (10) using Eq. (31). This set of equations can be solved with Mathematica to provide the following unknown constants,

Set 1: Choosing the set $c_0=-\frac{2 \sqrt{2} \sqrt{-\delta (\lambda +\tau )}}{\sqrt{\rho (2 \lambda +\tau )}},c_1=0,d_1=\frac{5 \sqrt{2} \sqrt{-\delta \lambda -\delta \tau }}{\sqrt{2 \lambda \rho +\rho \tau }}, {\alpha }=-\frac{\sqrt{\delta }}{\sqrt{2 \lambda +\tau }}$ the solitary wave solution is obtained under noise as follow,

$$\begin{aligned} H_{13}(x,t)= \left( \frac{5 \sqrt{2} \sqrt{-\delta \lambda -\delta \tau }}{\sqrt{2 \lambda \rho +\rho \tau } \left( 2-\tan \left( \frac{\sqrt{\delta } \left( x-\frac{2 \sqrt{\delta } t \tau }{\sqrt{2 \lambda +\tau }}\right) }{\sqrt{2 \lambda +\tau }}\right) \right) }-\frac{2 \sqrt{2} \sqrt{-\delta (\lambda +\tau )}}{\sqrt{\rho (2 \lambda +\tau )}}\right) e^{i \left( \theta +\delta t+\frac{\sqrt{\delta } x}{\sqrt{2 \lambda +\tau }}\right) +\varpi \beta (t)-\varpi ^{2} t}. \end{aligned}$$

(32)

Set 2: Choosing the set $c_0=-\frac{2 \sqrt{2} \sqrt{-\delta (\lambda +\tau )}}{\sqrt{\rho (2 \lambda +\tau )}},c_1=\frac{\sqrt{2} \sqrt{-\delta \lambda -\delta \tau }}{\sqrt{2 \lambda \rho +\rho \tau }},d_1=0, {\alpha }=\frac{\sqrt{\delta }}{\sqrt{2 \lambda +\tau }}$ the solitary wave solution is obtained under noise as follow,

$$\begin{aligned} H_{14}(x,t)= \left( \frac{\sqrt{2} \sqrt{-\delta \lambda -\delta \tau }}{\sqrt{2 \lambda \rho +\rho \tau }} \left( \tan \left( \frac{\sqrt{\delta } \left( \frac{2 \sqrt{\delta } t \tau }{\sqrt{2 \lambda +\tau }}+x\right) }{\sqrt{2 \lambda +\tau }}\right) +2\right) -\frac{2 \sqrt{2} \sqrt{-\delta (\lambda +\tau )}}{\sqrt{\rho (2 \lambda +\tau )}}\right) \nonumber \\e^{i \left( \theta +\delta t-\frac{\sqrt{\delta } x}{\sqrt{2 \lambda +\tau }}\right) +\varpi \beta (t)-\varpi ^{2} t}. \end{aligned}$$

(33)

Family of solution 9: If $[f_1, f_2, f_3, f_4]=[ 1, 2, 1, 1]$, $[r_1, r_2, r_3, r_4]=[ 1, 0, 1, 0]$ then Eq. (7) changes into,

$$\begin{aligned} \varphi (\eta )=\frac{e^{ \eta }+2}{e^{ \eta }+1}. \end{aligned}$$

(34)

The set of equations is derived by substituting Eq. (11) into Eq. (10) using Eq. (34). This set of equations can be solved with Mathematica to provide the following unknown constants,

Set 1: Choosing the set $c_0=\frac{3 \sqrt{\delta (\lambda +\tau )}}{\sqrt{\rho (\lambda +3 \tau )}},c_1=0,d_1=-\frac{4 \sqrt{\delta \lambda +\delta \tau }}{\sqrt{\lambda \rho +3 \rho \tau }}, {\alpha }=-\frac{\sqrt{2} \sqrt{\delta }}{\sqrt{-\lambda -3 \tau }},$ the exponential function solution is obtained under noise as follow,

$$\begin{aligned} H_{15}(x,t)= \left( \frac{3 \sqrt{\delta (\lambda +\tau )}}{\sqrt{\rho (\lambda +3 \tau )}}-\frac{4 \sqrt{\delta \lambda +\delta \tau }}{\sqrt{\lambda \rho +3 \rho \tau } \left( \frac{1}{\exp \left( -\frac{\sqrt{2} \sqrt{\delta } \left( x-\frac{2 \sqrt{2} \sqrt{\delta } t \tau }{\sqrt{-\lambda -3 \tau }}\right) }{\sqrt{-\lambda -3 \tau }}\right) +1}+1\right) }\right) \nonumber \\e^{i \left( \theta +\delta t+\frac{\sqrt{2} \sqrt{\delta } x}{\sqrt{-\lambda -3 \tau }}\right) +\varpi \beta (t)-\varpi ^{2} t}. \end{aligned}$$

(35)

Family of solution 10: If $[f_1, f_2, f_3, f_4]=[ 2, 1 , 1 , 1]$, $[r_1, r_2, r_3, r_4]=[ 1, 0, 1, 0]$ then Eq. (7) changes into,

$$\begin{aligned} \varphi (\eta )=\frac{e^{\eta }}{e^{\eta }+1}. \end{aligned}$$

(36)

The set of equations is derived by substituting Eq. (11) into Eq. (10) using Eq. (36). This set of equations can be solved with Mathematica to provide the following unknown constants,

Set 1: Choosing the set $c_0=\frac{3 \sqrt{\delta (\lambda +\tau )}}{\sqrt{\rho (\lambda +3 \tau )}},c_1=-\frac{2 \sqrt{\delta \lambda +\delta \tau }}{\sqrt{\lambda \rho +3 \rho \tau }},d_1=0, {\alpha }=-\frac{\sqrt{2} \sqrt{\delta }}{\sqrt{-\lambda -3 \tau }}$ the exponential function solution is obtained under noise as follow,

$$\begin{aligned} H_{16}(x,t)= \left( \frac{3 \sqrt{\delta (\lambda +\tau )}}{\sqrt{\rho (\lambda +3 \tau )}}-\frac{2 \sqrt{\delta \lambda +\delta \tau }}{\sqrt{\lambda \rho +3 \rho \tau }} \left( 2-\frac{1}{\exp \left( -\frac{\sqrt{2} \sqrt{\delta } \left( x-\frac{2 \sqrt{2} \sqrt{\delta } t \tau }{\sqrt{-\lambda -3 \tau }}\right) }{\sqrt{-\lambda -3 \tau }}\right) +1}\right) \right) \nonumber \\e^{i \left( \theta +\delta t+\frac{\sqrt{2} \sqrt{\delta } x}{\sqrt{-\lambda -3 \tau }}\right) +\varpi \beta (t)-\varpi ^{2} t}. \end{aligned}$$

(37)

Effect of noise on the optical solution of the RLSE

This section examines how multiplicative noise affects the RNLSE (2) solution. The values of the physical parameters in the dispersion and nonlinear coefficients are indicated by the behavior of the solutions for the RNLSE (2), which can be classified as solitons, dissipative, periodic, etc. For various noise strength values, we present some 2D, and 3D graphics. We use the Mathematica11.1 package in the following ways for our purposes. Set the settings to $\delta =1.1,$ $\theta =0.5,$ $\lambda =1.5,$ $\rho =1.3,$ and $\tau =-1.56$. We present several simulations for different values of $\varpi$ (noise intensity).

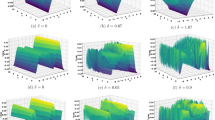
Figures 1, 3 and 4 are shows the dark solitons when we choose the noise $\varpi =0$ it provides the classical soliton for the solutions $H_1(x,t)$, $H_5(x,t)$ and $H_{11}(x,t)$ respectively. Further, we increase the noise $\varpi =0.3, 0.5$ and 0.9 which shows that how the noise is effected our solutions. However, we observe that the surface becomes more planer following minor transit behaviors when the noise arrives and the noise level $\varpi$ grows. This indicates that the solutions are affected by multiplicative noise, which stabilizes them. Figure 2 is shows the solitary wave solutions and their effect of noise on it for the solutions $H_3(x,t)$. Dark solitons and solitary wave solutions hold crucial importance for studying the dynamical aspects of the stochastic resonance nonlinear Schrödinger equation (SR-NLSE) because this equation describes wave propagation in nonlinear media which contains stochastic perturbations. Dark solitons occur as stable solutions which form localized intensity dips in defocusing nonlinear systems. The solitary wave packets found their relevance particularly in three scientific domains, optical fibers, Bose–Einstein condensates and plasma physics. Local waves known as solitary wave solutions exist because nonlinearity matches dispersion and permits their shape to persist. RNLSE solutions exhibit results from stochastic resonance because this phenomenon enables systems to improve their weak periodic signal detection with added noise. The theoretical framework of RNLSE finds important use in signal processing for noise-enhanced weak signal detection while mapping neural activity synchronization patterns in biophysics. RNLSE uses nonlinear interactions between noise and periodic forcing to investigate intricate wave patterns which apply to theoretical and practical settings (Figs. 3, 4).

Fig. 1

Impact of noise on dark soliton solutions $H_1(x,t)$ under the different values of parameters.

Fig. 2

Impact of noise on solitary wave solutions $H_3(x,t)$ under the different values of parameters.

Fig. 3

Impact of noise on dark soliton solutions $H_5(x,t)$ under the different values of parameters.

Fig. 4

Impact of noise on dark soliton solutions $H_{11}(x,t)$ under the different values of parameters.

Dynamical analysis

The sensitivity, chaotic, and bifurcation analyses of the resonance NLS equation were examined in this section. Equation (10) is transformed into a dynamical system using the Galilean transformation^43,44. Equation (10) is assumed such as

$$\begin{aligned} \hbar ''(\eta )+\theta \hbar +\tau \hbar ^3=0, \end{aligned}$$

(38)

where we let $\theta =\frac{(-\sigma +\xi j^2)}{ (\xi +\lambda )}$ and $\tau =\frac{\rho }{ (\xi +\lambda )}$.

Let $\hbar (\eta )=\mathbf {H_1}$ and $\mathbf {H_2}^{\prime }(\eta )=\mathbf {H_2}$

$$\begin{aligned} \left. \begin{array}{lll} \mathbf {H_1}^{\prime }& =& \mathbf {H_2},\\ \mathbf {H_2}^{\prime }& =& -\theta \mathbf {H_1} - \tau \mathbf {H_1}^3, \end{array} \right. \end{aligned}$$

(39)

To demonstrate the sensitivity of the dynamical system, we expressed the sensitivity of the solutions in this analysis. If we only make little adjustments to the original conditions, the system sensitivity will be reduced. The sensitivity plots are created using the parameters that were selected, such as $\theta =2$ and $\tau =2$. The system will be extremely sensitive, nevertheless, if it changes much as a result of minor changes to the initial conditions. We’ll look at how the frequency term affects the model under study. This will be accomplished by defining the physical characteristics of the model being studied and discussing the effects of the disturbance’s force and frequency on the system. The illustrations Fig. 7 illustrate how our dynamical behaves sensitively for varying initial condition values. It displays the sensitive behavior if we alter the initial conditions by changing the slit. The simulations for the sensitivity analysis is given in Fig. 5.

Fig. 5

Sensitive behavior of the dynamical system (39) under the different ICs.

The dynamical system (40) is obtained by applying the Galilean transformation to Eq. (10) and observing the chaotic behavior by adding $\chi \cos (\varpi t)$.

$$\begin{aligned} \left. \begin{array}{lll} \mathbf {H_1}^{\prime }& =& \mathbf {H_2},\\ \mathbf {H_2}^{\prime }& =& -\theta \mathbf {H_1} - \tau \mathbf {H_1}^3, \end{array} \right. \end{aligned}$$

(40)

The Fig. 6 shows the different chaotic behaviors for the different values of $\chi$ and $\varpi$. Now, we will investigate the Eq. (2) utilizing bifurcation theory^43,44. This system is Hamiltonian and has following integral

$$\begin{aligned} Q(\mathbf {H_1},\mathbf {H_2})= \frac{\mathbf {H_2}^2}{2}-\theta \frac{\mathbf {H_1^2}}{2} - \tau \frac{\mathbf {H_1}^4}{4}=q, \end{aligned}$$

(41)

where q is Hamiltonian constant. Now we analyze the bifurcations behavior of phase portraits of Eq. (39) in the parameter space c. By qualitative analysis, we gained the results. The three equilibrium points for the above system of differential equations are computed as (0, 0), $(-\frac{ \sqrt{-\theta }}{\sqrt{\tau }}, 0)$ and $( \frac{ \sqrt{-\theta }}{\sqrt{\tau }}, 0)$ on $\mathbf {H_1}$-axis. Also, the jacobian of the system will be:

$$\begin{aligned} J=(P_1,P_2)=\left| \begin{array}{cc} 0 & 1 \\ -\theta \mathbf {H_1} - \tau \mathbf {H_1}^3 & 0 \\ \end{array} \right| =-(-\theta \mathbf {H_1} - \tau \mathbf {H_1}^3). \end{aligned}$$

Thus $(\mathbf {H_1},0)$ is a saddle point for $J=(\mathbf {H_1},\mathbf {H_2})< 0$, it is a center for $J=(\mathbf {H_1},\mathbf {H_2}) > 0$ and a cuspidal point for $J=(\mathbf {H_1},\mathbf {H_2})= 0$.

Fig. 6

Chaotic behavior of the system (40).

Fig. 7

Phase portrait plots of the dynamical system 39.

Summary

The main summary of this article is, we explored the optical solitons and solitary wave solutions for the rasonance nonlinear NLS equation using the multiplicative time noise. A well-known approach is used name as the GERF method to explored these solutions. These solutions are obtained in the form of combo singular bright solutions, bell-shaped, exponential, and singular. The different effects of noise on the solutions are visualized for different values of $\varpi$ in the form of 3D and 2D. Moreover, the dynamical analysis of the underlying model is visualized to show the stability of the system. Bifurcation, sensitivity and chaotic behaviors are show in the form of 2D and 3D (Fig. 7).

Conclusion

The results of this work give us a better knowledge of the physical and dynamical properties of the rasonance nonlinear NLS system using GERF technique. The RNLS equation are mostly used to describe how light moves via planar wave guides and nonlinear optical fibres. Explicit solitary wave solutions are obtained for various kinds of stochastic wave structures. The observed solutions fall into categories such as combo singular bright solutions, bell-shaped, exponential, and singular. The outcomes show the methods usefulness and clarity, allowing it to be applied to more complex phenomena. Moreover, in the stochastic RNLS equations, bifurcation, chaos, and stability analysis has yielded important new information on optical fiber. The Galilean transformation gives us a dynamic structure that makes it easier to analyze bifurcations in detail. The obtained solutions are essential for comprehending a number of challenging physical processes due to the significance of the RNLS equation in nonlinear waves in a liquid-filled elastic tube, solitary wave and nonlinear instability problems, plasma waves and hydromagnetic, heat transfer in a solid, nonlinear optics, and propagation in the piezoelectric semi-conductors. Lastly, a few illustrations were added to show how the stochastic term affected the stochastic precise solutions of the stochastic RNLS equation. We concluded that the solutions of stochastic RNLS equation were stabilized by the multiplicative Wiener process. We can use additive noise to solve the RNLS equation in subsequent research. For the future direction, there are many nonlinear system