Introduction

Bridges are an essential component of any highway project that falls under the theme of urban development, but their position in seismically prone regions causes structural damage and economic breakdown. The physical damage to such structures is determined by various elements, including seismic parameters, geotechnical and geological setup, and material characterization1,2. Previous earthquakes in the United States, Taiwan, Japan, Nepal, and Turkiye caused damage to bridges, including both superstructure and substructure, as well as foundations. This resulted in the identification of risk factors, which were then assessed as part of the disaster risk reduction initiative3,4,5. Damage is classified into multiple classes based on the damage pattern caused by ground shaking. Previous researchers offered bridge damage classification using field observations, analytical investigations, and numerical modeling6. A probabilistic approach for measuring bridge resilience that incorporates empirical, analytical, and experimental data is utilized to generate consistent seismic damage limits, which are then confirmed using shaking table tests and calibrated fragility models7,8. Autoregressive models were presented to categorize damage and estimate stiffness in experimental structures by utilizing minimal damage-sensitive characteristics and sensors9,10,11,12,13,14.

Bi and Hao15 conducted a comprehensive numerical analysis using 3D finite element simulations to assess pounding damage and dislocation potentials in a two-span bridge under spatially variable seismic loads, which revealed realistic damage mechanisms. Mangalathu et al.16 proposed a machine learning-based approach for quick post-earthquake damage assessment of bridges, which achieved up to 82% accuracy by taking into account bridge-specific parameters such as span length and reinforcement ratio. Li et al.17 examined seismic damage data from 1069 reinforced concrete girder bridges affected by the 2008 Wenchuan earthquake and developed a nonlinear fragility model to measure vulnerability and improve future resilience research. Interlayer area damage model (IADM) with the Markov Chain Monte Carlo (MCMC) method was investigated for efficient seismic damage assessment in a high-speed rail bridge, highlighting the impact of ground motion on damage indices18.

The present study compiles damage data from 331 bridges impacted by 8 well-documented earthquake events (Table 1), aiming to propose a novel damage assessment method for bridges based on reported bridge damage. Details regarding bridge typology, construction materials, and other structural parameters are provided in Table 2. Additionally, risk factors affecting seismic bridge performance were identified, analyzed, and classified within a hierarchical framework. The seismic risk assessment was conducted using a fuzzy synthetic approach (FSA), with the effectiveness of the method demonstrated through February 6, 2023 Kahramanmaras (Turkiye) Earthquake (Mw 7.8) data.

Table 1 Bridges damaged during previous earthquakes.
Full size table
Table 2 Derived data summary from previous earthquakes.
Full size table

Classification of seismic bridge damages

Bridge damage is determined by the seismic hazard level at the site, which controls the intensity of ground motion. Damage can also result from earthquake-induced ground failures, such as liquefaction, fault displacements, or landslides. As a result, bridge damage classification should include these factors while also taking into account functionality and the level of physical damage, such as fracture dimensions and deformations. Bridge damage (BD) is classified into five categories: none for no visible damage, slight for minor cracking or spalling of structural components, moderate for damage that affects functionality, such as significant cracking, joint failure, or deck displacement, extensive for major cracking, girder damage, or pier dislocation, and collapse for complete structural failure (Table 3).

Table 3 Newly proposed seismic bridge damage patterns and their impact on traffic flow.
Full size table

This newly proposed classification of seismic damage is based on the extent of structural damage to the superstructure and substructure, quantified using specific crack widths (\({w}_{c}\)), crack lengths (\({l}_{c}\)), spalling severity, tilting angle (α), and settlement (\({S}_{s}\)). It integrates damage patterns with traffic functionality, categorizing bridges from “None (VL = very low)” to “Collapse (VH = very high)” based on structural integrity and accessibility. The classification reflects the progressive impact of seismic events on structural performance and operational capacity, aiding in post-earthquake assessments and decision-making for repairs or closures. The limit states are defined using quantitative thresholds for factors given in Table 3, with increasing values representing higher damage levels. System-level performance is set by combining these component limits, where the most critical damage in either the superstructure or substructure dictates the overall bridge functionality.

Primary risk factors for performance assessment

In this study, various data sources were used to identify risk factors influencing bridge seismic performance, including site-specific earthquake damage statistics, structural design reports, and case studies. Tables 1, 2 show the selected earthquake events and data sources for bridge damage. Based on these, Fig. 1 depicts a hierarchical system for assessing seismic risk of bridges.

Fig. 1
figure 1

Level based seismic risk assessment of bridges.

Full size image

The primary factors impacting bridge seismic performance are divided into three categories: (1) hazard parameters, (2) structural condition parameters, and (3) ground condition parameters. Each factor is detailed as follows:

Hazard parameters

Intensity levels

Earthquake magnitude, focal depth, and epicentral distance are the most important criteria for bridge engineering. Higher magnitudes, shallow focal depths, and proximity to the distance to fault rupture all contribute to increased seismic activity, increasing the likelihood of bridge damage45,46.

Ground motion parameters

The duration of intense ground motion has a substantial impact on bridge performance, generating cumulative fatigue failure or cracks in structural components. High-frequency ground motion can cause localized spalling or differential displacements in bridge components47,48. Amplification effects may occur if the wavelength of seismic waves coincides with the span of the bridge.

Structural condition parameters

Superstructure and substructure

The design and construction of superstructure features like girders and decks has an impact on seismic performance. Inadequate reinforcing and poor construction practices increase vulnerability to lateral stresses. Substructures, such as piers and abutments, exhibit seismic behavior that is determined by their stiffness and foundation depth49,50. Bridges with skewed or curved geometry are more sensitive to seismic forces.

Materials and aging

The seismic capacity of bridge components is greatly influenced by the aging effects and material composition. During seismic occurrences, older bridges with steel reinforcement or deteriorating concrete are more likely to fail. Resilience is enhanced through the use of advanced materials such as fiber-reinforced composites, as noticed in past earthquake scenarios51.

Ground condition parameters

Site geology

Bridges that are located in areas with unfavorable geological conditions, such as fault zones or liquefiable soils, are more vulnerable to foundation failures and differential settlements26. These weaknesses may be made worse by ground instability, which could result in uneven bridge pier support.

Foundation depth and stability

Deeper bridge foundations usually have stronger seismic resilience, but shallow foundations are more vulnerable to damage from increased ground motion. Sediment instability or lateral spreading close to bridge abutments can cause serious structural damage.

Landslides and fault displacements

Bridges on or near unstable slopes are particularly vulnerable to landslides caused by seismic activity. Bridge decking or piers may experience severe structural failure due to sudden, localized deformation brought on by fault movements9,52. By offering a methodical way to assess seismic risk factors for bridges, this hierarchical framework makes it possible to create focused mitigation plans that will increase resilience.

Fuzzy synthetic approach (FSA)

Fuzzy synthetic approach (FSA) serves as a robust decision-making framework that combines fuzzy logic with weighted criteria to analyze and quantify the behavior of complex systems under uncertain conditions. In this study, the methodology follows four principal steps outlined by Tesfamaraim and Saatcioglu53, which are elaborated below:

Identification and prioritization of risk factors

For assessing seismic vulnerability in bridges, a comprehensive set of risk factors (\({R}_{f}\)) is identified and prioritized, as defined by Kir and Yuan54. In Eq. (1), \({R}_{f}\) represents a vector of ten prioritized seismic risk factors defined for assessing bridge vulnerability (refer to Table 4).

Table 4 Fuzzy transformation of primary risk factors.
Full size table
$${R}_{f}=({R}_{f1}, {R}_{f2},{R}_{f3}, {R}_{f4},{R}_{f5}, {R}_{f6},{R}_{f7}, {R}_{f8},{R}_{f9}, {R}_{f10}, )$$
(1)

The ranking of these factors is linked to damage classification and is determined based on predefined levels: VL (very low), L (low), M (medium), H (high), and VH (very high), as discussed in previous section. This classification assess system-level seismic performance by quantifying component-level damage and integrating it based on bridge typology. For different bridge types (suspension, arch, truss, beam), the importance of components varies. For example, suspension bridges are highly sensitive to cable and anchorage integrity, while arch bridges depend on abutment stability. Factors like foundation depth and adverse geology may be more critical for arch and truss bridges, while traffic load capacity and support systems significantly impact beam bridges. Thus, components carry varying importance depending on structural behavior and seismic vulnerability.

Formation of fuzzy modules

The identified risk factors are standardized through a fuzzification process, where each factor is assigned to memberships corresponding to five defined risk levels. This transformation ensures comparability across parameters. These transformations link to observed bridge damages from eight earthquakes considered in this study (Table 2) by correlating risk factors (e.g., proximity to fault rupture, bridge type etc.) with damage patterns. The fuzzified values represent the degree of association between each factor and damage severity, reflecting how specific conditions influenced superstructure and substructure failures during the studied seismic events. Membership values are determined using a histogram-based method10,55 applied to earthquake damage datasets belonging to February 6, 2023 Kahramanmaras (Turkiye) Earthquake (Figs. 2, 3, 4, 5). The derived memberships are detailed in Table 4.

Fig. 2
figure 2

Distribution of primary risk factors from February 6, 2023 Kahramanmaras (Turkiye) Earthquake for: (a) distance to fault rupture (superstructure); (b) distance to fault rupture (substructure); (c) bridge type (superstructure) and (d) support system (superstructure).

Full size image
Fig. 3
figure 3

Distribution of primary risk factors from February 6, 2023 Kahramanmaras (Turkiye) Earthquake for: (a) support system (substructure); (b) construction quality (superstructure); (c) construction quality (substructure); (d) adverse geology (superstructure).

Full size image
Fig. 4
figure 4

Distribution of primary risk factors from February 6, 2023 Kahramanmaras (Turkiye) Earthquake for: (a) adverse geology (substructure); (b) foundation depth (substructure); (c) slope condition (superstructure); (d) slope condition (substructure).

Full size image
Fig. 5
figure 5

Distribution of primary risk factors from February 6, 2023 Kahramanmaras (Turkiye) Earthquake for: (a) fault movement (superstructure); (b) fault movement (substructure); (c) material type (superstructure); (d) material type (substructure) and (e) traffic load capacity (superstructure).

Full size image

Weight assignment using AHP

The relative significance of each risk factor is represented by a weight set \({W}_{r}\). The analytic hierarchy process (AHP), developed by Saaty56, is employed to calculate these weights through pairwise comparisons of factors. Equation (2) shows the comparison matrix \(\left(\Delta \right)\) which denotes the \(n\times n\) pairwise matrix where each element represents the ratio of seismic risk factors \(\left({R}_{fi}/{R}_{fj}\right)\) for the selected dataset. The widely recognized 1–9 scale57 is utilized in this study due to its ability to maintain the original order consistently, ensure a uniform scaling approach, and enhance perceptual clarity. The details of this scale are presented in Table 5.

Table 5 Weight intensity-based comparison scale58.
Full size table
$$\Delta =\left[{d}_{ij}\right]= {\left[\begin{array}{ccc}{R}_{f1}/{R}_{f1}& \cdots & {R}_{f1}/{R}_{fn}\\ \vdots & \ddots & \vdots \\ {R}_{fn}/{R}_{f1}& \cdots & {R}_{fn}/{R}_{fn}\end{array}\right]}_{n\times n}$$
(2)

The row geometric mean method (RGMM) is utilized to compute the weight of \({R}_{f}\) (\({w}_{ri}\)) and weight set (\({W}_{r})\), according to Crawford and Williams59.

$${w}_{ri}= \sqrt[n]{{\prod }_{j=1}^{j=n}{d}_{ij}}$$
(3)
$${W}_{r}= \left(\frac{{w}_{r1}}{\sum {w}_{ri}}, \frac{{w}_{r2}}{\sum {w}_{ri}}, \dots .., \frac{{w}_{rn}}{\sum {w}_{ri}}\right)$$
(4)

Consistency verification is performed using the geometric consistency index (\(GCI\)) given by Aguarón and Moreno-Jiménez60. In Eq. (5), \(GCI\) measure the consistency of the pairwise comparison matrix (\(\Delta\)) by evaluating the deviations between the matrix ratios (\({d}_{ij}\)) and the corresponding weights (\({w}_{ri}, {w}_{rj}\)).

$$GCI= \frac{2}{\left(n-1\right)\left(n-2\right)}\sum_{i<j}{\left(\text{log}\frac{{d}_{ij} . {w}_{rj}}{{w}_{ri}}\right)}^{2}$$
(5)

Thresholds for \(GCI\) are set at 0.31 for \(n\) = 3, 0.35 for \(n\) = 4, and 0.37 for \(n\) > 4. If the \(GCI\) exceeds the threshold, the matrix is adjusted to ensure logical consistency. Final weights are summarized in Table 6.

Table 6 AHP weights for bridge vulnerability assessment.
Full size table

Unified data architecture

The FSA employs the weighted mean method for aggregating parameters. Fuzzified inputs \(\left({\beta }_{VL},{\beta }_{L},{\beta }_{M},{\beta }_{H},{\beta }_{VH}\right)\) for \(n\) parameters form a fuzzy judgment matrix. The AHP-derived weights are multiplied with this matrix to compute the fuzzy evaluation result.

$$\left({\beta }_{VL},{\beta }_{L},{\beta }_{M},{\beta }_{H},{\beta }_{VH}\right)= {\left({w}_{r1},{w}_{r2},{w}_{r3}, \dots .., {w}_{rn} \right)}^{\alpha }\left[\begin{array}{ccc}{{\beta }_{VL}}^{1}& \cdots & {{\beta }_{VH}}^{1}\\ \vdots & \ddots & \vdots \\ {{\beta }_{VL}}^{n}& \cdots & {{\beta }_{VH}}^{n}\end{array}\right]$$
(6)

A fuzzy composite operator “\(\alpha\)” determines the interaction of aggregated factors. Finally, defuzzification translates the fuzzy output into a crisp index (\(I\)) for decision-making61. In Eq. (7), I is calculated by aggregating the weighted contributions (\({{\partial }_{i}\times \beta }_{i}\)) of \(n\) fuzzy risk factors.

$$I= {\sum }_{i=1}^{i=n}{{\partial }_{i}\times \beta }_{i}$$
(7)

This study adopted the weighted average method, assigning equal importance to five-tuple fuzzy sets (\({\partial }_{VL}=0,{\partial }_{L}=0.25,{\partial }_{M}=0.5,{\partial }_{H}=0.75,{\partial }_{VH}=1\)). This approach ensures that all risk factors contribute to the final assessment, preventing data loss.

Case study

On February 6, 2023, a major earthquake (Mw 7.8) devastated southeastern Turkiye and northern Syria, causing significant devastation. This event killed over 50 thousand people, injured thousands, and caused catastrophic infrastructural damage, with over 0.3 million buildings demolished or severely damaged42. The event’s economic toll surpassed $100 billion. The seismic intensity exceeded XI, inflicting significant damage to essential infrastructure, including bridges and transportation networks.

Following the event, a thorough investigation was carried out to assess the damage that 52 bridges, including railroad, pedestrian, and highway structures had incurred. As part of this study, engineering records, design documentation, and maintenance histories were reviewed. A GIS-based database that recorded each bridge’s parameters, including span length, materials, construction type, and comprehensive damage photos, was created in order to arrange the findings. Of the bridges examined, 18 needed immediate repairs because of significant damage, and the remaining bridges showed varied degrees of devastation. In order to anticipate the damage condition of bridges located within 50 km of the distance to fault rupture, FSA was conducted. The results, which were mostly conservative overestimations, showed good agreement with the conditions that were observed.

The analysis of bridge damage reveals that the distance to fault rupture played a significant role in the severity of structural failures. Approximately 65% of damaged bridges were located within 40 km of the distance to fault rupture, with the most severe damage observed within 20 km. For instance, the Elbistan Bridge and Hatay Coastal Bridge, positioned 10 to 15 km from the distance to fault rupture, experienced damage levels of 5 and 4, respectively. Additionally, the orientation of bridge spans relative to fault ruptures influenced damage intensity (Table 7). Bridges oriented at angles of 60° to 90°, such as the Goksun River Bridge (18 km, arch type), sustained the most severe damage. In contrast, bridges oriented parallel to fault lines, such as the Pazarcik Bridge, showed relatively lower damage level of 2 despite similar distance to fault rupture. Bridge-specific variations in damage severity were influenced by factors such as foundation depth, slope conditions, and traffic loads. For example, despite similar distances to fault rupture, the Gaziantep Old Bridge and Reyhanli Bridge displayed damage levels of 3 and 4, respectively, due to differences in support systems and construction quality. Bridges with flexible support systems, shallow foundations, and poor construction quality exhibited heightened vulnerability to seismic forces. The Bahce-Nurdagi Bridge, located within 12 km of the distance to fault rupture, suffered complete collapse due to its shallow foundation and inadequate reinforcement.

Table 7 Comparison of observed bridge damage from past earthquakes with estimated damage levels.
Full size table

The present study FSA demonstrated a closer alignment with observed damage levels compared to62,63 models (refer to Table 7). It accurately predicted 25 out of 33 cases, whereas Nasrollahzadeh’s model correctly estimated 16 cases, and Lin et al.’s model only matched 12 cases. The present study also outperformed other models in capturing extensive (level 4) and collapse (level 5) damage, reducing underestimations seen in previous models. The mismatch between the present study and observed damage primarily arises in cases of higher damage levels (collapse and extensive damage). This discrepancy may result from uncertainties in local geotechnical conditions, structural variations, or simplifications in model assumptions regarding load distribution and material degradation. While the present model reduces underestimation, it occasionally predicts one level lower due to conservatively calibrated parameters.

Nasrollahzadeh’s model frequently underestimated higher damage levels (5 and 4), indicating limitations in its damage amplification mechanism. Lin et al.’s model showed an even stronger underestimation bias, particularly for extensive and collapse damage cases, suggesting it lacks sensitivity to severe structural failures. These models are less capable of handling mismatch due to their lower predictive accuracy in high-damage scenarios. The present study model’s advantage lies in a more refined calibration, enabling better representation of collapse-prone cases.

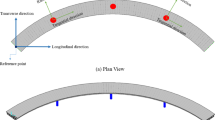
Figures 6 and 7 highlight the significant impact of the angle between bridge span direction and fault rupture on damage severity. On average, bridges oriented at 45°–65° angles experienced the most damage, with approximately 25 to 30% of the bridges collapsing or suffering extensive damage (red and orange bars). For instance, in subplots (b) and (f), about 20 to 25 bridges recorded moderate to extensive damage at angles of 45°, while fewer than 10 bridges sustained only slight damage. Comparatively, bridges at 15° or 85° angles had lower collapse rates, with slight to moderate damage dominating at an average of 50 to 60% of the total bridges. The data also indicates that the number of bridges with extensive damage (orange bar) peaked for the 45° to 65° angle range across multiple subplots, representing nearly 40% of total damaged structures in certain cases, such as shown in subplots (e) and (h). Conversely, slight damage (green bar) occurred more frequently for angles close to 15° and 85°, accounting for around 60 to 70% of cases. This trend underscores the vulnerability of bridges oriented obliquely (45° to 65°) to fault lines, where seismic forces act more destructively. In contrast, parallel or near-perpendicular orientations exhibit comparatively lower damage intensities, emphasizing the need for optimized span direction in seismic-prone zones. Table 8 summarizes the correlation between different factors and various bridge damage levels:

Fig. 6
figure 6

Effect of the angle between bridge span direction and fault on observed damage levels, examined under: (a) distance to fault rupture; (b) bridge type; (c) support system and (d) construction quality. The data presented here pertains to bridges damaged during the February 6, 2023, Kahramanmaras (Turkiye) Earthquake.

Full size image
Fig. 7
figure 7

Effect of the angle between bridge span direction and fault on observed damage levels, examined under: (a) adverse geology; (b) foundation depth; (c) slope condition; (d) material type and (e) traffic load capacity. The data presented here pertains to bridges damaged during the February 6, 2023, Kahramanmaras (Turkiye) Earthquake.

Full size image
Table 8 Influence of risk factors on bridge damage levels.
Full size table

The proposed FSA method demonstrated enhanced accuracy by integrating real earthquake damage data, particularly benefiting long-span beam-type bridges (e.g., Adiyaman Bridge: 1800 m) with rigid support and deep foundations. Compared to47,48, which relies on simulated records, the proposed FSA reduced uncertainty, especially for steep-slope structures (e.g., Nurdagi-Gaziantep Bridge). The Scozzese & Minnucci64 approach, which focuses on link slab bridges, is less applicable to the rigid support systems in most Turkish and Nepalese bridges. The Monteiro65 sampling-based method is computationally intensive for multi-span structures (e.g., Tarsus-Adana Bridge: 1600 m), whereas proposed FSA maintained efficiency across varied typologies. Chiu et al.66 consider corrosion effects, yet proposed FSA extended applicability beyond columns to complete structures, improving performance for composite bridges (e.g., Kilis Border Bridge). Monti & Nistico67 scenario-based model evaluated bridge response to specific earthquakes but lacks adaptability for bridges near active faults (e.g., Birecik Bridge: 95 km from rupture). The proposed FSA enhances reliability by considering diverse structural-geotechnical parameters, improving risk assessments across different seismic events.

Conclusions

This study introduces a novel damage classification system for evaluating bridge performance during seismic events, emphasizing the application of the fuzzy synthetic approach (FSA) to enhance the accuracy and reliability of damage assessments. Using data from the Kahramanmaras (Turkiye) earthquake (Mw 7.8), FSA enabled the integration of multiple uncertain and imprecise factors- such as seismic parameters, structural characteristics, and ground conditions, into a comprehensive damage evaluation framework. By incorporating fuzzy logic, the method effectively handled the inherent uncertainties in post-earthquake damage assessment, translating subjective expert judgments and field data into quantifiable damage indices. Key highlights and significant outcomes of this study include:

  • The FSA framework combined with the analytic hierarchy process (AHP) facilitated the prioritization and weighting of ten primary seismic risk factors. This integration allowed for a nuanced evaluation of damage patterns, revealing critical insights into common failure modes, including pier shear and flexural failures, deck displacements, bearing collapses, abutment instabilities, and severe girder cracking.

  • The FSA’s ability to manage vague and complex data proved essential in highlighting the influence of factors like distance to fault rupture, which emerged as a key determinant of damage severity. Moreover, FSA enabled the identification of structural vulnerabilities, such as the increased susceptibility of bridges with flexible supports, shallow foundations, and poor construction quality.

  • The proposed FSA offers a robust, data-driven, and globally adaptable framework that enhances accuracy, reduces subjectivity, and improves reliability in seismic bridge vulnerability assessments compared to existing methodologies62,63.

  • The proposed FSA model showed its enhanced precision, adaptability to various bridge types, which outperform traditional probability-based seismic risk assessment approaches.

Overall, the FSA proved instrumental in synthesizing complex datasets and expert judgments, providing a robust framework for damage assessment. These findings underscore the necessity of integrating fuzzy-based methods in bridge engineering to refine damage evaluations, enhance resilience, and ensure the long-term sustainability of critical infrastructure in seismically active regions.