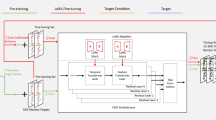
Abstract
Reservoir porosity is a crucial indicator of the physical properties of reservoirs, forming the foundation for oil and gas exploration, development design, and decision-making. Currently, it is primarily obtained through core testing or logging interpretation, but the lack of quantitative evaluation methods during drilling limits the timeliness and efficiency of porosity acquisition. Based on this, this study focuses on the tight sandstone reservoir in the East China Sea shelf basin, conducting modeling and rock-breaking simulations of 5 blade and 6 blade polycrystalline diamond compact (PDC) bits commonly used in the region. It investigates the relationships between rate of penetration (ROP), torque, mechanical specific energy (MSE), physical index, and other parameters for rocks with varying physical characteristics. A real-time quantitative prediction method for reservoir porosity, based on drilling and logging engineering parameters, is proposed. The results indicate that: (1) Significant differences in the response characteristics of rate of penetration, torque, and MSE are observed when drilling formations with identical mechanical characteristics, due to the influence of bit type. Therefore, these engineering parameters are not suitable for directly predicting reservoir porosity. (2) The relationship between the physical index and elastic modulus for 5 blade and 6 blade PDC bits is highly consistent, with both increasing logarithmically as elastic modulus increases. This suggests that the physical index can eliminate the influence of bit type and more accurately reflect changes in formation characteristics during drilling. (3) Using elastic modulus as an intermediary parameter, a model is established that relates porosity to the physical index, showing that porosity decreases as a power function of the physical index. The research findings were cross-verified in well NB13-4-A, with a 91.57% agreement between the porosity predicted by engineering parameters and the logging-derived porosity. The prediction method was applied to 20 exploration wells in the NB13-4 working area, yielding an average porosity consistency rate of 85.74%. This demonstrates that the method can provide timely, efficient, and accurate support for decision-making in exploration operations, such as intermediate testing and well completion.
Similar content being viewed by others
Introduction
Tight sandstone reservoirs are characterized by significant burial depth, high diagenetic strength, dense lithology, complex pore structures, and strong heterogeneity. Real-time, quantitative prediction of reservoir porosity during drilling is a key task in the exploration of tight sandstone reservoirs. Existing methods for evaluating reservoir physical properties include core identification, seismic wave monitoring, and imaging logging technologies1,2,3. Core identification relies on core porosity experiments, which require on-site core sampling and are costly and discontinuous. Seismic wave monitoring is a pre-drilling method that reflects reservoir physical properties using geophysical data, core or cuttings analysis, and crack observations. Due to multiple possible solutions, interpretation accuracy is low, and prediction reliability is insufficient. Imaging logging is a post-drilling method that uses logging instruments to measure porosity. Common logging methods include natural gamma, neutron, acoustic, and density logging4,5,6,7. Different logging methods can reflect changes in reservoir porosity to some extent, but they suffer from significant delays and cannot pro-vide real-time insights into the reservoir’s physical properties. This limits decision-making, such as advanced drilling, drilling depth adjustment, and mid-course testing, which in turn restricts deep and ultra-deep oil and gas exploration. For tight sandstone reservoirs, these porosity evaluation methods face issues such as low data quality, multiple solutions, and low accuracy, which pose challenges to effective reservoir prediction and identification. In recent years, some scholars have used MWD technology for qualitative identification of reservoir physical properties8,9,10, but few studies have explored its use for quantitatively explaining changes in these properties. Currently, numerical simulation methods are employed to develop geometric, kinematic, and interactive mechanical models of full bits, which are used to study the gradual maturation of cutter forces11,12,13,14,15,16,17,18. However, due to the coarse mesh used in finite element modeling, it is impossible to analyze the rock-breaking response of the entire bit. Furthermore, existing studies lack a comparative analysis of numerical simulation results for ROP, torque, and MSE.
Therefore, a PDC bit rock-breaking simulation was conducted in the NB13-4 working area, and the concept of the physical index was introduced. The relationship models between porosity and elastic modulus, as well as between the physical index and elastic modulus, were combined to establish a model linking the physical index and porosity through the elastic modulus. A quantitative method for predicting the porosity of tight sandstone reservoirs based on logging engineering parameters has been developed. This method offers advantages such as low cost, high precision, and real-time capability. Field applications of the physical property evaluation for tight sandstone reservoirs in the working area demonstrate that the method is both practical and effective. It provides real-time physical property data during drilling and logging, showing strong potential for future applications.
Engineering parameters of LWD and their derived values
Several types of sensors are installed at various locations on the well logging site, including the drill floor, mud pumps, and high-pressure manifold. These sensors monitor engineering parameters in real time, such as weight on bit, rotational speed, torque, mechanical penetration rate, pump stroke, riser pressure, and casing pressure. These parameters can indicate abnormal drilling conditions (e.g. bit passivation, bit mud packing, or tool failure) as well as reflect the geological characteristics of the formation, such as the physical properties of the reservoir. The drilling process can exhibit varying degrees of efficiency depending on these properties.
Individual parameters, such as weight on bit, rotational speed, torque, and mechanical penetration rate, exhibit certain responses to reservoir physical properties. However, these parameters are influenced by multiple factors, including downhole tools, bit types, and drilling conditions, which limits their ability to accurately reflect reservoir properties. Therefore, they are not reliable indicators for assessing reservoir characteristics.
MSE calculation model
MSE refers to the energy required by the bit to fracture rock per unit volume. It primarily consists of two components: the work done by bit weight (vertical work) and the work done by torque (tangential work). The classical MSE calculation model, pro-posed by R. Teale, is presented in Eq. (1)19.
where \(E\) represents the MSE (MPa); \(W\) represents the weight on bit (N); \(N\) represents the rotating speed of the turntable (r/min); \(T_{{\text{b}}}\) represents the torque (N·m); \(v_{{{\text{ROP}}}}\) represents the rate of penetration (m/h); and \(D_{{\text{b}}}\) represents the drill diameter (mm).
MSE combines parameters such as weight on bit, speed, torque, rate of penetration, and bit size into a single comprehensive metric. It is derived from the data acquired by the comprehensive logging instrument and can be continuously calculated in real time. The MSE varies depending on the reservoir’s physical properties. It is higher in hard and dense formations, and lower in formations with porosity and fractures.
Calculation method for the base value of MSE
The basic value of mechanical specific energy is obtained by sliding up and down the maximum value of mechanical specific energy, which can better indicate the entering and exiting reservoir. The calculation formula for the baseline value of MSE is presented in Eq. (2).
The formula for calculating the base value of MSE is presented in Eq. (3).
where: \(MSEU\) represents the MSE sliding up value (MPa), \(MSED\) denotes the MSE sliding down value (MPa), and \(MSEJ\) refers to the MSE base value (MPa).
-
(1)
\(MSEU\)(sliding up) is the mechanical specific energy from the top to the calculation point to take n values, take 2n/5 of the maximum values, and then take the average of 2n/5 of the maximum values, as shown in the blue line in Fig. 1.
-
(2)
\(MSED\) (sliding down) is to take n values from the calculation point to the bottom of the mechanical specific energy, take 2n/5 maximum values, and then take the average of these 2n/5 maximum values, as shown in the yellow line in Fig. 1.
-
(3)
The significance of \(MSEU\) is that it is more accurate to enter the reservoir and get stuck. The significance of \(MSED\) is that it is more accurate to exit the reservoir and get stuck.
-
(4)
The mechanical specific energy base value is the average of the mechanical specific energy base value (sliding up) and the mechanical specific energy base value (sliding down)..
Parameter derived from the physical index
To eliminate the influence of bit type and engineering parameters, a physical in-dexbased parameter is introduced for the dimensionless normalization of MSE. The physical index is defined as the ratio of MSE to its reference value, as shown in Eq. (4). The physical index reflects the variation in the formation’s physical properties. A physical index near 1 indicates low formation porosity, suggesting underdeveloped formation. If the physical index is below 1, it indicates high porosity and the presence of holes and fractures in the formation. The lower the physical index, the higher the porosity.
where \(P\) represents the physical index and \(MSEJ\) refers to the base value of the MSE (MPa).
Numerical simulation of the rock-breaking process using a PDC bit
The rock breaking mechanism of PDC bits
A PDC bit relies on shearing the rock to achieve a crushing effect. The shear rock-breaking method has relatively low crushing power; however, the PDC bit’s composite material offers high wear resistance and self-sharpening, enabling continuous and efficient rock breaking. The bit’s excellent wear resistance significantly reduces the passivation rate of the cutting edge, while its self-sharpening capability ensures effective rock penetration and breaking, even when worn. The PDC composite diamond layer has much higher wear resistance than the cemented carbide matrix. As the diamond wears, the cemented carbide matrix wears significantly faster, ensuring that the diamond layer remains sharp and continues to cut effectively20. This is the principle behind the self-sharpening effect of the PDC bit.
PDC bit geometry
The geometry of the PDC bit primarily describes the spatial positioning of the PDC bit cutters after the coordinate system is defined20. Based on this, mathematical equations for characteristic curves and surfaces are developed to define the positional relationship between the bit and the cutters. The geometric position of the PDC bit, cutting surface area, cutting angle, and cutting load model are all derived from the bit geometry.
Constitutive relationship of rocks in the elastic stage
Rock deformation in the elastic stage is minimal. The stress–strain curve indicates that the constitutive relationship of rocks in the elastic stage is approximately linear20. Therefore, a linear elastic model is commonly used to describe the constitutive behavior of rocks in the elastic stage.
Strength and yield criteria of rock in the plastic deformation stage
When the rock material transitions into the plastic state, the stress–strain curve becomes nonlinear, and the rock’s constitutive behavior becomes more complex. First, the stress–strain curve must be analyzed to determine whether the rock has reached the plastic state, which requires establishing appropriate yield conditions or failure criteria. Generally, the yield condition or failure criterion of a rock indicates a stress or strain state (or both) at which the rock loses its load-bearing capacity. Once it is deter-mined that the rock has entered the plastic state, the constitutive relationship for the plastic stage is established. At this point, the relationship between stress and strain is no longer one-to-one; instead, the relationship between stress and strain increments can only be established.
The Mohr–Coulomb and Drucker-Prager yield criteria (D-P yield criteria) are widely used to describe the yield behavior of rocks in the plastic stage. The Mohr–Coulomb criterion is an isotropic hardening–softening model, where rock yield-ing occurs if the shear stress in a plane exceeds a certain threshold. However, the Mohr–Coulomb criterion does not account for confining pressure. In contrast, the D-P yield criterion, which modifies the Mohr–Coulomb model, incorporates confining pressure and also reflects the expansion of rock caused by shear stress20.
PDC bit and rock simulation model
Assumed rock conditions
During the rock-breaking process with a PDC bit, the rock is heterogeneous and exhibits anisotropy. Rock anisotropy can be categorized into two types: the first type arises from the presence of micro-cracks and their directional arrangement and distribution. The first type of anisotropy, known as stress anisotropy, varies with changes in rock stress. The second type results from the directional alignment of rock particles and remains unaffected by variations in rock stress. The following assumptions apply to the PDC cutting gear and the rock:
① The PDC teeth and rocks are treated as homogeneous, continuous media, without considering the influence of porous structures.
② The entire rock cutting process is assumed to be adiabatic, neglecting fluid resistance.
③ The rock is treated as an infinite body, ignoring both the side effects and stress wave reflections at its boundary.
④ The overall motion of the rock is ignored, and the initial stress in both the particles and rock is assumed to be zero.
⑤ The PDC rock breaking process is assumed to be stable and uniform. A numerical simulation is conducted by applying a displacement load to the cutter. The resulting support reaction force is extracted from the post-processing data, and compared with experimental load measurements to verify the simulation accuracy.
The development of geometric models
The PDC bit is a rotary cutter with a diameter of 215.9 mm. The 5 blade bit has 44 main cutting teeth: 34 large teeth with a diameter of 12.6 mm and 10 small teeth with a diameter of 9.2 mm. The 6 blade drill has 52 main cutting teeth: 30 large teeth with a diameter of 16.2 mm and 22 small teeth with a diameter of 13.6 mm. The rock model is a cylinder with a diameter of 700 mm and a thickness of 200 mm. The geometric model is shown in Fig. 2.
Grid division
In finite element analysis, the mesh density influences both calculation accuracy and computational time. Thus, it is essential to balance accuracy and solving efficiency when determining mesh division. If the grid is too dense, the calculation will be time-consuming and require excessive memory. Conversely, if the mesh density is too sparse, the failure-induced rock fragments may not be visible during post-processing, or the detachment may be unrealistic, leading to errors in the output curve. Therefore, the cut portion of the rock’s geometric model is segmented. Based on the size of the cuttings, the mesh density is increased to 150 elements for the inner ring, while a coarser mesh with 60 elements is used for the outer ring. The drill mesh unit uses a C3D4 tetrahedral mesh, while the rock mesh unit employs a C3D8R hexahedral mesh. This choice ensures both accuracy and improved computational efficiency. Addition-ally, enhanced hourglass control is applied to minimize excessive mesh distortion. The grid division is illustrated in Fig. 3.
Define the material properties and the failure criteria
① Elastic constitutive relation.
Set the drill as a rigid unit and the other components as elastic units. The drill bit density is 7.9g/cm3, the elastic modulus is 206GPa, and the Poisson ratio is 0.3. According to the material properties of sandstone, it is assumed that the rock density is 2.6g/cm3, the elastic modulus is 20GPa, and the Poisson ratio is 0.25.
② D-P plastic constitutive relation.
The classical D-P model is extended using finite element simulation software, enabling the yield surface shape on the meridian plane to be simulated by linear, hyperbolic, or exponential functions. The extended linear D-P model is applied to simulate the rock’s structural and mechanical characteristics, accounting for the influence of confining pressure on yield properties and the shear-induced expansion of the rock.
The extended D-P model possesses the following characteristics:
① In numerical simulations of rock and soil materials, the yield limit increases with confining pressure.
② The material used to simulate tensile yield strength is much weaker than its compressive yield strength.
③ It permits isotropic hardening or softening of the material, accounting for its dilatancy.
④ It can model strain rate-dependent materials and simulate their properties under monotonic loading.
(5) Rock failure criteria.
The Johnson–Cook shear failure model relies on the equivalent plastic strain at the integration points of the elements, assuming material failure occurs when the failure parameter exceeds 1. If failure occurs at all integration points, the corresponding cell is removed from the grid. The failure parameter definition is provided in Eq. (5).
In this context, \(W\) represents the failure parameter, \(\Delta \varepsilon^{pl}\) denotes the increment in equivalent plastic strain, and \(\varepsilon_{f}^{pl}\) indicates the critical equivalent plastic strain.
The critical equivalent plastic strain is presented in Eq. (6).
where: \(\dot{\varepsilon }^{pl} /\dot{\varepsilon }_{0}\) represents the dimensionless plastic strain rate; \(p\) denotes the hydrostatic pressure; \(q\) refers to the Mises stress; \(\hat{\theta }\) indicates the dimensional temperature; \(d_{1} \sim d_{5}\) is the failure parameter at the transition temperature, determined through a tensile-torsion experiment; \(\dot{\varepsilon }_{0}\) is the reference strain rate.
Define the analysis steps, contact conditions, constraints, and applied loads
① Constraints and loads.
First, define an RP point and attach the cutter to the rigid body at this point. This approach allows for easy extraction of the final cutting force and enables load application in the storage. A displacement load is applied to the PDC bit in the tangential cut-ting direction, and the loading process is analyzed over time. The rotational speed is set to 60 r/min, and the weight on the bit is fixed at 55 kN. The boundary conditions are as follows: the constraint of rock freedom in the Z-direction on the X–Y plane, the constraint of freedom in the X-direction on the Y–Z plane, the constraint of freedom in the Y-direction on the X–Z plane, and the tangential movement of the cutting teeth in the cutting direction.
② Analysis step
In the rock-breaking process of a PDC bit, the interaction between the cutter and the rock mass is both nonlinear and stochastic, varying over time. The total duration for each analysis step is set to 20 s.
③ Contact each other.
Each rock node is in contact with the cutter face of the PDC bit. The friction penalty formula is selected in the tangential formula, and the friction mechanism between the cutter wear surface and the rock interface is analyzed by carrying out the indoor micro-PDC bit drilling experiment, and the friction coefficient between the rock and the cutter is obtained. The normal formula is the “hard contact” formula, the normal force model follows the “hard contact” approach. Specifically, when the gap between two surfaces reduces to zero, a contact constraint is applied, allowing unlimited transmission of contact pressure between the surfaces. If the contact pressure between the sur-faces becomes zero or negative, the surfaces will separate, and the constraints will be removed. The normal direction of the contact surface does not transmit tension, and nodes on the passive surface cannot penetrate the active surface elements.
Solving and generating ODB files and post-processing
The analysis file for the cut rock is created, and parallel computation is performed using the computer’s CPU processor. Finally, the drilling rate and torque of the PDC bit during rock breaking are extracted at the RP point.
Rock brake simulation
The dynamic analysis module of finite element simulation software was used to simulate drill bit and rock. In the established finite element model, the bit adopted 5/6 blade PDC bit, and set it as rigid unit, and other components were set as elastic unit. The rock is sandstone and its elastic–plastic mechanical properties are considered. In order to improve the accuracy of the solution, the cutting teeth of the PDC bit and the rock area mainly touched by the bit are respectively encrypted during the cell mesh division, so as to ensure that the fine degree of mesh division has no influence on the result. During the load setting process, a constant rotational angular speed is applied to the turntable and a constant bit weight is applied to the PDC bit combination. In terms of displacement constraints, Z-direction fixed constraints are applied to the X–Y ground, X-direction fixed constraints are applied to the Y–Z side, and y-direction fixed constraints are applied to the X–Z side. Through the setting of key modeling factors such as geometric model, mesh number and constitutive model, rock braking simulation is carried out to model rock breaking simulation model of PDC bit and analyze the characteristics of rock breaking response.
The parameters of PDC bit and rock geometry structure are shown in Table 1.
Characteristic analysis of rock breaking simulation response of PDC bit
This paper presents a rock-breaking experiment and simulation for the cutting unit, determining key modeling factors such as the basic geometric model, mesh scale, and constitutive model. Based on these, the modeling and verification of the drill rock-breaking simulation model are conducted.
The relationship between rate of penetration and elastic modulus
The elastic modulus was used as the parameter to characterize the formation’s mechanical properties. The response characteristics of drilling rate and elastic modulus for 5 blade and 6 blade PDC bits were obtained through rock-breaking simulations, as shown in Fig. 4.
The drilling rate of a 5 blade bit ranges from 3.07 to 4.45 m/h, while the rate for a 6 blade bit ranges from 2.26 to 3.88 m/h. Under the same elastic modulus, the drilling rate of the 5 blade bit is higher than that of the 6 blade bit. Both drilling rates decrease linearly as the elastic modulus increases.
The relationship between torque and elastic modulus
The elastic modulus was used as a parameter to characterize the mechanical properties of the formation. The response characteristics of torque and elastic modulus for 5 blade and 6 blade PDC bits were obtained through rock-breaking simulations, as shown in Fig. 5.
The rock-breaking torque of the 5 blade bit ranges from 5.42 kN·m to 7.21 kN·m, while that of the 6 blade bit ranges from 7.06 kN·m to 8.33 kN·m. With the same elastic modulus, the 5 blade bit exhibits a smaller torque, while the rock-breaking torque of both bit types increases logarithmically as the elastic modulus increases.
The relationship between MSE and elastic modulus
The elastic modulus was used as the parameter to characterize the formation’s mechanical properties. The response characteristics of MSE and elastic modulus for 5 blade and 6 blade PDC bits were obtained through rock-breaking simulations, as shown in Fig. 6.
The MSE of the 5 blade bit ranges from 131.53 MPa to 166.73 MPa, while for the 6 blade bit, it ranges from 160.98 MPa to 201.17 MPa. Under the same elastic modulus, the MSE of the 5 blade bit is lower. The MSE of both types of bits increases exponentially as the elastic modulus increases.
The relationship between physical index and elastic modulus
The baseline elastic modulus of the rock in the NB13-4 working area is 63.57 GPa. Using the relationship model between MSE and elastic modulus shown in Fig. 6, the baseline MSE of the 5 blade PDC bit is 176.10 MPa, while that of the 6 blade PDC bit is 213.47 MPa. The physical index for the 5 blade and 6 blade PDC bits is obtained by dividing the MSE shown in Fig. 6 by the corresponding baseline values. Figure 7 illustrates the response characteristics of the physical index and elastic modulus.
Figure 7 illustrates that, although the MSE of the 5 blade and 6 blade PDC bits in formations with the same elastic modulus differ significantly, their physical index values are quite similar. The relationship between the physical index and the elastic modulus is consistent, with both indices increasing exponentially as the elastic modulus increases, as described in Eq. (7).
When engineering parameters are used to characterize the mechanical properties of the formation, the physical index can eliminate the influence of bit type, making it more applicable than other indices.
Prediction of reservoir porosity using physical index
The relationship between porosity and elastic modulus
In general, an increase in porosity leads to a decrease in the formation’s elastic modulus. The relationship curve between porosity and elastic modulus, derived from the logging interpretation results of the working area, is presented in Fig. 8.
Porosity decreases exponentially as the elastic modulus increases. A regression analysis was used to establish a relationship model between porosity and elastic mod-ulus, as shown in Eq. (8).
In this equation, \(\phi\) represents the porosity (%) and \(E\) represents the elastic modulus (GPa).
The relationship between porosity and physical index
The relationship between porosity and the physical index is derived from Eqs. (7) and (8), as illustrated in Fig. 9.
The porosity decreases as a power function with the increasing physical index. The mathematical relationship between these two variables, as described by Eq. (9), can be used to quantitatively predict the porosity of tight sandstone reservoirs in the study area.
In this equation, \(\phi\) denotes porosity (%) and \(P\) represents the physical index.
Application of LWD engineering parameters for porosity prediction in field environments
The method for predicting reservoir physical properties based on engineering parameters obtained during drilling and logging has been applied to over 20 exploration wells in the tight sandstone reservoir of the NB13-4 area. The comprehensive logging tool continuously collects engineering parameters, including weight on bit, rotate speed, torque, and ROP. It calculates the MSE and physical index, predicts the reservoir porosity, and compares the predicted values with the actual logging porosity. As an example, well NB13-4-A's porosity verification results are presented in Table 2, and the field application analysis is illustrated in Fig. 10.
The predicted LWD porosity of well NB13-4-A ranges from 10.61 to 16.49%, with an average of 13.26%. The absolute porosity error ranges from 0.96 to 20.74%, with an average of 8.43%. The porosity coincidence rate of well NB13-4-A is 91.57%.
Similarly, 20 exploration wells in the tight sandstone reservoir of the NB13-4 working area in the East China Sea shelf basin were analyzed. The average agreement rate between porosity predicted by engineering parameters and logging porosity was 85.74%, demonstrating that the method can predict the physical properties of tight sandstone reservoirs in real time.
Cause analysis and future prospect of relative error rate of porosity
Alternating soft and hard bedding is a common phenomenon in tight sandstone formations, which are usually composed of thin layers or interlayers of different lithologies. The formation of alternating soft and hard strata is closely related to sedimentary cycles, tectonic compression or differential compaction . The possible reasons for the relatively large porosity error rate in Fig. 10 are as follows:
-
(1)
Rock composition and structure: with the increase of depth, rock composition and structure may change, resulting in the difference of mechanical properties in the drilling process, which will affect the numerical fluctuations of parameters such as bit weight, rotary speed, torque and mechanical specific energy.
-
(2)
To maintain drilling efficiency and safety: In order to maintain drilling efficiency and safety, the driller may make timely adjustments to bit weight and rotary speed according to the geological conditions and actual conditions of the drilling equipment, which directly leads to fluctuations in the value of related parameters.
-
(3)
Formation pressure and temperature: Formation pressure and temperature increase with the increase of depth, which may lead to the change of drilling fluid properties, and then affect the mechanical penetration rate and mechanical specific energy and other parameters.
-
(4)
Diversity of pore structure: the pore structure in tight sandstone reservoirs is complex and diverse, including fractures, solution pores and other types, which increases the difficulty of porosity measurement.
-
(5)
Limitations of prediction models: Current prediction models may not fully capture all geological factors affecting porosity, resulting in deviations between predicted results and actual measured values.
In future work, a comprehensive consideration should be given to logging parameters, drilling design and drilling parameters, and the mechanism of influence of geological factors on drilling parameters should be further studied, the drilling process and logging technology should be optimized, the measurement accuracy and data processing capability should be improved, and a more accurate and reliable porosity prediction model should be established.
Conclusions
Through the above research and analysis, the following conclusions can be drawn:
-
1.
The rock-breaking characteristics of 5 blade and 6 blade PDC bits were simulated and analyzed, with the elastic modulus as the primary parameter. Simulations were per-formed on strata with varying mechanical properties within the working area. The resulting torques for the 5 blade bit ranged from 5.42 to 7.21 kN·m, while those for the 6 blade bit ranged from 7.06 to 8.33 kN·m. The MSE for the 5 blade PDC bit ranged from 131.53 to 166.73 MPa, while for the 6 blade bit, it ranged from 160.98 to 201.17 MPa. Moreover, the rock-breaking torque and MSE were lower for the 5 blade PDC bit.
-
2.
The physical index is defined by comparing the MSE with its baseline value. The response characteristics of the physical index and the elastic modulus across various drill bit types exhibit strong consistency. Furthermore, the physical index effectively mitigates the influence of drill bit type, offering a more accurate representation of reservoir drilling characteristics.
-
3.
A relationship model between porosity and physical index has been established, and a prediction method for reservoir porosity during drilling has been developed. The re-search results were cross-validated in well NB13-4-A. The porosity predicted using engineering parameters showed a 91.57% correlation with the logging-derived porosity The prediction method was applied to 20 exploration wells in the NB13-4 area, achieving an average porosity correlation rate of 85.74%. This method has been proven to provide rapid support for decision-making in exploration operations, including mid-test evaluations and drilling completion.
Data availability
The utilized data in this study is available upon reasonable request from the corresponding author.
Abbreviations
- PDC:
-
Polycrystalline diamond compact
- ROP:
-
Rate of penetration
- MSE:
-
Mechanical specific energy
- WOB :
-
Bit weight
- \(\text{MSEJ}\) :
-
Mechanical specific energy base value
- \(\text{RPM}\) :
-
Rotate speed
- P:
-
Physical index
- LWD:
-
Logging while drilling
References
Liu, Q., Dong, N., Ji, Y. & Chen, T. Direct reservoir property estimation based on prestack seismic inversion. J. Petrol. Sci. Eng. 171, 1475–1486. https://doi.org/10.1016/J.PETROL.2018.08.028 (2018).
Lamoj, M. Laboratory and theoretical investigations of petroleum reservoir rock properties. J. Am. J. Energy Natl. Resour. (AJENR) 3(1), 10–20. https://doi.org/10.54536/ajenr.v3i1.2382 (2024).
Charkhi, A., Javaherian, A. & Nabi-Bidhendi, M. A reliable regression-based approach for seismic reservoir characterization. J. Explor. Geophys. 50(1), 86–93. https://doi.org/10.1080/08123985.2019.1570710 (2019).
Zhang, Q., Zhang, F., Yuan, C., Wang, X. & Zhang, X. A comparative study on the neutron-gamma density and gam-ma-gamma density logging. J. Petrol. Sci. Eng. 176, 792–799. https://doi.org/10.1016/J.PETROL.2019.02.007 (2019).
Xi, H., Sun, W., Tan, Z., Xue, J., Chen, Z., & Cheng, L. A design of natural gamma spectrum logging system. In International Conference on Electric Information and Control Engineering, 28–31. https://doi.org/10.1109/ICEICE.2011.5777582 (2011).
Zhang, Q., Zhang, F., Yuan, C., Deng, R. & Liu, G. Application analysis on the different neutron gamma density (NGD) logging methods. J. Appl. Radiat. Isotopes 172, 109672. https://doi.org/10.1016/j.apradiso.2021.109672 (2021).
Wang, H. et al. A new method for calculating bulk density in pulsed neutron-gamma density logging. J. Geophys. 85(6), 219–232. https://doi.org/10.1190/geo2018-0821.1 (2020).
Wu, Y. et al. A new logging-while-drilling method for resistivity measurement in oil-based mud. J. Sens. 20(4), 1075. https://doi.org/10.3390/s20041075 (2020).
Sun, J. et al. Real-time updating method of local geological model based on LWD process. J. Arab. J. Geosci. 14, 746. https://doi.org/10.1007/s12517-021-07034-1 (2021).
Nguyen, K., Fahmy, M., Dzhaykiev, B., Odiase, P., Al-Morakhi, R., Al-Ajmi, M., Verma, N., & Quttainah, R. Application of LWD - nuclear magnetic resonance in reservoir evaluation and geosteering: A case study in Marrat reservoir, Umm Roos Field, West Kuwait. Journal of ADIPEC. SPE-211699-MS. https://doi.org/10.2118/211699-MS (2022).
Zhang, C., Yang, Y., Qingliang, Q., Ren, H. & Wang, J. Research on numerical drilling technology of mesh-like cutting PDC bit. J. Energy Rep. 7, 2068–2080. https://doi.org/10.1016/J.EGYR.2021.04.013 (2021).
Kuang, Y. et al. Simulation and experimental research of PDC bit cutting rock. Failure Anal. Prev. 16, 1101–1107. https://doi.org/10.1007/s11668-016-0188-9 (2016).
Sun, Y., Liu, L., Jiang, H., Yu, J., Ji, G., Wu, Q., & Chen, C. Research on the rock cutting mechanism of non-planar PDC cutters based on the D-P criterion. In Conference on the 57th U.S. Rock Mechanics/Geomechanics Symposium, ARMA-2023-0556. https://doi.org/10.56952/arma-2023-0556 (2023).
Pryhorovska, T., Chaplinskiy, S. & Kudriavtsev, I. Finite element modelling of rock mass cutting by cutters for PDC drill bits. J. Petrol. Explor. Dev. 42(6), 888–892. https://doi.org/10.1016/S1876-3804(15)30087-2 (2015).
Panayirci, H. An experimental study on steering response of PDC drill bits. J. Petrol. Sci. Eng. 208(1), 109440. https://doi.org/10.1016/j.petrol.2021.109440 (2022).
Huang, H., Wu, M., , S., Chen, L., & Lu, C. Analysis of bit-rock interaction models using finite element simulation data ⋆. In Conference on the 39th Chinese Control Conference (CCC), 2329–2333. https://doi.org/10.23919/CCC50068.2020.9189430 (2020).
Zeng, Y. et al. Numerical simulation of the pressing of polycrystalline diamond compact cutter into the rock based on arbitrary Lagrangian-Eulerian algorithm. J. Alex. Eng. J. 59(3), 1381–1390. https://doi.org/10.1016/j.aej.2020.03.010 (2020).
Hanson, J., & Hansen, W. Dynamics Modeling of PDC Bits. In Conference on the SPE/IADC Drilling. Amsterdam, Netherlands. SPE-29401-MS. https://doi.org/10.2118/29401-MS (1995).
Teale, R. The concept of specific energy in rock drilling. J. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 2(1), 57–73. https://doi.org/10.1016/0148-9062(65)90022-7 (1965).
Yazhou. Peng. Research on numerical simulation method of PDC full-bit rock breaking. Master’s degree from Southwest Petroleum University (2015).
Acknowledgements
I would like to express my gratitude to Professor Ligang Zhang, Lecturer Zhaoyi Liu, Lecturer Hao Li, Dr. Junru Li and Master Chenxu Jiang for their guidance and full support throughout the research process.
Author information
Authors and Affiliations
Contributions
Software, writing-original drafts, writing-review & editing, X.D.; resources, methodology, conceptualizing, supervision, Z.L.; visualization, L.Z.; formal analysis, L. H.; data curation, L.J.; investigation, J.C. All authors have read and agreed to the published version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Xue, D., Zhang, L., Liu, Z. et al. Predicting porosity in tight sandstone reservoirs based on logging while drilling engineering parameters. Sci Rep 15, 14241 (2025). https://doi.org/10.1038/s41598-025-98311-6
Received:
Accepted:
Published:
Version of record:
DOI: https://doi.org/10.1038/s41598-025-98311-6