Introduction

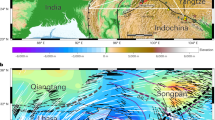
The Eastern Himalayan Syntaxis (EHS), the point where the Himalayan mountain range, the Indo-Myanmar Range, and the Hengduan Mountains converge, is a region of strong stress and deformation where the Indian Plate, Eurasian Plate, and Myanmar Plate meet and has experienced a variety of complex tectonic events, including collision, subduction, and rapid uplift, which have had an important impact on the evolution of the whole plateau1,2 (Fig. 1). Hence, the EHS region where tectonic escape is observed along the interface between the Indian and Eurasian plates, is considered to be an ideal place to study the dynamics of plate convergence from past to present3. Notably, the EHS region is prone to earthquakes, which have an immediate impact on local communities and may threaten water security because significant tectonic deformation accounts for the dramatically altered landforms and water drainage systems of the region4, which are essential to the livelihood of billions of inhabitants that depend on the Asian water tower.

Fig. 1
figure 1

Tectonic map of the Tibetan Plateau. The background color indicates elevation and was derived from ETOPO elevation data5 obtained from the National Geophysical Data Center (NGDC). The dashed green lines show the suture zones6. ATSZ: Altyn Tagh suture zone; EKSZ: Eastern Kunlun suture zone; JRSZ: Jinsha River suture zone; BNSZ: Bangong-Nujiang suture zone; IYSZ: Indo-Yarlung Zangbo suture zone; MBT: Main boundary fault; EHS: Eastern Himalayan syntaxis. The figure was created by using the software GMT7. (version: GMT 4.5.7, URL link: https://www.generic-mapping-tools.org/download/).

Full size image

The GPS velocity field and seismic anisotropy of southeastern Tibet show clockwise rotation around the EHS8,9, which indicates a connection between crustal extrusion and mantle flow. Clockwise tectonic rotation can result from the upper crust being dragged by the southeastward motion of the lower crust or upper mantle10. Thus, lower crustal flows have been widely accepted as the mechanism controlling the high torque of the EHS11. However, geological evidence from isotopic analyses shows that the igneous rocks at a depth of 30–40 km below the Gongga-Zheduo intrusive massif (east of the EHS) are derived from partial melting of the local crust, contradicting the long-distance crustal flow hypothesis12.

It has been proposed that upwelling of the asthenosphere contributes more to crustal deformation and uplift in this region12. Clarifying the crust-mantle material circulation process can provide insights into the tectonic evolution of the EHS and help us clearly understand how the surface topography responds to changes in deep extrusion. Previous studies have demonstrated that with the integration of various observations, numerical simulation can be an effective tool to investigate the viscous relaxation and elastic deformation of the overriding plate13,14. Large-scale mantle flow studies have revealed a clockwise rotation of mantle flow beneath the southeastern margin of the Tibetan Plateau15,16. However, mantle flow models combined with known slab geometries and velocities have not yet been applied to Tibet and the EHS, and the features of the underlying mantle flow have not yet been investigated. We aim to address these issues and investigate the evolution of 3D mantle flow fields below the EHS.

To accomplish this, we constructed a novel mantle flow model with the prescribed 3D geometry of the Indian plate based on the Slab2 model17 and 3D subduction velocities18,19. Considering that Slab2 data are currently lacking at the leading edge of the slab immediately below the EHS, we combined several seismic inversion results from previous studies and incorporated them into different models. The use of various Indian plate fronts enables better estimations of their effects on the 3D mantle flow field beneath eastern Tibet.

Materials and methods

Novel 3D models are developed from thermomechanical codes20 via the finite difference method (FDM). The model designed in this study has a length of 1700 km, a width of 1400 km, and a depth of 300 km (Fig. S1) and contains 72 × 72 × 72 grid points. The top of the model is set to be a rigid surface (equal to high crustal viscosity); the four vertical boundaries, the front, left, right, and back vertical surfaces and the bottom surface are set to be permeable. The slab guide is determined by Slab2, which is the latest 3D geometric model of global slabs proposed by Hayes et al.17, and other seismic inversion data (Fig. 2). Since the plate data range of the Tibetan Plateau region in the Slab2 model covers only the shallow part below the Himalayan orogenic belt, the slab geometry data at certain depths are calculated by extrapolation of the existing Slab2 and seismic inversion data (Fig. 2a). Notably, the inferred positions of the frontal boundary of the Indian plate have been debated in previous studies (see the Supplementary Materials, Indian lithosphere boundaries section), and the impact of this factor must be considered in modeling. Therefore, we set up three different frontal boundary cases (model I, model II, and model III.) to investigate the consequent changes in the calculated viscous flow field. The leading edge of the Indian plate in model I is based on Wang et al.21 and represents the case in which the Indian plate front has reached below the central Tibetan Plateau (Fig. 2b), with the northern boundary of the Indian plate gently subducting below the Bangong–Nujiang suture zone, and the southeast boundary steeply subducting below the Sibumasu block (dark blue dashed line in Fig. S2). In contrast, the Indian plate of model II is referenced by Jiang et al.22, indicating that the Indian front is restricted to some extent (Fig. 2c). The western boundary of the Indian plate in the model II confined is restricted to below the Indo-Yarlung Zangbo suture zone23. On the east side of model II, the Indian lithosphere below the EHS and the eastern side of the EHS is deeply subducted close to the Bangong-Nujiang suture zone and beneath the Myanmar block (yellow dashed line in Fig. S2), respectively. According to the inversion results of Peng et al.24, the structure of the Indian plate beneath the EHS was further constrained in model III (Fig. 2d). Owing to their results suggesting the presence of a fractured Indian plate window beneath the middle EHS, we set the Indian plate in this region as having a gap structure (pink dashed line in Fig. S2).

Fig. 2
figure 2

Schematic diagram of the subduction model of the Indian plate. (a) full subduction; (b) model I; (c) model II; (d) model III. The blocks in the tectonic setting of the Tibetan Plateau were delineated according to the results of He et al.25. JRSZ: Jinsha River suture zone; BNSZ: Bangong-Nujiang suture zone; QT: Qiangtang block; LS: Lhasa block; HM: Himalayan block; EHS: Eastern Himalayan Syntaxis; IYSZ: Indo-Yarlung Zangbo suture zone; MBT: Main boundary fault; CD: Chuan-Dian block; SM: Sibumasu block; SL: Simao-Lanping block; BM: Myanmar block. The figure was created by using the software Paraview (version: Paraview 5.4.1, URL link: https://www.paraview.org/download/).

Full size image

When subduction starts, the Indian plate gradually grows and subducts below Tibet within the prescribed slab guide, resulting in different viscous flow fields at each time step (Fig. S3). The velocities of the Indian plate relative to the Eurasian plate are derived from the MORVEL plate motion velocity dataset (DeMets et al., 2010); based on the coordinate transformation, the velocity data from MORVEL are transformed to those at the grid nodes under the X, Y, and Z axes of the model, as shown in Fig. S1. The timespan of the Indian plate movement in the model is set to ≥ 40 Myr according to the limits on the timing of the collision between the Indian and Eurasian plates6 and to ensure that the slab reaches the opposite model boundary and reaches a steady state19. The lithospheric structure of the EHS in receiver function inversion indicates that the thickness of the crust is 54 ~ 60 km26, so the crustal thickness of the Indian lithosphere is set to 60 km. Furthermore, the downgoing lithosphere geometry was kinematically prescribed without slab surface deformation during time step, and the density and viscosity of each layer (e.g., upper crust, lower crust, subducted slab, mantle lithosphere, and asthenosphere) remain constant. In the model, the upper crust (30 km thick) of the overriding plate does not contribute to the calculation of the viscous flow field and functions only as a boundary constraint. Except for this, the viscosity of all layers in the model is set to an initial value of 1 × 1020 Pa s and then changes at each time step according to the temperature, pressure, and strain-rate conditions present within the layer. Then, the viscous flow of the model domain is determined in the specified slab motion time range at each grid point. Meanwhile, the maximum depth of the model is set to 300 km to ensure sufficient space for viscous flow beneath continental plates. In addition, the equations associated with the model settings are described in detail in the Methods section of the Supplementary Materials and in Tables S1-S3.

Results

Calculated 3D viscous flow fields of models I, II, and III

After the specified 40 Myr subduction time, which allows the slab to reach the opposite/bottom model boundary and a quasisteady state in mantle flow, the mantle velocities of the three models are obtained (Fig. 3). In model I (Fig. 3a), the direction of viscous flow within the Indian lithosphere is NE direction, which is essentially the same direction of motion as the Indian plate. Furthermore, the viscous flow distribution within the overriding plate shows two different forms. In one form, the viscous flow continues to maintain the NE direction, such as the motion below the Bangong-Nujiang suture zone to the Simao-Lanping block. In the other form, the viscous flow direction appears to turn clockwise; for example, on the southeastern side of the EHS, the viscous flow direction rotates clockwise from the NEE direction to the SE direction.

Fig. 3
figure 3

Viscous flow field distribution of models. (a) model I; (b) model II; (c) model III. The arrows indicate the direction of the viscous flow, and the sizes of the arrows are proportional to the flow velocity. The figure was created by using the software Paraview (version: Paraview 5.4.1, URL link: https://www.paraview.org/download/).

Full size image

In model II (Fig. 3b), the viscous flow of the Indian lithosphere also follows the NE direction, with values ranging from 4.5 to 5.5 cm/yr. Compared with model I, model II shows a wider area of viscous flow distribution within the overriding plate, and this increase occurs in two regions: one region is beneath the Lhasa to Qiangtang block on the northern side of the Indian plate, and the other region is beneath the Myanmar block to Sibumasu block on the eastern side of the Indian plate. Additionally, our results show viscous mantle flow (5 ~ 6 cm/yr) beneath the Chuan-Dian block, which is potentially related to the lateral compression caused by the movement of the narrow Indian plate front along the NE direction.

Because the only difference between models III and II is the shape of the northeast leading edge of the Indian plate, the calculated viscous flow fields for both models are similar. In model III (Fig. 3c), the direction and magnitude of the mantle flow are similar to those in model II. In contrast, the narrowing of the Indian plate front in model III enables a greater distribution of mantle flow beyond the Indian plate. Although the narrower Indian plate front also produces lateral compression, this compression is weaker than that observed in model II, resulting in a maximum mantle flow of approximately 5.5 cm/yr beneath the Chuan-Dian block.

Calculated 2-D cross section of the viscous flow field

Next, to better observe the calculated mantle flow field, multiple 2D cross sections of the viscous flow field were plotted according to the coordinate axes of the three models. The results of the equally spaced horizontal sections are shown in Figs. 4–6, while the results of the equally spaced vertical sections are shown in Supplementary Materials (Figs. S5-S10). In model I, the viscous flow direction for the Indian crust is directed NE, with values ranging from 4 to 5 cm/yr at a depth of approximately 30 km (Fig. 4a). At approximately 80 km in depth, the flow direction of the Indian lithosphere is predominantly NE, while the viscous flow in the overriding plate rotates clockwise from NE to SW from the Jinsha River suture zone to the Sibumasu block (Fig. 4b). This clockwise rotation at a depth of approximately 80 km is quite clear, showing an overall gyratory change. At a depth of approximately 130 km, we see that as the Indian plate subducts further below the overriding mantle, the rotation of flows is significantly weakened (Fig. 4c). The mantle flow disappears at depths of approximately 180 km as a result of the subduction of the Indian lithosphere in the region beneath the Myanmar, Sibumasu, and Simao-Lanping blocks (Fig. 4d). The maximum rotated mantle flow occurs beneath the Sibumasu and Simao-Lanping blocks at depths of 80–180 km.

Fig. 4
figure 4

Horizontal profiles of model I at different depths. (a) horizontal profile at 31.25 km depth; (b) horizontal profile at 81.25 km depth; (c) horizontal profile at 131.25 km depth; (d) horizontal profile at 181.25 km depth. The arrows indicate the direction of the viscous flow, and the sizes of the arrows are proportional to the flow velocity. The figure was created by using the software GMT7. (version: GMT 4.5.7, URL link: https://www.generic-mapping-tools.org/download/).

Full size image

In models II and III, the maximum viscous flow of the overriding plate is located beneath the Chuan-Dian block due to a weaker extrusion effect than that observed in model I (Figs. 5 and 6). Interestingly, the viscous flow of the overriding plate in model III is weaker than that in model II below the eastern EHS, probably due to the lower subduction depth of the Indian plate at the EHS (Figs. 5b and 6b). In the upper and lower cross-sections, the results of the two models are similar, indicating that the EHS area is small and does not have sufficient influence on the mantle flow under the blocks to the southeast. This can be attributed to the extrusion of more materials in the overriding mantle during greater subduction of the Indian plate, resulting in greater transport of mantle at depths of 80–180 km, which indicates that the Indian plate subduction distance will significantly influence the scale and distance of tectonic extrusion around the EHS.

Fig. 5
figure 5

Horizontal profiles of model II at different depths. (a) horizontal profile at 31.25 km depth; (b) horizontal profile at 81.25 km depth; (c) horizontal profile at 131.25 km depth; (d) horizontal profile at 181.25 km depth. The arrows indicate the direction of the viscous flow, and the sizes of the arrows are proportional to the flow velocity. The figure was created by using the software GMT7. (version: GMT 4.5.7, URL link: https://www.generic-mapping-tools.org/download/).

Full size image
Fig. 6
figure 6

Horizontal profiles of model III at different depths. (a) horizontal profile at 31.25 km depth; (b) horizontal profile at 81.25 km depth; (c) horizontal profile at 131.25 km depth; (d) horizontal profile at 181.25 km depth. The arrows indicate the direction of the viscous flow, and the sizes of the arrows are proportional to the flow velocity. The figure was created by using the software GMT7. (version: GMT 4.5.7, URL link: https://www.generic-mapping-tools.org/download/).

Full size image

Discussion

Viscous flow field analysis

A comparison of the mantle flow fields of the three models (Figs. 4–6) shows that they are all similar in that the viscous flow direction of the overriding plate rotates clockwise from the NEE direction below the Bangong-Nujiang suture zone to the SE direction below the northern part of the Chuan-Dian block. This change is caused by the differences in subduction rates between the northern and southern regions of the EHS. The gentle subduction in the northern region21,24 is the mechanism that generates the high-velocity NE-oriented mantle flow. In contrast, the differences in the mantle flow field of the overriding mantle of the three models indicate that the location of the frontal boundary of the Indian plate significantly affects the strength of the mantle flow. Of the three models, the generated mantle flow field is strongest when the Indian plate subducts below the Bangong-Nujiang suture zone21 and the eastern boundary enters the deep part of the Myanmar block by steep subduction27,28. This not only produces mantle flow values of 4–6 cm/yr below the Myanmar block and the Sibumasu block (Figs. 4b-4d) but also mantle flow values of up to 6–7 cm/yr at depths of 50–80 km below the southeastern margin of the Tibetan Plateau (Fig. S6f.), even when there is enough flow space in the shallow part to produce a large gyration. Furthermore, the maximum values of mantle flow beneath the Myanmar block increase to 5 ~ 6 cm/yr (Fig. 4b), and this effect is related to the steep subduction of the Indian plate below the Myanmar block29,30. The dragging of the steeply subducting Indian plate accelerates the viscous flow velocity in the mantle near this location (Figs. S6e-S6f.). Overall, the slab geometric difference between the northern and southern EHS and the plate subduction distance likely determine the scale of tectonic rotation. The combined efforts of surface shearing and uplift processes greatly contribute to tectonic syntaxis growth.

In addition, the undulating changes in the viscous flow at various depths of the three models reflect the change in the shape of the Indian plate. For example, at a depth of 31.25 km and from the main boundary fault to the Himalayan block (Figs. 4a, 5a, and 6a), the Indian lithosphere exhibits an arcuate shape, which may represent the bending-related deformation of India beneath Tibet. This bending is also reflected in profile I-I’ (Fig. S6c). This profile crosses the EHS, where the Indian plate enters beneath the Tibetan Plateau in a gently subducting manner21,24, causing lateral viscous flow and leading to topographic uplift within the EHS. Moreover, the results at different depths (Figs. 4–6) show that the direction of mantle flow deflects in both the upward and downward directions, potentially exerting a buoyancy force on the base of the overriding crust. This result indicates that the dynamic bottom-up process is likely the dominant driving force in the formation of the Indian subduction system.

Estimating extrusion and dynamic mechanism analysis

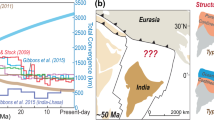
Reconstructions of the Indian and Eurasian continental plates based on paleomagnetic observations suggest that the distance between the two plates potentially shortened by approximately 3000 km over the last 50 Ma31,32. Although the average elevation of the Tibetan Plateau rose to approximately 5000 m and massive north–south retrograde thrusting occurred to form a very thick crust, these tectonic activities consumed less than half of the estimated total material mass, leaving approximately 1000–2000 km of unaccounted shortening3,11. Therefore, previous work has suggested that the plastic flow of material from deeper depths to the northeast and southeast margins could explain where the remaining 1000–2000 km of the material may be located33. To verify how much material was extruded from the southeast side of the EHS, a preliminary estimate of material extrusion was made based on the three Indian plate models. The average velocity of the Indian plate at the EHS was approximately 10 cm/yr from ~ 47 Ma, which was twice the present-day velocity34. In contrast, since 20 Ma, the average speed of motion of the Indian plate dropped by half to 5 cm/yr6. On the basis of the plate motion conditions under these two different phases, the total mass of the shortening produced from 47 Ma to the present was tentatively estimated as approximately 3700 km; in models II and III, the constructed extrusion width of the Indian plate on the southeast side of the EHS was approximately one-third of the total width, with more than 1000 km of material being extruded to the southeastern margin of the Tibetan Plateau. In contrast, the larger constructed extrusion width in model I results in more material being extruded. Thus, it is conservatively estimated in this study that more than 1000 km of material was potentially extruded from the southeast side of the EHS to the southeast margin of the Tibetan Plateau during 40 Myr of Indian plate motion.

Additionally, the tectonic stress field of the EHS reflects the joint action of the influence of multiple stress fields35. This can also be observed from the variation in the GPS horizontal velocity field36 (Fig. S11), where there are stress effects not only in a NE-oriented direction but also in other directions. Cao et al.10 suggested that the east or southeast material flow of the lower crust and upper mantle under the EHS was responsible for its clockwise rotation. However, no extruded material from central Tibet is found at a depth of 30–40 km below eastern Tibet12, indicating that the geological evidence does not support the large-scale crustal flow model hypothesis11. We compared the viscous flow field with previously observed crustal seismic anisotropy results8,37,38 and found that there are certain directional discrepancies between the two (Fig. 7). Given the rigidity of the upper crust, we infer that the crust of the Indian plate is unlikely to extend as far as the Bangong–Nujiang suture zone as in model I (Fig. 7a). In contrast, it is more likely to stop near the EHS, as represented in model III (Fig. 7c). Moreover, the seismic anisotropy provides insights into the orientation of internal deformation processes within the Earth39. In the upper mantle depths, we suggest that the stress direction exerts an eastward to southeastward force (Figs. 7b and 7d), which supports the clockwise rotation of the mantle viscous flow field beneath the southeastern margin of the Tibetan Plateau. The clockwise rotation of the mantle flow was key to the shearing and buoyancy effect in the overriding crust, laterally rotating the crust and forming the unique topographic features of the EHS.

Fig. 7
figure 7

Comparison between the horizontal viscous flow field in this study and the seismic wave anisotropy results from previous studies. (a) 31.25 km depth in model I; (b) 131.25 km depth in model I; (c) 31.25 km depth in model III; (d) 131.25 km depth in model III. The red arrows indicate the direction of the viscous flow, and the sizes of the arrows are proportional to the flow velocity. The blue lines indicate the fast wave polarization direction of Pms wave splitting38. The black lines indicate the fast wave polarization direction of SKS wave splitting8,37. The figure was created by using the software GMT7. (version: GMT 4.5.7, URL link: https://www.generic-mapping-tools.org/download/).

Full size image

In summary, mantle flow contributes greatly to the tectonic evolution of the EHS and the shaping of the regional surface topography. Notably, the rotational variation characteristics of the mantle simulated in our study occur under homogenized viscosity and density conditions. More geological and geophysical data need to be included in the future to verify and constrain the specific flow depth and deflection direction and to determine the correlation between surface elevation and deep stress field.

Conclusions

Through 3D subduction modeling of mantle flows in EHS, we obtained the following conclusions:

(1) The difference in the subduction of the Indian plate beneath the northern and southeastern parts of the eastern Himalayan syntaxis is the key mechanism driving the clockwise rotation in viscous flows of the upper mantle.

(2) Based on the constructed models, this study estimates that more than 1000 km of material may have been extruded from the eastern Himalayan syntaxis to the southeastern margin of the Tibetan Plateau in past 40 million years.

(3) Compared with the influence from crustal flow, the deep upper mantle viscous flow is the main reason accounting for the clockwise rotation of the crust. The clockwise rotational flow of the upper mantle can produce a lateral dragging effect on the crust, which causes the direction of GPS horizontal velocity field to significantly rotate around the eastern Himalayan syntaxis.